当前位置：文档之家 › 中考复习 杨辉三角ppt课件

中考复习 杨辉三角ppt课件

  • 格式：ppt
  • 大小：581.72 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

杨辉三角与二项式系数的性质一ppt课件

杨辉三角与二项式系数的性质一ppt课件

最大项与增减性
增减性的实质是比较 Cnk与Cnk1的大小.
Cnk
k
!
n! (n
k)!
n
k k
1
(k
1)!
n! (n
k
1)!
n
k k
1
C k1 n
所以C
k n
相对于C
k n
1的增减情况由
nk 1 1 k n1
nk k
1 决定．
k
可知，当
k
n
1
2
时，
2
二项式系数是逐渐增大的，由对称性可知它的后
1 C
0 6
C
1 6
C
2 6
C
3 6
C
4 6
C
5 6
C
6 6
6 15 20 15 6 1
你知道这是什么图表吗？
《 杨辉 三角
详
解
九 章
杨
算
辉
法
》
记
载
的
表
以上二项式系数表,早在我 国南宋数学家杨辉1261年所著的
《详解九章算法》一书里就已经出现了，这个表称为杨辉三角，
杨辉指出这个方法出于《释锁》算书，且我国北宋数学家贾宪
(3)a1 a3 a5 a7 (4)a0 a2 a4 a6
解 : 设f (x) (1 2x)7
(3) f (1) a0 a1 a2 a7 f (1) a0 a1a2 a3 a7
2(a1 a3 a5 a7) f (1) f (1)
a1 a3 a5 a7
倒序相加法
知识对接测查3
1.C110 C120
C 10 10
2_1_0__1_; 1023

杨辉三角ppt

杨辉三角ppt

大自然中的斐波那契数列
花瓣的数目
海棠（2）
铁兰（3）
大自然中的斐波那契数列
花瓣的数目
洋紫荊（5）
黃蝉（5）
蝴蝶兰（5）
大自然中的斐波那契数列
花瓣的数目
雏菊（13）
雏菊（13）
大自然中的斐波那契数列
树丫的数目
13 8
5 3 2 1 1
大自然中的斐波那契数列
种子的排列（松果）
大自然中的斐波那契数列
即
C C
第0行 第 1行 第 2行 第 3行 第 4行 第 5行 第 6行 第 7行 第 n行 1 C
1
1 1 3
1 2
1
1
3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1
1 n
CHale Waihona Puke 2 nC Cr r
r r 1
C
… …… … … …… … … …… … …
3 5 8 1 2 1 13 21 1 3 3 1 34 1 4 6 4 1 55 89 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 1
1
1
1 2
如图斜线中各数字的和，从第3条斜线中数字起，其后 各斜线中的和是前两条斜线中数字和之和。
再见
1
一、杨辉三角的基本性质
1、杨辉三角形的两条斜边都是数字1，
2、而其余的数都等于它肩上的两个数字相加. 即
C C
r n
r 1 n 1
C
r n 1
3、杨辉三角形的每一行中的数字左右对称.
r nr n n 4、杨辉三角的各行数字的和等于与之对应的(a+b)n 的展开式的各个系数的和为2n。

课件8：1.3.2　杨辉三角

课件8：1.3.2　杨辉三角

解：由图知，数列的首项是 C22，第 2 项是 C12，第 3 项是 C23， 第 4 项是 C13，…，第 18 项是 C110，第 19 项是 C211， ∴S19＝C22＋C21＋C32＋C31＋…＋C120＋C110＋C211 ＝(C12＋C13＋C14＋…＋C110)＋(C22＋C23＋C24＋…＋C211) ＝(2＋3＋4＋…＋10)＋(C33＋C23＋…＋C211) ＝2＋120×9＋C132＝54＋121××121××310＝274.
于是得到： (1)二项式系数和为 2n，即 Cn0＋Cn1＋C2n＋…＋Cnn＝2n. (2)二项式的奇数项的二项式系数和与偶数项的二项式 系数和相等，都等于 2n－1.即 C1n＋C3n＋C5n＋…＝C0n＋C2n ＋Cn4＋…＝2n－1.
在理解二项展开式的二项式系数和的有关性质 时，要掌握这种给字母赋值的思想(实际上是函数思 想)；具体到计算特定项的二项式系数时可以直接给字 母赋值，也可以联系二项式的展开式；对整体式子的 求值，用给字母赋值的方法非常方便．
1.3.2 杨辉三角
情景导入 幻方，在我国也称纵横图，
它的神奇特点吸引了无数人为之痴 迷．一天，时任台州地方官的杨辉外 出巡游，遇到一学童，学童正在为老 先生布置的题目犯愁：“把 1 到 9 的数字分行排列， 不论竖着加，横着加，还是斜着加，结果都等于 15”．
情景导入
杨辉看到这个题顿时兴趣大发，于是和学童一起研究 起来，直至午后，两人终于将算式摆出来了．杨辉回 到家后，反复琢磨，终于发现了规律，并总结成四句 话：“九子斜排，上下对易，左右相更，四维挺出．”
方法总结 (1)对形如(ax＋b)n、(ax2＋bx＋c)m(a，b，c ∈R，n，m∈N＋)的式子求其展开式的各项系数之和， 常用赋值法，只需令 x＝1 即可；对(ax＋by)n(a，b∈R， x∈N＋)的式子求其展开式的各项系数之和，只需令 x ＝y＝1 即可．

杨辉三角PPT优秀课件3

杨辉三角PPT优秀课件3
利用组合数的重要性质可得
( a b ) k 1 C k 0 1 a k 1 C k 1 1 a k b 1 C k r 1 1 a k r b r 1 C k k 1 1 b k 1
二.引入:
1. 斐波那契“兔子繁殖问题”:
r
n 1
n 1
第n行1
C
1 n
C
2 n
…
C
r n
…
…… … …
C n2 n 1
1
C n1 n
1
练习1:
（04. 上海春季高考）如图，在由二项式系
数所构成的杨辉三角形中，第__3_4__行中从
左至右第14与第15个数的比为 2 : 3 .
练习2：
1
2
2
34
3
47
74
5 11 14 11 5
65 66 68 72 8 0 96
则表中各数按从小到大的顺序排列， 第100个数是 多少？
分析:首先计算第100 个数位于表中第几行, ∵ 1 + 2 + 3 + … + 13 = 91 ∴第100 个数位于第 14 行,第 9 个数 其次计算第 14 行第1个数: 3 + 21 + 22 + … +213 = 16385 最后计算第 9 个数: 16385 + 20 +21 +22 + 23 + 24 + 25 + 26 + 27
第3行
13 3 1
第4行
14 6 4 1
第5行
1 5 10 10 5 1
第6行 1 6 15 20 15 6 1

杨辉三角上课用PPT课件

杨辉三角上课用PPT课件

(a+b)6…1 6 15 20 15 6 1
观察每一行的第一个和最后一个数有什么特点？
(1)对称性: Cn0 1,Cnn 1
与首末两端“等距离”的两个二项式系数相等．
这就是组合数的性质
1: Cnm
C nm n
第2页/共32页
(a性+b质)1…………… 1 1
(2)递推性:
除(a1+以b)外2…的…每…一个…数…都1等2于它1肩上两个数的和.
第15页/共32页
题型 证明不等式
例20．证明： 当n N*且n 1 2 (1 1)n 3
n
证明 (1
1 )n n
1 Cn1
1 n
Cn2
1 n2
11 Cn2
1 n2
2
通项
Cnk
1 nk
n(n
1)
k
(n !
k
1)
1 nk
nk k!
1 nk
1 k!
(1
1)n n
1
C
1 n
1 n
Cn2
1，1，2，3，5，8，13，21，34，．．．
第21页/共32页
探究：横行规律
第0行
1 2 3
4 5 6 7
8 9 10 11 12 13 14
15
1）杨辉三角中的第1，3，7，15，…行，即第 2n-1行的 各个数字为奇数？
则第2n行的数字有什么特点？除两端的1之外都是偶数.
第22页/共32页
解:?1二项式系数之和为C90 C91 C92 C99 29 512.
解 : 设2x 3y9 a0x9 a1x8y a2x7y2 a9y9. 2令x y 1得各项系数之和为a0 a1 a2 a9 21 319 1.

(展示)杨辉三角ppt_高三数学

(展示)杨辉三角ppt_高三数学
r n r −1 n−1
C = C +C …… …… 2 r n−2 r −1 1 … Cn−1 Cn−1 … Cn−1 第n-1行 1 Cn−1 Cn−1 行 r n−1 2 1 … … Cn Cn 第n行 1 Cn Cn 行 …… … …
r n−1
一.简介:杨辉三角的基本性质 简介: 表中每个数都是组合数， 1）表中每个数都是组合数，第n行的第 n ! r r+1个数是 r+1个数是 C =
3.杨辉三角与“纵横路线图” 3.杨辉三角与“纵横路线图” 杨辉三角与 “纵横路线图”是数学中的一类有趣 纵横路线图” 纵横路线图 的问题：如图是某城市的部分街道图， 的问题：如图是某城市的部分街道图， 纵横各有五条路，如果从A处走到 处走到B处 纵横各有五条路，如果从 处走到 处 (只能由北到南，由西向东 ，那么有多 只能由北到南， 只能由北到南 由西向东)， 少种不同的走法？ 少种不同的走法？
（2）斜看杨辉三角中各数的和，又有何规律？ 斜看杨辉三角中各数的和，又有何规律？
列斜线上的前Q个数之和等于第 列斜线上的第Q个数 第P列斜线上的前 个数之和等于第 列斜线上的前 个数之和等于第(P+1)列斜线上的第 个数。 列斜线上的第 个数。
（3）如图，写出斜线上各行数字的和，有什么规律？ 如图，写出斜线上各行数字的和，有什么规律？
= (C a + C a b +⋯+ C a b +⋯+ C )(a + b) 0 k+1 1 k r +1 k−r b+1 k k = Ck a + Cka b +⋯+ Ck a b +⋯+ Ck ab +
0 k k 1 k −1 1 k r k k −r r k k

杨辉三角优质课件

杨辉三角优质课件
n 1
n 1 n
C
n n
倒序相加法
思考3.在(3x -2y)20的展开式中，求：(1)二项 式系数最大的项;(2)系数绝对值最大的项;(3) 系数最大的项; 解:(2)设系数绝对值最大的项是第r+1项. 则 r 20 r r r 1 19 r r 1
C 20 3 C 3
r 20
2 C 20 3 2 C
r r 1 20
2
20 r
3
21 r
2
r 1
即
3(r+1)>2(207 r8 5 5
8
所以当r=8时，系数绝对值最大的项为 8 12 8 12 9 20
T C 3 2 x y
即
3(r+1)>2(20-r)
令a=1，b=－1得
C C C C
0 n 2 n 1 n 3 n
1答案 2答案


2 n

启示：在二项式定理中，对a,b赋予一些特定的值， 是解决二项式有关问题的一种重要方法——赋值法。
0 2 1 2 2 2 n 2 n ) (C n ) (C n ) (C n ) C2 思考2求证: (Cn n. 略证：由(1+x)n(1+x)n=(1+x)2n，两边展开 后比较xn的系数得：
m m m 1 C C 这就是组合数的性质 2: C n 1 n n
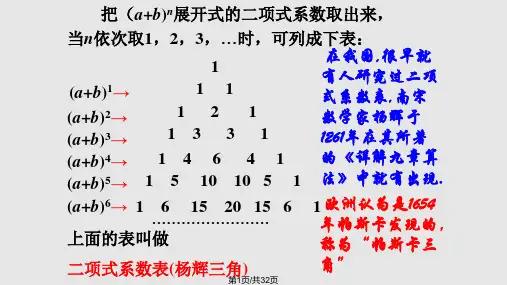
可运用函数的观点，结合“杨辉三角”和函数图象， 研究二项式系数的性质． f( r ) 20 n (a+b) 展开式的二项式系数是
C , C , C , , C ， , C .
0 n
1 n

中考复习 杨辉三角ppt课件

中考复习 杨辉三角ppt课件

C．5 2
D． 51
1 23 256 7 2 2 3 10 ………
9
4．【2015广西】将正整数按如图所示的规律排 列下去，若用有序数对（m，n）表示第m排，从 左到右第n个数，如（3，2）表示正整数5，（4， 3）表示正整数9，则（100，16）表示的正整数 是 4966 ．
10
5．(2018·枣庄)将从1开始的连续自然数按如下 规律排列：
所示的三角形，我们称之为“杨辉三角”从图中
取一列数：1，3，6，10，…，记a1=1，a2=3，;a11﹣2a10+10的值是
．
8
3．(2018·十堰)如图，是按一定规律排成的三
角形数阵，按图中数阵的排列规律，第9行从左
至右第5个数是 ( B )
A．2 10
B． 41
11 +
12 1 +
13 3 1 +
14 6 4 1
第5行
1 5 10 10 5 1
第6行
1 6 15 20 15 6 1
第7行
1 7 21 35 35 21 7 1
一般有
············
Cr r
Cr r1
Cr r2
Cr n1
C r1 (n n
r)
5
探究3
杨辉三角中试写出斜行直线上数字的和, 有
1.（2018年德州）我国南宋数学家杨辉所著的《详 解九章算术》一书中，用如图的三角形解释二项 式（a+b）n的展开式的各项系数，此三角形称为 “杨辉三角”根据”杨辉三角”请计算（a+b）8的 展开式中从左起第四项的系数为（ ） A．84 B．56 C．35 D．28
7
1（2018年孝感）我国古代数学家杨辉发现了如图

杨辉三角PPT优秀课件

杨辉三角PPT优秀课件

B 1
1 1 4
A
1 1 3
1
3
2
1
1
A
6 4 1 5 10 5 10 15 20 15 35 35 B70
2、杨辉三角的对称性：
C C .
r n
nr n
3、杨辉三角的第 n行就是二项式 (a b) 的展开式的系数，即：
n
(a b) C a C a b
n r 0 n n 1 n
2.1杨辉三角(1)
杨辉最重要的著作是《详解九章算法》． 为了使《九章算术》便于自学，杨辉对 该书的246个问题中较难的80题作了详解， 并增添了“图解、乘除算法和纂类”三卷． “详解”包括三个方面：一是“解题”，即解 释题意、名词术语，校勘文字，并对题目 作出评注；二是“细草”，即详细的解题过 程及必要的图示；三是“比类”，即增选与 原题算法相同或类似的例题进行对照分析． “纂类”是把《九章算术》中的全部问题按 解题方法由浅入深的顺序重新整理分类．
杨辉三角与“纵横路线图” “纵横路线图”是数学中的一类有趣 的问题．图 1 是某城市的部分街道 图，纵横各有五条路，如果从 A 处 走到 B 处 ( 只能由北到南，由西向 东 ) ，那么有多少种不同的走法？
我们把图顺时针转 45 度，使 A 在 正上方， B 在正下方，然后在交叉 点标上相应的杨辉三角数．有趣的 4 是， B 处所对应的数 C 8 =70 ， 正好是答案 ( 70) ． 一般地 , 每个交点上的杨辉三角数， 就是从 A 到达该点的方法数．由此 看来，杨辉三角与纵横路线图问题 有天然的联系．
n1
Ca
r n
n r
b C b
n n n
请用数学归纳法证明这一性质 。

《杨辉三角》_精品教学PPT人教版1

《杨辉三角》_精品教学PPT人教版1
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
解析：
由图1我们能发现，第1行中的数是 C10，C11 第2行中的数是 C02，C12，C22 第3行中的数是 C03，C13，C32，C33 则第n行中的数是 Cn0，C1n，Cn2， ，Cnn 设第n行中从左到右第14与第15个数的比为2 : 3
则 C1n3·C1n4 = 2 : 3 ，解得 n = 34
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
2.(1-x3)•(1+x)10的展开式中含x4的项的系数 2为00_____(用数字作答).
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
针对性练习
1. 如图１，在由二项式系数所构成的杨辉三 角中，第___3_4__行中从左到右第14与第15个数的 比为2:3 .
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版) 《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
课堂小结
1.二项式系数的三条性质
（1）对称性; （2）增减性与最大值; （3）各二项式系数的和; （4）递推性（杨辉三角中）.
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)
《 杨辉三 角》优 品教学P PT人教 版1-精 品课件 ppt(实 用版)

《“杨辉三角”与二项式系数的性质》ppt课件

《“杨辉三角”与二项式系数的性质》ppt课件
3）根据这两条规律，大家能写出下面的系数吗?
总结提炼1:
a).表中每行两端都是1。 b).除1外的每一个数都等
于它肩上两个数的和。
11
例如：2+1=3
1 22 11 1 3 33 1 1 44 66 4 1 1 5 1100 10 5 1 1 6 15 20 15 6 1
4C+106C=1110
因为：CC2120+C = C C2221 C2232 = 3
(a+b)1 (a+b)2 (a+b)3 (a+b)4 (a+b)5 (a+b)6
+ ++ +++ ++++
+++++
①每行两端都是1 Cn0= Cnn=1 ②从第二行起，每行除1以外的每一个数都等于它肩上 的两个数的和 Cn+1m= Cnm + Cnm-1
二项式系数的性质
(a b)n 展开式的二项式
0 6
C61
C62
C
3 6
C
4 6
C65
C
6 6
1 5 10 10 5 1 1 6 15 20 15 6 1
知识探究3:
11
(a+b)1
C10 C11
121
(a+b)2
C
0 2
C12
C
2 2
1 33 1
(a+b)3
(a+b)4 (a+b)5 (a+b)6
C
0 3
C13
C
2 3
C
3 3

14.2乘法公式--杨辉三角(共19张PPT)

14.2乘法公式--杨辉三角(共19张PPT)

(2)直接写出25+5×24×(-3)
+10×23×(-3)2+10×22×(-3)3
+5×2×(ー3)4+(-3)5=
；
(3)直接写出25-5×24+10×23-
10×22+5×2-1=
；
13
知识点二：利用“杨辉三角”解决规律问题
针对练习 1
(4)若(2xー1)2018＝a1x2018+a2x2017+a3 x2016+ …+a2017 x2+a2018 x+a2019， 求a1+a2+a3+…+a2017+a2018的值.
14
知识点二：利用“杨辉三角”解决规律问题
针对练习
我国古代数学的许多创新和发展都位居世界前列，如南宋 数学家杨辉(约13世纪)所著的《详解九章算术》一书中， 用下图所示的三角形解释二项式(a+b)n的展开式的各项系 数，此三角形称为“杨辉三
角”根据“杨辉三角”,计算(a+b)20
的展开式中第三项的系数为( D )
6
知识点一：“杨辉三角”的认识
新知探究
杨辉三角中斜行和水平行之间的关系
①
把斜行①中第7行之前的数
②
字相加得1+1+1+1+1+1+1=6
③
②：1+2+3+4+5=15
④ ⑤
⑥
③：1+3+6+10=20 ④：1+4+10=15 ⑤：1+5=6
⑥1
将上面得到的数字与第7行中的数字对比你有什么发现？

杨辉三角ppt PPT课件

杨辉三角ppt PPT课件
研究性课题：
杨辉三角
杨辉三角
第0行
1
第1行
11
第2行 第3行 第4行 第5行
12
4=1+3
10=6+4 1
15=5+10
1
4
3
6
1 6=3+3 3 1 10=6+4
4 1 20=10+10
1 5 10 10 5 1
第6行
1 6 15 20 15 6 1
…… ……
C
r n

C r1 n1

C
r n1
分析:设第 n 行的第 2 个数为 an ,则a2 = 2 , an+1 = an + n ∴ an = 2 + 2 + 3 +…+ ( n-1) n2 n 2
2
练习3：
3
56
9 10 12
17 18 20 24
33 34 36 40 48
65 66 68 72 8 0 96
则表中各数按从小到大的顺序排列， 第100个数是 多少？
奖品高于中间区奖品？
“概率三角形”
1
1
1
1
2
2
1
2
1
4
4
4
1
3
3
1
8
8
8
8
照这样计算第n+1层有n+1个通道， 弹子通过各通道的概率将是？
与杨辉三角有何关系？
3.杨辉三角与“纵横路线图”
“纵横路线图”是数学中的一类有趣的问题：如 图是某城市的部分街道图，纵横各有五条路，如 果从A处走到B处 (只能由北到南，由西向东)，那 么有多少种不同的走法？
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

11 +
12 1 +
13 3 1 +
14 6 4 1
第5行
1 5 10 10 5 1
第6行
1 6 15 20 15 6 1
第7行
1 7 21 35 35 21 7 1
一般有
············
Cr r
Cr r1
Cr r2
Cr n1
C r1 (n n
r)
5
探究3
杨辉三角中试写出斜行直线上数字的和, 有
1 + 5 +10 + 10 + 5 + 1= 32 , 1 + 6 +15 +20 + 15 + 6 + 1= 64 ,
············ 2n
4
探究2
杨辉三角中与腰平行的第m条斜线(从右上到
左下)上前n个数字的和, 与第m+1条斜线上的第n
个数有什么关系?
第0行
1
相等关系
第1行 第2行 第3行 第4行
1.（2018年德州）我国南宋数学家杨辉所著的《详 解九章算术》一书中，用如图的三角形解释二项 式（a+b）n的展开式的各项系数，此三角形称为 “杨辉三角”根据”杨辉三角”请计算（a+b）8的 展开式中从左起第四项的系数为（ ） A．84 B．56 C．35 D．28
7
1（2018年孝感）我国古代数学家杨辉发现了如图
中考复习 规律问题之杨辉三角
1
杨辉简介
杨辉 ( 约公元13世纪中叶至后 半叶 ) 字谦光, 钱塘 ( 今浙江杭州 ) 人, 是中国南宋末年的数学家、数 学教育家. 著作甚多, 他编著的数 学书共五种二十一卷, 著有《详解九章算法》十二 卷 (1261年)、《日用算法》二卷(1262年)、等.
“杨辉三角”出现在他编著的《详解九章算法》 一书中, 杨辉三角的发现要比欧洲早500年左右, 杨 辉是一位杰出的数学教育家、重视数学的普及．
ห้องสมุดไป่ตู้
什么规律? 第0行
1
从第3个数起, 任 一 个数是前2个数字的
第1行
11
和,是斐波那契数列.
第2行
12 1
第3行
1 3 31
第4行
14 6 4 1
第5行
1 5 10 10 5 1
第6行
1 6 15 20 15 6 1
第7行 1 7 21 35 35 21 7 1
第7行 1 8 28 56 70 56 28 8 1 6
C．5 2
D． 51
1 23 256 7 2 2 3 10 ………
9
4．【2015广西】将正整数按如图所示的规律排 列下去，若用有序数对（m，n）表示第m排，从 左到右第n个数，如（3，2）表示正整数5，（4， 3）表示正整数9，则（100，16）表示的正整数 是 4966 ．
10
5．(2018·枣庄)将从1开始的连续自然数按如下 规律排列：
2
杨辉三角
一
一
一
一二 一
一三三 一
一四 六 四 一
一五 十 十 五一
一六
十 五
二 十
十 五
六
一
3
探究1
计算杨辉三角中各行数字的和,我们有
第0行 第1行 第2行 第3行 第4行 第5行 第6行
第n行
1 1 + 1= 2 , 1 + 2 + 1= 4 , 1 + 3 + 3 + 1= 8 , 1 + 4 + 6 + 4 + 1= 16 ,
所示的三角形，我们称之为“杨辉三角”从图中
取一列数：1，3，6，10，…，记a1=1，a2=3，a3=6，
a4=10，…，那么a4+a11﹣2a10+10的值是
．
8
3．(2018·十堰)如图，是按一定规律排成的三
角形数阵，按图中数阵的排列规律，第9行从左
至右第5个数是 ( B )
A．2 10
B． 41
第1行
1
第2行
234
第3行
98765
第4行
10 11 12 13 14 15 16
第5行 25 24 23 22 24 20 19 18 17
…
…
• 则2 018在第__4_5___行．
11