用全等三角形证明线段相等的解题思路

初中数学—全等三角形解题方法、思路及技巧汇总全等三角形是初中数学中非常重要的内容，今天我们就把初二数学中，与全等三角形相关的方法、思路及技巧都来整理一下。

一、全等三角形的性质与判定。

五种判定方法：SSS，SAS，AAS，ASA，HL，其中HL是边边角（SSA的特例）。

全等三角形的对应边相等，对应角相等，一句话，凡是对应的，都相等。

二、寻找全等三角形常用方法1、直接从结论入手一般会有以下几种要求证的方向：•线段相等•角相等•度数•线段或者线段的和、差、倍、分关系然后根据题目要求证的方向，找到要证明的相关量分别在哪两个三角形中，再围绕这两个三角形进行研究。

2、从已知条件入手把所有能标注在图上的已经条件标注出来，注意用不同的标示进行区分，比如第一组相等的线段用一条短竖，第二组相等的线段用两条短竖，再比如第一组相等的角用一个小圆弧，第二组相等的角就用两个小圆弧等。

然后通过已知条件找到相关的两个三角形，再进行分析。

记住一句话：“充分利用已知条件”。

3、把已经条件和结论综合起来考虑找到所有的已知条件和隐藏条件，结合结论，找出可能全等的两个三角形，再进行分析。

4、如果上述方法都确定行不通，就考虑添加辅助线来构造全等三角形。

三、构造全等三角形的一般方法1、题目中出现角平分线（1）通过角平分线上的某个已知点，向两边作垂线，这是利用角平分线的性质定理或者逆定理来构造的全等三角形（2）在角平分线的某个已知点，作角平分线的垂线和两边相交，构造全等三角形。

（3）在该角的两边，距离角的顶点相等长度的位置上截取两点，分别连接这两点与角平分线上的某已知点，构造全等三角形2、题目中出现中点或者中线（中位线）（1）倍长中线法，把中线延长至二倍位置（2）过中点作某一条边的平行线3、题目中出现等腰或者等边三角形（1）找中点，倍长中线（2）过顶点作底边的垂线（3）过某已知点作一条边的平行线（4）三线合一4、题目中出现三条线段之间的关系通常用截长补短法，在某条线段上截取一段线段，使之与特定的线段相等，或者将某条线段延长，使之与特定线段相等。

数学篇学思导引在平面几何中，证明两条线段相等是一种常见的问题，其证明方法非常多，其中利用全等三角形对应边相等是证明线段相等的主要方法.但有些题目所给的图中没有现成的全等三角形，这就需要通过添加辅助线去构造全等三角形，再利用全等三角形的性质，找到解题的突破口.一、通过旋转构造全等三角形旋转前后，图形中的对应角的大小、线段的长短、面积的大小均不变.当三角形或正方形绕着图形的某个顶点顺时针（或逆时针）旋转一定角度以后，旋转前后的图形是全等的，其对应边及对应角是相等的.此外，旋转不同的角度（比如30°、45°、60°、90°等）还可以构造出新的图形（比如等边三角形、直角三角形等）、得到新的位置关系（垂直或平行），然后依据旋转后构造的条件即可顺利解题.例1如图1，四边形ABCD为正方形，DE//AC，AE=AC，AE与CD相交与F.求证：CE=CF.图1图1-1分析：此题ABCD是正方形，具有对称性，可以利用旋转图形来构造全等三角形.将△ADC旋转至△ABG处，可得到△ADC≌△ABG.然后再通过计算角度∠ABG和∠ABD，证得B、D、G三点共线.然后再利用BD是对角线，具有对称性，求得△ABG≌△CBG.从而证得△ADC≌△ABG≌△CBG，进而证明三角形ACG为等边三角形.再计算出相关角的大小，得出∠AEC=∠EFC=75°最后证明CE=CF.解：把△ADE绕点A顺时针旋转90°得到△ABG，连接CG，如图1-1.∵旋转前后的两个三角形全等，∴∠ABG=∠ADE=90°+45°=135°又∵BD是正方形ABCD的对角线，∴∠ABD=45°，∴∠ABG+∠ABD=135°+45°=180°，B、G、D共线，∴DG是∠AGC的角平分线，∴△AGB≌△CGB.∴AG=CG又∵△ADE≌△ABG，∴AG=AE，又∵AE=AC，∴AE=AG=AC=GC，∴△AGC为等边三角形，∴∠AGB=30°，∴∠DAE=∠BAG=∠ABD-∠AGB=45°-30°=15°，∴∠EAC=∠DAC-∠DAE=45°-15°=30°，又∵AE=AC，∴∠AEC=（180°-30°）÷2=75°，又∵∠EFC=∠DFA=45°+30°=75°，如何构造全等三角形证明线段相等江苏省盐城景山中学孔佩佩28数学篇∴∠AEC =∠EFC ，∴△CEF 为等腰三角形，∴CE =CF .评注：此题图形比较简单，但等量线段、全等三角形较少，直接解答比较困难，可考虑旋转三角形来构造全等三角形，创造等量关系.将△ADE 旋转到△ABG 后，利用正方形的对称性证明G 、B 、H 、D 四点共线，然后利用等量关系证明△AGC 为等边三角形，进而证明△CEF 为等腰三角形，完成证明.二、通过补形构造全等三角形许多几何问题常因图形复杂、不规则而给解题带来困难，这时可以考虑利用补形的方法构造特殊图形，通过证明三角形全等来求解.具体的步骤如下：第一，作垂线或平行线，构造正方形、长方形或特殊三角形；第二，找等量关系，从补形后的整体图形中找全等三角形确定边角的等量关系，或找相似三角形得到比例关系；第三，通过计算得到新的等量关系证明线段相等.例2设P 是正方形ABCD 一边BC 上的任意一点，PF ⊥AP ，CF 平分∠DCE .求证：PA =PF.图2图2-1分析：题中CF 与PF 构成的图形不完整，可以将其补全，经过分析发现补全后的图形是正方形，可以得到很多相等的线段，并求出一些角的度数.但题中的点P 是一个不确定的点，直接求解较难.不妨将图形问题转化为“数与式”的问题来解.设|AB |=a ，|BP |=b ，|CE |=c ，然后通过Rt△ABP ∽Rt△PEF 来求解出a 、b 、c 之间的关系.最后再分析出PA 与PF 之间的关系.解：过F 作FG ⊥CD 交CD 于G ，过F 作FE ⊥BC 交BC 于E ，如图2-1所示.∵四边形ABCD 是正方形，∴∠DCE =90°，又∵CF 平分∠DCE ，∴四边形CEFG 是正方形，∴EF =CE ，设|AB |=a ，|BP |=b ，|CE |=c ，则|PC |=a -b ，|EF |=|CE |=c ，在Rt△ABP 中，tan∠BAP =BP AB =b a，在Rt△PEF 中，tan∠EPF =EF PE，∵PE =PC +CE =(BC -BP )+CE =(a -b )+c =a -b +c ，∴tan∠EPF =EF PE =c a -b +c，∵PF ⊥AP ，∴∠APF =90°，∴△BAP ∽△EPF ，∴∠BAP =∠EPF ，∴tan∠BAP =tan∠EPF ，即b a =c a -b +c，∴ac =ab -b 2+bc ，整理得c (a -b )=b (a -b )，∴c =b ，∴BP =CE =EF ，又∵△BAP ∽△EPF ，∴△BAP ≌△EPF ，∴PA =PF ，评注：本题通过补全图形的方法将不规则的图形放入两个正方形中，由于P 点为任意一点，构造△ABP ∽△PEF ，得到BP 与EF的比例关系.再结合CF 是对角线，将△ABP ∽△PEF 转化为△ABP ≌△PEF ，从而证明结论.证明线段相等的方法多种多样，构造全等三角形的方法灵活多变，同学们在解题时要努力挖掘题设特征，巧妙合理地构造全等三角形，这样才能使方法简便.学思导引29。

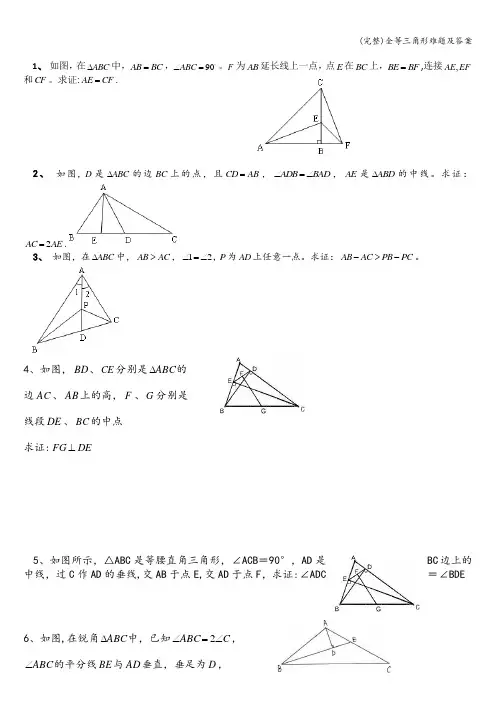
1、 如图，在ABC ∆中，AB BC =，90ABC ∠=。

F 为AB 延长线上一点，点E 在BC 上，BE BF =,连接,AE EF 和CF 。

求证:AE CF =.2、 如图,D 是ABC ∆的边BC 上的点，且CD AB =，ADB BAD ∠=∠，AE 是ABD ∆的中线。

求证：2AC AE =.3、 如图，在ABC ∆中，AB AC >，12∠=∠,P 为AD 上任意一点。

求证：AB AC PB PC ->-。

4、如图，BD 、CE 分别是ABC ∆的边AC 、AB 上的高，F 、G 分别是线段DE 、BC 的中点求证:DE FG ⊥5、如图所示，△ABC 是等腰直角三角形，∠ACB ＝90°，AD 是BC 边上的中线，过C 作AD 的垂线,交AB 于点E,交AD 于点F ，求证:∠ADC＝∠BDE6、如图,在锐角ABC ∆中，已知C ABC ∠=∠2,ABC ∠的平分线BE 与AD 垂直，垂足为D ，若cm BD 4=，求AC 的长参考答案1、 思路分析：可以利用全等三角形来证明这两条线段相等，关键是要找到这两个三角形.以线段AE 为边的ABE ∆绕点B 顺时针旋转90到CBF ∆的位置，而线段CF 正好是CBF ∆的边，故只要证明它们全等即可。

解答过程：90ABC ∠=，F 为AB 延长线上一点∴90ABC CBF ∠=∠=在ABE ∆与CBF ∆中AB BC ABC CBF BE BF =⎧⎪∠=∠⎨⎪=⎩∴ABE CBF ∆≅∆(SAS)∴AE CF =。

解题后的思考：利用旋转的观点，不但有利于寻找全等三角形，而且有利于找对应边和对应角。

小结：利用三角形全等证明线段或角相等是重要的方法，但有时不容易找到需证明的三角形。

这时我们就可以根据需要利用平移、翻折和旋转等图形变换的观点来寻找或利用辅助线构造全等三角形。

2、 思路分析：要证明“2AC AE =”，不妨构造出一条等于2AE 的线段，然后证其等于AC 。

初中数学三角形全等解题技巧全等三角形的内容是初二数学中的重点知识，也是教学中的难点。

许多学生由于基础知识薄弱或无法进行逻辑推理等原因，下面是小编为大家整理的关于初中数学三角形全等解题技巧，希望对您有所帮助。

欢迎大家阅读参考学习!1初中数学三角形全等解题技巧巧用三角形全等证明两线垂直通过对于数学知识的学习，学生在探究和实践中会了解三角形全等的方式，通常会通过“边边边”“边角边”“角边角”“角角边”“斜边直角边”的判定方法来证明三角形全等。

当了解了三角形全等后，很多数学问题就会迎刃而解，使学生可以借助全等三角形的性质和特点来进行进一步的证明和推理，完善自己的思维，提高自己的理解能力，在大脑中建构出数学模型。

学生在解题过程中可以利用三角形全等来证明两线垂直，这是三角形全等的一种常用法。

例如：AD为△ABC的高，E为AC上一点，BE交AD与F，且有BF=AC，FD=CD，求证BE⊥AC。

解决本题的关键就是证明∠BEC=90°，而证明∠BEC=90°，也就是说∠EBC+∠BCE=90°。

题目中已知AD为△ABC的高，BF=AC，FD=CD，也就是AD⊥BC，即∠ADB为90°，同时∠DBF+∠BFD=90°。

所以证明本题的关键就是证明，这样就可以证明∠BEC=90°。

在对于∠BFD=∠BCE的过程中，学生就可以利用三角形全等的性质，这样问题就顺利解决了。

解题过程中学生利用三角形全等来证明三角形中的内角相等，之后利用三角形内角和相等就可以证明两直线的垂直。

学生在解题过程中要善于利用自己的逻辑思维和推理判断以及对于知识的迁移能力，使学生可以灵活地转化已知条件之间的关系，证明三角形全等，之后进一步对个数量关系进行证明，提高自己的思维能力。

“倍长中线法”构造全等三角形全等三角形的应用是非常广泛的，学生在解题过程中要善于转化和构造，使已知的数学条件可以得到充分地利用。

1专题13 利用全等三角形的性质解决线段的证明与计算问题知识对接考点一、全等三角形的性质 （1）全等三角形对应边相等； （2）全等三角形对应角相等.考点二、怎样解运用全等三角形性质的问题证明两条线段相等或两个角相等时，常证明两条线段或两个角所在的三角形全等,运用全等三角形的性质，即全等三角形的对应边相等、对应角相等得到.专项训练一、单选题1．（2021·福建九年级）如图，点E ，F 在线段BC 上，ABF 与DEC 全等，点 A 和点D ，点B 和点C 是对应点，AF 和DE 交于点 M ，则与EM 相等的线段是（ ）A ．BEB ．EFC ．FCD ．MF【答案】D 【分析】根据ABF 与DEC 全等，点A 和点D ，点B 和点C 是对应点，可得AFB DEC ∠=∠，则有EM FM =． 【详解】解：∵ABF 与DEC 全等，点A 和点D ，点B 和点C 是对应点， ∵AFB DEC ∠=∠， ∵EM FM =， 故选：D ． 【点睛】本题考查了全等三角形的性质，等腰三角形的判定与性质，熟悉相关性质是解题的关键．2．（2021·山东九年级）如图，在菱形ABCD 中，6AB =，60BCD ∠=︒，E 是AD 中点，BE 交AC 于点F ，连接DF ，则DF 的长为（ ）A ．4BC ．D ．【答案】C 【分析】连接DB ， 四边形ABCD 为菱形，∵BCD =60°，可得∵ABD 为等边三角形，求出AF 的长度，再证明∵AEF ∵∵DEF ，即可求出DF 的长度． 【详解】 如图：连接DB∵四边形ABCD 为菱形，∵BCD =60°， ∵∵BCD =∵BAD =60°，∵AB =AD ，∵DAC =∵BAC =12∵DAB =30°，即∵ABD 为等边三角形， 又E 为AD 的中点， ∵BE ∵AD ，∵AE =12AD =12AB =3，cos ∵EAF =AE AF = cos AF 又在∵AEF 和∵DEF 中，∵AEF =∵DEF =90°，AE =DE ，EF =EF ，3∵∵AEF ∵∵DEF ， ∴DF =AF故选：C ． 【点睛】本题考查了菱形的性质，等边三角形的判定和性质，全等三角形的判定和性质，以及特殊锐角三角函数值，熟悉并灵活运用以上性质式解题的关键．3．（2021·天津和平·）如图，在AOB 中，15,6,OAB AOB OB OC ∠=∠=︒=平分AOB ∠，点P 在射线OC 上，点Q 为边OA 上一动点，则PA PQ +的最小值是（ ）A ．1B ．2C ．3D ．4【答案】C 【分析】在射线OB 上截取一点Q '，使得OQ OQ '=，则OPQ OPQ ∆≅∆'，可得PQ PQ ='．作AH OB ⊥于H ．可得PA PQ PA PQ +=+'，推出当A 、P 、Q '共线，且垂直OB 时，PA PQ +'的值最小，最小值为AH ，【详解】解：在射线OB 上截取一点Q '，使得OQ OQ '=，则OPQ OPQ ∆≅∆'，可得PQ PQ ='．作AH OB ⊥于H ． ∵'PA PQ PA PQ +=+，∵当A 、P 、Q '共线，且垂直OB 时，PA PQ +'的值最小，即最小值为AH ∵15OAB AOB ∠=∠=∵6OB AB ==，30OA B AO H B A B ∠+∠=∠=， 在Rt ABH 中， ∵·sin303AH AB ==，+的最小值为3，∵PA PQ故选C．【点睛】本题考查轴对称-最短问题、全等三角形，等腰三角形的性质、三角函数等知识，解题的关键在于能够熟练的掌握相关知识点．4．（2021·江苏南通田家炳中学九年级）如图，在直角坐标系中，已知点A(6，0)，点B为y轴正半轴上一动点，连接AB，以AB为一边向下作等边∵ABC，连接OC，则OC的最小值（）A B．3C．D．【答案】B【分析】以OA为对称轴作等边∵AMN，由“SAS”可证∵ANC∵∵AMB，可得∵AMB=∵ANC=60°，由直角三角形的性质可求∵AEN=30°，EO= ，则点C在EN上移动，当OC'∵EN时，OC'有最小值，即可求解．【详解】解：如图，以OA为对称轴作等边∵AMN，延长CN交x轴于E，∵∵ABC是等边三角形，∵AMN是等边三角形，∵AM=AN，AB=AC，∵MAN=∵BAC，∵AMN=60°=∵ANM，∵∵BAM=∵CAN，∵∵ANC∵∵AMB（SAS），∵∵AMB=∵ANC=60°，∵∵ENO=60°，∵AO=6，∵AMB=60°，AO∵BO，∵MO=NO=∵∵ENO=60°，∵EON=90°，5∵∵AEN=30°，， ∵点C 在EN 上移动，∵当OC'∵EN 时，OC'有最小值， 此时，O'C=12EO=3， 故选：B ．【点睛】本题考查了全等三角形的判定和性质，等边三角形的性质，垂线段最短，锐角三角函数，确定点C 的运动轨迹是解题的关键．5．如图，已知：在∵ABCD 中，E 、F 分别是AD 、BC 边的中点，G 、H 是对角线BD 上的两点，且BG ＝DH ，则下列结论中不正确的是（ ）A ．GF ∵FHB ．GF ＝EHC ．EF 与AC 互相平分D ．EG ＝FH【答案】A 【分析】连接EF 交BD 于O ，易证四边形EGFH 是平行四边形，然后证明是否得出选项． 【详解】连接EF 交BD 于点O ，在平行四边形ABCD 中的AD=BC ，∵EDH=∵FBG ， ∵E 、F 分别是AD 、BC 边的中点， ∵DE∵BF,DE=BF=12BC ，∵四边形AEFB 是平行四边形,有EF∵AB ， ∵点E 是AD 的中点，∵点O 是BD 的中点，根据平行四边形中对角线互相平分，故点O 也是AC 的中点，也是EF 的中点，故C 正确，又∵BG=DH,∵∵DEH∵∵BFG ， ∵GF=EH ，故B 正确，∵DHE=∵BGF ，∵∵GHE=∵HGF ， ∵∵EHG∵∵FGH ， ∵EG=HF ，故D 正确，∵GF∵EH ，即四边形EHFG 是平行四边形，而不是矩形，故∵GFH 不是90度， ∵A 不正确． 故选A. 【点睛】本题考查平行四边形的判定与性质和全等三角形的判定与性质，解题的关键是熟练掌握平行四边形的判定与性质和全等三角形的判定与性质.6．如图，ABC DEC ≌△△，A 和D ，B 和E 是对应点，B 、C 、D 在同一直线上，且5CE =，7AC =，则BD 的长为（ ）A ．12B ．7C ．2D ．14【答案】A 【分析】7根据全等三角形的性质即可得到结论． 【详解】解：如图，ABC DEC ∆≅∆，A 和D ，B 和E 是对应点，B 、C 、D 在同一直线上，且5CE =，7AC =，5BC EC ∴==，7CD AC ==，12BD BC CD ∴=+=．故选：A ． 【点睛】本题主要考查的是全等三角形的性质，熟练掌握全等三角形的性质是解题的关键． 7．如图：若ABE ACF ≌，且5,2==AB AE ，则EC 的长为（ ）A ．2B ．2.5C ．3D ．5【答案】C 【分析】根据全等三角形的性质得AC=AB=5，由EC=AC ﹣AE 求解即可． 【详解】解：∵ABE ACF ≌，AB=5， ∵AC=AB=5， ∵AE=2，∵EC=AC ﹣AE=5﹣2=3， 故选：C ． 【点睛】本题考查了全等三角形的性质、线段的和与差，熟练运用全等三角形的性质是解答的关键． 8．如图，ABC ADE △≌△，点D 在边BC 上，则下列结论中一定成立的是（ ）A．AC DE==B．AB BDC．ABD ADB∠=∠∠=∠D．EDC AED【答案】C【分析】根据全等三角形的性质可直接进行排除选项．【详解】△≌△，解：∵ABC ADE∵AB=AD，BC=DE，AC=AE，∵B=∵ADE，∵C=∵E，∵∵ABD=∵ADB，故A、B、D都是错误的，C选项正确；故选C．【点睛】本题主要考查全等三角形的性质，熟练掌握全等三角形的性质是解题的关键．9．如图，∵ACE∵∵DBF，AE//DF，AB＝3，BC＝2，则AD的长度等于（）A．2B．8C．9D．10【答案】B【分析】根据全等三角形的对应边相等解答．【详解】解：由图形可知，AC＝AB＋BC＝3＋2＝5，∵∵ACE∵∵DBF，∵BD＝AC＝5，9∵CD ＝BD−BC ＝3， ∵AD ＝AC ＋CD ＝5＋3＝8， 故选：B ． 【点睛】本题考查的是全等三角形的性质，掌握全等三角形的对应边相等是解题的关键．10．（2021·河北）如图，已知平行四边形ABCD ，3CD cm =，依下列步骤作图，并保留作图痕迹： 步骤1：以B 为圆心，BE 长为半径画弧∵，分别交AB ，BC 于点E ，F ； 步骤2：以A 为圆心，以BE 长为半径画弧∵，交AD 于点G ；步骤3：以G 为圆心，以EF 长为半径画弧∵，弧∵和弧∵交于点H ，过H 作射线，交BC 于点M ．则下列叙述不正确．．．的是：（ ）A ．AMC C ∠=∠B ．AM CD =C ．AM 平分BAD ∠ D ．BEF AGH ∆∆≌【答案】C 【分析】由作图痕迹，可以得到∵EBF∵∵GAH ，从而有∵EBF=∵GAH ，因此可以判断A 、B 、D 正确，因为C 不一定成立，故可以得到解答． 【详解】解：如图，连结E 、F 和G 、H ，由已知，在∵EBF 和∵GAH 中，AG=EB ，AH=BF ，HG=EF ，∵∵EBF∵∵GAH ，故D 正确； ∵∵EBF∵∵GAH ，∵∵EBF=∵GAH ，由平行四边形的性质可得：∵AMB=∵GAH ，∵∵EBF=∵AMB ，∵AB=AM ，又由平行四边形的性质可得：AB=CD ，∵AM=CD ，故B 正确；∵∵AMB+∵AMC=180°，∵∵EBF+∵AMC=180°，又由平行四边形的性质可得：∵EBF+∵C=180°，∵∵AMC=∵C ，故A 正确； ∵∵BAM=∵MAD 不一定成立，∵C 不正确， 故选C ． 【点睛】本题考查三角形全等的判定和应用，熟练掌握作一个角等于已知角的作法和依据是解题关键． 二、填空题11．如图，矩形ABCD 中，AD ＝2，E 为CD 上一点，连接AE ，将∵ADE 沿AE 折叠，点D 恰好落在BC 上，记为D ′，再将∵D ′CE 沿D ′E 折叠，若点C 的对应点C ′落在AE 上，则AB 的长为___．【分析】由折叠的性质得到ADE AD ED CE D C E ∆∆⎧⎨∆∆'''⎩'≌≌，能得到345∠=∠=∠，再用平角的性质得到34560∠=∠=∠=︒，再由1490∠+∠=︒，得到1230∠=∠=︒，可以求出6∠，最后可以求出cos AB AD BAD ''=⨯∠． 【详解】 如图：由折叠的性质得：ADE AD E D CE D C E ∆∆⎧⎨∆∆'''⎩'≌≌11∵123435AD AD ∠=∠∠=∠=⎧⎨∠=∠'⎩；； ∵345∠=∠=∠ ∵345180∠+∠+∠=︒ ∵34560∠=∠=∠=︒ ∵1490∠+∠=︒ ∵1230∠=∠=︒∵6901230∠=︒-∠-∠=︒ ∵'Rt ABD 中，'30BAD ∠=︒∵cos cos AB AD BAD AD BAD '''=⨯∠=⨯∠2==【点睛】本题考查了矩形与折叠，全等三角形的性质，三角函数，掌握它们的性质是解题的关键．12．（2021·江苏扬州市·九年级二模）如图，Rt ∵ABC ∵Rt ∵FDE ，∵ABC ＝∵FDE ＝90°，∵BAC ＝30°，AC ＝4，将Rt∵FDE 沿直线l 向右平移，连接BD 、BE ，则BD +BE 的最小值为___．【答案】【分析】根据平面直角坐标系，可以假设(E m ，则(1D m +，，则BD BE +求BD BE +的最小值，相当于在x 轴上找一点(,0)R m ，使得R 到(1M -，，N 的距离和的最小值，如图1中，作点N 关于x 轴的对称点N '，连接MN '交x 轴题意R ，连接RN ，此时RM RN +的值最小，最小值MN ='的长． 【详解】解：建立如图坐标系，在Rt ABC ∆中，90ABC ∠=︒，4AC =，30BAC ∠=︒， 122BC AC ∴==，AB ==∴斜边AC 上的高ABC FDE ∆≅∆，4EF AC ∴==，斜边EF∴可以假设(E m ，则(1D m +，，BD BE ∴+欲求BD BE +的最小值，相当于在x 轴上找一点(,0)R m ，使得R 到(1M -，，N 的距离和的最小值，如图1中，作点N 关于x 轴的对称点N '，连接MN '交x 轴题意R ，连接RN ，此时RM RN +的值最小，最小值MN ='BD BE ∴+的最小值为故答案为：13【点睛】本题考查轴对称最短问题，平面直角坐标系，勾股定理等知识，解题的关键是学会用转化的思想思考问题，属于中考填空题中的压轴题．13．（2021·浙江金华·九年级）如图，在ABC 中，1841B C ∠=︒∠=︒，，点D 是BC 的中点，点E 在AB 上，将BDE 沿DE 折叠，若点B 的落点B '在射线CA 上，则BA 与B D '所夹锐角的度数是________．【答案】80︒． 【分析】根据折叠可得三角形全等，根据全等三角形的性质以及中点的性质可得BD B D '=， DC DB '=，由等腰三角形性质以及三角形外角定理求得BDB '∠度数，在BOD 中根据内角和即可求得BA 与B D '所夹锐角的度数． 【详解】如下图，连接DE ，BA 与B D '相交于点O ，将 ∵BDE 沿 DE 折叠， BDE B DE '∴△≌△，BD B D '∴=,又∵D 为BC 的中点，BD DC =，BD B D '∴=，41DB C C '∴==︒∠∠, BDB DB C C =''∴=+︒∠∠∠82,18080BOD B BDB '∴=︒--=︒∠∠∠, 即BA 与B D '所夹锐角的度数是80︒．故答案为：80︒． 【点睛】本题考察了轴对称的性质、全等三角形的性质、中点的性质、三角形的外角以及内角和定理，综合运用以上性质定理是解题的关键．14．（2021·广东）如图，点M 是Rt ∵ABC 斜边AB 的中点，过点M 作DM ∵CM ，交AC 于点D ，若AD ＝2，BC ＝5，则CD ＝_______【分析】延长CM ，使CD ＝MN ，连接AN ，证明()AMN BMC SAS ∆∆≌，由全等三角形的性质得出5BC AN ==，NAM B ∠=∠，由勾股定理求出DN =【详解】解：延长CM ，使CD ＝MN ，连接AN ， 如图所示：∵点M 是Rt ABC ∆斜边AB 的中点， ∵AM BM =， 在AMN ∆和BMC ∆中， AM BM AMN BMC MN CM =⎧⎪∠=∠⎨⎪=⎩， ∵()AMN BMC SAS ∆∆≌，15∵5BC AN ==，NAM B ∠=∠， ∵//AN BC ， ∵90BCA ∠=︒， ∵90NAD ∠=︒，∵DN == ∵DM CM ⊥，CM MN =，∵CD DN ==【点睛】本题考查了全等三角形的判定与性质，勾股定理，中垂线的性质，直角三角形的性质，熟练掌握全等三角形的判定与性质是解题的关键．15．（2021·浙江）如图，已知： Rt Rt 90ABC CEF ABC CEF ∠=∠=︒≌，，306A AC ∠=︒=，．现将CEF △绕点C 逆时针旋转α度，线段CF 与直线AB 交于点O ，连接OE ．则当OE OB =时，线段OA 的长为________．【答案】【分析】过E 作EH ∵CF 于H ，得出ABC CEF ≅，设OF=x ，则OC=6-x ，根据勾股定理得出结果． 【详解】解：过E 作EH ∵CF 于H ， ∵ABC CEF ≅，∵6CF AC == ，30A ∠=︒， ∵9060EFC A ∠=︒-∠=︒， 设OF =x ，则OC =6-x ， 在Rt ∆OCB 中，2222(6)9OB OC BC x =-=--，在Rt ∆FEH 中，EH =EF FH =EF ·cos60º=32， ∵OH =x -32，在Rt ∆OEH 中，222223()2OE EH OH x =+=-+，又∵OE =OB ，∵2223()(6)92x x -+=--解得x =2，∵BO∵AO =AB -BO =故答案为【点睛】本题考查了全等三角形的性质，勾股定理及特殊角的三角函数，正确作出辅助线是解题的关键． 三、解答题16．（2021·云南）如图，AC ∵BD ，垂足点E 是BD 的中点，且AB =CD ，求证：AB //CD .【答案】详见解析 【分析】17先证明,BE DE = 再利用斜边直角边公理证明()Rt ABE Rt CDE HL ≌，可得A C ∠=∠，从而可得答案． 【详解】证明：∵点E 是BD 的中点 ∵BE ED =. ∵AC BD ⊥∵90AEB DEC ∠=∠=︒. 在Rt ABE △和Rt CDE △中AB CDBE ED =⎧⎨=⎩∵()Rt ABE Rt CDE HL ≌， ∵A C ∠=∠， ∵//AB CD ． 【点睛】本题考查的是利用斜边直角边证明两个三角形全等，以及全等三角形的性质，平行线的判定，掌握以上知识是解题的关键．17．如图，在正方形ABCD 中，点E 在BC 边的延长线上，点F 在CD 边的延长线上，且CE DF =,连接AE 和BF 相交于点M ． 求证：AE BF = ．【答案】证明见解析． 【分析】利用正方形的性质证明：AB=BC=CD ，∵ABE=∵BCF=90°，再证明BE=CF ，可得三角形的全等，利用全等三角形的性质可得答案． 【详解】证明：∵四边形ABCD 为正方形，∵AB=BC=CD ，∵ABE=∵BCF=90°， 又∵CE=DF ，∵CE+BC=DF+CD 即BE=CF ， 在∵BCF 和∵ABE 中，BE CF ABE BCF AB BC =⎧⎪∠=∠⎨⎪=⎩∵ABE BCF △△≌（SAS ）， ∵AE=BF ． 【点睛】本题考查的是正方形的性质，三角形全等的判定与性质，掌握以上知识是解题的关键． 18．（2021·吉林）综合与实践在数学活动课上，老师出示了这样一个问题：如图1，在ABC 中，90ACB ∠=︒，6AC =，8BC =，点D 为BC 边上的任意一点．将C ∠沿过点D 的直线折叠，使点C 落在斜边AB 上的点E 处．问是否存在BDE 是直角三角形？若不存在，请说明理由；若存在，求出此时CD 的长度．探究展示：勤奋小组很快找到了点D 、E 的位置．如图2，作CAB ∠的角平分线交BC 于点D ，此时C ∠沿AD 所在的直线折叠，点E 恰好在AB 上，且90BED ∠=︒，所以BDE 是直角三角形．问题解决:（1）按勤奋小组的这种折叠方式，CD 的长度为 ．（2）创新小组看完勤奋小组的折叠方法后，发现还有另一种折叠方法，请在图3中画出来． （3）在（2）的条件下，求出CD 的长． 【答案】（1）3；（2）见解析；（3）247CD = 【分析】（1）由勾股定理可求AB 的长，由折叠的性质可得AC=AE=6，CD=DE ，∵C=∵BED=90°，由勾股定理可求解；（2）如图所示，当DE∵AC，∵EDB=∵ACB=90°，即可得到答案；（3）由折叠的性质可得CF=EF，CD=DE，∵C=∵FED=90°，∵CDF=∵EDF=45°，可得DE=CD=CF=EF，通过证明∵DEB∵∵CAB，可得DE BD＝，即可求解．AC BC【详解】（1）∵∵ACB=90°，AC=6，BC=8，∵10AB=，由折叠的性质可得：∵ACD∵∵AED，∵AC=AE=6，CD=DE，∵C=∵BED=90°，∵BE=10-6=4，∵BD2=DE2+BE2，∵（8-CD）2=CD2+16，∵CD=3，故答案为：3；（2）如图3，当DE∵AC，∵BDE是直角三角形，（3）∵DE∵AC，∵∵ACB=∵BDE=90°，由折叠的性质可得：∵CDF∵∵EDF，∵CF=EF，CD=DE，∵C=∵FED=90°，∵CDF=∵EDF=45°，∵EF=DE，∵DE=CD=CF=EF，∵DE∵AC，∵∵DEB∵∵CAB，19∵DE BD AC BC ＝， ∵886DE DE -＝， ∵DE=247， ∵247CD =【点睛】此题考查几何变换综合题，全等三角形的性质，折叠的性质，相似三角形的判定和性质，勾股定理等知识，灵活运用这些性质进行推理是解题的关键．19．（2021·陕西西北工业大学附属中学九年级）如图，在平行四边形ABCD 中，E 为BC 边上一点，且B AEB ∠=∠．求证：AC DE =．【答案】证明见解析. 【详解】试题分析：由平行四边形的性质得：AB=DC ，180ABC BCD ∠+∠=︒，证得AEC BCD ∠=∠，从而可证AEC ∵DCE ，故可得结论.试题解析：∵四边形ABCD 是平行四边形， ∵AB DC =，180ABC BCD ∠+∠=︒． ∵AB DC =，∵ABE AEB ∠=∠，AE DC =． ∵180AEC AEB ∠+∠=︒， ∵AEC BCD ∠=∠． 又EC EC =， ∵AEC ∵DCE ， ∵AC ED =．20．（2021·广东九年级）如图，已知点E 、C 在线段BF 上，且BE =CF ，CM ∵DF ，（1）作图：在BC 上方作射线BN ，使∵CBN =∵1，交CM 的延长线于点A （用尺规作图法，保留作图痕迹，21不写作法）；（2）在（1）的条件下，求证：AC =DF ．【答案】（1）作图见解析；（2）证明见解析【详解】试题分析：（1）∵以E 为圆心，以EM 为半径画弧，交EF 于H ，∵以B 为圆心，以EM 为半径画弧，交EF 于P ，∵以P 为圆心，以HM 为半径画弧，交前弧于G ，∵作射线BG ，则∵CBN 就是所求作的角．（2）证明∵ABC ∵∵DEF 可得结论．试题解析：（1）如图，（2）∵CM ∵DF ，∵∵MCE =∵F ，∵BE =CF ，∵BE +CE =CF +CE ，即BC=EF ，在∵ABC 和∵DEF 中，∵1{CBN BC EF MCE F∠∠∠∠＝＝＝ ∵∵ABC ∵∵DEF ，∵AC =DF ．【点睛】本题考查了基本作图-作一个角等于已知角，同时还考查了全等三角形的性质和判定；熟练掌握五种基本作图：（1）作一条线段等于已知线段．（2）作一个角等于已知角．（3）作已知线段的垂直平分线．（4）作已知角的角平分线．（5）过一点作已知直线的垂线．21．定义：一条对角线垂直平分另一条对角线的四边形叫做筝形，如图，筝形ABCD 的对角线AC 、BD 相交于点O ．且AC 垂直平分BD ．（1）请结合图形，写出筝形两种不同类型的性质：性质1： ；性质2： ．（2）若AB ∵CD ，求证：四边形ABCD 为菱形．【答案】（1）对角线互相垂直，是轴对称图形；（2）见解析【分析】（1）由筝形的定义即可得出结论；（2）由垂直平分线的性质得出AB=AD ，BO=DO ，同理：BC=DC ，由AS 证明∵AOB∵∵CDO ，得出AB=CD ，因此AB=CD=BC=AD ，即可得出四边形ABCD 为菱形．【详解】解：（1）由筝形的定义得：对角线互相垂直，即AC∵BD ；是轴对称图形，对称轴为AC ；故答案为对角线互相垂直，是轴对称图形；（2）∵AC 垂直平分BD ，∵AB ＝AD ，BO ＝DO ，同理：BC ＝DC ，∵AB∵CD ，∵∵ABO ＝∵ODC ，在∵ABO 和∵CDO 中，ABO ODC BO DOAOB DOC ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∵∵AOB∵∵CDO （ASA ），∵AB ＝CD ，∵AB ＝CD ＝BC ＝AD ，∵四边形ABCD 为菱形．【点睛】本题考查了菱形的判定、筝形的性质、线段垂直平分线的性质、全等三角形的判定与性质；熟练掌握筝形的性质，证明三角形全等是解题的关键．22．（2021·湖北黄石·）如图，D 是ABC 的边AB 上一点，//CF AB ， DF 交AC 于E 点，DE EF =．23（1）求证：ADE ∵CFE ；（2）若5AB =，4CF =，求BD 的长．【答案】（1）证明见详解；（2）1．【分析】（1）根据ASA 证明即可；（2）根据（1）可得ADE CFE ∆≅∆，即由AD CF =，根据BD AB AD AB CF 求解即可．【详解】（1）证明：//AB FC ，∴∠=∠ADE F ，在ADE ∆和CFE ∆中，ADE FDE EF AED CEFADE CFE ASA ；（2）由（1）得ADE CFE ∆≅∆AD CF ∴=∵541BD AB AD AB CF ．【点睛】本题考查全等三角形的判定和性质、平行线的性质等知识，熟练掌握基本知识是解题的关键． 23．（2021·江苏南京·南师附中新城初中）如图,在正方形ABCD 中,E ､F ､G ､H 分别是各边上的点,且AE BF CG DH ===．求证:（1）AHE BEF ≌△△; （2）四边形EFGH 是正方形．【答案】（1）见解析;（2）见解析【分析】（1）在正方形ABCD 中,由AE BF CG DH ===可得:AH BE CF DG ===,即可求证;（2）由（1）可用同样的方法证得EBF FCG △≌△,FCG GDH ≌△△,可得到FCG GDH ≌△△,然后证明90HEF ∠=︒,即可求证．【详解】（1）证明:∵四边形ABCD 为正方形,∵AB BC CD DA ===,90A B ∠=∠=︒．又∵AE BF DH CG ===,∵AH BE CF DG ===．∵()SAS AHE BEF ≌△△ （2）由（1）得,AHE BEF ≌△△, 同理,EBF FCG △≌△,FCG GDH ≌△△, ∵EF FG GH HE ===,AEH BFE ∠=∠,∵90B ∠=︒,∵90EFB FEB ∠+∠=︒,∵90AEH FEB ∠+∠=︒,∵90HEF ∠=︒,∵四边形EFGH 为正方形．【点睛】本题主要考查了正方形的性质和判定,三角全等的判断和性质,熟练掌握并会灵活应用相应知识点是解题的关键．25。

全等三角形的及其相应的线段、角相等的证明方法知识点：全等三角形定义：能够完全重合的两个三角形叫全等三角形知识点：对应顶点，对应边，对应角要点诠释：两个全等三角形重合在一起，重合的顶点叫对应顶点，重合的边叫对应边，重合的角叫对应角。

知识点：全等三角形的性质要点诠释：全等三角形对应边相等，对应角相等知识点：三角形全等的判定定理（一）要点诠释：三边对应相等的两个三角形全等。

简写成“边边边”或“SSS”知识点：三角形全等的判定定理（二）要点诠释：两边和它们的夹角对应相等的两个三角形全等。

简写成“边角边”或“SAS”知识点：三角形全等的判定定理（三）要点诠释：两角和它们的夹边对应相等的两个三角形全等，简写成“角边角”或“ASA”知识点：三角形全等的判定定理（四）要点诠释：两个角和其中一个角的对边对应相等的两个三角形全等。

简写成“角角边”或“AAS”知识点：直角三角形全等的判定定理要点诠释：斜边和一条直角边对应相等的两个直角三角形全等。

简写成“斜边、直角边”或”三、规律方法指导1．探索三角形全等的条件：（1）一般三角形全等的判定方法有四种方法：①边角边（SAS）；②角边角(ASA);③角角边(AAS);④(SSS).（2）直角三角形的全等的条件:除了使用SAS、ASA、AAS、SSS判定方法外，还有一种重要的判定方法，也就是斜边、直角边（HL）判定方法.2．经验与提示：⑴寻找全等三角形对应边、对应角的规律①全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边．②全等三角形对应边所对的角是对应角，两个对应边所夹的角是对应角．③有公共边的，公共边一定是对应边．④有公共角的，公共角一定是对应角．⑤有对顶角的，对顶角是对应角．⑥全等三角形中的最大边(角)是对应边(角)，最小边(角)是对应边(角)⑵找全等三角形的方法①可以从结论出发，看要证明相等的两条线段（或角）分别在哪两个可能全等的三角形中；②可以从已知条件出发，看已知条件可以确定哪两个三角形全等；③从条件和结论综合考虑，看它们能一同确定哪两个三角形全等；④若上述方法均不行，可考虑添加辅助线，构造全等三角形。

证明三角形全等的常见思路全等三角形是初中几何的重要内容之一，全等三角形的学习是几何入门最关键的一步，这部分内容学习的好坏直接影响着今后的学习．而一些初学的同学，虽然学习了几种判定三角形全等的公理和推论，但往往仍不知如何根据已知条件证明两个三角形全等．通过对以下几种证明三角形全的分析，体会常见思路。

知识点睛全等三角形的性质：对应角相等，对应边相等，（对应线段相等）对应边上的中线相等，对应边上的高相等，对应角的角平分线相等，面积相等．寻找对应边和对应角，常用到以下方法：(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边． (2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角． (3)有公共边的，公共边常是对应边． (4)有公共角的，公共角常是对应角． (5)有对顶角的，对顶角常是对应角．(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角)，一对最短边(或最小角)是对应边(或对应角)．要想正确地表示两个三角形全等，找出对应的元素是关键． 全等三角形的判定方法：(1) 边角边定理(SAS)：两边和它们的夹角对应相等的两个三角形全等． (2) 角边角定理(ASA)：两角和它们的夹边对应相等的两个三角形全等． (3) 边边边定理(SSS)：三边对应相等的两个三角形全等．(4) 角角边定理(AAS)：两个角和其中一个角的对边对应相等的两个三角形全等． (5) 斜边、直角边定理(HL)：斜边和一条直角边对应相等的两个直角三角形全等． 2．证题的思路：⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧）找任意一边（）找两角的夹边（已知两角）找夹已知边的另一角（）找已知边的对角（）找已知角的另一边（边为角的邻边）任意角（若边为角的对边，则找已知一边一角）找第三边（）找直角（）找夹角（已知两边AAS ASA ASA AAS SAS AAS SSS HL SAS全等三角形的应用：运用三角形全等可以证明线段相等、角相等、两直线垂直等问题，在证明的过程中，注意有时会添加辅助线．一、已知一边与其一邻角对应相等1．证已知角的另一边对应相等，再用SAS证全等．例1 已知：如图1，点E、F在BC上，BE=CF，AB=DC，∠B=∠C .求证：AF=DE．证明∵BE=CF(已知)，∴BE+ EF=CF+EF，即 BF=CE．在△ABF和△DCE中，∴△ABF≌△DCE(SAS)．∴ AF=DE(全等三角形对应边相等)．2．证已知边的另一邻角对应相等，再用ASA证全等．例2 已知：如图2，D是△ABC的边AB上一点，DF交AC于点E，DE=FE，FC∥AB．求证：AE=CE．证明∵ FC∥AB(已知)，∴∠ADE=∠CFE(两直线平行，内错角相等)．在△ADE和△CFE中，∴△ADE≌△CFE(ASA).∴ AE=CE(全等三角形对应边相等)3．证已知边的对角对应相等，再用AAS证全等．例3 (同例2).证明∵ FC∥AB(已知)，∴∠A=∠ECF(两直线平行，内错角相等).在△ADE和△CFE中，∴△ADE≌△CFE(AAS).二、已知两边对应相等1．证两已知边的夹角对应相等，再用SAS证等．例4 已知：如图3，AD=AE，点D、E在BC上，BD=CE，∠1=∠2．求证：△ABD≌△ACE证明∵∠1=∠2(已知)，∠ADB=180°-∠1，∠AEC=180°-∠2(邻补角定义)，∴∠ADB = ∠AEC，在△ABD和△ACE中，∴△ABD≌△ACE(SAS).2．证第三边对应相等，再用SSS证全等．例5 已知：如图4，点A、C、B、D在同一直线上，AC=BD，AM=CN， BM=DN．求证： AM∥CN，BM∥DN．证明∵ AC=BD(已知)∴AC+BC=BD+BC，即 AB=CD.在△ABM和△CDN中，∴△ABM≌△CDN(SSS)∴∠A=∠NCD，∠ABM=∠D(全等三角应角相等)，∴ AM∥CN，BM∥DN(同位角相等，两直线平行)．三、已知两角对应相等1．证两已知角的夹边对应相等，再用ASA证全等．例6 已知：如图5，点B、F、C、E在同一条直线上，FB=CE，∠B=∠E，∠ACB=∠DFE.求证： AB=DE， AC=DF.证明∵ FB=CE(已知)∴ FB+FC=CE+FC，即 BC=EF，∴ AB=DE，AC=DF(全等三角形对应边相等)2．证一已知角的对边对应相等，再用AAS证全等．例7 已知：如图6，AB、CD交于点O，E、F为AB上两点，OA=OB，OE=OF，∠A=∠B，∠ACE=∠BDF. 求证：△ACE ≌△BDF.证明∵OA=OB，OE=OF已知)，∴OA-OE=OB-OF，即 AE=BF，在△ACE和△BDF中，∴△ACE≌△BDF(AAS).四、已知一边与其对角对应相等，则可证另一角对应相等，再利用AAS证全等例8 已知：如图7，在△ABC中，B、D、E、C在一条直线上，AD=AE，∠B=∠C．求证：△ABD≌△ACE.证明∵AD=AE(已知)∴∠1=∠2(等边对等角)，∵∠ADB=∠180°-∠1，∠AEC=180°-∠2(邻补角定义)，∴∠ADB=∠AEC，在△ABD和△ACE中，∴△ABD≌△ACE(AAS).全等三角形问题中常见的辅助线——倍长中线法△ABC中,AD是BC边中线方式1:直接倍长(图1)：延长AD到E，使DE=AD，连接BEAAB CED F C BAD CB A方式2：间接倍长1) （图2）作CF ⊥AD 于F ，作BE ⊥AD 的延长线于E, 连接BE 2) （图3）延长MD 到N ，使DN=MD ，连接CD【经典例题】1、已知，如图△ABC 中，AB=5，AC=3， 则中线AD 的取值范围是_________.（提示：画出图形，倍长中线AD ，利用三角形两边之和大于第三边）例2：已知在△ABC 中，AB=AC ，D 在AB 上， E 在AC 的延长线上， DE 交BC 于F ，且DF=EF.求证：BD=CE（提示：方法1：过D 作DG ∥AE 交BC 于G ，证明ΔDGF ≌ΔCEF 方法2：过E 作EG ∥AB 交BC 的延长线于G ，证明ΔEFG ≌ΔDFB方法3：过D 作DG ⊥BC 于G ，过E 作EH ⊥BC 的延长线于H ，证明ΔBDG ≌ΔECH ）例3、如图，△ABC 中，E 、F 分别在AB 、AC 上，DE ⊥DF ，D 是中点，试比较BE+CF 与EF 的大小.变式：如图，AD 为ABC ∆的中线，DE 平分BDA ∠交AB 于E ，DF 平分ADC ∠交AC 于 F. 求证：EF CF BE >+（提示：方法1： 在DA 上截取DG=BD ，连结EG 、FG ， 证明ΔBDE ≌ΔGDE ΔDCF ≌ΔDGF 所以BE=EG 、CF=FG 利用三角形两边之和大于第三方法2：倍长ED 至H ，连结CH 、FH ，证明FH=EF 、CH=BE ，利用三角形两三边）例4：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF （提示：方法1：倍长AD 至G ，连接BG ，证明ΔBDG ≌ΔCDA 三角形BEG 是等腰三角形。

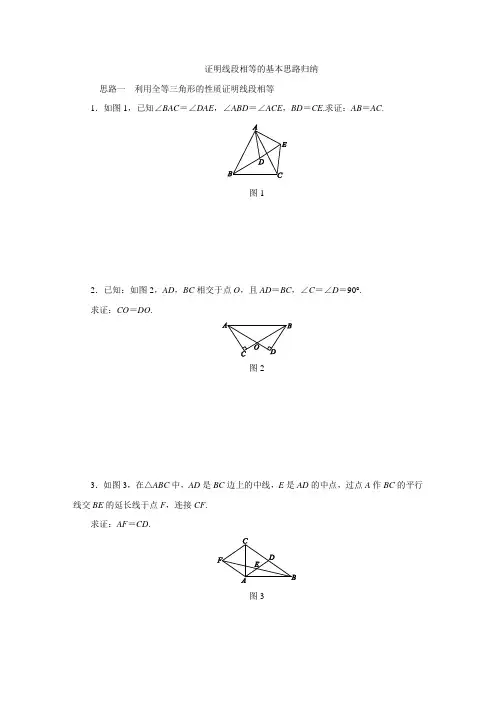
证明线段相等的基本思路归纳思路一利用全等三角形的性质证明线段相等1．如图1，已知∠BAC＝∠DAE，∠ABD＝∠ACE，BD＝CE.求证：AB＝AC.图12．已知：如图2，AD，BC相交于点O，且AD＝BC，∠C＝∠D＝90°.求证：CO＝DO.图23．如图3，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF.求证：AF＝CD.图3思路二利用等腰(边)三角形的性质与判定证明线段相等4．如图4，在等边三角形ABC中，E是AB上的动点，点E不与点A，B重合，点D在CB的延长线上，且CE＝ED.(1)如图①，若E是AB的中点，求证：BD＝AE.(2)如图②，若E不是AB的中点，(1)中的结论“BD＝AE”能否成立？若不成立，请直接写出BD与AE数量关系；若成立，请给予证明．图45．如图5，在△ABC中，AD是BC边上的高，BE⊥AC于点E，∠BAD＝∠CBE.求证：AB＝AC.图56．如图6，在△ABC中，AC＝BC，∠C＝120°，D为AB边的中点，DE，DF分别交AC，BC于点E，F.若EF∥AB，求证：DE＝DF.图67．如图7，在△ABC中，AD平分∠BAC，交BC于点D，E为AC的反向延长线上的一点，EG∥AD，分别交AB，BC于点F，G，找出图中的等腰三角形，并给出证明．图7思路三利用线段垂直平分线的性质与判定证明线段相等8．如图8，在△ABC中，AB＝AC，∠BAC＝120°，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F.求证：BM＝MN＝CN.图8思路四利用角平分线的性质与判定证明线段相等9．如图9，在△ABC中，∠BAC＝90°，AD⊥BC于点D，∠ACB的平分线交AD于点E，交AB于点F，FG⊥BC于点G.求证：AE＝FG.图910．如图10，在△ABC中，∠ABC的平分线与AC的垂直平分线MN交于点M，过点M作MD⊥AB，ME⊥BC，垂足分别为D，E.求证：AD＝CE.图101．证明：∵∠BAC ＝∠DAE ， ∴∠BAC －∠DAC ＝∠DAE －∠DAC ， 即∠BAD ＝∠CAE . 在△ABD 和△ACE 中， ⎩⎪⎨⎪⎧∠BAD ＝∠CAE ，∠ABD ＝∠ACE ，BD ＝CE ， ∴△ABD ≌△ACE . ∴AB ＝AC .2．证明：∵∠C ＝∠D ＝90°， ∴△ABC 和△BAD 都是直角三角形．在Rt △ABC 和Rt △BAD 中，⎩⎪⎨⎪⎧BC ＝AD ，AB ＝BA ，∴Rt △ABC ≌Rt △BAD (HL)． ∴∠ABC ＝∠BAD . ∴AO ＝BO . ∵BC ＝AD ， ∴BC －BO ＝AD －AO . ∴CO ＝DO .3．证明：∵AF ∥BC ，∴∠AFE ＝∠DBE . ∵E 是AD 的中点， ∴AE ＝DE .在△AFE 和△DBE 中，⎩⎪⎨⎪⎧∠AFE ＝∠DBE ，∠FEA ＝∠BED ，AE ＝DE ，∴△AFE ≌△DBE (AAS)．∴AF ＝BD . ∵AD 是BC 边上的中线， ∴BD ＝CD . ∴AF ＝CD .4．解：(1)证明：∵△ABC 是等边三角形，E 是AB 的中点， ∴∠ABC ＝∠ACB ＝60°，CE 平分∠ACB ，AE ＝BE . ∴∠BCE ＝30°. ∵ED ＝CE ， ∴∠D ＝∠BCE ＝30°. ∵∠ABC ＝∠D ＋∠BED ， ∴∠BED ＝30°. ∴∠D ＝∠BED . ∴BD ＝BE . ∴BD ＝AE . (2)BD ＝AE 成立．证明：过点E 作EF ∥BC 交AC 于点F ，如图所示，则∠AEF ＝∠ABC ，∠AFE ＝∠ACB . ∵△ABC 是等边三角形，∴∠ABC ＝∠ACB ＝∠A ＝60°，AB ＝AC ＝BC . ∴∠AEF ＝∠ABC ＝60°，∠AFE ＝∠ACB ＝60°， 则∠AEF ＝∠AFE ＝∠A ＝60°. ∴△AEF 是等边三角形．∴AE ＝EF . ∵∠AFE ＝∠ACB ＝∠ABC ＝60°，∴∠DBE ＝∠EFC ＝120°，∠D ＋∠DEB ＝∠ECF ＋∠ECD ＝60°. ∵ED ＝CE ，∴∠D ＝∠ECD . ∴∠DEB ＝∠ECF .在△DEB 和△ECF 中，⎩⎪⎨⎪⎧∠DEB ＝∠ECF ，∠DBE ＝∠EFC ，ED ＝CE ，∴△DEB ≌△ECF (AAS)． ∴BD ＝EF .∴BD ＝AE .5．证明：∵AD是BC边上的高线，BE⊥AC于点E，∴∠ADB＝∠BEC＝90°. ∴∠ABC＋∠BAD＝∠C＋∠CBE＝90°.∵∠BAD＝∠CBE，∴∠ABC＝∠C.∴AB＝AC.6．证明：∵AC＝BC，∠C＝120°，∴∠A＝∠B＝30°.∵EF∥AB，∴∠FEC＝∠A＝30°，∠EFC＝∠B＝30°.∴∠FEC＝∠EFC.∴EC＝FC.又∵AC＝BC，∴AE＝BF.∵D是AB的中点，∴AD＝BD.又∵∠A＝∠B，∴△ADE≌△BDF.∴DE＝DF.7．解：△AEF是等腰三角形．证明：∵AD平分∠BAC，∴∠BAD＝∠CAD.∵EG∥AD，∴∠E＝∠CAD，∠EF A＝∠BAD.∴∠E＝∠EF A.∴AE＝AF.∴△AEF是等腰三角形．8．证明：如图，连接AN，AM.∵ME垂直平分AB，NF垂直平分AC，∴BM＝AM，CN＝AN.∴∠MAB＝∠B，∠CAN＝∠C.∵∠BAC＝120°，AB＝AC，∴∠B＝∠C＝30°.∴∠AMN＝∠ANM＝60°，则△AMN是等边三角形．∴AM＝AN＝MN.∴BM＝MN＝CN.9．证明：∵CF 平分∠ACB ，∠BAC ＝90°，FG ⊥BC ， ∴FG ＝F A .∵∠AFC ＋∠ACF ＝90°，∠DEC ＋∠ECD ＝90°，且∠ACF ＝∠ECD ， ∴∠AFC ＝∠DEC . 又∵∠AEF ＝∠DEC ， ∴∠AFC ＝∠AEF . ∴AE ＝F A . ∴AE ＝FG .10．证明：连接MA ，MC .∵点M 在∠ABC 的平分线上，且MD ⊥AB ，ME ⊥BC ， ∴∠MDA ＝∠MEC ＝90°，MD ＝ME . ∵点M 在线段AC 的垂直平分线上， ∴MA ＝MC .在Rt △MAD 和Rt △MCE 中，⎩⎪⎨⎪⎧MD ＝ME ，MA ＝MC ， ∴Rt △MAD ≌Rt △MCE (HL)． ∴AD ＝CE .。

利⽤三⾓形相关知识证明线段相等的常⽤⽅法2019-09-22可以说证明两条线段相等是初中⼏何证明中⽐较基本的题⽬。

证明两条线段相等看似简单，但所适⽤的定理也⽐较多，要想熟练掌握，其实也不是⼀件容易的事情，为此，现就从三⾓形相关知识出发进⾏探究，仅供同学们参考。

⼀、利⽤两三⾓形⾯积相等地，等底必等⾼，等⾼必等底证明在三⾓形中需要证明等底或等⾼时，可以利⽤⾯积相等证明。

[例1] 求证：等腰三⾓形两腰上的⾼相等。

证明：如图1，在等腰中，作BDAC于D，CEAB于E，⽽AB=AC，BD=CE⼆、利⽤“直⾓三⾓形斜边上的中线等于斜边的⼀半”证明线段相等如果所证两线段所在的图形能构成直⾓三⾓形，并且可能构成斜边及斜边上的中线，⽤上⾯⽅法⼀时证不出来，可以考虑此法。

[例2]如图2，正⽅形ABCD中，E、F分别为AB、BC的中点，EC和DF相交于G，连接AG，求证：AG=AD。

证明：作DA、CE的延长线交于HABCD是正⽅形，E是AB的中点AE=BE，∠AEH=∠BEC，∠EBC=∠EAH=90°AEH≌BEC（ASA）AH=BC，AD=AH⼜F是BC的中点 RtDFC≌RtCEB∠DFC=∠CEB ∠GCF+∠GFC=∠ECB+∠CEB=90°∠CGF=90 DGH=∠CGF=90°DGH是Rt AD=AHAG==AD三、利⽤等腰三⾓形三线合⼀证明线段相等若要证明两条线段在同⼀直线上并且有共同端点，可以考虑此法。

[例3] 如图3，已知ABC为Rt，D为，DEAC于E，DFBC于F。

求证：AE=CE，BF=CF证明：连结CDD为RtABC的斜边AB的中点AD=CD=BD ADC与CDB均为等腰三⾓形⼜DEAC，DFBCAE=CE，BF=CF.（等腰三⾓形底边上的⾼线平分底边）四、利⽤等腰三⾓形的判定（等⾓对等边）证明线段相等如果两条所证线段在同⼀三⾓形中，证全等⼀时难以证明，可以考虑⽤此法。

初中几何证明线段相等的常用方法摘要：平面几何证明是中学生数学学习的一项重要任务，而证明线段相等是平面几何证明中经常会遇到的问题。

中学阶段的学生处于从具体形象思维向抽象逻辑思维转变的时期，学生对于几何证明问题往往不知如何下手。

本文在介绍证明线段相等的相关知识的基础上，归纳总结了证明线段相等的常用方法，并结合实例分别讨论了在何种情况下应该使用何种方法最为合适，有助于学生快速准确的解决证明线段相等的这类问题。

关键词：平面几何；线段相等；分类思想Abstract: The plane geometry is an important task for students,and that line segments equal plane geometry proof problem often encountered in middle school students. In the transformation from the specific image thinking period, the geometric proof of the problem students often do not know how to start. This paper introduces the related basic knowledge of that segment is equal the last, sums up the common methods that line segment equal, and examples are discussed in what circumstances should use what kind of method is most appropriate, help students to quickly and accurately solve this kind of problemthat is equal to the line.Key words: plane geometry; reasoning proof; line segment几何是一门逻辑性和系统性比较强的学科。

一、利用全等三角形证线段相等1.利用全等三角形证线段等1.已知：如图△ABC、△ADE都是等边三角形。

求证：CE=DB分析：本题属于证明两条线段相等的题型。

通常证明两条线段相等的解决方法是通过证明两条线段所在的三角形全等，从而利用全等三角形的对应边相等的性质得证。

或者通过证明两线段在等腰三角形的两腰上则两腰相等；或证明两条线段在等边三角形的任意两条边上则相等；或者证明这两条线段在是角平分线上一点到角的两边的距离，则根据角平分线上任意一点到角的两边的距离相等的性质得证。

证明两条线段相等最常用的方法是通过证明全等三角形，从而利用其对应边相等的性质得证。

证明全等三角形，首先要在图形中找到哪两个三角形全等。

寻找两全等三角形必须要熟记全等三角形有三种基本模式，即旋转型、平移型和翻转型。

（加粗部分）（加粗部分）如果图形中不能直接找到两个对应的全等三角形，就要根据题的已知条件和图形的特点构造全等三角形。

构造全等三角形是以三种基本全等三角形为模型来构造。

所以要熟记这三种基本全等三角形的模式。

CE与DB分别在两个三角形中，可以证明它们所在的三角形全等，从而利用全等三角形的性质：全等三角形的对应边相等，即CE=DB证明：∵△ABC为等边三角形（已知）∴AC=AB（等边三角形三条边相等）∴∠1=60°（等边三角形每个角等于60°）∵△ADE为等边三角形（已知）∴AD=AE（等边三角形三条边相等）∴∠2=60°（等边三角形每个角等于60°）∴∠1+∠3=∠2+∠3（等式性质）即∠CAE=∠BAD在△CAE和△BAD中∴△CAE≌△BAD（SAS）∴CE=DB（全等三角形对应边相等）附：此题的图形还有以下五种形式证明的方法与上例大体相同2.如图2，已知EG∥AF,请你从下面三个条件中，再选出两个作为已知条件，另一个作为结论，推出一个正确的命题。

（写出所有的情况）错误！未找到引用源。

在证明线段相等的教学中锻炼学生思维能力东莞市寮步镇香市中学 廖大渭【摘要】证明线段相等是初中平面几何学习中一个重要的组成部分。

如何运用证明线段相等的具体方法来锻炼学生的思维能力，是数学教师值得探究的问题。

反思证明线段相等的教学过程，教师想要让学生学会创造性地解决问题，就必须在平时的教学中将问题解决的思路探索过程充分“暴露”在学生面前，使学生从中学会解决问题的思路探索方法，从而让学生的思维能力得到更好的锻炼。

【关键词】线段相等；思维能力初中数学平面几何证明题的教学在数学课堂教学中，向来用时多，收效少。

如何打破这种尴尬的教学现状，更好地解决这个一直困扰着数学教师的老大难问题。

笔者从事初中数学教学多年，结合平时的教学经验, 在平面几何教学方面做了一些大胆的尝试,发现问题的症结在于：学生分析问题能力差,解题方法单一,思路无法拓展，在解答推理说明性问题上不够严谨。

由此可见，在教学中教给学生分析问题、解决问题的不同方法,拓展思路,是平面几何教学的必由之路。

现以证明“线段相等”为例,来谈谈如何训练学生多角度分析问题、解决问题的能力。

1 平面几何证明线段相等的重要性证明线段相等是平面几何学习中一个重要的组成部分。

初中阶段，学生所遇到的几何问题多为证明线段、角的相等、线段的和差倍分问题。

解决线段相等的问题，学生需要综合应用三角形全等、等腰三角形的有关性质、直角三角形的性质、线段中垂线性质及角平分线性质等知识。

因此，对于初学几何证明的学生而言，能否很好地掌握证明两条线段相等的方法，既是学习平面几何的基础要求，也有利于提升学生解决平面几何求证问题的能力，同时能有效地锻炼学生的思维能力。

2 证明线段相等的具体方法在平面几何教学的过程中，教师要教会学生看懂题目，了解已知条件和清楚求证结论，正确判断求证结论的关键方向。

要证明两条线段相等，教学中，教师首先要明确告诉学生，平面几何中两条线段分布的位置主要有三种：①在同一个三角形中；②分别在两个三角形中；③在同一直线上。

【高整理】【全等三角形】常考题型+解题思路整理！全等三角形的性质对应角相等，对应边相等，对应边上的中线相等，对应边上的高相等，对应角的角平分线相等，面积相等。

寻找对应边和对应角，常用到以下方法：（1）全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边。

（2）全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角。

（3）有公共边的，公共边常是对应边。

（4）有公共角的，公共角常是对应角。

（5）有对顶角的，对顶角常是对应角。

（6）两个全等的不等边三角形中一对最长边（或最大角）是对应边（或对应角），一对最短边（或最小角）是对应边（或对应角）。

【解题关键】要想正确地表示两个三角形全等，找出对应的元素是关键。

全等三角形的判定方法（1）边角边定理（SA S）：两边和它们的夹角对应相等的两个三角形全等。

（2）角边角定理（A S A）：两角和它们的夹边对应相等的两个三角形全等。

（3）边边边定理（SS S）：三边对应相等的两个三角形全等。

（4）角角边定理（A A S）：两个角和其中一个角的对边对应相等的两个三角形全等。

（5）斜边、直角边定理（H L）：斜边和一条直角边对应相等的两个直角三角形全等。

全等三形的应用运用三角形全等可以证明线段相等、角相等、两直线垂直等问题，在证明的过程中，注意有时会添加辅助线。

【拓展】通过判定两个三角形全等，可证明两条线段间的位置关系和大小关系。

而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础。

找全等三角形的方法（1）可以从结论出发，寻找要证明的相等的两条线段（或两个角）分别在哪两个可能全等的三角形中；（2）可以从已知条件出发，看已知条件可以确定哪两个三角形全等；（3）可从条件和结论综合考虑，看它们能确定哪两个三角形全等；（4）若上述方法均不可行，可考虑添加辅助线，构造全等三角形。

三角形中常见辅助线的作法①延长中线构造全等三角形；②利用翻折，构造全等三角形；③引平行线构造全等三角形；④作连线构造等腰三角形。

利用三角形全等是证明线段相等的重要方法之一，但有时不能直接应用，就需要根据条件通过作辅助线构造全等三角形，使题目中的条件集中.构造全等三角形的方法主要有翻折，旋转，截取，延长等.1.翻折法构造全等三角形【例1】如下图所示，已知△ABC中，AC=BC，∠ACB=90°，BD平分∠ABC，求证：AB=BC+CD.【分析】要证AB=BC+CD，由BD平分∠ABC，我们想到翻折△BCD，使得BC与AB重合，如上图，翻折了以后再证明AE＝DE就可以了.证明：BD平分∠ABC，将△BCD沿BD翻折180°，点C落在BA上的E点，则有BC=BE，在△BCD和△BED中，∴△BCD≌△BED（SAS）∴∠DEＢ=∠ACB=90°，CD=DE，（全等三角形对应边，对应角相等）∴∠DEＡ=90°，∵△ABC中，∠ACB=90°，AC=BC，∴∠A=45°，∴∠EDA=∠A=45°，∴DE=EA，∴AB=BE+EA=BC+CD，即AB=BC+CD.2.旋转法构造全等三角形【例2】如下图所示，已知点E、F分别在正方形ABCD的边BC、CD上，并且AF平分∠EAD.求证：BE+DF=AE.【分析】由于要证结论是BE+DF=AE，我们自然想到把BE、DF放在同一条直线上.由于四边形是正方形，所以旋转△ADF可实现我们的设想.证明：将△ADF绕点A顺时针旋转90°至△ABG，则△ADF≌△ABG，∴∠G=∠AFD，∠GAB=∠FAD，DF=BG，∴BE+DF=BE+BG=GE.又∵AF平分∠EAD，∴∠FAD=∠FAE=∠GAB.∴∠GAB+∠BAE=∠FAE+∠BAE，即∠GAE=∠BAF.又∵AB∥CD，∴∠BAF=∠AFD＝∠GAE=∠G.∴在△EAG中，AE=GE，即BE+DF=AE.【点评】利用旋转巧妙地将两条分离的线段“连接”在一起从而得证，利用旋转构造三角形全等是经常用到的方法.3.延长法构造全等三角形【例3】如下图所示，△ABC中，∠C=2∠B，∠1=∠2，求证：AB=AC+CD.“【分析】本题要证的结论也是两条线段长度之和等于一条线段的长度，与前面例2的思路相同，我们想到使不共线两条线段AC、CD组合成一条线段，延长AC是必然的（如上图）.由于有条件∠1＝∠2，然后再证明△ABD≌△AED就轻而易举.证明：延长AC至E，使AE=AB，连接DE，在△ABD和△AED中，∴△ABD≌△AED.∴∠B=∠E.∵∠ACD=∠E+∠CDE，∠ACD=2∠B，∴∠ACD=2∠E.∴∠E=∠CDE.∴CD=CE. ∴AB=AC+CD.【小结】本例中用到的方法叫“补短法”，是将较短的线段AC补长，构造全等三角形，从而达到求解目的.也可采用“截长法”，即在AB上截取AF=AC，连接DF，构造三角形全等，这两种方法通常适合于证明一条线段等于两条线段的和.4.截取法构造全等三角形【例4】如下图所示，在△ABC中，AD为BC边上的高，∠B=2∠C.求证：CD=AB+BD.【分析】在DC上截取DE=DB后显然△ADE≌△ADB，然后再证明AE＝EC就可以了.证明：在DC上截取DE=DB，连接AE，则△ADE≌△ADB.∴AE=AB，∠AEB=∠B，∵∠AEB=∠C+∠CAE，∠B=2∠C，ED=BD，∴∠AEB=2∠C.∴∠C=∠CAE，故CE=AE=AB.∴CD=CE+ED=AE+ED=AB+BD.5.作平行线构造全等三角形【例5】如下图所示，在△DEF中，DE=DF，过EF上一点A作直线分别与DE、DF的延长线交于点B、C，且BE=CF.求证：AB=AC.【分析】要证AB=AC，我们很自然想到过点B做CD的平行线，然后再证△AGB≌△AFC.条件DE=DF 和BE=CF结合所作的平行线可得出BG＝CF，有了边的相等关系证△AGB≌△AFC就容易多了.证明：过B作BG∥CD交EF于G.∵BG∥CD，∴∠EGB=∠EFD.∵DE=DF，∴∠E=∠EFD，∴∠E=∠EGB，∴BE=BG.∵BE=CF，∴BG=CF.∵BG∥CD.∴∠GBA=∠ACF，∠AGB=∠AFC.在△AGB和△AFC中，∴△AGB≌△AFC.∴AB=AC.。

祥子数理化用全等三角形证明线段相等的解题思路例题: E 是/ AOB 的平分线上一点，EC丄OA, ED± 0B,垂足为C, D。

求证：（1）OC=OD, （2）DF=CR思路:要证明OC=OD就是要证明三角形全等（两边相等用全等三角形）将OC放到三角形中（将一条边放进三角形中）列出所有三角形△ OCD △ OCF △ OCE在剩下的里面选择三角形显然OA丄EC,和厶OCE有关所以用△ OCE（看哪个三角形能用上已知条件就选那个三角形）△ OCE找出要证明的和这三角形全等的对应三角形一般已知条件里很容易找出两个，/ COF=/ DOF（OE是/ AOB的平分线）△OCE^A ODE （AAS）条件齐全，三角形全等，写上对应判定定理OC=OD（两线段相等）参照这条思路练习第二问（第一问在第二问里可以当做已知，若第一问是证全等，第二问必然会用到全等例得到的新条件--这就是全等的真正用处。

）对于稍微难点的题目，我们会发现在寻找全等三角形的时候找不出来，这时候需要辅助线构造全等三角形。

构造的原则还是尽量利用已知。

0C、OD处于同一△种，不要（该否定的否定掉）△ ODE寻找已知条件（需要三个条件,/ ECO=Z EDO（EC丄OA, ED丄OD）用全等定理确定第三个是什么,OE=OE（角平分线的公共边）再寻找）1、如下左1图，已知AB// DE, BC// EF,练习D, C在AF上，且AD= CF,求证: BC=EF2、如上左2图，点E在厶ABC的外部，点D在BC边上，DE交AC于点F,若/ 1 = / 2= / 3, AC=AE求证: AB=AD。

3、如上左3图，△ ABC为等边三角形，点M、N,分别在BC AC上，且BM=CN, AM与BN交于Q点，求/ AQN的度数。

祥子数理化在 △ ABC 中，点 D 是BC 的中点， DE 丄AB , DF 丄AC, E 、F 为垂足，DE = DF ,求证:26、如上左3图，A 、F 、C 、D 四点在一直线上， AF=CD AB//DE ,且AB=DE,27、如上左4图，AB=AC, BD_AC, CE_AB ,垂足分别为 D 、E, BD 、CE 相交于点F ,求证：BE=CD 28、如上左 5 图，D 、E 在 BC 上,且 BD=CE / ADE=Z AEDb 求证：AB=ACo 4、如上左4图,D 是AB 上一点，DF 交AC 于点E , AE=CE FC// AB,求证：DE=EF 5、如下左1图, E , B ，F ，C 四点在同一直线上，/ 7、如上左 图, AE , FC 都垂直于 BD,垂足为 E 、F , AD=BC BE=DF O 求证：0A=0G 图, AB=CD D 、B 至U AC 的距离 DE=BF 求证：AB /CD.11、如上左 BE=CF 12、如上左 占八B , E , C, F 在同一直线上, AB / DE ,且 AB=DE, BE=CF 求证：AC=DF O 13、如下左1AD 丄BC 于 D , AD=BD , AC=BE 。

证明线段相等的方法(共10页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--平面几何中线段相等的证明几种方法平面几何中线段相等的证明看似简单，但方法不当也会带来麻烦，特别是在有限的两个小时考试中。

恰当选用正确的方法，可取得事半功倍的效果。

一、利用全等三角形的性质证明线段相等这种方法很普遍，如果所证两条线段分别在不同的三角形中，它们所在三角形看似全等，或者，通过简单处理，它们所在三角形看似全等，可考虑这种方法。

［例1］如图，C是线段AB上一点，△ACD和△BCE是等边三角形。

求证：AE=BD。

证明∵△ACB和△BCE都是等边三角形∴∠ACD=60°，∠BCE=60°，∠DCE=60°∴∠ACE=∠ACD＋∠DCE=120°∠BCD=∠BCE＋∠DCE=120°∴AC=CD，CE=CB∴△ACE≌△DCB（SAS）∴AE=DB［例2］如图，已知△ABC中，AB=AC，点E在AB上，点F在AC的延长线上，且BE=CF，EF与BC交于D，求证：ED=DF。

证明：过点E作EG//AF交BC于点G∴∠EGB=∠ACB，∠EGD=∠FCD∵AB=AC∴∠B=∠ACB，∠B=∠FGB，BE=GE∵BE=CF，∴GE=CF在△EGD和△FCD中，∠EGD=∠FCD，∠EDG=∠FDC，GE=CF∴△EGD≌△FCD（AAS）∴ED=FD二、利用等腰三角形的判定（等角对等边）证明线段相等如果两条所证线段在同一三角形中，证全等一时难以证明，可以考虑用此法。

［例1］如图，已知在△ABC中，AD是BC边上的中线，E是AD上的一点，且BE=AC，延长BE交AC于F。

求证：AF=EF。

证明：延长AD到G，使DG=AD，连结BG。

∵AD=GD，∠ADC=∠GDB，CD=BD∴△ADC≌△GDB∴AC=GB，∠FAE=∠BGE∵BE=AC∴BE=BG，∠BGE=∠BEG∴∠FAE=∠BGE=∠BEG=∠AEF∴AE=EF［例2］如图，已知△ABC中，AB=AC，DF⊥BC于F，DF与AC交于E，与BA的延长线交于D，求证：AD=AE。

证明三角形全等找边相等的方法法一：利用等角对等边（注意：必须在同一个三角形中才能考虑）1.如图，已知∠1=∠2，∠3=∠4，求证：AB=CD法二：利用公共边相等（若果要证明的两个全等三角形有两个相同的对应点，那么可么马上得出它们具有公共边）2.AB=AC ，DB=DC ，F 是AD 的延长线上的一点。

求证：BF=CF3.已知：如图所示，AB ＝AD ，BC ＝DC ，E 、F 分别是DC 、BC 的中点，求证： AE ＝AF 。

4.如图，在四边形ABCD 中，E 是AC 上的一点，∠1=∠2，∠3=∠4，求证: ∠5=∠6．法三：利用等量代换（即AB+公共边=DE+公共边，那么AB=DE)5.如图：AB=CD ，AE=DF ，CE=FB 。

求证：AF=DE 。

F D C B A FEBA D BCA FE 654321E DC BA .3421DC B A6.已知：点A 、F 、E 、C 在同一条直线上， AF ＝CE ，BE∥DF，BE ＝DF ．求证：△ABE≌△CDF．7.已知AB ∥DE ，BC ∥EF ，D ，C 在AF 上，且AD ＝CF ，求证：△ABC ≌△DEF ．法四：利用三角形中线定理，或者等边三角形（三角形一条中线将三角形一边平分为相等的两条想段）8.如图：AB=AC ，ME ⊥AB ，MF ⊥AC ，垂足分别为E 、F ，ME=MF 。

求证：MB=MC9.如图所示，已知AE ⊥AB ，AF ⊥AC ，AE=AB ，AF=AC 。

求证：（1）EC=BF ；（2）EC ⊥BF法五：利用三角形角平分线定理（三角形角平分线上的点到角两边的距离相等注意1、必须是角平分线上的点 2、必须是点到直线的距离，垂直距离）10.如图，在ΔABC 中，D 是边BC 上一点，AD 平分∠BAC ，DE 垂直AB,DC 垂直AC,连结DE ，已知DE=2cm ，BD=3cm ，求线段BC 的长。