水力学第六章 第三节

1． 水力最优断面
均匀流基本公式
3
/23
/52/12/13/21χn A i i AR n Ri AC Av Q ==== i 、n 已定时，过水能力Q 取决于过水断面的大小和形状。

过水面积A 一定时，使流量Q 最大，即湿周χ最小的断面定义为水力最优断面。

推导边坡系数m 一定时的梯形水力最优断面：
几何关系
h mh b )(+=A
212m h b ++=χ 从中解得mh h A -=b ，代入湿周式
212m h mh h
A ++-=
χ 对上式求)(h f =χ的极小值，得水力最优梯形断面宽深比
)21(2m m h
b -+==β 说明：
（1）当m=0时得矩形水力最优断面宽深比2=β。

（2）若代入水力半径，得R=h/2。

即在任何边坡m 下，水力最优梯形断面的水力半径为水深的一半。

（3）“水力最优”并非“技术经济最优”，对小型渠道接近“技术经济最优”。

2． 允许流速
（1） 不冲最大允许流速[v]max ；
（2） 不淤最小允许流速[v]min ；
（3） 设计流速或实际流速应
[v]max >v>[v]min。

第六章 流动阻力与能量损失本章首先讨论实际流体在运动过程中的能量损失的分类和计算公式，公式中损失系数的确定将是这一章主要的内容。

由于粘性的影响，实际流体的流动会呈现出两种不同的型态 — 层流和紊流，它们的流场结构和动力特性区别很大，必须加以判别，并分别研究。

由均匀流流动的特点，导出了均匀流的沿程损失与切应力之间的关系，圆管层流类似于均匀流，因此得到了圆管层流的沿程损失的计算方法。

由于在紊流流场中存在随机的脉动量，须对瞬时量取统计平均，分别讨论平均流动和脉动量。

紊流中切应力包含了粘性切应力和附加切应力（雷诺应力），采用混合长度理论建立起附加切应力与时均流速之间的关系。

本章还紊流运动中的局部水头损失的计算方法。

§6—1 流动阻力和能量损失的两种形式● 实际流体在渐变流段中流动，由流管壁面上粘性切应力形成的阻力称为沿程阻力或摩擦阻力。

在均匀流段上这种阻力是沿程不变的。

为克服沿程阻力形成的能量损失，称为沿程损失，沿程损失随着流程的增加而增加。

在均匀流段上每单位流程上的沿程损失是常数，沿程损失与流程长度呈正比例关系。

单位重量流体的沿程损失用 hf 表示，称为沿程水头损失。

计算公式为：gv d l h f 22λ= ● 在流管边壁沿程急剧变化，流速分布急剧调整的局部区段上，集中产生的流动阻力称为局部阻力。

由局部阻力引起的水头损失，称为局部水头损失，以 hj 表示，如管道进口、异径管、弯管、三通、阀门等各种管件处的水头损失，都是局部水头损失。

计算公式为：gv h j 22ζ= ● 若断面1至断面2的一段管路由若干段渐变流段组成，其间又有若干处局部损失，则这段管路的能量损失为所有沿程损失和局部损失的总和。

§6—2 流动的两种型态● 实际流体的流动会呈现出两种不同的型态：层流和紊流，它们的区别在于：流动过程中流体层之间是否发生混掺现象。

在紊流流动中存在随机的脉动量，而在层流流动中则没有。

● 1883年，雷诺试验表明：圆管中恒定流动的流态转化取决于雷诺数νvdR e =，d 是圆管直径，v 是断面平均流速，ν是流体的运动粘性系数。

1． 流动特点由于水流重力在流动方向上的分力与阻力不平衡，所以断面流速和水深一般沿程变化，水面线为曲线，水力坡度J 、水面坡度J p 和渠道底坡i 一般互不相等。

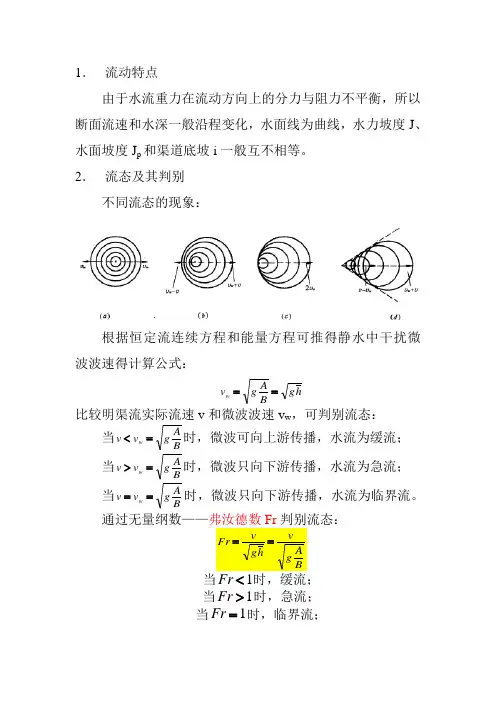
2． 流态及其判别不同流态的现象：根据恒定流连续方程和能量方程可推得静水中干扰微波波速得计算公式：h g BAgv w == 比较明渠流实际流速v 和微波波速v w ，可判别流态：当BA g v v w =<时，微波可向上游传播，水流为缓流；当BA g v v w =>时，微波只向下游传播，水流为急流；当BA g v v w ==时，微波只向下游传播，水流为临界流。

通过无量纲数——弗汝德数Fr判别流态：当时，缓流； 当1>Fr 时，急流； 当1=Fr 时，临界流；从量纲分析知，弗汝德数Fr 的力学意义是水流惯性力与重力的比值，重力作用占优势时为缓流，水深流缓；惯性作用占优势时，水浅流急。

3． 断面单位能与明渠流态 断面单位能（断面比能）E s 定义：22222gA Q h gv h E s αα+=+=断面单位能E s 沿程可能增大、减小或不变，这一点与断面单位重量水体的总机械能E （g v h z E 220α++=）不同。

比能曲线——当流量Q 和渠道断面形状大小一定时，断面单位能仅仅是水深h 的函数，)(h f E s =曲线即比能曲线。

为进一步了解比能曲线的变化规律，将E s 对h 取导：2211Fr BAg v dh dE s -=-=α 由此可见断面比能随水深的变化与断面流态的关系。

临界水深h c ——流量、渠道断面形状和大小一定时，相比较实际水深和临界水深判断断面流态：h>h c ；缓流 h<h c ；急流 h=h c ；临界流4．底坡与明渠均匀流流态缓坡上的均匀流为缓流；陡坡上的均匀流为急流。

显然，临界底坡既要满足临界流方程又要满足均匀流基本方程，据此计算临界底坡值。

1． 明渠均匀流特性和形成条件由受力平衡推得f F G =θsin说明均匀流中重力分力与摩阻力平衡。

由能量方程推得21-=f h z ∆说明势能的减少等于克服摩阻力产生的能耗。

均匀流产生的条件：恒定、流量不变、糙率不变的长直正坡棱柱形渠。

2． 基本公式（谢才公式、曼宁公式）K ——流量模数，即底坡为1时通过的流量。

Ri C v =611R n C =i K Ri AC Av Q ===21321i R nv =3． 计算类型正常水深h 0：即均匀流水深，以区别于非均匀流水深。

1) 校核过水能力计算已知渠道边界条件（b 、m 、n 、i ）和实际水深(h)，求流量Q 。

Ri AC Q =2) 渠道设计计算——常用试算和图算✧ 底坡设计：已知渠道断面条件（b 、h 、m 、n ）以及流量Q ，求底坡i 。

R AC K =22KQ i = ✧ 底宽设计：已知流量Q 、底坡i 、边坡系数m 及糙率n ，水深h 另由通航、防洪或施工条件限定作为已知值，求底宽b 。

设不同b 值，由R AC K =作)(b f K =曲线，根据已知条件，由iQ K =实际值查对应的底宽b 。

✧ 渠深设计：水深h 加上一定超高就是渠深。

此类设计相当于已知流量Q 、底坡i 、边坡系数m 及糙率n ，底宽b 另由地形或施工条件限定，求水深h 。

与上相似，作)(h f K =曲线，查已知的实际K 值对应的水深h 。

✧ 宽深比hb =β已定，设计相应的b 、h ：流量Q 、底坡i 、边坡系数m 及糙率n 已知，宽深比β由水力最优或综合技术经济条件给出，此时b 、h 中只有一个独立未知量，可用前述方法计算。

✧ 限定最大允许流速[v]max ，求相应b 、h ：流量Q 、底坡i 、边坡系数m 及糙率n 为已知，此时渠道过水断面面积和水力半径为定值。

m ax][v Q A = 2/32/1m ax )][(i v n R = 由几何关系h mh b )(+=A212)(m h b h mh b A +++==χR联立可解b 、h 。

第六章明渠恒定均匀流人工渠道、天然河道以及未充满水流的管道等统称为明渠。

明渠流(Open Channel Flow)是一种具有自由表面的流动，自由表面上各点受当地大气压的作用，其相对压强为零，所以又称为无压流动。

与有压管流不同，重力是明渠流的主要动力，而压力是有压管流的主要动力。

明渠水流根据其水力要素是否随时间变化分为恒定流和非恒定流动。

明渠恒定流动又根据流线是否为平行直线分为均匀流和非均匀流。

明渠流动与有压管流的一个很大区别是：明渠流的自由表面会随着不同的水流条件和渠身条件而变动，形成各种流动状态和水面形态，在实际问题中，很难形成明渠均匀流。

但是，在实际应用中，如在铁路、公路、给排水和水利工程的沟渠中，其排水或输水能力的计算，常按明渠均匀流处理。

此外，明渠均匀流理论对于进一步研究明渠非均匀流也具有重要意义。

§6-1 概述1．明渠的分类由于过水断面形状、尺寸与底坡的变化对明渠水流运动有重要影响，因此在水力学中把明渠分为以下类型。

(1)棱柱形渠道和非棱柱形渠道凡是断面形状及尺寸沿程不变的长直渠道，称为棱柱形渠道，否则为非棱柱形渠道。

前者的过水断面面积A仅随水深h变化，即A=f(h)；后者的过水断面面积不仅随水深变化，而且还随着各断面的沿程位置而变化，即A=f(h,s)，s为过水断面距其起始断面的距离。

(2)顺坡(正坡)、平坡和逆坡(负坡)渠道明渠渠底线(即渠底与纵剖面的交线)上单位长度的渠底高程差，称为明渠的底坡(Bottom slope)，用i表示，如图6-1a，1-1和2-2两断面间，渠底线长度为Δs，该两断面间渠底高程差为(a1-a2)=Δa，渠底线与水平线的夹角为θ，则底坡i为。

图6-1θsin 21=∆∆=∆-=sas a a i (6-1-1) 在水力学中，规定渠底高程顺水流下降的底坡为正，因此，以导数形式表示时应为dsdai -= (6-1-2) 当渠底坡较小时，例如i ＜0.1或θ＜6°时，因两断面间渠底线长度Δs ，与两断面间的水平距离Δl ，近似相等，Δs ≈Δl ，则由图6-1a 可知θtan =∆∆≈∆∆=la s a ii=sin θ≈tg θ (6-1-3) 所以，在上述情况下，两断面间的距离Δs 可用水平距离Δl 代替，并且，过水断面可以看作铅垂平面，水深h 也可沿铅垂线方向量取。