算法_流程图

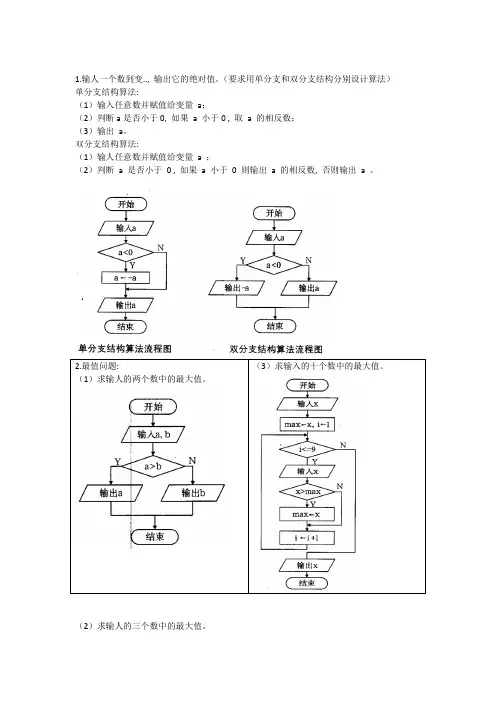
1.输人一个数到变.., 输出它的绝对值。

（要求用单分支和双分支结构分别设计算法）单分支结构算法:
（1）输入任意数并赋值给变量a；
（2）判断a是否小于0, 如果a 小于0 , 取a 的相反数；
（3）输出a。

双分支结构算法:
（1）输人任意数并赋值给变量 a ；
（2）判断a 是否小于0 , 如果a 小于0 则输出a 的相反数, 否则输出a 。

（3）求输入的十个数中的最大值。

2.最值问题:
（1）求输人的两个数中的最大值。

（2）求输人的三个数中的最大值。

3.循环求和（不同的控制循环方法）
1.求输.
2.个数的和。

(知道循环次数, 可以采用循环变量i 来控制循环次数)
计数法2.求输入的若干个学生成绩
的和, 输.-1表示结束。

（不能确定次数, 可以用输
入的数据的值来进行控制）
标志法
3.对输入的数据求和, 当所求
的和超.10.则停止输入并输出
求和结果（设此题中输人的数
皆为正数）。

（没有指出输人数据的具体个
数, 且不能依据对输入数据的
值来控制循环, 控制循环的关
键就在于对循环体中变量s
的判断）
（没有指出输人数据的具体个
数，且不能依据对输入数据的
值来控制循环，控制循环的关
键就在于对循环体中变量s
的判断）
输出如下图形:
**********
**********
**********
**********
**********
如下算法能输出哪种图形？（A）。

1.2 流程图1．流程图的概念流程图是由一些图框和流程线组成的，其中图框表示各种操作的类型，图框中的文字和符号表示操作的内容，流程线表示操作的先后次序．2．流程图的图形符号及其应用依次进行多个处理的结构称为顺序结构．顺序结构的形式如图所示，其中A和B两个框是依次执行的．顺序结构是任何一个算法都离不开的最简单、最基本的结构．4．选择结构先根据条件作出判断，再决定执行哪一种操作的结构称为选择结构，也称为分支结构．如图所示，虚线框内是一个选择结构，它包含一个判断框，当条件p成立(或称为“真”)时执行A，否则执行B．思考1：一个选择结构只能有两个执行选项吗？[提示] 一个选择结构只能有两个执行选项．思考2：若有多于两种选项的情况怎样处理？[提示] 可以用多个选择结构嵌套组合来处理．5．循环结构(1)定义：在算法中，需要重复执行同一操作的结构称为循环结构．(2)分类：循环结构分为当型循环和直到型循环．①当型循环：先判断所给条件p是否成立，若p成立，则执行A，再判断条件p是否成立；若p仍成立，则又执行A，如此反复，直到某一次条件p不成立时为止，这样的循环结构称为当型循环．其示意图如图1所示：图1 图2②直到型循环：先执行一次循环体，再判断所给条件是否成立，若不成立，则继续执行循环体，如此反复，直到条件成立时为止，这样的循环结构称为直到型循环．其示意图如图2所示．1．下列对流程图的描述，正确的是( )A．流程图中的循环可以是无止境的循环B．选择结构的流程图有一个入口和两个出口C．选择结构中的两条路径可以同时执行D．循环结构中存在选择结构D[根据选择结构与循环结构的定义可知，A、B、C不正确．D正确．特别提醒：本题易错选B，判断框是一个入口和两个出口，但是选择结构中的两条路径，只能执行其一，不能同时执行，故B不正确．]2．如图所示的流程图的运行结果是________．第2题图第3题图5 2[根据流程图的意义可知，当a＝2，b＝4时，S＝24＋42＝52.]3．阅读如图所示的流程图，运行相应的算法，输出的结果是________．11 [第一次运行，a＝3；第二次运行a＝11,11<10不成立，退出．] 4．如图是求实数x的绝对值的算法流程图，则判断框①中可填________．x >0或x ≥0 [根据绝对值定义解答，|x |＝⎩⎪⎨⎪⎧x ， x ≥0，－x ， x <0.]①流程图中的图形符号可以由个人来确定； ②也可以用来执行计算语句； ③输入框只能紧接在起始框之后；④用流程图表示算法，其优点是将算法的基本逻辑结构展现得非常直接．④ [①中框图中的图形符号有严格标准，不能由个人确定；②中只能执行判断语句，不能执行计算语句；③中输入框不一定只能紧接在起始框之后．故①②③不正确，④正确．]1．理解流程图中各框图的功能是解此类题的关键，用流程图表示算法更直观、清晰、易懂．2．起止框用“”表示，是任何流程不可少的，表明程序的开始和结束．3．输入、输出框图用“”表示，可用在算法中任何需要输入、输出的位置，需要输入的字母、符号、数据都填在框内．4．处理框图用“”表示，算法中处理数据需要的算式、公式等可以分别写在不同的用以处理数据的处理框内，另外，对变量进行赋值时，也用到处理框．5．判断框是唯一具有超过一个退出点的图框符号．1．流程图中，符号“”可用于________．(填序号) ①输入；②输出；③赋值；④判断．③ [流程图中矩形方框的功能是赋值和计算．]2．对于流程图的图框符号的理解，下列说法中正确的是________．(填序号) ①输入框、输出框有严格的位置限定； ②任何一个流程图都必须有起止框；③对于一个流程图而言，判断框中的条件是唯一确定的； ④判断框是唯一具有超过一个退出点的图框符号．②④ [任何一个流程图都必须有开始和结束，因此必须有起止框；输入框和输出框可以用在算法中的任意需要输入和输出的位置；判断框中的条件不是唯一的．]思路点拨：对于套用公式型的问题，要注意所给公式中变量的个数及输入、输出部分的设计．先写出算法，再画出对应的流程图．本题可用顺序结构解决．[解] 算法如下： S1 输入a ，b ，h ； S2 S ←12(a ＋b )·h ；S3 输出S . 流程图如图．应用顺序结构表示算法的步骤(1)仔细审题，理清题意，找到解决问题的方法； (2)梳理解题步骤；(3)用数学语言描述算法，明确输入量，计算过程，输出量； (4)用流程图表示算法过程． 提醒：规范流程图的画法 (1)使用标准的框图符号；(2)框图一般按从上到下、从左到右的方向画，流程线要规范； (3)除判断框外，其他框图符号只有一个进入点和一个退出点； (4)在图形符号内描述的语言要非常简练、清楚．3．已知x ＝4，y ＝2，画出计算w ＝3x ＋4y 的值的流程图．[解] 本题可用顺序结构解决，利用流程图的定义及符号之间的联系即可画出流程图． 流程图如图：4．已知一个圆柱的底面半径为R ，高为h ，求圆柱的体积．设计一个解决该问题的算法，并画出相应的流程图．[解] 算法如下： 第一步，输入R ，h . 第二步，计算V ←πR 2h .第三步，输出V . 流程图如图所示：【例3】 设计一个算法，输入x 的值，计算并输出y 的值，且y ＝⎩⎪⎨⎪⎧－x ＋1，x <0，1，x ＝0，x ＋1，x >0，试画出该算法的流程图．[解] 该函数是分段函数，当给出一个自变量x 的值时，必须先判断x 的范围，然后确定利用哪一段的解析式求对应的函数值．因为解析式分了三段，所以判断框需要两个，即进行两次判断．算法步骤如下： 第一步 输入x ；第二步 若x <0，则y ←－x ＋1；否则执行第三步； 第三步 若x ＝0，则y ←1；否则，y ←x ＋1； 第四步 输出y . 流程图如图所示：1．选择结构是在需要进行分类讨论时所应用的逻辑结构，但是在某些问题中，需要经过几次分类才能够将问题讨论完全，这样就需要选择结构的嵌套．所谓嵌套，是指选择结构内，又套有小的分支，对条件进行两次或更多次的判断．常用于一些分段函数的求值问题．选择结构中算法的流程要根据条件流向不同的方向，此结构中的主要部分是判断框．选择结构的嵌套中可以含有多个判断框．一般地，如果是分三段的函数，需要引入两个判断框；如果是分四段的函数，需要引入三个判断框…以此类推．其流程图如图所示．2．在选择结构中，反映的是“先判断，后执行”的思想．选择结构的两个分支在写算法时实质上是一个步骤，不能写成两个步骤．如果一个分支中还有两个子分支，这时有两种处理方法：(1)直接嵌套在这一步中； (2)用“转到”某一步．提醒：根据分段函数，设计算法流程图时，必须引入判断框，运用选择结构，当题目出现多次判断时，一定要先分清判断的先后顺序，再逐层设计流程图．5．如图所示的流程图，若输入的x的值为0，则输出的结果为________．1 [这是一个嵌套的选择结构，当输入x＝0时，执行的是y←1，即y＝1.故输出的结果为1.]6．设计一个求解一元二次方程ax2＋bx＋c＝0的算法，并画出流程图．[解] 依据求解一元二次方程的方法步骤设计算法，算法步骤如下：S1 输入3个系数a，b，c；S2 计算Δ←b2－4ac；S3 判断Δ≥0是否成立．若是，则计算p←－b2a，q←Δ2a；否则，输出“方程没有实数根”，结束算法；S4 判断Δ＝0是否成立．若是，则输出x1＝x2＝p；否则，计算x1←p＋q，x2←p－q，并输出x1，x2.流程图如图所示：[1．循环结构有哪两种形式？[提示] 循环结构有当型循环结构和直到型循环结构两种常见形式．2．当型循环结构和直到型循环结构有何区别？[提示] 当型循环结构与直到型循环结构的区别为当型循环结构首先进行条件的判断，然后再执行循环体，而直到型循环结构是先执行一次循环体，然后再进行条件的判断．3．当型循环结构和直到型循环结构是否可以相互转化？[提示] 这两种循环结构可以相互转化，需要注意的是，两者相互转化时，所满足的条件不同．【例4】指出图中流程图的功能．如果用的是循环结构，则写出用的是哪一种循环结构，并画出用另一种循环结构表示的流程图．思路点拨：依据当型循环和直到型循环的结构特征判断、改写．图中是先执行再判断，故采用的直到型循环结构，可用当型循环结构改写．[解] 题图所示的是计算12＋22＋32＋…＋992的值的一个算法的流程图，采用的是直到型循环结构，可用当型循环结构表示，如图所示：1．读如图所示的流程图，完成下面各题：(1)循环体执行的次数是________．(2)输出的结果为________．(1)49 (2)2 450 [(1)∵i←i＋2，∴当2n＋2≥100时循环结束，此时n≥49.(2)S＝0＋2＋4＋6＋…＋98＝2 450.]2．指出图中流程图的功能，如果是循环结构，指出是哪一种循环结构，并画出用另一种循环结构表示的流程图．[解] 依据当型循环和直到型循环结构的特征判断改写．此流程图的功能是计算1×3×5×7×…×97的值．是当型循环结构，可用直到型循环结构表示，如图所示：1．循环结构主要用于解决有规律的重复计算问题，如累加求和、累乘求积等．如果算法问题里涉及的运算进行了多次重复的操作，且先后参与运算的各数之间有相同的变化规律，就可以引入循环变量参与运算，构成循环结构．2．要用好循环结构，需要注意三个环节：(1)确定循环变量和初始值，初始值的确定要结合具体问题，这是循环的基础；(2)确定循环体，循环体是算法中反复执行的部分，是循环进行的主体；(3)确定终止循环的条件，因为一个算法必须在有限步骤内完成．3．转化与化归思想在循环结构中有重要应用．循环结构的两种形式，当型循环结构与直到型循环结构可以相互转化，需要注意的是，相互转化时所满足的判断条件不同．1．本节课的重难点是理解流程图的作用，能用顺序结构，选择结构，循环结构书写算法．2．含条件结构问题的求解策略(1)理清所要实现的算法的结构特点和流程规则，分析功能；(2)结合框图判断所要填入的内容或计算所要输入或输出的值；(3)明确要判断的条件是什么，判断后的条件对应着什么样的结果．3．利用循环结构表示算法的步骤利用循环结构表示算法，第一要先确定是利用当型循环结构，还是直到型循环结构；第二要选择准确的表示累计的变量；第三要注意在哪一步开始循环，满足什么条件不再执行循环体.1．任何一种算法都离不开的基本结构为( )A．顺序结构B．选择结构C．循环结构D．顺序结构和选择结构A[顺序结构是最简单、最基本的结构，是任何一个算法都离不开的基本结构．]2．下列关于流程线的说法，不正确的是( )A．流程线表示算法步骤执行的顺序，用来连接图框B．流程线只要是上下方向就表示自上向下执行，可以不要箭头C．流程线无论什么方向，总要按箭头的指向执行D．流程线是带有箭头的线，它可以画成折线B[依据流程线的画法及其功能判断，A、C、D正确，B不正确．]3．根据所给流程图，当输入x＝10时，输出的y的值为________．14．1 [由流程图可知，该流程图的作用是计算分段函数y ＝⎩⎪⎨⎪⎧1.2x ， x ≤7，.9x －4.9， x ＞7的函数值．当输入x ＝10时，输出的y 值为1.9×10－4.9＝14.1.]4．设计求1＋3＋5＋7＋…＋99的算法，并画出相应的流程图．[解] 这是求50个数和的一道题，多次求和，可以利用循环结构完成．用变量S 存放求和的结果，变量I 作为计数变量，每循环一次，I 的值增加2.算法如下： S1 S ←0； S2 I ←1；S3 如果I ≤99，那么转S4，否则转S6； S4 S ←S ＋I ； S5 I ←I ＋2，转S3； S6 输出S . 流程图如图所示：。

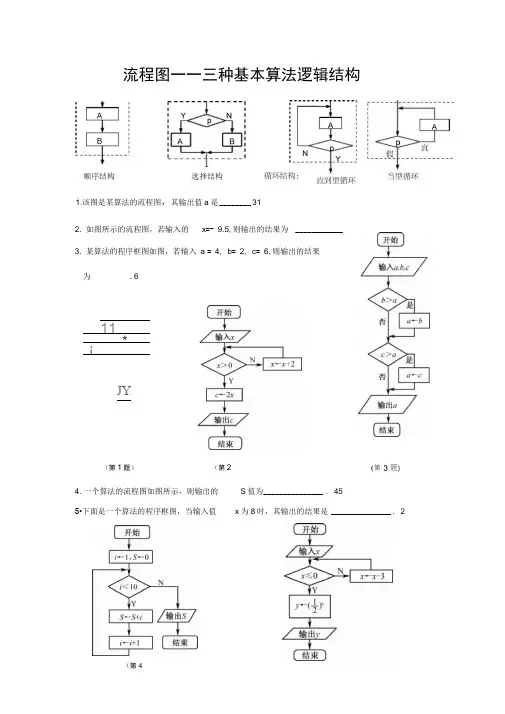
1.该图是某算法的流程图，其输出值a是________ 312. 如图所示的流程图，若输入的x=- 9.5,则输出的结果为 ____________3. 某算法的程序框图如图，若输入a = 4, b= 2, c= 6,则输出的结果为.611*iJY（第1题）4. 一个算法的流程图如图所示，则输出的5•下面是一个算法的程序框图，当输入值S值为_______________ . 45x为8时，其输出的结果是_______________ . 2流程图一一三种基本算法逻辑结构顺序结构选择结构（第2题）（第4题）6. 运行如图所示的程序框图，则输出的结果 S = ___________ . 617. 如图所示的算法流程框图中， 若输入a = 4,b = 48,则最后输出的a 的值是 ________________ .96 8. 如图，程序执行后输出的结果为 _________ 6410.阅读下面的流程图，若输入______________a = 10, b = 6,则输出的结果是 211. _____________________________________________ 右图是一个算法的流程图，则输出 S 的值是 _________________________________________________ 7500开始/输出P/ 卩/9•按如图所示的流程图运算 ,则输出的S 二 _________20 （第6题）（第7题）I —12. ___________________________________________ 右图是一个算法的流•程图，最后输出的k= _________________ . 1113•阅读右边的流程图,则输出S= ________ . 3015、图中是一个算法流程图，则输出的n= ______ 1116. 右图是一个算法的流程图，最后输出的x= ________ .-1017.执行右边的程序框图，若p =15,则输出的n二fT-li S^-0（第16题）5/输入/n=l,S=0沪針严/5丽7ZE~~TM=n+1 ［结束］（第15题）（第17题））如图所示，其输出结果是127开始（第14 题）结束14•程序框图（即算法流程图（第12题）（第13题）c-2cr+'l/输出口/18. 根据如图所示的算法流程图，可知输出的结果i为______________ .719. 右图是一个算法的流程图，最后输出的n = ____________ .10020. 右图是一个算法的流程图，则输出a的值是_____________. log2321. 已知某算法的流程图如图所示，若将输出的数组（x, y）依次记为（X1, y1）, （X2, y2），…, （X n, y n）,…，则程序运行结束时输出的最后一个数组为22. _________________________________ 如图,该程序运行后输出的结果为______________________________ 1623•执行右边的程序框图，若p= 9，则输出的s= _（第19题）（第18题）（开始〕1 rm2托（第20题）(第22 题)—• (27,—6)2.5苏州市第六中学2014数学必修三（算法）。

常用算法流程图及程序
1、枚举法：1??47（百位和千位被涂抹掉了）是个五位数，要逐一输出所有能被57或67整除的五位数，并统计这样的五位数有几个。

2、枚举法：1? 4?7（十位和千位被涂抹掉了）是个五位数，要逐一输出所有能被57或67整除的五位数。

3、枚举法：逐一输出所有3位数水仙花数（即个位数3+十位数3+百位数 3 =
这个数）
4、枚举法：百鸡百钱问题：100元买100只鸡（三种鸡，5元一只公鸡，3元一只母鸡，1元三只小鸡），输出每一种买法的各种鸡的数量。

5、枚举法：输出1000以内的所有的素数之和
6、冒泡排序：对十个数按非递减方式（即升序）冒泡排序，并输出排序后的这十个数。

其中i 是外循环变量，用来控制需要进行多少次处理，j 是内循环变量，用来控制每次处理需要进行多少次的俩俩比较。

7、顺序查找：100个数中顺序查找key，如找到则输出是第几个元素，否则输出0（如果输出0的话，表示没找到）。

8、对分查找：100个数（必须事先排好序）中对分查找key，如找到则输出是第几个元素，否则输出0（如果输出0的话，表示没找到）。

i 是用来表示对分查找的起点变量，j是用来表示对分查找的终点变量。

算法与流程图算法与流程图是计算机科学中常用的两种工具。

算法是解决问题的一系列有序的步骤，而流程图则是以图形的形式展示算法的执行过程。

本文将介绍算法与流程图的概念、基本结构，以及它们在实际应用中的作用。

算法是一种抽象的表示方法，它描述了一个问题的解决方案。

一个好的算法应该满足以下几个标准：可行性、确定性、有穷性、有界性和有效性。

可行性表示算法能够解决特定问题，确定性表示算法的每一步都是确定的，有穷性表示算法能在有限时间内结束，有界性表示算法的输入和输出都是有限的，有效性表示算法的执行效率应尽可能高。

算法通常由一系列的步骤组成，每个步骤都是精确的、清晰的、可执行的。

算法可以使用伪代码、流程图或编程语言来表示。

伪代码是用自然语言描述的算法步骤，流程图则是以图形的方式表示算法的执行过程。

流程图通常由图形符号、箭头和标注组成。

图形符号代表不同的操作，箭头代表控制流的方向，标注用来描述操作的目的和属性。

一个标准的流程图包含以下几个基本结构：开始、输入、处理、输出和结束。

开始结构用于表示算法的起始点，输入结构用于接收数据，处理结构用于执行算法的主要计算，输出结构用于展示结果，结束结构用于表示算法的结束点。

流程图还可以包含条件结构和循环结构，用于实现分支和循环控制。

算法与流程图在实际应用中发挥着重要的作用。

它们可以帮助程序员理清思路，设计出高效、可靠的程序。

算法与流程图还可以为团队协作提供一个共同的语言，方便沟通与合作。

此外，算法与流程图还是程序设计、软件工程等课程中的重要学习内容，通过学习算法与流程图，学生能够培养逻辑思维、问题分析和解决问题的能力。

总结来说，算法与流程图是计算机科学中常用的解决问题的工具。

算法描述了一个问题的解决方案，而流程图以图形的方式展示算法的执行过程。

算法与流程图在实际应用中发挥着重要的作用，帮助程序员设计出高效、可靠的程序，并提供一个共同的语言用于团队协作。

通过学习算法与流程图，学生能够培养逻辑思维和解决问题的能力。