汉明码系统

汉明码编码电路的工作原理
汉明码编码电路是一种通过增加冗余位来检测和纠正数据传输错误的编码器。

其工作原理如下：
1. 数据输入：将需要传输的数据输入到汉明码编码电路的数据输入端。

2. 编码器：编码器根据预定的汉明码编码规则对输入的数据进行编码。

具体编码规则包括确定冗余位的位置和计算校验位的值。

冗余位的个数根据数据的长度和校验位确定。

3. 冗余位计算：编码器通过对数据进行一系列的逻辑运算，计算出冗余位的值。

冗余位的值是根据数据中的每一位进行计算的，它代表了数据的的校验信息。

4. 编码输出：编码器将编码后的数据和计算的冗余位一起输出。

5. 传输过程：编码后的数据和冗余位被传输给解码器。

6. 解码器：解码器根据汉明码编码规则对接收到的数据进行解码，计算出接收到的数据中是否存在错误，并尝试纠正错误。

7. 错误检测和纠正：解码器通过对接收到的数据和冗余位进行逻辑运算，判断是否存在错误。

如果存在错误，解码器会尝试根据冗余位的值来纠正错误的数据。

如果无法纠正错误，解码器会发出错误报警信号。

通过增加冗余位和校验位，汉明码编码电路可以在数据传输过程中检测出错误，并在一定程度上纠正这些错误。

这使得数据传输变得更加可靠，提高了系统的容错性。

74汉明码编码1. 线性分组码是一类重要的纠错码，应用很广泛。

在（n ，k ）分组码中，若 冗余位是按线性关系模2相加而得到的，则称其为线性分组码。

现在以(7,4)分组码为例来说明线性分组码的特点。

其主要参数如下：码长：21m n =-信息位：21m k m =--校验位：m n k =-，且3m ≥最小距离：min 03d d ==其生成矩阵G （前四位为信息位，后三位为冗余位）如下：系统码可分为消息部分和冗余部分两部分，根据生成矩阵，输出码字可按下式计算：所以有信息位 冗余位由以上关系可以得到(7,4)汉明码的全部码字如下所示。

1000110010001100101110001101G ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦3210321010001100100011(,,,)(,,,)00101110001101b a a a a G a a a a ⎡⎤⎢⎥⎢⎥=•=•⎢⎥⎢⎥⎣⎦63524130b a b a b a b a ====231013210210b a a a b a a a b a a a =⊕⊕=⊕⊕=⊕⊕2.用C++编写(7,4)汉明码的思路如下：16个不同信息序列的产生：调用stidlib包中的rand(）产生二进制伪随机序列,为了产生16个不同信息序列，共分两步产生：第一步：先产生一个伪随机序列并保留，将它赋给第一个信息序列V[0];i=0;for(j=0;j<4;j++)v[i][j]=rand()%2;第二步：同样产生一个序列，产生后要与在它以前产生的信息序列相比较，如果产生的信息序列与前面的序列都不同，则保留这个信息序列，并进行产生下一个信息序列；如果产生的信息序列与前面的序列有相同的，则此次产生的序列无效，需从新产生信息序列。

此过程中需定义一个比较函数进行比较，其代码如下：for(i=1;i<16;i++){Lable:for(j=0;j<4;j++)v[i][j]=rand()%2;for(k=0;k<i;k++){ //判断随机产生的信息序列与前面的信息序列是否相同if( vedict( v[i],v[k]))continue; //如果产生的信息序列与前面的序列都不同，则保留这个信息序列，并进行产生下一个信息序列elsegoto lable; //如果产生的信息序列与前面的序列有相同的，则此次产生的序列无效，跳转到标签lable处，从新产生信息序列}}进行判断的函数为：bool vedict(int a[],int b[]){int m;for(m=0;m<4;m++){switch(m){case 0:if(a[m]!=b[m])return true;else continue;break;case 1:if(a[m]!=b[m])return true;elsecontinue;break;case 2:if(a[m]!=b[m])return true;else continue;break;case 3:if(a[m]!=b[m])return true;elsereturn false;}}}74汉明码的生成：利用线性关系式 ： 信息位冗余位用两个for 循环，并分两部分求解:前四位用信息位方程，后三位用 冗余位方程（通过异或运算求得);其代码如下：for(i=0;i<16;i++){for(j=0;j<7;j++){if(j<4)u[i][j]= v[i][j];if(j==4)u[i][j]=(v[i][0]^v[i][2])^v[i][3];if(j==5)u[i][j]=(v[i][0]^v[i][1])^v[i][2];if(j==6)u[i][j]=(v[i][1]^v[i][2])^v[i][3];cout << u[i][j] << " ";}cout << endl;}3. 其总代码为：#include<iostream.h>#include<stdlib.h>void main(){int g[4][7]={{1,0,0,0,1,1,0},{0,1,0,0,0,1,1},{0,0,1,0,1,1,1},{0,0,0,1,1,0,1}};//声明生成矩阵63524130b a b a b a b a ====231013210210b a a a b a a a b a a a =⊕⊕=⊕⊕=⊕⊕int v[16][4];//声明信息序列int u[16][7];int i,j,k;cout << "生成矩阵为：" << endl;//输出生成矩阵for(i=0;i<4;i++){for(j=0;j<7;j++)cout << g[i][j] << " ";cout << endl;}bool vedict(int a[],int b[]);//声明判断函数cout << "消息序列:"<< endl;//随机产生信息位序列i=0;for(j=0;j<4;j++)v[i][j]=rand()%2;for(i=1;i<16;i++){lable:for(j=0;j<4;j++)v[i][j]=rand()%2;for(k=0;k<i;k++){ //判断随机产生的信息序列与前面的信息序列是否相同if( vedict( v[i],v[k]))continue; //如果产生的信息序列与前面的序列都不同，则保留这个信息序列，并进行产生下一个信息序列elsegoto lable; //如果产生的信息序列与前面的序列有相同的，则此次产生的序列无效，跳转到标签lable处，从新产生信息序列}}for(i=0;i<16;i++){ //输出信息序列for(j=0;j<4;j++)cout << v[i][j] << " ";cout << endl;}cout << "74汉明码为：" <<endl;for(i=0;i<16;i++){for(j=0;j<7;j++){if(j<4)u[i][j]= v[i][j];if(j==4)u[i][j]=(v[i][0]^v[i][2])^v[i][3];if(j==5)u[i][j]=(v[i][0]^v[i][1])^v[i][2];if(j==6)u[i][j]=(v[i][1]^v[i][2])^v[i][3];cout << u[i][j] << " ";}cout << endl;}}bool vedict(int a[],int b[]){int m;for(m=0;m<4;m++){switch(m){case 0:if(a[m]!=b[m])return true;else continue;break;case 1:if(a[m]!=b[m])return true;elsecontinue;break;case 2:if(a[m]!=b[m])return true;else continue;break;case 3:if(a[m]!=b[m])return true;elsereturn false;}}}编译、运行结果为：。

ecc算法汉明码原理
ECC（Error Correction Code）算法是一种用于检测和纠正数据传输中错误的编码技术。

而汉明码（Hamming Code）是一种特定类型的ECC，它是由理查德·汉明在1950年提出的。

汉明码的原理是通过在数据中添加冗余位来检测和纠正错误。

具体来说，汉明码通过在数据位中插入校验位（也称为冗余位）来实现这一点。

这些校验位的位置是事先确定的，并且被用于确保数据的正确传输和接收。

在汉明码中，校验位的位置是通过二进制数的位置来确定的，例如第1、2、4、8等位置。

这些位置上的校验位被用来检测特定数据位的错误，并且可以通过简单的异或运算来进行纠正。

当数据传输时，接收端会使用汉明码的算法来检测是否有错误发生，并且尝试通过校验位来纠正这些错误。

总的来说，汉明码的原理是利用添加的冗余位来检测和纠正数据传输中的错误。

通过在数据中添加校验位，并且利用这些校验位进行纠错，汉明码可以提高数据传输的可靠性，确保数据在传输过
程中不会受到损坏而导致错误。

这种技术在计算机网络、存储系统和通信领域中被广泛应用，以确保数据的完整性和可靠性。

汉明码的原理汉明码是一种错误检测和纠正的编码方式，它以理论家理查德·汉明的名字命名。

汉明码通过在数据中插入冗余位来检测和纠正错误。

它的原理是在发送数据的时候，根据一定的规则生成一组冗余位，并将其附加到原始数据中。

接收方在接收到数据后，通过对数据进行校验，可以检测出错误的位置，并进行纠正。

汉明码的生成规则如下：假设发送方要发送一个m位的数据，需要生成r位的冗余位。

冗余位的数量r需要满足以下条件：2^r ≥ m + r + 1。

也就是说，冗余位的数量需要满足能够容纳原始数据和冗余位的总长度。

生成冗余位的方法是通过对原始数据进行一系列的异或运算。

首先，确定冗余位的位置，通常是2的幂次方位置，比如第1位、第2位、第4位等。

然后，对于每一个冗余位，计算其值，即将与其相关的原始数据位进行异或运算，并将结果作为冗余位的值。

最后，将生成的冗余位附加到原始数据中，形成最终的发送数据。

接收方在接收到数据后，需要对数据进行校验。

校验的过程是将接收到的数据和冗余位进行一系列的异或运算，然后检查结果。

如果结果为0，则说明数据没有错误；如果结果不为0，则说明数据存在错误，并且错误的位置对应于校验结果中值为1的位。

在纠正错误的时候，可以通过计算错误位置的二进制表示来确定具体是哪一位出现了错误。

例如，如果校验结果中值为1的位的位置是5，则说明第5位出现了错误。

接下来，将错误位的值进行取反操作，即从0变成1，或者从1变成0，然后将纠正后的数据发送给上层应用。

汉明码的好处是能够检测出错误的位置并进行纠正，从而提高数据传输的可靠性。

它广泛应用于通信和存储系统中，特别是在数据传输距离较远或者噪声较大的情况下，汉明码可以有效地保证数据的完整性和准确性。

总结起来，汉明码是一种通过插入冗余位来实现错误检测和纠正的编码方式。

它的原理是在发送数据的时候，根据一定的规则生成一组冗余位，并将其附加到原始数据中。

接收方在接收到数据后，通过对数据进行校验，可以检测出错误的位置，并进行纠正。

汉明码原理一、什么是汉明码汉明码是一种在数字通信和信息理论中常用的错误检测和纠正编码技术。

它由美国数学家理查德·汉明提出，用于在传输过程中检测和纠正由于噪声引起的位错误。

汉明码通过在原始数据中添加冗余位，使得接收端能够根据编码规则检测出错误，并且在一定程度上纠正这些错误。

二、汉明码的原理汉明码的原理是基于一种称为”奇偶校验”的技术。

通过添加冗余位，汉明码能够检测并纠正单比特错误。

它通过在传输的数据中添加冗余位，使得数据在传输过程中能够容忍一定数量的错误。

三、汉明码的结构汉明码通常由n个信息位和m个校验位组成，总共有n+m个位。

校验位的数量由信息位的数量决定。

汉明码的一大特点是校验位与信息位之间的位置关系。

3.1 校验位的位置在汉明码中，校验位的位置是关键。

校验位的位置被选择为2的幂次（从0开始计数），也就是在二进制表示中只有一个位为1，其余位为0。

例如，第1个校验位的位置是1，第2个校验位的位置是2，以此类推。

3.2 校验位的计算校验位的计算方式是将校验位所对应的位置上的所有信息位相加，并根据结果计算校验位的值。

如果校验位的计算结果为奇数，则校验位的值为1；如果计算结果为偶数，则校验位的值为0。

3.3 例子以一个汉明码(7,4)为例，其中有4个信息位和3个校验位。

校验位的位置是1、2和4。

假设要发送的信息是1011，根据校验位的位置，计算校验位的值：1.计算第1个校验位的值：根据校验位的位置，需要计算第1个、第2个和第4个位的和。

对应的信息位是1、0和1。

计算结果为2，为偶数，所以第1个校验位的值为0。

2.计算第2个校验位的值：根据校验位的位置，需要计算第2个、第3个和第4个位的和。

对应的信息位是0、1和1。

计算结果为2，为偶数，所以第2个校验位的值为0。

3.计算第4个校验位的值：根据校验位的位置，需要计算第4个位和第3个位。

对应的信息位是1和1。

计算结果为2，为偶数，所以第4个校验位的值为0。

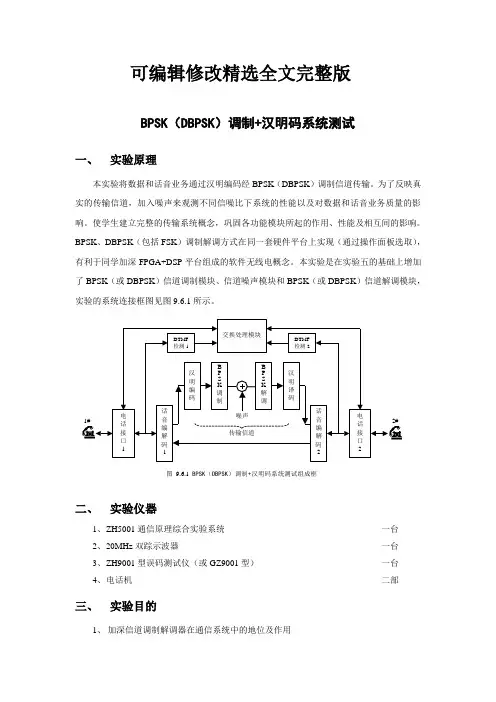
可编辑修改精选全文完整版BPSK （DBPSK ）调制+汉明码系统测试一、 实验原理本实验将数据和话音业务通过汉明编码经BPSK （DBPSK ）调制信道传输。

为了反映真实的传输信道，加入噪声来观测不同信噪比下系统的性能以及对数据和话音业务质量的影响。

使学生建立完整的传输系统概念，巩固各功能模块所起的作用、性能及相互间的影响。

BPSK 、DBPSK （包括FSK ）调制解调方式在同一套硬件平台上实现（通过操作面板选取），有利于同学加深FPGA+DSP 平台组成的软件无线电概念。

本实验是在实验五的基础上增加了BPSK （或DBPSK ）信道调制模块、信道噪声模块和BPSK （或DBPSK ）信道解调模块，实验的系统连接框图见图9.6.1所示。

二、 实验仪器1、 Z H5001通信原理综合实验系统 一台2、 20MHz 双踪示波器一台 3、 Z H9001型误码测试仪（或GZ9001型） 一台 4、 电话机二部三、 实验目的1、 加深信道调制解调器在通信系统中的地位及作用2#1#图9.6.1 BPSK （DBPSK ）调制+汉明码系统测试组成框图2、熟悉信道误码对话音通信业务的影响3、加深认识纠错编码在通信系统中的作用及性能四、实验内容准备工作：（1）本实验在实验五基础上进行，先按实验五要求设置各选择开关；（2）将汉明编码模块工作方式选择开关SWC01设置在和汉明编码器工作（H_EN），开关位置00010000；将汉明译码模块输入数据和时钟选择开关KW01、KW02设置在CH位置（左边），汉明译码使能开关KW03设置在工作ON位置（左端）；将输入数据选择开关KC01设置在DT-SYS(左端：同步数据输入)；（3）将解调器模块载波提取环路开关KL01设置在1_2位置（左端：闭环），输入信号选择开关KL02设置在1_2位置（左端），加入噪声；（4）将噪声模块输出电平选择开关SW01设置最小噪声电平位置（10000001），此时信噪比较高；（5）用中频电缆连接K002和JL02，建立中频自环；（6）将2部电话机分别接入PHONE1和PHONE2插座。

汉明码编码原理汉明码是一种用于检错和纠错的编码方式，它是由理查德·汉明在1950年提出的。

汉明码通过在数据中添加校验位来实现错误检测和纠正，从而保证数据的可靠性。

在计算机领域，汉明码被广泛应用于存储系统、通信系统以及数字电子设备中，以确保数据传输的准确性和完整性。

汉明码的编码原理主要是通过添加校验位来实现错误检测和纠正。

在汉明码中，校验位的位置是按照2的幂次方来确定的，例如第1位、第2位、第4位、第8位等。

这些校验位的作用是对数据位进行奇偶校验，使得在接收端可以通过对校验位的检测来判断数据是否出现错误，并且可以根据校验位的信息来进行错误的纠正。

通过这种方式，汉明码可以实现对多位错误的检测和单位错误的纠正，保证了数据传输的可靠性。

汉明码的编码原理还涉及到了海明距离的概念。

海明距离是指两个等长字符串之间对应位置上不同字符的个数。

在汉明码中，通过调整校验位的位置，使得任意两个有效码之间的海明距离至少为3，这样可以实现对单个错误的检测和纠正。

同时，通过添加更多的校验位，还可以实现对多个错误的检测和纠正，从而提高了数据传输的可靠性。

除了在数据传输中的应用，汉明码还被广泛应用于存储系统中。

在硬盘、闪存等存储设备中，为了保证数据的可靠性，通常会采用汉明码来进行错误检测和纠正。

通过在存储数据时添加汉明码，可以有效地避免数据在读写过程中出现错误，从而保证了数据的完整性和可靠性。

总之，汉明码作为一种重要的编码方式，在数据传输和存储领域发挥着重要的作用。

它通过添加校验位来实现错误检测和纠正，保证了数据传输和存储的可靠性。

随着信息技术的不断发展，汉明码在各种数字系统中的应用将会更加广泛，为数据的安全传输和存储提供了有力的保障。

hammin(汉明)码编码规则计算机汉明码编码规则若编成的海明码为Hm，Hm-1…H2H1，则海明码的编码规律为：(1)校验位分布：在m位的海明码中，各校验位Pi分布在位号为2^(i-1)的位置，即校验位的位置分别为1，2，4，8，…，其余为数据位；数据位按原来的顺序关系排列。

如有效信息码为…D5D4D3D2D1，则编成的海明码为…D5P4D4D3D2P3D1P2P1。

(2)校验关系：校验关系指海明码的每一位Hi要有多个校验位校验，其关系是被校验位的位号为校验位的位号之和。

如D1(位号为3)要由P2(位号为2) 与P1(位号为1)两个校验位校验，D2(位号为5)要由P3(位号为4)与P1两个校验位校验，D3(位号为6)要由P2与P3两个校验位校验，D4(位号为7)要由P1，P2，P3三个校验位校验，……。

这样安排的目的是希望校验的结果能正确反映出出错位的位号。

(3)在增大合法码的码距时，使所有码的码距尽量均匀增大，以保证对所有码的校验能力平衡提高。

汉明距离在一个码组集合中，任意两个码字之间对应位上码元取值不同的位的数目定义为这两个码字之间的汉明距离。

即d(x,y)=∑x[i]⊕y[i]，这里i=0,1,..n-1，x,y都是n位的编码，⊕表示异或例如，(00)与(01)的距离是1，(110)和(101)的距离是2。

在一个码组集合中，任意两个编码之间汉明距离的最小值称为这个码组的最小汉明距离。

最小汉明距离越大，码组越具有抗干扰能力。

下面我们用d表示码组的最小汉明距离。

1。

当码组用于检测错误时，设可检测e个位的错误，则d >=e + 1设有两个距离为d的码字A和B，如果A出现了e个错误，则A变成了以A为圆心，e位半径的球体表面的码字。

为了能够准确地分辨出这些码字既不是A也不是B，那么A 误码后变成的球面上的点与B至少应该有一位距离（如果B在球面上或在球面内部则无法分辨出到底B是不是A的错误码），即A与B之间的最小距离d >= e+1。

（7，4）汉明码编译码原理程序说明书1、线性分组码假设信源输出为一系列二进制数字0和1.在分组码中，这些二进制信息序列分成固定长度的消息分组（message blocks ）。

每个消息分组记为u ，由k 个信息位组成。

因此共有2k 种不同的消息。

编码器按照一定的规则将输入的消息u 转换为二进制n 维向量v ，这里n>k 。

此n 维向量v 就叫做消息u 的码字（codeword ）或码向量（code vector ）。

因此，对应于2k 种不同的消息，也有2k 种码字。

这2k 个码字的集合就叫一个分组码（block code ）。

一个长度为n ，有2k 个码字的分组码，当且仅当其2k 个码字构成域GF （2）上所有n维向量空间的一个k 维子空间时被称为线性（linear ）（n ，k ）码。

对于线性分组码，希望它具有相应的系统结构（systematic structure ），其码字可分为消息部分和冗余校验部分两个部分。

消息部分由k 个未经改变的原始信息位构成，冗余校验部分则是n-k 个奇偶校验位（parity-check ）位，这些位是信息位的线性和（linear sums ）。

具有这样的结构的线性分组码被称为线性系统分组码（linear systematic block code ）。

本实验以（7，4）汉明码的编译码来具体说明线性系统分组码的特性。

其主要参数如下：码长：21mn =-信息位：21mk m =-- 校验位：m n k =-，且3m ≥ 最小距离：min 03d d ==由于一个（n ，k ）的线性码C 是所有二进制n 维向量组成的向量空间n V 的一个k 维子空间，则可以找到k 个线性独立的码字，0,1,1k g g g -…… ，使得C 中的每个码字v 都是这k 个码字的一种线性组合。

（7，4）汉明码的生成矩阵如下，前三位为冗余校验部分，后四位为消息部分。

0123 1 1 0 1 0 0 00 1 1 0 1 0 01 1 1 0 0 1 01 0 1 0 0 0 1g g G g g ⎧⎫⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪==⎨⎬⎨⎬⎪⎪⎪⎪⎪⎪⎪⎪⎩⎭⎩⎭如果()0123u u u u u =是待编码的消息序列，则相应的码字可如下给出：()0101230011223323g g v u G u u u u u g u g u g u g g g ⎧⎫⎪⎪⎪⎪===+++⎨⎬⎪⎪⎪⎪⎩⎭编码结构即码字()0123456v v v v v v v v =，对于（7，4）线性分组码汉明码而言，3456,,,v v v v 为所提供的消息序列，而0356v v v v =⊕⊕，1345v v v v =⊕⊕，2456v v v v =⊕⊕。

课程设计报告题目：汉明码编译码器的SystemView仿真设计学生姓名：XX学生学号：1008XX系别：电气信息工程学院专业：电子信息科学与技术届别：2014指导教师：XX2013年5月目录1 任务与要求 (1)1.1 设计的目的 (1)1.2 设计的基本内容 (1)2 汉明码的简介 (1)2.1 汉明码介绍 (1)2.2 编码原理 (1)2.3译码原理 (3)3 SystemView软件简介 (4)3.1 SystemView基本特点 (4)3.2 各单元模块功能介绍及电路设计 (4)3.3 各模块的原理及介绍 (6)3.4 图符库选择按钮 (6)3.5 system view 的操作步骤 (7)3.6 分析窗的接收计算器 (8)4 系统仿真和调试 (9)4.1 系统整体电路图 (9)4.2 系统测试 (10)4.3 子系统仿真 (11)4.4 数据分析 (12)5 总结 (15)5.1 设计小结 (15)5.2 心得体会 (15)参考文献 (16)汉明码编译码器的SystemView仿真设计学生：XXX指导教师：XXX电气学院XXXXX专业1 任务与要求1.1 设计的目的这次的课程设计就是基于SystemView软件的汉明编码器编码系统仿真设计，要学会运用SystemView，理解汉明编码系统的原理，知道如何解调和调制，并用SystemView进行设计。

1.2 设计的基本内容SystemView是一种动态系统分析软件，也是一个非常好的仿真工具。

它能按照物理概念直接建立分析和仿真，对通信技术的发展起到很大的作用。

本次课程设计就是利用软件SystemView对（7,4）汉明码编译码器进行可视化仿真，对信息数据的编码，传输及译码等功能的实现，充分展示了SystemView在通信仿真中灵活的应用实例。

2 汉明码的简介2.1 汉明码介绍汉明码是一种线性分组码，其具有很多优点。

首先，线性码比非线性码更容易编码和译码。

74汉明码编码原理汉明码（Hamming Code）是一种用于检错和纠错的编码方式。

它是由美国数学家理查德·汉明（Richard Hamming）在1950年提出的。

汉明码的设计目标是，通过在发送的数据中附加冗余位（校验位）来检测和纠正传输错误。

汉明码的原理是利用了冗余位与数据位之间的异或运算。

在汉明码编码中，将n个数据位编码为m个码字，其中m>n，并在码字中加入冗余位。

通过校验位的计算与比较，可以检测错误的发生位置，并进行纠正，使得接收方可以准确地恢复原始数据。

汉明码的编码过程如下：1.确定数据位的数量n和校验位的数量m。

汉明码要求数据位的数量n加上校验位的数量m等于码字的位数，即m+n=k，其中k是码字的位数。

2.确定校验位的位置。

校验位的位置有两种方式：水平位置和垂直位置。

在水平位置编码中，校验位出现在码字的最左边，依次向右排列。

在垂直位置编码中，校验位出现在码字的最上方，依次向下排列。

3.计算校验位的值。

校验位的计算方法是使得每个校验位对应的数据位加上校验位的数量等于偶数个1例如，对于一个校验位对应两个数据位的汉明码，校验位的值是根据对应的两个数据位的奇偶性进行计算的。

若两个数据位中1的个数为奇数，则校验位的值为1；若两个数据位中1的个数为偶数，则校验位的值为0。

4.将数据位和校验位合并形成码字。

将数据位和校验位按照一定的顺序合并形成码字。

合并的方式可以采用水平合并或垂直合并。

5.发送码字。

将编码后的码字发送给接收方。

汉明码的解码过程如下：1.接收码字。

接收方接收到发送方发送的码字。

2.计算校验位的值。

对接收到的码字，按照相同的校验位计算方法重新计算校验位的值。

3.比较校验位的值。

将接收到的校验位的值与重新计算得到的校验位的值进行比较，如果两者不一致，则说明发生了错误。

4.纠正错误。

如果发现错误发生，则根据校验位的位置和计算出的校验位值，确定错误的位置，并进行纠正。

5.提取数据位。

汉明码译码的快速性及纠错特点与应用汉明码是一种用于错误检测和纠正的编码技术，具有快速性和纠错特点，在通信和存储等领域有广泛的应用。

汉明码译码的快速性是指译码过程相对简单且效率高。

汉明码在编码时添加了一些校验位，用于检测和纠正错误。

在译码过程中，接收方将收到的编码进行解码，通过比较校验位和数据位的差异，确定出错的位置，并进行相应的纠错。

由于校验位的设计和计算方法简单，译码过程可以通过简单的逻辑运算完成，因此快速性较高。

汉明码的纠错特点是能够检测和纠正多个比特的错误。

汉明码的设计目标是能够检测和纠正所有的单比特错误，并尽可能多地纠正多比特错误。

在传输和存储过程中，由于各种原因可能导致比特的错误，包括传输中的噪声、干扰或存储介质的问题等。

汉明码通过添加校验位的方式，在接收过程中可以检测出这些错误，并进行相应的纠正，从而保障数据的完整性和准确性。

汉明码在通信和存储领域有广泛的应用。

在通信中，汉明码常用于数字通信系统中的信道编码，用于检测和纠正在传输过程中产生的错误。

汉明码还被应用于无线通信系统中，用于提高数据传输的可靠性。

在存储中，汉明码被应用于磁盘驱动器、闪存存储器等设备中，用于检测和纠正存储介质上的错误，提高数据的存储可靠性。

除了通信和存储领域，汉明码还被广泛应用于计算机内存系统中。

计算机内存中的错误可能导致严重的系统故障，因此对于内存错误的检测和纠正非常重要。

汉明码被用于内存系统中，通过添加校验位的方式，实时检测并纠正内存中可能发生的错误。

通过应用汉明码进行内存错误检测和纠正，可以提高计算机系统的可靠性和稳定性。

总之，汉明码译码具有快速性和纠错特点，在通信和存储领域有广泛的应用。

通过快速、有效地检测和纠正错误，汉明码可以提高数据传输和存储的可靠性，并保障系统的稳定性和性能。