电子科技大学大物上机实验(滕保华)
- 格式:doc
- 大小:572.04 KB
- 文档页数:14
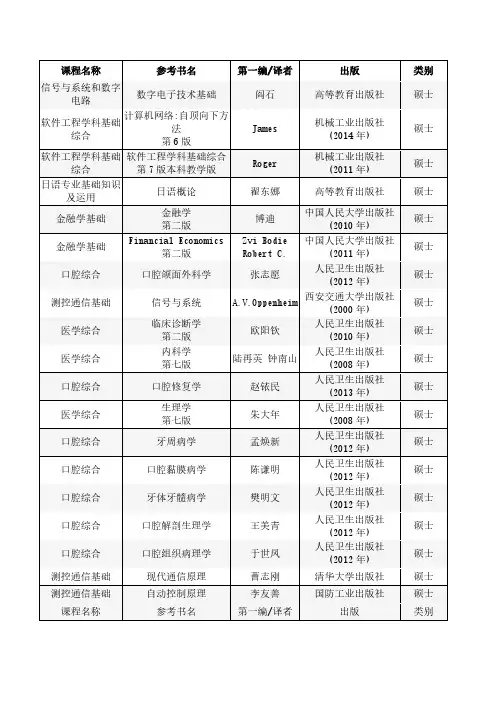


两表面层铁电薄膜体介质层效应理论研究王春栋; 滕保华; 程登木; 周飞【期刊名称】《《四川师范大学学报(自然科学版)》》【年(卷),期】2011(034)005【总页数】6页(P684-689)【关键词】铁电薄膜; 相图; 体介质层; 两表面层【作者】王春栋; 滕保华; 程登木; 周飞【作者单位】电子科技大学物理电子学院四川成都610054; 电子科技大学微电子与固体电子学院四川成都610054; 南京航空航天大学高新技术研究院江苏南京210016【正文语种】中文【中图分类】BH77.80铁电薄膜材料由于具有压电效应、热释电效应、电光效应、声光效应、光折变效应、非线性光学效应和高介电系数等优良特性,所以近几十年来铁电薄膜及集成铁电器件一直是材料科学工程、电解质物理、微电子与光电子等领域科技人员关注和研究的热点之一.其中Pb(ZrxTi1-x)O3(PZT)薄膜由于具有低工作电压、高介电常数、相对大的剩余极化强度和压电常数等特点,成为铁电非易失存储器、微机电系统、热电传感器和场效应晶体管的首选材料.然而由于其显著的疲劳特性及高退火温度容易形成烧绿石相,使人们不断通过各种方法从实验上和理论上进行其改性研究[1].理论上,运用最多的是P.G.de Gennes[2]提出的微观的横场伊辛模型(TFIM)来研究铁电薄膜的性质.该模型假设铁电薄膜是由横场中具有交换相互作用的赝自旋组成.虽然早在1944年L.Onsager[3]就发表了平面正方二维伊辛模型的精确解,然而三维的TIM至今还没有得到精确解.近年来发展了许多近似方法及格林函数法来处理该模型,J.M.Wesselinowa[4-5]运用格林函数系统地研究了铁电薄膜的TIM相图和动力学性质.王春雷等[6]和H.K.Sy[7]运用平均场近似理论研究了铁电薄膜和铁电超晶格相变中的表面效应和尺寸效应.曲保东等[8]研究了铁电薄膜的自然极化特点和介电磁化系数.滕保华等[9]运用高阶退耦合近似格林函数方法研究了各参量对相图的影响.最近从理论上研究了插入层[10]和晶种层[11]对薄膜的影响,发现选择交换相互作用大的而横场参量小的插入层和晶种层能明显提高薄膜的居里温度和极化.本文基于横场伊辛模型,获得了一个适合于研究具有体介质层的任意层数两表面层铁电薄膜相变性质的递归公式.基于该公式讨论具有两层表面层铁电薄膜的体介质层的交换相互作用和横场参量对相图的影响.研究体介质层的交换相互作用参量过渡值和横场参量之间的关系,体介质层的横场参量过渡值和交换相互作用参量之间的关系及两表面层对整个铁电薄膜的影响.1 模型及其理论处理为了简单起见,下面的讨论中将体介质层视为交换相互作用参量比原铁电薄膜(A材料)的交换相互作用参量大、而横场参量比原来小的另外一种铁电材料(B材料).这样具有两个表面层的带有体介质层的铁电薄膜就可以用具有两个表面层的A/B型(两种不同材料结构)简立方格子赝自旋模型来表示(见图1).该系统的哈密顿量[6-12]可写成下列形式其中,Ωi是横场参量,和是格点i处自旋算符沿x和z方向的分量,Jij是第i个和第j个格点位置处的交换相互作用参量只对最近邻的格点求和.如图1所示,ΩA和ΩB分别代表A材料(原铁电薄膜层)和B材料(体介质层)的横场参量;ΩSA为与原铁电薄膜层相接触的两表面层横场参量;ΩSB为与体介质层相接触的两表面层横场参量;JA为材料A的层间和层内的交换相互作用参量;JB是体介质层材料B的层间和层内交换相互作用参量;JSA为与原铁电薄膜层相接触的两表面层的交换相互作用参量;JSB为与体介质层材料B相接触的两表面层的交换相互作用参量.在界面处,A和B材料层的两体交换相互作用参量[13]为横场参量为采用类似于于文献[10]中用的平均场近似理论,并假设同一层的赝自旋具有相同值,则第i层沿z方向的自旋平均值可表示成如下形式当温度接近居里温度时,〈〉将趋于零,对于具有体介质层的两表面层铁电薄膜将有下列线性方程:对于与原铁电薄膜层相接触的两表面层有对于原铁电薄膜层(材料A)有对于体介质层薄膜(材料B)有对于与体介质层接触的两表面层有其中,Si代表基于方程(5)~(13),可得到系数矩阵(14),其中类似于对同种材料组成的n层铁电薄膜[7]的讨论,这一系数矩阵可写成下列递归方程其中并且有A0=1,A-1=0,B0=1,B-1=0,以及基于方程(15),就可讨论任意层数体介质层对带有两个表面层铁电薄膜相变性质的影响.2 计算结果及分析主要运用方程(15)展示体介质层对具有两表面层铁电薄膜的影响.如上面已经提及的,为简单起见,在本文中将体介质层考虑成与原铁电薄膜不同的另一种材料(材料B),通过比较不同的介质层的较大的交换相互作用参量和较小的横场参量对相图的影响,来研究介质层对铁电薄膜相图的影响.本文中相图主要讨论居里温度与表面交换相互作用参量JSB的关系[7,9],同时也列举了居里温度和表面横场参量ΩSB的关系相图[10-12].文中沿用滕保华等[9]的定义,用FPD代表铁电相决定相图,PPD代表顺电相决定相图.为简单起见,本文研究共10层铁电薄膜情形,其中4层表面层,3层介质层(材料B),3层原铁电薄膜层(材料A).数值计算结果展示在图2中.图2展示了体介质层的横场参量对相图的影响,即对不同的ΩB的JSB-TC曲线.从图中可以发现相图敏感地依赖于介质层的横场参量ΩB.图2(a)中当体介质层的横场参量较大时,如图中的ΩB/J=3.542 8时,相图中的铁电区只占很小的一部分,而顺电相占据相图中的大部分面积,这就是顺电相决定相图PPD.而当体介质层的横场参量取较小值,如ΩB/J=2.101 3时,此时情况正好相反,铁电相占据相图大部分面积,而顺电相只占据小部分,这就是铁电相决定相图(FPD).同时还可以发现图2(a)中存在从铁电相向顺电相的过渡区,即图中的ΩB/J=2.833 29所对应的曲线(其曲线上每一点所对应的温度即为居里温度),称该过渡曲线所对应的值为过渡值.从图2中可看到,随着温度增加时,越过该过渡曲线,便由铁电区进入了顺电区,这也就是该相图的过渡特征.同时比较图2(a)、(b)、(c),会发现随着介质层交换相互作用参量的增加(本文中所讨论的介质层的交换相互作用参量值比原铁电薄膜的大),介质层的横场参量的过渡值在增加,同时相图中的铁电区也在增加.这说明介质层的交换相互作用的增大将导致薄膜的居里温度增加.综上所述,说明横场参量是顺电相产生的原因,交换相互作用是铁电相产生的原因.铁电相和顺电相的出现是横场参量和交换相互作用参量相互竞争的结果.所以实验中要选择交换相互作用参量大而横场参量小的介质层来提高整个薄膜的居里温度,改善薄膜的铁电性能.图2中通过比较(a)、(b)、(c)讨论了体介质层的交换相互作用参量对相图的影响.为了更直观的展现其对相图的影响,在图3中,将在同一图中比较体介质层的交换相互作用参量对相图的影响.与图2中所讨论的体介质层的横场参量过渡值相类似,本图中也存在体介质层的交换相互作用参量的过渡值.而与图2中横场参量对相图影响不同的是在本图中可以发现体介质层的交换相互作用越大铁电区越大.这一结论与对通常铁电薄膜的研究相一致[7].观察图4,可发现当介质层的交换相互作用参量增加时,其横场参量的过渡值也在增加.此即表示对于较大的JB/J,需要较大的ΩB/J才能导致从铁电相向顺电相的转变.换言之,增大介质层的交换相互作用参量将增大从铁电相向顺电相转变的难度.另外从图4中还能发现随着JB/J增加,横场参量的过渡值增加速率也在增加. 从图5中也能看到当介质层的横场参量增加时,交换相互作用参量的过渡值也在增加,即对于较大的ΩB/J,只有较大的JB/J才能导致从顺电相向铁电相的转变.而图5的特征与图4的特征不一样,ΩB/J和 JBC/J存在线性关系,其线性关系为JBC/J=0.359ΩB/J+0.049.这说明体介质层的交换相互作用参量对相图的影响要比其横场参量对相图的影响稍大些.在图2、3中研究了体介质层的横场参量和交换相互作用参量对相图的影响,发现横场参量和交换相互作用参量均存在过渡值,并且发现材料的这两个参量并不是互相独立的,而是相互影响相互制约的,故在图5、6中将分别研究体介质层的交换相互作用参量对横场参量过渡值的影响及介质层的横场参量对其交换相互作用参量的过渡值的影响.在图2~5中研究了体介质层的交换相互作用参量和横场参量对相图的影响及对相互之间的过渡值的影响.图6中将研究当体介质层(B材料)和原铁电薄膜(A材料)的交换相互作用参量和横场参量都取确定值(本图中选取体介质层的交换相互作用比原铁电薄膜的大,而横场参量比原铁电薄膜的小的情形)时,与体介质层相接触的表面的交换相互作用对相图ΩSB-TC的影响.从图中发现当JSB/J从0.1增加到0.25时,铁电区将敏感地随之增加,同时也发现当取确定的ΩSB时,表面相互作用JSB/J的增加也将导致整个薄膜居里温度的增加.这一结果与文献[7]对通常铁电薄膜的表面效应的研究相一致.3 结语本文基于横场伊辛模型,运用理论上获得的适合于研究具有体介质层的任意层数两表面层铁电薄膜相变性质的递归公式,讨论了体介质层的加入对整个铁电薄膜相变性质的影响.结果显示,体介质层的交换相互作用参量的增大,能导致相图中铁电区的增加、薄膜的居里温度增大、横场参量过渡值的增大;体介质层的横场参量的增大,能导致相图中铁电区的减小、薄膜居里温度的减小、交换相互作用参量过渡值的增大;而体介质层的交换相互作用参量对薄膜的影响比其横场参量稍大些.此外,与体介质层接触的表面层对相图和居里温度也有很大的影响.尽管文中所呈现的体介质层效应是定性的,希望能对实验中铁电薄膜性能改性有所理论指导.参考文献[1]王英龙,魏同茹,刘保亭,等.外延PbZr0.4Ti0.6O3薄膜厚度对其铁电性能的影响[J].物理学报,2007,56(5):2931-2936.[2]de Gennes P G.Collective motions of hydrogen bonds[J].Solid State Commun,1963,1(6):132-137.[3]Onsager L.Crystal statistics I:A two-dimensional model with anorder-disorder transition[J].Phys Rev,1944,B65:117-149.[4]Wesselinowa J M.On the theory of thin ferroelectric films[J].Phys Stat Sol(b),2001,223:737-743.[5]Wesselinowa J M.Properties of ferroelectric thin films with a first-order phase transitions[J].Solid State Commun,2002,121(2):89-92. [6]Wang C L,Xin Y,Wang X S,et al.Phase transition properties offerroelectric superlattices with three alternative layers[J].Phys Lett,2000,A268:117-122.[7]Sy H K.Surface effects in an alternating magnetic superlattice[J].Phys Rev,1992,B45(1):4454-4459.[8]Qu Bao-dong,Zhong Wei-lei,Zhang Pei-lin.Phase-transition behavior of the spontaneous polarization and suspeptibility of ferroelectric thin film[J].Phys Rev,1995,B52(2):766-770.[9]Teng B H,Sy H K.Green’s function investigati on of transition properties of the transverse Ising model[J].Phys Rev,2004,B70(10):104115-104120.[10]Wang Chun-dong,Teng Bao-hua,Zhang Xian-jun,et al.Phase transition properties of ferroelectric thin film with one distinct inserting-layer[J].Mod Phys Lett,2008,B22(31):1-13.[11]Wang Chun-dong,Teng Bao-hua,Zhang Xian-jun,etal.Investigation of the seeding-layer effect on a ferroelectric thin film with the transverse Ising model[J].Phys,2009,A388(38):1472-1478. [12]Kaneyoshi T.Phase diagrams of a transverse Ising superlattice based on two theoretical frameworks[J].Phys,2001,A293(1):387-398. [13]Qu Bao-dong,Zhong Wei-lei,Zhang Pei-lin.Ferroelectric supperlattice with first-order transition[J].Ferroelectrics,1997,197:23-26.[14]Wang Chun-lei,Qin Zi-kai,Zhang Jing-bo.Green’s function theory of phase transition in PbHPO3and PbDPO4ferroelectrics[J].Ferroelectrics,1988,77:21-29.[15]Zhou Jing,Lv Tian-quan,Cui Lian,et al.Phase transition properties of finite size ferroelectric thin film with structural transition zones[J].J Appl Phys,2008,104:124105-124112.[16]Lu Z X,Teng B H,Lu X H,et al.Investigation of the crossover properties for the interaction parameters of a ferroelectric thin film [J].Solid State Commun,2009,149(29/30):1176-1179.[17]穆轶,侯邦品.增加光子对和减少光子对相干态的等阶Y压缩效应[J].四川师范大学学报:自然科学版,2007,30(5):610-614.[18]丁迎春,徐明,沈益斌,等.γ-Si3N4在高压下的光学性质研究[J].四川师范大学学报:自然科学版,2007,30(6):755-759.。


两电容与两电感分别连接前后能量变化的类比分析
余静;滕保华;李学敏
【期刊名称】《物理与工程》
【年(卷),期】2011(21)6
【摘要】本文从电学中两个具有初始电压的电容连接前后的能量变化出发,类比地讨论了磁学中两个具有初始电流的电感连接前后的能量变化,并分析了初始电压及初始电流的方向对其能量损失的影响,从而从本质上加深对电磁现象的认识.
【总页数】3页(P14-15,21)
【作者】余静;滕保华;李学敏
【作者单位】电子科技大学2009级英才实验班,四川成都611731;电子科技大学物理电子学院,四川成都610054;电子科技大学2009级英才实验班,四川成都611731
【正文语种】中文
【相关文献】
1.两套自制教具在电容和电感教学中的应用 [J], 阙永华
2.电容器、电感线圈的两个特征及应用 [J], 华兴恒
3.换路后两个连接电容电场能量变化分析 [J], 齐超;王子誉;杨瀚潮;齐赛
4.关于R、L、C串联交流电路中电容、电感两端电压最大值的微探 [J], 李能武
5.两电平静止无功发生器连接电感计算方法研究 [J], 韩文辉
因版权原因,仅展示原文概要,查看原文内容请购买。
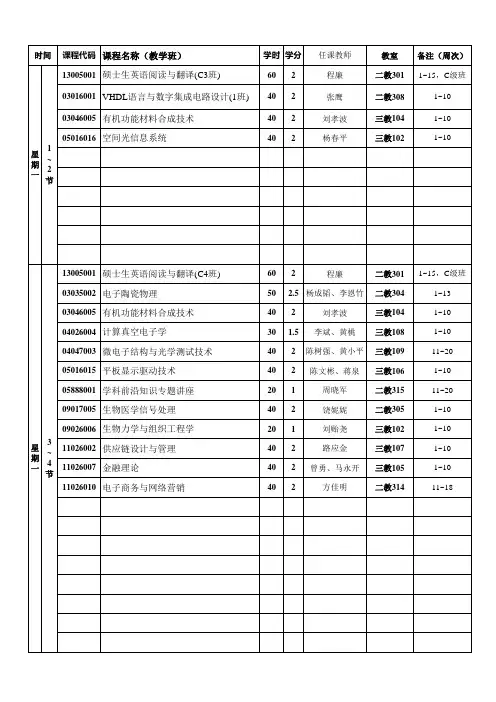



电子技术应用实验1(数字电路基础实验)_电子科技大学中国大学mooc课后章节答案期末考试题库2023年1.电源电压为5V的TTL门电路的阈值电压最接近以下哪个值?参考答案:1V2.电源电压为5V的CMOS门电路的阈值电压大约为多少?参考答案:2.5V3.用芯片74LS00(4个2输入与非门)实现反相器,未使用的引脚应该如何处理?参考答案:接另一个输入引脚_直接悬空_接5V电源4.在测量电源电压Vcc时,实验箱上指示灯亮,用万用表测量电源电压为5V,但示波器测出为0V,原因可能是示波器探头耦合方式未设置为()。
参考答案:直流5.在Verilog语言中assign语句是?参考答案:连续赋值语句6.关于Verilog语言中的always语句不正确的是?参考答案:只有wire类型数据可以在这个语句中被赋值7.Vivado中仿真文件的后缀为?参考答案:.v8.74LS163工作于计数状态,CP为2KHzTTL信号。
若用四个发光二极管去看74LS163的四个输出端,四个发光二极管看起来。
参考答案:常亮9.示波器探头衰减开关置为时,输入阻抗更大。
参考答案:10X档10.示波器探头设置中,在探头比为10х时的输入电容比探头比为1X时大。
参考答案:错误11.用双踪示波器同时测试频率不同、周期成整数倍的两个时序波形时,当某信号显示不同步时可能需要。
参考答案:调节触发释抑时间_重新选择示波器的触发源_调节示波器的触发电平位置12.用示波器只观察信号中的交流成分时,输入耦合应选择。
参考答案:交流耦合13.若CD4511输入为4位二进制码1011,其驱动的七段显示器显示是参考答案:无显示14.74LS00用作反相器使用时,下列哪种连接方法正确?参考答案:一个输入端接信号,另一个输入端接高电平_一个输入端接信号,另一个输入端悬空_两个输入端并接信号15.用示波器测量某点的直流电压值,示波器需要做以下哪些设置?参考答案:通道探头的设置和探头上的开关设置相对应_输入耦合方式为直流_对应通道的0V标志在屏幕上_能够在屏幕上看到该直流信号16.在测试74X139的逻辑功能实验中,当G'、A1、A0分别接0、1、0时,哪个端口的输出有效()。

·1·常用电子测量仪器的使用一部第分第一部分 常用电子测量仪器的使用本部分主要涉及实验要用到的三种仪器:数字示波器、信号发生器和稳压电源。
学生在自学了《电子技术应用实验教程 综合篇》(后称教材)第一章内容后,填空完成这部分的内容。
一、学习示波器的应用,填空完成下面的内容示波器能够将电信号转换为可以观察的视觉图形,便于人们观测。
示波器可分为 模拟示波器 和 数字示波器 两大类。
其中, 模拟示波器 以连续方式将被测信号显示出来;而 数字示波器 首先将被测信号抽样和量化,变为二进制信号存储起来,再从存储器中取出信号的离散值,通过算法将离散的被测信号以连续的形式在屏幕上显示出来。
我们使用的是 数字示波器 。
使用双踪示波器,能够同时观测两个时间相关的信号。
信号通过探头从面板上的 通道1 和 通道2 端送入,分别称为CH1和CH2。
在使用示波器时,需要注意以下几点:(1)正确选择触发源和触发方式触发源的选择:如果观测的是单通道信号,就应选择 该信号 作为触发源;如果同时观测两个时间相关的信号,则应选择信号周期 大 (大/小)的通道作为触发源。
(2)正确选择输入耦合方式应根据被观测信号的性质来选择正确的输入耦合方式。
如图1.1所示,输入耦合方式若设为交流(AC ),将阻挡输入信号的直流成分,示波器只显示输入的交流成分;耦合方式设为直流(DC ),输入信号的交流和直流成分都通过,示波器显示输入的实际波形;耦合方式设为接地(GND ),将断开输入信号。
t0U1V 5V(A )tU 1V5V 图1.2 被测信号实际波形tU (B )t0U-2V2V (C )图1.1 输入耦合开关示意图图1.3 不同输入耦合方式时的波形已知被测信号波形如图1.2所示,则在图1.3中, C 为输入耦合方式为交流(AC )·2·DIANZI JISHU YINGYONG SHIYAN JIAOCHENG SHIYAN BAOGAO电子技术应用实验教程实验报告综合篇时的波形, A 为输入耦合方式为直流(DC )时的波形, B 为输入耦合方式为接地(GND )时的波形。
第15卷 第4期强激光与粒子束Vol.15,No.4 2003年4月HIGH POWER LASER AND PAR TICL E B EAMS Apr.,2003 文章编号: 100124322(2003)0420409203多脉冲叠加高压系统及测量技术Ξ肖明珠1,2, 谈效华2, 姚永和2, 陈光 1(1.电子科技大学自动化系CAT实验室,四川成都610054; 2.中国工程物理研究院电子工程研究所,四川绵阳621900) 摘 要: 介绍了多脉冲叠加高压系统的核心部件:一个双次级绕组高压脉冲变压器,它能形成多路脉冲并叠加合成为梯形脉冲波,从而改善了波形的上升下降沿。
该系统输出电压由3个衰减正弦波叠加而成,脉冲幅度大于100kV,脉冲宽度2~5μs。
同时,在双次级绕组高压脉冲变压器上设计一个小型结构型电容分压装置,解决了变压器与其它装置对接装配后高压的监测和测量。
关键词: 脉冲功率; 高压; 多脉冲叠加; 测量 中图分类号: TM531 文献标识码: A 利用电容器充放电可以建造高压脉冲系统,国内外均有该类系统的大量报道[1~3]。
但该类系统通常输出衰减正弦波或指数波高压脉冲,波形上升沿和下降沿较缓,对负载的有效作用时间小,能量利用率低[4~6]。
为了克服上述缺点,俄罗斯专家率先提出了一种多脉冲叠加高压系统,如图1所示。
在该系统中,有2个储能电容和1个多初次级绕组的高压脉冲变压器。
P1,P2,P3为初级绕组,S1,S2为次级绕组。
这样该系统有多个放电回路,能形成多路高压脉冲,负载Z上电压由2个次级绕组S1,S2产生的电压叠加而成,多个脉冲波形叠加合成了矩形或梯形高压脉冲,从而改变波形的上升沿和下降沿。
我国对多脉冲叠加高压系统的设计方法研究很少,对其分析也停留在一些定性层面。
本文提出了一种双次级变压器多脉冲叠加的高压系统,如图2所示。
该系统能输出2~5μs高压脉冲,电压幅度在100kV以上,带负载能力大于85%,能量利用率高,且结构简单,容易实现。
实验一ARM汇编基础实验1.掌握ARM汇编指令2.学习掌握C与汇编混合编程基础3.熟练使用ARM调试工具RVDS进行调试操作1.熟悉ARM汇编2.用ARM汇编实现1+2+...+N3.C调用汇编实验(实现字符串拷贝功能)4.汇编调用C实验5.ARM汇编实现冒泡算法(选做)1.ARM汇编、C语言2.RVDS工具硬件:PC机PentiumlOO以上软件:Windows操作系统,RVDS软件1.在汇编中使用C定义的全局变量在汇编和C之间进行一些数据的传递,最简便的办法就是使用全局变量。
在汇编中调用C中定义的全局变量,需要在汇编中IMPORT对应的全局变量。
IMPORT伪指令用于通知编译器要使用的标号或变量在其他的源文件中定义。
例如:汇编文件asmfile.s想调用C文件cfile.c中定义的全局变量a,则在汇编文件asmfile.s 前面要添加:IMPORT a2.在汇编中调用C的函数要在汇编中调用C文件中定义的函数,主要做两方面的工作:首先:需要在汇编中IMPORT对应的C函数名。
其次:在调用该C函数之前还需要通过汇编语言传递该函数的参数。
C和汇编之间的参数传递是通过ATPCS (ARM Thumb Procedure Call Standard)的规定来进行的。
简单的说就是如果函数有不多于四个参数,对应的用ARM寄存器R0-R3来进行传递, 多于4个时借助栈。
函数的返回值通过R0来返回。
3.在C中调用汇编的函数在C中调用汇编文件中的函数,要做的主要工作有两个:一:是在C中声明函数原型,并加extern关键字;二:是在汇编中用EXPORT导出函数名,并用该函数名作为汇编代码段的标识,最后用mov pc, lr返回。
然后,就可以在C中使用该函数了。
EXPORT伪指令用于在程序中声明一个全局的标号,该标号可在其他的文件中引用。
1、用ARM汇编实现l+2+-.n的运算。
2、理解C和汇编,并用汇编程序实现字符串拷贝,并在C程序中调用该汇编程序。
电子科技大学经济与管理学院标准实验报告(实验)课程名称企业经营决策模拟电子科技大学教务处制表电子科技大学实验报告学生姓名:学号:指导教师:曹欢实验地点:经管大楼A403实验时间:一、实验室名称:经管大楼A403二、实验项目名称:运用《人机对抗——网络版》系统,进行决策仿真实践三、实验学时:8四、实验原理:根据上机实验操作,运用所学的相关知识,对所遇到问题进行分析,提出解决方案。
利用决策仿真,巩固已学的相关知识,增加实践经验。
五、实验目的:(1)掌握决策时所需要考虑的因素(2)在环境发生变化时采取相应的措施(3)进一步从整体上考虑企业的优化决策,进而激发创新意识,提高创新能力六、实验内容:对相关的理论知识进行强化、熟悉人机对抗版的操作步骤,上机实际操作,针对实验结果进行讨论七、实验器材(设备、元器件):东华大学现代企业经营决策仿真系统软件、电脑、投影仪八、实验步骤:(1)有重点地学习部分理论知识,分别侧重于竞争条件下的产品市场需求预测、产品市场销售决策、生产方案决策、物料采购决策、决策方案全面预算和方案成果盈亏计算等现代企业决策的各个主要方面及其相互联系和影响。
(2)正式运用《人机对抗——网络版》系统,进行决策仿真实践。
九、实验数据及结果分析:(需要粘贴软件中第六步骤的四张表格)!!十、实验结论:结果如何,为什么会造成这样的结果的分析。
例如,战胜电脑,个人的策略是什么?控制了哪些关键点?输给电脑,或成绩不理想,是由于哪些环节出了问题?十一、总结及心得体会:请根据个人的思考和分析来填写。
例如,在这次实验中的体会。
以及在将来的实践操作中,需要注意的地方:战略?市场?生产?如何将这几个环节综合进行思考?十二、对本实验过程及方法、手段的改进建议:报告评分:指导教师签字:电子科技大学实验报告学生姓名:学号:指导教师:曹欢实验地点:经管大楼A403实验时间:一、实验室名称:经管大楼A403二、实验项目名称:运用《决策仿真——群体对抗web版》系统,进行决策仿真实践三、实验学时:4四、实验原理:根据上机实验操作,运用所学的知识,对所遇到问题进行分析,提出解决方案。
电子科技大学计算机工程学院标准实验报告(实验)课程名称电子科技大学教务处制表电子科技大学实验报告实验一学生姓名:穆萨·图拉克学号:2012060090033 指导教师:实验地点:主楼A2-412 实验时间:19:00~一、实验室名称:二、实验项目名称:汇编源程序的上机调试操作基础训练三、实验学时:四、实验原理:(包括知识点,电路图,流程图)DEBUG 的基本调试命令;汇编数据传送和算术运算指令MASM宏汇编开发环境使用调试方法五、实验目的:1. 掌握DEBUG 的基本命令及其功能2. 学习数据传送和算术运算指令的用法3. 熟悉在PC机上编辑、汇编、连接、调试和运行汇编语言程序的过程六、实验内容:(介绍自己所选的实验内容)1. DEBUG命令的使用2. 程序的调试与运行3. 编写程序计算以下表达式:Z=(5X+2Y-7)/2设X、Y的值放在字变量V ARX、V ARY中,结果存放在字节单元V ARZ中。
七、实验器材(设备、元器件):WinXP PC机,MASM,50 ,VisulASM软件平台。
八、实验步骤:(编辑调试的过程)1.编辑源程序,建立一个以后缀为.ASM的文件.2.汇编源程序,检查程序有否错误,有错时回到编辑状态,修改程序中错误行。
无错时继续第3步。
3.连接目标程序,产生可执行程序。
4.用DEBUG程序调试可执行程序,记录数据段的内容。
九、实验数据及结果分析:(实验运行结果介绍或者截图,对不同的结果进行分析)程序说明:功能:本程序完成Z=(5X+2Y-7)/2这个等式的计算结果求取。
其中X 与Y是已知量,Z是待求量。
结构:首先定义数据段,两个DB变量VARX与VARY(已经初始化),以及结果存放在VARZ,初始化为?。
然后定义堆栈段,然后书写代码段,代码段使用顺序程序设计本程序,重点使用MOV和IMUL以及XOR,IDIV完成程序设计。
详细内容见程序注释。
程序清单:DATA SEGMENTVARX DB10VARY DB10VARZ DB?DATA ENDSSTACK SEGMENT PARA STACKSTACK ENDSCODE SEGMENTASSUME CS:CODE,DS:DATA,SS:STACKMAIN:MOV AX,DATAMOV DS,AXMOV AL,VARXMOV AH,VARYSAL AL,1SAL AL,1ADD AL,VARXSAL AH,1ADD AL,AHSUB AL,7SAR AL,1MOV VARZ,ALMOV AH,4CHINT21HCODE ENDSEND MAIN程序框图:结束调试说明:将汇编语言(.asm文件)通过masm命令转换为目标程序(.obj 文件),通过link命令转换为目标程序可执行程序(.exe文件); 这次试验还要用-p参数以及d参数显示结果为:十、实验结论:(联系理论知识进行说明)通过本次实验,我们学习了解掌握了DEBUG 的基本命令及其功能,学习了数据传送和算术运算指令的用法,熟悉了在PC机上编辑、汇编、连接、调试和运行汇编语言程序的过程。
实验一一.实验名称:范德瓦尔斯方程分析二.实验目的:熟练运用Mathcad, 对理想气体方程和范德瓦尔斯方程比较分析。
三.实验原理:理想气体物态方程只适用于压强不太大,温度不太低的气体。
但当气体压强比较大,温度比较低即气体分子的数密度n 比较大时,气体分子间的实际间距没有理想气体间距那么大,分子间的相互作用力和分子本身的体积就加以考虑,所以需要找出实际气体的物态方程。
荷兰物理学家范德瓦耳斯改进了气体的状态方程,把分子间的作用力和分子的有限体积放进方程中去。
他论证了,分子间距离较远时,它们间必定存在吸引力,这一作用附加到容器壁施加的压强上去。
他进一步提供论据,假设附加产生的压强反比于气体比容的平方。
还有,由于分子占有体积,它们可利用的空间必须减少,或者说,减少的总体积就正比于分子在相互接触时所占有的体积。
于是一摩尔真实气体的状态方程变成 2V V m m a b RT p --=或 RT b m a p V V m =-+))(2(这简单方程包含两个常数,即a 和b ,对于每一种物质它们可由实验确定。
R 是普适气体数学。
后来人们称之为范德瓦耳斯方程。
他还导出了b 是分子体积的4 倍。
这个方程不仅能解释安德纽斯的实验结果及J .汤姆生的见解,而且能从常数a 、b 值计算出临界参数。
范德瓦尔斯方程的引出,是从理论分析出发导出气体状态方程的一个典型例子。
范德瓦尔斯方程只不过是用两个常数很粗略地考虑了气体内分子运动的行为,所以还不能精确地表述气体的p-v-t 关系。
但是,它为用理论方法研究状态方程开拓了道路。
特别是它在定性上能反映出物质气—液相变的性质。
按照范德瓦尔斯状态方程在p-v 图上作出的定温线称为范德瓦尔斯定温线。
因为该方程可以展开成摩尔体积V m 的三次方程:0)(23=-++-ab a m RT pb m p V V V m 将范德瓦尔斯方程代入式式中T c ,p c 是临界点的温度和压力值,称为物质的临界温度和压力值。
在临界点物质骤然全部地发生气—液相转变,在实验中可以观察到临界乳光现象发生,由此可以测定出临界点参数。
在测定临界温度和压力以后,可按上式计算出范德瓦尔斯常数。
四.实验内容:(1)不同气体在相同温度状态下的范德瓦尔斯等温线与理想气体等温线的对比。
分别作出不同气体的p-v曲线。
由图中可见在气压较低、压强较大的情况下,范德瓦尔斯对理想气体公式的修正参数影响是显著的。
气压较低、压强较大时压强对体积的变化率较大,在此范围内使用理想气体公式是不合适的。
这在一定程度上说明了理想气体的适用条件之一,即压强不太大。
同种气体在不同温度状态下的范德瓦尔斯曲线及其与对应理想气体曲线的对比。
作二氧化碳气体的p-v 曲线。
试分析T 与a 与b 对1mol 二氧化碳气体的影响,这里的a 与b 的取值范围:)(5~5.0:22mol l atm a ⋅⋅)(05.0~02.0:1-⋅mol l b(1)探究a 对二氧化碳气体的影响随着a的增加p-v图的第一个极小值的数值在不断减小,整个曲线的下凹部分逐渐明显,可以得出气体压强变化的剧烈程度随着a的增大而加强的结论。
总体气体压强随着a的增加而减小,但当v趋于无穷时,压强趋同。
(2)探究b对二氧化碳气体的影响随着b的增加,p-v图的第一个极小值逐渐明显,且压强变化的剧烈度随着b的增加而增强。
总体看来,气体压强随着b的增加而减小,且当v趋于无穷时,p 将趋于稳定。
(3)探究T对二氧化碳气体的影响随着温度的升高,p-v图的变化趋势趋于指数形式。
从红线图到绿色虚线图,p-v图的极值点越来越不明显,到紫色虚线图时,极点甚至消失了。
可以得出结论:温度影响气体分子的运动剧烈度,破坏较高气体摩尔密度下的p-v特性。
同时随着温度的上升,压强总体增加。
五.实验结论:范德瓦尔斯方程是对理想气体方程的修正。
同时,范德瓦尔斯方程也具有局限性。
范德瓦尔斯方程能相当近似地解释实际气体在一定温度和压强范围内的宏观表现。
范德瓦尔斯方程等温线与真实气体的实验等温线作比较,二者都有一条临界等温线。
在临界等温线以上,二者比较接近;在温度很高时,二者之间没有区别。
在临界等温线以下,二者却有显著的区别。
范德瓦尔斯等温线的是一个三次曲线,曲线中有一段的斜率为正,意味着体积愈膨胀,压强越大,因而无法平衡。
真实气体的等温线有一个液化过程,也就是说有一个汽液共存区域,在汽液共存区当体积逐渐减小时,压力基本不变,近似为一水平直线。
实验二一.实验名称:对于磁滞回线用Mathcad进行作图。
二.实验目的:用Mathcad对磁滞回线直观的进行分析,进一步熟悉Mathcad,的使用。
三.实验原理:(1)实验研究铁磁质时通常把它做成环状,外面绕上若干匝线圈,构成具有铁芯的螺绕环。
改变电流,可以得到一系列H和B的值,这样就可以绘出一条关于磁铁质H-B的关系曲线来表示铁磁质的磁化特点。
这样的曲线叫磁化曲线。
如果从磁铁质完全没有磁化开始,逐渐增大H,所得曲线叫起始磁化曲线。
如图中ONP线段是从实验得出的某一铁磁质开始磁化时的H-B曲线,即起始磁化曲线。
从曲线中可以看出B和H之间是非线性关系。
当H从零逐渐增大时,B急剧地增加,这是因为磁畴在磁场的作用下迅速沿外磁场排列的缘故;到达点N以后,再增大H时,B增加地就比较慢了;当达到P点以后,再增加外磁场强度H时,B的增加就十分缓慢,呈现出磁化已饱和的程度。
点P所对应的B值一般叫做饱和磁感应强度B m,这时,在铁磁质中,几乎所有磁畴都已沿着外磁场方向排列了。
这时的磁场强度用H m表示。
当磁场强度达到B m后就开始减小,在H减小的过程中,H-B曲线不是按原来的起始磁化曲线退回来。
当外磁场由H m逐渐减小时,磁感强度B并不沿起始曲线ONP减小,而是沿着另一条曲线PQ比较缓慢地减小。
这种B的变化落后于H的变化的现象,叫做磁滞现象,简称磁滞。
(2)顺磁质的磁导率μ很小,但是是一个常量,不随外磁场变化而变化,故顺磁质的B和H的关系是线性关系。
但铁磁质不是这样,不仅它的磁导率比顺磁质大得多,而且,当外磁场改变时,它的磁导率μ还随磁场强度H的变化而变化。
由于磁滞的缘故,当磁场强度减小到零(即H=0)时,磁感强度B并不等于零,而是仍有一定数值B r,B r叫做剩余磁感强度,简称剩磁。
这是铁磁质特有的性质。
如果一铁磁质有剩磁存在,这就表明它已被磁化过。
由图可以看出,随着反向磁场的增加,B逐渐减小,当达到H c=时,B等于零,这时铁磁H-质的剩磁就消失了,铁磁质也就不显现磁性。
通常把称为H c矫顽力,时,材料它表示铁磁质抵抗去磁的能力。
当反向磁场不断增强到-Hm的反向磁化同样能达到饱和点P'。
此后,反向磁场逐渐减弱到零,B-H 线便沿P'Q'变化,从而完成一个循环。
所以,由于磁滞,B-H 曲线就形成一个闭合曲线,这个闭合曲线叫做磁滞回线,研究磁滞回线不仅可以了解铁磁质的性质,而且也有实用价值,因为铁磁材料往往是应用于交变磁场中的。
需要指出,铁磁质在交变磁场中被反复磁化时,磁滞效应是要损耗能量的,而所损耗的能量与磁滞回线包围的面积有关,面积越大,能量的损耗也越多。
(3).一般的铁磁质都有对应的的磁滞回线——即当磁场强度周期性变化时,表示铁磁性物质或亚铁磁性物质磁滞现象的闭合磁化曲线。
相对于坐标原点对称的磁滞回线称为“正常磁滞回线”。
其中磁矩m 与周期性外磁场H (t )和温度T 有关系:])(tanh[Tt H m m dt dm ++-=四.实验过程:1.使用Mathcad 软件,输入ω=0.1, h=0.6, T=0.5按以下图示输入,得到如图所示图线:改变一定条件探究磁滞回线与相图关系: 1.当其他条件一定,h取不同值:令T=0.5, =0.2当h=0.14,0.18,0.24,0.28; 磁滞回线如图:磁滞回线随着h增大而由内到外依次排列,同时我们发现这一组的磁滞回线是不对称的。
当h=0.4 ,0.7 ,1.0 ,1.4 ,1.8磁滞回线随着h增大而由内到外依次排列,同时我们发现这一组的磁滞回线是对称的。
由实验可知,在温度和频率一定的条件下,磁滞回线形状是与振荡幅度有关的。
当h0值较小,系统呈现铁磁性且平均磁化并不消失。
当h0值较大,系统呈现顺磁性且平均磁化会消失。
随着h0值的增加,磁回滞线包围封闭图形的面积扩大。
磁回滞线形状趋近于长方形但仍不能呈现长方形的外观形态。
2.当其他条件一定,ω取不同值:令T=0.5, h=0.6当ω=1.5,1.8,2.2,2.6磁滞回线随ω增大从外向内排列,磁滞回线呈现不对称形态。
当ω=0.1,0.2,0.4,0.6,1.0磁滞回线随ω增大从外向内排列,磁滞回线呈现中心对称形态。
由实验可知,温度和振荡幅度一定时,磁回滞线与振荡外场的频率有关。
ω值较大,系统呈现铁磁性,平均磁化并不消失。
ω值越大,系统平均磁化强度越强。
ω值较小,系统呈现顺磁性且平均磁化会消失。
取值较小ω值,磁回滞线的形态才大致与矩形相仿。
五.实验结论:由实验可知磁滞回线形状是与振荡幅度和频率有关的,不同的振荡幅度和频率会产生不同的磁滞回线形状。
当h0值较小,系统呈现铁磁性且平均磁化并不消失。
当h0值较大,系统呈现顺磁性且平均磁化会消失。
随着h0值的增加,磁回滞线包围封闭图形的面积扩大。
磁回滞线形状趋近于长方形但仍不能呈现长方形的外观形态。
当ω值较大,系统呈现铁磁性,平均磁化并不消失。
ω值越大,系统平均磁化强度越强。
ω值较小,系统呈现顺磁性且平均磁化会消失。
取值较小ω值,磁回滞线的形态才大致与矩形相仿。