2011年迎春杯六年级初赛(详细解答)

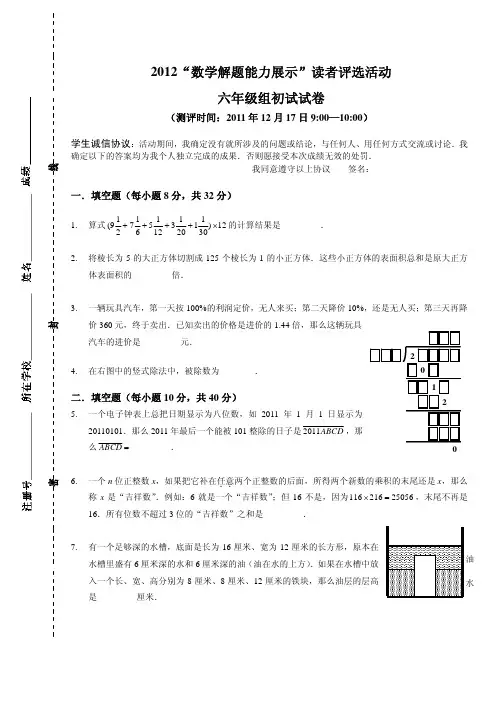
2012“数学解题能力展示”读者评选活动六年级组初赛试题（测评时间：2011年12月17日9：00—10：00）一．填空题（每小题8分，共32分） 1.算式11111(97531)1226122030++++⨯的计算结果是_________． 2.将棱长为5的大正方体切割成125个棱长为1的小正方体．这些小正方体的表面积总和是原大正方体表面积的_________倍．3.一辆玩具汽车，第一天按100%的利润定价，无人来买；第二天降价10%，还是无人买；第三天再降价360元，终于卖出．已知卖出的价格是进价的1.44倍，那么这辆玩具汽车的进价是_________元．4.在右图中的竖式除法中，被除数为________．二．填空题（每小题10分，共40分）5.一个电子钟表上总把日期显示为八位数，如2011年1月1日显示为20110101．那么2011年最后一个能被101整除的日子是2011ABCD ，那么ABCD =_________．6.一个n 位正整数x ，如果把它补在任意．．两个正整数的后面，所得两个新数的乘积的末尾还是x ，那么称x 是“吉祥数”．例如：6就是一个“吉祥数”；但16不是，因为11621625056⨯=，末尾不再是16．所有位数不超过3位的“吉祥数”之和是_________．7.有一个足够深的水槽，底面是长为16厘米、宽为12厘米的长方形，原本在水槽里盛有6厘米深的水和6厘米深的油（油在水的上方）．如果在水槽中放入一个长、宽、高分别为8厘米、8厘米、12厘米的铁块，那么油层的层高是_________厘米．水8.有一个66⨯的正方形，分成36个11⨯的正方形．选出其中一些11⨯的正方形并画出它们的对角线，使得所画出的任何两条对角线都没有公共点，那么最多可以画出 条对角线．三．填空题（每小题12分，共48分）9.甲车由A 地开往B 地，同时乙车也从B 地开往A 地．甲车速度是每小时80千米，乙车速度是每小时70千米．甲车在中途C 地停车，15分钟后乙车到达C 地，这时甲车继续行驶．如果两车同时到达目的地，那么AB 两地相距_________千米．10.如果自然数a 的各位数字之和等于5，那么称a 为“龙腾数”．将所有的“龙腾数”从小到大排成一列，2012排在这一列数中的第_________个．11.在右图中，将一个每边长均为12厘米的正八边形的8个顶点间隔地连线，可以连出两个正方形．图中阴影部分的面积是_________平方厘米．12.用横向或纵向的线连接所有的黑点和白点并形成自身不相交的回路．这个回路在黑点处必须拐直角弯，且前一格和后一格都必须直行通过；在白点处必须直行通过，且在前一格或者后一格（至少一处）拐直角弯．例如，图2的画法是图1的唯一解．如果按照这个规则在图3中画出回路，那么这条回路一共拐了_________次弯．图1 图2 图3【参考答案】一．填空题（每小题8分，共32分）1.算式11111(97531)1226122030++++⨯的计算结果是_________．知识点：分数四则运算难易度：☆（半颗星）答案：310解析：11111(97531)1226122030111111111 (97531)12(1)12223344556 30010310++++⨯=++++⨯+-+-+-+-+-⨯=+=2.将棱长为5的大正方体切割成125个棱长为1的小正方体．这些小正方体的表面积总和是原大正方体表面积的_________倍．知识点：立体几何难易度：☆（半颗星）答案：5解析：把大正方体切割成小正方体，需要切12刀，一共增加了24个5×5的面．原来有6个面，切割后增加到了30个面，因此小正方体的表面积总和是原大正方体表面积的5倍．3.一辆玩具汽车，第一天按100%的利润定价，无人来买；第二天降价10%，还是无人买；第三天再降价360元，终于卖出．已知卖出的价格是进价的1.44倍，那么这辆玩具汽车的进价是_________元．知识点：经济问题难易度：★（一颗星）答案：1000解析：设进价为“1”，则第一天定价为“2”，第二天定价为“1.8”，最终售价为“1.44”．“1.8”与“1.44”的差价等于360元，可知进价“1”=1000元．4.在右图中的竖式除法中，被除数为________．知识点：数字谜与数阵图难易度：★★★（三颗星）答案：20952解析：首先，X ＝1，Y ＝9，则Z ＝1； 由ABC ×D ＝10□，知D ＝1，A ＝1，B ＝0；由C 10×E ＝9□2，知E ＝9，C ＝8；从而Y □2＝972；由Y □2＝972知PQ 取值38～47，又据108×F ＝PQ □，得F ＝4． 所以，被除数108×194＝20952．二．填空题（每小题10分，共40分）5.一个电子钟表上总把日期显示为八位数，如2011年1月1日显示为20110101．那么2011年最后一个能被101整除的日子是2011ABCD ，那么ABCD =_________． 知识点：整除问题 难易度：★★（两颗星） 答案：1221解析：因为是最后一个能被101整除的日子，所以先看12月有没有，令12AB =．判断能否被101整除要用两位截断后奇偶作差能否被101整除．偶数段的和是201232+=，那么奇数段的和可能是32、133．后面一个不可能，只能是32．那么321121CD =-=，1221ABCD =．6.一个n 位正整数x ，如果把它补在任意．．两个正整数的后面，所得两个新数的乘积的末尾还是x ，那么称x 是“吉祥数”．例如：6就是一个“吉祥数”；但16不是，因为11621625056⨯=，末尾不再是16．所有位数不超过3位的“吉祥数”之和是_________．供题者：西城实验中学-王宁知识点：余数问题难易度：★★★（三颗星）答案：1114解析：可知只要一个数的平方的末尾还是这个数，这个数就是吉祥数．当1n =时，显然1,5,6x =是“吉祥数”．当2n =时，这个两位“吉祥数”的个位数字也一定是1、5、6中的一个．如果个位数字是1，设这个数是101a +，()22101100201a a a +=++，个位数字是1，十位数字是2a 的个位数字．而2a 的个位数字不可能是a ，所以两位“吉祥数”的各位数字不可能是1；如果个位数字是5，设这个数是105a +，()2210510010025a a a +=++，末两位数字是25，这个“吉祥数”就是25；如果个位数字是6，设这个数是106a +，()2210610012036a a a +=++，个位数字是6，十位数字是2a +3的个位数字．那么有2310a a +-=（减10是因为会进位），7a =．这个“吉祥数”就是76．可知两位的“吉祥数”只有25和76．类似地，当3n =时，可知三位“吉祥数”的末两位是两位“吉祥数”．如果末两位是25，设这个数为10025a +，()2210025100005000625a a a +=++，末三位是625，这个“吉祥数”就是625；如果末两位是76，设这个数为10076a +，()221007610000152005776a a a +=++，末两位是76，百位数字是27a +的个位数字，即2710a a +-=，3a =．这个“吉祥数”就是376．三位“吉祥数”只有625和376．因此，所有不超过3位的“吉祥数”之和为15625766253761114++++++=．7.有一个足够深的水槽，底面是长为16厘米、宽为12厘米的长方形，原本在水槽里盛有6厘米深的水和6厘米深的油（油在水的上方）．如果在水槽中放入一个长、宽、高分别为8厘米、8厘米、12厘米的铁块，那么油层的层高是_________厘米．知识点：立体几何难易度：★★★（三颗星）答案：7解析：铁块被放入以后，“水层”的底面积变成了128平方厘米，“水层”高 度变成了9厘米，说明9厘米高的铁块没入水中，3厘米高的铁块浸入油中．“油层”增加的体积是388192⨯⨯=立方厘米，增加的高度是19216121÷÷=厘米．因此“油层”的高度是7厘米．8.有一个66⨯的正方形，分成36个11⨯的正方形．选出其中一些11⨯的正方形并画出它们的对角线，使得所画出的任何两条对角线都没有公共点，那么最多可以画出 条对角线．知识点：构造论证难易度：★★★（三颗星）水油答案：21解析：如下左图，可以画出21条对角线．如下右图，标记了21个格点，画出的每条1×1正方形的对角线都要以这21个标记格点中的某一个为顶点．而据题意，所画出的任何两条对角线都没有公共点，所以每个标记格点至多画出一条对角线，从而至多画出21条对角线．三．填空题（每小题12分，共48分）9.甲车由A 地开往B 地，同时乙车也从B 地开往A 地．甲车速度是每小时80千米，乙车速度是每小时70千米．甲车在中途C 地停车，15分钟后乙车到达C 地，这时甲车继续行驶．如果两车同时到达目的地，那么AB 两地相距_________千米．知识点：行程问题难易度：★★（两颗星）答案：140解析：设全长为x 千米，则15708060x-，解得140x =．或者这样做：甲乙两车的速度比是8:7，所走的路程相同，所以甲乙所用的时间比是7:8．又因为乙车比甲车多走了15分钟，可知乙车一共走了()15878120÷-⨯=分钟，即两小时．所以AB 间的路程是140千米．10.如果自然数a 的各位数字之和等于5，那么称a 为“龙腾数”．将所有的“龙腾数”从小到大排成一列，2012排在这一列数中的第_________个．知识点：不定方程及其它难易度：★★★（三颗星）答案：38解析：先计算位数小于四位的“龙腾数”的个数，相当于不定方程5a b c ++=的自然数解(,,)a b c 的组数，有2721C =组（a =0、b =0对应一位“龙腾数”，a =0、b ≠0对应两位“龙腾数”，a ≠0对应三位“龙腾数”）；再计算以1开头的四位“龙腾数”的个数，相当于不定方程4a b c ++=的自然数解(,,)a b c 的组数，有2615C =组．考虑到2012是第二个以2开头的四位“龙腾数”，因此答案是2012是这一列数中的第38个．11.在右图中，将一个每边长均为12厘米的正八边形的8个顶点间隔地连线，可以连出两个正方形．图中阴影部分的面积是_________平方厘米．知识点：图形的切拼；弦图与勾股定理难易度：★★★★（四颗星）答案：288解析：如下左图，记AD = a ，由对称性知，DB = a ，BC = a ．取E 为DC 中点，连接BE ，将△ABC 分成直角三角形ABE 和等腰直角三角形BEC ． 四个△BEC 可以拼成一个边长a 的正方形．记BE = b ，则CE = a ，DE = a由AE = a + b ，BE = b 知：由4个△ABE 和一个以a 为边长的正方形可拼成一个以AB 为边长的正方形（如下右弦图）．题中阴影可看做8个△ABE 的面积，△ABE 的面积等于36平方厘米，因此本题答案为288平方厘米．12.用横向或纵向的线连接所有的黑点和白点并形成自身不相交的回路．这个回路在黑点处必须拐直角弯，且前一格和后一格都必须直行通过；在白点处必须直行通过，且在前一格或者后一格（至少一处）拐直角弯．例如，图2的画法是图1的唯一解．如果按照这个规则在图3中画出回路，那么这条回路一共拐了_________次弯．知识点：一笔画与图论B图1图2图3难易度：★★★★★（五颗星） 答案：20解析：依题意，黑点和白点处的画线方式应如图4所示．按照图3摆放方式的，我们可以先确定其中1个黑点和4个白点的画线方式，如图5所示．在图5的基础上，可以确定2个黑点的画线方式，如图6所示．在图6的基础上，可以确定剩下黑点和1个白点的画线方式，如图7所示．在图7的基础上，可以完成这个回路，一共拐了20次弯．图8图7 图6图5 图4。

全国小学生英语竞赛（六年级组）2011年初赛试题及详解听力部分（共四大题，计30分）I.听辨单词（Words）（共5小题，计5分）听音，从A，B，C三个选项中选出你所听到的句子中含有的单词。

每个句子读两遍。

1.A.WhatB.WhoC.How2.A.dayB.weekC.month3.A.bankB.shopC.store4.A.actorB.artistC.actressputerB.magazineC.dictionary【答案与解析】1.C录音中问到，你怎么去学校，结合所给单词，可知答案是C项。

2.B录音中讲到，一周有七天，结合所给单词，可知答案是B项。

week[wi:k]，意为“星期”。

day[deɪ]，意为“天”。

month[mʌnθ]，意为“月”。

3.A录音中讲到，我爸爸在银行上班，结合所给单词，可知答案是A项。

bank[bæŋk]，意为“银行”。

shop[ʃɔp]，意为“商店，店铺”。

store[stɔ:(r)]，意为“商店”。

4.C录音中讲到，她将成为一名演员，结合所给单词，可知答案是C项。

注意actor是男演员，而句中的主语为she。

actress[ˈæktrəs]，意为“女演员”。

artist[ˈɑ:tɪst]，意为“艺术家”。

5.C录音中问到，我能不能借你的字典用用，结合所给单词，可知答案是C项。

dictionary[ˈdɪkʃənri]，意为“字典”。

computer[kəmˈpju:tə(r)]，意为“电脑”。

magazine[ˌmægəˈzi:n]，意为“杂志”。

【录音原文】1.How do you get to school?2.There are seven days in a week.3.My father works in a bank.4.She is going to be an actress.5.May I borrow your dictionary?II.句子理解（Sentences）（共5小题，计5分）听音，判断下列图片与你所听到的句子意思是（Y）否（N）相符。

2021年“迎春杯〞数学解题能力展示复赛试卷〔小高组〕一、填空题Ⅰ〔每题8分，共40分〕1．〔8分〕定义一种新运算a☆b满足：a☆b＝b×10+a×2，那么2021☆130＝．2．〔8分〕从1999年到2021年的12年中，物价涨幅为150%〔即1999年用100元能购置的物品，2021年要比原来多花150元才能购置〕．假设某个企业的一线员工这12年来工资都没有变，按购置力计算，相当于工资下降了%．3．〔8分〕如图中大圆的半径是20厘米，7个小圆的半径都是10厘米．那么阴影图形的面积是平方厘米〔π取3.14〕．4．〔8分〕某届“数学解题能力展示〞读者评选活动初试共有12000名学生参加，分为初中、小学高年级、小学中年级三个组别、小学的两个组共占总人数的，不是小学高年级组的占总人数的．那么小学中年级组参赛人数为人．5．〔8分〕如图是一个除法竖式，这个除法竖式的被除数是多少？二、填空题Ⅱ〔每题10分，共50分〕6．〔10分〕算式1!×3﹣2!×4+3!×5﹣4!×6+…+2021!×2021﹣2021!×2021+2021!的计算结果是．7．〔10分〕春节临近．从2021年1月17日〔星期一〕起工厂里的工人陆续回家过年，与家人团聚．假设每天离厂的工人人数相同，到1月31日，厂里还剩下工人121名，在这15天期间，统计工厂工人的工作量是2021个工作日〔一人工作一天为1个工作日，工人离厂当天及以后不需要统计〕，其中周六、日休息，且无人缺勤，那么截止到1月31日，回家过年的工人共有人．8．〔10分〕有一个整数，它恰好是它的约数个数的2021倍，这个整数的最小值是．9．〔10分〕一个新建5层楼房的一个单元每层有东西2套房：各层房号如下图，现已有赵、钱、孙、李、周五家入住，一天他们5人在花园中聊天：赵说：“我家是第3个入住的，第1个入住的就住我对门．〞钱说：“只有我一家住在最高层．〞孙说：“我家入住时，我家的同侧的上一层和下一层都已有人入住了．〞李说：“我家是五家中最后一个入住的，我家楼下那一层全空着．〞周说：“我家住在106号，104号空着，108号也空着．〞他们说的话全是真话，设第1、2、3、4、5家入住的房号的个位数依次为A、B、C、D、E，那么五位数＝．10．〔10分〕6支足球队，每两队间至多比赛一场如果每队恰好比赛了2场，那么符合条件的比赛安排共有种．三、填空题Ⅲ〔每题12分，共60分〕11．〔12分〕0～9可以组成两个五位数A和B，如果A+B的和是一个末五位数字相同的六位数，那么A×B的不同取值共有个．12．〔12分〕甲乙两人分别从A、B两地同时出发，在A、B往返行走；甲出发的同时，丙也从A出发去B．当甲乙两人第一次迎面相遇在C地时，丙还有100米才到C；当丙走到C时，甲又往前走了108米；当丙到B时，甲乙正好第二次迎面相遇．那么A、B两地间的路程是多少米？13．〔12分〕如图，大正方形被分成了面积相等的五块．假设AB长为3.6厘米，那么大正方形的面积为平方厘米．14．〔12分〕用36个3×2×1的实心小长方体拼成一个6×6×6的大正方体，在各种拼法中，从大正方体外的某一点看过去最多能看到个小长方体．15．〔12分〕平面中有15个红点，在这些红点间连一些线段，一个红点连出了几条线段，就在这个红点上标几．所有标有相同数的红点之间互不连线，那么这15个红点间最多连了条线段．2021年“迎春杯〞数学解题能力展示复赛试卷〔小高组〕参考答案与试题解析一、填空题Ⅰ〔每题8分，共40分〕1．〔8分〕定义一种新运算a☆b满足：a☆b＝b×10+a×2，那么2021☆130＝5322．【解答】解：根据分析可得，2021☆130＝130×10+2021×2＝1300+4022＝5322；故答案为：5322．2．〔8分〕从1999年到2021年的12年中，物价涨幅为150%〔即1999年用100元能购置的物品，2021年要比原来多花150元才能购置〕．假设某个企业的一线员工这12年来工资都没有变，按购置力计算，相当于工资下降了60%．【解答】解：100+100×150%＝100+150＝250〔元〕1﹣100÷250＝1﹣40%＝60%答：按购置力计算，相当于工资下降了60%．故答案为：60．3．〔8分〕如图中大圆的半径是20厘米，7个小圆的半径都是10厘米．那么阴影图形的面积是942平方厘米〔π取3.14〕．【解答】解：观察图象可知阴影局部的面积＝7个小圆面积﹣一个大圆面积＝7•π•102﹣π•202＝300π＝942，故答案为：942．4．〔8分〕某届“数学解题能力展示〞读者评选活动初试共有12000名学生参加，分为初中、小学高年级、小学中年级三个组别、小学的两个组共占总人数的，不是小学高年级组的占总人数的．那么小学中年级组参赛人数为5250人．【解答】解：1﹣＝，﹣＝，12000×＝5250〔人〕；答：小学中年级组参赛人数为5250人．故答案为：5250．5．〔8分〕如图是一个除法竖式，这个除法竖式的被除数是多少？【解答】解：由题意，除数的两个倍数分别是2□□和91□，如果2□□是除数的2倍，根据余数为130，除数为131以上，149以下，这样91□只能是除数的7倍，131×7＝917，那么第三个被除数为91□或81□，它等于除数的某个倍数减1，只能是7倍减1，即916，被除数等于131×277﹣1＝36286，经检验符合题意；如果2□□是除数的1倍，那么91□是除数的4倍，可能是912或916，除数可能是228或229，第三个被除数为91□或81□，除以除数之后余数为130，可能是228×3+130＝814或229×3+130＝817，被除数相应为228×143+130＝32734或229×143+130＝32877，但无论哪种，第一个差都是两位数，所以不符合题意．综上所述，被除数等于36286，除数为131，商为276．二、填空题Ⅱ〔每题10分，共50分〕6．〔10分〕算式1!×3﹣2!×4+3!×5﹣4!×6+…+2021!×2021﹣2021!×2021+2021!的计算结果是1．【解答】解：分组找规律：2021!×2021﹣2021!×2021+2021!＝2021!〔2021﹣2021×2021+2021×2021〕＝2021!那么2007!×2021﹣2021!×2021+2021!＝2007!〔2021﹣2021×2021+2021×2021〕＝2007!由奇数项向前裂变抵消规律得原式＝2021!×2021﹣2021!×2021+2021!+…+5!×7﹣4!×6+3!×5﹣2!×4+1!×3＝1!＝1故答案为：17．〔10分〕春节临近．从2021年1月17日〔星期一〕起工厂里的工人陆续回家过年，与家人团聚．假设每天离厂的工人人数相同，到1月31日，厂里还剩下工人121名，在这15天期间，统计工厂工人的工作量是2021个工作日〔一人工作一天为1个工作日，工人离厂当天及以后不需要统计〕，其中周六、日休息，且无人缺勤，那么截止到1月31日，回家过年的工人共有120人．【解答】解：依题意可知：设每天回家的人数为x人，那么15天共走15x人，其中有2个周六周日共4天休息不工作．周末剩余人数为9x〔周六〕，8x〔周日〕，2x〔周六〕，x〔周日〕．121×11+〔3+4+5+6+7+10+11+12+13+14〕x＝2021∴x＝8，15x＝120〔人〕故答案为：1208．〔10分〕有一个整数，它恰好是它的约数个数的2021倍，这个整数的最小值是16088．【解答】解：用列举法因为2021×8＝16088，所以，满足条件的最小整数为16088，故答案为16088．9．〔10分〕一个新建5层楼房的一个单元每层有东西2套房：各层房号如下图，现已有赵、钱、孙、李、周五家入住，一天他们5人在花园中聊天：赵说：“我家是第3个入住的，第1个入住的就住我对门．〞钱说：“只有我一家住在最高层．〞孙说：“我家入住时，我家的同侧的上一层和下一层都已有人入住了．〞李说：“我家是五家中最后一个入住的，我家楼下那一层全空着．〞周说：“我家住在106号，104号空着，108号也空着．〞他们说的话全是真话，设第1、2、3、4、5家入住的房号的个位数依次为A、B、C、D、E，那么五位数＝69573．【解答】解：根据分析，因为104和108都空着，而孙的楼上楼下都有人了，所以孙住在左侧，只有钱一家住在最高层，说明剩余4人住在101，102，103，105，106，107，里面的6家，全空着的一层只能是第一层或第二层，这样才能使得孙和楼上楼下都有人．如果全空着的是第一层，那么李住在第二层的103，李氏最后入住的，所以孙住在107，且105和109都在这之前有人住了，赵是第三个入住的，所以孙一定是第四个入住的，根据钱的话，钱住在109，有对门的是105和106，周住在106，所以赵住在105，而且周的第一个入住的，故答案是：69573．10．〔10分〕6支足球队，每两队间至多比赛一场如果每队恰好比赛了2场，那么符合条件的比赛安排共有70种．【解答】解：6支球队分2组每组3支，这3支球队间相互比赛：分组方法：〔6×5×4〕÷〔3×2×1〕÷2＝10〔选3支球队和剩3支球队重复，所以除2〕；6支球队围成圈，相邻的球队之间比赛：方法：5×4×3×2×1÷2＝60 〔顺时针与逆时针重复，所以除2〕，所以符合条件的比赛安排共有10+60＝70种．答：符合条件的比赛安排共有70种．故答案为：70．三、填空题Ⅲ〔每题12分，共60分〕11．〔12分〕0～9可以组成两个五位数A和B，如果A+B的和是一个末五位数字相同的六位数，那么A×B的不同取值共有384个．【解答】解：依题意可知：六位数字的首位一定是1，根据弃九法后5位都是7．所以这两个五位数的首位之和是17．后四个数字和为7的数字两两配对．把和为7的数字两两配对，首位是9的那个五位数有8×6×4×2＝384〔种〕．根据不同情况下两个五位数的差不同，差小积大，这384个乘积也各不相同．故答案为：384．12．〔12分〕甲乙两人分别从A、B两地同时出发，在A、B往返行走；甲出发的同时，丙也从A出发去B．当甲乙两人第一次迎面相遇在C地时，丙还有100米才到C；当丙走到C时，甲又往前走了108米；当丙到B时，甲乙正好第二次迎面相遇．那么A、B两地间的路程是多少米？【解答】解：甲从A走到C时，丙走了100÷＝1250〔米〕，AC的距离为1250×＝1350〔米〕，甲乙速度之和是丙的速度的3倍，那么乙的速度是丙的〔3﹣〕倍，BC的距离为1250×〔3﹣〕＝2400〔米〕，所以AB的距离为1350+2400＝3750〔米〕答：A、B两地间的路程是3750米．13．〔12分〕如图，大正方形被分成了面积相等的五块．假设AB长为3.6厘米，那么大正方形的面积为1156平方厘米．【解答】解：根据分析，设正方形边长为一个单位，如图，因为正方形分成面积相等的五份，故每一份的面积都等于，故AG＝，D到FH的距离＝C到EF的距离＝，因为A到左边EG的距离等于A到上边EF的距离的，所以C到EG的距离也等于C 到EF的距离的，即；C到FH的距离为1﹣＝，类似，D到右边FH的距离为，因为C到EF的距离：C到右边FH的距离＝＝10：21，故D到EF的距离也等于D到FH的距离的，即：×＝，故D到GH的距离＝1﹣＝；又三角形BDH的面积＝，故BH＝＝，AB＝1﹣﹣＝÷＝34〔厘米〕，正方形的面积＝34×34＝1156平方厘米．故答案是：1156．14．〔12分〕用36个3×2×1的实心小长方体拼成一个6×6×6的大正方体，在各种拼法中，从大正方体外的某一点看过去最多能看到31个小长方体．【解答】解：如图，为了从外面看到的个数最多，需要使外面看到的长方形尽可能“深入〞正方形里面，结果如下：共6×3+3×4+3×1+1＝31〔个〕．故答案为：31．15．〔12分〕平面中有15个红点，在这些红点间连一些线段，一个红点连出了几条线段，就在这个红点上标几．所有标有相同数的红点之间互不连线，那么这15个红点间最多连了85条线段．【解答】解：将15个点分为5组，每组分别有1，2，3，4，5个点，〔1×14+2×13+3×12+4×11+5×10〕÷2＝170÷2＝85〔条〕答：这15个红点间最多连了85条线段．故答案为：85．。

第一讲计算与计数常用公式1、()21321+=++n n n Λ 末项＝首项＋（项数一1) ×公差；数列和＝（首项＋末项）×项数÷2；项数=（末项-首项）÷公差＋1；公差=（末项－首项）÷（项数－1）；2、()()612121222++=+++n n n n Λ 3、()()412121222333+=++=+++n n n n ΛΛ 4、131171001⨯⨯⨯=⨯=abc abc abcabc 6006610016131177877=⨯=⨯⨯⨯=⨯⇒如： 5、()()b a b a b a -+=-226、()()212311321n n n n =+++++++-++++ΛΛ7、1211111=⨯ 12321111111=⨯ 112345654321111112=8、111111111912345679=⨯9、()kn n k n n k +-=+⨯11 10、()()()112231123n n n n n ⨯+⨯++⨯+=++L11、完全平方和公式：()2222b ab a b a ++=+ 12、完全平方差公式：()2222b ab a b a +-=- 循环小数一、把循环小数的小数部分化成分数的规则①纯循环小数小数部分化成分数：将一个循环节的数字组成的数作为分子，分母的各位都是9，9的个数与循环节的位数相同，最后能约分的再约分。

②混循环小数小数部分化成分数：分子是第二个循环节以前的小数部分的数字组成的数与不循环部分的数字所组成的数之差，分母的头几位数字是9，9的个数与一个循环节的位数相同，末几位是0，0的个数与不循环部分的位数相同。

【1】（2010年迎春杯初赛六年级第1题）{{{10015022541112224442010个个个…＋…＋…＋计算结果的数字和是 ．【2】（2011年迎春杯初赛六年级第7题） 定义运算：a b a b a b ⨯♥=+，算式920102010201020102010♥♥♥♥♥♥L 144444424444443共颗“”的计算结果是 ．【3】（2009年迎春杯初赛六年级第6题） 计算：89109101110111211121378910111178910＋＋＋＋＋＋＋＋－＋－＝－＋－________．【4】（2015年迎春杯初赛六年级第1题） 算式2015143199163135115131⨯⎪⎭⎫ ⎝⎛+++++的计算结果是 ．【5】（2009年迎春杯初赛五年级第9题） 5717191155(+)234345891091011⨯+++⨯⨯⨯⨯⨯⨯⨯⨯…= ．【6】（2010年迎春杯初赛六年级第3题）满足图中算式的三位数abc 最小值是______．【7】（2012年迎春杯初赛六年级第4题）在右图中的除法竖式中，被除数为 ．a b c21⨯【8】（2015年迎春杯初赛六年级第2题）如图，一道除法竖式中已经填出了“2015”和“0”，那么被除数是 ．【9】（2011年迎春杯初赛六年级第15题）已知算式19.1220102=-+-I GHF DE ABC 中的A ,B ,C ,D ,E ,F ,G ,H ,I 表示1～9中各不相同的数字．那么，五位数ABCDE ＝ ．【10】（2013年迎春杯初赛六年级第6题）在3×3的九宫格内填入数字1至9（每个数字都恰好使用一次），满足圆圈内的数恰好为它周围四个方格的数字之和，例如A +B +D +E =28，那么ACEGI 组成的五位数是 ．【11】（2013年迎春杯初赛六年级第4题）由2、0、1、3四个数字组成（可重复使用）的比2013小的四位数有个．【12】（2015年迎春杯初赛六年级第8题）甲、乙、丙三户人家打算订阅报纸，共有7种不同的报纸可供选择，已知每户人家都订三份不同的报纸，并且知道这三户人家每两户所订的报纸恰好有一份相同，那么三户人家共有种不同的订阅方式．【13】（2009年迎春杯初赛六年级第7题）将5枚棋子放入下图编号的4×4表格的格子中，每个格子最多放一枚，如果要求每行，每列都有棋子，那么共有_____种不同放法．1 2 3 45 6 7 89 10 11 1213 14 15 16【14】（2012年迎春杯初赛六年级第10题）如果自然数a 的各位数字之和等于5，那么称a 为“龙腾数”。

目录第1届“迎春杯”数学竞赛刊赛试题... .............................................................. . 1 第2届“迎春杯”数学竞赛决赛试题... .............................................................. . 5 第3届“迎春杯”数学竞赛决赛试题... .............................................................. . 8 第4届“迎春杯”数学竞赛决赛试题... ............................................................ .. 10 第5届“迎春杯”数学竞赛决赛试题... ............................................................ .. 11 第6届“迎春杯”数学竞赛决赛试题... ............................................................ .. 13 第7届“迎春杯”数学竞赛决赛试题... ............................................................ .. 16 第8届“迎春杯”数学竞赛决赛试题... ............................................................ .. 18 第9届“迎春杯”数学竞赛决赛试题... ............................................................ .. 20 第10 届“迎春杯”数学竞赛决赛试题... .......................................................... (23)第11 届“迎春杯”数学竞赛初赛试题... ........................................................... (25)第11 届“迎春杯”数学竞赛决赛试题... ........................................................... (27)第12 届“迎春杯”数学竞赛决赛试题... .......................................................... (29)第12 届“迎春杯”数学竞赛决赛试题... .......................................................... (31)第13 届“迎春杯”数学竞赛初赛试题... .......................................................... (33)第13 届“迎春杯”数学竞赛决赛试题... .......................................................... (35)第14 届“迎春杯”数学竞赛决赛试题... .......................................................... (37)第14 届“迎春杯”数学竞赛决赛试题... .......................................................... (39)第15 届“迎春杯”数学竞赛初赛试题... .......................................................... (41)第15 届“迎春杯”数学竞赛决赛试题... .......................................................... (43)第16 届“迎春杯”数学科普活动日区县邀请赛试题... .................................. (45)第17 届“迎春杯”数学科普活动日队际交流试题... ....................................... . 47 第18 届“迎春杯”数学科普活动日队际交流试题... ....................................... . 50 第19 届“迎春杯”数学科普活动日计机交流试题... ....................................... . 52 第19 届“迎春杯”数学科普活动日队际交流试题... ....................................... . 54 第20 届“迎春杯”数学科普活动日试题... ....................................................... .. 55 第21 届“迎春杯”数学科普活动日解题能力展示初赛试题... ...................... (57)第21 届“迎春杯”数学解题能力展示读者评选活动复试计算机交流试题... (58)第22 届“迎春杯”数学解题能力展示读者评选活动中年级初试试题... ..... .. 60 第22 届“迎春杯”数学解题能力展示读者评选活动中年级复试试题... ..... .. 62 第22 届“迎春杯”数学解题能力展示评选活动高年级初试试题... .............. . 64第22 届“迎春杯”数学解题能力展示评选活动高年级复试试题... .............. . 66第23 届“迎春杯”数学解题能力展示评选活动中年级初试试题... .............. . 69第23 届“迎春杯”数学解题能力展示评选活动中年级复试试题... .............. . 71第23 届“迎春杯”数学解题能力展示评选活动高年级初试试题... .............. . 73第23 届“迎春杯”数学解题能力展示评选活动高年级复试试题... .............. . 75第24 届“迎春杯”数学解题能力展示评选活动三年级初试试题... .............. . 77第24 届“迎春杯”数学解题能力展示评选活动四年级初试试题... .............. . 79第24 届“迎春杯”数学解题能力展示评选活动中年级复试试题... .............. . 81第24 届“迎春杯”数学解题能力展示评选活动五年级初试试题... .............. . 83第24 届“迎春杯”数学解题能力展示评选活动六年级初试试题... .............. . 85第24 届“迎春杯”数学解题能力展示评选活动高年级复试试题... .............. . 88第25 届“迎春杯”数学解题能力展示评选活动三年级初试试题... .............. . 90第25 届“迎春杯”数学解题能力展示评选活动四年级初试试题... .............. . 92第25 届“迎春杯”数学解题能力展示评选活动中年级复试试题... .............. . 94第25 届“迎春杯”数学解题能力展示评选活动五年级初试试题... .............. . 96第25 届“迎春杯”数学解题能力展示评选活动六年级初试试题... .............. . 98第25 届“迎春杯”数学解题能力展示评选活动高年级复试试题... ........... .. 100 第26 届“迎春杯”数学解题能力展示评选活动三年级初试试题... ........... .. 102 第26 届“迎春杯”数学解题能力展示评选活动四年级初试试题... ........... .. 104 第26 届“迎春杯”数学解题能力展示评选活动中年级复试试题... ........... .. 106 第26 届“迎春杯”数学解题能力展示评选活动五年级初试试题... ........... .. 108 第26 届“迎春杯”数学解题能力展示评选活动六年级初试试题... ........... .. 110 第26 届“迎春杯”数学解题能力展示评选活动高年级复试试题... ........... .. 112 第27 届“迎春杯”数学解题能力展示评选活动三年级初试试题... ........... .. 114 第27 届“迎春杯”数学解题能力展示评选活动四年级初试试题... ........... .. 116 第27 届“迎春杯”数学解题能力展示评选活动中年级复试试题... ........... .. 118第 27届“迎春杯”数学解题能力展示评选活动六年级初试试题... .......... .. 122 第 27届“迎春杯”数学解题能力展示评选活动高年级复试试题... .......... .. 124 第 28届“迎春杯”数学解题能力展示评选活动三年级初试试题... .......... .. 126 第 28届“迎春杯”数学解题能力展示评选活动四年级初试试题... .......... .. 128 第 28届“迎春杯”数学解题能力展示评选活动中年级复试试题... .......... .. 130 第 28届“迎春杯”数学解题能力展示评选活动五年级初试试题... .......... .. 132 第 28届“迎春杯”数学解题能力展示评选活动六年级初试试题... .......... .. 134 第 28届“迎春杯”数学解题能力展示评选活动高年级复试试题... .......... .. 136 第 29届“迎春杯”数学解题能力展示评选活动三年级初试试题... .......... .. 138 第 29届“迎春杯”数学解题能力展示评选活动四年级初试试题... .......... .. 140 第 29届“迎春杯”数学解题能力展示评选活动中年级复试试题... .......... .. 141 第 29届“迎春杯”数学解题能力展示评选活动五年级初试试题... .......... .. 143 第 29届“迎春杯”数学解题能力展示评选活动六年级初试试题... .......... .. 144 第 29届“迎春杯”数学解题能力展示评选活动高年级复试试题... .......... .. 145第 1 届“迎春杯”数学竞赛刊赛试题1．天安门广场是世界上最大的广场，面积约44万平方米，合____亩。

第一讲应用题行程问题行程问题的三个基本量是距离、速度和时间。

其互逆关系可用乘、除法计算，方法简单，但应注意行驶方向的变化，按所行方向的不同可分为三种：（1）相遇问题；（2）相离问题；（3）追及问题。

行程问题的主要数量关系是：距离=速度×时间。

它大致分为以下三种情况：（1）相向而行：相遇时间=距离÷速度和（2）相背而行：相背距离=速度和×时间。

（3）同向而行：速度慢的在前，快的在后。

追及时间=追及距离÷速度差在环形跑道上，速度快的在前，慢的在后。

追及距离=速度差×时间。

解决行程问题时，要注意充分利用图示把题中的情节形象地表示出来，有助于分析数量关系，有助于迅速地找到解题思路。

例题1.甲、乙两辆汽车同时从两城相对开出，甲车每小时行55千米，乙车每小时行45千米，经过3小时相遇，问两城之间相距多少千米?例题2．一辆公共汽车和一辆小轿车同时从相距450千米的两地相向而行，公共汽车每小时行40千米，小轿车每小时行50千米，问几小时后两车相距90千米?例题3．甲、乙两列火车从相距770千米的两地相向而行，甲车每小时行45千米，乙车每小时行41千米，乙车先出发2小时后，甲车才出发。

甲车行几小时后与乙车相遇?例题4。

李明和王亮同时分别从两地骑车相向而行，李明每小时行18千米，王亮每小时行16千米，两人相遇时距全程中点3千米。

问全程长多少千米?例题5.两地相距900米，甲、乙二人同时、同地向同一方向行走，甲每分钟走80米，乙每分钟走100米，当乙到达目标后，立即返回，与甲相遇，从出发到相遇共经过多少分钟?例题6.一个圆形操场跑道的周长是500米，两个学生同时同地相背而行。

甲每分钟走66米，乙每分钟走59米。

经过几分钟才能相遇?工程问题在解答工程问题时，如果对题目提供的条件孤立、分散、静止地看，则难以找到明确的解题途径，若用“组合法”把具有相依关系的数学信息进行恰当组合，使之成为一个新的基本单位，便会使隐蔽的数量关系立刻明朗化，从而顺利找到解题途径。

迎春杯考试历年真题及答案2、小红、小明、小方三个人在玩一个叫“屠龙”的游戏，需要若干20个面的骰子。

为了杀死小明的恶龙，小红掷了25个20面骰子，其总和却只有70。

小方安慰他说，在那个和下，骰子的点数乘积达到了最大值。

小红掷的骰子中有____________________个点数是2。

【解析】两个数的和一定时，数越接近乘积越大。

所以70÷25=2余20所以20个3和5个2连乘乘积最大。

结果为5。

【答案】：53、一个月的第一个星期日和最后一个星期日的日期数之和能取到的所有自然数中，最多包含____________________个连续的自然数。

【解析】七日为一个周期，每月最少28天，最多31天。

当一号为周日时，最后一个周日可能为22号和29号。

2号为周日时最后一个周日可能为23和30号。

以此类推，共可能的和为23、25、27、29、30、31、32、33、34、35。

其中29到35连续7天。

【答案】：74。

定义g□K=gK+g2，g◇K=g+3K，则(2□3)(3◇2)=____________________。

【解析】2□3=2×3+22=103◇2=3+3×2=910×9=90【答案】：905。

喜羊羊每星期一、二、四说谎，其他日子说实话；懒羊羊每星期一、三、六说谎，其他日子说实话。

一周内（从星期一到星期日），灰太狼问喜羊羊和懒羊羊“昨天是不是你说谎的日子？”那么这七天中，有____________________天喜羊羊和懒羊羊回答相同（都回答“是”或者都回答“否”）。

【解析】6、如图所示，每行每列都是1到5各一次，则最右一列从上到下组成的五位数是____________________。

□□＜□□□∨□□□□□∨□□＞□□＜□∨□□□□□∧□□□＜□＜□【解析】突破口一□4＜5□□∨□3□□□∨□2＞1□＜□∨□□□□□∧□□□＜□＜□突破口二□□＜□□□∨□□□□□∨□□＞□□＜□∨□5□□□∧□1□＜□＜□突破口三□□＜□□□∨□□□□□∨□□＞□□＜□∨□□□□□∧□□3＜4＜5进而确定每一个数，最终答案为21435。

迎春杯2011年-2017年中高年级初赛复赛试题真题整理2011年少儿迎春杯三年级初赛(试题)2010年12月19日“数学解题能力展示”读者评选活动三年级组初赛试题（活动时间：12月19日11:00—12:00；满分150）一、填空题Ⅰ（每题8分，共40分） 1.计算：82-38+49-51= .2.超市中的某种汉堡每个10元，这种汉堡最近推出了“买二送一”的优惠活动，即花钱买两个汉堡，就可以免费获得一个汉堡，已知东东和朋友需要买9个汉堡，那么他们最少需要花元钱。

3.小亮家买了72个鸡蛋，他们家还养了一只每天都下一个蛋的母鸡；如果小亮家每天吃4个鸡蛋，那么，这些鸡蛋够他们家连续吃天。

4.5个只由数字8组成的自然数之和为1000，其中最大的数与第二大的数之差是.5．已知：1×9+2=1112×9+3=111123×9+4=1111……△×9+○=111111那么△+○= .二、填空题Ⅱ（每题10分，共50分）6.四月份共有30天，如果其中有5个星期六和星期日，那么4月1日是星期.（星期一至星期日用数字1至7表示）7．小明把三支飞镖掷向下图所示的镖盘上，然后把三支飞镖的得分相加，镖盘上的数字代表这个区域的得分，未中镖盘记0分.那么小明不可能得到的总分最小是.8.一天中午，孙悟空吃了10个桃子，猪八戒吃了25个包子，孙悟空说猪八戒太能吃了，但猪八戒说自己的包子比桃子小得多，还是孙悟空吃的多.聪明的沙僧用天平得到了下面两种情况，（圆圈是桃子，三角是包子长方形表示重量为所标数值的砝码），那么1个桃子和1个包子共重克.9．在算式 =2010中，不同的字母代表不同的数字. 那么，A+B+C+D+E+F+G=.10．红星小学组织学生参加队列演练，一开始只有40个男生参加，后来调整队伍，每次调整减少3个男生，增加2个女生，那么调整次后男生女生人数就相等了.三、填空题Ⅲ（每题12分，共60分）11．如图1是一个3×3的方格表，每个方格（除了最后一个方格）都包含了1～9中某个数字和一个箭头，每一个方格中的箭头都正好指向了下一个数字所在方格的方向，如1号方格的箭头指向右方，代表2号方格在1号方格右方，2号方格指向斜下，代表3号方格在2号斜下方，3号方格指向上方，代表4号方格在3号方格上方，……（指向的方格可以不相邻），这样正好从1到9走完整个方格表。

经典例题【考点分析】约数个数定理【教学提示】因为大家学的都不好，所以出题人特别爱出.约数个数定理是六年级迎春杯的常客.本题比较难说服学生的是为何只有因子2和3而无其他.【解析【解析】】假设无因子3，则其3倍的约数个数为原数的2倍，则原数有3个约数，说明其必为某质数的平方数；但不论其为22还是其他质数的平方数，都不满足第一个条件.则此数必有因子3.再假设无因子2，则其2倍的约数个数为原数的2倍，则原数有2个约数，说明其必为3本身，这就不符合第二个条件，说明必有因子2.再假设这个数只能含2和3的因子，因为如果它还有别的因子，例如5，那么最后增加的个数要比给定的数字大.设23a b x =⋅，它的约数有()()11a b ++个，它的2倍为123a b +⋅，它的约数有()()111a b +++个.()()()()1111112a b a b b +++−++=+=，1b =同样的，它的3倍为123a b +⋅，它的约数为()()111a b +++个，比原数多3个()()()()1111113a b a b a +++−++=+=，2a =所以这个数的形式是22312⋅=【拓展】(2009年迎春杯五年级初赛)200名同学编为1至200号面向南站成一排．第1次全体同学向右转（转后所有的同学面朝西）；第2次编号为2的倍数的同学向右转；第3次编号为3的倍数的同学向右转；……；第200次编号为200的倍数的同学向右转；这时，面向东的同学有名．【考点分析】约数个数定理【解析【解析】】显然每位同学转的次数等于其编号的约数个数．从面南到面东，应转了3次或7次或11次…．由于3、7、11...都是奇数，则这些数首先是平方数，枚举200内14个平方数的约数个数发现：22，23，25，27，211，213有3个正约数；62有7个正约数，4223×有15个正约数；综上所述，面向东的同学有8名．【考点分析【考点分析】】“物不知其数”【教学提示】可通过改数字增加题目难度.【解析】对这批书补2本，则图书总数同时是24，28，32的整数倍，而[]242832672=，，且67221000×>，所以共有6722670−=（本）．【考点分析】位值原理，最值【解析】25()A B C D E A B C D E ××××=×++++，令5D E ==且A B C ≥≥，则有：()555525A B C A B C ××××=++++×，即10A B C A B C ××=+++⑴若9A =，则919BC B C =++，3BC =时8B C +=，显然无解.⑵若8A =，则818BC B C =++，3BC =时6B C +=，无解.⑶若7A =，则717BC B C =++，3BC =时4B C +=3,1B C ⇒==.得最大值75531；【拓展】(2010年迎春杯五年级初赛)已知一个五位回文数等于45与一个四位回文数的乘积（即45abcba deed =×）,那么这个五位回文数最大的可能值是.【考点分析】位值原理，整除性质【解析】45⇒5abcba 且9abcba .显然5a =，再令9b =，分析59959□⇒8=□，五位数最大为59895；【考点分析】枚举树【解析】标上字母如右图，Q Q A C E D F H BH F D E B→→→→→→→→→→→→↘从A 若第一次到C ，共有2种，经过F 、D 点也分别有2种.∴共有6种.【考点分析】分类枚举【教学提示【教学提示】】枚举法是计数问题的基础，其最高准则为“不重不漏”，这看似容易，实际上对孩子要求很高，这类题的错误率是极高的，应引起全面重视【解析【解析】】显然马至少要走4步，第一步必须走到如图A1、A2、A3处，第三步必须走到B1、B2、B3处，研究第二步的可能性：(1,1)1f A B =,(1,2)2f A B =,(1,3)0f A B =(2,1)2f A B =,(2,2)2f A B =,(2,3)2f A B =(3,1)0f A B =,(3,2)2f A B =,(3,3)1f A B =可见，共有12条.A1A2A3B1B2B3的方格表，现将数字1~6填入空白方格中，使得每一行、每一列数字1~6都恰好出现一次；图中已经填了一些数字．那么剩余空格满足要求的填写方法一共有种．【考点分析】数独、乘法原理【教学提示】高度对称数阵，其填法也是高度对称【解析】如图，图中4个a 地位平等，都只能填1或6，显然只有2种填法同理，4个b、4个c、4个d 都有2种填法，因此全表共有222216×××=种填法.a ac cd db bd db ba ac c表格的格子中，每个格子最多放一枚，如果要求每行,每列都有棋【考点分析】加乘原理、排列组合【教学提示】不重不漏的分类非易事【解析【解析】】显然必有一行拥有2枚棋子，从而首先任取一行再从本行中任取两格，共124424C C⋅=种情况.图1为24种情况之一.此时，第二列的棋子可能在前两枚棋子下，也可能不在其下；在其下时，三四行的棋子只有2种方法，不在其下时，三四行有2417×−=种方法：可见全图共有24(2227)432××+×=种放法.日组织同学们看电影，确定好日期后，老师告诉了班长，但是由于或者把10听成4），班长又把日期告诉那么小明认为看电影的日期是正确的可能性为_____%【考点分析】概率【教学提示】六年级专项考点【解析】小明认为正确的情况有两种：（1）班长正确、小明正确，共（1−10%）×（1−10%）=81%；（2）班长错误、小明错误，10%×10%=1%.共81%+1%=82%.☆☆☆☆☆☆☆☆【考点分析】竖式数字谜，最值【教学提示】数字谜最值的绝招：从理论最值试起.【解析】最小值为102：10225225704×=【考点分析】横式数字迷【教学提示】显然，突破口在小数部分.【解析】ABC DE−是整数，所以，小数只能由22010FIGH−产生.2010I在12356I=，，，，时为整数，这要求2FGH的尾数为19，不可能.2010I在7I=、9时除不开，7I≠、9.4I=时，2010502.5I=，2690.69100FGH⎧⎫==⎨⎩⎭无解.∴8I=时，2010251.25I=，244110.4410025FGH⎧⎫===⎨⎬⎩⎭223662525F⇒==符合条件.3612.19251.2526225ABC DE−=+−=；剩下1，3，4，7，9，简单试验可知34179262−=，故34179ABCDE=实战演练1.(2007年迎春杯高年级初赛)甲、乙两个三位数的乘积是一个五位数，这个五位数的后四位为1031．如果甲数的数字和为10，乙数的数字和为8，那么甲乙两数之和是_________．【考点分析】弃九法【教学提示】有数字和的地方就有弃九法【解析】根据弃九法可得知，乘积是310313171113=×××，适当组合可得知两数为317217×=和1113143×=，和为360．2.(2009年迎春杯五年级初赛)从1、2、3、4、5、6中选取若干个数，使得它们的和是3的倍数，但不是5的倍数．那么共有种不同的选取方法．【考点分析】分类枚举、对应法【教学提示】对应法的应用是本题的亮点【解析】和只能为3,6,9,12,18和21，依次枚举：(21)1f=，(18)(3)2f f==，(12)(9)5f f==，(6)4f=，共有142(25)19++×+=种3.(2006年迎春杯六年级初赛)有两个三位数，百位上的数字分别是5和4，十位上的两个数字分别是6和7，个位上的数字分别是3和4．当时这两个三位数分别是和时，它们的乘积最大．【解析】和一定时差小积大：563474×最大.4.(2008年迎春杯高年级复赛)在图中55×的方格表中填入A、B、C、D四个字母，要求：每行每列中四个字都出现一次；如果某行的左边标有字母，则它表示这行中第一个出现的字母；如果某行的右边标有字母，则它表示这行中最后一个出现的字母；类似的，如果某列的上边（或者下边）标有字母，则它表示该列的第一个（或者最后一个）出现的字母.那么A、B、C、D在第二行从左到右出现的次序是.ABCDAAD【解析】如右图ABCDAAD AA B C DB C D AD A B CA B C DC D A B5.(2009年迎春杯高年级复赛)从1至999中选出连续6个自然数，使得它们的乘积的末尾恰有4个0，一共有种选法.【解析【解析】】6个数的乘积中必须含有4个因子5和4个因子2，而6个数中最多只有2个5倍，这就需要6数中必有125倍和625倍．如果6个数中不含625，那么必须含有一个125的倍数和一个5的倍数，此时乘积恰有4个5和4个2，共有6212×=（种）选法；如果6个数中含有625，只有621~626，622~627，623~628，624~629，625~630这6种选法，其中620~625的乘积末尾有5个0，不满足要求，其它5种都满足要求（625~630的乘积中含有5个5，4个2，满足要求，满足要求））．综上所述，共12517+=（种）选法．。