金属电子论习题

一、金属材料1.定义：凡由金属元素或以金属元素为主而形成的，并具有一般金属特性的材料称为金属材料。

2.纯金属与合金纯金属：基本上由一种金属元素组成的材料或物质。

杂质：无益的、偶尔混入的或难于净除而存留下来的元素。

（合金也含）合金：将两种或两种以上的金属元素或金属与非金属元素，经熔炼、烧结或其它方法形成具有金属特性的新物质称为合金。

合金元素：有益的、有意的加入或存留在某一金属材料中的一定数量的元素。

二、金属材料的一般性能1.工艺性能：在冷、热加工条件下表现出来的性能，在于能不能保证生产和制作的问题。

如铸造性、锻造性、焊接性、冲压性能、切削性及热处理性能等。

2.使用性能：在使用条件下表现出来的性能，在于保证能不能应用的问题。

（1）机械性能：材料受不同外力时所表现出来的特性，叫材料的力学性能又称机械性能。

（2）物理性能：包括密度、熔点、膨胀系数、导热性、电磁性等。

（3）化学性能：主要指常温或高温下工作时抵抗各种化学作用的能力。

三、决定金属材料性能的一般因素包括成分、组织、结构。

1.成分：组成金属材料的成分不同，性能不同；2.组织：指用肉眼或借助于各种不同放大倍数的显微镜所观察到的金属材料的内部情景，如晶粒的大小、形状、种类以及各种晶粒之间的相对数量和相对分布。

a）组织的分类：根据放大倍数的不同将组织分为三类：低倍组织或宏观组织：用肉眼或几十倍的放大镜所观察到的组织。

高倍组织或显微组织：用放大100--2000倍的显微镜所观察到的组织。

电镜显微组织或精细组织：用放大几千倍到几十万倍电子显微镜所观察到的组织。

b）有关组织的几个基本概念晶粒：组织的基本组成单位。

晶界：晶粒之间的界面。

亚晶粒：晶粒中的晶粒。

亚晶界：亚晶粒之间的界面。

3.结构：指原子集合体中各原子的具体组合状态。

对组织结构不敏感的性能：当化学成分给定时，金属材料的某些性能对结构的变化，特别是对组织的变化很不敏感，以致从应用角度，可忽略不记，这类性能为对组织结构不敏感性能。

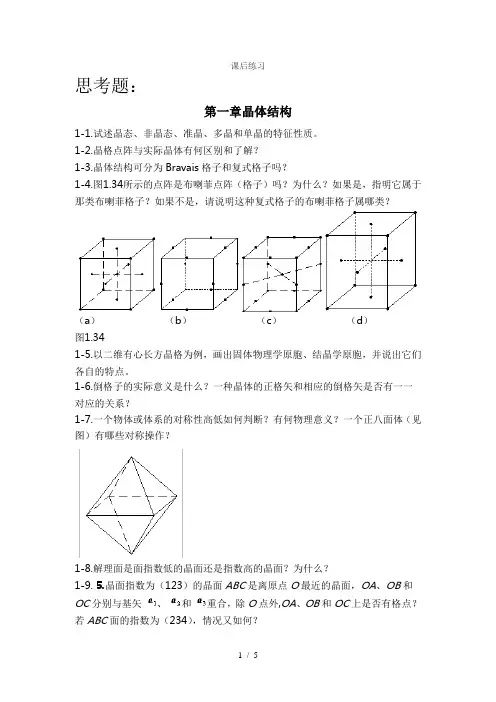
课后练习思考题：第一章晶体结构1-1.试述晶态、非晶态、准晶、多晶和单晶的特征性质。

1-2.晶格点阵与实际晶体有何区别和了解？1-3.晶体结构可分为Bravais格子和复式格子吗？1-4.图1.34所示的点阵是布喇菲点阵（格子）吗？为什么？如果是，指明它属于那类布喇菲格子？如果不是，请说明这种复式格子的布喇菲格子属哪类？（a）（b）（c）（d）图1.341-5.以二维有心长方晶格为例，画出固体物理学原胞、结晶学原胞，并说出它们各自的特点。

1-6.倒格子的实际意义是什么？一种晶体的正格矢和相应的倒格矢是否有一一对应的关系？1-7.一个物体或体系的对称性高低如何判断？有何物理意义？一个正八面体（见图）有哪些对称操作？1-8.解理面是面指数低的晶面还是指数高的晶面？为什么？1-9. 5.晶面指数为（123）的晶面ABC是离原点O最近的晶面，OA、OB和OC分别与基矢、和重合，除O点外,OA、OB和OC上是否有格点？若ABC面的指数为（234），情况又如何？1-10.带轴为[001]的晶带各晶面，其面指数有何特点？1-11. 与晶列[l1l2l3]垂直的倒格面的面指数是什么?1-12. 在结晶学中,晶胞是按晶体的什么特性选取的?1-13. 六角密积属何种晶系?一个晶胞包含几个原子?1-14.体心立方元素晶体, [111]方向上的结晶学周期为多大?实际周期为多大?1-15. 面心立方元素晶体中最小的晶列周期为多大?该晶列在哪些晶面内?1-16. 在晶体衍射中，为什么不能用可见光？第二章固体的结合2-1.试述离子键、共价键、金属键、范德瓦尔斯键和氢键的基本特征.2-2.有人说“晶体的内能就是晶体的结合能”，对吗？2-3.当2个原子由相距很远而逐渐接近时，二原子间的力与势能是如何逐渐变化的？2-4.为什么金属比离子晶体、共价晶体易于进行机械加工并且导电、导热性良好？2-5.是否有与库仑力无关的晶体结合类型?2-6.如何理解库仑力是原子结合的动力?2-7.晶体的结合能,晶体的内能,原子间的相互作用势能有何区别?2-8.原子间的排斥作用取决于什么原因?2-9.原子间的排斥作用和吸引作用有何关系?起主导的范围是什么?2-10.共价结合为什么有“饱和性”和“方向性”?2-11.共价结合,两原子电子云交迭产生吸引,而原子靠近时,电子云交迭会产生巨大的排斥力,如何解释?2-12.试解释一个中性原子吸收一个电子一定要放出能量的现象.2-13.如何理解电负性可用电离能加亲和能来表征?2-14.何为杂化轨道?2-15.你认为固体的弹性强弱主要由排斥作用决定呢,还是吸引作用决定?第三章晶格振动与晶体的热学性质3-1.什么是简谐近似？3-2.试定性给出一维单原子链中振动格波的相速度和群速度对波矢的关系曲线，并简要说明其意义。

第四章 金属自由电子理论1.金属自由电子论作了哪些假设？得到了哪些结果？解：金属自由论假设金属中的价电子在一个平均势场中彼此独立，如同理想气体中的粒子一样是“自由”的，每个电子的运动由薛定谔方程来描述；电子满足泡利不相容原理，因此，电子不服从经典统计而服从量子的费米－狄拉克统计。

根据这个理论，不仅导出了魏德曼－佛兰兹定律，而且而得出电子气对晶体比热容的贡献是很小的。

2.金属自由电子论在k 空间的等能面和费米面是何形状？费米能量与哪些因素有关？解：金属自由电子论在k 空间的等能面和费米面都是球形。

费米能量与电子密度和温度有关。

3.在低温度下电子比热容比经典理论给出的结果小得多，为什么？解：因为在低温时，大多数电子的能量远低于费米能，由于受泡利原理的限制基本上不能参与热激发，而只有在费米面附近的电子才能被激发从而对比热容有贡献。

4.驰豫时间的物理意义是什么？它与哪些因素有关？解：驰豫时间的物理意义是指电子在两次碰撞之间的平均自由时间，它的引入是用来描写晶格对电子漂移运动的阻碍能力的。

驰豫时间的大小与温度、电子质量、电子浓度、电子所带电量及金属的电导率有关。

5.当2块金属接触时，为什么会产生接触电势差？解：由于2块金属中的电子气系统的费米能级高低不同而使热电子发射的逸出功不同，所以这2块金属接触时，会产生接触电势差。

6.已知一维金属晶体共含有N 个电子，晶体的长度为L ，设0=T K 。

试求： （1）电子的状态密度； （2）电子的费米能级； （3）晶体电子的平均能量。

解：(1)该一维金属晶体的电子状态密度为：dEdkdk dZ dE dZ E ⋅==)(ρ …………………………（1） 考虑在k 空间中，在半径为k 和dk k +的两线段之间所含的状态数为：dk Ldk dZ π=∆=k 2 …………………………（2） 又由于 mk E 222η=所以 mkdk dE 2η= …………………………（3） 将（2）和（3）式代入（1）式，并考虑到每个状态可容纳2个自旋相反的电子，得该一维金属晶体中自由电子的状态密度为：EmL E 22)(ηπρ= (4)（2）由于电子是费米子，服从费米—狄拉克统计，即在平衡时，能量为E 的能级被电子占据的几率为：11)(+=-TK E E B F eE f (5)于是，系统中的电子总数可表示为：⎰∞=)()(dE E E f N ρ (6)由于0=T K ，所以当0F E E >，有0)(=E f ，而当0F E E ≤，有1)(=E f ，故（6）式可简化为：⎰=)(FE dE E N ρ＝⎰0022FE dE E m L ηπ＝240FmE L ηπ由此可得： 222208mL N E Fηπ= (7)（3）在0=T K 时，晶体电子的平均能量为： ⎰∞=0)()(1dEE E Ef N E ρ＝dE EmL E N FE 2210⎰⋅ηπ＝230)(232F E m N L ηπ＝022223124F E mL N =ηπ 7.限制在边长为L 的正方形中的N 个自由电子，电子的能量为)(2),(222y x y x k k mk k E +=η。

u tΔΔS为平均附加速度:v0.23~2.4 nm电子在发生碰撞前可自由穿过10个晶格。

A. Sommerfeld下，电子的能量和动量不随时间或位置改变，此时可以用: ，其中的方向为平面波的方向，(E)和动量(P)由德布罗意关系表示n 2、n 3是整数。

从上述分析可见，在k 空间，电子的状态是分立的，只允许波矢k 具有确定的分立值。

这样k 可以被解释为量子数。

因此单电子的本征能量亦取分立值。

由于单电子的本征能量为：的区域所允许的k 点(许可态)的数目个电子对许可k 态的占据，简单地由泡利不相容原理态，电子自旋能够取两个可能值：k 空间的电子态密度自由电子气系统的基态T=0K ，N 个自由电子的基态，可从能量最态开始，按能量从低到态两个电子，依次填充个电子，它的空间具有最k F 为半费米球，其。

对于基态，费米球内所有状态都被电子占据，而费米球外的状态全部未被定义为费米球的表面，在基态它把占据态和未N 个自由电子的基态为电子浓度。

相对应的能量称为费米能量：所受到的外力为：由于自由电子的动量与波矢之间的关系：则由牛顿第二定律可知：从上式可以看出，波矢k将随时间变化。

时刻将电场施加到电子气的基态，则在后一时刻费米球中心将移到新的位置：如果不发生碰撞，恒定的外加电场将使k空间中的费米球匀速移动。

由于电子与离子实的碰撞将使电子失τ为迟豫时间，Δk决定电子的漂移速度(平均速度) 。

不同的是，在量子体系中，由于非平衡费米球中与E=0时费米球交叠部分，方向上分布的对称性，对电流没有贡献。

电流来源于原费米球面撞，费米球整体的位移Δk和外力F的关系可由下式给出：为电子的漂移速度。

项为自由电子加速度而项表示碰撞效应项(相当于电子遭受碰撞而引入的摩擦阻力。

作用在一个电子上的洛仑兹力为：数为零，于是：则运动方程为：轴平行于磁场，于是运动方程可写为：其中。

：固体的界面效应和表面效应在金属自由电子模型中，金属内部被假设为均匀势场，离子实提供一个正电背景。

《固体物理学》习题解答黄昆 原着 韩汝琦改编 （陈志远解答，仅供参考）第一章 晶体结构、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1） a=2r ， V=3r 34π，Vc=a 3，n=1∴52.06r8r34a r 34x 3333=π=π=π=（2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 3（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个（5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证：六方密排堆积结构中633.1)38(ac 2/1≈=证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是：NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

…、证明：面心立方的倒格子是体心立方；体心立方的倒格子是面心立方。

证明：（1）面心立方的正格子基矢（固体物理学原胞基矢）：123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩r r r r r rr r r由倒格子基矢的定义：1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ，223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r同理可得：232()2()b i j k ab i j k aππ=-+=+-r rr r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。

金属学原理习题库第一章1. 原子中一个电子的空间位置和能量可用哪四个量子数来决定？2. 在多电子的原子中，核外电子的排布应遵循哪些个原则？3. 铬的原子序数为24，共有四种同位数：4.31%的Cr 原子含有26 个中子，83.76%含有28 个中子，9.55%含有29 个中子，且2.38%含有30 个中子。

试求铬的原子量。

4. 铜的原子序数为29，原子量为63.54，它共有两种同位素Cu63 和Cu65，试求两种铜的同位素之含量百分比。

5. 已知Si 的原子量为28.09，若100g 的Si 中有5×1010 个电子能自由运动，试计算：(a)能自由运动的电子占价电子总数的比例为多少？(b)必须破坏的共价键之比例为多少？6. 何谓同位素？为什么元素的相对原子质量不总为正整数？7. 已知Si 的相对原子质量为28.09，若100g 的Si 中有5×1010 个电子能自由运动，试计算：(a)能自由运动的电子占价电子总数的比例为多少？(b)必须破坏的共价键之比例为多少？第二章1. 试证明四方晶系中只有简单立方和体心立方两种点阵类型。

2. 为什么密排六方结构不能称作为一种空间点阵？3. 标出面心立方晶胞中（111）面上各点的坐标。

4. 标出具有下列密勒指数的晶面和晶向：a)立方晶系(421)，(-123)，(130)，[2-1-1]，[311]；b)六方晶系(2-1-11)，(1-101)，(3-2-12)，[2-1-11]，[1-213]。

5. 试计算面心立方晶体的(100)，(110)，(111)，等晶面的面间距和面致密度，并指出面间距最大的面。

6. 平面A 在极射赤平面投影图中为通过NS 及核电0°N，20°E 的大圆，平面B的极点在30°N，50°W 处，a)求极射投影图上两极点A、B 间的夹角；b)求出A 绕B 顺时针转过40°的位置。

《固体物理学》习题解答黄昆 原着 韩汝琦改编 （陈志远解答，仅供参考）第一章 晶体结构、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1） a=2r ， V=3r 34π，Vc=a 3，n=1∴52.06r8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 3（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯n=1232126112+⨯+⨯=6个（5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证：六方密排堆积结构中633.1)38(ac 2/1≈=证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是：NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

…、证明：面心立方的倒格子是体心立方；体心立方的倒格子是面心立方。

证明：（1）面心立方的正格子基矢（固体物理学原胞基矢）：123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩r r r r r rr r r由倒格子基矢的定义：1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ，223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r 同理可得：232()2()b i j k ab i j k aππ=-+=+-r rr r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。

第一章 晶体结构1、把等体积的硬球堆成下列结构，求球可能占据的最大体积和总体积之比。

（1）简立方 （2）体心立方 （3）面心立方（4）金刚石 解：（1）、简立方，晶胞内含有一个原子n=1，原子球半径为R ，立方晶格的顶点原子球相切，立方边长a=2R,体积为()32R ，所以 ()33344330.5262n R R K V R πππ⋅==== （2）、体心立方晶胞内含有2个原子n=2，原子球半径为R ，晶胞边长为a ，立方晶格的体对角线原子球相切，体对角线长为4个原子半径，所以43a R =3334423330.68843n R R K V R πππ⋅⨯====⎛⎫⎪⎝⎭（3）、面心立方晶胞内含有4个原子n=4，晶胞的面对角线原子球相切，面对角线长度为4个原子半径，立方体边长为a,所以42a R =3334442330.74642n R R K V R πππ⋅⨯====⎛⎫⎪⎝⎭(4)、金刚石在单位晶格中含有8个原子，碳原子最近邻长度2R 为体对角线14长，体对角线为83R a = 3334483330.341683n R R K V R πππ⋅⨯====⎛⎫⎪⎝⎭2、证明面心立方和体心立方互为倒格子。

09级微电子学专业《固体物理》期末考复习题目至诚 学院 信息工程 系 微电子学 专业 姓名： 陈长彬 学号： 2109918033、证明：倒格子原胞体积为()3*2cvvπ=，其中v c为正格子原胞的体积。

4、证明正格子晶面 与倒格矢正交。

5能写出任一晶列的密勒指数，也能反过来根据密勒指数画出晶列；能写出任一晶面的晶面指数，也能反过来根据晶面指数画出晶面。

见课件例题 以下作参考： 15.如图1.36所示，试求：（1） 晶列ED ，FD 和OF 的晶列指数；（2） 晶面AGK ,FGIH 和MNLK 的密勒指数； （3） 画出晶面（120），（131）。

密勒指数：以晶胞基矢定义的互质整数( )。

u tΔΔS为平均附加速度:v0.23~2.4 nm电子在发生碰撞前可自由穿过10个晶格。

A. Sommerfeld下，电子的能量和动量不随时间或位置改变，此时可以用: ，其中的方向为平面波的方向，(E)和动量(P)由德布罗意关系表示n 2、n 3是整数。

从上述分析可见，在k 空间，电子的状态是分立的，只允许波矢k 具有确定的分立值。

这样k 可以被解释为量子数。

因此单电子的本征能量亦取分立值。

由于单电子的本征能量为：的区域所允许的k 点(许可态)的数目个电子对许可k 态的占据，简单地由泡利不相容原理态，电子自旋能够取两个可能值：k 空间的电子态密度自由电子气系统的基态T=0K ，N 个自由电子的基态，可从能量最态开始，按能量从低到态两个电子，依次填充个电子，它的空间具有最k F 为半费米球，其。

对于基态，费米球内所有状态都被电子占据，而费米球外的状态全部未被定义为费米球的表面，在基态它把占据态和未N 个自由电子的基态为电子浓度。

相对应的能量称为费米能量：所受到的外力为：由于自由电子的动量与波矢之间的关系：则由牛顿第二定律可知：从上式可以看出，波矢k将随时间变化。

时刻将电场施加到电子气的基态，则在后一时刻费米球中心将移到新的位置：如果不发生碰撞，恒定的外加电场将使k空间中的费米球匀速移动。

由于电子与离子实的碰撞将使电子失τ为迟豫时间，Δk决定电子的漂移速度(平均速度) 。

不同的是，在量子体系中，由于非平衡费米球中与E=0时费米球交叠部分，方向上分布的对称性，对电流没有贡献。

电流来源于原费米球面撞，费米球整体的位移Δk和外力F的关系可由下式给出：为电子的漂移速度。

项为自由电子加速度而项表示碰撞效应项(相当于电子遭受碰撞而引入的摩擦阻力。

作用在一个电子上的洛仑兹力为：数为零，于是：则运动方程为：轴平行于磁场，于是运动方程可写为：其中。

：固体的界面效应和表面效应在金属自由电子模型中，金属内部被假设为均匀势场，离子实提供一个正电背景。

《固体物理学》习题解答黄昆 原着 韩汝琦改编 （陈志远解答，仅供参考）第一章 晶体结构、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1）a=2r ， V=3r 34π，Vc=a 3，n=1 ∴52.06r8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 3（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 （5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证：六方密排堆积结构中633.1)38(a c 2/1≈= 证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是： NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

…、证明：面心立方的倒格子是体心立方；体心立方的倒格子是面心立方。

证明：（1）面心立方的正格子基矢（固体物理学原胞基矢）：123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩r r r r r rr r r由倒格子基矢的定义：1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ，223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r同理可得：232()2()b i j k ab i j k aππ=-+=+-r rr r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。