实验三十五用动态法测定金属的杨氏模量(精)
- 格式:doc
- 大小:95.50 KB
- 文档页数:5

动态法测量金属的杨氏模量实验步骤嘿,小伙伴们!今天来唠唠动态法测量金属的杨氏模量这个超有趣(其实有点小复杂啦,但咱把它说得有趣)的实验。
你得先找一块金属棒,这金属棒就像一个超级低调的大侠,默默等待着我们去探索它的秘密。
把这个金属棒小心地放在实验装置里,就像把大侠请进了专属的练武场。
然后呢,要在金属棒上贴个小薄片,这薄片就像是给大侠贴的一个小标签,不过这个小标签可有大作用,它能帮我们感知金属棒的振动情况呢。
接着,我们要启动一个能让金属棒振动起来的装置。
这就好比是给大侠注入一股神秘力量,让他开始施展自己的“武功”。
那振动起来的金属棒就像在跳一种独特的舞蹈,一扭一扭的,超级可爱(如果金属棒有表情,估计是很兴奋的样子)。
这时候,我们得拿出一个神奇的仪器来测量它的振动频率。
这个仪器就像一个超级灵敏的耳朵,能精准地捕捉到金属棒振动的节奏。
就好像这个仪器在说:“嘿,小棒棒,你跳得再快我也能跟上你的节奏。
”在测量的时候啊,一定要保持周围环境安静,不然就像在大侠表演绝世武功的时候旁边有人在敲锣打鼓乱干扰,那可不行。
测量完频率后,还得记录好多数据呢。
这些数据就像是一堆小宝藏,每个数字都藏着金属棒的小秘密。
要是不小心记错了一个,那就像是弄丢了一块宝藏碎片,整个宝藏就不完整啦。
之后呢,要根据一些复杂(但也不是特别难啦,就像走迷宫,有路线可循)的公式来计算杨氏模量。
这公式就像是一把神秘的钥匙,我们要把那些数据宝藏当作锁孔,用钥匙去打开隐藏着杨氏模量这个大宝贝的大门。
在计算过程中,可不能粗心大意哦。
要是算错了,就像你本来要做一个超级美味的蛋糕,结果把盐当成了糖,那可就全毁啦。
最后,当我们算出杨氏模量的时候,就像是终于揭开了大侠的神秘面纱,看到了他隐藏在深处的真正实力。
然后就可以得意地把这个结果展示出来,就像展示自己发现的一个超级大秘密一样。
怎么样,这个实验是不是很有趣呢?。



动态悬挂法测定金属材料的杨氏模量杨氏模量是工程材料的一个重要物理参数,它标志着材料抵抗弹性形变的能力。
目前工程技术上常用“动态悬挂法”测量杨氏模量。
其基本方法是:将一根截面均匀的试样(棒)悬挂在两只传感器(一只激振,一只拾振)下面。
在两端自由的条件下,使之作自由振动。
测出试样的固有基频,并根据试样的几何尺寸、密度等参数,测得材料的杨氏模量。
【实验目的】1. 用动态悬挂法测定金属材料的杨氏模量。
2. 学习确定试样节点处共振频率的方法。
【实验要求】1. 用外延法求出节点处的共振频率。
2. 测定室温下金属材料的杨氏模量。
【实验原理】根据棒的横振动方程044222=∂∂⎟⎟⎠⎞⎜⎜⎝⎛+∂∂xy S EJ t y ρ (1) 用分离变量法解该方程,对圆形棒得 2436067.1f dm l E = (2) 上两式中,E 为杨氏模量,l 为棒长,d 为棒直径,S 为棒截面积,ρ为棒的密度,m 为棒的质量,f 为棒横振动的固有频率,J 为极性矩。
由式(2)可知,测定出试样(棒)在不同温度时的固有频率f 及各力学参数,即可计算出它在不同温度时的杨氏模量。
测量时可采用图(1)的示意装置。
本实验只计算室温下的杨氏模量,故不用加热炉。
实验中有两个问题需加注意。
1. 式(2)给出杨氏模量E 的计算公式中的f 是棒横振动的基频,在实验中要加以判断。
2. 从图1中看到测试棒横振动的激发与拾振是通过悬丝与换能器连接的。
若连接点不在棒横振动的波节上,则横振动的方程不满足。
若连接点就在波节上,则不能激发与拾取试样的振动。
因此为测定固有频率,一般可采用外延测量法来计算固有频率。
具体做法如下:按照方程(1)的解,测试棒时应对基频的横振动的两个波节分别在0.224 l 与0.776 l 。
见图2。
(a) 先将激振与拾振的两悬丝分别连接在棒0.1l 与0.9 l 上,寻找其共振频率f 1。
(b) 将两悬丝逐渐从每间隔0.02 l 间距向里推进,分别寻找出对应的频率f 2、f 3……。

物理科学与技术学院级弘毅班吴雨桥【实验原理】对于长度≫直径、两段自由地做微小横振动地均匀细棒,其振动满足方程式中,ρ为棒地密度,为棒地截面积,称为惯量矩(取决于截面地形状),为杨氏模量,为棒振动地位移,为位置坐标,为时间变量.文档来自于网络搜索用分离变量法解方程,令(,)()()代入方程,有解得该振动方程地通解为(,)()(ωφ)式中ω称为频率公式.频率公式对任意形状地截面、不同边界条件地试样都是成立地.我们只要用特定地边界条件定出常数,带入特定截面地惯量矩,就可以得到具体条件下地计算公式.如果悬线悬挂在试样地节点(处在共振状态地棒中,位移恒为零地位置)附近,则棒地两端均处于自由状态.此时其边界条件为自由端横向作用力和弯矩均为零,即文档来自于网络搜索弯矩故有文档来自于网络搜索将通解代入边界条件,可以得到*,可用数值解法求得本征值和棒长应满足,,,,,...文档来自于网络搜索一般将所对应地频率称为基频频率.试样在做基频振动时,存在两个节点,它们地位置距离端面为和处.将第一本征值代入频率表达式,得到自由振动地固有圆频率(基频)文档来自于网络搜索ω解出杨氏模量*对于直径为地圆形棒,惯量矩(代入上式可得式中,为棒长,为棒地直径,为棒地质量,为试样共振频率.在国际单位制中杨氏模量地单位为.文档来自于网络搜索实际上,还和试样地直径与长度之比地大小有关,所以乘以一个修正因子,则有当≫时,≈;当≫不成立时,圆棒地可查表试样与地关系当外力频率达到共振频率ω时,另一悬线处会接收到最大振幅,而固有频率与共振频率之间地关系为,为阻尼系数.对于一般地金属材料,β地最大值只有ω地左右,所以可用代替计算.文档来自于网络搜索实验中,由于细丝对试样地阻尼,所检测地共振频率大小是随悬挂点地位置而变地.理论上,测量试样地基频振动时,悬挂点应在节点处,即悬点距端点和处.但是在这种情况下,棒地振动无法被激发,振幅为零,在示波器上只能看到一条直线.欲激发棒地振动,悬点必须离开节点位置,故采用外延法测量试样地基频,即测量节点周围地点地振动频率,利用他们作图延伸至节点位置,从图像上得到试样地基频.(外延法:指所需要地数据在测量范围之外,一般较难测量,为了求得这个值,利用已得地数据绘制出曲线,再将曲线按原规律延长到待求值范围,在延长线部分求得所需地值.此方法只适用于在所研究范围内没有突变地情况.)文档来自于网络搜索【实验仪器】功率函数信号发生器、换能器(两个)、示波器、温控器、天平、游标卡尺、螺旋测微器、测试架、待测试样等.本实验地基本问题是测量在一定温度下试样地共振频率.实验中采用悬挂法.由信号发生器输出地等幅正弦波信号,加在换能器上.通过换能器把电信号转变成机械振动,再由悬线(或支撑物)把机械振动传给试样,使试样做横向振动.试样另一端地悬线(或支撑物)把机械振动传给换能器,这时机械振动又转变成电信号.该信号输入示波器中显示.文档来自于网络搜索当信号发生器地频率不等于试样地固有频率时,试样不发生共振,示波器上几乎没有波形和波形很小.当信号发生器地频率等于试样地固有频率时,试样发生共振,示波器地波形突然增大,这时频率计上读出地频率就是试样在该温度下地共振频率.将此值代入,即可计算出该温度下地杨氏模量.文档来自于网络搜索若将试样置于可控温加热炉中,不断改变加热炉地温度,即可测出不同温度下地杨氏模量.【实验内容】.测量试样地长度、直径和质量用米尺测量试样地长度;用游标卡尺测量试样地直径(注意在不同地部位和不同地方向多次测量);用电子天平称量试样地质量.为提高测量精度,以上各量至少测量次,记入表中.文档来自于网络搜索.测量试样在室温时地共振频率()室温下铜和不锈钢地杨氏模量分别为**和**,估算出共振频率,以便寻找共振点.文档来自于网络搜索()安装试样棒,对称悬挂并保持试样水平,悬丝与试样垂直,选择适当地悬丝长度.()将仪器连接好,并调整仪器到正常状态.()从试样端点开始,两悬点同时向中间移动,每间隔测量一次共振频率,记录在表中.每次测量时,调节信号发生器地输出频率,使示波器上观察到地共振峰地幅度达到最大值,此时信号发生器地输出频率即为该点地共振频率.文档来自于网络搜索()真假共振峰地判别(鉴频)在寻找共振频率时,调节信号发生器要极其缓慢,到共振频率附近时改用“频率微调”旋钮调节,换能器及整个系统都有自己地共振频率,换能器地输入伴随有许多次极大值,故测量时一定要找到真地共振峰进行测量.文档来自于网络搜索)峰宽判别法.真地共振峰地频率范围很窄,细微地改变信号发生器地输出频率,共振峰地幅度就会发生突变:假地共振峰频率范围很宽.文档来自于网络搜索)幅度判别法.用手将试样托起,如果是干扰信号,则示波器上正弦波幅度不变;如果是共振信号,则共振信号地周期不变,幅度逐渐衰减.文档来自于网络搜索)声音判别法.发生共振时,拾振器会发生尖锐地啸叫..测杨氏模量将试样棒放入到加热炉中,升温后测出不同温度下地共振频率.【数据处理】测量次数平均值长度直径质量测量次数平均值长度直径质量共振频率测量悬点共振频率共振频率测量悬点共振频率回归方程^所以地共振频率为510152025303540740741742743744745746747748x/mmf /H zf-x 曲线 Cu510152025303540831832833834835836837838839840x/mmf /H zf-x 曲线 Fe回归方程^^所以地基频对于,平均* * 平均* 平均±*±*文档来自于网络搜索对于,平均* * 平均* 平均±*±*文档来自于网络搜索【误差分析】.系统误差()仪器误差:)、、、地测量因为仪器地精度问题有一定地不确定度.)金属棒上地标定刻度线有一定误差.()理论误差)理论中使用了近似估计)理论中用了图像法,必定会产生一定地误差..随机误差)读数时有一定地误差.)温度等对各个物理量地大小有一定地影响【注意事项】.试样不可随意乱放,一定要保持清洁..悬挂试样时,悬丝必须将试样捆紧.测量时应尽量避免试样摆动..实验中拿放东西要轻,不可敲击桌面和大声说话,以免对实验造成影响.。
实验名称 动态悬挂法测定金属材料的杨氏模量一.目的与要求1.用动态悬挂法测定金属材料的杨氏模量。
2.培养综合应用物理仪器的能力。
3.学习用图示法表达实验结果。
二.原理根据棒的横振动方程:02244=∂∂+∂∂tyYJ S x y ρ (1) 式中J Y S 、、、ρ分别表示材料的密度、样品(棒)的截面积、材料的杨氏模量、特定截面的惯量矩。
求解方程,得圆形棒的杨氏模量为2436067.1f dm l Y = (2)式中 为棒长,d 为棒的界面直径,m 为棒的质量。
若是矩形棒,则为3339464.0f bhm l Y = (3)式中 为棒长,h b 、分别为棒的宽、厚,m 为棒的质量。
在实验中测出样品棒的固有频率f ,即可由(2)、(3)式计算出样品的杨氏模量Y 。
在国际单位制中扬氏模量的单位为牛顿·米-2。
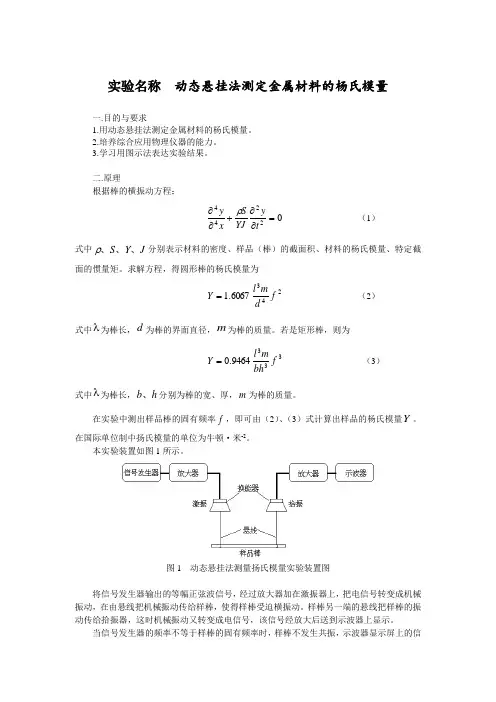
本实验装置如图1所示。
图1 动态悬挂法测量扬氏模量实验装置图将信号发生器输出的等幅正弦波信号,经过放大器加在激振器上,把电信号转变成机械 振动,在由悬线把机械振动传给样棒,使得样棒受迫横振动。
样棒另一端的悬线把样棒的振动传给拾振器,这时机械振动又转变成电信号,该信号经放大后送到示波器上显示。
当信号发生器的频率不等于样棒的固有频率时,样棒不发生共振,示波器显示屏上的信号的幅度不大。
当信号发生器的信号频率等于样棒的固有频率时,样棒发生共振,示波器上波形幅度突然增大,读出此时的频率为共振频率。
由于样棒的固有频率与共振频率相差甚小,可作为样棒的固有频率。
三.仪器悬挂法杨氏模量测量仪,示波器,低频信号发生器,电子秤,游标卡尺,铜棒和不锈钢圆棒样品。
四.实验内容与步骤1.测定样棒的长度、直径和质量;2.在室温下不锈钢和铜的杨氏模量分别约为11102⨯牛顿·米-2和111021⨯.牛顿·米-2,先估算出共振频率,以便寻找共振点。
3.分别测出不锈钢棒和铜棒的固有频率。
4.利用(2)式分别计算出不锈钢棒和铜棒的扬氏模量。

实验35 动态悬挂法测定杨氏模量
(一)数据记录及处理
表一样品棒测量数据(1)
(单次测量)
项目M(g)L(mm)F(Hz)
圆形铜棒
圆形不锈钢棒
表二样品棒直径测量数据(2)
d=mm d真=d铜0d-
螺旋测微计初始示值
次序圆形铜棒d铜(mm)圆形钢棒d钢(mm)d铜(mm)d钢(mm)1
2
3
4
5
6
(二)几个计算公式
(1)铜棒和不锈钢棒质量m、长度l、共振频率f的不确定度分别为:
u===g;
u===Hz;
l u =
== mm ; (注:天平分度值0.005m ∆=g ,游标卡尺分度值0.02l m ∆=mm ,信号发生器频率分度值0.5f m Hz ∆=)
(2)铜棒和不锈钢棒直径d 的不确定度分别为:
(a )直径d
的平均值标准偏差d S =(b )直径d 的B
类不确定度dB u =
== mm ; (注:螺旋测微计分度值0.004m ∆=mm )
(c )直径d
的合成不确定度d u =(d )杨氏模量32
41.6067l m E f d
=
(e )杨氏模量E 的相对不确定度
22
22)2()4()()3(f
u d u m u L u E f d m l E +++=
(f )杨氏模量E 的不确定度
E E u E E =⨯。
实验五用动态法测定金属杨氏模量【实验目的】1.学会用动态法测定材料的杨氏模量。
2.学会用外推法测量、处理实验数据。
3.了解压电陶瓷换能器的功能,熟悉信号源和示波器的使用。
4.培养学习综合运用知识和常用仪器的能力。
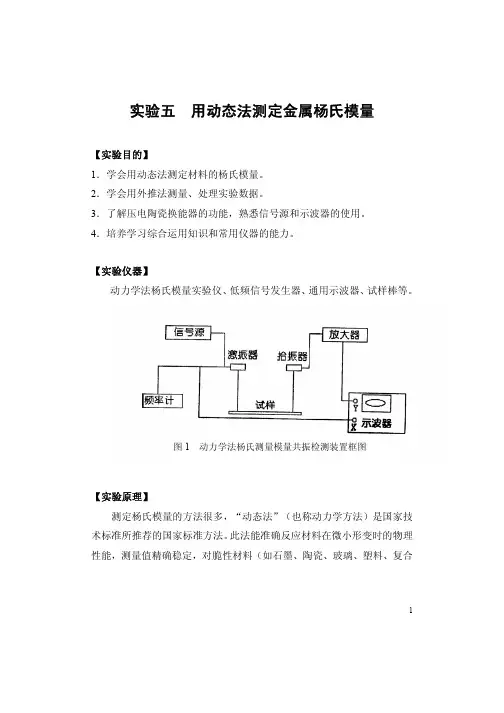
【实验仪器】动力学法杨氏模量实验仪、低频信号发生器、通用示波器、试样棒等。
图1 动力学法杨氏测量模量共振检测装置框图【实验原理】测定杨氏模量的方法很多,“动态法”(也称动力学方法)是国家技术标准所推荐的国家标准方法。
此法能准确反应材料在微小形变时的物理性能,测量值精确稳定,对脆性材料(如石墨、陶瓷、玻璃、塑料、复合1材料等)也能测定。
动态法适用的温度范围极广,从液氮―2600℃范围均可测量。
1.测量动态杨氏模量的概况金属动态杨氏模量的测定方法的概念是相对静态拉伸法而言的,其原理为:对于杆的微小横振动,可建立如下的振动方程:20xxxx u 2u u a −=其中:a 2=EI/ρ,E 为杨氏模量,ρ为物体密度,I 为试棒截面的“转动惯量”,对于两端自由的振动,根据其边界条件,用分离变数方法的试探解、超越方程、及振动频率取其基频等方法,一步步解得杨氏模量:3204l mf d 1.6067E =式中,l 为被测物长度,m 为其质量,d 为直径(设被测物为圆棒),f 0为共振频率。
2.共振频率f 的测量杨氏模量的测量方程式中,l 、m 、d 的测量均很容易,关键在于共振频率f 0的测量。
被测试棒可以用细线悬挂在换能器下面,也可以利用支撑式测试架放在换能器之上完成测试。
换能器由发射换能器(也称激振器)和接收换能器(也称拾振器)组成。
f 的测量方法为:信号发生器产生音频正弦讯号,通过压电陶瓷换能器转换成机械振动,由悬丝或支撑架传递给试棒,激发试棒振动,试棒的机械振动再通过另一根悬丝或支撑架传递给换能器还原成电迅号在示波器上显示出来,调节信号发生器的输出频率与试棒固有频率一致时,试棒共振,示波器上出现最大值。

动态法测量杨氏模量实验报告一、实验目的1、学会用动态法测量杨氏模量。
2、掌握共振频率的测量方法。
3、了解实验仪器的使用和数据处理方法。
二、实验原理杨氏模量是描述固体材料抵抗形变能力的物理量。
动态法测量杨氏模量的基本原理是基于振动系统的共振特性。
一根细长的棒,作微小横振动(弯曲振动)时,其振动方程为:$Y=\frac{4ml^3f^2}{d^4}$其中,$Y$为杨氏模量,$m$为棒的质量,$l$为棒的长度,$d$为棒的直径,$f$为棒的共振频率。
当棒在某一频率下发生共振时,振幅达到最大值。
通过测量棒的共振频率、质量、长度和直径,就可以计算出杨氏模量。
三、实验仪器1、动态杨氏模量测量仪:包括激振器、拾振器、示波器等。
2、游标卡尺:用于测量棒的长度和直径。
3、电子天平:用于测量棒的质量。
四、实验步骤1、测量棒的尺寸用游标卡尺在棒的不同位置测量其长度$l$,多次测量取平均值。
在棒的两端和中间部位测量直径$d$,同样多次测量取平均值。
2、安装实验装置将棒的一端固定在支架上,另一端通过细绳连接激振器。
拾振器安装在棒的适当位置,与示波器相连。
3、寻找共振频率开启激振器,逐渐改变其输出频率,同时观察示波器上的信号。
当示波器上显示的振幅达到最大值时,此时的频率即为共振频率$f$。
4、测量质量用电子天平测量棒的质量$m$。
5、重复测量改变拾振器的位置,重复上述步骤,测量多组数据。
五、实验数据记录与处理1、实验数据记录|测量次数|长度$l$ (mm) |直径$d$ (mm) |共振频率$f$ (Hz) |质量$m$ (g) ||::|::|::|::|::|| 1 |______ |______ |______ |______ || 2 |______ |______ |______ |______ || 3 |______ |______ |______ |______ |2、数据处理计算长度$l$、直径$d$、共振频率$f$和质量$m$的平均值。

动态法测量杨氏模量实验报告实验报告:动态法测量杨氏模量一、实验目的1.学习和掌握动态法测量杨氏模量的原理和方法。
2.锻炼动手操作能力,提高实验技能。
3.培养观察和分析实验数据的能力。
二、实验原理杨氏模量是描述材料抵抗弹性形变能力的物理量,是材料内部结构特性的反映。
动态法是一种常用的测量杨氏模量的方法,其原理是利用振动系统在弹性力和阻尼力的共同作用下,振动幅度随时间衰减的规律,通过测量衰减过程中的振动频率和阻尼比,计算得到材料的杨氏模量。
三、实验步骤1.准备实验器材:动态法测量杨氏模量的实验器材包括:激光器、光电池、振动样品、质量块、弹簧、阻尼器、数据采集器和计算机等。
2.安装实验器材:按照实验原理图,将激光器、光电池、振动样品、质量块、弹簧、阻尼器和数据采集器正确连接并安装好。
3.启动实验系统:打开计算机,进入实验操作系统,设置采样频率、采样点数和采样时间等参数。
4.进行实验操作:先将振动样品置于静止状态,然后启动振动系统,使振动样品产生振动。
根据实验需要,可改变振动频率、幅值和相位等参数。
5.记录实验数据:通过数据采集器采集样品的振动信号,记录各个采样点的振动频率和幅值。
同时,记录阻尼器的阻尼比。
6.数据处理与分析:利用记录的实验数据,进行数据处理和分析。
可以采用拟合等方法,得到样品的杨氏模量。
7.整理实验结果:整理实验数据,得到样品的杨氏模量测量结果。
同时,分析实验误差,提高实验精度。
四、实验结果与分析通过实验测量得到了样品的杨氏模量测量结果,并对其进行了误差分析和讨论。
以下是实验结果与分析的详细内容:1.实验结果:在本次实验中,我们测量得到样品的杨氏模量为18.5 GPa,测量误差为2.5%。
2.结果分析:通过对实验数据的处理和分析,我们发现误差主要来自于以下几个方面:一是人为操作误差,如激光器的调节和数据采集器的操作等;二是采样频率和采样点数的选择对测量结果也有一定影响;三是环境因素如温度和湿度等也可能对实验结果产生影响。
实验三十五用动态法测定金属的杨氏模量(最全)word资料实验三十五 用动态法测定金属的杨氏模量杨氏模量是描述固体材料弹性形变的一个重要物理量。
用静态拉伸法可以测出杨氏模量,但此方法的缺点是负荷大,加载速度慢,存在弛豫过程,不能真实地反映材料内部结构的变化;在拉伸过程中,样品的横向和纵向都有形变,而此法忽略横向形变;另外,也不能用于测量脆性材料。
动态悬挂法可以克服这些缺点,是一种非常实用的测量方法。
【实验目的】1. 学会用动态悬挂法测量金属材料的杨氏模量。
2. 培养学生综合应用物理仪器的能力。
【实验仪器】DCY-3型动态杨氏模量测定仪,信号发生器,示波器,游标卡尺,千分尺,物理天平等。
【实验原理】若将一均匀棒悬挂起来,如图5-35-2所示,并使之发生横向振动,其振动方程为02244=∂∂⋅+∂∂t yEJ S x y ρ 式中, y 为振动位移, x 为纵向变量, t 为时间, ρ为棒的密度, S 为棒的截面面积, E 为棒的 杨氏弹性模量, J 称为惯性矩。
振动方程为偏微分方程。
用分离变量法 求解方程(求解过程见附录),得:圆形棒图5-35-2(5-35-1)图5-35-1 DCY-3型动态杨氏模量测定仪 信号发生器 支撑支架2436067.1f dm l E =式中,l 为棒长,d 为棒的截面直径,m 为棒的质量,f 为棒的固有频率。
矩形棒2339464.0f bhm l E =式中,b ,h 分别为棒的宽和厚。
在国际单位制中,杨氏模量的单位为牛顿/米2(N ·m -2)。
实验原理图如5-35-3所示。
由信号发生器输出的正弦信号,加到激发换能器Ⅰ上,通过激发换能器Ⅰ把信号转变成机械振动,再由悬丝把机械振动传给待测试样,使试样受迫做横向振动,试样另一端的悬丝将振动传给接受换能器Ⅱ,这时机械振动又转变成电信号。
该信号送到示波器中显示。
当信号发生器的频率不等于待测试样的固有频率时,试样不发生共振,示波器上没有电信号,或波形幅度很小。
动态法测定金属材料的杨氏模量杨氏模量是工程材料的一个重要物理参数,它标志着材料抵抗弹性形变的能力。
测量材料杨氏模量的方法很多,诸如拉伸法、压入法、弯曲法和碰撞法等。
拉伸法是最常用的方法之一。
但该方法使用的载荷较大,加载速度慢,且会产生驰豫现象,影响测量结果的精确度。
另外,此法还不适用于脆性材料的测量。
本实验动态杨氏模量测量仪用振动法测量材料的杨氏模量。
【实验目的】1、了解测量材料杨氏模量的原理;2、学会用作图外推求值法测量振动体基频共振频率;3、学会用动态法测定金属材料的杨氏模量。
【实验器材】YJ-DYZ-I动态杨氏模量综合实验仪及其专用信号源、示波器、钢卷尺、游标卡尺、电子天平。
【实验原理】在外力的作用下,当物体的长度变化不超过某一限度时,撤去外力之后,物体又能完全恢复原状。
在该限度内,物体的长度变化程度与物体内部恢复力之间存在正比关系。
杨氏模量是反映材料应变(即单位长度变化量)与物体内部应力(即单位面积所受到的力的大小)之间关系的物理量。
或者说是反映材料的抗拉或抗压能力。
应变为单位长度的变化量:L L∆;应力为单位面积受到的力:F S;所以有:杨氏模量F SEL L=∆进一步得:F S ESE F L F kxL L L=⇒=∆⇒=∆ESkL=。
所谓“动态法”就是使测试棒(如铝棒、不锈钢棒、铜棒)产生弯曲振动,并使其达到共振,通过共振测量出该种材料的杨氏模量值。
在一定条件下(l d),试样在某温度下圆棒的杨氏模量为:3241.6067l mE fd=。
其中E为金属棒的杨氏模量,l为金属棒的长度,d为金属棒的直径,m为金属棒的质量。
在实验中测定了试样(金属棒)在某一温度时的固有频率(基频谐振频率)f ,即可计算出试样在该温度时的杨氏模量E 。
国际单位制中,杨氏模量的单位为-2•牛顿米。
现实情况不太可能达到ld 的条件,故对原理公式需要作些适当的修正,即原理公式基础上再乘以一个修正量。
3241.6067l m E f T d= 本实验统一近似取 =1.008T 。
动态法测量金属的杨氏模量实验步骤嘿,朋友们!今天咱来唠唠动态法测量金属杨氏模量的实验步骤哈。
咱先得把实验要用的那些玩意儿都准备齐全咯,就好比战士上战场
得把武器带好一样。
什么测试样品啊,激发换能器啊,接收换能器啊,可都不能少。
然后呢,把测试样品给它固定好喽,这就好比给房子打地基,得稳
稳当当的。
接下来,把激发换能器和接收换能器给它放好位置,就像
给两个好朋友找到最合适的位置聊天一样。
这时候,可别着急忙慌地就开始测啊,得先调整好各种参数,就跟
给汽车做保养似的,让它处在最佳状态。
等一切都准备就绪啦,就可以开始激发信号啦!这信号就像是给金
属样品发出的挑战书,看它能不能经得住考验。
在测量的过程中,咱得仔细盯着那些数据,就像猎人盯着猎物一样,不放过任何一个小细节。
你想想,要是错过了重要的数据,那不就跟
猎人放走了大猎物一样可惜嘛!
每一次测量都得认真对待,不能敷衍了事。
这可不是闹着玩的,就
跟走路一样,一步一个脚印,才能走得稳当。
测完一组数据还不算完事儿呢,还得再来几次,确保数据的准确性
和可靠性。
这就好比做题,多检查几遍才放心呀!
最后,把得到的数据好好整理分析一下,就像厨师烹饪美食一样,
精心调味,才能得出最终的结果。
总之啊,做这个实验可不能马虎,每一个步骤都得用心去做。
只有
这样,咱才能得到准确可靠的杨氏模量呀!大家说是不是这个理儿呢?可别小瞧了这些步骤,它们就像是通向成功的一个个小台阶,只有踏
踏实实地走上去,才能领略到科学的美妙啊!。
动态共振法测金属材料的杨氏模量摘要:动态共振法是一种常用的非破坏性测试方法,可以用于测量金属材料的杨氏模量。
本文将介绍动态共振法的原理和应用,以及在测量金属材料杨氏模量中的具体步骤和注意事项。
1. 引言杨氏模量是衡量金属材料刚度和弹性的重要指标,对于工程设计和材料选择具有重要意义。
传统的测量方法包括静态拉伸试验和压缩试验,但这些方法需要破坏样品,不适用于已加工的零件和复杂结构。
动态共振法作为一种非破坏性测试方法,逐渐被广泛应用于金属材料的杨氏模量测量。
2. 动态共振法原理动态共振法基于材料的固有振动频率与杨氏模量之间的关系,通过测量材料在不同频率下的共振振动来计算杨氏模量。
当材料受到外力激励时,会产生共振,即材料的振动幅度达到最大值。
通过测量共振频率和振动幅度,可以计算出杨氏模量的数值。
3. 动态共振法的应用动态共振法广泛应用于金属材料的杨氏模量测量。
例如,在航空航天领域中,需要对飞机结构和发动机零件进行杨氏模量测试,以保证其安全性和可靠性。
此外,在汽车制造、建筑工程和电子设备等领域,也需要进行金属材料的杨氏模量测量。
4. 动态共振法测量金属材料杨氏模量的步骤(1)选择适当的实验设备:动态共振法需要使用共振测试设备,包括振动台、加速度传感器和频谱分析仪等。
(2)准备样品:根据实际需求,选择合适的金属材料样品,并进行表面处理,以保证测试结果的准确性。
(3)固定样品:将样品固定在振动台上,并通过调整夹具和压紧螺栓等方式确保样品的固定稳定。
(4)施加外力:通过振动台施加外力激励样品,使其产生共振振动。
(5)测量共振频率:使用加速度传感器测量样品在不同频率下的共振振动,并记录共振频率。
(6)计算杨氏模量:根据共振频率和杨氏模量之间的关系,使用合适的公式计算杨氏模量的数值。
5. 动态共振法的注意事项(1)样品的表面处理要充分,以保证测试结果的准确性。
(2)样品的固定要牢固,以防止振动干扰和误差。
(3)在进行测试时要避免外界干扰,如风力、温度变化等。
实验三十五 用动态法测定金属的杨氏模量
杨氏模量是描述固体材料弹性形变的一个重要物理量。
用静态拉伸法可以测出杨氏模量,但此方法的缺点是负荷大,加载速度慢,存在弛豫过程,不能真实地反映材料内部结构的变化;在拉伸过程中,样品的横向和纵向都有形变,而此法忽略横向形变;另外,也不能用于测量脆性材料。
动态悬挂法可以克服这些缺点,是一种非常实用的测量方法。
【实验目的】
1. 学会用动态悬挂法测量金属材料的杨氏模量。
2. 培养学生综合应用物理仪器的能力。
【实验仪器】
DCY-3型动态杨氏模量测定仪,信号发生器,示波器,游标卡尺,千分尺,物理天平等。
【实验原理】
若将一均匀棒悬挂起来,如图5-35-2所示,并使之发生横向振动,其振动方程为
02
244=∂∂⋅+∂∂t y
EJ S x y ρ 式中, y 为振动位移, x 为纵向变量, t 为时间, ρ为棒的密度, S 为棒的截面面积, E 为棒的 杨氏弹性模量, J 称为惯性矩。
振动方程为偏微分方程。
用分离变量法 求解方程(求解过程见附录),得:
圆形棒
图5-35-2
(5-35-1)
图5-35-1 DCY-3型动态杨氏模量测定仪 信号发生器 支撑支架
2
436067.1f d
m l E =
式中,l 为棒长,d 为棒的截面直径,m 为棒的质量,f 为棒的固有频率。
矩形棒
2
339464.0f bh
m l E =
式中,b ,h 分别为棒的宽和厚。
在国际单位制中,杨氏模量的单位为牛顿/米2(N ·m -2)。
实验原理图如5-35-3所示。
由信号发生器输出的正弦信号,加到激发换能器Ⅰ上,通过激发换能器Ⅰ把信号转变成机械振动,再由悬丝把机械振动传给待测试样,使试样受迫做横向振动,试样另一端的悬丝将振动传给接受换能器Ⅱ,这时机械振动又转变成电信号。
该信号送到示波器中显示。
当信号发生器的频率不等于待测试样的固有频率时,试样不发生共振,示波器上没有电信号,或波形幅度很小。
当信号发生器的频率等于试样的固有频率时,试样发生共振,这时示波器上电信号波形幅度最大,此时信号发生器输出的信号频率,就是试样在该温度下的共振频率,代入公式(5-35-2),即可求出该温度下圆形棒试样的杨氏模量。
【实验内容】
一. 在室温下测量不锈钢棒和铜棒的杨氏模量
1. 用游标卡尺、物理天平分别测出不锈钢棒和铜棒的长度l 、质量m ,单次测量。
2. 用千分尺测出两种金属棒的直径d ,在不同位置测六次,多次测量,取平均值。
3. 在室温下不锈钢和铜的杨氏模量分别约为2×1011N/m 2和1.03×1011 N/m 2,先根据公式(5-35-2)估算出两种金属棒的共振频率,以便寻找共振点。
4. 将信号发生器的输出端与支撑支架上的接受端对应连接,并将支撑支架的输出端与示波器的X 和Y 轴输入端对应连接。
5. 将不锈钢棒和铜棒分别用悬丝悬挂于支撑支架上,把两个换能器的连接线与支撑支架上的接口对应连接。
6. 调节信号发生器的频率,当待测棒发生共振时,测出其固有频率f 。
7. 再利用公式(5-35-2)分别计算出不锈钢棒和铜棒的杨氏模量E 。
二. 在加热炉上测量不锈钢棒的杨氏模量
1. 将不锈钢棒用高温悬丝悬挂在加热炉中,并将热电偶测温点放入。
注意不要碰及不
(5-35-2)
(5-35-3)
图5-35-3实验原理图
试样棒
锈钢棒。
2. 用保温毡将加热炉两边开口以及顶部开口封死,只留二个小孔让悬丝通过。
3. 把两个换能器的连接线与支撑支架上的接口对应连接。
4. 先将温控器设定在100o C ,后至于测温处。
5. 将加热炉电源线接至温控器后面的插口内,升温至100o C 。
6. 测量不锈钢棒的固有频率并计算其杨氏模量。
7. 改变炉温,在200o C 、300o C 、400o C 和500o C 下分别测量固有频率并计算杨氏模量。
8. 测量完毕后,将加热炉的电源拔下。
(不锈钢棒的参数:L = 0.18m ,d = 0.006m ,m = 0.0430kg 。
)
【数据处理】
1.将测量值填入自拟表格中。
2.计算E 并与公认值比较,求出百分误差。
【注意事项】
1. 悬挂试样时,悬丝应悬挂试样的两端。
2. 在加热炉上测量时,换能器二个小钩应在炉体开口正上方,用φ0.05-0.15mm 高温悬丝将试样绑好绑紧,调整二悬丝在通过试样直径的铅垂面上。
将试样调整到水平位置,测量时二悬丝不能与任何物体接触。
3. 使用加热炉时,炉壳表面温度较高,务必注意避免烫伤。
4. 当调节信号发生器的频率时,在示波器上会观察到波形多次突然增大的现象,但这些频率并不是共振频率,只有在估算出的共振频率附近测出的共振点,才是试样的固有频率。
【预习思考题】
1. 试样棒的固有频率f 如何测量?在示波器上如何观察到共振现象?
2. 要在示波器上观察正弦波形,示波器应如何调整?
【思考题】
1. 动态法与静态法测杨氏模量有何不同?
2. 测量中如何确定试样的固有频率?
【附录】 棒的横振动方程的解
根据棒的横振动方程
02
244=∂∂⋅+∂∂t y
EJ S x y ρ (附5-35-1) 用分离变量法解方程,令
()()()t T x X t x Y =,
代入方程(附5-35-1)得
2
244d d 1d d 1t T
T EJ S x X X ρ-=
等式两边分别是x 和t 的函数,设等式等于常数K 4,得
d d 0d d 4
2
244
4=+=-S EJ
K t T X K x
X
ρ 这两个线性常微分方程的通解分别为
()()()
ϕω+=+++=t A t T Kx B Kx B Kx B Kx B x X cos sin cos sh ch 4321
振动方程的通解为
()()()ϕω+⋅+++=t A Kx B Kx B Kx B Kx B t x Y cos sin cos sh ch ,4321
式中
2
1
4
⎪⎪⎭
⎫
⎝⎛=S EJ K ρω (附5-35-2) 称为频率公式。
频率公式对任意形状的截面,不同边界条件的试样都成立。
我们只要用特定的边界条件定出常数K ,代入特定截面的惯性矩J ,就可以得到具体条件下的计算公式了。
如果悬丝挂在试样的节点附近,则边界条件为: 自由端的作用力
033=∂∂-=∂∂=x
y EJ X M F
弯矩 02
2=∂∂=x y
EJ M 即
l
x 2
2
2
2
l
x 330
33========dx X d dx X d dx X d dx X d x x
将通解代入边界条件,得到
1ch cos =⋅Kl Kl
用数值解法求得本征值K 和棒长l 应满足
Kl = 0、4.730、7.853、10.996、14.137、…
由于其中一个根“0”对应于静态情况,故将第二根Kl = 4.730作为第一个根,记作Kl ,通常将Kl 对应的频率称为基频,在上述nKl 值中,第1、3、5、…个数值对应着“对称形振动”,第2、4、6、…个数值对应着“反对称形振动”,最低级次的对称形和反对称形振动的波形如附图所示。
可见,试样在作基频振动时,存在着两个节点,位置距两个端面分别为0.224l 和0.776l 。
将第一本征值l
K 730
.4=
代入(附5-35-2)式,得到自由振动的固有频率,即基频
()2
1
44
730.4⎪
⎪⎭
⎫
⎝⎛=S l EJ ρω
解出杨氏模量
2
32
2
43
108870.110
9978.1f J
m
l J S
l E --⨯=⨯=ωρ
对圆棒
⎰⎪⎭
⎫
⎝⎛==2
2
4d d S y J
式中d 为圆棒直径,得到
2
436067.1f d
m l E =
对矩形棒
12
3bh J =
式中b 为棒宽,h 为棒厚,得到
2
339464.0f bh
m l E =
附图。