工程展开计算方法

建筑面积和展开面积的关系
在建筑设计和规划中，建筑面积和展开面积是两个重要的概念。

建筑面积是指
建筑物在平面上所覆盖的水平投影面积，通常用平方米（m²）为单位表示。

而展
开面积则是指建筑物各层平面展开后的总面积，也是一个重要的计算指标。

建筑面积和展开面积之间的换算一般是通过建筑物的高度和层高来进行计算的。

假设建筑物的平面形状为矩形，建筑面积为A平方米，高度为H米，层高为h米，则展开面积S可以通过以下公式来计算：
S = A + 2 * H * A / h
其中，A、H和h分别代表建筑面积、高度和层高。

通过这个公式，可以方便
地将建筑面积和展开面积进行换算。

在实际的建筑设计中，展开面积通常用于计算建筑物的总建筑面积和总建筑成本，是一个重要的参考指标。

除了矩形形状的建筑物，对于其他形状的建筑物，如圆形、多边形等，换算建
筑面积和展开面积的方法也可以通过适当的数学模型和计算来进行。

不同形状的建筑物可能有不同的换算方式，但总体原理是相似的，即通过建筑物的形状和尺寸参数来进行计算。

在建筑设计过程中，准确计算建筑面积和展开面积是非常重要的，可以帮助设
计师和规划者更好地评估建筑物的空间利用效率和功能性，同时也有助于控制建筑成本和资源利用。

因此，建筑面积和展开面积的换算是建筑设计中一个重要的计算环节。

拉伸件展开计算方法(一)拉伸件展开计算介绍拉伸件展开计算是在工程中常用的一种计算方法，通过对拉伸件进行展开计算，可以得到其在平面上的真实形态，为后续加工和制作提供便利。

本文将介绍几种常见的拉伸件展开计算方法，帮助读者更好地理解和应用这一技术。

直线法直线法是最简单和常用的拉伸件展开计算方法之一。

其基本原理是将拉伸件按照一定比例进行展开，使得各个部分的长度保持不变。

具体步骤如下： 1. 根据拉伸件的图纸确定其展开比例和展开方向。

2. 将拉伸件的边线按照展开比例进行延长，形成展开后的直线。

3.按照展开方向将拉伸件的各个部分进行展开，并标注相应的长度。

开发法开发法是比直线法更复杂一些的展开计算方法，适用于曲线较多或曲线形状复杂的拉伸件。

其基本原理是将拉伸件按照形状进行展开，保证展开后的形态与拉伸件的表面形状一致。

具体步骤如下： 1. 将拉伸件的图纸上的曲线边线，根据其曲率进行等分。

2. 沿着每个等分点的曲率方向，将对应的拉伸件边线延长。

3. 连接延长后的拉伸件边线，形成展开图形。

4. 对展开图形进行修整，使其与拉伸件表面形状一致。

三视图法三视图法是一种较为直观的展开计算方法，通过绘制拉伸件的三视图，可以得到其在各个投影面上的展开形态。

具体步骤如下： 1. 根据拉伸件的三视图，绘制其正视图、俯视图和侧视图。

2. 将三视图分别投影在展开平面上，得到对应的展开图形。

3. 将三个展开图形进行叠加，得到最终的拉伸件展开图形。

现代计算法随着计算机技术的发展，现代计算法在拉伸件展开计算中得到了广泛应用。

在计算机辅助设计软件的帮助下，可以通过数学模型和计算方法，准确地进行拉伸件的展开计算。

现代计算法的优点是快速、准确且易于修改，适用于各种复杂的拉伸件展开计算任务。

总结拉伸件展开计算是工程中重要的一环，不同的方法适用于不同的情况和要求。

直线法和开发法是传统的手工计算方法，适用于简单的拉伸件展开计算。

三视图法提供了更直观的展开计算方法，适用于适中复杂程度的拉伸件。

模板工程展开面积计算方案一、前言模板工程是指在建筑设计施工过程中，为了提高工程施工效率和资金利用效率而制定出的一套标准化施工方案。

在这个过程中，展开面积的计算就显得尤为重要。

展开面积是指建筑物在平面上的有效展开的面积，它是确定建筑物施工进度、材料运输、人员配置等的重要依据。

因此，建筑设计中展开面积的准确计算具有重要意义。

二、展开面积计算的相关知识展开面积是建筑物在平面上的有效展开的面积，它是建筑物的外形面积。

展开面积的计算是依据建筑物平面图纸上所标示的建筑物的各面积，计算出建筑物的展开面积。

建筑的展开面积主要包括墙体、楼板等。

1. 墙体展开面积的计算墙体展开面积是指在平面上所呈现的建筑物墙体的展开面积。

通常情况下，墙体展开面积的计算需要首先测量建筑物墙体的实际长度和高度，然后通过相应的公式进行计算。

墙体展开面积计算公式如下：展开面积 = 墙体的长度 × 墙体的高度2. 楼板展开面积的计算楼板展开面积是指建筑物楼板在平面上的展开面积。

通常情况下，楼板展开面积的计算需要测量建筑物楼板的实际面积，然后通过相应的公式进行计算。

楼板展开面积计算公式如下：展开面积 = 楼板的实际面积以上是墙体和楼板展开面积的计算方法，但是在实际的工程中，为了更准确地计算展开面积，还需要考虑一些特殊情况的处理，比如在墙体展开面积的计算中，要考虑窗户、门洞等的占据情况，而在楼板展开面积的计算中，也要考虑到梁柱的影响等。

三、模板工程展开面积计算方案在进行模板工程展开面积计算时，一般需要按照以下步骤进行：1. 收集设计图纸首先需要收集建筑物的设计图纸，包括平面图、立面图、剖面图等。

这些图纸可以作为展开面积计算的依据。

2. 分析平面图分析平面图的图形结构，确定建筑物的墙体、楼板等的展开面积计算方式。

要注意考虑到窗户、门洞等的影响，合理确定墙体的展开面积。

3. 计算展开面积按照上述所述的墙体和楼板展开面积计算公式，计算建筑物的展开面积。

封头展开计算公式
对于圆形封头来说，其展开计算公式非常简单，只需要知道封头的直径D即可。

圆形封头的表面积及圆弧长可以通过如下公式计算：表面积=π*D^2/4
圆弧长=π*D/2
对于椭圆形封头来说，其展开计算相对复杂些，需要知道封头的长轴a和短轴b。

椭圆形封头的表面积及圆弧长可以通过如下公式计算：表面积=π*a*b
圆弧长= π * (3 * (a+b) - sqrt((3*a+b)*(a+3*b)))
对于扁平形封头来说，展开计算也相对较为复杂，需要知道封头的外径Do、内径Di和高度h。

扁平形封头的表面积及圆弧长可以通过如下公式计算：
表面积=π*((Do-Di)*(Di+Do)+4*h^2)/4
圆弧长=π*(Do+Di)/2
这些计算公式在实际工程设计中非常实用，可以根据封头的形状和尺寸计算出封头的表面积和圆弧长等参数。

通过这些参数，可以进行封头的制造和装配设计，确保封头与压力容器的其他部分相匹配，并能够承受所需的压力。

在实际应用中，为了方便计算，常常使用计算机辅助设计（CAD）软件或者编写程序来进行封头展开计算。

这样可以提高计算的精度和效率，并且可以快速根据实际需求进行计算和调整。

总之，封头展开计算公式是工程设计中重要的计算方法，它可以帮助
设计人员确定封头的几何参数，从而确保封头的制造和装配设计符合要求。

在实际应用中，可以通过使用计算机软件或编写程序来进行封头展开计算，以提高计算的准确性和效率。

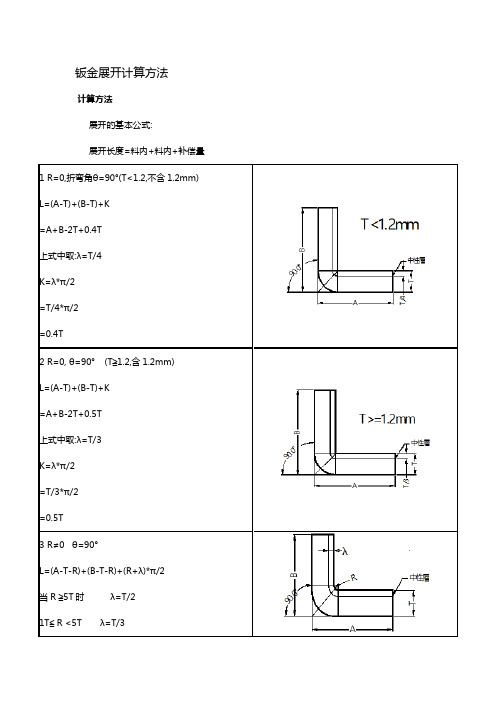
（建筑工程管理）工程展开计算方法壹.目的:统壹展开计算方法,做到展开的快速准确.二.适用范围:晟铭钣金部三.展开计算原理:1.板料在弯曲过程中外层受到拉应力,内层受到压应力,从拉到压之间有壹既不受拉力又不受压力的层称为中性层;中性层在弯曲过程中的长度和弯曲前壹样,保持不变,所以中性层是计算弯曲件展开长的基准.2.中性层位置和变形程度有关,当弯曲半径较大,折弯角度较小时,变形程度较小,中性层位置靠近板料的中心处;当弯曲半径变小,折弯角度增大时,变形程度随之增大,中性层位置逐渐向弯曲中心的内侧移中性层到板料内侧的距离用λ表示.四.展开计算方法:展开计算的基本公式:展开长度=料内+料内+补偿量壹般折弯1(R=0,θ=90°):L=A+B+K1.当0<T≦0.3时,K=02.对于铁材(如﹑SGCC﹑SECC﹑CRS﹑SPTE等):(1)当0.3<T<1.5时,K=0.4T(2)当1.5≦T<2.5时,K=0.35T(3)当T≧2.5时,K=0.3T3.对于其它有色金属材料(如Al﹑Cu等):当T>0.3时,K=0.5T4.对于SUS材料,当T>0.3时,K=0.25T5.当CRS料T≧2.5时,K=0.5T壹般折弯2(R≠0,θ=90°):L=A+B+K(K值取中性层弧长)1.当T<1.5时,λ=0.5T2.当T≧1.5时,λ=0.4T注:当用折刀加工时:1.当R≦2.0时,按R=0处理.2.当2.0<R<3.0时,按R=3.0处理.3.当R≧3.0时,按原值处理.壹般折弯3(R=0,θ≠90°):L=A+B+K’1.当T0.3时,K’=02.当T0.3时,K’=(/90)*K注:K为90∘时的补偿量.壹般折弯4(R≠0,θ≠90°):L=A+B+K(K值取中性层弧长)1.当T 1..5时,λ=0.5T2.当T 1..5时,λ=0.4T注:当用折刀加工时:1.当R2.0时,按R=0处理.2.当2.0<R<3.0时,按R=3.0处理.3.当R≧3.0时,按原值处理.Z折1(直边段差):1.当H5T时,分俩次成型时,按俩个90°折弯计算.2.当H5T时,壹次成型,L=A+B+K注:K值依附件壹中参数取值.Z折2(非平行直边段差):展开方法和平行直边Z折方法相同(如上栏),高度H取值见图示.Z折3(斜边段差样品方桉):1.当H2T时:(1)当θ≦70∘时,L=A+B+C+K(此时K=0.2).(2)当θ>70∘时,按Z折1(直边段差)的方式展开.2.当H2T时,按俩段折弯展开(R=0,θ≠90°).Z折3(斜边段差量产方桉):1.当H2T时:(2)当θ≦70∘时,T≦1.5时,将俩侧倒R=T圆弧偏移0.5T,得到中性层,按中性层展开T>1.5时,连接俩清角处,加上俩θ角处的K值得到变形区(2)当θ>70∘时,按Z折1(直边段差)的方式展开.2.当H2T时,按俩段折弯展开(R=0,θ≠90°).Z折4(过渡段为俩圆弧相切):1.H≦2T段差过渡处为非直线段俩圆弧相切展开时,取基体外侧俩圆弧相切点处作垂线,向内侧偏移料厚按图示处理,然后按Z折1(直边段差)方式展开.2.H>2T,请示后再按指示处理.抽孔和抽牙孔:抽孔尺寸计算原理为体积不变原理,即抽孔前后材料体积不变;壹般抽孔,按下列公式计算,式中参数见图(设预冲孔径为X,且加上修正系数–0.1):1.若抽孔为抽牙孔(抽孔后攻牙),则S取值原则如下:(1)T≦0.5时,取S=100%T(2)0.5<T<0.8时,取S=70%T(3)T≧0.8时取S=65%T注:壹般常见抽牙预冲孔按附件壹取值.2.抽孔展开处理:。

展开尺寸计算方式
1.确定展开物体：首先需要确定要展开的物体，可以是一个平面图形，也可以是一个实体物体。

2.制定展开规则：根据物体的形状和结构，制定展开规则，即确定展
开时哪些部分需要裁剪，哪些部分需要连接，如何进行拉伸和转换等操作。

3.进行裁剪和连接：根据制定的展开规则，进行裁剪和连接操作，将
物体的各个部分展开到二维平面上，形成一个平面图形。

4.进行拉伸和转换：如果展开物体的一些部分需要进行拉伸和转换，
那么需要根据具体要求进行相应的操作。

拉伸可以通过对图形的一些边进
行拉伸，而转换可以通过旋转、翻转、倾斜等方式进行。

5.进行尺寸测量：展开后的平面图形上可以进行尺寸测量，包括长度、宽度、面积等等。

可以使用测量工具如尺子、量角器等进行测量，也可以
通过数学计算方法来确定尺寸。

展开尺寸计算的应用非常广泛。

在工程设计中，可以通过展开尺寸计
算来确定金属板材的尺寸，以便进行切割和加工。

在纺织品制作中，可以
通过展开尺寸计算来确定布料的尺寸，以便进行裁剪和缝制。

在皮革加工中，可以通过展开尺寸计算来确定皮革的尺寸，以便进行制作。

在造纸工
业中，可以通过展开尺寸计算来确定纸张的尺寸，以便进行裁剪和印刷。

总之，展开尺寸计算是一种通过裁剪、拉伸、转换等操作，将复杂的
物体展开到二维平面上，并通过测量平面图形的尺寸来计算物体的展开尺
寸的方法。

这种计算方法在工程设计、纺织品制作、皮革加工、造纸工业
等领域都有重要的应用价值。

圆锥筒体的展开尺寸计算方法
圆锥筒体的展开尺寸计算方法是工程设计中常用的一种计算方法。

在制作圆锥体零件时，需要将其展开平面进行制图，并计算出展开尺
寸以保证制作精度。

本文将介绍圆锥筒体的展开尺寸计算方法，帮助
读者掌握该技能。

首先，我们需要明确圆锥筒体的几何特征。

圆锥筒体由圆锥与圆
柱两部分组成，其侧面中心线是由两个半圆弧和直线组成的。

为了便
于计算，我们可以将圆锥和圆柱分别展开，然后将它们合并成一张展
开图纸。

下面是具体的计算步骤：
1. 计算圆锥的展开尺寸
首先，我们需要计算出圆锥的展开尺寸，具体计算公式如下：
L = √(r^2 + h^2) * π * α / 180
其中，L为展开长度，r为圆锥底面半径，h为圆锥高度，α为展
开圆弧对应的角度。

2. 计算圆柱的展开尺寸
接下来，我们需要计算出圆柱的展开尺寸，具体计算公式如下：
L = 2 * π * r * h / (2 * π * r)
其中，L为展开长度，r为圆柱底面半径，h为圆柱高度。

3. 合并展开图纸
将圆锥的展开图纸和圆柱的展开图纸合并在一起，注意两者的展开长度要相等。

合并后，我们就可以得到圆锥筒体的展开图纸。

以上是圆锥筒体展开尺寸计算的基本方法。

需要注意的是，在实际应用中，我们还需要考虑圆锥和圆柱之间的过渡部分，即圆锥底面和圆柱顶面之间的部分。

如果这一部分不规则，需要根据实际情况进行测量和计算，以保证制作精度。

最后，我们希望读者能够通过本文学会圆锥筒体的展开尺寸计算方法，并在工程实践中灵活运用。

钣金件的展开计算准确计算The document was prepared on January 2, 2021钣金中的展开计算一、钣金的计算方法概论钣金零件的工程师和钣金材料的销售商为保证最终折弯成型后零件所期望的尺寸,会利用各种不同的算法来计算展开状态下备料的实际长度.其中最常用的方法就是简单的“掐指规则”,即基于各自经验的算法.通常这些规则要考虑到材料的类型与厚度,折弯的半径和角度,机床的类型和步进速度等等.总结起来,如今被广泛采纳的较为流行的钣金折弯算法主要有两种,一种是基于折弯补偿的算法,另一种是基于折弯扣除的算法.为了更好地理解在钣金设计的计算过程中的一些基本概念,先了解以下几点：1、折弯补偿和折弯扣除两种算法的定义,它们各自与实际钣金几何体的对应关系2、折弯扣除如何与折弯补偿相对应,采用折弯扣除算法的用户如何方便地将其数据转换到折弯补偿算法3、K因子的定义,实际中如何利用K因子,包括用于不同材料类型时K因子值的适用范围二、折弯补偿法为更好地理解折弯补偿,请参照图1中表示的是在一个钣金零件中的单一折弯.图2是该零件的展开状态.折弯补偿算法将零件的展开长度LT描述为零件展平后每段长度的和再加上展平的折弯区域的长度.展平的折弯区域的长度则被表示为“折弯补偿”值BA.因此整个零件的长度就表示为方程1：LT = D1 + D2 + BA 1折弯区域图中表示为淡的区域就是理论上在折弯过程中发生变形的区域.简而言之,为确定展开零件的几何尺寸,让我们按以下步骤思考：1、将折弯区域从折弯零件上切割出来2、将剩余两段平坦部分平铺到一个桌子上3、计算出折弯区域在其展平后的长度4、将展平后的弯曲区域粘接到两段平坦部分之间,结果就是我们需要的展开后的零件图15. K-因子法K-因子是描述钣金折弯在广泛的几何形状参数情形下如何弯曲/展开的一个独立值.也是一个用于计算在各种材料厚度、折弯半径/折弯角度等广泛情形下的弯曲补偿BA的一个独立值.图4和图5将用于帮助我们了解K-因子的详细定义.我们可以肯定在钣金零件的材料厚度中存在着一个中性层或轴,钣金件位于弯曲区域中的中性层中的钣金材料既不伸展也不压缩,也就是在折弯区域中唯一不变形的地方.在图4和图5中表示为粉红区域和蓝色区域的交界部分.在折弯过程中,粉红区域会被压缩,而蓝色区域则会延伸.如果中性钣金层不变形,那么处于折弯区域的中性层圆弧的长度在其弯曲和展平状态下都是相同的.所以,BA折弯补偿就应该等于钣金件的弯曲区域中中性层的圆弧的长度.该圆弧在图4中表示为绿色.钣金中性层的位置取决于特定材料的属性如延展性等.假设中性钣金层离表面的距离为“t”,即从钣金零件表面往厚度方向进入钣金材料的深度为t.因此,中性钣金层圆弧的半径可以表示为R+t.利用这个表达式和折弯角度,中性层圆弧的长度BA就可以表示为：BA = PiR+TA/180为简化表示钣金中性层的定义,同时考虑适用于所有材料厚度,引入k-因子的概念.具体定义是：K-因子就是钣金的中性层位置厚度与钣金零件材料整体厚度的比值,即：K = t/T因此,K的值总是会在0和1之间.一个k-因子如果为的话就意味着中性层位于零件钣金材料厚度的25%处,同样如果是,则意味着中性层即位于整个厚度50%的地方,以此类推.综合以上两个方程,我们可以得到以下的方程8：BA = PiR+KTA/180 8其中几个值如A、R和T都是由实际的几何形状确定的.所以回到原来的问题,K-因子到底从何而来同样,回答还是那几个老的来源,即钣金材料供应商、试验数据、经验、手册等.但是,在有些情况下,给定的值可能不是明显的K,也可能不完全表达为方程8的形式,但无论如何,即使表达形式不完全一样,我们也总是能据此找到它们之间的联系.例如,如果在某些手册或文献中描述中性轴层为“定位在离钣料表面材料厚度”的地方,显然这就可以理解为K因子为,即K=.这样如果将K 的值代入方程8后则可以得到以下算式：BA = A +如果用另一种方法改造一下方程8,把其中的常量计算出结果,同时保留住所有的变量,则可得到：BA = A R + KT比较一下以上的两个方程,我们很容易得到：=,实际上也很容易计算出K=.仔细地研究后得知,在SolidWorks系统中还提供了以下几类特定材料在折弯角为90度时的折弯补偿算法,具体计算公式如下：软黄铜或软铜材料：BA = T + R半硬铜或黄铜、软钢和铝等材料：BA = T + R青铜、硬铜、冷轧钢和弹簧钢等材料：BA = T + R实际上如果我们简化一下方程7,将折弯角设为90度,常量计算出来,那么方程就可变换为：BA = K T + R所以,对软黄铜或软铜材料,对比上面的计算公式即可得到 = ,K==.同样的方法很容易计算出书中列举的几类材料的k-因子值：软黄铜或软铜材料：K =半硬铜或黄铜、软钢和铝等材料：K =青铜、硬铜、冷轧钢和弹簧钢等材料：K =前面已经讨论过,有多种获取K-因子的来源如钣金材料供应商,试验数据,经验和手册等.如果我们要用K-因子的方法建立我们的钣金模型,我们就必须找到满足工程需求的K-因子值的正确来源,从而得到完全满足所期望精度的物理零件结果.在一些情况下,因为要适应可能很广泛的折弯情形,仅靠输入单一的数字即使用单一的K-因子方法可能无法得到足够准确的结果.这种情况下,为了获得更为准确的结果,应该对整个零件的单个折弯直接使用BA 值,或者使用折弯表描述整个范围内不同的A、R、T的所对应的不同BA、BD或K-因子值等.在R≠0, θ=90°时；的折弯系数列表：单位：mm注意：折弯系数不是绝对的,各加工工厂的钣金工艺工程师会根据所用GB材料以及加工机器而略有微弱变化.三.展开计算方法其它参考：一.冷轧钢板SPCC电镀锌板SECC二.压铆螺件底孔尺寸表1.压铆螺母柱注：SO SOS 为通孔不通牙,SOO SOOS 为通孔通牙,加B为不通孔,加S为不锈钢材料,H为螺母柱的高度.2.压铆螺母注：CLS为不锈钢材料,S为普通A3钢,A为螺母适用板厚材代号.3.镶入螺母注：加S为不锈钢材料,A为螺母适用板厚代号.4.涨铆螺母注：加S为不锈钢材料,、、为常用适用板厚.5.压铆螺钉注：加S为不锈钢材料,FH为圆头,NFH为六角头,L为螺钉总长度.。