2016-2017学年度第一学期期中六校联考高一地数学试卷

2016-2017学年度第一学期六校联考高一地理（考试时间90分钟，满分100分）一、单项选择题（每小题2分，共22小题，44分。

在每小题给出的四个选项中，只有一个选项符合题目要求。

）1、以下与我们的视觉对应正确的是A、星云-----一闪即逝B、行星-----圆缺多变C、彗星------拖着长尾D、月亮-----轮廓模糊2、下列关于太阳和太阳活动的叙述，正确的是A．太阳的主要成分是氮和氧B．黑子在太阳大气的光球层C．太阳黑子的活动周期大约是17年D．太阳大气层从外到里依次是光球层、色球层、日冕层读“太阳黑子与温带乔木年轮相关性曲线图”，完成3-4题。

3、图中年轮宽度与太阳黑子相对数之间的关系是A.正相关B.负相关C.成反比D.没有相关性4、此图所反映的问题是A.太阳活动能影响地球气候，进而影响地球植物的生长B.太阳活动发射的电磁波能扰动地球的电离层C.太阳活动时，抛出的带电粒子流扰动地球磁场，产生“磁暴”现象D.太阳活动时，太阳风使两极地区出现极光，从而影响中高纬度地区树木的生长读图“地球圈层结构示意图”，完成5—7题。

5、关于图中各圈层的正确叙述是A．地球外部圈层由A、B、C三部分组成，其中C为生物圈B．地球内部圈层由E、F、G三部分组成，其中G为地核C．E、F合为岩石圈D．各圈层间相互联系、相互制约，形成自然环境6、一般认为，岩浆的主要发源地是A．软流层 B．下地幔C．图中D层 D．图中G层7、下列关于地球内部圈层结构的叙述，正确的是A．划分依据是各层温度的变化 B．地壳由岩石组成，厚度均一C．岩石圈是指地壳和上地幔的顶部 D．莫霍界面是地幔与地核的分界面8、下列与地球自转运动有关的叙述中，正确的是A. 地球上不同地点自转线速度都相同B. 地球上任何地点每24小时昼夜都更替一次C. 受惯性离心力影响，地球成为两极稍鼓的旋转椭球体D. 受地转偏向力影响，长江自西向东流的河段，南岸受河水冲刷作用较强9、在下面四幅图的a、b、c、d四点中，处于黄昏的是10、地球上经度相同，纬度不同的两地A、日出日落时刻相同B、正午太阳高度相同C、昼夜长短的相同D、地方时相同11、关于时区与区时的叙述正确的是A、北京时间（东八区）比东京时间（东九区）要早B、北京（东八区）与洛杉矶（西八区）时差为24小时C、伦敦（零时区）早上10点时，纽约（西五区）是15点D、从东十二区进入西十二区，区时不变，日期减一12、下图是两条大河的河口图，图中航道通航条件较好的是A．甲、丙 B．乙、丙 C．甲、丁 D．乙、丁13、下列四幅昼夜分布图(图中阴影部分表示夜半球，箭头表示地球自转方向)中，表示北半球夏至日的是A B C D14、下列四组城市中，按9月23日正午太阳高度从大到小排序正确的是A、北京、伦敦、新加坡、悉尼B、新加坡、悉尼、北京、伦敦C、伦敦、北京、悉尼、新加坡D、悉尼、新加坡、伦敦、北京读下图，回答15～17题。

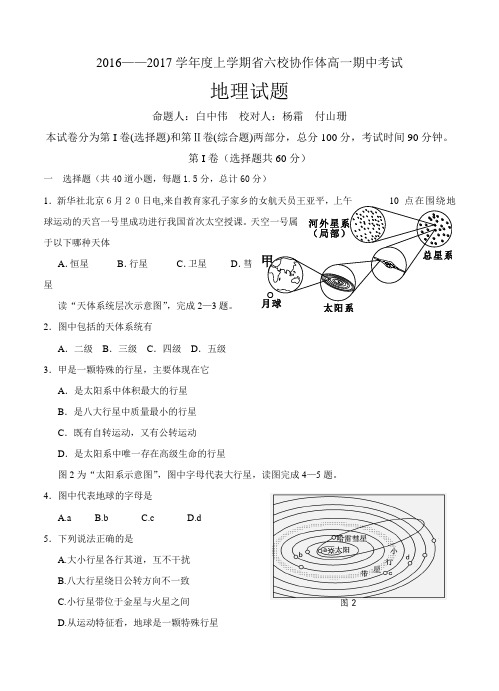
图22016——2017学年度上学期省六校协作体高一期中考试地理试题命题人：白中伟 校对人：杨霜 付山珊本试卷分为第I 卷(选择题)和第Ⅱ卷(综合题)两部分，总分100分，考试时间90分钟。

第I 卷（选择题共60分）一 选择题（共40道小题，每题1.5分，总计60分）1．新华社北京６月２０日电,来自教育家孔子家乡的女航天员王亚平，上午10点在围绕地球运动的天宫一号里成功进行我国首次太空授课。

天空一号属于以下哪种天体A ．恒星B ．行星C ．卫星D ．彗星读“天体系统层次示意图”，完成2—3题。

2．图中包括的天体系统有A ．二级B ．三级C ．四级D ．五级 3．甲是一颗特殊的行星，主要体现在它 A ．是太阳系中体积最大的行星 B ．是八大行星中质量最小的行星 C ．既有自转运动，又有公转运动 D ．是太阳系中唯一存在高级生命的行星图2为“太阳系示意图”，图中字母代表大行星，读图完成4—5题。

4．图中代表地球的字母是A.aB.bC.cD.d 5．下列说法正确的是A.大小行星各行其道，互不干扰B.八大行星绕日公转方向不一致C.小行星带位于金星与火星之间D.从运动特征看，地球是一颗特殊行星2015年10月12日至18日，国家天文台在日面上观测到多次黑子和耀斑活动。

据此完成6—7题。

6.有关太阳活动的正确叙述是A.太阳活动是太阳内部的变化B.黑子和耀斑的活动周期约为11年C.耀斑出现在太阳光球层D.黑子是色球层上出现的暗黑的斑点7.太阳活动剧烈时，对地球产生的影响可能是A.干扰地球磁场引发“磁暴”现象B.地面无线电长波通信受到影响C.全球各地降水量都明显增多D.两极地区产生极昼极夜现象8. 太阳辐射能量来源于太阳内部的A. 核裂变反应B. 核聚变反应C. 耀斑爆发D. 太阳风9．下列现象与太阳辐射无关的是A.利用地热能发电B.煤、石油、天然气等矿物燃料的形成C.地球上大气的运动D.地球上的水循环10．耀斑形成于A．色球层 B．光球层C．太阳内部 D．日冕层地球表面某区域经纬网示意图,回答11--12题。

2016-2017学年第一学期高一数学上册期中试题(含答案)2016-2017学年第一学期期中考试高一数学试题第Ⅰ卷（选择题共60分）一、选择题：（本大题共12小题，每小题分，共60分，在每个小题给出的四个选项中，只有一项是符合题目要求的）1设集合U={1,2,3,4,},A={1,2,3},B={2,},则A U B等于( )A{2} B{2,3} {3} D{1,3}2已知且，则A的值是（）A7 B D 983若a>0且a≠1，且，则实数a的取值范围是（）A．0<a<1 B．．D．或a>14函数（>0且≠1）的图象必经过点（）A（0,1） B (1,1) (2,3) D(2,4)三个数之间的大小关系是（）A B D6函数= 在[1,3]上的最大值与最小值的和为1，则a =（）A B 2 3 D7下列函数中，在区间（0，2）上不是增函数的是（）A B D8函数与（）在同一坐标系中的图像只可能是( ）9 下列各式:①＝a;②(a2－3a＋3)0＝1③＝其中正确的个数是()A 0B 12 D 310计算()A BD 111 f(x)= 则f =()A -2B -39 D12 已知幂函数的图象经过点(9,3),则( )A 1 BD第Ⅱ卷（非选择题共90分）二、填空题：（每小题分，共20分）13 已知f(x)是定义在R上的奇函数,当x>0时,f(x)=1+ ,则f(-2)=14若函数在区间内单调递减,则a的取值范围是______________ 1函数的定义域是．16求值：＝________ _．三、解答题：（本题共包含个大题，共70分）17 求值:（10分）(1) ;(2)求lg2．6．2+lg +ln + 的值．18 已知={x| -2≤x≤}, N={x| a+1≤x≤2a-1},若N，求实数a的取值范围（12分）19 已知函数f(x)=lga(3+2 x),g(x)=lga(3-2x)(a>0,且a≠1)（12分）(1)求函数=f(x)-g(x)的定义域(2)判断函数=f(x)-g(x)的奇偶性,并予以证明20 已知函数且（12分）(1)判断的奇偶性,并证明;(2)求使的的取值范围21已知函数f(x)＝lg(1＋x)＋lg(1－x)．（12分）(1)求函数f(x)的定义域；(2)判断函数f(x)的奇偶性；(3)若f(x)＝lg g( x)，判断函数g(x)在(0,1)内的单调性并用定义证明．22设函数（12分）(1)设,用表示,并指出的取值范围;(2)求的最值,并指出取得最值时对应的x的值2016-2017学年第一学期期中考试高一数学试卷答案一、选择题（60）1-12 DBDD ABA B二、填空（20）13 -14116 49 B【解析】令a=-1，n=2时，＝1，①错;因为a2－3a＋3>0,所以②正确; = ，③显然错误所以选项B错误10 A【解析】• lg23• ,故选A11 【解析】因为f =lg3 =-2,所以f =f(-2)= =9,故选12 B【解析】设f(x)= 由幂函数的图象经过点(9,3)，则f(9)= ，所以f(x)= ，故选B三、（70分）17（10分）(1) 原式(2) 解：原式＝2－2＋ln ＋＝＋6＝18（12分）解：①当N=Φ时，即a＋1＞2a－1，有a＜2；②当N≠Φ，则，解得2≤a≤3，综合①②得a的取值范围为a≤319 （12分）(1) =f(x)-g(x)= lga(3+2x)-lga(3-2x),要使该函数有意义,则有,解得<x<所以函数=f(x)-g(x)的定义域是(2) 由第1问知函数=f(x)-g(x)的定义域关于原点对称f(-x)-g(-x)=lga(3-2x)-lga(3+2x)= -[lga(3+2x)-lga(3-2x)]=-[f(x)-g(x)],所以函数=f(x)-g(x)是奇函数20 （12分）(1) 由,得故的定义域为∵,∴是奇函数(2) 当时,由,得,所以,当时,由,得,所以故当时, 的取值范围是;当时, 的取值范围是21 （12分）22 （1 2分）(1) 设,因为,所以此时, ，即,其中(2) 由第1问可得,因为,函数在单调递增,在单调递减,所以当,即,即时, 取得最大值;当,即,即时, 取得最小值。

2016-2017年第一学期高一数学上册期中试题（有答案）高一第一学期期中考试数学试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分共1 0分，考试时间120分钟。

注意事项：答题前考生务必将考场、姓名、班级、学号写在答题纸的密封线内。

选择题每题答案涂在答题卡上，非选择题每题答案写在答题纸上对应题目的答案空格里，答案不写在试卷上。

考试结束，将答题卡和答题纸交回。

第Ⅰ卷（选择题，共60分）一、选择题：本大题共12小题，每小题分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的1．已知集合A＝{－1,1}，B＝{x|ax＋1＝0}，若B⊆A，则实数a的所有可能取值的集合为()A．{－1} B．{1} ．{－1,1} D．{－1,0,1}2．函数＝1lnx－1的定义域为()A．(1，＋∞)B．[1，＋∞)．(1,2)∪(2，＋∞) D．(1,2)∪[3，＋∞)3．已知f(x)＝fx－，x≥0，lg2－x，x<0，则f(2 016)等于()A．－1 B．0 ．1 D．24、若α与β的终边关于x轴对称，则有()A．α＋β＝90° B．α＋β＝90°＋•360°，∈Z．α＋β＝2•180°，∈Z D．α＋β＝180°＋•360°，∈Z、设1＝409，2＝8048，3＝(12)－1，则()A．3＞1＞2B．2＞1＞3．1＞2＞3D．1＞3＞26．在一次数学试验中，运用图形计算器采集到如下一组数据：x－20－100100新标x b1 200300024011202398802则x，的函数关系与下列哪类函数最接近？(其中a，b为待定系数)()A．＝a＋bxB．＝a＋bx．＝ax2＋bD．＝a＋bx7．定义运算a⊕b＝a，a≤b，b，a＞b则函数f(x)＝1⊕2x的图象是()8、设偶函数f(x)满足f(x)＝2x－4(x≥0)，则不等式f(x－2)>0的解集为()A．{x|x<－2，或x>4}B．{x|x<0，或x>4}．{x|x<0，或x>6} D．{x|x<－2，或x>2}9．函数＝lg12(x2－x＋3)在[1,2]上的值恒为正数，则的取值范围是()A．22<<23B．22<<72．3<<72D．3<<2310 已知1＋sinxsx＝－12，那么sxsinx－1的值是()A12 B．－12 ．2 D．－211．设∈R，f(x)＝x2 －x＋a(a＞0)，且f()＜0，则f(＋1)的值() A．大于0 B．小于0 ．等于0D．不确定12、已知函数f(x)＝1lnx＋1－x，则＝f(x)的图象大致为()第Ⅱ卷（非选择题共90分）二、填空题：本大题4小题，每小题分，共20分13．已知集合A＝{x∈R||x＋2|<3}，集合B＝{x∈R|(x－)(x－2)<0}，且A∩B＝(－1，n)，则＋n＝________14 函数f(x)＝x＋2x在区间[0,4]上的最大值与最小值N的和为__ 1．若一系列函数解析式相同，值域相同，但定义域不同，则称这些函数为“同族函数”，那么函数解析式为＝x2，值域为{1,4}的“同族函数”共有________个．16 已知f(x)＝ax2＋bx＋3a＋b是偶函数，且其定义域为[a－1,2a]，则＝f(x)的值域为________．三、解答题：本大题共6小题，共70分，解答应写出字说明，证明过程或演算步骤17．（本小题10分）已知集合A＝{x|x2－3x＋2＝0}，B＝{x|x2－ax＋a－1＝0}，若A∪B ＝A，求实数a的值．18．(本小题满分12分)已知扇形的圆心角是α，半径为R，弧长为l(1)若α＝60°，R＝10 ，求扇形的弧长l(2)若扇形的周长是20 ，当扇形的圆心角α为多少弧度时，这个扇形的面积最大？(3)若α＝π3，R＝2 ，求扇形的弧所在的弓形的面积．19．（本小题满分12分）已知定义域为R的函数f(x)＝－2x＋b2x＋1＋a是奇函数．(1)求a，b的值；(2)若对任意的t∈R，不等式f(t2－2t)＋f(2t2－)＜0恒成立，求的取值范围．20、（本小题满分12分）已知函数f(x)＝4x＋•2x＋1有且仅有一个零点，求的取值范围，并求出该零点．21．（本小题满分12分）如图，建立平面直角坐标系x，x轴在地平面上，轴垂直于地平面，单位长度为1千米．某炮位于坐标原点．已知炮弹发射后的轨迹在方程＝x－120(1＋2)x2(＞0)表示的曲线上，其中与发射方向有关．炮的射程是指炮弹落地点的横坐标．(1)求炮的最大射程；(2)设在第一象限有一飞行物(忽略其大小)，其飞行高度为32千米，试问它的横坐标a不超过多少时，炮弹可以击中它？请说明理由．22．(本小题满分12分)设函数f(x)＝ax－a－x(a>0且a≠1)是定义域为R的奇函数．(1 )若f(1)>0，试求不等式f(x2＋2x)＋f(x－4)>0的解集；(2)若f(1)＝32，且g(x)＝a2x＋a－2x－4f(x)，求g(x)在[1，＋∞)上的最小值．高一数学期中测试卷参考答案1．解析：由题意知集合B的元素为1或－1或者B为空集，故a＝0或1或－1，选D答案：D2 解析由ln(x－1)≠0，得x－1>0且x－1≠1由此解得x>1且x≠2，即函数＝1lnx－1的定义域是(1,2)∪(2，＋∞)．答案3 解析f(2 016)＝f(1)＝f(1－)＝f(－4)＝lg24＝2答案 D4 解析：根据终边对称，将一个角用另一个角表示，然后再找两角关系．因为α与β的终边关于x轴对称，所以β＝2•180°－α，∈Z，故选答案：解析：1＝409＝218，2＝8048＝2144，3＝(12)－1＝21由于指数函数f(x)＝2x在R上是增函数，且18＞1＞144，所以1＞3＞2，选D 答案：D6 解析：在坐标系中将点(－2,024)，(－1,01)，(0,1)，(1,202)，(2,398)，(3,802)画出，观察可以发现这些点大约在一个指数型函数的图象上，因此x与的函数关系与＝a＋bx最接近．答案：B7 解析：f(x)＝1⊕2x＝1，x≥0，2x，x＜0故选A答案：A8 解析：当x≥0时，令f(x)＝2x－4>0，所以x>2又因为函数f(x)为偶函数，所以函数f(x)>0的解集为{x|x<－2，或x>2}．将函数＝f(x)的图象向右平移2个单位即得函数＝f(x－2)的图象，故f(x －2)>0的解集为{x|x<0，或x>4}．答案：B9 解析：∵lg12(x2－x＋3)>0在[1,2]上恒成立，∴0<x2－x＋3<1在[1, 2]上恒成立，∴<x＋3x>x＋2x在[1,2]上恒成立又当1≤x≤2时，＝x＋3x∈[23，4]，＝x＋2x∈[22，3]．∴3<<23答案：D10 解析：设sxsinx－1＝t，则1＋sinxsx•1t＝1＋sinxsx•sinx－1sx＝sin2x－1s2x＝－1，而1＋sinxsx＝－12，所以t＝12故选A答案：A11 解析：函数f(x)＝x2－x＋a的对称轴为x＝12，f(0)＝a，∵a＞0，∴f(0)＞0，由二次函数的对称性可知f(1)＝f(0)＞0∵抛物线的开口向上，∴由图象可知当x＞1时，恒有f(x)＞0∵f()＜0，∴0＜＜1∴＞0，∴＋1＞1，∴f(＋1)＞0答案：A12 解析：(特殊值检验法)当x＝0时，函数无意义，排除选项D中的图象，当x＝1e－1时，f(1e－1)＝1ln1e－1＋1－1e－1＝－e<0，排除选项A、中的图象，故只能是选项B中的图象．(注：这里选取特殊值x＝(1e－1)∈(－1,0)，这个值可以直接排除选项A、，这种取特值的技巧在解题中很有用处)答案：B13 答案0 解析由|x＋2|< 3，得－3<x＋2<3，即－<x<1又A∩B＝(－1，n)，则(x－)(x－2)<0时必有<x<2，从而A∩B＝(－1,1)，∴＝－1，n＝1，∴＋n＝014 解析：令t＝x，则t∈[0,2]，于是＝t2＋2t＝(t＋1)2－1，显然它在t∈[0,2]上是增函数，故t＝2时，＝8；t＝0时N＝0，∴＋N＝8答案：81 解析：值域为{1,4}，则定义域中必须至少含有1，－1中的一个且至少含有2，－2中的一个．当定义域含有两个元素时，可以为{－1，－2}，或{－1,2}，或{1，－2}，或{1,2}；当定义域中含有三个元素时，可以为{－1,1，－2}，或{－1，1,2}，或{1，－2,2}，或{－1，－2,2}；当定义域含有四个元素时，为{－1,1，－2,2}．所以同族函数共有9个．答案：916 解析：∵f(x)＝ax2＋bx＋3a＋b是偶函数，∴其定义域[a－1,2a]关于原点对称，即a－1＝－2a，∴a＝13∵f(x)＝ax2＋bx＋3a＋b是偶函数，即f(－x)＝f(x)，∴b＝0，∴f(x)＝13x2＋1，x∈[－23，23]，其值域为{|1≤≤3127}．答案：{|1≤≤3127}17 答案a＝2或a＝3解析A＝{1,2}，∵A∪B＝A，∴B⊆A，∴B＝∅或{1}或{2}或{1,2}．当B＝∅时，无解；当B＝{1}时，1＋1＝a，1×1＝a－1，得a＝2；当B＝{2}时，2＋2＝a，2×2＝a－1，无解；当B＝{1,2}时，1＋2＝a，1×2＝a－1，得a＝3综上：a＝2或a＝318 【解析】(1)α＝60°＝π3，l＝10×π3＝10π3(2)由已知得，l＋2R＝20，所以S＝12lR＝12(20－2R)R＝10R－R2＝－(R－)2＋2所以当R＝时，S取得最大值2，此时l＝10，α＝2(3)设弓形面积为S弓．由题知l＝2π3S弓＝S扇形－S三角形＝12×2π3×2－12×22×sin π3＝(2π3－3) 2 【答案】(1)10π3 (2)α＝2时，S最大为2(3)2π3－3 219 解：(1)因为f(x)是定义在R上的奇函数，所以f(0)＝0，即b－1a＋2＝0ͤb＝1，所以f(x)＝1－2xa＋2x＋1，又由f(1)＝－f(－1)知1－2a＋4＝－1－12a＋1ͤa＝2(2)由(1)知f(x)＝1－2x2＋2x＋1＝－12＋12x＋1，易知f(x)在(－∞，＋∞)上为减函数．又因f(x)是奇函数，从而不等式：f(t2－2t)＋f(2t2－)＜0等价于f(t2－2t)＜－f(2t2－)＝f(－2t2)，因f(x)为减函数，由上式推得：t2－2t＞－2t2，即对t∈R有：3t2－2t－＞0，从而Δ＝4＋12＜0ͤ＜－1320 解：∵f(x)＝4x＋•2x＋1有且仅有一个零点，即方程(2x)2＋•2x＋1＝0仅有一个实根．设2x＝t(t＞0)，则t2＋t＋1＝0当Δ＝0时，即2－4＝0∴＝－2时，t＝1；＝2时，t＝－1(不合题意，舍去)，∴2x＝1，x＝0符合题意．当Δ＞0时，即＞2或＜－2时，t2＋t＋1＝0有两正或两负根，即f(x)有两个零点或没有零点．∴这种情况不符合题意．综上可知：＝－2时，f(x)有唯一零点，该零点为x＝021 解：(1)令＝0，得x－120(1＋2)x2＝0，由实际意义和题设条知x＞0，＞0，故x＝201＋2＝20＋1≤202＝10，当且仅当＝1时取等号．所以炮的最大射程为10千米．(2)因为a＞0，所以炮弹可击中目标⇔存在＞0，使32＝a－120(1＋2)a2成立⇔关于的方程a22－20a＋a2＋64＝0有正根⇔判别式Δ＝(－20a)2－4a2(a2＋64)≥0⇔a≤6所以当a不超过6(千米)时，可击中目标．22 答案(1) {x|x>1或x<－4}(2)－2解析∵f(x)是定义域为R的奇函数，∴f(0)＝0，∴－1＝0，∴＝1(1)∵f(1)>0，∴a－1a>0又a>0且a≠1，∴a>1∵＝1，∴f(x)＝ax－a－x当a>1时，＝ax和＝－a－x在R上均为增函数，∴f(x)在R上为增函数．原不等式可化为f (x2＋2x)>f(4－x)，∴x2＋2x>4－x，即x2＋3x－4>0∴x>1或x<－4∴不等式的解集为{x|x>1或x<－4}．(2)∵f(1)＝32，∴a－1a＝32，即2a2－3a－2＝0∴a＝2或a＝－12(舍去)．∴g(x)＝22x＋2－2x－4(2x－2－x)＝(2x－2－x)2－4(2x－2－x)＋2令t＝h(x)＝2x－2－x(x≥1)，则g(t)＝t2－4t＋2∵t＝h(x)在[1，＋∞)上为增函数(由(1)可知)，∴h(x)≥h(1)＝32，即t≥32∵g(t)＝t2－4t＋2＝(t－2)2－2，t∈[32，＋∞)，∴当t＝2时，g(t)取得最小值－2，即g(x)取得最小值－2，此时x＝lg2(1＋2)．故当x＝lg2(1＋2)时，g(x)有最小值－2。

天津市六校联考2016-2017学年高一（上）期中数学试卷一．选择题（本大题共8小题，每题4分共32分）1．（4分）已知集合A={0，1}，B={﹣1，0，a+3}，且A⊆B，则a等于（）A．1 B．0 C．﹣2 D．﹣32．（4分）设全集U=R，A={x∈N|1≤x≤5}，B=x∈R|x2﹣x﹣2=0}，则图中阴影表示的集合为（）A．{﹣1} B．{2} C．{3，4，5} D．{3，4}3．（4分）函数f（x）=+lg（x﹣1）+（x﹣3）0的定义域为（）A．{x|1＜x≤4}B．{x|1＜x≤4且x≠3}C．{x|1≤x≤4且x≠3}D．{x|x≥4}4．（4分）已知a=log0.60.5，b=ln0.5，c=0.60.5．则（）A．a＞b＞c B．a＞c＞b C．c＞a＞b D．c＞b＞a5．（4分）设函数f（x）=ln（1﹣x）﹣ln（1+x），则f（x）是（）A．奇函数，且在（0，1）上是增函数B．奇函数，且在（0，1）上是减函数C．偶函数，且在（0，1）上是增函数D．偶函数，且在（0，1）上是减函数6．（4分）函数y=2x-1+x﹣1的零点为x0，则x0∈（）A．（﹣1，0）B．（0，）C．（，1）D．（1，）7．（4分）已知f（x）=log（x2﹣2x）的单调递增区间是（）A．（1，+∞）B．（2，+∞）C．（﹣∞，0）D．（﹣∞，1）8．（4分）已知函数f（x）=，若存在x1∈（0，+∞），x2∈（﹣∞，0]，使得f（x1）=f（x2），则x1的最小值为（）A．log23 B．log32 C．1 D．2二．填空题（本大题共6小题，每题4分共24分）9．（4分）已知集合A={1，2a}，B={a，b}，若A∩B={}，则A∪B为．10．（4分）设函数f（x）=，则f（2）=．11．（4分）已知定义域为[a﹣4，2a﹣2]的奇函数f（x）=2016x3﹣5x+b+2，则f（a）+f（b）的值为．12．（4分）若幂函数在（0，+∞）上是增函数，则m=．13．（4分）已知函数f（x）=log a x+b（a＞0，a≠1）的定义域、值域都是[1，2]，则a+b=．14．（4分）已知函数f（x）是定义在R上的奇函数，若f（x）=，则关于x的方程f（x）+a=0（0＜a＜1）的所有根之和为．三.解答题（本大题共5题）15．（12分）已知：函数f（x）=+lg（3x﹣9）的定义域为A，集合B={x|x﹣a＜0，a∈R}，（1）求：集合A；（2）求：A∩B≠∅，求a的取值范围．16．（12分）设集合A={x|（x﹣2m+1）（x﹣m+2）＜0}，B={x|1≤x+1≤4}．（1）若m=1，求A∩B；（2）若A∩B=A，求实数m的取值集合．17．（13分）已知函数f（x）=+bx（其中a，b为常数）的图象经过（1，3）、（2，3）两点．（I）求a，b的值，判断并证明函数f（x）的奇偶性；（II）证明：函数f（x）在区间[，+∞）上单调递增．18．（13分）已知函数f（x）=（a＞0且a≠1）（1）若a=2，解不等式f（x）≤5；（2）若函数f（x）的值域是[4，+∞），求实数a的取值范围．19．（14分）已知f（x）是定义在[﹣1，1]上的奇函数，且f（1）=1，若m，n∈[﹣1，1]，m+n≠0时，有＞0．（Ⅰ）证明f（x）在[﹣1，1]上是增函数；（Ⅱ）解不等式f（x2﹣1）+f（3﹣3x）＜0（Ⅲ）若f（x）≤t2﹣2at+1对∀x∈[﹣1，1]，a∈[﹣1，1]恒成立，求实数t的取值范围．参考答案一．选择题（本大题共8小题，每题4分共32分）1．C【解析】∵集合A={0，1}，B={﹣1，0，a+3}，且A⊆B，∴a+3=1∴a=﹣2故选C【点评】本题考查集合关系中的参数取值问题，解题的关键是由集合之间的关系得出参数所满足的方程或不等式，从而解同参数的取值范围，集合中参数的取值范围问题，是集合知识综合运用题，需要运用集合中的相关知识综合判断，正确转化，考查了推理判断能力及转化的思想2．A【解析】阴影部分为B∩（C R A），而A={x∈N|1≤x≤5}，B={x∈R|x2﹣x﹣2=0}={﹣1，2}，∴B∩（C R A）={x|x=﹣1}，故选A．【点评】本题考查集合的基本运算和韦恩图，真确理解韦恩图表达的集合是解决本题的关键．3．B【解析】要使f（x）有意义，则：；解得1＜x≤4，且x≠3；∴f（x）的定义域为{x|1＜x≤4，且x≠3}．故选B．【点评】考查函数定义域的概念及求法，以及对数函数的定义域，并清楚x0中的x≠0．4．B【解析】log0.60.5＞1，ln0.5＜0，0＜0.60.5＜1，即a＞1，b＜0，0＜c＜1，故a＞c＞b，故选：B【点评】本题主要考查函数值的大小比较，利用指数函数和对数函数的单调性是解决本题的关键．5．B【解析】∵函数f（x）=ln（1﹣x）﹣ln（1+x）=ln，由，求得﹣1＜x＜1，可得它的定义域为（﹣1，1）．再根据f（﹣x）=ln=﹣ln=﹣f（x），可得它为奇函数．在（0，1）上，ln（1﹣x）是减函数，﹣ln（1+x）是减函数，故函数f（x）=ln（1﹣x）﹣ln（1+x）是减函数，故选：B．【点评】本题主要考查函数的奇偶性、单调性的判断和证明，属于中档题．6．B【解析】设f（x）=2x﹣1+x﹣1，∵，，即，∴函数的零点．故选B．【点评】本题考查函数零点的存在性．掌握零点存在性定理并能运用是关键．属于基础题．7．C【解析】令t=x2﹣2x＞0，求得x＜0，或x＞2，故函数的定义域为（﹣∞，0）∪（2，+∞），且f（x）=log（x2﹣2x）=g（t）=log t．根据复合函数的单调性，本题即求函数t=x2﹣2x在定义域内的减区间．再利用二次函数的性质可得函数t=x2﹣2x在定义域内的减区间为（﹣∞，0），故选：C．【点评】本题主要考查复合函数的单调性，二次函数的性质，体现了转化的数学思想，属于中档题．8．B【解析】x≤0，f（x）≥1∵存在x1∈（0，+∞），x2∈（﹣∞，0]，使得f（x1）=f（x2），∴﹣1≥1，∴≥2，∴x1≥log32，∴x1的最小值为log32．故选：B．【点评】本题考查分段函数，考查函数的值域，考查学生分析解决问题的能力，正确转化是关键．二．填空题（本大题共6小题，每题4分共24分）9．{﹣2，1，}【解析】集合A={1，2a}，B={a，b}，若A∩B={}，则2a=，即有a=﹣2，b=．则A∪B={﹣2，1，}．故答案为：{﹣2，1，}．【点评】本题考查集合的运算，主要是交集和并集的运算，考查运算能力，属于基础题．10．19【解析】函数f（x）=，∵2＜6，∴f（2）=f（2+3）=f（5）；又5＜6，∴f（5）=f（5+3）=f（8）；8＞6，∴f（8）=3×8﹣5=19．所以得f（2）=19．故答案为：19．【点评】本题考查了对函数的定义域和解析式的理解和带值计算能力．属于基础题．11．0【解析】根据奇函数f（x）=2016x3﹣5x+b+2得定义域为[a﹣4，2a﹣2]，可得a﹣4+（2a﹣2）=0，求得a=2，故条件为奇函数f（x）=2016x3﹣5x+b+2得定义域为[﹣2，2]，∴f（0）=b+2=0，求得b=﹣2，∴f（x）=2016x3﹣5x，∴f（a）+f（b）=f（2）+f（﹣2）=f（2）﹣f（2）=0，故答案为：0．【点评】本题主要考查奇函数的定义和性质，属于基础题．12．﹣1【解析】∵幂函数在（0，+∞）上是增函数，∴，解得m=﹣1．故答案为﹣1．【点评】熟练掌握幂函数的定义和单调性是解题的关键．13．或3【解析】当0＜a＜1时，易知函数f（x）为减函数，由题意有解得：a=，b=2，符合题意，此时a+b=；当a＞1时，易知函数为增函数，由题意有，解得：a=2，b=1，符合题意，此时a+b=3．综上可得：a+b的值为或3．故答案为：或3．【点评】本题考查对数函数的性质以及分类讨论的思想方法．分类讨论函数的单调性是正确解决本题关键．属于易错题．14．1﹣2a【解析】∵f（x）为定义在R上的奇函数∴f（﹣x）=﹣f（x），∵当x≥0时，f（x）=，∴当x＜0时，f（x）=作出图象：∵关于x的方程f（x）+a=0（0＜a＜1）的根转化为f（x）的图象与y=﹣a（0＜a＜1）图象的交点问题．从图象上依次零点为：x1，x2，x3，x4，x5，根据对称性得到零点的值满足x1+x2=﹣6，x4+x5=6，x3满足：log（1﹣x3）=﹣a，解得：故得x1+x2+x3+x4+x5=1﹣2a故答案为：1﹣2a．【点评】本题考查了分段函数性质，图象以及应用，考查了函数的零点与函数的交点问题，属于中档题．三.解答题（本大题共5题）15．解（1）∵f（x）=+lg（3x﹣9）∴4﹣x≥0且3x﹣9＞0，即x≤4且x＞2，则A={x|2＜x≤4}（2）B={x|x﹣a＜0，a∈R}={x|x＜a}，由A∩B≠∅，因此a＞2，所以实数a的取值范围是（2，+∞）．【点评】本题主要考查了函数的定义域及其求法，以及并集及运算和子集的概念，属于基础题．16．解集合B={x|0≤x≤3}．…（1分）（1）若m=1，则A={x|﹣1＜x＜1}，则A∩B={x|0≤x＜1}．…（4分）（2）当A=∅即m=﹣1时，A∩B=A；当A≠∅即m≠﹣1时，（ⅰ）当m＜﹣1时，A=（2m﹣1，m﹣2），要使得A∩B=A，A⊆B，只要，所以m的值不存在．（ii）当m＞﹣1时，A=（m﹣2，2m﹣1），要使得A∩B=A，A⊆B，只要，∴m=2．综上所述，m的取值集合是{﹣1，2}．【点评】本题考查集合的运算与关系，考查分类讨论的数学思想，考查学生的计算能力，属于中档题．17．解（Ⅰ）∵函数f（x）的图象经过（1，3）、（2，3）两点∴，得a=2，b=1，∴函数解析，定义域为：（﹣∞，0）∪（0，+∞），关于原点对称，又∵，∴函数f（x）是奇函数；（II）设任意的，且x1＜x2，∵=∵，∴x2﹣x1＞0，且2﹣x1x2＜0，所以f（x1）﹣f（x2）＜0，即f（x1）＜f（x2），∴函数f（x）在区间上单调递增．【点评】本题考查函数的奇偶性和单调性．判断奇偶性注意定义域要关于原点对称，这是必要条件；证明单调性问题关键是第二步作差，正确变形是关键．18．解（1）∵函数f（x）=（a＞0且a≠1），∴a=2时，，∵f（x）≤5，∴当x≤2时，﹣x+6≤5，解得x≥1，∴1≤x≤2；当x＞2时，3+log2x≤5，解得x≤4，∴2＜x≤4．综上，不等式f（x）＜5的解集为{x|1≤x≤4}．…（7分）（2）∵函数f（x）=（a＞0且a≠1）的值域是[4，+∞），∴当x≤2时，f（x）=﹣x+6≥4，解得x≤2，∴x=2时，f（x）=﹣x+6=4；当x＞2时，f（x）=3+log a x≥4，∴log a x≥1，当0＜a＜1时，x≤a，由x＞2，得a≥2，无解；当a＞1时，x≥a，由x＞2，得a≤2，∴1＜a≤2．∴实数a的取值范围是（1，2]．…（14分）【点评】本题考查不等式的解法，考查实数的取值范围的求法，是中档题，解题时要认真审题，注意分段函数的定义、对数的性质及运算法则、不等式性质的合理运用．19．解（Ⅰ）任取﹣1≤x1＜x2≤1，则，∵﹣1≤x1＜x2≤1，∴x1+（﹣x2）≠0，由已知，∴f（x1）﹣f（x2）＜0，即f（x1）＜f（x2），∴f（x）在[﹣1，1]上是增函数；（Ⅱ）∵f（x）是定义在[﹣1，1]上的奇函数，且在[﹣1，1]上是增函数，∴不等式化为f（x2﹣1）＜f（3x﹣3），∴，解得；（Ⅲ）由（Ⅰ）知f（x）在[﹣1，1]上是增函数，∴f（x）在[﹣1，1]上的最大值为f（1）=1，要使f（x）≤t2﹣2at+1对∀x∈[﹣1，1]恒成立，只要t2﹣2at+1≥1⇒t2﹣2at≥0，设g（a）=t2﹣2at，对∀a∈[﹣1，1]，g（a）≥0恒成立，∴，∴t≥2或t≤﹣2或t=0．【点评】本题考查抽象函数的单调性、奇偶性，考查抽象不等式的求解，可从恒成立问题，考查转化思想，考查学生灵活运用知识解决问题的能力．。

“四地六校”联考2016—2017学年上学期第一次月考高一数学试卷（考试时间:120分钟 总分：150分）第Ⅰ卷 （选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的。

1。

设集合{}1>∈=x N x A ，则（ )A. A ∉φB.A ∉1 C 。

A ∈1 D 。

{}A ⊆1 2。

下列各组函数中，表示同一函数的是 （ ) A 。

1=y ，0x y = B. 211,1y x x y x =-+=-C 。

33,x y x y == D ．2)(|,|x y x y ==3。

下列函数中,在其定义域内既是奇函数又是减函数的是( ) A 。

);(R x x y ∈= B 。

);0(1≠=x xyC 。

);(R x x y ∈=D 。

).(3R x xy ∈-=4.函数14)(-+=x a x f 的图象恒过定点P ，则点P 的坐标是 （ )A 。

()5,1 B. ()4,1 C 。

（-1,4） D. （0，4）5.已知函数23)12(+=+x x f 且2)(=a f ，则a 的值等于( )A. —1 B 。

5 C. 1 D 。

86。

若函数1)12()(2+-+=x a xx f 在区间(]2,∞-上是减函数，则实数a 的取值范围是（ ）A 。

⎪⎭⎫⎢⎣⎡+∞-,23 B 。

⎥⎦⎤ ⎝⎛-∞-23, C 。

⎪⎭⎫⎢⎣⎡+∞,23 D.⎥⎦⎤ ⎝⎛∞-23,7。

函数x x x f ++=12)(的值域是（）A 。

[)+∞,0B 。

]0,(-∞C 。

),21[+∞- D. [)+∞,18. 1(0,1)xy aa a a=-≠≠函数且的图像可能是（ )A ．B ．C ．D ．9.已知2.05.05.0,2,5.0===c b a ，则c b a ,,三者的大小关系是（)A 。

a c b >>B 。

2016-2017学年度第一学期期中六校联考高一数学试卷宝坻一中 张国铭 杨村一中 崔立梅一. 选择题(本大题共8小题，每题4分共32 分)1.已知集合 A 二{0 ,1}, B 二{ _1,0, a 3},且 A? B,则 a 等于()7.已知f(x) RogMx 2 -2x)的单调递增区间是()2x8. 已知函数f (X ) = F 2 2x>° ,若存在为已(0,+比)，x 2w (q ,0】,使得l x +1, x^0f X 1二f X 2，则X 1的最小值为()(A) 1(B) 0 (C)-2(D)-32. 设全集U =R, A ={x • N |1乞x 乞5}, B = x • R|x 2 - x-2 = 0}，则图中阴影表示的集合为( )(A) { -1} (B){2}(C) {3,4,5} (D) {3,4}3. 函数 f x =-x • lg(x -1) • (x -3)° 的定义域为()(A) : x 1 ：： x _ 4』 (B): x 1 ：： x _ 4且 x =3:(C)「x1Ex 乞4 且 x=3? (D)1xx_4；(A ) a b c (B ) a c b (C ) cab (D ) c b a5.设函数 f(x)= l n(1-x) -1 n(1+x)，则 f(x)是()(A)奇函数，且在(0,1)上是增函数 B .奇函数，且在(0,1)上是减函数 6.函数y Wx-1的零点为X 。

，则3 ( )…0 (B)°，： (C)2，1 (D)(A)(1, =)(B)(2(C)(」：，0)(D)(A) log2 3 (B) log3 2 (C) (D) 2二.填空题(本大题共6小题，每题4分共24分)r1】9. 已知集合A={l,2a}, B={a,b},若A c B=]-,，则AU B为.1.4 J 7 ------------10. 设函数f(x)二3x-5,(x_6)，则f .I f(x+3),(x c6)11. 已知定义域为！a-4,2a-2]的奇函数f x = 2016x^5x b 2 ,则f a f b 的值为.212. 若幕函数y =(m2-m-1)x m‘心在(0,=)上是增函数，则m= .13. 已知函数f(x)=log a x+b(a>0，a^1)的定义域、值域都是11,2]，则a b = .[Iog2(x + 1),x"0,1)14. 已知函数f (x)是定义在R上的奇函数，若f(x)二127 ，则-x -3x —,x [1,：：) 2 2 关于x的方程f(x) • a = 0(0 :：: a <1)的所有根之和为.三.解答题(本大题共5题)15. ( 12分)函数f(x)「口」g(3x—9)的定义域为A,集合B =x -a ：0 ,a R?.(I) 求集合A;(II) 若A，B -一，求a的取值范围.16. (12 分)设集合 A = {x (x—2m+1 I x—m+2 0〉，B = <x 1 兰x+1 兰4〉.(I)若m =1 时，求ARB ;(I I)若A" B = A，求实数m的取值集合.17. (13分)已知函数f(x) =a bx(其中a , b为常数)的图象经过(1,3)、(2,3)两x占八、、・(I) 求a ,b的值，判断并证明函数f(x)的奇偶性；(II) 证明：函数f(x)在区间迈，二上单调递增.18. ( 13 分)已知函数 f (x) x 6，x " 2，(a . 0 且a=1)3 +log a x, X >2,(I) 若a =2，解不等式f(x)空5 ;(II) 若函数f(x)的值域是4，•::,求实数a的取值范围.19 . ( 14分)已知f(x)是定义在1-1,11上的奇函数，且f(1) =1，若m,n 1-1,1，m n = 0 时，有f (m) f (n)m +n(I) 证明f(x)在［-1,1】上是增函数；(II) 解不等式f(x2 -1) f(3-3x) ：：0 ;(III) 若f (x)乞t2-2at • 1对-l-1,1】,a・丨-1,11恒成立，求实数t的取值范围•2016-2017学年度第一学期期中六校联考高一数学答题纸选择题、填空题9、10、11、12、13、14、三、解答题15、16、17、18、19、2016-2017学年度第一学期期中六校联考高一数学答案、选择题C A B B B B C C•填空题：1 5 a 9. -2,1 10.19 11.0 12. -1 13.3 或14. 1-21 4 J 2三、解答题："4-xZ0 ‘X 兰415. 解：(I)要使函数f(x)有意义，只需满足」，解得彳，3X-9A0 'XA2即2 e x兰4，从而求出集合A = {x2v x兰4} 6 分(II)由(1)可得集合A = {x2v x兰4}，而集合B={xxva }若a兰2，贝U ，所以a 2，即a的取值范围是(2, •：：). 6 分16. 解：集合B = <x0 兰x 兰3〉.(I) 若m=1，则A={x-1v x<1}.则A「|B 二「X 0 岂x ：：：1〉 4 分(II) 当A W即m - -1 时，A p]B=A ；当A=_即m = -1时： 6 分当m ：： -1 时，A = (2m-1, m-2)，要使得A"B 二A,A- B ,丄2m -1 丄0—1只要m^5，所以m的值不存在；8 分[m-2 兰3 2当m •-1 时，A = (m-2 ,2m-1)，要使得A5 B ,□冷m—2-O 八只要=m = 2. 10 分[2m—1 兰3综上，m的取值集合是{-1 , 2} . 12 分17.解：(I) •••函数f (x)的图像经过(1,3)、(2,3)两点2•••函数解析式 f(x)=「x ，定义域(-：：，o )u (0 ,+：：)x22f ( -X ) ( -X )- - (— ' x) - - f (x)-X x2•函数解析式f(x) x 是奇函数7 分x(II)设任意的x 1、x 2［迈 ,r )，且 X i ：：: X 22(x 2一為)/、2 (x2- % ) = ( x2- x i)( 1)X j X 2X i X 22—^x 2=(x 2-为)——ii分MX ?T 为 _、2 , x 2 . 2，且 x i::: x 2二 x i X 2 2，则 2 - X j X 2 ：： 0，且 x 2 - 为 0 得 f(x ,) —f (x 2) ：：0,艮卩 f(xj ：： f(x 2) •函数f (x)在区间［「2,=)上单调递增.i3分 -x 6,x _ 2口i8.解：(I)将a =2代入函数f x 二a ・0且a = i 中，3 + log ax,x>2f —x+6,x^2口得 f xa 0 且 a = i ;3 +log 2x,x >2f (x) _5，即-x ■ 6 一5或3 log 2x _ 5，4 分解得：i 乞x^2或2：：：x 乞4， 综上：i 乞x 乞4;•不等式f(x)空5的解集为「xi 乞x 空4? ； 7分(II) •••当 x — 2时，f x〔4「：，函数 f (x)的值域是 ----------- 9分f (X i ) - f (X 2)=2 2 X 1x 2X iX 2•••当x 2时，f x =3 log a x - 4，即log a x — 1 ；当0 ：：：a ::: 1时，显然不符合题意，ii 分2故 a 1，贝V log ax 丄log aa = 1，解得 a ^x , ■ - 1 ：： a < 2.•••实数a 的取值范围为 1,2].13 分19.解：(I)任取-1乞X 1 ：：: X 2叮，贝Uf (x 1)- f(x 2)= f (x 1)f (-X 2)='(x1- x 2 )2分X 〔 一 X ?一1 乞花：：x 2 乞 1,. %(—x 2) = 0 ,f (xj + f (—X 2) c-由已知 -0, X^ X 2:: 04分% —x 2.f (xj - f(X 2)::： 0,即 f (x)在 1-1,1 上是增函数5 分(II )因为f (x)是定义在1-1,1上的奇函数，且在1-1,11上是增函数-仁3x-3叮(III )由 (1 )知f(x)在〔-1,1上是增函数，所以 f(x)在I- 1,11上的最大值为 f(1)=1，f (x)乞t 2 -2at 1 对—x '-1,11a I-1,112 • — 2 t 一 2at 1 _ 1 = t - 2at _ 0 10设 g(a)二t 2 -2at,对-a 1-1,1, g(a) 一 0 恒成立, 11 所以,g(_1) =t 2 +2t 二0 丿 2 n * 飞⑴=t 2—22 0 >0 或 t< -2 t 启2或t^O 13所以 t 一2或 t< -2或t =0 .14不等式2化为 f (x -1) :： f (3x - 3)，所以< 2X 2 -1c3x-32( 41< -1兰 x -1兰1 ，解得。

安义中学2016-2017学年度上学期高一年级期中考试数 学 试 卷一、选择题（在每小题给出的四个选项中，只有一项是符合题目要求的.本大题共12小题，每小题5分，共60分.）1．全集为实数集R ，M ＝{}{}），则（＜，M C x x N x x R 122=≤≤-∩N ＝( ) A ．{}2-＜x xB ．{}12＜＜x x -C ．{}1＜x xD ．{}12＜x x ≤-2．下列图形中，可以表示以M=｛x |0≤x ≤1｝为定义域，以N=｛y ｜0≤y ≤1｝为值域的函数的图象是 ( )A B C D3．设f ，g 都是由集合A 到A 的映射，其对应法则如下表（从上到下）；x 1 2 3 4 x 1 2 3 4f(x) 3421g(x) 4321则f [g (1)]的值为( ) A ．1 B ．2 C ．3 D ．44．函数y =a x -2－1（a ＞0且a ≠0）图象必经过点( )A ．(0，1)B ．(1，1)C ．(2，0)D ．(2，2)5．若函数y=f(x)的图像与y=1nx 的图像关于y=x 对称，则f (1)＝( )A ．1B ．eC ．e 2D ．1n(e －1)6．函数f (x )=4x 2－m x ＋5在区间[－2，＋∞]上是增函数，在区间(－∞，2)上是减函数，则f (1)等于( ) A ．－7 B ．1 C ．－16 D ．25 7．若a=20.5，b=log π3，c=1n 31，则( ) A ．b ＞c ＞aB ．b ＞a ＞cC ．a ＞b ＞cD ．c ＞a ＞b8．f (x )=⎪⎩⎪⎨⎧=00002＜ ＞ x x x x π，则f {f [f (－3)]}等于( )A ．0B ．πC ．9D ．π29．已知函数f (x )=等于，则，若)()(111a f b a f xxg-=+-( ) A ．bB ．－bC ．b 1D ．－b110．已知f (x )={)1(1)1(413≥+-x x og x a x a a ＜）（是（－∞，+∞）上的减函数，那么a 的取值范围是( )A ．[3171，）B ．（0，31） C ．（71，1） D ．（31，1） 11．若函数f (x )为偶函数，且在)[∞+，0上是增函数，又f (－3)＝0，则不等式(x －2)f （x ）＜0的解集为( )A ．(－∞，－3)∪(2，3)B ．(－3，2)∪(3，＋∞)C ．(－3，3)D ．(2，3)12．对于实数m ，n 定义运算“⊕”：m ⊕n ＝⎪⎩⎪⎨⎧-≤-+-nm mn n nm mn m ＞ 2212，设f (x )＝（2x －1）⊕(x －1)，且关于x 的方程f (x )＝a 恰有三个互不相等的实数根x 1，x 2，x 3，则x 1x 2x 3 的取值范围是( )A ．(－321，0) B ．(－161，0) C ．(0，321) D ．(0，161) 二、填空题：（本大题共4小题，每小题5分，满分20分）13．函数f (x )=1n x +2x －6的零点在区间(a ，a+1)，a ∈Z 内，则a ＝ . 14．A 若{}20172017201b ab a a a b a ++=⎭⎬⎫⎩⎨⎧，则，，，，的值为 .15．函数f (x )=)32(1313-2++-x g xx 的定义域为 .16．给出下列五个命题：①函数y =f (x )，x ∈R 的图象与直线x=a 可能有两个不同的交点； ②函数y=log 2x 2与函数y=2log 2x 是相等函数；③对于指函数y=2x 与冥函数y =x 2，总存在x 0，当x ＞x 0时，有2x ＞x 2成立； ④对于函数y =f (x )，x ∈[a ，b ],若有f (a )×f (b )＜0，则f (x )在(a ，b )内有零点； ⑤已知x 1是方程x +1g x =5的根，x 2是方程x +10x =5的根，则x 1+x 2=5. 其中正确的序号是三、解答题（本大题共6小题，共70分） 17．(本小题满分10分) 计算下列各式的值：(1)31021)278()53()412(　-+-- (2)++1001lg 25.6log 5.2In 3log 122++e18．(本小题满分12分)已知集合A={}{}4)2(log 362＜，或+=-≤≥x x B x x x . (1)求B C A R ⋂;(2)已知{}B C R a a x a x C ⊆∈+=，若＜＜)(12，求实数a 的取值范围.19．(本小题满分12分) 设函数，则：244)(+=x xx f (1)证明：1)1()(=-+x f x f ；(2)计算：)20152014()20153()20152()20151(f f f f +⋯+++.20．(本小题满分12分)已知函数12)(2-+-=a ax x x f 在区间[0，1]上有最小值－2，求a 的值.21．(本小题满分12分)据市场分析，广饶县驰中集团某蔬菜加工点，当月产量在10吨至25吨时，月生产总成本y （万元）可以看成月产量x(吨)的二次函数. 当月产量为10吨时，月总成本成为20万元；当月产量为15吨时，月总成本最低为17.5万元.(1)写出月总成本y (万元)关于月产量x (吨)的函数有关系； (2)已知该产品销售价为每吨1.6万元，那么月产量为多少时，可获最大利润，最大利润多少?22．(本小题满分12分) 已知函数).23()11(1)(，恒过定点且＞，　≠+=-a a ax f a x(1)求实数a ；(2)在(1)的条件下，将函数f(x)的图象向下平移1个单位，再向左平移a 个单位后得到函数g(x)，设函数g(x )的反函数为h(x )，求h(x )的解析式；(3)对于定义在[1，9]的函数y =h(x )，若在其定义域内，不等式[h(x )+2]2≤h (x 2)+m +2恒成立，求m 的取值范围.。

2016~2017学年度第一学期高一地理期中联考试卷一、单项选择题：（每小题2分，共50分） 1．在天体系统各层次中，最高一级是A.总星系B.河外星系C. 太阳系D.地月系 2.离地球最近的天体是A ．太阳 B.月球 C. 火星 D.金星 3．下列关于太阳活动的叙述，正确的是（ ）A ．在黑子数目最多的地方和时期，耀斑等其他形式的太阳活动就很少出现B ．太阳黑子的多少和大小，可以作为太阳活动强弱的标志C ．太阳黑子多少的变化周期大约为11年，耀斑多少的变化周期大约只有若干分钟D ．太阳大气层从里到外分为光球、色球和日冕三层，黑子和耀斑都出现在光球层里 下图表示12月22日a 、b 、c 、d 四城市昼夜长短情况示意图，阴影部分为黑夜，据图回答4—5题。

4．四城市中地球自转线速度最大的是： A ．cB ．bC ． aD ．d5．由南向北排出a 、b 、c 、d 四城市的顺序：A ．acbdB ．acdbC ．dcabD ． cadb 6. 下列四幅图中（图1-1），能正确表示地球自转方向的是（ ）A ．④B ．③C ．②D ．①7.图中正确表示北半球水平运动物体偏转方向的是：(虚线为原运动方向，实线为偏转方向)（ ）S① ②N④900W ③900W 图1—1A B C D8．天安门广场上的国旗与太阳同时升起，下列日期中升旗仪式最早的是（）A．5月1日B．8月1日C． 7月1日D．10月1日9．从冬至日到夏至日（）A．赤道以北的地区正午太阳高度不断增大B．地球绕日公转的速度越来越慢C．赤道以北的地区白昼越来越长D．太阳直射点位于赤道和北回归线之间读右图，回答10～11题。

10．如果图中的虚线为晨线，则此时的北京时间是：A．6时B．12时C．3时20分D．15时20分11．若从A点沿经线向B方向发射一颗射程为4000千米的导弹，则关于导弹落点的叙述，正确的是：A．导弹落在B点的东南方向、A点的东北方向B．导弹落点所在地一年之中有两次太阳直射C．导弹落在低纬度地区D．导弹将落在北半球、西半球12.今天（11月5日前后）南昌昼夜长短状况是A.昼最短夜最长B.昼短夜长，且昼渐短夜渐长C.昼夜等长D.昼长夜短，且昼渐长夜渐短13.下列现象中，与大气对太阳辐射的削弱作用无关的是：A、多云的夜晚通常比晴朗的夜晚温暖些B、日出前天已亮，日落后天不黑C、平流层的气温随高度增加而增加D、夏季白天多云时，气温不会太高14.下图中昼夜温差最小的是15.秋季，晴朗的夜晚，农民点燃田地里的秸秆，烟雾弥漫，据说能防霜冻，原因是烟雾：A、能减少大气逆辐射B、能增加地面辐射C、能使地面辐射减弱D、能增加大气逆辐射16.图一中四幅热力环流图与图二所示气压分布状态图相符的是：17.某气压带的南面盛行西北风，北面盛行东南风，该气压带是：Ａ、北半球副热带高压带Ｂ、北半球副极地低压带Ｃ、南半球副热带高压带Ｄ、南半球副极地低压带18.关于气压带、风带季节移动的规律，叙述正确的是Ａ、夏季向北移，冬季向南移Ｂ、北半球夏季北移冬季南移Ｃ、北半球夏季南移冬季北移Ｄ、风带位置季节移动，必然导致风向的季节变化19.下列叙述正确的是Ａ、盛行西风与信风在南北纬60度附近相遇Ｂ、赤道地区上空，水平气压梯度力指向低纬地区Ｃ、赤道低压附近为东北信风带与东南信风带Ｄ、南北纬30度附近上空，空气受热上升20.读北半球中高纬度环流示意图，下列说法正确的是：Ａ、②盛行西南风Ｂ、乙点位于30ºＮ附近Ｃ、①是冷性气流Ｄ、甲点位于30ºＮ附近21.当我国各地白昼时间最短时，下列四幅图所示气压带、风带分布正确的是：陆地陆地B海洋海洋C图二图一①②ＡＢ Ｃ Ｄ22.南半球的气压带基本呈带状分布，而北半球的气压带则断裂成块状，主要原因是： Ａ、海陆分布状况不同Ｂ、气压带和风带的季节移动Ｃ、太阳直射点的位置不断变化Ｄ、地形起伏状况不同读“某月某条经线上部分气压带、风带和气流相互关系示意图”，完成22～23题：23.图中②气压带或风带的气流运动方向及性质分别为： A 、上升，湿润 B 、下沉，干燥C 、由高纬流向低纬，干燥D 、由低纬流向低纬，湿润24.下面四幅图表示的热力环流中，错误的是：A B C D25.下列四幅风带图中，对西欧温带海洋性气候的形成有重要影响的是：A B C D 二、综合题（50分）26、读图，回答问题（20分）30º60º 60º30º 30º0º 15º15º 0º 气压带风带 ① ②③副极地低气压带赤道南极30ºＳ60ºＳ（1）此图所示的日期是。