汕头金山中学高三理科数学测试题

广东省汕头帀金山中学2019届咼三数学上学期期中试题 理温馨提示：先做你会做的题是得高分的必要条件。

先做难题，下次将有更大的增长空间。

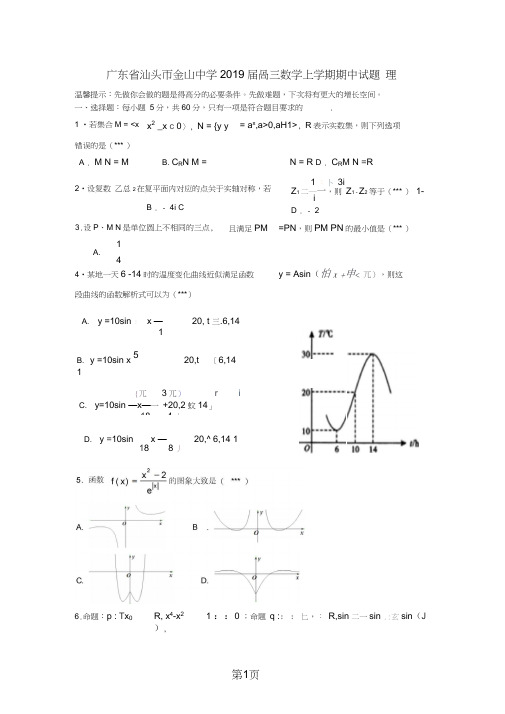
一、选择题：每小题 5分，共60分，只有一项是符合题目要求的 .1 •若集合M = <x 错误的是（*** ）1 A.46.命题：p : T x 0R, x 4-x 21 ：：0 ；命题 q :：：匕，： R,sin 二一sin .:玄sin （J）,x 2 _x c 0〉, N = {y y = a x ,a>0,aH1>, R 表示实数集，则下列选项A . M N = M B. C R N M = N = R D . C R M N =R2•设复数 乙总2在复平面内对应的点关于实轴对称，若B . - 4i C1 ：卜 3iZ 1 二―一，则 Z 1 - Z 2 等于（*** ） 1-iD . - 23.设P 、M N 是单位圆上不相同的三点,且满足PM=PN ，则PM PN 的最小值是（*** ）4•某地一天6 -14时的温度变化曲线近似满足函数 y = Asin （怕x +申< 兀），则这段曲线的函数解析式可以为（***） A. y =10sin ： x —20, t 三.6,14 1184B. y =10sin x520,t〔6,141184{兀 3兀） riC. y=10sin —x —一 +20,2 蚊14」18 4丿D. y =10sinx — 20,^ 6,14 1 18 8丿则下列命题中的假命题为（*** ） B- (—p) (—q)C - (一p) (—q) D. p q3x - y - 6 乞 0 I7.设x, y 满足x - y • 2 _0 ,若函数z =ax • y(a . 0)的最大值为18，则a 的值为(*** )x _ 0, y _ 0A .3B. 5C. 7D.9&若 f (x)==2sin( x )( 门＞0 ）的图像在［0,1］上恰有3个最咼点，则-■的范围为（*** ）A r 19 兀 ,2?： )B . 9 二 13 17二 25 二、[, )C •[,,」 D .[4 二,6二）A .[4 4 2 2 4 49.图1所示，一棱长为2的正方体被削去一个角后所得到的几何体的直观图，其中DD^1 ,10•已知棱长为 J3的正方体ABCD -ABQ 1D 1内部有一圆柱，此圆柱恰好以直线 AG 为轴，则该圆柱侧面积的最大值为（***）2 3- D . 3.2-自然对数的底数，则实数a 的取值范围为（*** ）A . a ：： -eB . a 1C . a eD . a ：： —3或 a 11112.记min'abc 』为a,b,c 中的最小值，设x, y 为任意正实数，则M = min 2x, , yI yx j的最大值为（***） A. 1'、2 B. 2 C.22 D. 3二、填空题：本大题共 4小题，每小题5分，共20分.13•如图所示，在边长为1的正方形OABC 中任取一点P , 则点P 恰好取自阴影部分的概率为 __________________ . 14•向量a，b,c 满足：〔aF4 , |b | = 4&, b 在 a 上的投影为 4,（a P e-c ） =0,A - p (—q)AB = BC = AA =2，若此几何体的俯视图如图 2所示，则可以作为其正视图的是（***）11.已知函数 f (x) =ax eln x 与 g(x)2一x的图象有三个不同的公共点x -eln x则b c的最大值为.二，n为奇数15. 数列｛a*｝且a* =n 2n ___________ ,若S n为数列：a"的前n项和，则S2018 = .sin - , n为偶数42x _ 3 x16. 已知函数y=f(x)(x・R)满足f(x)・f(_x)=6，函数g(x) ，若曲x-1 x + 1线y = f(x)与y =g(x)图象的交点分别为(为『)、区皿)、…、(X m,y m),则mZ (Xi +yj= _____________ (结果用含有m的式子表示).i 4三、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.17. (12分)已知等差数列 g 的公差为d，且关于x的不等式ax2 - dx-3 ：：：0的解集为(-1,3),(an巧(I)求数列:a n ?的通项公式；(n)若b n =2 2•务，求数列 Z 前n项和久18. (12分)如图，在ABC中，内角A,B,C的对边分别为a,b,c，且2acosC-c = 2b .(I)求角A的大小；兀(n)若• ABC , AC边上的中线BD的6长为35，求ABC的面积.19. (10分)已知函数f (x) = x-1|+|x — 3 .(I)解不等式：f (x^l x 1 ；(n)设函数f (x)的最小值为c,实数a, b满足a 0,b 0,a ^c ,2 b2求证：- 1 .a+1 b+120. (12分)四棱锥S - ABCD的底面ABCD为直角梯形，AB/ /CD , AB _ BC , AB =3 , BC =1 , CD =2 ,SAD为正三角形.(I)点M为棱AB上一点，若BC //平面SDM , AM丄■ AB，求实数'的值;(n)若BC _ SD，求二面角A - SB -C的余弦值.21. (12 分)已知圆C1:(x 3)2(^1)^4和圆Sf则b c 的最大值为.2 2C 2 ： (x -4) (y -5) = 4.(I)若直线l 过点A(4,0)且被圆C 1截得的弦长为2 3，求直线丨的方程；(n)设平面上的点 P 满足：存在过点 P 的无穷多对互相垂直的直线 |1和|2，它们分别与 圆C i 和圆C 2相交，且直线l i 被圆C i 截得的弦长与直线12被圆C 2截得的弦长相等，试求所 有满足条件的点 P 的坐标。

汕头市金山中学2015-2016学年度第一学期期中考试高三理科数学 试题卷本试题分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，时间120分钟.第Ⅰ卷 （选择题 共60分）一、选择题：(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知i 为虚数单位，若复数()()()211a a i a R -+-∈是纯虚数，则实数a 的值为（ ） A ．1±B ．1-C ．0D ．12．“23sin =θ”是“3πθ=”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件 3．已知数列{}n a 为等比数列，191,3a a ==，则5a =（ ）A ． 2 BD．4．如图，正方体1111ABCD A B C D -中，E 为棱1BB 的中点，用过点1,,A E C 的平面截去该正方体的上半部分，则剩余几何体的左视图为（ ）A B CD5．设双曲线()22221,0,0x y a b a b-=>>错误!未找到引用源。

的渐近线方程为错误!未找到引用源。

，则该双曲线的离心率为（ ） A ．错误!未找到引用源。

B ．2 C ．错误!未找到引用源。

D ．错误!未找到引用源。

6．已知平面向量22(2sin ,cos )a x x =r ，22(sin ,2cos )b x x =-r ，()f x a b =⋅r r ，要得到2cos 2y x x =-的图像，只需将()y f x =的图像（ ）ABCDA B C D 1111E第4题图A ．向左平移6π个单位长度 B ．向右平移6π个单位长度 C ．向左平移3π个单位长度 Ｄ．向右平移3π个单位长度7．设,x y 满足约束条件2208400 , 0x y x y x y -+≥⎧⎪--≤⎨⎪≥≥⎩，若目标函数()0,0z abx y a b =+>>的最大值为8，则a b +的最小值为（ ）A ．3B ．4C ．8D ．98．定义平面向量的正弦积为sin 2a b a b θ•=r r r r错误!未找到引用源。

高中数学学习材料鼎尚图文*整理制作2015-2016汕头金山中学高三理科数学期末考试试题命题人：彭志敏第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．复数z 满足2(1)(1)i z i -+=+，其中i 为虚数单位，则在复平面上复数z 对应的点位于（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 2．已知向量25,10),1,2(=+=⋅=→→→→→b a b a a ，则=→b （） A. 5 B.10 C.5 D.253.已知M ，N 为集合I 的非空真子集，且M ，N 不相等，若N ∩∁I M ＝∅，则M ∪N ＝( )A ．MB ．NC ．ID ．∅ 4．定义域为R 的函数2009()f x xx a b =++是奇函数的充要条件是（） :0A ab = :0B a b +=:0bC a= 22:0D a b +=5．已知P 为抛物线x y 42=上一个动点，Q 为圆1)4(22=-+y x 上一个动点，那么点P 到点Q 的距离与点P 到抛物线的准线距离之和最小值是( ) A ．5 B ．8 C.25+ D.171-6. 在∠AOB 的OA 边上取m 个点，在OB 边上取n 个点(均除O 点外)，连同O 点共m +n +1个点，现任取其中三个点为顶点作三角形，可作的三角形有( )1212121212121112211111A.C C C C B.C C C C C.C C C C C C D.C C C C m n n m m n n m m n n m m n m n m n +++++++++7．某几何体的三视图如图7-1所示，若这个几何体的体积为24，则h =（）444 h正视图侧视图俯视图图7-1A ．2B ．3C ．4D ．58 ．已知条件2|1:|>+x p ,条件a x q >|:|,且p ⌝是q ⌝的必要不充分条件,则实数a 的取值范围是（ ）A ．10≤≤aB ．31≤≤aC ．1≤aD ．3≥a9.设m ，n ∈R ，若直线(m +1)x +(n +1)y －2＝0与圆(x －1)2+(y －1)2＝1相切，则m+n 的取值范围是( ) A ．［13-，13+］ B ．(－∞，13-］∪［13+，+∞)C ．［222-，222+］D ．(－∞，222-］∪［222+，+∞) 10．已知定义在[)0,+∞上的函数()f x 满足()()22f x f x =+，当[)0,2x ∈时()22+4f x x x =-，设()f x 在[)22,2n n -上的最大值为n a ()n N *∈，且{}n a 的前n 项和为n S ，则n S =（ ） A ．1122n --B ．2142n --C ．122n -D ．1142n -- 11.已知函数f (x )=A sin(ωx+φ)(A ,ω,φ均为正的常数)的最小正周期为π,当x=时,函数f (x )取得最大值,则下列结论正确的是( )A .f (2)<f (-2)<f (0)B .f (0)<f (-2)<f (2)C .f (-2)<f (0)<f (2)D .f (2)<f (0)<f (-2)12．已知函数:2342015()12342015x x x x f x x =+-+-++,2342015()12342015x x x x g x x =-+-+-- 设函数()(3)(5)F x f x g x =+⋅-,且函数()F x 的零点均在区间),,](,[Z ∈<b a b a b a 内,则-b a 的最小值为（ ）A ．8B ．9C ．10D ．11第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题5分，共20分． 13、已知411e n dx x =⎰，那么3()n x x-展开式中含2x 项的系数为 14.若直线2y x =上存在点(,)x y 满足约束条件30,230,,x y x y x m +-≤⎧⎪--≤⎨⎪≥⎩则实数m 的取值范围为.15.已知实数,x y 满足221x y +=，则x y +的最大值是.16、已知函数()23log (1)1132x x kf x x x k x a -+-≤<⎧=⎨-+≤≤⎩，若存在k 使得函数()f x 的值域为[]0,2，则实数a 的取值范围是三．解答题（共6小题，前五题为必答题，每题满分12分，后三题为选做题，每题满分10分） 17. 在△ABC 中，角A ，B ，C 对应的边分别是a ，b ，c .已知cos 2A －3cos(B ＋C )＝1. （1）求角A 的大小；（2）若△ABC 的面积53S =，b ＝5，求sin sin B C ⋅的值． 18. 数列{}n a 的前n 项和为nS , 已知 nn Sa n +=-(*n N ∈) 恒成立.(1) 求数列{}n a 的通项公式;(2) ln(1),n n na nb a n +⎧⎪=⎨⎪⎩为奇数，为偶数，求{}n b 的前2n 项和T 2n .19. 在四棱锥P ABCD -中，AB //CD ，AB AD ⊥，4,22,2AB AD CD ===，PA ⊥平面ABCD ，4PA =.（Ⅰ）设平面PAB平面PCD m =，求证：CD //m ；（Ⅱ）求证：BD ⊥平面PAC ；（Ⅲ）设点Q 为线段PB 上一点，且直线QC 与平面PAC所成角的正弦值为33，求PQPB 的值．20．已知直线330x y +-=经过椭圆C ：()222210x y a b a b+=>>的右焦点和上顶点． （1）求椭圆C 的标准方程； （2）过点()0,2-的直线l 与椭圆C 交于不同的A 、B 两点，若AOB ∠为钝角，求直线l 斜率k 的取值范围；（3）过椭圆C 上异于其顶点的任一点P 作圆O ：222x y +=的两条切线，切点分别为,M NPDCBA（,M N 不在坐标轴上），若直线MN 在x 轴、y 轴上的截距分别为m 、n ，证明：221143mn+为定值．21．已知函数2()(0)f x x ax a =-≠，()ln g x x =，()f x 图象与x 轴交于点M （M 异于原点），()x f 在M 处的切线为1l ，()1-x g 图象与x 轴交于点N 且在该点处的切线为2l ，并且1l 与2l 平行. (Ⅰ)求(2)f 的值；(Ⅱ)已知实数R t ∈，求函数[][()+],1,y f xg x t x e =∈的最小值；(Ⅲ)令()()'()F x g x g x =+，给定1212,(1,),x x x x ∈+∞<，对于两个大于1的正数βα,，存在实数m 满足：21)1(x m mx -+=α，21)1(mx x m +-=β，并且使得不等式12|()()||()()|F F F x F x αβ-<-恒成立，求实数m 的取值范围.请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一题计分，作答时请写清题号． 22、选修4-1：几何证明选讲如图，圆周角C ∠BA 的平分线与圆交于点D ，过点D 的切线与弦C A 的延长线交于点E ，D A 交C B 于点F ．()I 求证：C//D B E ；()II 若D ，E ，C ，F 四点共圆，且AC BC =，求C ∠BA ．23、选修4-4：坐标系与参数方程已知椭圆C:22143x y +=，直线:l 3323x ty t⎧=-+⎪⎨=+⎪⎩（t 为参数）． ()I 写出椭圆C 的参数方程及直线l 的普通方程；()II 设()1,0A ，若椭圆C 上的点P 满足到点A 的距离与其到直线l 的距离相等，求点P 的坐标．24、选修4-5：不等式选讲 已知函数()21f x x a x =-++．()I 当1a =时，解不等式()3f x <； ()II 若()f x 的最小值为1，求a 的值．高三理数期末考试参考答案 DCADDCBC DBBD ；-12；(],1-∞；-2；[1,3]；17解：（1）由cos 2A －3cos(B ＋C )＝1，得2cos 2A ＋3cos A －2＝0，……2分解得cos A ＝12或cos A ＝－2(舍去)．……3分 因为0＜A ＜π，所以A ＝3π.……5分（2）由S ＝12bc sin A ＝53，得bc ＝20.又b ＝5，知c ＝4.……7分 由余弦定理得a 2＝b 2＋c 2－2bc cos A ＝25＋16－20＝21，……9分故由正弦定理得sin B ⋅sin C ＝2sin 5()7A bc a ⋅=.……12分 18解：（1）由 n n S a n +=-得 n=1时，1111111, 2S a S a a +=-=∴=-…….1分 2n ≥时,1nn n a S S -=-…….2分1111 (1) ()1n n n n n n n n S a n S a n S a S a ----+=-⇒+=--∴+-+=- 11212(1)1n n n n a a a a --∴=-∴+=+…….3分1111111100 2212n n a a q a -++=-+=≠∴==≠+ {}1n a ∴+是以12为首项，公比12q =的等比数列…….4分 1111(1)2n n n a a q -∴+=+=112n n a ∴=-…….6分 (2)ln 2,112n nn n b n -⎧⎪=⎨-⎪⎩为奇数，为偶数，…….8分2422111ln 2[13(21)]()22211ln 2[1()]34n n T n n n n=-⋅+++-++++-=-⋅+--…….12分19．（Ⅰ）证明：因为AB //CD ，CD ⊄平面PAB ，AB ⊂平面PAB ，所以CD //平面PAB . …………1分因为CD ⊂平面PCD ，平面PAB 平面PCD m =，所以CD //m . …………………………3分z yxPD CB A（Ⅱ）证明：因为AP ⊥平面ABCD ，AB AD ⊥，所以以A 为坐标原点，,,AB AD AP 所在的直线分别为x 轴、y 轴、z 轴建立空间直角坐标系，则(4,0,0)B ，(0,0,4)P ，(0,22,0)D ，(2,22,0)C . ………4分所以(4,22,0)BD =-，(2,22,0)AC =，(0,0,4)AP =，所以(4)22222000BD AC ⋅=-⨯+⨯+⨯=，(4)0220040BD AP ⋅=-⨯+⨯+⨯=. 所以BD AC ⊥，BD AP ⊥. ……………6分因为 AP AC A =，AC ⊂平面PAC ，PA ⊂平面PAC ，所以BD ⊥平面PAC . …………………………………7分（Ⅲ）解：设PQPBλ=（其中01λ≤≤），(,,)Qxyz ，直线QC 与平面PAC 所成角为θ.所以PQ PB λ=.所以(,,4)(4,0,4)x y z λ-=-.∴4,0,44,x y z λλ=⎧⎪=⎨⎪=-+⎩即(4,0,44)Q λλ-+∴(42,22,44)CQ λλ=---+. ……………8分由（Ⅱ）知平面PAC 的一个法向量为(4,22,0)BD =-.因为sin cos ,CQ BD CQ BD CQ BDθ⋅=<>=⋅，得2234(42)8326(42)8(44)λλλ---=⋅-++-+. 解得7[0,1]12λ=∈.所以712PQ PB =. …………12分法2：(II) 依题意：Rt BAD ∆∽Rt ADC ∆,所以ABD DAC ∠=∠，又因为090ABD ADB ∠+∠=， 所以090ADB DAC ∠+∠=，所以BD AC ⊥…..4分又因为PA ⊥平面ABCD ，BD ABCD ⊂平面，所以BD AP ⊥…..6分因为 APAC A =，AC ⊂平面PAC ，PA ⊂平面PAC ，所以BD ⊥平面PAC . ………7分20.（1）依题椭圆的右焦点为()1,0，上顶点为()0,3，故1c =，3b =，222a b c =+=，∴ 可求出椭圆标准方程为22143x y +=．……3分（2）设直线l 方程为2y kx =-，设11(,)A x y 、22(,)B x y由222143y kx x y =-⎧⎪⎨+=⎪⎩得：22(43)1640k x kx +-+=， ∵ 21230k ∆=->，∴ 214k >， 又1221643k x x k +=+，122443x x k =+ ∵ AOB ∠为钝角，∴ 0OA OB ⋅<， 即12120x x y y +<， ∴ 1212(2)(2)0x x kx kx +--<，∴ 21212(1)2()40kx x k x x +-++>，∴ 222416(1)2404343k k k k k +⋅-⋅+<++，即221216043k k -+<+， ∴ 243k >，解得233k <-或233k >，∴ 所求直线斜率的取值范围是2323,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭．……8分 （3）设点()00,Px y ，则以OP 为直径的圆的方程为()()000x x x y y y -+-=④，④式与圆O ：222x y +=方程两式相减可得切点弦MN 的方程为002x x y y +=， 令0y =，得02m x =，令0x =得02n y =， ∴ 02x m =，02y n=，又点()00,P x y 在椭圆C 上， ∴ 2222143m n ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭+=，即22111434m n +=，∴ 221143m n +为定值．……12分21解: ()y f x =图象与x 轴异于原点的交点(,0)M a ，'()2f x x a =-(1)ln(1)y g x x =-=-图象与x 轴的交点(2,0)N ，1'(1)1g x x -=- 由题意可得12l l k k =，即1a =，∴2(),f x x x =-，2(2)222f =-= ………………2分（2）2[()+][ln +](ln +)y f xg x t x x t x x t ==-=22(ln )(21)(ln )x x t x x t t +-+-………4分令ln u x x =，在 []1,x e ∈时，'ln 10u x =+>， ∴ln u x x =在[]1,e 单调递增，0,u e ≤≤…………5分22(21)y u t u t t =+-+-图象的对称轴122tu -=，抛物线开口向上 ①当1202tu -=≤即12t ≥时，2min 0|u y y t t ===-②当122t u e -=≥即122e t -≤时，22min |(21)u e y y e t e t t ===+-+- ③当1202t e -<<即12122e t -<<时，22min 12212121|()(21)224tu t t y y t t t -=--==+-+-=-…………7分1(3)()()'()ln F x g x g x x x =+=+,22111'()0x F x x x x-=-=≥1x ≥得 所以()F x 在区间(1,)+∞上单调递增 ∴1x ≥当时，F F x ≥>（）（1）0①当(0,1)m ∈时，有12111(1)(1)mx m x mx m x x α=+->+-=，12222(1)(1)mx m x mx m x x α=+-<+-=，得12(,)x x α∈，同理12(,)x x β∈， …………………10分∴ 由)(x f 的单调性知 0<1()()F x F α<、2()()F F x β<从而有12|()()||()()|F F F x F x αβ-<-，符合题设. ………………11分 ②当0m ≤时，12222(1)(1)mx m x mx m x x α=+-≥+-=，12111(1)(1)m x mx m x mx x β=-+≤-+=，由)(x f 的单调性知 0<12()()()()F F x F x F βα≤<≤， ∴12|()()||()()|F F F x F x αβ-≥-，与题设不符③当1m ≥时，同理可得12,x x αβ≤≥，得12|()()||()()|F F F x F x αβ-≥-，与题设不符.∴综合①、②、③得(0,1)m ∈…………………12分22、解：（Ⅰ）证明：因为∠EDC ＝∠DAC ，∠DAC ＝∠DAB ，∠DAB ＝∠DCB ， 所以∠EDC ＝∠DCB ， 所以BC ∥DE ． …4分 （Ⅱ）解：因为D ，E ，C ，F 四点共圆，所以∠CFA ＝∠CED 由（Ⅰ）知∠ACF ＝∠CED ，所以∠CFA ＝∠ACF ． 设∠DAC ＝∠DAB ＝x ， 因为AC ⌒＝BC ⌒，所以∠CBA ＝∠BAC ＝2x ， 所以∠CFA ＝∠FBA ＋∠FAB ＝3x ，在等腰△ACF 中，π＝∠CFA ＋∠ACF ＋∠CAF ＝7x ，则x ＝ π7， 所以∠BAC ＝2x ＝2π7．…10分23、解：（Ⅰ）C ：⎩⎨⎧x ＝2cos θ，y ＝3sin θ（θ为为参数），l ：x －3y ＋9＝0．…4分（Ⅱ）设P (2cos θ，3sin θ),则|AP |＝(2cos θ－1)2＋(3sin θ)2＝2－cos θ，P 到直线l 的距离d ＝|2cos θ－3sin θ＋9|2＝2cos θ－3sin θ＋92． 由|AP |＝d 得3sin θ－4cos θ＝5，又sin 2θ＋cos 2θ＝1，得sin θ＝ 35， cos θ＝－ 45． 故P (－ 8 5， 335)．…10分24、解：（Ⅰ）因为f (x )＝|2x －1|＋|x ＋1|＝⎩⎪⎨⎪⎧－3x ，x ≤－1；－x ＋2，－1≤x ≤ 1 2；3x ，x ≥ 12 且f (1)＝f (－1)＝3，所以，f (x )＜3的解集为{x |－1＜x ＜1}；…4分（Ⅱ）|2x －a |＋|x ＋1|＝|x －a 2|＋|x ＋1|＋|x －a 2|≥|1＋a 2|＋0＝|1＋a2| 当且仅当(x ＋1)(x －a 2)≤0且x －a2＝0时，取等号． 所以|1＋a2|＝1，解得a ＝－4或0．…10分ADBFCE。

汕头市金山中学2012-2013学年度第一学期期中考试高三理科数学 试题卷本试题分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，时间120分钟.第Ⅰ卷 （选择题 共40分）一、选择题：(本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.)1．o 660sin 等于（ ）A ．23 B ．21 C ．21- D ．23-2．设R x ∈, 那么“0<x ”是“3≠x ”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件 3．已知单位向量,i j 满足(2)j i i -⊥，则,i j 夹角为（ ） A ．4π B ．6πC ．3π D ．23π4．已知函数()sin y x ωϕ=+0,02πωϕ⎛⎫><≤ ⎪⎝⎭，且此函数的图象如图所示，则点(),ωϕ的坐标是（ ）A ．2,4π⎛⎫⎪⎝⎭B ．2,2π⎛⎫⎪⎝⎭ C ．4,4π⎛⎫⎪⎝⎭D ．4,2π⎛⎫⎪⎝⎭5．函数1ln --=x e y x的图象大致是（ ）6．已知,x y 满足线性约束条件1020410x y x y x y -+≥⎧⎪+-≤⎨⎪++≥⎩，若(,2)x =-a ，(1,)y =b ，则z =⋅a b 的最大值是（ ）A. 1-B. 5C. 52- D. 77．若函数()f x 的零点与函数()422x g x x =+-的零点之差的绝对值不超过0.25，则()f x 可以是（ ）A. ()1x f x e =-B. ()1ln 2f x x ⎛⎫=-⎪⎝⎭C. ()41f x x =-D. ()2(1)f x x =- 8．对于下列命题：①在△ABC 中，若sin2sin2A B =，则△ABC 为等腰三角形；②已知a ，b ，c 是△ABC 的三边长，若2a =，5b =，6A π=，则△ABC 有两组解；③设2012sin3a π=，2012cos 3b π=，2012tan 3c π=,则a b c >>；④将函数2sin 36y x π⎛⎫=+ ⎪⎝⎭图象向左平移6π个单位，得到函数2cos 36y x π⎛⎫=+ ⎪⎝⎭图象。

2019届广东省汕头市金山中学 高三上学期期中考试 数学（理）试题 数学 注意事项： 1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、单选题1．若集合M ={x|x 2−x <0}，N ={y|y =a x (a >0,a ≠1)}，R 表示实数集，则下列选项错误的是A ．M ∩N =MB ．M ∪N =RC ．M ∩C R N =ϕD ．∁R M ∪N =R2．设复数z 1，z 2在复平面内对应的点关于实轴对称，若z 1=1+3i1−i ，则z 1+z 2等于A ．4iB ．−4iC ．2D ．−23．已知P 、M 、N 是单位圆上互不相同的三个点,且满足|PM ⃗⃗⃗⃗⃗⃗|=|PN ⃗⃗⃗⃗⃗⃗ |，则PM ⃗⃗⃗⃗⃗⃗ ⋅PN ⃗⃗⃗⃗⃗⃗的最小值是A ．−14B ．−12C ．−34 D ．−14．如图所示，某地一天6~14时的温度变化曲线近似满足函数，则这段曲线的函数解析式可以为（ ）A ．,B ．,C ．,D ．, 5．函数f(x)=x 2−2e |x|的图象大致是 A ． B ． C ． D ． 6．命题：p ：∃x 0∈R ，x 4−x 2+1<0；命题q ：∀α，β∈R ，sinα−sinβ≤sin(α−β)，则下列命题中的假命题为 A ．p ∨(￢q) B ．(￢p)∨(￢q) C ．(￢p)∧(￢q) D ．p ∧q 7．设x ，y 满足约束条件{3x −y −6≤0x −y +2≥0x ≥0,y ≥0 若目标函数z =ax +y(a >0)的最大值为18，则a 的值为 A ．3 B ．5 C ．7 D ．9 8．已知函数()2sin 4f x x πω⎛⎫=+ ⎪⎝⎭（0ω>）的图象在区间[]0,1上恰有3个最高点，则ω的取值范围为 A ．1927,44ππ⎡⎫⎪⎢⎣⎭ B ．913,22ππ⎡⎫⎪⎢⎣⎭ C ．1725,44ππ⎡⎫⎪⎢⎣⎭ D ．[)4,6ππ 9．如图1所示，是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图，其中11DD =， 12AB BC AA ===，若此几何体的俯视图如图2所示，则可以作为其正视图的是此卷只装订不密封班级姓名准考证号考场号座位号A ．B ．C ．D ．10的正方体1111ABCD A B C D -内部有一圆柱，此圆柱恰好以直线1AC 为轴，则该圆柱侧面积的最大值为ABCD11．已知函数()ln f x ax e x =+与,其中e 为自然对数的底数,则实数a 的取值范围为A ．a e <-B ．1a >C ．a e >D ．3a <-或1a > 12．记{}min ,,a b c 为,,a b c 中的最小值，若,x y 为任意正实数，最大值是AB ．2 CD二、填空题13．如图所示，在边长为1的正方形OABC 中任取一点M ．则点M 恰好取自阴影部分的概率是 ．14．向量a ⃗ ,b ⃗ ,c ⃗ 满足：|a ⃗ |=4，|b ⃗ |=4√2，b ⃗ 在a ⃗ 上的投影为4，(a ⃗ −c ⃗ )⋅(b ⃗ −c ⃗ )=0，则b ⃗ ⋅c ⃗ 的最大值是______．15．数列{a n }且a n ={1n 2+2n ,n 为奇数sin nπ4,n 为偶数，若S n 为数列{a n }的前n 项和，则S 2018=______．16．已知函数f(x)(x ∈R)满足f(x)+f(−x)=6，函数g(x)=2x−3x−1+x x+1，若曲线y =f(x)与y =g(x)图象的交点分别为(x 1,y 1)，(x 2,y 2)，…，(x m ,y m ).则∑(m i=1x i +y i )=______ 三、解答题 17．已知等差数列{a n }的公差为d ，且关于x 的不等式a 1x 2−dx −3<0的解集为(−1,3)， (Ⅰ)求数列{a n }的通项公式； (Ⅱ)若b n =2(a n +12)+a n ，求数列{b n }前n 项和S n ． 18．如图，在ΔABC 中，内角A,B,C 所对的边分别为a,b,c ，且2acosC −c =2b ． （1）求角A 的大小； （2）若∠ABC =π6，AC 边上的中线BD 的长为√35，求∆ABC 的面积． 19．已知函数f(x)=|x −1|+|x −3|． （1）解不等式f(x)≤x +1； （2）设函数f(x)的最小值为c ，实数a ，b 满足a >0,b >0,a +b =c ，求证：a 2a+1+b 2b+1≥1． 20．四棱锥S −ABCD 的底面ABCD 为直角梯形，AB//CD ，AB ⊥BC ，AB =2BC =2CD =2，△SAD 为正三角形． (Ⅰ)点M 为棱AB 上一点，若BC//平面SDM ，AM ⃗⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ ，求实数λ的值； (Ⅱ)若BC ⊥SD ，求二面角A −SB −C 的余弦值． 21．在平面直角坐标系xOy 中，已知圆C 1：(x ＋3)2＋(y －1)2＝4和圆C 2：(x －4)2＋(y －5)2＝4.(1)若直线l过点A(4，0)，且被圆C1截得的弦长为l的方程；(2)设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线l1和l2，它们分别与圆C1和圆C2相交，且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等，试求所有满足条件的点P的坐标．22．已知函数f(x)=(x+b)(e x−a)，(b>0)，在(−1,f(−1))处的切线方程为(e−1)x+ey+ e−1=0.（1）若n≤0，证明：f(x)≥nx2+x；（2）若方程f(x)=m有两个实数根x1，x2，且x1<x2，证明：x2−x1≤1+m(1−2e)1−e ..2019届广东省汕头市金山中学高三上学期期中考试 数学（理）试题数学 答 案参考答案1．B【解析】【分析】先化简M ，N ，再根据集合的运算和集合的之间的关系即可求出.【详解】∵集合M ={x|x 2−x <0}=(0,1)，N ={y|y =a x (a >0,a ≠1)}=(0，+∞)，∴M ∩N =M ，M ∪N =(0,+∞)，∁R N =(−∞,0]，∁R M =(−∞,0]∪[1,+∞)，∴ M ∩C R N =ϕ，∁R M ∪N =R 故选：B ．【点睛】本题考查集合的运算及包含关系的判断及应用，属于基础题．2．D【解析】【分析】利用复数的运算法则可得：z 1，再利用几何意义可得z 2．【详解】z 1=1+3i 1−i =(1+3i)(1+i)(1−i)(1+i)=−2+4i 2=−1+2i ，∵复数z 1，z 2在复平面内对应的点关于实轴对称，∴z 2=−1−2i ，则z 1+z 2=−2．故选：D ．【点睛】本题考查了复数的运算法则、几何意义，考查了推理能力与计算能力，属于基础题．3．B【解析】试题分析：解：根据题意，不妨设点P 的坐标为(1,0),点M 的坐标为(cosθ,sinθ),点N 的坐标为,其中0<θ<π则PM ⃗⃗⃗⃗⃗⃗ =(cosθ−1,sinθ),PN ⃗⃗⃗⃗⃗⃗ =(cosθ−1,−sinθ)所以PM ⃗⃗⃗⃗⃗⃗ ·PN ⃗⃗⃗⃗⃗⃗ =(cosθ−1,sinθ)⋅(cosθ−1,−sinθ)=(cosθ−1)2−sin 2θ =cos 2θ−2cosθ+1−sin 2θ=2cos 2θ−2cosθ=2(cosθ−12)2−12 所以当cosθ=12时，PM ⃗⃗⃗⃗⃗⃗ ·PN ⃗⃗⃗⃗⃗⃗ 有最小值−12 考点：1、单位圆与三角函数的定义；2、向量的数量积；3、一元二次函数的最值问题. 4．A20b =， ，过点()14,30有：A. 5．D 【解析】 【分析】 根据函数的奇偶性和代入特殊点即可选出答案． 【详解】 函数f(x)=x 2−2e |x|，可得f(−x)=f(x)，可知f(x)是偶函数，排除A ； e |x|>0，当x 2−2=0时，即x =±√2时，f(x)有两个零点，x =0时，可得f(0)=−2.；排除B ； 当x >√2或x <−√2时，可得e |x|>x 2−2，图象逐渐走低； 故选：D ． 【点睛】 本题主要考查了函数奇偶性及图象变换，属于中档题． 6．D 【解析】 【分析】 利用配方法求得x 4−x 2+1>0说明p 为假命题，举例说明q 为假命题，再由复合命题的真假判断得答案． 【详解】∵x 4−x 2+1=(x 2−12)2+34>0，∴命题p 为假命题；∀α，β∈R ，sin(α−β)=sin α−sin β不正确，比如α=90∘，β=−90∘，sinα−sinβ=2，而sin(α−β)=0，故命题q 为假命题，则p ∨(￢q)为真命题；(￢p)∨(￢q)为真命题；(￢p)∧(￢q)为真命题；p ∧q 为假命题． 故选：D ．【点睛】本题主要考查了复合命题的真假判断与应用，考查利用配方法求函数的最值，考查三角函数值的大小判断，属于中档题．7．A【解析】【分析】由线性约束条件画出可行域，然后结合目标函数的最大值，求出a 的值．【详解】画出约束条件{3x −y −6≤0x −y +2≥0x ≥0,y ≥0的可行域，如图：目标函数z =ax +y(a >0)最大值为18，即目标函数z =ax +y(a >0)在{x −y +2=03x−y−6=0 的交点M(4,6)处，目标函数z 最大值为18，所以4a +6=18，所以a =3．故选：A ．【点睛】本题主要考查了线性规划问题，作出可行域是解题的关键，属于中档题.8．C （0ω>）的图象在区间[]0,1上恰有3个最高点，所， ω的取值范围为 C.【方法点晴】本题主要考查三角函数的图象、三角函数的周期性，属于难题．三角函数的图象与性质是高考考查的热点之一，在复习时要注意基础知识的理解与落实．三角函数的性质由函数的解析式确定，在解答三角函数性质的综合试题时要抓住函数解析式这个关键，在函数解析式较为复杂时要注意使用三角恒等变换公式把函数解析式化为一个角的一个三角函数形式，然后利用正弦（余弦）函数的性质求解． 9．C 【解析】由题意，根据该几何体的直观图和俯视图知，其正视图的长应为底面正方形的对角线长，宽应为正方体的棱长，故排除B ，D ，而在三视图中看不见的棱用虚线表示，故排除A ，所以正确答案为C. 点睛：此题主要考查空间几何体的三视图等有关方面的知识，属于中低档题型，也是最近几年高考的必考题型.此题有与以往有不同之处，就是给出了空间几何体的三视图各俯视图，去寻找正视图，注意的是，由实物图画三视图或判断选择三视图时，需要注意“长对正、高平齐、宽相等”的原则，还看得见棱的画实线，看不见的棱要画虚线. 10．D 【解析】 如图由正方体的对称性可知，圆柱的上底面必与过A 点的三个面相切， 且切点分别在线段11,,AB AC AD 上，设线段1AB 上的切点为E ， 1AC ⋂面12A BD O =，圆柱上底面的圆心为1O ，半径即为1O E 记为r ，则 ，由12//O E O F 知D。

汕头市金山中学2020届高三第一学期期中考试数 学（理科）一、单选题（本题共12小题，每小题5分，共60分。

在每小题的四个选项中，只有一项是符合题目要求的) 1．已知集合，则等于（ ）A. B. C.D.2．已知复数12z i =+，且复数12,z z 在复平面内对应的点关于实轴对称，则12z z =( ) A ．1i +B ．3455i + C ．3455i - D ．413i +3．下列说法正确的是（ ）A ．命题“若21x =，则1x =”的否命题为：“若21x =，则1x ≠”B ．已知()y f x =是R 上的可导函数，则“()00f x '=”是“x 0是函数()y f x =的极值点”的必要不充分条件C ．命题“存在x ∈R ，使得210x x ++<”的否定是：“对任意x ∈R ，均有210x x ++<”D ．命题“角α的终边在第一象限角，则α是锐角”的逆否命题为真命题 4．已知函数2()cos cos f x x x x =+，则（ ） A ．()f x 的图象关于直线6x π=对称 B ．()f x 的最大值为2 C ．()f x 的最小值为1-D ．()f x 的图象关于点(,0)12π-对称5．一物体在力F (x )＝3x 2－2x ＋5(力单位：N ，位移单位：m)作用力下，沿与力F (x )相同的方向由x ＝5 m 直线运动到x ＝10 m 处做的功是( )． A ．925 J B ．850 J C ．825 J D ．800 J 6．如果'()f x 是二次函数，且'()f x的图象开口向上，顶点坐标为，那么曲线()y f x =上任一点的切线的倾斜角α的取值范围是（ ）A ．(0,]3πB ．[,)32ππC ．2(,]23ππD ．[,)3ππ7．已知()()sin (0,0,,)2f x A x A x R πωϕωϕ=+>><∈在一个周期内的图像如图所示，则()y f x =的图像可由函数cos y x =的图像（纵坐标不变）（ ）得到．A ．先把各点的横坐标缩短到原来的12倍，再向左平移6π单位 B ．先把各点的横坐标缩短到原来的12倍，再向右平移12π单位C ．先把各点的横坐标伸长到原来的2倍，再向左平移6π单位D ．先把各点的横坐标伸长到原来的2倍，，再向左平移12π单位 8．已知函数，，则下列说法正确的是（ ）A.与的定义域都是B.为奇函数，为偶函数C.的值域为，的值域为 D.与都不是周期函数9．设向量a 与b 的夹角为θ，定义a 与b 的“向量积”：a b ⨯是一个向量，它的模sin a b a b θ⨯=⋅⋅，若()()3,1,1,3a b =--=，则a b ⨯=（ ）A ．2BC ．D ．410．如图，可导函数()y f x =在点00(,())P x f x 处的切线方程为()y g x =，设()()()h x g x f x =-，)'(h x 为()h x 的导函数，则下列结论中正确的是（ ）A ．0'()0h x =，0x 是()h x 的极大值点B ．0'()0h x =，0x 是()h x 的极小值点C ．0'()0h x ≠，0x 不是()h x 的极值点D ．0'()0h x ≠，0x 是()h x是的极值点11．已知函数()()f x x ∈R 满足，若函数与()y f x =图像的交点为1122(,),(,),,(,),m m x y x y x y ⋅⋅⋅ 则1()mi i i x y =+=∑ （ ）（A ）0 （B ）m （C ）2m （D ）4m 12．设a 为常数，函数()()2ln 1f x x x ax =--，给出以下结论：（1）若2a e -=，则()f x 存在唯一零点 （2）若1a >，则()0f x < （3）若()f x 有两个极值点12,x x ，则1212ln ln 1x x x x e-<-其中正确结论的个数是（）A.3B.2C.1D.0二、填空题（本题共4小题，每小题5分，共20分)13．已知一个扇形的周长为，则当该扇形的半径__________时，面积最大.14．如图，在直角三角形ABC 中，2AB =，60B ∠=，AD BC ⊥，垂 足为D ，则 AB AD ⋅的值为_____ 15．已知角3πα+的始边是x 轴非负半轴．其终边经过点34(,)55P --，则sin α的值为__________．16．下列是有关ABC ∆的几个命题，①若tan tan tan 0A B C ++>，则ABC ∆是锐角三角形；②若sin2sin2A B =，则ABC ∆是等腰三角形；③若()0AB AC BC +⋅=，则ABC ∆是等腰三角形；④若 cos sin A B =，则ABC ∆是直角三角形； 其中所有正确命题的序号是_______三、解答题（共70分。

汕头市金山中学2024届高三第一学期阶段性考试数学一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合}032|{2≤--=x x x A ，},3|{N x x x B ∈≤=，则=B A （）A ．)3,1[-B ．}3,2,1,0,1{-C ．}3,2,1,0{D ．}3,2,1{2．已知角a 的始边与x 轴非负半轴重合，终边过点)2,1(--P ,则α2sin =()A ．52B ．54C ．55D ．5523．ABC ∆中，“B A >”是“B A sin sin >”的()A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．已知等差数列{}n a 的前n 项和为n S ，若2,552==S S ,则7S =()A ．7B ．－7C ．－10D ．105．教室通风的目的是通过空气的流动，排出室内的污浊空气和致病微生物，降低室内二氧化碳和致病微生物的浓度，送进室外的新鲜空气按照国家标准，教室内空气中二氧化碳日平均最高容许浓度应小于等于01%．经测定，刚下课时，空气中含有0.2%的二氧化碳，若开窗通风后教室内二氧化碳的浓度为y %，且y 随时间t （单位：分钟）的变化规律可以用函数)(05.0101R e y ∈+=-λλ，描述，则该教室内的二氧化碳浓度达到国家标准至少需要的时间为()（参考数据1.13n 1≈）A ．11分钟B ．14分钟C ．15分钟D ．20分钟6．已知1817=a ，,31cos =b 31sin 3=c ，则()A ．a b c >>B ．c a b >>C ．c b a >>D ．bc a >>7．若过点)0)(,(>m n m 可作曲线x x y 33-=三条切线，则()A ．m n 3-<B ．mm n 33->C ．m m n 33-=或m n 3-=D ．mm n m 333-<<-8．己知函数⎪⎩⎪⎨⎧>+-≤=0,20,)(2x x x x xe x f x ，若函数)(2)()]([3)(22R m m x mf x f x g ∈--=恰有5个零点54321,,,x x x x x ，且54321x x x x x <<<<，)()(43x f x f =，则)2()()(2331x f x f x f -++的取值范围是()A ．⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-e e 1,00,23 B ．⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-e e 1,00,32 C ．⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-32,00,23e e D ．⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-32,00,32e e二、多选题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有错选的得0分．9．己知复数z 满足2)1(=+i z ，则()A ．2||=z B ．iz +=1C ．iz 22=D ．2=⋅z z 10．已知AB 为圆4:22=+y x C 的直径，直线1:+=kx y l 与y 轴交于点M (A ，B ，M 三点不共线)，则()A ．l 与C 恒有公共点B ．ABM ∆是钝角三角形C ．ABM ∆的面积的最大值为lD ．l 被C 截得的弦的长度最小值为3211．如图，正方体1111D C B A ABCD -的棱长为a ，E 是棱DD 1的动点，则下列说法正确的是()A ．若E 为DD 1的中点，则直线//1EB 平面BD A 1B ．三棱锥CE BC 11-的体积为定值361a C ．E 为DD 1的中点时，直线E B 1与平面11C CDD 所成的角正切值为552D ．过点1B ，C ，E 的截面的面积的范围是⎥⎦⎤⎢⎣⎡222,23a a 12．设定义在R 上的函数)(x f 与)(x g 的导函数分别为)(x f '和)(x g '，若,2)3()(=--x f x g )1()(-'='x g x f ，且)2(+x g 为奇函数，则下列说法中一定正确的是()A ．函数)(x g 的图象关于1=x 对称B ．)(x f 的周期为4C ．∑==20231)(k k g D ．4)4()2(=+f f 三、填空题：本题共4小题，每小题5分，共20分．13．5)1(x x -的展开式中x 2项的系数是（用数字作答）14．已知函数3sin )(3++=x b ax x f ，若,1)(=m f 则)(m f -=.15．设函数，)(x f 是定义在R 上的偶函数，)(x f '为其导函数，当x >0时，0)()(>+'x f x f x，，则不等式0)(>x f 的解集为．16．已知函数)(sin )(ϕω+=x x f ，（其中0>ω，2πϕ<），T 为)(x f 的最小正周期，且满足⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛T f T f 2131,若函数)(x f 在区间()π,0上恰有2个极值点，则ω的取值范围是.四、解答题：本题共6小题，共70分，解答应写出必要的文字说明、证明过程及演算步骤.17．（本小题满分10分）在ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c ，且.sin 2cosB a Ab =(1)求角A 的大小；(2)若D 为BC 边中点，且2=AD ，求a 的最小值.18．（本小题满分12分）已知数列{}n a 满足11=a ,⎩⎨⎧+=+为偶数为奇数n a n a a n n n ,2,21(1)记n n a b 2=，求证：数列{}2+n b 是等比数列；(2)若,21n n a a a T +++= 求n T 2.19．（本小题满分12分）己知函数132)(23+++=ax x x x f 在)0,1(-上有两个极值点1x ，2x ，且21x x <(1)求实数a 的取值范围；(2)证明：当021<<-x 时，1211)(>x f 20．（本小题满分12分）如图，在三棱锥BCD A -中，平面ABD ⊥平面BCD ，ADAB =O 为BD 的中点，OCD ∆是边长为l 的等边三角形，且63=-BCD A V (1)证明：CDOA ⊥(2)在棱AD 上是否存在点E ，使二面角E-BC-D 的大小为45°？若存在，并求出DEAE的值．21．（本小题满分12分）已知)0,6(1-F ，)06(2，F 为双曲线C 的焦点，点)1,2(-P 在C上.(1)求C 的方程；(2)点A ，B 在C 上，直线PA ，PB 与y 轴分别相交于M ，N 两点，若0=+ON OM ,证明：直线AB 过定点.22．（本小题满分12分）己知函数xk x x f +=ln )(,12)(1+=-xe x g ，其中k 为实数．(1)求)(xf 的极值；(2)若)()()(x f x g x h -=有4个零点，求k 的取值范围．数学参考答案CBCBAADBBDABDBCD ABC-55),1()1,(+∞⋃--∞⎥⎦⎤ ⎝⎛617,61117．解：(1)B a A b sin 2cos= ，由正弦定理得B A AB sin sin 2cos sin ⋅=⋅……1分0sin =/B ,2cos 2sin 2sin 2cos AA A A ==∴……2分02cos =/A,212sin =∴A ……3分又220π<<A ,62π=∴A ,3π=∴A ……5分(2) D 为BC 边中点，AC AB AD +=∴2,即2)(AC AB +=……6分2=AD ，,cos 21622A bc b c ++=∴bc c b -=+∴1622……7分bc c b bc -=+≤∴16222，即316≤bc ，当且仅当334==c b 时取等号，……8分bc bc c b A bc c b a 216cos 222222-=-+=-+= ……9分3163162162=⨯-≥∴a ，即334≥a 故a 的最小值为334……10分18．解：(1)因为11=a ,所以3212=+=a a 故,321==a b 故52221=+=+a b ……2分当2≥n 时，.2222221221)22(121)12(2+=+=+=+===--+--+-n n n n n n n b a a a a a b 故)2(221+=+-n n b b ……5分所以数列}2{+n b 是首项为5，公比为2的等比数列；……6分(2)由(1)知：1252-⨯=+n n b ，故2251.-⨯=-n n b ……7分其中,22222212422421231n b b b n a a a a a a a a a n n n n -+++=-+++=-++-+-=+++- ……8分故,2)(2)()(2124212312212n b b b a a a a a a a a a T n n n n n -+++=+++++++=+++=- ……9分设,52252)221(5121--⨯=-+++⨯=+++=-n n b b b S n n n n ……11分故106252212--⨯=-=+n n S T n n n ……12分19．(1)解：,132)(23+++=ax x x x f ,22)(2a x x x f ++='∴…．．1分 函数.132)(23+++=ax x x x f 在)0,1(-上有两个极值点21x x ，，且21x x <∴由题意知方程0222=++a x x 在)0,1(-上有两不等实根， (2)设a x x x g ++=22)(2，其图像的对称轴为直线,21=x 故有⎪⎪⎪⎩⎪⎪⎪⎨⎧<+-+=⎪⎭⎫ ⎝⎛->=>=-0)1(21210)0(0)1(a g a g a g ，解得210<<a ∴实数a 的取值范围是⎪⎭⎫⎝⎛21,0……5分(2)证明：由题意知x 2是方程0222=++a x x 的较大的根，故⎪⎭⎫⎝⎛-∈0212x ……6分由于210<<a ,2221x ax >∴,32322222222221()1 1.332f x x x ax x x x ∴=+++>+++…8分设12132)(23+++=x x x x h ，⎪⎭⎫ ⎝⎛-∈021x ，021212)(2>+⎪⎭⎫ ⎝⎛+='x x h ……9分)(x h ∴在⎪⎭⎫⎝⎛-021，单调递增，……10分121121)(=⎪⎭⎫ ⎝⎛->∴h x h ，即1211)(2>x f 成立……11分∴当021<<-x 时，1211)(>x f ……12分20．(1)证明：AD AB = ,O 为BD 的中点BD OA ⊥∴……1分又∴平面ABD ⊥平面BCD ,平面⋂ABD 平面,BD BCD =⊂OA 平面ABD ,⊥∴OA 平面BCD ……3分⊂CD 平面BCD ,CD OA ⊥∴……4分(2)解：分别取CB ，CD 的中点为F ，G ，连结OF ，OG ，O 为BD 的中点，OCD ∆是边长为1的等边三角形∴△BCD 是直角三角形，22==OD BD ,1=CD ,3)()(.22=-=CD BD BC ……5分 CB ，CD 的中点为F ，G ，CD OF //∴,,//BC OG OGOF ⊥由(1)得，AO 是三棱锥A-BCD 底面BCD 的高，AOB ∆是直角三角形63132131=⨯⨯⨯⨯⨯⨯=∆-AO S AO V BCD BCD A ,,1=∴AO ……6分以O 点为坐标原点，分别以OF ，OG,OA 所在的直线为x,y,z 轴，如图建立空间直角坐标系，则)0,0,0(O ,)0,0,21(F ,)0,23,0(G ,)1,0,0(A ,)0,23,21(B ),0,23,21(C )0,23,21(D ……7分若在棱AD 上存在点E ，使二面角E-BC-D 的大小为45°，设)10(≤≤=λλAD AE )0,30(，=BC ，)1,23,21(-=AB ，⎪⎪⎭⎫ ⎝⎛-=1,23,21AD ，⎪⎪⎭⎫ ⎝⎛--==λλλλ,23,21AD AE ⎪⎪⎭⎫ ⎝⎛+-++-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-=1,2)1(3,211,23,21,23,21λλλλλλAB AE BE …8分)1,0,0(=OA 是平面BCD 的一个法向量……9分设),,(2222z y x n =是平面BCE 的一个法向量，则⎪⎩⎪⎨⎧=⋅=⋅0022BE n BC n 即⎪⎩⎪⎨⎧==+-++++-30)1(2)1(3212222y z y x λλλ取)1(22-=λx ，12--=λz ，)1,0,22(2---=λλn ……10分二面角E-BC-D 的大小为45°22==∴,即22)1()22(122=++-+λλλ……11分整理得，031032=+-λλ，解得，31=λ或3=λ（舍去）,31ADAE=∴即,31ADAE=21=DEAE∴在棱AD上存在点E，使二面角E-BC-D大小为45°，21=DEAE……12分21解：(1)设双曲线C的方程为,12222=-byax),0,0(>>ba由题意知⎪⎪⎩⎪⎪⎨⎧=+=-=6,11462222babac,解得⎪⎪⎩⎪⎪⎨⎧==33ba,∴双曲线C的方程为;13322=-yx……4分(2)设直线AB的方程为,mkxy+=),,(11yxA),,(22yxB)1,2(-P⎩⎨⎧=-+=322yxmkxy消去y，得.032)1(222=----mkmxxk则,012=/--k,0)3)(1(442222>+-+=∆⋅mkmk22112kkmxx-=+，,13222|1kmx x---=……6分∴直线PA方程为,1)2(2111---+=xxyy令,0=x则⎪⎭⎫⎝⎛-+11122,0x yxM,同理),22,0(222xyxN-+……7分由0=+ONOM,可得,02222222112=-++-+xyxxyx,02)(22)(2222111=-+++-++∴xmkxxxmkxx.0)2](2)12[()2](2)12[(1221=-+++-++xmxkxmxk,08)24())(224(2121=++-+-+∴mxxkxxmk,0813)24(12)224(222=+---+--⋅+-∴mkmkkkmmk,0)1(4)3)(12(2)12(22=-++++⋅+-∴k m m k km m k ,04436222422222=-++++++-∴mk m m k km km km m k ,036)42(2=++++∴k m k m 即0)12)(3(=+++k m m ……10分当012=++k m 时，,12--=k m 此时直线AB 方程为1)2(--=x k y ，恒过定点)1,2(-P 显然不可能；……11分3-=∴m ，此时直线AB 方程为,3-=kx y ，恒过定点)3,0(-E ……12分22解：解：(1)因为xkx x f +=ln )(，),,0(+∞∈x 所以,1n 1)(2xk x x f -+-='令,0>'x f 解得,01ke x -<<令0)(<'xf ，解得,1ke x ->……2分所以，)(x f 在),0(1ke-上单调递增，在),(1+∞-k e 上单调递减，所以)(x f 在k e x -=1处取得极大值，即11)()(--==k ke ef x f 极大值无极小值……4分(2)由0)(=x h 即,0)12(n 11=+-+-x e xkx 可得,0n 121=--+-k x x xe x 令k x x xex F x--+=-n 12)(1，则⋅--=⎪⎭⎫ ⎝⎛--='---111)2)(1(12)1()(x x xxe e x x x e x x F …5分设12)(--=x ex x p ，则,2)(1--='x e x p 由0)(>'x p 得,12n 10+<<x 由0)(<'x p 得,12ln +>x 所以)(x p 在)12n 1,0(+上单调递增，在),12(ln +∞+上单调递减，且,1)1(=p 06)3(2<-=e p ，0525154<-=⎪⎭⎫ ⎝⎛e p ，即0)1(51<⎪⎭⎫ ⎝⎛p p ，,0)3()1(<p p 所以存在⎪⎭⎫⎝⎛∈1,511x ，)3,1(2∈x 使得,0)(1=x p ,0)(2=x p 即1112-=x ex ，1222-=x ex ①，…….7分故)(x F 在(0，x 1)上单调递减，在)1,(1x 上单调递增，在),1(2x 上单调递减，在),(2+∞x上单调递增，故)(x F 的极大值为,3)1(k F -=极小值为)(1x F 和)(2x F 对①式两边取对数可得2n 11n 111--=x x ，②2n 11n 122--=x x 将①②代入)(1x F 得kk x x e e k x x e x x F x x x -+=-+---=-+-=---2n 12)2n 11(n 12)(111111111121同理可得,2n 12)(2k x F -+=……9分要使)(x F 有四个零点，则必有⎩⎨⎧>-=<-+==03)1(02ln 2)()(21k F k x F x F 解得32ln 2<<+k ……10分而,03ln e2)(331333>->--+=------k k e e e e F e 05n 125n 1555n 110)5(4>->-->-+-=-k k e F ……11分由零点存在定理可知，当32ln 2<<+k 时)(x F 有且仅有4个零点，即)(x h 有4个零点，所以实数k 的取值范围为)3,2n 12(+……12分。

一、选择题（每题5分，共50分）1. 已知函数f(x) = 2x + 3，则f(2)的值为（）A. 7B. 5C. 4D. 6答案：A2. 下列哪个数是无理数？（）A. √4B. √9C. √16D. √25答案：C3. 已知等差数列{an}的前三项分别为1，3，5，则第10项an的值为（）A. 19B. 20C. 21D. 22答案：B4. 下列哪个函数是奇函数？（）A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = x^5答案：B5. 已知复数z = 3 + 4i，则|z|的值为（）A. 5B. 7C. 9D. 11答案：C6. 已知圆的方程为x^2 + y^2 = 25，则该圆的半径为（）A. 5B. 10C. 15D. 20答案：A7. 已知直线的方程为y = 2x + 1，则该直线的斜率为（）A. 2B. -2C. 1/2D. -1/2答案：A8. 下列哪个不等式是正确的？（）A. 2 < 3 < 4B. 4 < 3 < 2C. 3 < 2 < 1D. 1 < 2 < 3答案：A9. 已知函数f(x) = x^2 - 4x + 4，则f(2)的值为（）A. 0B. 4C. 8D. 12答案：A10. 下列哪个数是正数？（）A. -3B. 0C. 3D. -5答案：C二、填空题（每题5分，共25分）11. 若等差数列{an}的首项为2，公差为3，则第5项an的值为______。

答案：2 + 4d = 2 + 34 = 1412. 已知函数f(x) = x^2 - 3x + 2，则f(1)的值为______。

答案：1^2 - 31 + 2 = 013. 若复数z = 5 - 2i，则|z|^2的值为______。

答案：|z|^2 = (5^2 + (-2)^2) = 25 + 4 = 2914. 圆的方程为x^2 + y^2 - 4x + 6y - 12 = 0，则该圆的圆心坐标为______。

汕头市金山中学毕业考试高考最新模拟试题理科数学本试卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分100分，考试时间120 分钟。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷（选择题，共50分）注意事项： 1．答第I 卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不能答在试题卷上。

一、选择题（本卷有25道题，每小题2分，共50分。

在每题列出的四个选项中，只有一项是最符合题目要求的。

） 参考公式：如果事件A 、B 互斥，那么 正棱锥、圆锥的侧面积公式P （A+B ）=P （A ）+（B ） cl S 21=锥侧如果事件A 、B 相互独立，那么P （A·B ）=P （A ）·P （B ） 其中c 表示底面周长，l 表示斜高或母线长 如果事件A 在一次试验中发生的概率是 球的体积公式 P ，那么n 次独立重复试验中恰好发生k 334R V π=球次的概率kn k k n n P P C k P --=)1()( 其中R 表示球的半径一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，选择一个符合题目要求的选项。

1．已知复数2121,21,3z z i z bi z 若-=-=是实数，则实数b 的值为 （ ）A ．0B ．23-C ．6D ．－62．已知中心在原点，焦点在y 轴的双曲线的渐近线方程为x y 21±=，则此双曲线的离心率 为（ ）A ．25B ．5C ．25 D ．53．下列四个命题 ①线性相差系数r 越大，两个变量的线性相关性越强；反之，线性相关性越小； ②残差平方和越小的模型，拟合的效果越好；③用相关指数R 2来刻画回归效果，R 2越小，说明模型的拟合效果越好。

④随机误差e 是衡量预报精确度的一个量，它满足E （e ）=0 A ．①③ B ．②④ C ．①④ D ．②③ 4．已知程序框图如右图所示，则该程 序框图的功能是 （ ）A ．求数列}1{n 的前10项和*)(N n ∈B ．求数列}21{n 的前10项和*)(N n ∈C ．求数列}1{n 的前11项和*)(N n ∈D ．求数列}21{n的前11项和*)(N n ∈5．已知函数,1cos sin )(++=x x a x f )4(x f -π且),4(x f +=π则a 的值为（ ）A ．1B ．－1C ．22D ．26．以原点为圆心的圆全部在区域⎪⎩⎪⎨⎧≥++≤-+≥+-0943042063y x y x y x 内，则圆面积的最大值为（ ）A ．π518B ．π516 C ．π2581 D ．π2564 7．已知=+⋅====++)(,1||||||,543则且（ ）A ．0B ．53C ．－53 D ．－54 8．在2006)2(-x 的二项展开式中，含x 的奇次幂的项之和为S ，当2=x 时，S 等于（ ）A ．23008B ．－23008C ．23009D ．－230099．已知等差数列1,}{>m S n a n n 若项和为的前，且m S a a a m m m m 则,38,012211==-+-+-等于（ ）A ．38B ．20C ．10D ．910．已知n m b a b x a x x f ,),)()((1)(<---=是)(x f 的零点，且n m <，则实数a 、b 、m 、n 的大小关系是 （ ）A ．n b a m <<<B ．b n m a <<<C ．n b m a <<<D ．b n a m <<<11．设O 为坐标原点，F 为抛物线x y 42=的焦点，A 为抛物线上的一点，若4-=⋅，则点A 的坐标为（ ）A ．（2，22±） B ．（1，±2） C ．（1，2）D ．（2，22）12．正四面体ABCD 的棱长为1，棱AB //平面α，则正四面体上的所有点在平面α内的射影构成图形面积的取值范围是 （ ）A ．]43,42[B ．]43,66[C ．]21,43[D ．]21,42[第Ⅱ卷（共90分）注意事项：1．用钢笔或圆珠笔直接答在试题卷中。