2013年杭州市西湖区一模数学卷答案

2013年浙江省杭州市高考数学一模试卷（文科）学校:___________姓名：___________班级：___________考号：___________一、选择题(本大题共10小题，共50.0分)1.若复数z=2+，其中i是虚数单位，则复平面上，复数z所对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【解析】试题分析：把复数z中的分式部分利用复数的除法运算进行化简，得到复数z的实部和虚部，则答案可求．由=．复数z的实部为2，虚部为-1，所以复数z对应的点在第四象限．故选D．2.平面向量与的夹角为60°，=(2，0)，||=1，则|+2|=()A. B. C.4 D.12【答案】B【解析】试题分析：根据向量的坐标求出向量的模，最后结论要求模，一般要把模平方，知道夹角就可以解决平方过程中的数量积问题，题目最后不要忘记开方．由已知|a|=2，|a+2b|2=a2+4a•b+4b2=4+4×2×1×cos60°+4=12∴|a+2b|=，故选B3.设a∈R，则“a=4”是“直线l1：ax+2y-3=0与直线l2：2x+y-a=0平行”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】C【解析】试题分析：根据直线ax+2y-3=0与直线l2：2x+y-a=0的斜截式，求出平行的条件，验证充分性与必要性即可．当a=4时，直线4x+2y-3=0与2x+y-4=0平行，∴满足充分性；当：ax+2y-3=0与直线l2：2x+y-a=0平行⇒a=4，∴满足必要性．故选C4.设函数f(x)=2|x|，则下列结论正确的是()A.f(-1)＜f(2)＜f(-)B.f(-)＜f(-1)＜f(2)C.f(2)＜f(-)＜f(-1)D.f(-1)＜f(-)＜f(2)【答案】D【解析】试题分析：由函数的解析式，可判断出函数f(x)=2|x|为偶函数且在[0，+∞)上为增函数，将三个自变量化到同一单调区间内，进而利用单调性可比较大小．当x≥0时，f(x)=2|x|=2x为增函数又∵f(-x)=2|-x|=2|x|=f(x)故函数f(x)=2|x|为偶函数故f(-1)=f(1)，f(-)=f()∵2＞＞1故f(2)＞f()＞f(1)即f(-1)＜f(-)＜f(2)故选D5.设等差数列{a n}的前n项和为S n，若-a7＜a1＜a8，则必定有()A.S7＞0，且S8＜0B.S7＜0，且S8＞0C.S7＞0，且S8＞0D.S7＜0，且S8＜0【答案】C【解析】试题分析：由已知-a7＜a1＜a8，可得a7+a1＞0，d＞0，a8＞a7，结合等差数列的求和公式可判断∵-a7＜a1＜a8，∴a7+a1＞0，7d=a8-a1＞0∴d＞0，a8＞a7∴＞0∵S8=4(a1+a8)＞4(a1+a7)＞0故选C6.若程序框图如图所示，则该程序运行后输出k的值是()A.5B.6C.7D.8【答案】A【解析】试题分析：根据所给数值判定是否满足判断框中的条件，然后执行循环语句，一旦不满足条件就退出循环，执行语句输出k，从而到结论．当输入的值为n=5时，n不满足第一判断框中的条件，n=16，k=1，n不满足第二判断框中的条件，n满足第一判断框中的条件，n=8，k=2，n不满足第二判断框中的条件，n满足第一判断框中的条件，n=4，k=3，n不满足第二判断框中的条件，n满足第一判断框中的条件，n=2，k=4，n不满足第二判断框中的条件，n满足第一判断框中的条件，n=1，k=5，n满足第二判断框中的条件，退出循环，即输出的结果为k=5，故选A．7.设α是第三象限角，且tanα=2，则=()A. B. C. D.【答案】B【解析】本题考查诱导公式及同角的三角函数关系式，由条件利用同角三角函数的基本关系求得cosα=-，化简要求的式子为cosα，从而求得结果．解∵α是第三象限角，且tanα==2，可得sin2α+cos2α=1，可得cosα=-．故==cosα=-，故选B．8.设函数f(x)=|log a x|(0＜a＜1)的定义域为[m，n](m＜n)，值域为[0，1]，若n-m的最小值为，则实数a的值为()A.或B.或C.或D.或【答案】B【解析】试题分析：通过分类讨论和利用对数函数的单调性即可得出．①若1≤m＜n，则f(x)=-log a x，∵f(x)的值域为[0，1]，∴f(m)=0，f(n)=1，解得m=1，n=，又∵n-m的最小值为，∴，及0＜a＜1，当等号成立时，解得a=．②若0＜m＜n＜1，则f(x)=log a x，∵f(x)的值域为[0，1]，∴f(m)=1，f(n)=0，解得m=a，n=1，又∵n-m的最小值为，∴，及0＜a＜1，当等号成立时，解得a=．③若0＜m＜1＜n时，不满足题意．9.已知F1，F2分别是双曲线C：的左右焦点，以F1F2为直径的圆与双曲线C在第二象限的交点为P，若双曲线的离心率为5，则cos∠PF2F1等于() A. B. C. D.【答案】C【解析】试题分析：设|PF1|=n，|PF2|=m，则由双曲线的定义可得m-n=2a①，再由m2+n2=4c2②，以及=5可得m=8a，故cos∠PF2F1==，运算求得结果．设|PF1|=n，|PF2|=m，则由双曲线的定义可得m-n=2a①，且三角形PF1F2为直角三角形，故有m2+n2=4c2②．再由=5可得c=5a．把①和②联立方程组解得m=8a，故cos∠PF2F1====，故选C．10.已知函数∞∞，则函数F(x)=xf(x)-1的零点个数为()A.4B.5C.6D.7【答案】C【解析】试题分析：求函数F(x)=xf(x)-1的零点个数，我们可以转化为求函数y=f(x)与函数y=图象交点的个数，根据函数y=f(x)的解析式，我们在同一坐标系中分别画出两个函数图象，由图象即可求出两个函数的交点个数，即函数F(x)=xf(x)-1的零点个数．∵∞∞，则函数F(x)=xf(x)-1的零点个数等于函数y=f(x)与函数y=图象交点的个数，在同一坐标系中画出两个函数图象如下图所示：由图可知函数y=f(x)与函数y=图象共有6个交点故函数F(x)=xf(x)-1的零点个数为6个，二、填空题(本大题共7小题，共28.0分)11.在等比数列{a n}中，若a2=1，a5=-8则a8= ．【答案】64【解析】试题分析：利用等比数列的通项公式或性质即可得出．设等比数列{a n}的公比为q，则a2=a1q=1，=8，两式相除得q3=8，∴=8×8=64．或利用=a2a8解得．故答案为64．12.若sinx+cosx=1，则= ．【答案】±1【解析】试题分析：由sinx+cosx=1，可求得sin2x=0，从而可求得cos2x，继而可得答案．∵sinx+cosx=1，∴(sinx+cosx)2=1+sin2x=1，∴sin2x=0，∴cos2x=±1，∴==±1．故答案为：±1．13.若正数x，y满足x+y=1，则的最小值为．【答案】9【解析】试题分析：将x+y=1代入所求关系式，利用基本不等式即可求得答案．∵x＞0，y＞0，x+y=1，∴+=(+)(x+y)=4+1++≥5+2=9(当且仅当x=，y=时取等号)．故答案为：9．14.无穷数列1，2，2，3，3，3，4，4，4，4，5…的首项是1，随后两项都是2，接下来3项都是3，再接下来4项都是4，…，以此类推．记该数列为{a n}，若a n-1=7，a n=8，则n= ．【答案】29【解析】试题分析：利用已知条件，判断出数列中的各项特点，判断出数8所在的组，求出第28项为7，之后的8项就是8，从而得出n的值．∵一个数列{1，2，2，3，3，3，4，4，4，4，5，…}，它的首项是1，随后两项都是2，接下来3项都是3，再接下来4项都是4，…，依此类推，对任意的正整数k，该数列中恰有k个k，则当n=7，1+2+3+…+n===28，∴a28=7，a29=a30= (8)若a n-1=7，a n=8，则n=29．故答案为：29．15.在△ABC中，角A，B，C的对边分别为a，b，c，若a2+b2=，则直线ax-by+c=0被圆x2+y2=9所截得的弦长为．【答案】2【解析】试题分析：求出圆心到直线的距离，利用弦心距、半径、半弦长满足勾股定理，求出半弦长，即可求出结果．圆心(0，0)到直线的距离d==，再由a2+b2=，可得d=．而圆的半径为3，故弦长为2=2=2，故答案为2．16.若实数x，y满足不等式组，则2x+y的最大值为．【答案】【解析】试题分析：作出题中不等式组表示的平面区域，得如图的阴影部分，再将目标函数z=2x+y对应的直线进行平移，可得当x=y=时，目标函数z=2x+y取得最大值．作出不等式组表示的平面区域，得到直线y-x=0的下方且在直线x+y-7=0的上方，即如图的阴影部分，设z=F(x，y)=2x+y，将直线l：z=2x+y进行平移，当l经过点A(，)时，目标函数z达到最大值∴z最大值=F(，)=2×+=故答案为：17.设Q为圆C：x2+y2+6x+8y+21=0上任意一点，抛物线y2=8x的准线为l．若抛物线上任意一点P到直线l的距离为m，则m+|PQ|的最小值为．【答案】-2【解析】试题分析：先根据圆的方程求得圆心坐标和半径，抛物线方程求得焦点坐标和准线方程，根据根据抛物线的定义可知，P到准线的距离等于点P到焦点F的距离，根据图象可知当P，Q，F三点共线时，P到点Q的距离与点P到抛物线的焦点距离之和的最小，为圆心到焦点F的距离减去圆的半径．圆C：x2+y2+6x+8y+21=0即(x+3)2+(y+4)2=4，表示以C(-3，-4)为圆心，半径等于2的圆．抛物线y2=8x的准线为l：x=-2，焦点为F(2，0)，根据抛物线的定义可知点P到准线的距离等于点P到焦点F的距离，进而推断出当P，Q，F三点共线时P到点Q的距离与点P到抛物线的焦点距离之和的最小为：|FC|-r=-2=-2，故答案为-2．三、解答题(本大题共5小题，共72.0分)18.设f(x)=6cos2x-sin2x(x∈R)．(Ⅰ)求f(x)的最大值及最小正周期；(Ⅱ)在△ABC中，角A，B，C的对边分别为a，b，c，锐角A满足f(A)=3，B=，求的值．【答案】解：(Ⅰ)f (x)===2cos(2x+)+3，当时，f (x)取得最大值为2+3；最小正周期T==π．(Ⅱ)由f (A)=3-2得2cos(2A+)+3=3-2，∴cos(2A+)=-1，又由0＜A＜，得＜2A+＜π+，故2A+=π，解得A=．又B=，∴C==．由余弦定理得=2cos C=0．【解析】(Ⅰ)利用倍角公式和两角和差的正弦、余弦公式、三角函数的单调性和周期性即可得出；(Ⅱ)利用三角函数的单调性和余弦定理即可得出．19.在△ABC中，角A，B，C的对边分别为a，b，c，向量=(1，λsin A)，=(sin A，1+cos A)，且∥(Ⅰ)若λ=2，求角A的大小；(Ⅱ)若sin B+sin C=sin A，求实数λ的取值范围．【答案】解：(Ⅰ)由∥，得2sin2A-1-cos A=0，化为2cos2A+cos A-1=0，解得cos A=或cos A=-1(舍去)，∴A=．(Ⅱ)∵sin B+sin C=sin A，由正弦定理得b+c=a，由∥，得λsin2A-1-cos A=0，化为λcos2A+cos A+1-λ=0，解得cos A=或cos A=-1(舍去)．又cos A===，综上，λ需要满足，解得λ≥．【解析】(Ⅰ)利用向量共线的充要条件即可得出；(Ⅱ)利用正弦、余弦定理及基本不等式即可得出．20.设在等差数列{a n}和等比数列{b n}中，a1=1，b1=2，b n＞0(n∈N*)，且b1，a2，b2成等差数列，a2，b2，a3+2成等比数列．(Ⅰ)求数列{a n}，{b n}的通项公式；(Ⅱ)设c n=，数列{c n}的前n项和为S n，若恒成立，求实数t的取值范围．【答案】解：(Ⅰ)设等差数列{a n}的公差为d，等比数列{b n}的公比为q(q＞0)．由题意，得，解得d=q=3．∴a n=3n-2，．(Ⅱ)∵c n==3b n-2=3×2×3n-1-2=2×3n-2．∴S n=c1+c2+…+c n=2×(31+32+…+3n)-2n==3n+1-3-2n．∴==3n+1．∵恒成立，∴3n+1＜2×3n+t恒成立，即t＞(-3n+1)max，n∈N*．由于函数y=-3x+1在(0，+∞)上单调递减，∴-3n+1≤-31+1=-2，故t＞-2．【解析】(Ⅰ)利用等差数列、等比数列的定义及通项公式即可得出；(Ⅱ)利用等比数列的前n项和公式、函数的单调性即可得出．21.设函数f(x)=x2-(a+2)x+alnx，(其中a＞0)(Ⅰ)当a=1时，求函数f(x)的极小值；(Ⅱ)当a=4时，给出直线l1：5x+2y=m=0和l2：3x-y+n=0，其中m，n为常数，判断直线l1或l2中，是否存在函数f(x)的图象的切线，若存在，求出相应的m或n的值，若不存在，说明理由．【答案】解：(Ⅰ)当a=1时，f′(x)=2x-3+=，当时，f′(x)＞0；当时，f′(x)＜0；当x＞1时，f′(x)＞0．所以当x=1时，f(x)取极小值-2．…(7分)(Ⅱ)当a=4时，f′(x)=2x-6+，∵x＞0，∴f′(x)=2x+-6≥，故l1或l2中，不存函数图象的切线．由2x+-6=3得x=，或x=4，当x=时，可得n=，当x=4时，可得n=4ln4-20．(15分)【解析】(Ⅰ)把a=1代入，求导数，由导数的正负可得单调区间，进而可得极值；(Ⅱ)把a=4代入可得导数≥，故l1或l2中，不存函数图象的切线，令导数=3，可得n值．22.已知抛物线C：y2=2px(p＞0)和⊙M：x2+y2+8x-12=0，过抛物线C上一点P(x0，y0)(y0≥0)作两条直线与⊙M相切与A、B两点，圆心M到抛物线准线的距离为．(Ⅰ)求抛物线C的方程；(Ⅱ)当P点坐标为(2，2)时，求直线AB的方程；(Ⅲ)设切线PA与PB的斜率分别为k1，k2，且k1•k2=，求点P(x0，y0)的坐标．【答案】解：(Ⅰ)由⊙M：x2+y2-8x+12=0，配方得(x-4)2+y2=4，∴圆心M(4，0)，半径r=2．由题意知：，解得p=1，∴抛物线C的方程为y2=2x．(Ⅱ)设P(2，2)，∵P，A，B，M四点共圆，∴此圆的方程为：(x-4)(x-2)+(y-2)(y-0)=0，①又⊙M：x2-8x+y2+12=0，②又由①-②得直线AB的方程：x-y-2=0．(Ⅲ)设过P的直线l方程为y-y0=k(x-x0)，由于⊙M与直线l相切，得到，整理得到：，∴，即，∴x0=2或10，经检验得点P坐标为．【解析】(Ⅰ)利用抛物线的定义即可得出；(Ⅱ)利用两圆的根轴即可得出；(Ⅲ)利用直线与圆相切的充要条件、点到直线的距离公式即可得出．高中数学试卷第11页，共11页。

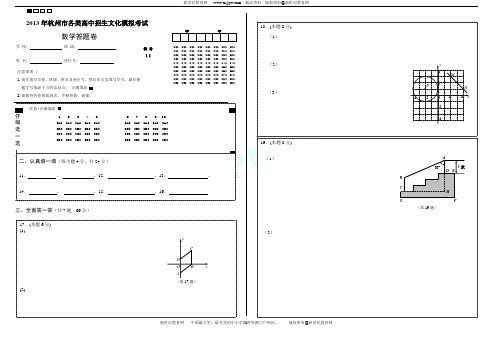
新世纪教育网精品资料版权所有@新世纪教育网2013 年杭州市各类高中招生文化模拟考试学 号18．(本题 8 分) （1）数学答题卷学 校： 姓 名： 注意事项 : 1.请先填写学校、班级、姓名及座位号，然后在右边填写学号，最后根 据学号填涂下方的信息点； 正确填涂 2.请保持答卷卷面清洁，不要折叠、破损。

班 级： 座位号：缺 考 [ ][0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [0] [1] [2] [3] [4] [5] [6] [7] [8] [9]（2）y4M N2 4P2 0 -2（3）-4 -2x一 仔 细 选 一 选注意:正确填涂1 2 3 4 5 6 7 8 9 10-4[A] [A] [A] [A] [A] [B] [B] [B] [B] [B] [C] [C] [C] [C] [C] [D] [D] [D] [D] [D][A] [A] [A] [A] [A] [B] [B] [B] [B] [B] [C] [C] [C] [C] [C] [D] [D] [D] [D] [D]19．(本题 8 分) （1）660 A D E 1米二、认真填一填（每小题 4 分，共 24 分）11． 14． ， ， ，12． ，15． ，13． ，16． ， .B C G H F （第 19 题）三、全面答一答（共 7 题, 66 分）17．(本题 6 分) (1)y C D O A B x（2）（第 17 题）(2)1 新世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。

2013年杭州市西湖区一模试卷答案与解析一1. B解析：此题考查字音的识记情况。

A、归省（xǐng）C、匮乏（kuì）D长吁短叹（xū）2. C解析：此题考查字形的掌握情况。

A 绵延B休养生息D志同道合3. B解析：此题考查词义的辨析。

“秩序”应改成“顺序”4. D解析：此题考查文学常识的掌握情况。

奥楚蔑洛夫是契诃夫笔下的“变色龙”形象。

5. D解析：此题考查病句的辨析。

A.宾语残缺“明显低龄化”后加“趋势”B.搭配不当“建立”应为“培养”或“增强”C.语义重复去掉“最高”6.①风正一帆悬江春入旧年②长风破浪会有时直挂云帆济沧海③蹴尔而与之乞人不屑也④无丝竹之乱耳无案牍之劳形7.①影响我们人生的绝不是环境，而是我们对这一切持有什么样的态度。

②态度决定我们的生活。

或：想要有美好的人生，就要具有积极的态度。

解析：此题考查语意的连贯。

联系上下文分析可知：①处为转折句，②处为总结句。

8、西湖区全面推进“三改一建”打造美丽西湖。

解析：此题考查语言的简明。

步骤：①确定新闻主体——西湖区。

②找出具体事件——“三改一建”行动正在全面进行。

届时，美丽西湖将成为美丽中国、美丽杭州的缩影。

③整合答案：主体+事件+目的（参考2011杭州中考概括题评分标准）9、“这位朋友，打扰一下，这次演出是不可以用闪光灯拍照的，请您不要拍照，谢谢！”解析：此题考查语言的表达。

要求语义明确，语言得体。

答案的组织一般包括三个方面：合适的称呼、准确的表达、恰当的礼貌用语。

10、答案示例：夏/却能感到火热的阳光/辽阔的田野/就荡漾沁人的麦香解析：此题考查句子的仿写。

句子的仿写要达到三点要求：内容切题、修辞一致、句式相同。

可用填空法，展开联想和想象组织答案。

二、11答案：①在狂风暴雨中依然坚强挺立,经过磨难洗礼，愈加青翠，繁盛，坚强面对一切无常；不顾误解嘲讽自己攀援高枝，坚定信仰，不停攀援，为更高的向往和追求，;虽然谦卑柔弱但依然阐释同枯同荣，生死与共的侠肝义胆。

2013学年第一学期九年级期末教学质量调研数学试题卷一、仔细选一选1. 若x ：y =6：5，则下列等式中不成立的是( )A . x x −y =6B . x −y y = 15C . x +y y = 115D . y y −x =52. 一个袋子中装有6个红球3个白球，这些球除颜色外，形状、大小、质地等完全相同，在看不到球的条件下，随机地从这个袋子中摸出一个球，摸到红球的概率为( ) A . 12 B . 19 C . 13 D . 23 3. 二次函数y =3−2(x −1)2的图象的顶点坐标是( )A . (3，−1)B . (1，3)C . (1，−3)D . (−1，−3) 4. 在平面直角坐标系中，若☉O 是以原点为圆心，10为半径的圆，则点A (−6，8)( )A . 在☉O 内B . 在☉O 外C . 在☉O 上D . 不能确定5. 已知(x 1，y 1)，(x 2，y 2)，(x 3，y 3)是反比例函数y =− 4x 的图象上三点，且x 1<0<x 2<x 3，则y 1，y 2，y 3的大小关系是( ) A . y 1<0<y 2<y 3 B . y 3<y 2<0<y 1 C . y 1<0<y 3<y 2 D . y 2<y 3<0<y 16.2A . 抛物线与x 轴的一个交点为(3，0)B . 抛物线与y 轴的交点为(0，6)C . 抛物线的对称轴是直线x =0.5D . 在x <1时，y 随x 增大而增大 7. 已知α为锐角，且tan (α−10°)= √33，则锐角α的度数是( )A . 20°B . 40°C . 50°D . 70°8. 把一个半圆纸片卷成圆锥的侧面，那么圆锥母线之间的最大夹角为( )A . 30°B . 45°C . 60°D . 90°9. 如图，在平行四边形ABCD 中，E 为CD 上一点，DE ：CE =2：3，连结AE ，BD 交于点F ，则S △DEF ：S △ADF ：S △ABF 等于( ) A . 2：3：5 B . 4：9：25 C . 4：10：25 D . 2：5：25FABCED10. (2012浙江湖州)如图，已知点A (4，0)，O 为坐标原点，P 是线段OA 上任意一点(不含端点O ，A )过P 、Q 两点的二次函数y 1和过P A 两点的二次函数y 2的图象开口均向下，它们的顶点分别为B 、C ，射线OB 与AC 相交于点D ，当OD =AD =3时，这两个二次函数的最大值之和等于( )A . √5B . 4√53C . 3D . 4二、认真填一填11. 如图，半径为10的☉O 中，弦AB 的长为16，则这条弦的弦心距为______________ 12. 如图，在△ABC 中，DE //BC ，若AD =3，DB =5，DE =3.3，那么BC =______________ 13. 如图，点A 、B 、C 是半径为3cm 的☉O 上三个点，且∠ABC =30°，则劣弧AC 的长是_________________cm14. 小明画了函数y = a x −1的图象如图，则关于x 的分式方程 ax −1=2的解估计是__________15. 从数−2，−1，1，2，3中任取两个，其和的绝对值为3的概率为_____________16. (2008湖北咸宁)两个反比例函数y = k x (k ≠0，k 为常数)和y = 1x 在第一象限内的图象如图所示，点P 在y = k x 的图象上，PC ⊥x 轴于点C ，交y = 1x 的图象于点A ，PD ⊥y 轴于点D ，交y = 1x 的图象于点B ，当点P 在y = kx 的图象上运动时，以下结论：①△ODB 与△OCA 的面积相等；②四边形P AOB 的面积不会发生变化；③P A 与PB 始终相等；④当点A 是PC 的中点时，点B 一定是PD 的中点，其中一定正确的结论是___________________(填序号)第12题第11题第10题ADEBC 1第16题第14题第13题B三、全面答一答17. 如图，菱形ABCD 放置在平面直角坐标系中，边AD 经过原点O ，已知A (0，−3)，B (4，0)1) 求点D 的坐标2) 求经过点C 的反比例函数解析式18. 如图，AB 是☉O 的直径，AD 是弦，∠A =22.5°，延长AB 到点C ，使得∠ACD =45°1) 求证：CD 是☉O 的切线2) 若AB =2√2，求OC 的长19. 如图，在一个坡角为15°的斜坡上有一棵树，高为AB ，当太阳光线与水平线成54°角时，测得该树在斜坡上的树影BC 长为10m ，延长AB ，交过点C 的水平线于点D ，求BD 与树高AB (精确到0.1m )，(已知sin 15°≈0.259，cos 15°≈0.966，tan 15°≈0.268，sin 54°≈0.809，cos 54°≈0.588，tan ≈54°1.376，供选用)A20. 如图，点E 、A 、B 在同一直线上，AD //BC ，AB =√3AD ，BC =√3AE1) 求证：△ABC ~△DAE 2) 若∠CAD =90°，AD =BC ，AE =1，求BD 的长21. 如图，抛物线y =ax 2+2与y 轴交于点A ，抛物线上的一点P 在第四象限，连结AP与x 轴交于点C ， AC CP = 12，且S △AOC =1，过点P 作PB ⊥y 轴于点B 1) 求BP 的长2) 求抛物线与x 轴交点坐标22. 已知一次函数y 1=x +b 的图象与二次函数y 2=a (x 2+bx +3)(a ≠0，a ，b 为常数)的图象交于A 、B 两点，且点A 的坐标为(0，3)1) 求出a ，b 的值，并写出函数y 1，y 2的解析式2) 验证点B 的坐标为(−2，1)，并写出当y 1≥y 2时x 的取值范围3) 设s =y 1+y 2，t =y 1−y 2，若n ≤x ≤m 时，s 随着x 的增大而增大，且t 也随着x 的增大而增大，求n 的最小值和m 的最大值E23.(2012无锡锡山区一模)抛物线y=ax2+bx+c的顶点为C(0，−√3)，与x轴交于点A、B，连结AC、BC，得等边△ABC，T点从B点出发，以每秒1个单位的速度向点A运动，同时点S从点C出发，以每秒√3个单位的速度向y轴负方向运动，TS交射线BC于点D，当点T到达A点时，点S停止运动，设运动时间为t秒1)求二次函数的解析式2)设△TSC的面积为S，求S关于t的函数解析式3)以点T为圆心，TB为半径的圆与射线BC交于点E，试说明：在点T运动的过程中，线段ED的长是一定值，并求出该定值。

2012-2013学年浙江省杭州市西湖区八年级（下）期末数学试卷2012-2013学年浙江省杭州市西湖区八年级（下）期末数学试卷一．仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的，请把正确选项前的字母填在答题卷中相应的格子内，注意可以用多种不同的方法来选取正确答案.1．（3分）要使式子有意义，则x的取值范围是（）224．（3分）（2012•泰州）下列四个命题：①一组对边平行且一组对角相等的四边形是平行四边形；②对角线互相垂直且相等的四边形是正方形；③顺次连接矩形四边中点得到的四边形是菱形；5．（3分）（2007•滨州）关于x的一元二次方程（m+1）+4x+2=0的解为（）6．（3分）（2012•泸州）已知三角形两边的长分别是3和6，第三边的长是方程x2﹣6x+8=0的根，则这个三角形的7．（3分）如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD（围墙MN最长可利用25m），现在已备足可以砌50m长的墙的材料，若设计一种砌法，使矩形花园的面积为300m2．则AB长度为（）8．（3分）阅读材料：对于任何实数，我们规定符号的意义是．按照这个规定，请你计算：当x2﹣4x+4=0时，的值（）9．（3分）（2012•安徽）为增加绿化面积，某小区将原来正方形地砖更换为如图所示的正八边形植草砖，更换后，图中阴影部分为植草区域，设正八边形与其内部小正方形的边长都为a，则阴影部分的面积为（）10．（3分）已知，在平面直角坐标系中放置了5个如图所示的正方形（用阴影表示），点B1在y轴上，点C1、E1、E2、C2、E3、E4、C3均在x轴正半轴上．若已知正方形A1B1C1D1的边长为1，∠B1C1O=60°，且B1C1∥B2C2∥B3C3，则点A3的坐标是（）），二．认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清楚题目的条件和要填写的内容，尽量完整地填写答案11．（4分）化简：=_________．12．（4分）已知如图，在线段BG同侧作正方形ABCD和正方形CEFG，其中BG=10，BC：CG=2：3，则S△ECG= _________，S△AEG=_________．13．（4分）（2012•包头）关于x的两个方程x2﹣x﹣2=0与有一个解相同，则a=_________．14．（4分）已知下列命题：①若a＞0，b＞0，则a+b＞0；②若a2≠b2，则a≠b；③对角线互相垂直的平行四边形是菱形；④直角三角形斜边上的中线等于斜边的一半．其中原命题与逆命题均为真命题的序号是_________．15．（4分）如图，是一个长为30m，宽为20m的矩形花园，现要在花园中修建等宽的小道，剩余的地方种植花草．如图所示，要使种植花草的面积为532m2，那么小道进出口的宽度应为_________米．16．（4分）如图，矩形ABCD的边AB在x轴上，AB的中点与原点重合，AB=2，AD=1，过定点Q（0，2）和动点P（a，0）的直线与矩形ABCD的边有公共点，则：（1）a的取值范围是_________；（2）若设直线PQ为：y=kx+2（k≠0），则此时k的取值范围是_________．三．全面答一答（本题有7个小题，共66分）解答应写出必要的文字说明、证明过程或推演步骤.如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以.17．（6分）（1）解方程：（x+1）（x﹣5）=1（2）关于x的一元二次方程x2+bx+c=0（c＜0）是否有实数解，请你作出判断并说明理由．18．（8分）已知在如图4×4的方格中，有一个格点三角形ABC（三个顶点均在格点上），其中AB=，BC=，AC=．（1）请你在方格中画出该三角形；（2）求△ABC的面积；（3）求△ABC中AC边上的高的长（结果保留根号）．19．（8分）一次测试八年级若干名学生1分钟跳绳次数的频数分布直方图如图所示，请根据这个直方图回答下列问题：（1）已知自左至右第2、3组（组中值分别为145、155）的频率之和为0.28，第3、4、5组（组中值分别为155、165、175）的频率之和为0.8，则参加测试的总人数有_________人，第3组的频数为_________人，第4组的频率为_________，并将直方图补充完整；（2）若图中自左至右各组的跳绳平均次数分别为137次，146次，156次，164次，177次，则参加测试的学生跳绳的平均次数为_________（只需列出算式，不用计算结果）；（3）若测试所得数据的中位数是160次，则测试次数为160次的学生至少有_________人．（直方图中每一组包括前一个边界值，不包括后一个边界值）20．（10分）如图，已知AG⊥BD，AF⊥CE，BD，CE分别是∠ABC和∠ACB的角平分线，若BF=2，ED=3，GC=4．（1）求FG的长；（2）求△ABC周长．21．（10分）平行四边形ABCD中，对角线AC、BD相交于点O，若E、F是线段AC上的两动点，分别从A、C 两点以1cm/s的速度向C、A运动，若BD=12cm，AC=16cm．（1）四边形DEBF是平行四边形吗？请说明理由；（2）当运动时间t为多少时，四边形DEBF是矩形．22．（12分）（2012•南京）某汽车销售公司6月份销售某厂家的汽车，在一定范围内，每部汽车的进价与销售量有如下关系：若当月仅售出1部汽车，则该部汽车的进价为27万元，每多售出1部，所有售出的汽车的进价均降低0.1万元/部，月底厂家根据销售量一次性返利给销售公司，销售量在10部以内（含10部），每部返利0.5万元；销售量在10部以上，每部返利1万元．（1）若该公司当月售出3部汽车，则每部汽车的进价为_________万元；（2）如果汽车的售价为28万元/部，该公司计划当月盈利12万元，那么需要售出多少部汽车？（盈利=销售利润+返利）23．（12分）已知直角梯形ABCD如图放置在平面直角坐标系中，∠DCB=30°，AB边在y轴上，点D的横坐标为6，CQ⊥x轴，垂足为Q，点Q的横坐标为12，过CD的直线l交x轴于点E，E点坐标为（18，0）．（1）求直线l的解析式，以及点A和点B的坐标；（2）P为线段CD上一动点，连结PQ、OP，探究△POQ的周长，并求出当周长最小时，P的坐标及此时的该三角形的周长；（3）点N从点Q（12，0）出发，沿着x轴以每秒1个单位长度的速度向点O运动，同时另一动点M从点B开始沿B﹣C﹣D﹣A的方向绕梯形ABCD运动，运动速度为每秒为2个单位长度，当其中一个点到达终点时，另一点也停止运动，设运动时间为t秒，连结MO和MN，试探究当t为何值时MO=MN．2012-2013学年浙江省杭州市西湖区八年级（下）期末数学试卷参考答案与试题解析一．仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的，请把正确选项前的字母填在答题卷中相应的格子内，注意可以用多种不同的方法来选取正确答案.1．（3分）要使式子有意义，则x的取值范围是（）224．（3分）（2012•泰州）下列四个命题：①一组对边平行且一组对角相等的四边形是平行四边形；②对角线互相垂直且相等的四边形是正方形；③顺次连接矩形四边中点得到的四边形是菱形；5．（3分）（2007•滨州）关于x的一元二次方程（m+1）+4x+2=0的解为（）6．（3分）（2012•泸州）已知三角形两边的长分别是3和6，第三边的长是方程x2﹣6x+8=0的根，则这个三角形的7．（3分）如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD（围墙MN最长可利用25m），现在已备足可以砌50m长的墙的材料，若设计一种砌法，使矩形花园的面积为300m2．则AB长度为（）8．（3分）阅读材料：对于任何实数，我们规定符号的意义是．按照这个规定，请你计算：当x2﹣4x+4=0时，的值（）∴9．（3分）（2012•安徽）为增加绿化面积，某小区将原来正方形地砖更换为如图所示的正八边形植草砖，更换后，图中阴影部分为植草区域，设正八边形与其内部小正方形的边长都为a，则阴影部分的面积为（）AC=BC===AC=BC=××，正八边形周围是四个全等三角形，面积和为：10．（3分）已知，在平面直角坐标系中放置了5个如图所示的正方形（用阴影表示），点B1在y轴上，点C1、E1、E2、C2、E3、E4、C3均在x轴正半轴上．若已知正方形A1B1C1D1的边长为1，∠B1C1O=60°，且B1C1∥B2C2∥B3C3，则点A3的坐标是（）），1=，=，×，=×==×==×=×=，M=+×=N=×=××）﹣=+++++，，二．认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清楚题目的条件和要填写的内容，尽量完整地填写答案11．（4分）化简：=π﹣3．二次根式的性质：=12．（4分）已知如图，在线段BG同侧作正方形ABCD和正方形CEFG，其中BG=10，BC：CG=2：3，则S△ECG= 18，S△AEG=18．×××﹣13．（4分）（2012•包头）关于x的两个方程x2﹣x﹣2=0与有一个解相同，则a=4．代入=中得：=14．（4分）已知下列命题：①若a＞0，b＞0，则a+b＞0；②若a2≠b2，则a≠b；③对角线互相垂直的平行四边形是菱形；④直角三角形斜边上的中线等于斜边的一半．其中原命题与逆命题均为真命题的序号是③④．15．（4分）如图，是一个长为30m，宽为20m的矩形花园，现要在花园中修建等宽的小道，剩余的地方种植花草．如图所示，要使种植花草的面积为532m2，那么小道进出口的宽度应为1米．16．（4分）如图，矩形ABCD的边AB在x轴上，AB的中点与原点重合，AB=2，AD=1，过定点Q（0，2）和动点P（a，0）的直线与矩形ABCD的边有公共点，则：（1）a的取值范围是﹣2≤a≤2；（2）若设直线PQ为：y=kx+2（k≠0），则此时k的取值范围是k≤﹣1或k≥1．三．全面答一答（本题有7个小题，共66分）解答应写出必要的文字说明、证明过程或推演步骤.如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以.17．（6分）（1）解方程：（x+1）（x﹣5）=1（2）关于x的一元二次方程x2+bx+c=0（c＜0）是否有实数解，请你作出判断并说明理由．；18．（8分）已知在如图4×4的方格中，有一个格点三角形ABC（三个顶点均在格点上），其中AB=，BC=，AC=．（1）请你在方格中画出该三角形；（2）求△ABC的面积；（3）求△ABC中AC边上的高的长（结果保留根号）．，；．19．（8分）一次测试八年级若干名学生1分钟跳绳次数的频数分布直方图如图所示，请根据这个直方图回答下列问题：（1）已知自左至右第2、3组（组中值分别为145、155）的频率之和为0.28，第3、4、5组（组中值分别为155、165、175）的频率之和为0.8，则参加测试的总人数有50人，第3组的频数为8人，第4组的频率为0.4，并将直方图补充完整；（2）若图中自左至右各组的跳绳平均次数分别为137次，146次，156次，164次，177次，则参加测试的学生跳绳的平均次数为（只需列出算式，不用计算结果）；（3）若测试所得数据的中位数是160次，则测试次数为160次的学生至少有8人．（直方图中每一组包括前一个边界值，不包括后一个边界值）=0.12；20．（10分）如图，已知AG⊥BD，AF⊥CE，BD，CE分别是∠ABC和∠ACB的角平分线，若BF=2，ED=3，GC=4．（1）求FG的长；（2）求△ABC周长．21．（10分）平行四边形ABCD中，对角线AC、BD相交于点O，若E、F是线段AC上的两动点，分别从A、C 两点以1cm/s的速度向C、A运动，若BD=12cm，AC=16cm．（1）四边形DEBF是平行四边形吗？请说明理由；（2）当运动时间t为多少时，四边形DEBF是矩形．AO=CO=BD=6cm22．（12分）（2012•南京）某汽车销售公司6月份销售某厂家的汽车，在一定范围内，每部汽车的进价与销售量有如下关系：若当月仅售出1部汽车，则该部汽车的进价为27万元，每多售出1部，所有售出的汽车的进价均降低0.1万元/部，月底厂家根据销售量一次性返利给销售公司，销售量在10部以内（含10部），每部返利0.5万元；销售量在10部以上，每部返利1万元．（1）若该公司当月售出3部汽车，则每部汽车的进价为26.8万元；（2）如果汽车的售价为28万元/部，该公司计划当月盈利12万元，那么需要售出多少部汽车？（盈利=销售利润+返利）23．（12分）已知直角梯形ABCD如图放置在平面直角坐标系中，∠DCB=30°，AB边在y轴上，点D的横坐标为6，CQ⊥x轴，垂足为Q，点Q的横坐标为12，过CD的直线l交x轴于点E，E点坐标为（18，0）．（1）求直线l的解析式，以及点A和点B的坐标；（2）P为线段CD上一动点，连结PQ、OP，探究△POQ的周长，并求出当周长最小时，P的坐标及此时的该三角形的周长；（3）点N从点Q（12，0）出发，沿着x轴以每秒1个单位长度的速度向点O运动，同时另一动点M从点B开始沿B﹣C﹣D﹣A的方向绕梯形ABCD运动，运动速度为每秒为2个单位长度，当其中一个点到达终点时，另一点也停止运动，设运动时间为t秒，连结MO和MN，试探究当t为何值时MO=MN．∴∴；当y=），x∴，，∴s6+综上可得：参与本试卷答题和审题的老师有：dbz1018；sjzx；yangwy；WWF；gsls；lanyan；zhjh；sd2011；星期八；HLing；zjx111；HJJ；caicl；xiawei（排名不分先后）菁优网2014年6月19日。

2013年浙江省杭州市西湖区中考数学一模试卷一.仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的，请把正确选项前的字母在答题卡中相应的方框内涂黑.注意可以用多种不同的方法来选取正确答案.．是正数是2的平方根C D．是分数3．（3分）（2011•昭通）已知两圆的半径R，r分别为方程x2﹣3x+2=0的两根，这两圆的圆心距为3，则这两圆的4．（3分）（2013•西湖区一模）母亲节快到了，某校团委随机抽取本校部分同学，进行母亲生日日期了解情况调查，分“知道、不知道、记不清”三种情况．下面图①、图②是根据采集到的数据，绘制的扇形和条形统计图．请你根据图中提供的信息，若全校共有990名学生，估计这所学校所有知道母亲的生日的学生有（）名．5．（3分）（2009•宁波）反比例函数y=在第一象限的图象如图所示，则k的值可能是（）6．（3分）（2013•西湖区一模）如图，x的值可能为（）7．（3分）（2013•西湖区一模）已知m为﹣9，﹣6，﹣5，﹣3，﹣2，2，3，5，6，9中随机取的一个数，则m4＞100的概率为（）．C D．8．（3分）（2014•路北区二模）若n个数的平均数为p，从这n个数中去掉一个数q，余下的数的平均数增加了2，9．（3分）（2014•路北区二模）如图，平面直角坐标系中，△ABC的顶点坐标分别是A（1，1），B（3，1），C（2，2），当直线与△ABC有交点时，b的取值范围是（）≤≤≤≤10．（3分）（2013•西湖区一模）如图（1）所示，E为矩形ABCD的边AD上一点，动点P、Q同时从点B出发，点P以1cm/秒的速度沿折线BE﹣ED﹣DC运动到点C时停止，点Q以2cm/秒的速度沿BC运动到点C时停止．设P、Q同时出发t秒时，△BPQ的面积为ycm2．已知y与t的函数关系图象如图；（2）（其中曲线OG为抛物线的一部分，其余各部分均为线段），则下列结论：①当0＜t≤5时，y=t2；②当t=6秒时，△ABE≌△PQB；③cos∠CBE=；④当t=秒时，△ABE∽△QBP；其中正确的是（）二、认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清楚题目的条件和要填写的内容，尽量完整地填写答案．11．（4分）（2013•西湖区一模）数据3，1，1，6，1，3的中位数是_________；众数是_________．12．（4分）（2013•西湖区一模）分解因式：a3﹣4a（a﹣1）=_________．13．（4分）（2012•杭州）某企业向银行贷款1000万元，一年后归还银行1065.6多万元，则年利率高于_________%．14．（4分）（2013•西湖区一模）一个由若干个大小完全相同的立方体堆成的立体图形的三视图如图所示，则组成这样的立体图形的小立方体的个数最多有_________个，最少有_________个．15．（4分）（2013•西湖区一模）如图，在梯形ABCD中，AD∥BC，∠B=90°，AD=2，BC=5，E为DC中点，tan∠C=．则AE的长度为_________．16．（4分）（2013•西湖区一模）如图，定长弦CD在以AB为直径的⊙O上滑动（点C、D与点A、B不重合），M 是CD的中点，过点C作CP⊥AB于点P，若CD=3，AB=8，PM=l，则l的最大值是_________．三、全面答一答（本题有7个小题，共66分）解答应写出文字说明、证明过程或推演步骤．如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以．17．（6分）（2013•西湖区一模）已知四边形ABCD是菱形，在平面直角坐标系中的位置如图，边AD经过原点O，已知A（0，﹣3），B（4，0）．（1）求点D的坐标；（2）求经过点C的反比例函数解析式．18．（8分）（2013•西湖区一模）如图，⊙P与y轴相切，圆心为P（﹣2，1），直线MN过点M（2，3），N（4，1）．（1）请你在图中作出⊙P关于y轴对称的⊙P′；（不要求写作法）（2）求⊙P在x轴上截得的线段长度；（3）直接写出圆心P′到直线MN的距离．19．（8分）（2013•西湖区一模）某学校体育场看台的侧面如图阴影部分所示，看台有四级高度相等的小台阶，每级小台阶都为0.4米．现要做一个不锈钢的扶手AB及两根与FG垂直且长均为l米的不锈钢架杆AD和BC（杆子的底端分别为D，C），且∠DAB=66°．（1）求点D与点C的高度差DH的长度；（2）求所用不锈钢材料的总长度l（即AD+AB+BC，结果精确到0.1米）．（参考数据：sin66°≈0.91，cos66°≈0.41，tan66°≈2.25，cot66°≈0.45）y=ax2+bx+c（a≠0）中的x，y满足下表：的值为_________；（2）若A（p，y1），B（p+1，y2）两点都在该函数的图象上，且p＜0，试比较y1与y2的大小．21．（10分）（2013•西湖区一模）如图，在梯形ABCD中，AD∥BC，∠BCD=90°，BC=DC，点E在对角线BD上，作∠ECF=90°，连接DF，且满足CF=EC．（1）求证：BD⊥DF．（2）当BC2=DE•DB时，试判断四边形DECF的形状，并说明理由．22．（12分）（2013•西湖区一模）如图1，△ABC内接于半径为4cm的⊙O，AB为直径，长为．（1）计算∠ABC的度数；（2）将与△ABC全等的△FED如图2摆放，使两个三角形的对应边DF与AC有一部分重叠，△FED的最长边EF恰好经过的中点M．求证：AF=AB；（3）设图2中以A、C、M为顶点的三角形面积为S，求出S的值．23．（12分）（2013•西湖区一模）已知：如图，在平面直角坐标系xOy中，边长为的等边△ABC随着顶点A在抛物线上运动而运动，且始终有BC∥x轴．（1）当顶点A运动至与原点重合时，顶点C是否在该抛物线上？（2）△ABC在运动过程中有可能被x轴分成两部分，当上下两部分的面积之比为1：8（即S上部分：S下部分=1：8）时，求顶点A的坐标；（3）△ABC在运动过程中，当顶点B落在坐标轴上时，直接写出顶点C的坐标．2013年浙江省杭州市西湖区中考数学一模试卷参考答案与试题解析一.仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的，请把正确选项前的字母在答题卡中相应的方框内涂黑.注意可以用多种不同的方法来选取正确答案.．是正数是2的平方根C D．是分数估算无理数的大小；实数．是正数，是2的一个平方根，＜＜，是无理数，不是分数，根据以上内容判断即可．是、∵＜＜是无理数，不是分数，错误，故本选项正确；3．（3分）（2011•昭通）已知两圆的半径R，r分别为方程x2﹣3x+2=0的两根，这两圆的圆心距为3，则这两圆的4．（3分）（2013•西湖区一模）母亲节快到了，某校团委随机抽取本校部分同学，进行母亲生日日期了解情况调查，分“知道、不知道、记不清”三种情况．下面图①、图②是根据采集到的数据，绘制的扇形和条形统计图．请你根据图中提供的信息，若全校共有990名学生，估计这所学校所有知道母亲的生日的学生有（）名．÷=90×=5505．（3分）（2009•宁波）反比例函数y=在第一象限的图象如图所示，则k的值可能是（），＜6．（3分）（2013•西湖区一模）如图，x的值可能为（）7．（3分）（2013•西湖区一模）已知m为﹣9，﹣6，﹣5，﹣3，﹣2，2，3，5，6，9中随机取的一个数，则m4＞．C D．的概率为：．．8．（3分）（2014•路北区二模）若n个数的平均数为p，从这n个数中去掉一个数q，余下的数的平均数增加了2，9．（3分）（2014•路北区二模）如图，平面直角坐标系中，△ABC的顶点坐标分别是A（1，1），B（3，1），C（2，2），当直线与△ABC有交点时，b的取值范围是（）≤≤≤≤）的坐标分别代入直线中，可得+b=1；中，可得；的取值范围是﹣10．（3分）（2013•西湖区一模）如图（1）所示，E为矩形ABCD的边AD上一点，动点P、Q同时从点B出发，点P以1cm/秒的速度沿折线BE﹣ED﹣DC运动到点C时停止，点Q以2cm/秒的速度沿BC运动到点C时停止．设P、Q同时出发t秒时，△BPQ的面积为ycm2．已知y与t的函数关系图象如图；（2）（其中曲线OG为抛物线的一部分，其余各部分均为线段），则下列结论：①当0＜t≤5时，y=t2；②当t=6秒时，△ABE≌△PQB；③cos∠CBE=；④当t=秒时，△ABE∽△QBP；其中正确的是（）====，ty=BQ PF=×t=中，t=PD=﹣﹣，=，∵=，==∴二、认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清楚题目的条件和要填写的内容，尽量完整地填写答案．11．（4分）（2013•西湖区一模）数据3，1，1，6，1，3的中位数是2；众数是1．=212．（4分）（2013•西湖区一模）分解因式：a3﹣4a（a﹣1）=a（a﹣2）2．13．（4分）（2012•杭州）某企业向银行贷款1000万元，一年后归还银行1065.6多万元，则年利率高于 6.56%．14．（4分）（2013•西湖区一模）一个由若干个大小完全相同的立方体堆成的立体图形的三视图如图所示，则组成这样的立体图形的小立方体的个数最多有18个，最少有12个．15．（4分）（2013•西湖区一模）如图，在梯形ABCD中，AD∥BC，∠B=90°，AD=2，BC=5，E为DC中点，tan∠C=．则AE的长度为．DM=CF=，C==．故答案为：16．（4分）（2013•西湖区一模）如图，定长弦CD在以AB为直径的⊙O上滑动（点C、D与点A、B不重合），M 是CD的中点，过点C作CP⊥AB于点P，若CD=3，AB=8，PM=l，则l的最大值是4．三、全面答一答（本题有7个小题，共66分）解答应写出文字说明、证明过程或推演步骤．如果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以．17．（6分）（2013•西湖区一模）已知四边形ABCD是菱形，在平面直角坐标系中的位置如图，边AD经过原点O，已知A（0，﹣3），B（4，0）．（1）求点D的坐标；（2）求经过点C的反比例函数解析式．=5的反比例函数解析式为，所求的解析式为；18．（8分）（2013•西湖区一模）如图，⊙P与y轴相切，圆心为P（﹣2，1），直线MN过点M（2，3），N（4，1）．（1）请你在图中作出⊙P关于y轴对称的⊙P′；（不要求写作法）（2）求⊙P在x轴上截得的线段长度；（3）直接写出圆心P′到直线MN的距离．轴上截得的线段长度为：MN==2，=19．（8分）（2013•西湖区一模）某学校体育场看台的侧面如图阴影部分所示，看台有四级高度相等的小台阶，每级小台阶都为0.4米．现要做一个不锈钢的扶手AB及两根与FG垂直且长均为l米的不锈钢架杆AD和BC（杆子的底端分别为D，C），且∠DAB=66°．（1）求点D与点C的高度差DH的长度；（2）求所用不锈钢材料的总长度l（即AD+AB+BC，结果精确到0.1米）．（参考数据：sin66°≈0.91，cos66°≈0.41，tan66°≈2.25，cot66°≈0.45）即可求得∵AB=y=ax2+bx+c（a≠0）中的x，y满足下表：（1）m的值为0；（2）若A（p，y1），B（p+1，y2）两点都在该函数的图象上，且p＜0，试比较y1与y2的大小．21．（10分）（2013•西湖区一模）如图，在梯形ABCD中，AD∥BC，∠BCD=90°，BC=DC，点E在对角线BD上，作∠ECF=90°，连接DF，且满足CF=EC．（1）求证：BD⊥DF．（2）当BC2=DE•DB时，试判断四边形DECF的形状，并说明理由．，∴22．（12分）（2013•西湖区一模）如图1，△ABC内接于半径为4cm的⊙O，AB为直径，长为．（1）计算∠ABC的度数；（2）将与△ABC全等的△FED如图2摆放，使两个三角形的对应边DF与AC有一部分重叠，△FED的最长边EF恰好经过的中点M．求证：AF=AB；（3）设图2中以A、C、M为顶点的三角形面积为S，求出S的值．，OM=FH=AC=4∵长为∴OBC=的中点，ABOM=FH=ABAC=4中，是MCN=∠，即，∴∴23．（12分）（2013•西湖区一模）已知：如图，在平面直角坐标系xOy中，边长为的等边△ABC随着顶点A在抛物线上运动而运动，且始终有BC∥x轴．（1）当顶点A运动至与原点重合时，顶点C是否在该抛物线上？（2）△ABC在运动过程中有可能被x轴分成两部分，当上下两部分的面积之比为1：8（即S上部分：S下部分=1：8）时，求顶点A的坐标；（3）△ABC在运动过程中，当顶点B落在坐标轴上时，直接写出顶点C的坐标．，代入抛物线的解析式可BC=AC=∴当时，）∴的边长为∴∴的坐标为3=x=或﹣+点横坐标为y=的坐标为。

2013年杭州市各类高中招生文化考试一模考试数学试卷考生须知：1．本试卷满分120分，考试时间100分钟．2．答题前，请在答题卷密封区内写明校名、姓名和准考证号．3．所有答案都必须做在答题卷标定的位置上，务必注意试题序号和答题序号相对应．4．考试结束后，上交试题卷和答题卷．试题卷一、仔细选一选(本题有10个小题, 每小题3分, 共30分)下面每小题给出的四个选项中, 只有一个是正确的，注意可以用多种不同的方法来选取正确答案．1．3的相反数是A ．3B ．3C ．31D ．312．下列各等式一定成立的是A ．22)(a aB ．33)(a aC ．22aaD ．33aa3．对于一组统计数据：3，7，6，2，9，3，下列说法错误．．的是A ．众数是 3B ．极差是7C ．平均数是 5D ．中位数是 44．选择用反证法证明“已知：在△ABC 中，∠C=90o．求证：∠A ，∠B 中至少有一个角不大于45o．”时，应先假设A ．∠A ＞45o，∠B ＞45o B ．∠A ≥45o ，∠B ≥45oC ．∠A ＜45o ，∠B ＜45oD ．∠A ≤45o，∠B ≤45o5．右图是一个由7个同样的立方体叠成的几何体，则这一几何体的三视图中，既是轴对称图形又是中心对称图形的是A ．主视图和俯视图 B.俯视图C ．俯视图和左视图 D. 主视图6．已知21m，21n，则代数式mn nm322的值为A. 9B. ±3C. 3D.5（第5题）7.如图，在四边形ABCD 中，E ，F 分别是AB ，AD 的中点，若EF =2，BC=5，CD=3，则sinC等于A.43 B.34 C.54 D.538．如图，在平面直角坐标系中，过格点A ，B ，C 作一圆弧，点B 与下列格点的连线中，能够与该圆弧相切的是A ．点(0，3)B ．点(2，3)C ．点(6，1)D ．点(5，1)9．在平面直角坐标系中，经过二、三、四象限的直线l 过点（-3，-2）.点(-2，a ），(0，b)，(c ，1)，(d ，-1)都在直线l 上，则下列判断正确的是A ．a= -3B ．b> -2C ．c< -3D ．d= -210．点A ，B 的坐标分别为（-2,3）和（1,3），抛物线c bxaxy2(a<0)的顶点在线段AB 上运动时，形状保持不变，且与x 轴交于C ，D 两点（C 在D 的左侧），给出下列结论：①c ＜3；②当x ＜-3时，y 随x 的增大而增大；③若点D 的横坐标最大值为5，则点C 的横坐标最小值为-5；④当四边形ACDB 为平行四边形时，34a.其中正确的是A ．②④B ．②③C ．①③④D ．①②④二、认真填一填（本题有6个小题，每小题4分，共24分）要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案．11．如图，△ABC 中，21FCAF EBAE ，若△AEF 的面积为1，则四边形EBCF 的面积为．（第9题）（第8题）（第7题）(第11题)12．在一个口袋中有三个完全相同的小球，把它们分别标上数字﹣1，0，2，随机地摸出一个小球记录数字然后放回，再随机地摸出一个小球记录数字．则两次的数字和是正数的概率为．13．已知1x 是一元二次方程0102bx ax 的一个解，且b a ，则ba ba2222的值为．14．某市居民用电价格改革方案已出台，为鼓励居民节约用电，对居民生活用电实行阶梯制价格（见表）：“一户一表”用电量不超过a 千瓦时超过a 千瓦时的部分单价（元/千瓦时）0.50.6小芳家二月份用电200千瓦时，交电费105元，则a= .15．无论a 取什么实数，点P （12a，3a）都在直线l 上，Q （m ，n ）是直线l 上的点，则2)12(nm的值为．16．如图，□ABCD 中，AC ⊥AB ．AB=6cm ，BC=10cm ，E 是CD 上的点，DE=2CE ．点P 从D 点出发，以1cm/s 的速度沿DA →AB →BC 运动至C 点停止．则当△EDP 为等腰三角形时，运动时间为s ．三、全面答一答（本题有8个小题，共66分）解答应写出文字说明、证明过程或推演步骤．如果觉得有的题目有点困难，你们把自己能写出的解答写出一部分也可以．17．（本小题满分6分）阅读材料，解答问题：观察下列方程：①23xx；②65xx；③127xx；,；（1）按此规律写出关于x 的第4个方程为，第n 个方程为；（2）直接写出第n 个方程的解，并检验此解是否正确.(第16题)18．（本小题满分8分）如图，在平面直角坐标系中，∠AOB =60°，点B 坐标为（2，0），线段OA 长为6，将△AOB 绕点O 逆时针旋转60°后，点A 落在点C 处，点B 落在点D 处.（1）请你在图中用直尺和圆规作出△COD （保留作图痕迹，不必写作法）；（2）求△AOB 旋转过程中点A 所经过的路程.19．（本小题满分8分）如图，AD 为△ABC 外接圆的直径，ADBC ，垂足为点F ，AB C 的平分线交AD 于点E ，连接BD ，C D ．请判断B ，E ，C 三点是否在以D 为圆心、D B 长为半径的圆上？并说明理由．20．（本小题满分10分）光明中学欲举办“校园吉尼斯挑战赛”，为此学校随机抽取男女学生各50名进行一次“你喜欢的挑战项目”的问卷调查，每名学生都选了一项．根据收集到的数据，绘制成如下统计图（不完整）：根据统计图表中的信息，解答下列问题：（1）在本次随机调查中，女生最喜欢“踢毽子”项目的有人，男生最喜欢“乒乓球”项目的有人；（2）请将条形统计图补充完整；(第18题)（第19题）（第20题）（3）若该校有男生400人，女生450人，请估计该校喜欢“羽毛球”项目的学生总人数．21．（本小题满分10分）在直角梯形ABCD 中，AB ∥CD ，∠ABC=90°，∠A=60°，AB=2CD ，E ，F 分别为AB ，AD 的中点，连结EF ，EC ，BF ，CF ．（1）求证△CBE ≌△CFE ；（2）若CD ＝a ，求四边形BCFE 的面积．22．（本小题满分12分）如图，已知2tan EOF，点C 在射线OF 上，OC =12.点M 是EOF内一点，OF MC于点C ，MC=4.在射线CF 上取一点A ，连结AM 并延长交射线OE 于点B ，作BD ⊥OF 于点D .（1）当AC 的长度为多少时，△AMC 和△BOD 相似；（2）当点M 恰好是线段AB 中点时，试判断△AOB 的形状，并说明理由；（3）连结BC.当BOC AMCS S △△时，求AC 的长.23．（本小题满分12分）如图，已知一次函数b kxy的图象与x 轴相交于点A ，与反比例函数xc y的图象相交于B （－1，5），C （25，d ）两点．（1）求k ，b 的值；（2）设点P （m ，n ）是一次函数b kxy 的图象上的动点．①当点P 在线段AB （不与A ，B 重合）上运动时，过点P 作x 轴的平行线与函数xc y的图象相交于点D ，求出△PAD 面积的最大值．②若在两个实数m 与n 之间（不包括m 和n ）有且只有一个整数，直接写出实数m的取值范围．(第21题)（第22题）（第23题）2013年杭州市各类高中招生文化考试一模试卷数学（参考答案及评分标准）一、仔细选一选(本题有10个小题, 每小题3分, 共30分) 题号 1 2 3 4 5 6 7 8 9 10 选项BADABCCDCA二、认真填一填（本题有6个小题，每小题4分，共24分）11. 8； 12.95； 13. 5； 14. 150；15. 16； 16. 4，4.8，,3105214136三、全面答一答（本题有8个小题，共66分）17.（本小题满分6分）（1）920xx ，-------------------------1分12)1(nx nn x---------------2分（2）1,21nx n x --------------------2分检验----------------------------------1分18.（本小题满分8分）（1）画图略，4分（可画正三角形得到60°角，不用圆规画60°扣2分）（2）2180660l，即点A 旋转过程中所经过的路程为2,,,,4分（其中n ，R 的值正确给2分）19.（本小题满分8分）解：B ，E ，C 三点在以D 为圆心，以D B 为半径的圆上.理由：∵A D 为直径，AD B C ，∴AD 平分弦BC 所对的弧，即BDC D.∴BD C D.-----------------------------------------3分∵BD C D ，∴B A DC BD .∵D BE C BDC BE ，D EBBAD ABE ，C BEAB E ，∴D BED EB .∴D B DE . ------------------------------------------------3分.∴D BD ED C .（第19题）∴B ，E ，C 三点在以D 为圆心，以D B 为半径的圆上. -------------------2分20.（本小题满分10分）解：（1）女生最喜欢“踢毽子”项目的有 10人，男生最喜欢“乒乓球”项目的有 20人；----------------------------------------4分（2）补充条形统计图如右图；---------------2分（3）193509450%28400.所以估计该校喜欢“羽毛球”项目的学生总人数为193人. ---------------------------------------------4分21.（本小题满分10分）（1）连接DE.90,,//ABC BE CDBE CD ∴四边形BCDE 是矩形----------------------------------------1分F 为AD 中点，90DEA ∴AFEF60A∴AEF是正三角形------------------------2分∴EF AE ，60EFABE AE，DF=AF∴EF BE，CD=DFAECD //∴120180A CDF ∴DFC=30°∴CFE=90°=CBE---------------2分又∵EF BE ，CE=CE ，∴Rt △CBE ≌Rt △CFE （HL ）------------------------------------2分（其它方法酌情给分）(2)aCD ∴a BE AE 60A∴aDEBC3∴223aSBCE∴23aS BCFE四边形------------3分(第21题)22.（本小题满分12分）（1）∵∠MCA =∠BDO =Rt ∠∴当DOBD ACMC =2tanEOF或DOBD MCAC =2tanEOF时，△AMC 和△BOD 相似∵MC=4，∴AC=2或AC=8时，△AMC ∽△BOD ---------------4分（2）△ABO 为直角三角形.------------------------------------------ 1分理由如下：∵MC ∥BD ，∴△AMC ∽△ABD ∴ADAC ABAM BDMC ，∠AMC=∠ABD ，∵M 为中点，∴BD=8 ∵2tanEOF，∴OD=4，∴CD=8 ∴AC=8由（1）得，此时△AMC ∽△BOD ∴∠DBO=∠CAM ，∴∠ABO=∠ABD+∠DBO=∠AMC+∠CAM=90°-----------------3分（3）连结BC ，设OD=a ，则BD=2a ∴BOCS △12a∵BOCAMCS S △△∴AC=6a ∵△AMC ∽△ABD ∴ADAC BDMC 即aaa a126624解得31a ，342a （舍去）∴AC=18-------------------------------------------------4分23.（本小题满分12分）解:（1）将点B 的坐标代入x c y ，得15c ，解得c=－5∴反比例函数解析式为x y5将点C （25，d ）的坐标代入xy5，得2255d∴C （25，－2）--------------1分∵一次函数b kx y 的图象经过B （－1，5）、C （25，－2）两点，（第22题）∴bkbk 2525，解得32bk -------------------------------------------------------------2分（2）点P （m ，n ）是一次函数b kx y 的图象上的动点．①令y=0，即－2x ＋3=0，解得x=23∴A （23，0）由题意，点P （m ，n ）在线段AB 上运动（不含A 、B ）.设P （23n，n ）∵DP ∥x 轴，且点D 在x y5的图象上，∴y D =y P =n ，x D =－n5，即D （－n5，n ）∴△PAD 的面积为1649)23(41)523(21212n n nnOP PDS---------2分∴S 关于n 的二次函数的图象开口向下，有最大值.又∵n =－2m ＋3，－1＜m ＜23，得0＜n ＜5，而0＜n=23＜5------------------------1分∴当n=23时，即P （23,43）时，△PAD 的面积S 最大，为1649.-------------------------2分②实数m 的取值范围为21≤m ＜1或1＜m ≤23(写成21≤m ≤23且m ≠1也对)------------------------------------------------------4分(漏等号每处扣1分,未舍去m=1扣1分)。

2013年西湖区一模试题Ⅱ，笔试部分（95分）四、单项填空（共15小题，计l5分）从A. B. C.D四个选项中，选出可以填入空白处的最佳选项。

16 :Can you find the sound／eə／in the underlined parts of the following words?A. hereB.clear C,chair D.ear17: The data of PM 2.5is giving us a big______．Can we do something about it?A. breakB. excuseC.handD.headache18. There is _______as good as the taste of a fresh apple, especially in the fall.A. nothingB.everythingC. somethingD.anything19.- -The song is, I have to say, not a bit beautiful.--Why? It’s________ than the songs I have ever heard.A. any less beautiful B: much less beautifulC: many more beautiful D:much more beautiful20.--You went late _____ the gym yesterday evening, didn't you?-- Yes. The teacher was very angry.A. forB. withC. toD. at21.- -Didn't you have a good time at the party?--Of course I did. In fact I had such fun that time seemed to _____ so quickly.A: go by B. go away C.go out D. go over22.The doctors in Beijing did all they_____ to save Shao Zhanwei, mayor of Hangzhou, but hestill died of heart attack at the,age of 58.A.would . B could C.must D,might .23.--I'm going to the Century Mart. ---_____ you're there, can you get me a bag of salt?A.As B/While C.Because D.If24.--We can't enter the house. I can't find the key! --Is it possible that you _____ it in the car?A.caughtB.changedC.foundD. left25.--Why are you still here? It's already seven o'clock.--Because I ______ my work. Don't worry. It's almost done.A:wasn't finishing .B. wouldn't finish C. haven't finished D. won't finish26. --Do you know ______? ---To meet her friends from America.A. where Anna is goingB. who is Anna's best friendC. how Anna goes to the airportD. why Anna is going to the airport27. ________me two more days, and I'll finish the report.A.GivingB.GivenC. GiveD.To give28.-- Nick, you clean the blackboard today, ______?---With pleasure. I cleaned it yesterday, though.A.Will youB.do youC.don't youD.didn't you29. --Do you know the man ______came to China as the ambassador for the Chinese SuperLeague? ---You mean David Beckham?A.whichB.where C, who D.what30. ---I'm too stressed out these days. Could you give me some advice?---__________.Tell me all about it and I'll do what I can.A.Never mindB. No wayC. No problemD. Forget it五：完形填空（共15小题，计15分）通读下面短文，掌握其大意，然后在各题所给的四个选项（A、B、C和D）中选出一个最佳选项。

浙江省杭州市西湖区 2013 年 4 月模拟考试数学试卷考生须知: 1. 本试卷分试题卷和答题卷两部分. 满分 120 分, 考试时间 100 分钟. 2. 答题时, 不能使用计算器,在答题卷指定位置内写明校名, 姓名和班级，填涂考生号. 3. 所有答案都做在答题卡标定的位置上, 请务必注意试题序号和答题序号相对应.2 4. 参考公式: 抛物线 y  ax2  bx  c(a  0) 的顶点坐标（  b ， 4ac  b ） 2a 4a一. 仔细选一选 (本题有 10 个小题, 每小题 3 分, 共 30 分) 下面每小题给出的四个选项中, 只有一个是正确的, 请把正确选项前的字母在答题卡中相应 的方框内涂黑. 注意可以用多种不同的方法来选取正确答案. 1. 在-5，0，-3，6 这四个数中，最小的数是（ A．-3 B．0 ） ） C．-5 D．62. 下列有关 2 叙述错误的是（ ．．A． 2 是正数B． 2 是 2 的平方根C． 1 22D．2 是分数 23. 已知两圆半径分别是方程 x - 3x + 2 = 0 的两根，两圆圆心距为 3，则两圆位置关系是 （ ） A．外切2B．外离C．相交D．内切4. 母亲节快到了，某校团委随机抽取本校部分同学，进行母亲生日日期了解情况调查，分 “知道、不知道、记不清”三种情况.下面图①、图②是根据采集到的数据，绘制的扇形 和条形统计图. 请你根据图中提供的信息， 若全校共有 990 名学生， 估计这所学校有知道 母亲的生日的学生有（ ）名.不知道记不清 120° 知道图① A．440 5. 反比例函数 y  B．495 C．550 D．660图②k 在第一象限的图象如图所示，则 k 的值可能是（ xC．2 D．1）y 2 1 O 1 2 x（第 5 题）A．4 B．3 6. 如图，x 的值可能为（ ）（第 6 题）A．10 C．7B．9 D．67. 已知 m 为-9 , -6 , -5 , -3 , -2 , 2 , 3 , 5 , 6 , 9 中随机取的一个数，则 m > 100 的概率为 （ ） A．41 5）B．3 10C．1 2D．3 58. 若 n 个数的平均数为 p ，从这 n 个数中去掉一个数 q ，余下的数的平均数增加了 2，则 q 的值为（A. p - 2n + 2B. 2 p - nC. 2 p - n + 2D. p - n + 29．如图，平面直角坐标系中，△ABC 的顶点坐标分别是 A(1，1),B(3，1),C(2，2),当直 线y1 x  b 与△ABC 有交点时，的取值范围是（ 2B. －）y C A B xA.－1≤ b ≤1 C. －1 ≤ b ≤1 21 1 1 o ≤b ≤ D. －1≤ b ≤ 2 2 2 （第 9 题） 10. 如图(1)所示，E 为矩形 ABCD 的边 AD 上一点，动点 P、Q 同时从点 B 出发，点 P 以 1cm/秒的速度沿折线 BE—ED—DC 运动到点 C 时停止， Q 以 2cm/秒的速度沿 BC 运 点 动到点 C 时停止．设 P、Q 同时出发 t 秒时，△BPQ 的面积为 ycm2．已知 y 与 t 的函数 关系图象如图(2)(其中曲线 OG 为抛物线的一部分，其余各部分均为线段)，则下列结 论：①当 0＜t≤5 时，y＝ ④当 t＝4 2 1 t ；②当 t＝6 秒时，△ABE≌△PQB；③cos∠CBE＝ ； 5 2y A P B Q C E D40 20 G29 秒时，△ABE∽△QBP； 2） B．①③④ D．①②④MN其中正确的是（ A．①② C．③④O5 10 14t（第 10 题图 1） （第 10 题图 2）二、认真填一填 (本题有 6 个小题, 每小题 4 分, 共 24 分)要注意认真看清楚题目的条件和 要填写的内容，尽量完整地填写答案． 11. 数据 3，1，1，6，1，3 的中位数是 ▲_ ；众数是 ▲ ． 12. 分解因式： a - 4a(a - 1) =_3▲ ___． ▲ %．13. 某企业向银行贷款 100 万元，一年后归还银行 106.6 多万元，则年利率高于14. 一个由若干个大小完全相同的立方体堆成的立体图形的三视图如图所示，则组成这样的 立体图形的小立方体的个数最多有_ 最少有_ ▲_ 个． ▲ _个，（第 14 题）15. 如图， 在梯形 ABCD 中， AD∥ BC， B=90° AD=2， ∠ ， BC=5， 为 DC 中点， E tan∠ C=4 ． 则 3AE 的长度为_ ▲ __． 16. 如图，定长弦 CD 在以 AB 为直径的⊙O 上滑动（点 C、D 与点 A、B 不重合） 是 CD ，M 的中点， 过点 C 作 CP⊥AB 于点 P， CD=3， 若 AB=8， PM=l， l 的最大值是 则 ▲ ． D A D C MEAPOBB（第 15 题）C（第 16 题）三、 全面答一答 （本题有 7 个小题， 66 分） 共 解答应写出文字说明、 证明过程或推演步骤． 如 y 果觉得有的题目有点困难，那么把自己能写出的解答写出一部分也可以． 17. (本题满分 6 分) 已知四边形 ABCD 是菱形，在平面直角坐标系中 的位置如图，边 AD 经过原点 O，已知 A（0，－3） ，B（4，0） ． （1）求点 D 的坐标； （2）求经过点 C 的反比例函数解析式． 18. (本题满分 8 分) 如图，⊙P 与 y 轴相切，圆心为 P（－2，1） ， 直线 MN 过点 M（2，3） ，N（4，1）. (1) 请你在图中作出⊙P 关于 y 轴对称的⊙P′； （不要求写作法） (2) 求⊙P 在 x 轴上截得的线段长度； (3) 直接写出圆心 P′到直线 MN 的距离．-4C D O A y4 2 0 -2 -4 （第 18 题） 2 4Bx（第 17 题）M N xP-219. (本题满分 8 分) 某学校体育场看台的侧面如图阴影部分所示， 看台有四级高度相等的小台阶， 每级小台阶都为 0.4 米.现要做一个不锈钢的扶手 AB 及两根 与 FG 垂直且长均为 l 米的不锈钢架杆 AD 和 BC （杆子的底端分别为 D， ， DAB  66 . C）且（1）求点 D 与点 C 的高度差 DH 的长度；660A D E 1米（2）求所用不锈钢材料的总长度（即 AD＋AB＋BC） ．B（结果精确到 0.1 米.参考数据： sin 66  0.91 ，C G （第 19 题）H Fcos 66  0.41 ， tan 66  2.25 ） 20．(本题满分 10 分)已知：二次函数 y  ax2  bx  c (a  0) 中的 x， y 满足下表：x y„ „100123„ „343m（1）求 m 的值； （2）根据上表求 y  0 时的 x 的取值范围； （3）若 A( p，y1 ) ， B( p  1 y2 ) 两点都在该函数图象上，且 p  0 ，试比较 y1 与 y2 的 ， 大小.21．(本题满分 10 分)如图，在梯形 ABCD 中，AD∥BC，∠BCD=90° ，BC=DC，点 E 在对 角线 BD 上，作∠ECF=90° ，连接 DF，且满足 CF=EC． （1）求证：BD⊥DF． （2）当 BC  DE  DB 时，试判断四边形 DECF 的形状，并说明理由．2A EDF B（第 21 题） C 22． (本题满分 12 分) 如图 1， △ABC 内接于半径为 4cm 的⊙O， 为直径， 长为 AB BC（1）计算∠ABC 的度数；4 cm ． 3（2） 将与△ABC 全等的△FED 如图 2 摆放， 使两个三角形的对应边 DF 与 AC 有一部分 重叠，△FED 的最长边 EF 恰好经过  的中点 M．求证：AF=AB； AB （3）设图 2 中以 A、C、M 为顶点的三角形面积为 S，求出 S 的值． E F M · C CA.OD B A.OB（第 22 题图 1）（第 22 题图 2）23．(本题满分 12 分)如图，在平面直角坐标系 xOy 中，等边 △ ABC 中，BC∥ x 轴，且 BC= 2 3 ，顶点 A 在抛物线 y  x 2  2 3x 上运动． （1）当顶点 A 运动至与原点重合时，顶点 C 是否在该抛物线上？ （2） △ ABC 在运动过程中有可能被 x 轴分成两部分，当上下两部分的面积之比为 1:8 （即 S上部分 : S下部分  1 : 8 ）时，求顶点 A 的坐标； （3） △ ABC 在运动过程中，当顶点 B 落在坐标轴上时，直接写出顶点 C 的坐标．（第 23 题）参考答案一、选择题（本大题共 10 个小题；每小题 3 分，共 30 分）题号 答案 1 C 2 D 3 A 4 C 5 B 6 B 7 D 8 A 9 B 10 D二、填空题（每小题 4 分，共 24 分）11．2,1 12． a(a - 2)2 13．6.6 14．18,12 15．65 216． 4三、解答题（本题共 8 小题，共 66 分）17． （本题 6 分） （1）由已知，AB= 32  42 =5 ∵四边形ABCD是菱形， ∴AD= AB=5 ∵边AD经过原点O ，A（0，－3） ∴点D（0，2）„„„„3分 （2）由（1）得，点 C 坐标为（4，5） 设经过点 C 的反比例函数解析式为 y  y C D O A B xk xk ，解得：k=20 4 20 ∴所求的解析式为 y  x得： 5  18. （本题 8 分） （1）图略，正确（第 17 题）„„„„3分„„„„3 分（点 P′画对得 1 分） „„„„3 分（2）⊙P 在 x 轴上截得的线段长度为 2 22 - 1 = 2 3 （3）由图可知，P′M=2，P′N=2，△P′MN 为直角三角形 ∴MN= 2 2  2 2 =2 2 ， ∴点 P′到直线 MN 的距离=P M  P N 2  2   2 MN 2 2„„„„2 分A19. （本题8分） （1）DH＝ 0.4  3 ＝ 1.2 （米）. „„„„„„„„„„„„„3分 （2）过点B作BM⊥AH，垂足为M. B 由题意得：MH＝BC＝AD= 1， A  66 .6601米 D EMH FC G∴AM＝AH－MH＝ 1  1.2  1 ＝ 1.2 . „„„„„„„2分 在 Rt△AMB 中， ∵ cos A AM AM 1.2   2.92 （米）. „„„„„1分 ，∴AB＝ AB cos 66 0.41 ∴＝AD＋AB＋BC  1  2.92  1  4.9 （米）. „„„„„„„„„„1分答：点D与点C的高度差DH为 1.2 米；所用不锈钢材料的总长度约为 4.9 米. „„1分 20. （本题 10 分） （1）m = 0； （2） y  0 ，则 x < - 1 或 x > 3 ； （3） p  0 ， p  p  1  1 „„„3 分 „„„„4 分 „„„„1 分又因为抛物开口向上，对称轴为 x  1 ， 21． （本题 10 分） y1  y2„„„„2 分（1）证明：∵ BCD  ECF  90 ， ∴ BCE  DCF ∵ BC  DC, EC  CF ，∴ BCE ≌ DCF ∴ EBC  FDC ∵ BC  DC, BCD  90 ，∴ DBC  BDC  45 ∴ FDC  45 ，∴ FDB  90 ∴ BD  DF „„„„„„„„„„„„„„„„„„„„„„5 分 (2) 四边形 DECF 是正方形„„„„„„„„„„„„„„„„„„„1 分2 ∵ BC  DE  DB, BC  DC ，∴ DC  DE  DB ， ∴2DC DE  DB DC∵ CDE  BDC ∴ CDE ∽ BDC ∴ DEC  DCB  90 ∵ FDE  ECF  90 ， ∵ CE  CF ， 22. （本题 12 分） （1）连结 OC ⌒长为 4 cm ，⊙O 的半径为 4cm ∵ BC ∴四边形 DECF 是矩形∴四边形 DECF 是正方形„„„„„„„„„„„„4 分 C A3 4  n 4  ∴ 180 3∵OB=OCO.B∴n=60即∠BOC=60°∴∠ABC=∠OBC=180  60  60 2„„„„4 分（2）连结 OM，过点 F 作 FH  AB 于 H ∵AB 为直径 ∴∠ACB=90° ∴∠A=180－90－60=30° ∴在 Rt△FAH 中， FH  ⌒ AB A1 AF 2E DM ·F C B.OH∵点 M 为的中点∴OM⊥AB 且 OM =1 AB 2∵△ABC 与△FED 全等 ∴EF∥AB OM=FH=∴∠A=∠EFD=30°1 AB 2E D A M · F C B∴AF=AB „„„„4 分 （3）连结 AM、CM，过点 M 作 MN⊥AC 于点 N 在 Rt△ABC 中，AB=8，∠A=30° ∴AC=4 3 在 Rt△AMO 中， AM  设 MN=x ，∵∠MCN =2.ONMO2  AO2  4 2⌒ AM =45°2 2m12∴MN=NC=x2 即x  4 3 x在 Rt△AMN 中， AM  AN  MN  4 2 22x1  2 3  2 ， x2  2 3  2 （舍去）∴ x  2 3  2∴S 1  4 3  (2 3  2)  12  4 3 2„„„„4 分23. （本题 12 分） （1）当顶点 A 运动至与原点重合时，设 BC 与 y 轴交于点 D，如图所示． ∵BC∥x 轴，BC=AC= 2 3 ， ∴ CD  3 ， AD  3 ． ∴C 点的坐标为 ( 3 ,  3) ． ∵当 x  „„„„„2 分3 时， y  ( 3) 2  2 3  3  3 ．∴当顶点 A 运动至与原点重合时，顶点 C 在抛物线上．„„„„„2 分 （2）过点 A 作 AD  BC 于点 D， 设点 A 的坐标为（ x ， x  2 3x ） ．2∵ S上部分 : S下部分  1 : 8 ， ∴ AD  3( x 2  2 3x) ．„„„„1 分 ∵等边 △ ABC 的边长为 2 3 ， ∴ AD  AC  sin 60  3 ． ∴ 3( x 2  2 3x)  3 ． ∴ x  2 3x  1  0 ．2·解方程，得 x 3 2．∴顶点 A 的坐标为 ( 3  2 , 1) 或 ( 3  2 , 1) ．„„„„„„„„„„4 分 （3）当顶点 B 落在坐标轴上时，顶点 C 的坐标为 (2 3  6 , 0) 、 (2 3  6 , 0) 、(2 3 ,  6) ． „„„„„„„„„„„„„„„„„„„„„„„3 分。