2011年上海16区县二模压轴汇编

2011上海市英语各区二模答案卢湾Section A1-5 BDCCD 6-10 DBBDBSection B11-13 BAA 14-16 BCDSection C17. 1808 18. toilet 19. leaking 20. three-day21. angry customers 22. transferred to Boston23. Early next month 24. location and reputationII. Grammar and VocabularySection A25. B 26. C 27. B 28. A 29. D 30. C 31. B 32. D33. C 34. D 35. A 36. D 37. C 38. A 39. B 40. ASection B41. H 42. E 43. D 44. A 45. C 46. F 47. B 48. I49. GIII. Reading ComprehensionSection A50-54 CBCBD 55-59 BABCB 60-64 AACDCSection B65-68 DBDC 69-71 BCD 72-75 DDBASection C76-80 FECADSection D81. she received words of praise from that father82. earn / win / make friends all over the world/from all parts of the world83. Praise is a sort of spiritual reward for our work./Praise is a sort of recognition of our work.84. To tell us to take every chance to praise others第II卷（45分）I. TranslationDirections: Translate the following sentences into English, using the words given in the brackets.1. 分值：3分词的用法（形容词的固定搭配，比较级固定句型）低碳生活日益受到年轻人的推崇。

例 2011年上海市闸北区中考模拟第25题直线113y x=-+分别交x轴、y轴于A、B两点，△AOB绕点O按逆时针方向旋转90°后得到△COD，抛物线y＝ax2＋bx＋c经过A、C、D三点．(1) 写出点A、B、C、D的坐标；(2) 求经过A、C、D三点的抛物线表达式，并求抛物线顶点G的坐标；(3) 在直线BG上是否存在点Q，使得以点A、B、Q为顶点的三角形与△COD相似？若存在，请求出点Q的坐标；若不存在，请说明理由．图1动感体验请打开几何画板文件名“11闸北25”，拖动点Q在直线BG上运动，可以体验到，△ABQ的两条直角边的比为1∶3共有四种情况，点B上、下各有两种．请打开超级画板文件名“11闸北25”，思路点拨1．图形在旋转过程中，对应线段相等，对应角相等，对应线段的夹角等于旋转角．2．用待定系数法求抛物线的解析式，用配方法求顶点坐标．3．第（3）题判断∠ABQ＝90°是解题的前提．4．△ABQ与△COD相似，按照直角边的比分两种情况，每种情况又按照点Q与点B 的位置关系分上下两种情形，点Q共有4个．满分解答（1）A(3，0)，B(0，1)，C(0，3)，D(－1，0)．（2）因为抛物线y＝ax2＋bx＋c经过A(3，0)、C(0，3)、D(－1，0) 三点，所以930,3,0.a b cca b c++=⎧⎪=⎨⎪-+=⎩解得1,2,3.abc=-⎧⎪=⎨⎪=⎩所以抛物线的解析式为y＝－x2＋2x＋3＝－(x－1)2＋4，顶点G的坐标为(1，4)．（3）如图2，直线BG的解析式为y＝3x＋1，直线CD的解析式为y＝3x＋3，因此CD//BG．因为图形在旋转过程中，对应线段的夹角等于旋转角，所以AB⊥CD．因此AB⊥BG，即∠ABQ＝90°．因为点Q在直线BG上，设点Q的坐标为(x，3x＋1)，那么BQ ==．Rt △COD 的两条直角边的比为1∶3，如果Rt △ABQ 与Rt △COD 相似，存在两种情况：①当3BQBA=3=．解得3x =±．所以1(3,10)Q ，2(3,8)Q --．②当13BQBA =13=．解得13x =±．所以31(,2)3Q ，41(,0)3Q -．图2 图3考点伸展第（3）题在解答过程中运用了两个高难度动作：一是用旋转的性质说明AB ⊥BG ；二是BQ ==．我们换个思路解答第（3）题：如图3，作GH ⊥y 轴，QN ⊥y 轴，垂足分别为H 、N ．通过证明△AOB ≌△BHG ，根据全等三角形的对应角相等，可以证明∠ABG ＝90°． 在Rt △BGH 中，sin 1∠=cos 1∠=①当3BQBA =时，BQ =在Rt △BQN 中，sin 13QN BQ =⋅∠=，cos 19BN BQ =⋅∠=．当Q 在B 上方时，1(3,10)Q ；当Q 在B 下方时，2(3,8)Q --．②当13BQ BA =时，BQ =．同理得到31(,2)3Q ，41(,0)3Q -．。

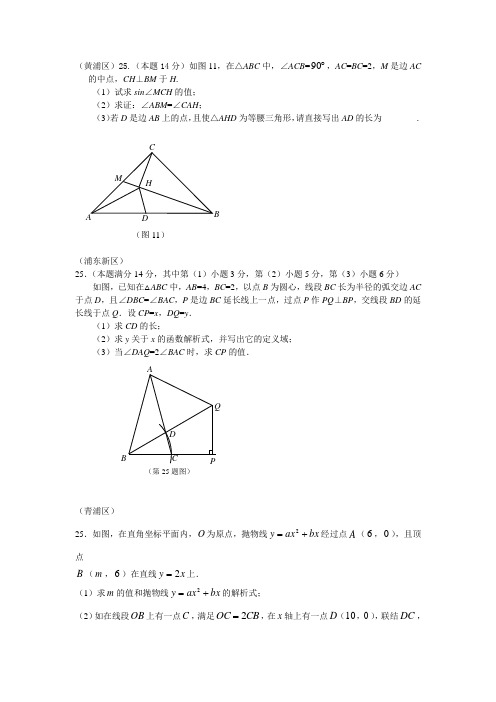
MA B C DH （图11） （黄浦区）25.（本题14分）如图11，在△ABC 中，∠ACB =︒90，AC =BC =2，M 是边AC 的中点，CH ⊥BM 于H .（1）试求sin ∠MCH 的值； （2）求证：∠ABM =∠CAH ； （3）若D 是边AB 上的点，且使△AHD 为等腰三角形，请直接写出AD 的长为________.（浦东新区） 25．（本题满分14分，其中第（1）小题3分，第（2）小题5分，第（3）小题6分）如图，已知在△ABC 中，AB =4，BC =2，以点B 为圆心，线段BC 长为半径的弧交边AC 于点D ，且∠DBC =∠BAC ，P 是边BC 延长线上一点，过点P 作PQ ⊥BP ，交线段BD 的延长线于点Q ．设CP =x ，DQ =y ．（1）求CD 的长；（2）求y 关于x 的函数解析式，并写出它的定义域； （3）当∠DAQ =2∠BAC 时，求CP 的值．（青浦区）25．如图，在直角坐标平面内，O 为原点，抛物线bx ax y +=2经过点A （6，0），且顶点B （m ，6）在直线x y 2=上．（1）求m 的值和抛物线bx axy +=2的解析式；（2）如在线段OB 上有一点C ，满足CB OC 2=，在x 轴上有一点D （10，0），联结DC ，A B C D （第25题图） Q P且直线DC 与y 轴交于点E ． ①求直线DC 的解析式；②如点M 是直线DC 上的一个动点，在x 轴上方的平面内有另一点N ，且以O 、E 、M 、N 为顶点的四边形是菱形，请求出点N 的坐标．（直接写出结果，不需要过程．）（松江区）25．（本题满分14分，第（1）小题4分，第（2）小题4分，第（3）小题6分）如图，在Rt △ABC 中，∠C =90°，AC =4，BC =5，D 是BC 边上一点，CD =3，点P 在边AC 上（点P 与A 、C 不重合），过点P 作PE // BC ，交AD 于点E ．（1）设AP =x ，DE =y ，求y 关于x 的函数解析式，并写出x 的取值范围；（2）当以PE 为半径的⊙E 与DB 为半径的⊙D 外切时，求DPE 的正切值；（3）将△ABD 沿直线AD 翻折，得到△AB /D ，联结B /C ．如果∠ACE =∠BCB /，求AP 的值．（奉贤区）25．（本题满分14分，第（1）、（2）小题每小题满分5分，第（3）小题满分4分）已知，在边长为6的正方形ABCD 的两侧如图作正方形BEFG 、正方形DMNK ，恰好使得N 、A 、F 三点在一直线上，联结MF 交线段AD 于点P ，联结NP ，设正方形BEFG 的ABEC （第25题图）DOxyABEC（第25题备用图）DO xy备用图 D C B AE P D C B A （第25题图）边长为x ，正方形DMNK 的边长为y ，（1）求y 关于x 的函数关系式及自变量x 的取值范围； （2）当△NPF 的面积为32时，求x 的值；（3）以P 为圆心，AP 为半径的圆能否与以G 为圆心，GF 为半径的圆相切，若能请求x 的值，若不能，请说明理由。

2011届上海各区县高考二模作文题汇总一、命题作文1、卢湾区法国文学家罗曼·罗兰说“与其花许多时间与经历去凿许多浅井，不如花同样的时间和精力去凿一口深井”，有人却不以为然。

请以《深井与浅并》为题展开联想，写一篇不少于800字的文章(不要写成诗歌) 2、普陀区总有些人常常牢骚满腹，怨天尤人，觉得世界太小，没有自己的用武之地。

其实，这是把“我”放得太大的缘故。

把“我”放得太大，心中便只有了自己，容不下别人也装不下世界，这样自然既看不见别人的长处，也无法发现世界的精彩。

把自己放小，才会觉得世界的广大和精彩。

请以《小我大世界》为题，写一篇800字左右的文章。

不要写成诗歌。

3、崇明区考试失败，老师鼓励：还有下一次；事业不成功，朋友安慰，还有下一次；比赛没有夺冠，教练激励，还有下一次；遭受挫折，我们也会原谅自己，或者给自己一个借口，还有下一次......你可以把“还有下一次”看作一句口头禅，或一种现象，也可以是一段故事。

请以《还有下—次》为题，写一篇不少于800字的文章，文体不限，不要写成诗歌。

4、黄浦区以“底色与着色”为题目，写一篇不少于800字的文章。

二、材料作文1、虹口区著名作家哈里斯和朋友在报摊上买报纸，那朋友很有礼貌的对报贩说了一声谢谢。

但报贩却冷口冷脸，没发一言。

“这家伙态度很差，是不是？”他们继续前行时，哈里斯问道。

“他每天都这样的。

”朋友说。

“那你为什么还要对他这么客气？”哈里斯问他。

朋友答道：“为什么我要让他决定我的行为。

”选取一个角度，自拟题目，写一篇不少于800字的文章。

2、长宁区根据下面材料，选取一个角度，自拟题目，写一篇不少于800字的文章(诗歌除外)。

公园里有两位老人在下围棋，他们下棋的速度非常缓慢，观棋的人都感到不耐烦了。

老人风趣地说：“你们不知道，围棋要慢慢下才好。

下得慢，可以细细体会棋局的无穷变化和乐趣；下得快则杀气腾腾，不像是朋友对弈。

何况，当第一颗子落下，一局棋就开始走向死路，下得急了，棋盘很快就填满了，棋也就死了。

2011年上海初中物理二模计算压轴题汇编2011年闵行区初中学业模拟考试计算题（第19、20、21、22题分别为4、5、6、9分，共24分）19．北京奥运会跳水池池深为5.4米。

求：距水面5米处水的压强。

20．一个质量为0.2千克的西红柿漂浮在水面上。

求：⑴西红柿受到的浮力。

⑵西红柿排开水的体积。

21.2011年安徽春晚舞台上，广州军区战士杂技团表演的《东方天鹅》将芭蕾舞的高雅、优美与杂技的高难度技巧揉为一体，赢得了观众的阵阵掌声。

如图16所示是“天鹅”轻盈立在王子的肩上的情景，若女演员的质量为45千克，脚尖与男演员肩膀接触面积约为1×10-3 米2，男演员的质量为65千克，双脚与地面接触面积约为3.5×10-2 米2。

求：⑴女演员的重力。

⑵男演员对地面的压强。

⑶《东方天鹅》的成功背后凝结着演员们辛勤的汗水。

由于男演员要承受较大压强，肩上甚至出现了溃烂，但还是忍着伤痛进行排练。

同学们，你有什么办法可以减小压强吗？请说出一种方法。

图1622．在图17(a)所示的电路中，电源电压为6伏且保持不变，电阻R 1的阻值为10欧，滑动变阻器R 2上标有“50 2A ”字样。

闭合电键S ，移动滑片P 到某位置时，电压表V 1的示数如图17（b ）所示，电流表A 的指针指在图17(c)的某个位置。

求： ⑴电阻R 1消耗的电功率。

⑵滑动变阻器R 2接入电路的阻值。

⑶若改变滑片P 的位置，请判断下列情况是否可能出现：①电压表V 1与电流表A 指针偏离零刻度线的角度相同， （可能/不可能）。

②电压表V 与电流表A 指针偏离零刻度线的角度相同， （可能/不可能）。

若有可能，请求出R 2的值。

2011年青浦区初中学业模拟考试计算题（共24分）请将计算过程和答案写入答题纸的相应位置。

19．质量为5千克的水，水的温度升高了20℃。

求：水吸收的热量Q 吸。

[水的比热容为4.2×103焦/（千克·℃）]图17（a ）图17（b ） 图17（c ）20．一艘小船在河中静止时，排开水的体积为2米3。

OMNxyP2011年上海市各区县高三数学二模新颖试题2011年3—4月的上海市各区县第二次模拟试题都以数学主干内容为载体，强调知识内容和思想方法的融会贯通，注重知识间的纵横联系，尤其突出新增内容的考查，突出考查学生的基本数学素养．模拟试题体现以下特点：重视传统基础，关注新增内容，突出能力立意，着力内容创新，解题方法求新，还涌现出了一大批新颖试题，它们内涵丰富，立意新颖，背景鲜活，设问独特，闪耀着命题者智慧的光芒，给人以赏心悦目、回味无穷的感受．它对考查学生的阅读理解能力、知识迁移能力、类比猜想能力、数学探究能力、数学创新意识等有良好的作用．仔细研究这些试题，可以使我们明晰高考数学命题的动向和趋势，提高高三数学复习迎考的针对性和有效性．一、鲜明的立意各区县的模考命题，传承高考的命题思路，一般以能力立意命题，就是首先确定试题在能力方面的考查目的，然后根据能力考查的要求，选择适当的考查内容，设计恰当的设问方式．各区县模考数学把具有创新特色的新颖试题根据以能力立意命题的指导思想，把具有发展能力价值，富有发展潜力、再生性强的能力、方法和知识作为切入点，从测量学生的发展性学力和创造性学力着手突出能力考查．1．考查基础知识的灵活应用 例1、（浦东新区13）设),(11y x M 、),(22y x N 为不同的两点，直线l ：0=++c by ax ，cby ax cby ax ++++=2211δ,以下命题中正确的序号为 ．（1）不论δ为何值，点N 都不在直线l 上；（2）若1=δ，则过N M ,的直线与直线l 平行； （3）若1-=δ，则直线l 经过MN 的中点；（4）若1>δ，则点M 、N 在直线l 的同侧且直线l 与线段MN 的延长线相交. 答案：（1）、（2）、（3）、(4) ．其中（1）依据δ有意义，分母不等于0，点N 都不在直线l 上；（2）、（3）、（4）都可以由等价变形，推出其成立．该题对思维能力、运算能力进行了全面考查，既考查了观察、联想、估算等直觉思维能力，又考查了等价变形等运算能力．学生通过对四道小题的逐一分析，计算推出结论，计算量控制较好．同样的既重视思维、又关注运算的问题，还有许多，略举三例： 1、（浦东新区14（理））函数2()f x ax bx c =++的图像关于任意直线l 对称后的图像依然为某函数图像，则实数,,a b c 应满足的充要条件为 ．（答案20,40a b ac <-=）2、（卢湾区14（理））已知集合2(21)cos ,n A x x n m -π⎧⎫==∈⎨⎬⎩⎭Z ，当m 为4022时，集合A 的元素个数为 ．（答案：1006）3、（闵行区11（理））如图，设P 是单位圆和x 轴正半轴的交点，M N 、是单位圆上的两点，O是坐标原点，3POM π∠=，PON α∠=,[]0απ∈，,()f OM ON α=+，则()αf 的范围为．（答案[]1,2）2．考查基本的数学思想方法众所周知，高考数学考查基础知识、思想方法和能力素质．数学思想方法在探寻解题思路、优化解题方法、加深问题理解、洞察问题本质等方面有广泛的应用．因此，高考对数学思想方法的考查力度很大，应引起足够的重视．数学思想方法应在概念的形成、命题的发现、问题的探究、解题的分析等教学活动中着意渗透、自然揭示、灵活A BO A 1 A 2运用和总结提炼．例2、（闵行区21（理），本题共有2个小题，第1小题满分4分，第2小题满分10分）已知O 是线段AB 外一点，若OA a = ，OB b = ．（1）设点1A 、2A 是线段AB 的三等分点，1OAA △、12OA A △及2OA B △的重心依次为123G G G 、、，试用向量a 、b 表示123OG OG OG ++；（2）如果在线段AB 上有若干个等分点，你能得到什么结论？请证明你的结论．说明：第（2）题将根据结论的一般性程度给予不同的评分.解：（理）（1）如图：点1A 、2A 是线段AB 的三等分点， 111211()()323OG OA OA OA OA ⎡⎤=+=+⎢⎥⎣⎦，同理可得：2121()3OG OA OA =+ ，321()3OG OA OB =+ ，（2分）则1231212()()33OG OG OG a b OA OA ++=+++1212()()()3333a b a b a a b a ⎡⎤=+++-++-⎢⎥⎣⎦()a b =+ （4分） （2）层次1：设1A 是AB 的二等分点，则12a b OA +=；122()3OG OG a b +=+； 设123A A A 、、是AB 的四等分点，则()12332a b OA OA OA +++=；或设121,,,n A A A - 是AB 的n 等分点，则OA OA OA OB k n k +=+-等等（结论2分，证明2分） 层次2：设12,,,n A A A- 是AB 的n等分点，12321()2n n n a b OA OA OA OA OA --++++++=（结论2分，证明4分）层次3：设121,,,n A A A - 是AB 的n 等分点， 则12321()3n n n a b OG OG OG OG OG --++++++=； （结论3分，证明7分）证：12112112()()33n n OG OG OG a b OA OA OA --+++=+++++12121()()()()33n a b a b a a b a a b a n n n -⎡⎤=+++-++-+++-⎢⎥⎣⎦12121121()(1)()()33n n a b n a b a n n n n n n --⎡⎤=++-++++-+++⎢⎥⎣⎦ 12(1)()()()3323n n a b a b a b -=++⋅+=+ （文）（1）如图：点P 、Q 是线段AB 的三等分点OP OA AP =+1()3OA OB OA =+- ，则2133OP a b =+ ，同理1233OQ a b =+， （2分）所以 O P O Q a b +=+ （4分）ABOPQA 1 （2）层次1：设1A 是AB 的二等分点，则12a bOA += ； 设123A A A 、、是AB 的四等分点，则 ()12332a b OA OA OA +++=等等（结论2分,证明2分） 层次2：设121,,,n A A A - 是AB 的n 等分点， 则OA OA OA OB k n k +=+-等；（结论2分，证明4分）层次3：设121,,,n A A A - 是AB 的n 等分点， 则1211()2n n OA OA OA a b --∴+++=+； （结论3分，证明7分） 证：121,,,n A A A - 是线段AB 的)3(≥n n 等分点，先证明这样一个基本结论:k n k OA OA OA OB -+=+*(11,)k n n k ≤≤-∈N 、. 由=k k OA OA AA + ,=n k n k OA OB BA --+ ,因为k AA 和n k BA -是相反向量， 则0k n k AA BA -+= , 所以 k n k OA OA OA OB -+=+ .记12321n n S OA OA OA OA OA --=+++++ ，1221n n S OA OA OA OA --=++++相加得1122112()()()(1)()n n n S OA OA OA OA OA OA n OA OB ---=++++++=-+1211()2n n OA OA OA a b --∴+++=+说明：本题（1），考察最基本的向量加法的平行四边形法则，（2）则在能力要求方面，由结论的一般性程度给予不同的评分，其载体平实，上手不难，对由特殊到一般的分析问题、解决问题的能力作了充分的考核．类似的问题，在各区县模拟试题中屡见不鲜．3．考查以数学思维能力为重点的数学能力数学科考试着重考查的数学能力为：思维能力、运算能力、空间想象能力、实践能力和创新意识，在这些能力中以思维能力为考查重点．数学创新型试题没有固定的模式，难有现成的方法和套路，思维水平要求高，思维容量大，运算量较小，能有效考查学生的思维水平和创造意识，分析和解答这样的试题需要有较高的能力与素质，依靠“死记硬背”、“题海战术”和“强化训练”往往难以奏效．例3、（静安等四区14（理））已知函数()f x 满足：①对任意(0,)x ∈+∞，恒有(2)2()f x f x =成立；②当(1,2]x ∈时，()2f x x =-.若()f a =)2020(f ，则满足条件的最小的正实数a 是 ．(文科学生做) 在平面直角坐标系中，O 是坐标原点，已知点(3,3)A ，点(,)P x y 的坐标满足303200x y x y y ⎧-≤⎪⎪-+≥⎨⎪≥⎪⎩，设z 为OA 在OP 上的投影，则z 的取值范围是 ．解：（理）∵2820202048)102420202(2)10242020(2)22020(2)2020(1010=-=-===f f f ，∴28)(=a f ，又∵要使满足条件的正实数a 最小，此时a a f -=64)(，∴2864=-a ，36=a 即为所求；（文）∵||OA OP z OP ⋅==cos OA AOP ⋅∠ =23cos AOP ∠，31πθ= Oxy A P 62πθ=63πθ=5[,]66AOP ππ∠∈，∴当6AOP π∠=时，m a x 23cos 6z π==3，当56AOP π∠=时，m i n 523cos 6z π==－3，∴z 的取值范围是[3,3]-．本题初看，已知条件简洁明了，但题目的背景比较新颖，给人一种难以下手的感觉．这就需要我们实际操作和巧妙设计，要求学生要具有灵活的思维和应变能力，能根据题目的条件和结论进行观察、分析、探索、决策．类似的问题，如：（闵行区14）已知等差数列{}n a ，对于函数()f x 满足：53222(2)(2)(2)6f a a a -=-+-=，53201020102010(4)(4)(4)6f a a a -=-+-=-，n S 是其前n 项和，则2011S = ．（答案：6033.）4．考查应用意识和探究意识“坚持数学应用，考查应用意识”是上海高考命题者坚持的一个命题方向．各区县模拟试卷突出数学的应用性，关注现实生活中鲜活的素材，反映出高中数学在解决实际问题中的重要作用．研究型、探索型、开放型试题是创新型试题的基本题型，有利于测试学生的能力与素质，有利于考查学生的探究精神．例4、（浦东新区21)某地发生特大地震和海啸，使当地的自来水受到了污染，某部门对水质检测后，决定往水中投放一种药剂来净化水质.已知每投放质量为m 的药剂后，经过x 天该药剂在水中释放的浓度y (毫克/升) 满足()x mf y =，其中()()()⎪⎪⎩⎪⎪⎨⎧>-≤<+=4264024x x x x x f ，当药剂在水中释放的浓度不低于4 (毫克/升)时称为有效净化；当药剂在水中释放的浓度不低于4 (毫克/升) 且不高于10(毫克/升)时称为最佳净化.（1）如果投放的药剂质量为4=m ，试问自来水达到有效净化一共可持续几天?（2）如果投放的药剂质量为m ，为了使在7天之内（从投放药剂算起包括7天）的自来水达到最佳净化，试确定应该投放的药剂质量m 的值.解：（1）因为4=m ，所以()()⎪⎩⎪⎨⎧>-≤<+=4224408x x x x y ,当40≤<x 时48≥+x 显然符合题意，当4>x 时4224≥-x 84≤<⇒x ． 综上80≤<x ，所以自来水达到有效净化一共可持续8天．（2）由()x f m y ⋅==()()⎪⎪⎩⎪⎪⎨⎧>-≤<+4264024x x m x m m x, 知在区间(]4,0上单调递增，即m y m 32≤<；在区间(]7,4上单调递减，即m y m356<≤． 综上m y m356≤≤， 为使104≤≤y 恒成立，只要456≥m 且103≤m 即可，即310=m . 所以，为了使在7天之内的自来水达到最佳净化，投放的药剂质量m 应该为310．很明显，本例是针对今年3月11日日本东北大地震命制的．类似的问题，今年各地普遍关注的一线城市治理交通拥堵问题，是一个社会热点，如普陀区20，见于例题11．二、新颖的情境情境是实现立意的材料和介质．情境与问题相伴，问题是情境的焦点，情境因问题而存在．问题既是考查的内容也是考查的手段．情境的新颖性是高考数学创新型试题的一个共同的特点．情境新颖的试题，对广大学生来讲是全新的、公平的，靠“解题套路”、“猜题押宝”、“密卷”，“宝典”和“题海战术”是难以凑效的．在高考中，学生对付情境新颖的试题，一般需要具有自主学习的能力，学习能力是指学生阅读并理解数学新知识的能力，这里的新知识可以是新的概念、新的定理、新的方法、新的公式、新的规则等．学习能力还包括会搜集、提炼、加工信息，对阅读的内容进行概括和理解，看清问题的本质，然后运用新的知识通过分析、演算，归纳、猜想，类比或论证等方法解决一些新的数学问题．1.定义新概念、给出新性质定义一个新概念，要求学生面对陌生情境，迅速提取有用信息，要善于挖掘概念的内涵与本质，并合理迁移运用已学的知识加以解决.这类问题较好地考查学生的转化能力、知识迁移能力以及学生探究性学习的潜能．例5、（徐汇等区22）定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”．如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比．已知椭圆221:14x C y +=．(1) 若椭圆222:1164x y C +=，判断2C 与1C 是否相似？如果相似，求出2C 与1C 的相似比；如果不相似，请说明理由；(2) 写出与椭圆1C 相似且短半轴长为b 的椭圆b C 的方程；若在椭圆b C 上存在两点M 、N 关于直线1y x =+对称，求实数b 的取值范围？如图：直线y x =与两个“相似椭圆”2222:1x y M a b+=和22222:(0,01)x y M a b a bλλλ+=>><<分别交于点,A B 和点,C D ， 试在椭圆M 和椭圆M λ上分别作出点E 和点F （非椭圆顶点），使CDF ∆和ABE ∆组成以λ为相似比的两个相似三角形，写出具体作法．（不必证明）解：（1）椭圆2C 与1C 相似．因为椭圆2C 的特征三角形是腰长为4，底边长为43的等腰三角形，而椭圆1C 的特征三角形是腰长为2，底边长为23的等腰三角形，因此两个等腰三角形相似，且相似比为2:1.（2）椭圆b C 的方程为：22221(0)4x y b b b+=>.设:MN l y x t =-+，点1122(,),(,)M x y N x y ，MN 中点为00(,)x y ，则222214y x tx yb b =-+⎧⎪⎨+=⎪⎩，所以222584()0x tx t b -+-=，则12004,255x x t t x y +===因为中点在直线1y x =+上，所以有4155t t=+，53t =-，即直线MN l 的方程为：5:3MN l y x =--，由题意可知，直线MN l 与椭圆b C 有两个不同的交点，即方程2225558()4[()]033x x b --+--=有两个不同的实数解，所以224025()454()039b ∆=-⨯⨯⨯->，即53b >．（3）作法1：过原点作直线(1)y kx k =≠，交椭圆M 和椭圆M λ于点E 和点F ，则CD F ∆和ABE ∆即为所求相似三角形，且相似比为λ．作法2：过点A 、点C 分别做x 轴（或y 轴）的垂线，交椭圆M 和椭圆M λ于点E 和点F ，则CDF ∆和ABE ∆即为所求相似三角形，且相似比为λ．本题考查了学生抽象概括能力，同时也考查了学生对新事物接受能力和探究精神.要求解题者通过观察、阅读、归纳、探索进行迁移，即读懂和理解新情境，获取有用的新信息，然后运用这些有用的信息进一步推理、运算．同样的问题如：1、（奉贤区13（理）、14（文））在平面直角坐标系中，设点),(y x P ，定义||||][y x OP +=，其中O 为坐标原点．对于以下结论：①符合1][=OP 的点P 的轨迹围成的图形的面积为2；②设P 为直线0225=-+y x 上任意一点，则][OP 的最小值为1；③设P 为直线),(R b k b kx y ∈+=上的任意一点，则“使][OP 最小的点P 有无数个”的必要不充分条件是“1±=k ”；其中正确的结论有________(填上你认为正确的所有结论的序号)答案：①③．2、（闵行区23（理））定义：对于任意*n ∈N ，满足条件212n n n a a a +++≤且n a M ≤（M 是与n 无关的常数）的无穷数列{}n a 称为T 数列．（1）若29n a n n =-+(*n ∈N )，证明：数列{}n a 是T 数列；（2）设数列{}n b 的通项为3502nn b n ⎛⎫=- ⎪⎝⎭，且数列{}n b 是T 数列，求常数M 的取值范围；（3）设数列1n pc n=-(*n ∈N ，1p >)，问数列{}n c 是否是T 数列？请说明理由．解： (1) 由29n a n n =-+，得：2)1(18)1(2)2(9)2(9222212-=+-+++++-+-=-+++n n n n n n a a a n n n所以数列{}n a 满足212nn n a a a +++≤． 又298124n a n ⎛⎫=--+ ⎪⎝⎭，当n =4或5时，n a 取得最大值20，即n a ≤20．综上，数列{}n a 是T 数列． (2)因为11331350(1)50502222n n nn n b b n n ++⎛⎫⎛⎫⎛⎫-=+--+=- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭，所以当1350022n⎛⎫-≥ ⎪⎝⎭即11n ≤时，10n n b b +->，此时数列{}n b 单调递增．当12n ≥时，10n n b b +-<，此时数列{}n b 单调递减；故数列{}n b 的最大项是12b ，所以，M 的取值范围是 1236002M ⎛⎫≥- ⎪⎝⎭．（3）①当12p <≤时， 当1n =时1231,1,1,23p pc p c c =-=-=-由13252203p c c c +-=-≤得65p ≤，即当615p <≤时符合122++≤+n n n c c c 条件． 若2n ≥，则1≤n p ，此时1n pc n=-，于是 2122(1)(1)2(1)021(1)(2)n n n p p p pc c c n n n n n n ++-+-=-+---=<++++， 又对于*n ∈N 有11n p c n=-<，所以当615p <≤时数列{}n c 是T 数列；②当23p <≤时， 取1n =则：1231,1,1,23p pc p c c =-=-=-由0322231>-=-+pc c c ，所以23p <≤时数列{}n c 不是T 数列．③当3p >时， 取1n =则1231,1,1,23p pc p c c =-=-=-由1325206pc c c +-=>，所以3p >时数列{}n c 不是T 数列． 综上：当615p <≤时数列{}n c 是T 数列；当65p >时数列{}n c 不是T 数列．2.规定新运算，设定新规则例6、（静安等四区18）已知有穷数列A ：n a a a ,,,21⋅⋅⋅（N n n ∈≥,2）.定义如下操作过程T ：从A 中任取两项j i a a ,,将ji j i a a a a ++1的值添在A 的最后，然后删除j i a a ,,这样得到一系列1-n 项的新数列A 1 (约定:一个数也视作数列)；对A 1的所有可能结果重复操作过程T 又得到一系列2-n 项的新数列A 2，如此经过k 次操作后得到的新数列记作A k . 设A ：31,21,43,75-,则A 3的可能结果是 （ ） （A ）0； （B ）34； （C ）13； （D ）12.答案：B同样的问题，如： 1、（奉贤区17（理））已知函数f(x) =2x+1，x ∈R.规定：给定一个实数x 0，赋值x 1= f(x 0)，若x 1≤255，则继续赋值x 2= f(x 1) …，以此类推，若x n-1≤255，则x n = f(x n-1)，否则停止赋值，如果得到x n 后停止，则称赋值了n 次（n ∈N *）.已知赋值k 次后该过程停止，则x 0的取值范围是 （ ）（A ）（2k-9 ,2 k-8] （B ）（2 k-8 -1, 2k-9-1] （C ）（28-k -1, 29-k -1] （D ）（27-k -1, 28-k -1]答案：C ．2、（浦东新区18）．对于给定的自然数n ，如果数列12,,...,()m a a a m n >满足：1,2,3,...,n 的任意一个排列都可以在原数列中删去若干项后按数列原来顺序排列而得到，则称12,,...,()m a a a m n >是“n 的覆盖数列”.如1,2,1 是“2的覆盖数列”；1,2,2则不是“2的覆盖数列”，因为删去任何数都无法得到排列2,1，则以下四组数列中是 “3的覆盖数列”为 （ ）（A ）1,2,3,3,1,2,3 （B ）1,2,3,2,1,3,1 （C ）1,2,3,1,2,1,3 （D ）1,2,3,2,2,1,3 答案：C ．以上几题考查了阅读和理解能力，同时考查了学生对新知识、新事物接受能力和加以简单运用的能力，考查了探究精神．要求解题者通过观察、阅读、归纳、探索进行迁移，即读懂和理解新情境，获取有用的新信息，然后运用这些有用的信息进一步推理，综合运用数学知识解决问题的能力和探索能力（多想少算甚至不算）．因此，“开放探索,考查探究精神，开拓展现创新意识的空间”在上海的高考试题中常有体现，用知识归类、套路总结，强化训练等传统教学方法难以解决高考中不断出现的新颖试题．三、深刻的背景 1．高等数学背景高等数学的一些基本思想，基本概念、基本方法为设计创新型试题提供了深刻的背景，这是因为高等数学的基本思想和方法是考查学生进一步学习潜能的良好素材．数学创新型试题一般都有比较深刻的高等数学背景，这类题目形式新颖，在课本例习题、复习资料和模拟试题中难以找到．解答这类题目没有现成方法可借鉴，会使一些学生感到难以人手，从而使该类题目有很好的区分度，这类试题有利于检测学生进入高等学校进一步学习的潜能，因此，命题教师都十分青睐含有高等数学背景的试题．例7、（黄浦区14（文））已知点221122()()A x x B x x ，、，是函数2y x =的图像上任意不同两点，依据图像可知，线段AB 总是位于A 、B 两点之间函数图像的上方，因此有结论2221212()22x x x x++>成立．运用类比思想方法可知，若点1122()()A x x B x x ，lg 、，lg 是函数lg ()y x x R +=∈的图像上的不同两点，则类似地有 成立．(理科)已知点1212(2)(2)x x A x B x ，、，是函数2xy =的图像上任意不同两点，依据图像可知，线段AB 总是位于A 、B 两点之间函数图像的上方，因此有结论121222222x x x x ++>成立．运用类比思想方法可知，若点1122(sin )(sin )A x x B x x ，、，是函数sin ((0))y x x =∈π，的图像上的不同两点，则类似地有 成立．答案： (文科)1212lg lg lg 22x x x x++<， (理科)1212sin sin sin 22x x x x ++<．本题以高等代数中函数图象的凹凸性为背景，将二次函数与对数函数、指数函数与正弦函数的相关知识有机地融合在一起，让人印象深刻．破解以高等数学为背景的试题，关键在阅读理解，抓住问题本质，将已掌握的知识迁移到新情景中去，将问题解决.需要指出的是，不宜提倡将高等数学的一些定理和背景知识作为教学的补充内容，因为这样做既会加重学生学习的负担，也与高考考查创新型试题的初衷相悖．2．课程改革背景各区县模拟试题重视新增内容的考查，体现高考新要求，充分重视将新增内容的考查，尤其注重知识间的糅合，虽然大多以小题出现，但却充分体现了上海高考的新要求．一些创新型试题的基本走向是坚持课程改革的方向，充分体现《课程标准》的精神，出现了不少以课程改革为背景的新题好题，体现了新课程理念．因此，教师应认真学习、研究《课程标准》，积极参与数学课程改革．例8、（1）（奉贤区18）行列式12365472131x x⎪⎭⎫ ⎝⎛中，第3行第2列的元素的代数余子式记作()x f ，()x f +1的零点属于区间 （ ）B A O O a S (a )123321S (a )a DC OO a 321S (a )321S (a )ayxO 332211y=a（A ）（1,32）； （B ）（32,21）； （C ）（21,31）； （D ）（31,0）；（2）（长宁区12（理））矩阵⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛nn n n n n n a a an a a a a a a a a a 32333322232211312321中每一行都构成公比为2的等比数列，第i 列各元素之和为i S ，则_________2lim2=⋅∞→nn n n S ． （3）（长宁区14（文））对于任意的实数b a ,，记{}()().,m a x ⎩⎨⎧<≥=b a b b a a b a 若()()(){}(),,max R x x g x f x F ∈=其中函数()()R x x f y ∈=是奇函数，且当0>x 时，()();212--=x x f 函数()()R x x g y ∈=是正比例函数，其图象与0>x 时函数()x f y =的图象如图所示，则下列关于函数()x F y =的说法中，y=F （x ）为奇函数；②y=F （x ）在（—3，0） 上为增函数 ；③y=F （x ）的最小值为—2，最大值为2．其中不正确的是.___________（填写你认为不正确的所有结论序号）(4) （奉贤区14（理））在空间直角坐标系O xyz -中，满足条件[][][]2221x y z ++≤的点(,,)x y z 构成的空间区域2Ω的体积为2V （[][][],,x y z 分别表示不大于,,x y z 的最大整数），则2V = _（5）（长宁区17（理）18（文））（文）图中的阴影部分由底为1，高为1的等腰三角形及高为2和3的两矩形所构成．设函数()(0)S S a a =≥是图中阴影部分介于平行线0y =及y a =之间的那一部分的面积，则函数()S a 的图象大致为（ ）答案：（1）B ； （2）41； （3）①②③； （4）8； （5）C . 3．联系实际生活背景应用题是对学生综合实力的考查，是考查能力与素质的良好题型，各区县应用题的编拟更加重视语言简洁、准确，背景清新、近人，模型具体、简明，方法熟悉、简便，所涉及的都是数学基本内容，思想和方法，摒弃繁琐的数学运算，突出了对数学思想，方法和实践能力的考查. 例9、（奉贤区11（文））为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图，如下图，由于不慎将部分数据丢失，但知道前40.30.1 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0 5.1 5.2 视力 组距频率 组的频数成等比数列，后6组的频数成等差数列，设最大频率为a ，视力在4.6到5.0之间的学生数为b ，则b 的值为答案：78．4．以课本经典内容研究方法为背景 例10、（浦东新区22(文)， 本题满分16分，第（1）小题4分，第（2）小题4分，第（3）小题8分)已知点),(11y x A 在圆22(2)4x y -+=上运动，点),4(0y B 在直线4x =上运动，异于点B 的动点(,)M x y 满足OB OM //，OM AB =.动点M 的轨迹C 的方程为0),(=y x F .（1）试用点M 的坐标y x ,表示110,,y x y ； （2）求动点M 的轨迹方程0),(=y x F ；（3）以下给出曲线C 的五个方面的性质，请你选择其中的三个方面进行研究，并说明理由（若你研究的方面多于三个，我们将只对试卷解答中的前三项予以评分）.① 对称性；（2分） ② 顶点坐标；（2分）（定义：曲线与其对称轴的交点称为该曲线的顶点） ③ 图形范围；（2分） ④ 渐近线；（3分）⑤ 对方程0),(=y x F ，当0≥y 时，函数)(x f y =的单调性.（3分） 解：（1）),(y x OM =，),4(0y OB =，),4(101y y x AB --=因为OB OM //，所以当0=x 时，0y R ∈；当0≠x 时，xyy 40=. 因为O M A B = ，所以⎩⎨⎧-=-=1014y y y x x ，则当0=x 时，11040x y y =⎧⎨==⎩；当0≠x 时，⎪⎩⎪⎨⎧-=-=y x yy x x 4411. 综上可知，当0=x 时，11040x y y =⎧⎨==⎩；当0≠x 时，x y y 40=，⎪⎩⎪⎨⎧-=-=y x yy xx 4411.……4分 yx-3-2-1123455-4-3-2-14321B AO（2）由点A 在圆上，则4)2(2121=+-y x .当0≠x 时，4)4()24(22=-+--y xy x ，整理得，32240x xy y +-=或4x =（舍） 当0=x 时，点)0,0(满足方程32240x xy y +-=.故，所求动点M 的轨迹C 的方程为32240x xy y +-=. …………8分（3）① 关于x 轴对称；将方程中的(,)x y 换成(,)x y -，方程的形式不变，则曲线C 关于x 轴对称. ② 曲线C 的顶点为（0，0）；在方程32240x xy y +-=中，令0y =，得0x =.则曲线C 的顶点坐标为（0，0）.③ 图像范围：04,x y R ≤<∈； 3204x y x=≥-，得04,x y R ≤<∈. ④ 直线4x =是曲线C 的渐近线；04x ≤<，324x y x=-，当4→x 时，y →∞. 则直线4x =是曲线C 的渐近线. ⑤ 当0≥y 时函数)(x f y =在[0,4)上单调递增；32(04)4x y x x=≤<-. 设1204x x ≤<<，则 333322121221121212(4)(4)44(4)(4)x x x x x x y y x x x x ----=-=----221212211212()[(4)(4)4]0(4)(4)x x x x x x x x x x --+-+=<--. 则2212y y <，即12y y <，所以当0≥y 时函数)(x f y =在[0,4)上单调递增. 本题主要考查了解方程组、求动点M 的轨迹方程、研究曲线C 的五个方面的性质、阅读理解能力和基本运算能力，其背景可以追溯到解析几何中经典的圆锥曲线的研究方法，耐人寻味．四、开放的设计数学开放型问题有条件开放型问题和结论开放型问题.1．条件开放型问题条件开放型问题，即没有确定的已经条件，其特征是缺少确定的条件，即求解问题所需的条件过多或不足，学生无法直接根据给出的条件来解决问题.设计条件开放型问题的目的是加强对学生信息整合力的考查.信息整合国是个体立足于社会的最基本能力之一，现实世界纷繁复杂，信息浩如烟海且更新速度很快，而获取信息的渠道多种多样，如果没有很强的整合力，个体就会被繁杂的信息所掩埋.例11、（普陀区20）为了缓解城市道路拥堵的局面，某市拟提高中心城区内占道停车场的收费标准，并实行累进加价收费．已公布的征求意见稿是这么叙述此收费标准的：“（中心城区占道停车场）收费标准为每小时10元，并实行累进加价制度，占道停放1小时后，每小时按加价50%收费．”方案公布后，这则“累进加价”的算法却在媒体上引发了争议（可查询2010年12月14日的相关国内新闻）．请你用所学的数学知识说明争议的原因，并请按照一辆普通小汽车一天内连续停车14小时测算：根据不同的解释，收费各应为多少元？解：争议的原因是收费标准中对于“每小时按加价50%收费”的含义出现了歧义．以下给出三种不同的理解：解释一：第一小时为10元，以后每小时都为15元.14小时总收费为：101513205+⨯=元；解释二：第一小时为10元，以后每小时都比前一小时增加5元．可以理解为等差数列求和，则14小时总收费为141414101355952S =⨯+⋅⋅=元. 解释三：第一小时为10元，以后每小时都增加50%.可以理解为等比数列求和， 则14个小时的收费为()1414101 1.55818.591 1.5S -==-元．【说明】以上三种解释中能任意给出两种即可得满分．本题考查学生分析问题和解决问题的能力．考查学生的创新意识，对学生的阅读理解能力及中学数学的领悟程度能有效检测．2. 结论开放型问题结论开放型问题，即没有明确的结果，其特征是结果的非唯一性．数学问题复杂多变，往往得到的不是唯一答案．高考命题者已有意识的设计结论开放型问题，引导学生摆脱数学是“答案唯一”的僵化思维模式，引导学生联系自己的知识经验考虑可能出现的多种情况，根据不同的情况，求得不同的答案．这两类问题又可分为归纳猜想型和探索发现型两类．例12、（浦东新区23，本题满分18分，本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分）对于定义域为D 的函数()y f x =，若有常数M ，使得对任意的1x D ∈，存在唯一的2x D ∈满足等式12()()2f x f x M +=，则称M 为函数y =f (x )的“均值”．（1）判断1是否为函数()21(1f x x =+-≤x ≤1)的“均值”，请说明理由；（2）若函数2()2(12,f x ax x x =-<<a 为常数）存在“均值”，求实数a 的取值范围；（3）若函数()f x 是单调函数，且其值域为区间I ．试探究函数()f x 的“均值”情况（是否存在、个数、大小等）与区间I 之间的关系，写出你的结论（不必证明）．说明：对于（3），将根据结论的完整性与一般性程度给予不同的评分．解：（1）对任意的1[1,1]x ∈-，有1[1,1]x -∈-，当且仅当21x x =-时，有1212()()112f x f x x x +=++=， 故存在唯一2[1,1]x ∈-，满足12()()12f x f x +=， ……………………2分 所以1是函数()21(11)f x x x =+-≤≤的“均值”． ……………………4分 (另法：对任意的1[1,1]x ∈-，有1[1,1]x -∈-，令21x x =-，则2[1,1]x ∈-，且1212()()112f x f x x x +=++=， 若2[1,1]x '∈-，且12()()12f x f x '+=，则有22()()f x f x '=，可得22x x '=， 故存在唯一2[1,1]x ∈-，满足12()()12f x f x +=， ……………………2分 所以1是函数()21(11)f x x x =+-≤≤的“均值”． ……………………4分）（2）当0a =时，()2(12)f x x x =-<<存在“均值”，且“均值”为3-；…………5分 当0a ≠时，由2()2(12)f x ax x x =-<<存在均值，可知对任意的1x ，都有唯一的2x 与之对应，从而有2()2(12)f x ax x x =-<<单调， 故有11a ≤或12a ≥，解得1a ≥或0a <或102a <≤， ……………………9分 综上，a 的取值范围是12a ≤或1a ≥． ……………………10分（另法：分0,a =1111,12,2a a a≤<<≥四种情形进行讨论） （3）①当I (,)a b =或[,]a b 时，函数()f x 存在唯一的“均值”．这时函数()f x 的“均值”为2a b +； …………………12分 ②当I 为(,)-∞+∞时，函数()f x 存在无数多个“均值”．这时任意实数均为函数()f x 的“均值”； ……………………14分③当I (,)a =+∞或(,)a -∞或[,)a +∞或(,]a -∞或[,)a b 或(,]a b 时，函数()f x 不存在“均值”． ……………………16分[评分说明：若三种情况讨论完整且正确，但未用等价形式进行叙述，至多得6分；若三种情况讨论不完整，且未用等价形式叙述，至多得5分]①当且仅当I 形如(,)a b 、[,]a b 其中之一时，函数()f x 存在唯一的“均值”．这时函数()f x 的“均值”为2a b +； ……………………13分 ②当且仅当I 为(,)-∞+∞时，函数()f x 存在无数多个“均值”．这时任意实数均为函数()f x 的“均值”； ……………………16分③当且仅当I 形如(,)a +∞、(,)a -∞、[,)a +∞、(,]a -∞、[,)a b 、(,]a b 其中之一时，函数()f x 不存在“均值”． ……………………18分（另法：①当且仅当I 为开区间或闭区间时，函数()f x 存在唯一的“均值”．这时函数()f x 的均值为区间I 两端点的算术平均数； ……………………13分②当且仅当I 为(,)-∞+∞时，函数()f x 存在无数多个“均值”．这时任意实数均为函数()f x 的“均值”； ……………………16分③当且仅当I 为除去开区间、闭区间与(,)-∞+∞之外的其它区间时，函数()f x 不存在“均值”． ……………………18分）[评分说明：在情形①与②中，等价关系叙述正确但未正确求出函数“均值”，各扣1分]试题科学、试卷平稳是高考命题的首要目标，展露新意、闪现亮点是高考命题的第二追求，由此可以预测：新颖题、亮点题必将还会在上海高考中出现．一般说来，新颖题、亮点题除以上特色外，还具有以下一些特征：第一，多属新信息迁移题，在教学中既要适当拓宽学生的数学知识视野，也要加强自主获取知识能力的训练与培养；第二，常规考点经过适当包装，要求学生不为表象所惑，善于抓住问题本质；第三，常规考点的组合联袂，在解答时只需抓住基本知识，加以合适组合，问题便可迎刃而解；第四，属于能力立意的，知识虽是新的，能力却不超纲，在教学中除了强调知识的获取，也要注意能力的培养．应对创新型试题的最好办法是让学生进行研究性学习，要让学生在新课学习和复习课中经历数学探究的过程，这个过程应该包括学生自己主动地观察数学现象、分析数学材料，提出数学问题、探究数学规律，猜想数学命题、寻找解题思路等．。

2011年上海中考数学二模试题及答案一、 选择题： 1．3的倒数是（ ）A .-3B .3C .13 D .13- 2．计算232(3)x x ⋅-的结果是（ ）A .56x - B .56x C .62x - D .62x3．⊙O 的半径为4，圆心O 到直线l 的距离为3，则直线l 与⊙O 的位置关系是（ ）A .相交B .相切C .相离D . 无法确定 4．使分式24xx -有意义的x 的取值范围是（ ） A . 2x = B .2x ≠ C .2x =- D .2x ≠-5．不等式组2030x x ->⎧⎨-<⎩的解集是（ ）A .2x >B .3x <C .23x <<D .无解 6．如图，⊙O 的直径CD 过弦EF 的中点G ，∠EOD =40°，则∠DCF 等于（ ）A .80°B . 50°C . 40°D . 20° 7．如图，是有几个相同的小正方体搭成的几何体的三种视图， 则搭成这个几何体的小正方体的个数是.（ ） A .3 B .4 C . 5 D . 68．观察市统计局公布的“十五”时期重庆市农村居民人均 收入每年比上一年增长率的统计图，下列说法正确的是（ ） A .2003年农村居民人均收入低于2002年B .农村居民人均收入比上年增长率低于9%的有2年C .农村居民人均收入最多时2004年OCFG DE俯视图左视图主视图时间：（年）20052004200320022001D .农村居民人均收入每年比上一年的增 长率有大有小，但农村居民人均收入在持续增加9．免交农业税，大大提高了农民的生产积极性，镇政府引导农民对生产的耨中土特产进行春节期间，这三种不同的包装的土特产都销售了1200千克，那么本次销售中，这三种包装的土特产获得利润最大是（ ）A .甲B . 乙C .丙D . 不能确定10.现有A 、B 两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）。

作图题（共6分）17. 一块重为20牛的正方体木块浸没于水中，放手后木块上浮，请在图14中画出木块在上浮过程中所受重力G 的图示。

18．如图15所示，请标出通电螺线管和小磁针的N 、S 极。

2011年青浦区初中学业模拟考试作图题（共6分）请将图直接画在答题纸的相应位置，作图必须使用2B 铅笔。

17．重为16牛的物体静止在水平地面上，用力的图示法在图8中画出物体所受的重力G 。

18．在图9中，画出物体AB 在平面镜MN 中所成的像A ＇B ＇。

图14图15MAB图9图8作图题（共6分）请将图直接画在答题纸的相应位置，作图题必须使用2B 铅笔。

17．重为10牛的物块静止在水平面上，请用力的图示法在图7中画出它所受到的重力G 。

18．在图8中，根据给出的反射光线OB 画出入射光线AO ，并标出入射角及其度数。

2011年崇明、杨浦区初中学业模拟考试物理部分作图题（共10分）19．在图10中，根据给出的反射光线OB 画出入射光AO ，并标出入射角及其度数。

20．在图11中画出物体AB 在平面镜中的像A ’ B’21．在图12中，用5牛的水平力将一个重为3牛的A 木块压在墙壁上，用力的图示法画出A 木块受到的重力。

图7图8 B图10图1122．在图13中，标出磁感线方向，小磁针的N ，S 极和电源的正负极。

23．请在图14中的O 内正确填入电压表、电流表的符号，使两个小灯都能发光。

2011年静安区初中学业模拟考试理化试卷作图题（共6分）请将图直接画在答题纸的相应位置，作图必须使用2B 铅笔。

17．图10中，重为30牛的物体A 静止在水平面上。

请按给定的标度，在图中用力的图示法画出A 所受的重力G 。

18．请在图11中，标出通电螺线管和小磁针的N 、S 极及磁感线的方向。

10牛2011年宝山、嘉定区初中学业模拟考试作图题（共6分）请将图直接画在答题纸的相应位置，作图题必须使用2B 铅笔。

17．重为6牛的物体A 静止在水平地面上，用力的图示法在图8中画出物体A 所受的重力G 。

2011年上海市普陀区中考数学二模试卷一、选择题（共6小题，每小题4分，满分24分）1．（2010•顺义区）下列计算正确的是（）A．x3+x2=x5B．x4÷x=x4C．x3•x2=x5D．（x3）2=x52．一元二次方程2x2﹣bx=1的常数项为（）A．﹣1 B．1 C．0 D．±1．被遮盖的两个数据依次是（）A．3℃，2 B．3℃，4 C．4℃，2 D．4℃，44．（2002•南通）已知两圆的半径分别是3cm和4cm，圆心距为2cm，那么两圆的位置关系是（）A．内含B．相交C．内切D．外离5．（2011•内江）如图，把一块直角三角板的直角顶点放在直尺的一边上，如果∠1=32°，那么∠2的度数是（）A．32°B．58°C．68°D．60°6．如图，D，E分别△ABC的边AB，AC的中点，给出下列结论：①BC=2DE；②△ADE∽△ABC；③AD：AE=AB：AC；④S△ADE：S四边形BCED=1：3．其中正确的结论有（）A．4个B．3个C．2个D．1个二、填空题（共12小题，每小题4分，满分48分）7．（2005•三明）计算：=_________．8．（2010•密云县）分解因式：a3﹣ab2=_________．9．方程的根是_________．10．成功、精彩、难忘的中国2010年上海世博会，众多境外参观者纷至沓来．国家统计局上海调查总队调查显示：上海世博会境外参观者近4250000人次．4250000人次可用科学记数法表示为_________人次．11．（2009•上海）已知函数f（x）=，那么f（3）=_________．12．在平面直角坐标系中，反比例函数（k＜0）图象的两支分别在第_________象限．13．一件卡通玩具进价a元，如果加价60%出售，那么这件卡通玩具可盈利_________元．14．在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、正方形和圆．在看不见图形的情况下随机摸出1张，这张卡片上的图形是中心对称图形的概率是_________．15．如图，已知AB=AD，在不添加任何辅助线的前提下，要使△ABC≌△ADC还需添加一个条件，这个条件可以是DC=BC．（只需写出一个）16．如图，在△ABC中，边BC、AB上的中线AD、CE相交于点G，设向量，，如果用向量，表示向量，那么=_________．17．等腰梯形ABCD中，AD∥BC，∠B=45°，AD=4，BC=10，那么梯形ABCD的周长是_________．18．已知：如图，直角△ABC中，∠ACB=90°，AC=BC=1，的圆心为A，如果图中两个阴影部分的面积相等，那么AD的长是_________（结果不取近似值）．三、解答题（共7小题，满分78分）19．解不等式组把它的解集在数轴上表示出来，并写出它的自然数解．20．解方程：．21．如图，矩形纸片ABCD的边长AB=4，AD=2．翻折矩形纸片，使点A与点C重合，折痕分别交AB、CD于点E、F，（1）在图中，用尺规作折痕EF所在的直线（保留作图痕迹，不写作法），并求线段EF的长；（2）求∠EFC的正弦值．22．国家教育部规定“中小学生每天在校体育活动时间不低于1小时”．2011年，为了了解我市毕业班学生体育活动情况，随机对我市240名毕业班学生进行调查，调查内容为：第一问你平均每天在校参加体育活动的时间是多少？A．超过1小时B．0.5～1小时C．低于0.5小时如果第一问没有选A，请继续回答第二问第二问在校参加体育活动的时间没有超过1小时的原因是什么？A．不喜欢B．没时间C．其他以下是根据所得的数据制成的统计图的一部分．根据以上信息，解答下列问题：（1）每天在校锻炼时间超过1小时的人数是_________；（2）请将条形图补充完整；（3）2011年我市初中毕业生约为8.4万人，请你估计今年全市初中毕业生中每天锻炼时间低于0.5小时的学生约有_________万人．23．如图，等腰三角形ABC中，AB=AC，AH垂直BC，点E是AH上一点，延长AH至点F，使FH=EH，（1）求证：四边形EBFC是菱形；（2）如果∠BAC=∠ECF，求证：AC⊥CF．24．如图，在平面直角坐标系xOy中，半径为的⊙C与x轴交于A（﹣1，0）、B（3，0）两点，且点C在x轴的上方．（1）求圆心C的坐标；（2）已知一个二次函数的图象经过点A、B、C，求这二次函数的解析式；（3）设点P在y轴上，点M在（2）的二次函数图象上，如果以点P、M、A、B为顶点的四边形是平行四边形，请你直接写出点M的坐标．25．直角三角板ABC中，∠A=30°，BC=1．将其绕直角顶点C逆时针旋转一个角α（0°＜α＜120°且α≠90°），得到Rt△A′B′C，（1）如图，当A′B′边经过点B时，求旋转角α的度数；（2）在三角板旋转的过程中，边A′C与AB所在直线交于点D，过点D作DE∥A′B′交CB′边于点E，连接BE．①当0°＜α＜90°时，设AD=x，BE=y，求y与x之间的函数解析式及定义域；②当时，求AD的长．2011年上海市普陀区中考数学二模试卷参考答案与试题解析一、选择题（共6小题，每小题4分，满分24分）1．（2010•顺义区）下列计算正确的是（）A．x3+x2=x5B．x4÷x=x4C．x3•x2=x5D．（x3）2=x5考点：同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方。