下载文档原格式
LLC原理讲解与传统PWM（脉宽调节）变换器不同，LLC是一种通过控制开关频率（频率调节）来实现输出电压恒定的谐振电路。
它的优点是：实现原边两个主MOS开关的零电压开通(ZVS)和副边整流二极管的零电流关断(ZCS)，通过软开关技术，可以降低电源的开关损耗，提高功率变换器的效率和功率密度。
学习并理解LLC，我们必须首先弄清楚以下两个基本问题：1.什么是软开关；2.LLC电路是如何实现软开关的。
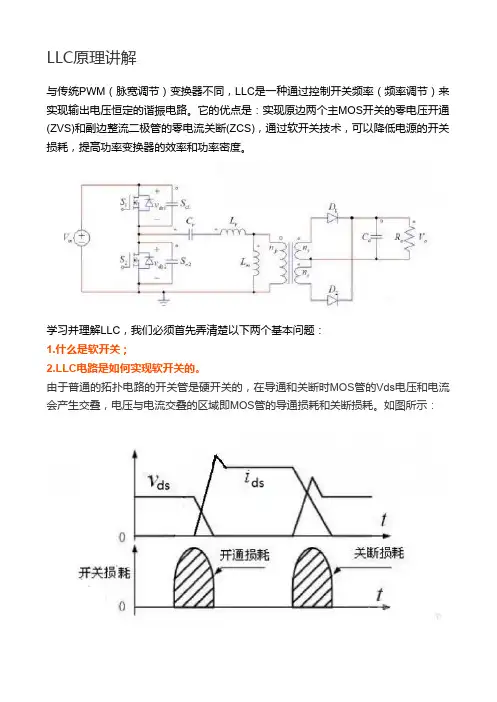
由于普通的拓扑电路的开关管是硬开关的，在导通和关断时MOS管的Vds电压和电流会产生交叠，电压与电流交叠的区域即MOS管的导通损耗和关断损耗。
如图所示：为了降低开关管的开关损耗，提高电源的效率，有零电压开关(ZVS) 和零电流开关（ZCS)两种软开关办法。
1零电压开关 (ZVS)开关管的电压在导通前降到零，在关断时保持为零。
2零电流开关（ZCS)使开关管的电流在导通时保持在零，在关断前使电流降到零。
由于开关损耗与流过开关管的电流和开关管上的电压的成绩（V*I）有关，当采用零电压ZVS导通时，开关管上的电压几乎为零，所以导通损耗非常低。
►Vin为直流母线电压，S1，S2为主开关MOS管（其中Sc1和Sc2分别为MOS管S1和S2的结电容，并联在Vds上的二极管分别为MOS管S1和S2的体二极管），一起受控产生方波电压；►谐振电容Cr 、谐振电杆Lr 、 励磁电杆Lm一起构成谐振网络；►np，ns为理想变压器原副边线圈；►二极管D1, 二极管D2，输出电容Co一起构成输出整流滤波网络。
那么LLC电路是怎么实现软开关的呢？要实现零电压开关，开关管的电流必须滞后于电压，使谐振槽路工作在感性状态。
LLC 开关管在导通前，电流先从开关MOS管的体二极管（S到D）内流过，开关MOS 管DS之间电压被箝位在接近0V（二极管压降），此时让开关MOS管导通，可以实现零电压导通；在关断前，由于DS 间的电容电压为0V而且不能突变，因此也近似于零电压关断（实际也为硬关断）。
LLC集成变压器推导计算LLC(L-L-C)集成变压器是一种绝缘变压器，由三个独立的电感器组成，分别是L1、L2和L3、它还包括两个电容器C1和C2以及一个输出变压器T。
LLC集成变压器在一些功率因数纠正电路和逆变器应用中非常常见。
在这个推导计算中，我们将使用一些基本电路理论来分析LLC集成变压器的性能。
首先，我们将定义一些符号：- Vin：输入电压- Vout：输出电压-Vc1,Vc2：分别是C1和C2的电压-IL1,IL2,IL3：分别是L1、L2和L3的电流-Io：输出电流-N1,N2：输入和输出变压器的匝数比现在，让我们开始推导计算LLC集成变压器。
1. 首先，我们可以利用电路分压原理来计算输入电压Vin与C1的电压Vc1之间的关系。
根据电路分压公式，我们可以得到以下方程：Vin = Vc1 + Vc22.接下来，我们可以利用电感器方程来计算各个电感器上的电流。
根据电感器方程，我们可以得到以下方程：Vc1 = L1 * diL1/dtVc2 = L2 * diL2/dtVout = L3 * diL3/dt3. 如果我们假设输出电流Io保持恒定，我们可以使用输出变压器的方程来计算输出电压Vout与输出电流Io之间的关系。
根据输出变压器方程，我们可以得到以下方程：Vout = N2 * Io * diL3/dt4. 最后，我们可以应用Laplace变换来得到传输函数，通过将所有未知量表示为频率域的复数变量。
通过代入以上方程，我们可以得到LLC集成变压器的传输函数：H(s) = Vout(s) / Vin(s) = (N2 * Io) / (s * (s * (L1 * L2 +L1 * L3 + L2 * L3) + (L1 + L2) * (C1 * (L1 * L2 + L1 * L3 + L2 * L3) + N2^2 * Io^2)))这个传输函数可以用于根据输入电压Vin和输出电流Io来计算LLC集成变压器的输出电压Vout。
llc 电路工作原理
LLC电路是一种用于变频调节的开关电源电路，它的工作基
于变压器的原理。
这种电路的核心是一个能够产生高频脉冲的开关器件，通常是MOSFET或IGBT。
通过控制开关管的通断状态，可以实现对输入电源的有效调节。
在LLC电路中，变压器的一侧接收输入电源信号，另一侧用
于输出可调节的直流电压。
开关管的开关状态由一个控制电路控制，该控制电路根据输出电压的变化来自动调节开关管的通断时间。
当输出电压低于设定值时，开关管开启，从而使得输入电源通过变压器传递能量到输出端。
当输出电压达到设定值时，开关管关闭，断开输入电源与输出端的连接。
LLC电路的工作原理可以通过以下几个步骤来解释：
1. 开始时，控制电路检测到输出电压低于设定值，发送信号给开关管。
2. 开关管导通，连接输入电源与变压器的输入端。
电流通过变压器的初级线圈，产生磁场。
3. 由于变压器的工作原理，磁场会在次级线圈中感应出电压，该电压经过整流和滤波后成为输出电压。
4. 控制电路检测输出电压达到设定值，发送信号给开关管。
5. 开关管截断，断开输入电源与变压器的连接。
由于电感的特性，变压器的磁场会崩溃，并使得次级线圈中的电流继续流动。
6. 根据电感的自感作用，电流通过磁场的能量得以传输到输出端。
7. 控制电路继续监测输出电压，如有需要，会再次控制开关管导通，周期性地实现能量传输。
通过这种方式，LLC电路能够实现高效、稳定的电能转换。
同时，由于采用了变频调节，可以通过调整开关管的通断时间来适应不同的负载要求，达到节能的目的。
LLC半桥谐振电路的基本原理LLC谐振变换的直流特性为为零电压工作区和零电流工作区。
这种变换有两个谐振频率。
一个是Lr和Cr的谐振点，另个一个谐振点由LM,CR以及负载条件决定。
负载加重，谐振频率将会下降。
这两个谐振点的计算公式如下：考虑到尽可能提搞效率，设计电路时需把工作频率设定在FR1附件。
其中，FR1为CR,LR串联谐振腔的谐振频率。
当输入电压下降时，可以通过降低工作频率来获得较大的增益。
通过选择合适的谐振参数，可以让LLC谐振变换无论是负载变化或是输入电压变化都能工作在零电压的工作区内。
总体来说LLC半桥谐振电路的开关动作和半桥电路无异，但是由于谐振腔的加入，LLC半桥谐振电路中的上下MOS工作情况大不一样，它能实现MOS零电压开通。
其工作波形图如下：上图为理想半桥谐振电路工作波形图，图中，VGS1,VGS2分别是Q1,Q2的驱动波表，IR为谐振电感 LR电感电流波形，IM为变压器的励磁电感LM的电流波形，ID1和ID2分别是次级侧的输出整流二极管波形，IDS1则为Q1导通电流。
IDS2则为Q2导通电流.波形图根据不同工作状态被分成6个阶段，下面具体分析各个状态，LLC谐振电路工作情况：TO-T1: Q1 关断、Q2开通；这个时候谐振电感上的电流为负，方向流向Q2.在此阶段，变压器主电感不参与谐振，CR，LR组成谐振频率，输出能量来自于CR 和LR.这个阶段随着Q2关断而结束。
上图3为LLC半桥谐振电路在T0-T1工作阶段各个元器件工作状态。
T1-T2: Q1关断、Q2关断；此时为半桥电路死区时间，谐振电感上的电流仍为负，谐振电流对Q1的输出电容（COSS1)进行放电，并且对Q2的输出电容（COSS2)进行充电，直到Q2的输出电容的电压等于输入电压（VIN),为Q1下次导通创造零电压开通的条件。
由于Q1体内二极管此时处于正向偏置，而Q2的体内二极管处于反向偏置，两个电感上的电流相等。
输出电压比变压器二次侧电压高，D1\D2处于反向偏置状态，所以输出端与变压器脱离。
LLC电路基本原理分析及公式推导LLC电路由LLC谐振电容器（C1，C2）和功率变压器（L1）组成。
当输入电压施加在谐振电容器上时，电容器开始充电。
同时，在电容器充电期间，电感器储存能量。
当电容器充电完毕后，电容器开始放电，电感器开始释放储存的能量。
由于谐振电容和电感在电路中的互连特性，电流和电压之间存在相位差，从而实现了电压和电流的变换。
在LLC电路中，我们需要推导出谐振频率和输出电压的公式。
1. 谐振频率（fr）的计算:在LLC电路中，谐振频率可以通过电感、谐振电容和输出电容的参数计算得出。
谐振频率的计算公式如下：\[f_r = \frac{1}{2\pi\sqrt{L_1(C_1 + C_2)}}\]2. 输出电压（Vout）的计算:在LLC电路中，输出电压的计算是通过电感、谐振电容和输入电压的参数计算得出。
输出电压的计算公式如下：\[V_{out} = \frac{N_1}{N_2} \cdot \frac{D}{1-D} \cdotV_{in}\]其中，N1和N2分别代表输入电感和输出电感的匝数，D代表占空比，Vin代表输入电压。
在设计LLC电路时，我们需要根据应用要求确定电感、谐振电容和输入电容的参数。
1.电感（L1）的选择:电感的选择主要取决于输出功率和应用电压。
通常，较大的输出功率和较高的应用电压需要选择较大的电感。
2.谐振电容（C1和C2）的选择:谐振电容的选择需要根据设计功率和应用电压来确定。
谐振电容的选择应当满足LLC电路的谐振频率要求。
3. 输入电容（Cin）的选择:输入电容的选择要根据应用要求和电压稳定性要求来确定。
输入电容一般起到平滑输入电压的作用，可减小输入电压的波动。
综上所述，LLC电路是一种利用电感和谐振电容在电路中的特性实现电流和电压变换的电力电子转换器。
通过计算谐振频率和输出电压的公式，可以根据设定参数来设计LLC电路的电感、谐振电容和输入电容的选择。
llc谐振开关电源电路原理LLC谐振开关电源电路原理LLC谐振开关电源电路是一种高效、稳定和可靠的电源设计方案，广泛应用于各种电子设备中。
本文将为您介绍LLC谐振开关电源电路的原理和工作方式。
LLC谐振开关电源电路由LLC谐振变压器、开关管、电容和电感等元件组成。
其工作原理基于LLC谐振拓扑结构，通过定时开关的方式将输入电源转换为所需的输出电压。
LLC谐振变压器是LLC电源电路的关键组件。
它由主绕组和副绕组组成，主要负责电压转换。
当输入电压施加到主绕组时，通过副绕组的电感和电容产生谐振，从而实现电压的转换。
谐振的频率由电感和电容的数值决定，通过合理选择电感和电容的数值，可以使LLC谐振变压器在高效、稳定的工作状态下运行。
开关管是LLC谐振开关电源电路的关键控制元件。
开关管的开关操作由控制电路控制，根据输入电压和输出负载的变化情况，控制电路会调整开关管的开关频率和占空比，以保持输出电压的稳定性。
开关管的开关操作使LLC谐振变压器工作在LLC谐振状态下，从而提高了电源的效率和稳定性。
电容和电感是LLC谐振开关电源电路中的重要元件，它们分别用于储存和释放能量。
电容通过吸收和储存电能，电感则通过积累和释放磁能。
它们与LLC谐振变压器共同实现了能量的转换和传递，从而实现了电源的高效工作。
总的来说，LLC谐振开关电源电路通过LLC谐振变压器、开关管、电容和电感等元件的协同工作，实现了输入电源到输出电压的转换。
其工作原理基于LLC谐振拓扑结构，通过合理选择电感和电容的数值，通过控制开关管的开关操作，使电源工作在LLC谐振状态下，从而提高了电源的效率和稳定性。
LLC谐振开关电源电路具有许多优点，例如高效、稳定和可靠。
相较于传统的开关电源电路，LLC谐振电路可以减少电源的能量损耗，提高电源的效率。
同时，LLC谐振电路还具有较低的输出电压波动和较高的输出电流能力，可以满足各种电子设备对电源的要求。
LLC谐振开关电源电路是一种高效、稳定和可靠的电源设计方案。
LLC原理讲解范文LLC原理的基本原理是通过一个谐振电路(LC谐振)来实现能量的存储、交换和传输。
LLC电路主要由一个电感器(L)、一个电容器(C)和一个磁性元件（如变压器）组成，并通过一个开关元件进行控制。
LLC电路通过施加适当的电压和电流波形来实现能量转换和传输。
LLC电路的工作原理可以分为以下几个步骤：1.谐振过程：在初始时刻，当开关元件关闭时，电感器和电容器处于充电状态。
在这个过程中，电感器和电容器的电流和电压之间是正弦波的谐振状态。
2.能量存储：当开关元件打开时，电感器和电容器之间的能量开始存储在磁性元件中。
此时，电感器的电流递减，并将能量传输给电容器。
3.能量传输：当电容器达到峰值电压时，开关元件再次关闭，电容器开始释放能量。
该能量通过磁性元件传输给负载。
4.能量交换：在能量传输的同时，电容器也在充电，以供应下一个工作周期的能量需求。
这种能量交换和传输的循环可以持续进行。
LLC电路通过谐振电感器和电容器之间的能量交换，实现高效率和高品质的能量传输和转换。
它的一个重要特点是能适应不同输入/输出电压和功率的需求，从而具有较大的灵活性。
除了上述基本原理外，LLC原理还有几个关键特点和应用：1.零电压开关(ZVS)：LLC电路的开关元件在开启和关闭时能够实现零电压过渡，减少了开关过程中的功耗和电压损耗。
这也使得LLC电路具有高效率和低压降的特点。
2.谐振频率调谐：通过调节电容器和电感器的数值，可以调节LLC电路的谐振频率，以适应不同应用和工作条件。
这种频率调谐能力可以提高电路的稳定性和性能。
3.电源和逆变器应用：LLC电路广泛应用于电源和逆变器等领域，以实现高效能的能量转换和稳定的交流输出。
总结起来，LLC原理通过使用谐振电路实现能量的存储、传输和转换，具有高效能、高品质和灵活性的特点。
它的工作原理包括谐振过程、能量存储、能量传输和能量交换等步骤。
LLC电路常用于电源和逆变器等应用中，具有广泛的应用前景。
Simplified Analysis and Design of Series-resonant LLC Half-bridge ConvertersMLD GROUPINDUSTRIAL & POWER CONVERSION DIVISIONOff-line SMPS BU Application LabI&PC Div. - Off-line SMPS Appl. LabPresentation Outline•LLC series-resonant Half-bridge: operation and significant waveforms•Simplified model (FHA approach)•300W design exampleI&PC Div. - Off-line SMPS Appl. LabSeries-resonant LLC Half-Bridge Topology and featuresQ1CrLsVinQ2 LpLLC tank circuit Preferably integrated into a singlemagnetic structure3 reactive elements, 2 resonant frequencies1f r12⋅π⋅Ls⋅Crf>fr1r2Center-tapped output with full-wave rectification(low voltage and high current)VoutVoutSingle-ended output withbridge rectifiication(high voltage and low current)Multiresonant LLCtank circuitVariable frequency controlFixed50%duty cycle for Q1&Q2Deadtime between LGandHGtoallow MOSFET’s ZVS@turnonfsw≈fr,sinusoidal waveforms:lowturnofflosses,low EMIEqual voltage¤t stressforsecondary rectifiers;ZCS,then norecovery lossesNooutputchoke;cost savingIntegrated magnetics:both L’scanbe realized with thetransformer.Highefficiency:>96%achievablefr212⋅π⋅(Ls+Lp)⋅CrI&PC Div. - Off-line SMPS Appl. LabLLC Resonant Half-bridgeWaveforms at resonance (f sw = f r1)Dead-timeGate-drivesignalsHB mid-pointVoltageResonant capvoltage Tank circuit current is sinusoidal Magnetizing current is triangularTransformercurrentsDiodevoltagesOutput currentCCM operationDiodecurrentsI&PC Div. - Off-line SMPS Appl. LabSwitching details at resonance (f sw = f r1)Dead-time Gate-drivesignalsZVS !HB mid-pointVoltageResonant capvoltageTank circuit current >0Magnetizing current Transformer currentsV(D1)<0Diodevoltages I(D1)=0 ZCS !DiodecurrentsI&PC Div. - Off-line SMPS Appl. LabOperating Sequence at resonance (Phase 1/6) 1/6Q Q Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1is OFF,Q2is OND1is OFF,D2is ON;V(D1)=2VoutLp is dynamically shorted:V(Lp)=nVout.Cr resonates with Ls,f r1appearsOutputenergy comes from Cr andLsPhase ends when Q2is switched offI&PC Div. - Off-line SMPS Appl. LabOperating Sequence at resonance (Phase 2/6) 2/6Q1 OFF Q2 ON Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1andQ2areOFF(deadtime)D1andD2areOFF;V(D1)=V(D2)=0;transformer’s secondary is openI(Ls+Lp)charges C OSS2anddischargesC OSS1,until V(C OSS2)=Vin;Q1’sbodydiodes tarts conducting,energy goes backto VinI(D2)is exactly zeroatQ2switch offPhase ends when Q1is switched onI&PC Div. - Off-line SMPS Appl. LabOperating Sequence at resonance (Phase 3/6) 3/6Q1 OFF Q2 ON Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1is ON,Q2is OFFD1is ON,D2is OFF;V(D2)=2VoutLp isdynamicallyshorted:V(Lp)=nVout.CrresonateswithLs,f r1appearsI(Ls)flows throughQ1’sR DS(on)backtoVin(Q1is workinginthe3rd quadrant)Phase ends when I(Ls)=0I&PC Div. - Off-line SMPS Appl. LabOperating Sequence at resonance (Phase 4/6)4/6Q1 OFF Q2 ONQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1is ON,Q2is OFFD1is ON,D2is OFF;V(D2)=2VoutLp isdynamicallyshorted:V(Lp)=nVout.CrresonateswithLs,f r1appearsI(Ls)flows throughQ1’sR DS(on)from Vinto groundEnergy is taken from Vin andgoes to VoutPhase ends when Q1is switched offI&PC Div. - Off-line SMPS Appl. LabOperating Sequence at resonance (Phase 5/6)5/6Q1 OFF Q2 ON Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1andQ2areOFF(deadtime)D1andD2areOFF;V(D1)=VD(2)=0;transformer’s secondary is openI(Ls+Lp)charges C OSS1anddischargesC OSS2,until V(C OSS2)=0;Q2’sbodydiodestarts conductingI(D1)is exactly zeroatQ1switch offPhase ends when Q2is switched onI&PC Div. - Off-line SMPS Appl. LabOperating Sequence at resonance (Phase 6/6)6/6Q1 OFF Q2 ON Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1is OFF,Q2is OND1is OFF,D2is ONLp isdynamicallyshorted:V(Lp)=nVout.CrresonateswithLs,fr1appearsI(Ls)flows throughQ2’sR DS(on)(Q2isworkinginthe3rd quadrant)Outputenergy comes from Cr andLsPhase ends when I(Ls)=0,Phase1starts I&PC Div. - Off-line SMPS Appl. LabWaveforms above resonance (f sw > f r1)Dead-timeGate-drivesignalsHB mid-pointVoltageResonant capvoltage Tank circuit current Magnetizing current is triangularTransformercurrentsSinusoid @ f=f r1 ~ Linear portionDiodevoltagesOutput currentCCM operationDiodecurrentsI&PC Div. - Off-line SMPS Appl. LabLLC Resonant Half-bridgeSwitching details above resonance (f sw > f r1)Dead-time Gate-drivesignalsZVS !HB mid-pointVoltageResonant capvoltage Tank circuit current >0 Slope ~ -(Vc-n·Vout)/LsMagnetizing currentTransformercurrentsV(D1)<0Diodevoltages ZCS ! Output currentI(D1)=0DiodecurrentsI&PC Div. - Off-line SMPS Appl. LabLLC Resonant Half-bridgeOperating Sequence above resonance (Phase 1/6) 1/6Q Q Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1is OFF,Q2is OND1is OFF,D2is ON;V(D1)=2VoutLp is dynamically shorted:V(Lp)=nVout.Cr resonates with Ls,f r1appearsOutputenergy comes from Cr andLsPhase ends when Q2is switched off I&PC Div. - Off-line SMPS Appl. LabLLC Resonant Half-bridgeOperating Sequence above resonance (Phase 2/6) 2/6Q1 OFF Q2 ON Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1andQ2areOFF(deadtime)D1andD2areOFF;V(D1)=V(D2)=0;transformer’s secondary is openI(Ls+Lp)charges C OSS2anddischargesC OSS1,until V(C OSS2)=Vin;Q1’sbodydiodes tarts conducting,energy goes backto VinV(D2)reverses as I(D2)goes to zeroPhase ends when Q1is switched onI&PC Div. - Off-line SMPS Appl. LabOperating Sequence above resonance (Phase 3/6)3/6Q1 OFF Q2 ON 1 ON2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1is ON,Q2is OFFD1is ON,D2is OFF;V(D2)=2VoutLp isdynamicallyshorted:V(Lp)=nVout.CrresonateswithLs,f r1appearsI(Ls)flows throughQ1’sR DS(on)backtoVin(Q1is workinginthe3rd quadrant)Phase ends when I(Ls)=0I&PC Div. - Off-line SMPS Appl. LabOperating Sequence above resonance (Phase 4/6)4/6Q1 OFF Q2 ON QQQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1is ON,Q2is OFFD1is ON,D2is OFF;V(D2)=2VoutLp isdynamicallyshorted:V(Lp)=nVout.CrresonateswithLs,f r1appearsI(Ls)flows throughQ1’sR DS(on)from Vinto groundEnergy is taken from Vin andgoes to VoutPhase ends when Q1is switched off I&PC Div. - Off-line SMPS Appl. LabOperating Sequence above resonance (Phase 5/6)5/6Q1 OFF Q2 ON Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1andQ2areOFF(deadtime)D1andD2areOFF;V(D1)=VD(2)=0;transformer’s secondary is openI(Ls+Lp)charges C OSS1anddischargesC OSS2,until V(C OSS2)=0;Q2’sbodydiodestarts conductingOutputenergy comes from CoutPhase ends when Q2is switched onI&PC Div. - Off-line SMPS Appl. LabOperating Sequence above resonance (Phase 6/6)6/6Q1 OFF Q2 ON Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1is OFF,Q2is OND1is OFF,D2is ONLp isdynamicallyshorted:V(Lp)=nVout.CrresonateswithLs,fr1appearsI(Ls)flows throughQ2’sR DS(on)(Q2isworkinginthe3rd quadrant)Outputenergy comes from Cr andLsPhase ends when I(Ls)=0,Phase1starts I&PC Div. - Off-line SMPS Appl. LabWaveforms below resonance (f sw < f r1)Dead-timeGate-drivesignalsHB mid-pointVoltageResonant capvoltage Tank circuit current Magnetizing currentSinusoid @ f=f r2TransformercurrentsSinusoid @ f=f r2Diodevoltages Output currentDCM operationDiodecurrentsI&PC Div. - Off-line SMPS Appl. LabLLC Resonant Half-bridgeSwitching details below resonance (f sw < f r1)Dead-time Gate-drivesignalsZVS !HB mid-pointVoltage Resonant cap voltageTank circuitcurrent = Magnetizing current >0 Portion of sinusoid @ f=f r2TransformercurrentsV(D1)<0DiodevoltagesZCS ! Output currentI(D1)=0DiodecurrentsI&PC Div. - Off-line SMPS Appl. LabOperating Sequence below resonance (Phase 1/8) 1/8Q1 ON Q2 OFF Q1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1is OFF,Q2is OND1is OFF,D2is ON;V(D1)=2VoutLp is dynamically shorted:V(Lp)=nVout.Cr resonates with Ls,f r1appearsOutputenergy comes from Cr andLsPhase ends when I(D2)=0Operating Sequence below resonance (Phase 2/8) 2/8Q1 OFF Q2 ON Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q2is ON,Q1is OFFD1andD2areOFF;V(D1)=V(D2)=0;transformer’s secondary is openCr resonates with Ls+Lp,f r2appearsOutputenergy comes from CoutPhase ends when Q2is switched offOperating Sequence below resonance (Phase 3/8) 3/8Q1 OFF Q2 ON Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1andQ2areOFF(deadtime)D1andD2areOFF;V(D1)=V(D2)=0;transformer’s secondary is openI(Ls+Lp)charges C OSS2anddischargesC OSS1,until V(C OSS2)=Vin;Q1’sbodydiodes tarts conducting,energy goes backto VinPhase ends when Q1is switched onI&PC Div. - Off-line SMPS Appl. LabOperating Sequence below resonance (Phase 4/8) 4/8Q1 OFF Q2 ON Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1is ON,Q2is OFFD1is ON,D2is OFF;V(D2)=2VoutLp isdynamicallyshorted:V(Lp)=nVout.CrresonateswithLs,f r1appearsI(Ls)flows throughQ1’sR DS(on)backtoVin(Q1is workinginthe3rd quadrant)Energy is recirculating into VinPhase ends when I(Ls)=0Operating Sequence below resonance (Phase 5/8) 5/8Q1 OFF Q2 ON Q1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1is ON,Q2is OFFD1is ON,D2is OFF;V(D2)=2VoutLp isdynamicallyshorted:V(Lp)=nVout.CrresonateswithLs,f r1appearsI(Ls)flows throughQ1’sR DS(on)from Vinto groundEnergy is taken from Vin andgoes to VoutPhase ends when I(D1)=0Operating Sequence below resonance (Phase 6/8)6/8Q1 OFF Q2 ON Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1is ON,Q2is OFFD1andD2areOFF;V(D1)=V(D2)=0;transformer’s secondary is openCr resonates with Ls+Lp,f r2appearsOutputenergy comes from CoutPhase ends when Q1is switched offOperating Sequence below resonance (Phase 7/8)7/8Q1 OFF Q2 ON Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1andQ2areOFF(deadtime)D1andD2areOFF;V(D1)=VD(2)=0;transformer’s secondary is openI(Ls+Lp)charges C OSS1anddischargesC OSS2,until V(C OSS2)=0,then Q2’sbodydiode starts conductingOutputenergy comes from CoutI&PC Div. - Off-line SMPS Appl. LabOperating Sequence below resonance (Phase 8/8)8/8Q1 OFF Q2 ON Q1 ONQ2 OFFQ1 OFFQ2 ONQ1Coss1VinLsCr n:1:1D1CoutCoss2VoutLpQ2D2Q1is OFF,Q2is OND1is OFF,D2is ONLp isdynamicallyshorted:V(Lp)=nVout.CrresonateswithLs,fr1appearsI(Ls)flows throughQ2’sR DS(on)(Q2isworkinginthe3rd quadrant)Outputenergy comes from Cr andLsPhase ends when I(Ls)=0,Phase1startsI&PC Div. - Off-line SMPS Appl. LabCapacitive mode (f sw ~ f r2): why it must be avoidedCapacitivemodeis encountered when f sw gets close to f r2Although incapacitivemodeZCScanbe achieved,however ZVSis lost,which causes:Hardswitching ofQ1&Q2:highswitching losses atturnonandvery highcapacitivelosses atturn offBodydiode ofQ1&Q2is reverserecovered:highcurrent spikes atturnon,additionalpowerdissipation;MOSFETswill easily blow up.Highlevel ofgenerated EMILarge andenergetic negativevoltage spikes intheHBmidpoint that may causethecontrolICto failAdditionally,feedbackloop sign could change from negativeto positive:Incapacitivemodetheenergy vs.frequency relationship is reversed Converteroperatingfrequencywouldrunawaytowardsitsminimum(ifMOSFETshavenotblownupalready!)I&PC Div. - Off-line SMPS Appl. LabWaveforms in capacitive mode (f sw ~ f r2)Dead-timeGate-drivesignalsHB mid-pointVoltageResonant capvoltage Tank circuit current is piecewise sinusoidal Magnetizing currentSinusoid @ f=f r2Transformercurrents Sinusoid @ f=f r1DiodevoltagesOutput currentDiodecurrentsI&PC Div. - Off-line SMPS Appl. LabSwitching details in capacitive mode (f sw ~ f r2)Gate-drivesignalsHARD SWITCHING !Very high voltage on Cr!HB mid-pointVoltage Resonant cap voltageMagnetizing currentTank circuit current is <0Transformer currentsCurrent is flowing in Q1’s body diode Q1’s body diode is recoveredDiodevoltagesOutput currentDiodecurrents I&PC Div. - Off-line SMPS Appl. LabApproximate analysis with FHA approach: BasicsBASICPRINCIPLES Input sourceC SN (ControlledSwitch Network)Resonant tankIdealtransformerUncontrolledrectifierLow-passfilterLoadCSNprovides asquare wave voltage atafrequency fsw,deadtimes are neglectedResonant tank responds primarily to its fundamental component,then: Tank waveforms areapproximated by their fundamental components Uncontrolled rectifier+lowpass filter’s effect is incorporated into theload.VinQ1Q2Cr Lsa:1Cout RLpVoutVinVin2Q1 ONQ2 OFF 0Q1 OFFQ2 ON2πVinNote:Cr is both resonant anddc blocking capacitorIts ac voltage is superimposed onadc componentequal to Vin/2(duty cyle is50%for both Q1andQ2) I&PC Div. - Off-line SMPS Appl. LabLLC Resonant Half-bridgeEquivalent model with FHA approachTheactualcircuitturnsintoanequivalentlinearcircuitwheretheacresonanttankis excitedbyaneffectivesinusoidalinputsourceanddrivesaneffectiveresistiveload. Standardacanalysiscanbeusedtosolvethecircuit Functions ofinterest:InputImpedance Z in (j ω)andForward TransferFunction M(j ω).It is possible to showthat thecomplete conversion ratioVout/Vin is:controlled switchrectifier withM (j ω)low-pass filterdc outputiiIS Routvac resonant tankRVout RRe8 = aR 2 Re2πdc inputIinvSZin (jω)⇒Vin2v S=Vin⋅sin(2π⋅fs⋅t)πVoutVin=M(jω) 2 2 1I=i cos(ϕ)=v Rein S Zs SππIout=2πa iRi ThisresultisvalidforanyresonanttopologyI&PC Div. - Off-line SMPS Appl. LabLLC Resonant Half-bridge Transformer model (I)Physical model All-Primary-Side equivalent model used for LLC analysisL1 Ideal Transformer L L2aLn:1:1 Sec. leakageinductanceLs Ideal Transformera:1:1Prim. leakage inductance LµSec. leakageinductanceLpMagnetizing inductance LL2bResults from theanalysis ofthemagnetic structure(reluctance modelappraach)nis theactual primarytosecondary turnratioL models themagnetizing flux linking all windings L L1models theprimary flux not linked to secondary L L2a andL L2b modelthesecondary flux not linked to primary;symmetrical windings:L L2a=L L2b APSequivalent model:terminalequations arethe same,internal parameters aredifferentais not theactual primarytosecondary turnratioLs is theprimary inductance measured with all secondaries shorted outLp is thedifference between theprimaryinductance measured with secondaries openandLsNOTE:L L1+L=Ls+Lp=L1primary winding inductance I&PC Div. - Off-line SMPS Appl. Lab。
