02热力学第一定律
- 格式:doc
- 大小:101.00 KB
- 文档页数:2


热力学第一定律与第二定律热力学是研究能量与热的转化和传递规律的科学,它是自然科学中重要的分支之一。
在热力学中,第一定律和第二定律是两个基本的定律,它们定义了能量守恒和能量转化的方向,对于理解热力学系统的行为和实际应用具有重要意义。
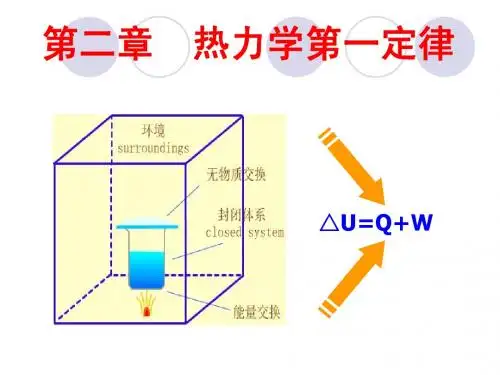
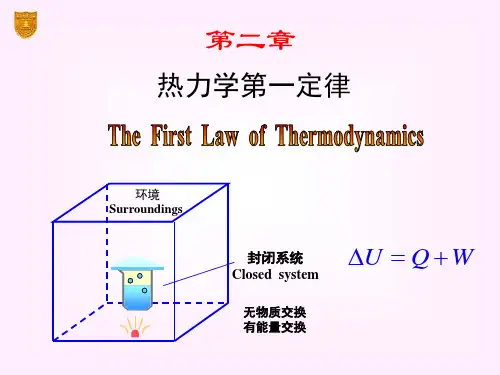
1. 热力学第一定律热力学第一定律,也称为能量守恒定律,表明能量在系统与环境之间的传递和转化后总量保持不变。
它可以通过下式表达:ΔU = Q - W其中,ΔU表示系统内能的变化,Q表示系统吸收的热量,W表示系统对外界做的功。
根据热力学第一定律,一个封闭系统的能量是守恒的,能量既不能被创造也不能被销毁,只能从一种形式转化为另一种形式。
热力学第一定律还可以用来推导出热机效率的表达式。
在一个热机中,根据热力学第一定律,系统吸收的热量等于系统对外界做的功加上系统内能的变化。
根据这个原理,我们可以得到热机效率的公式:η = 1 - Qc/Qh其中,η表示热机的效率,Qc表示热机向冷源放出的热量,Qh表示热机从热源吸收的热量。
这个公式表明,在一个热机中,不能把吸收的热量完全转化为功,一部分热量必须放出到冷源中,效率小于1。
2. 热力学第二定律热力学第二定律是热力学中最重要的定律之一,它表明热量不能自发地从低温物体传递到高温物体,而是自发地从高温物体传递到低温物体。
热力学第二定律有多种等效的表述方式,其中最常见的是克劳修斯表述和开尔文表述。
克劳修斯表述中,热量不会自发地从冷热源传递到热热源,即不存在一个热机,它只从一个热源吸热,然后完全转化为功,再把一部分热量放到冷热源上,不对环境产生任何影响。
这相当于说,在一个封闭系统中,不存在一个循环过程,使得系统对外界做的功等于输入的热量。
这个等效表述被称为克劳修斯表述。
开尔文表述中,不可能制造一个只从一个热源吸热,然后完全转化为功的热机,而不对环境产生任何影响。
这相当于说,在一个封闭系统中,不存在一个循环过程,使得系统吸收的热量完全转化为功,不放出热量到冷热源。






1第二章热力学第一定律2.1 热力学概论2.2 热力学的一些基本概念2.3 热力学第一定律2.4 焓和热容2.5 理想气体的热力学能和焓2.6 几种热效应2.7 化学反应的焓变22.1 热力学概论1. 热力学的研究对象2. 热力学的研究方法和局限性化学热力学是用热力学基本原理研究化学过程或与化学有关的物理过程。
热力学是研究宏观系统的热与其他形式能量之间的相互转换关系及其转换过程中所遵循的规律。
32.1.1 热力学的研究对象1. 研究化学过程及其与化学密切相关的物理过程中的能量转换关系。
2. 判断某条件下指定的热力学过程如相变、化学变化等的变化方向以及可能达到的最大限度。
根据第一定律计算变化过程中的能量变化,根据第二定律判断变化的方向和限度。
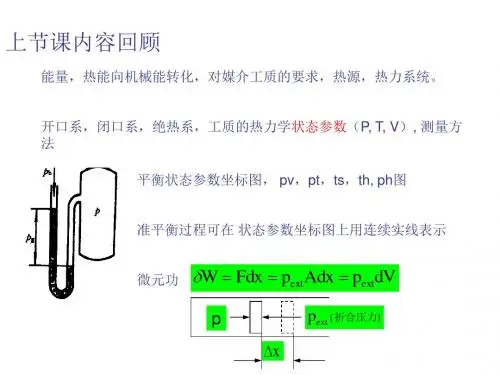
42. 1.2 热力学的研究方法和局限性研究方法•研究对象是大数量分子的集合体,研究宏观性质,所得结论具有统计意义。
•只考虑变化前后的净结果,不考虑物质的微观结构和反应机理。
•不研究系统的宏观性质与微观结构之间的关系局限性•不知道反应的机理、速率和微观性质•只讲可能性,不讲现实性•能判断变化能否发生以及进行到什么程度,但不考虑变化所需要的时间。
52.2 热力学的一些基本概念1. 系统和环境2. 系统的宏观性质3. 热力学平衡态4. 状态函数5. 过程和途径62.2.1 系统和环境系统(system )在科学研究中,把被划定的研究对象称为系统,亦称为物系或体系。
环境(surroundings)与系统密切相关、有相互作用或影响所能及的部分称为环境。
系统环境系统与环境72.2.1 系统和环境根据系统与环境之间的关系,把系统分为三类:(1)敞开系统(open system )系统与环境之间既有物质交换,又有能量交换。
环境有物质交换有能量交换敞开系统经典热力学不研究敞开系统82.2.1 系统和环境(2)封闭系统(closed system )系统与环境之间无物质交换,但有能量交换。
1
热力学第一定律
一、选择题
1. 理想气体向真空作绝热膨胀。
(A) 膨胀后,温度不变,压强减小;
(B) 膨胀后,温度降低,压强减小;
(C) 膨胀后,温度升高,压强减小;
(D) 膨胀后,温度不变,压强不变。
2. 氦、氮、水蒸气(均视为理想气体),它们的摩尔数相同,初始状态相同,若使它们在体积不变情况下吸收相等的热量,则
(A) 它们的温度升高相同,压强增加相同;
(B) 它们的温度升高相同,压强增加不相同;
(C) 它们的温度升高不相同,压强增加不相同;
(D) 它们的温度升高不相同,压强增加相同。
3. 如图所示,一定量理想气体从体积1V 膨胀到体积2V 分别经历的过程是:A →B 等压过程;A →C 等温过程;A →D 绝热过程。
其中吸热最多的过程
(A) 是A →B ;
(B) 是A →C ;
(C) 是A →D ;
(D) 既是A →B ,也是A →C ,两过程吸热一样多。
4. 一个绝热容器,用质量可忽略的绝热板分成体积相等的两部分。
两边分别装入质量相等、温度相同的H 2和O 2。
开始时绝热板P 固定,然后释放之,板P 将发生移动(绝热板与容器壁之间不漏气且摩擦可以忽略不计)。
在达到新的平衡位
置后,若比较两边温度的高低,则结果是:
(A) H 2比O 2温度高; (B) O 2比H 2温度高;
(C) 两边温度相等, 且等于原来的温度;
(D) 两边温度相等, 但比原来的温度降低了。
5. 如图所示,一绝热密闭的容器,用隔板分成相等的两部分,
左边盛有一定量的理想气体,压强为0p ,右边为真空。
今将隔
板抽去,气体自由膨胀,当气体达到平衡时,气体的压强是
0(A)p (B )2/0p 02(C)p γ (D) γ2/0p
(v p C
C /=γ) 6. 1 mol 的单原子分子理想气体从状态A 变为状态B ,如果不知是什么气体,变化过程也不知道,但A 、B 两态的压强、体积和温度都知道,则可求出:
(A) 气体所作的功;
(B) 气体内能的变化;
(C) 气体传给外界的热量; (D) 气体的质量。
二、填空题
1. 一定量的理想气体处于热动平衡状态时,此热力学系统不随时间变化的三个宏观量是 ,而随时间不断变化的微观量是 。
2. 不规则地搅拌盛于良好绝热容器中的液体,液体温度在升高,若将液体看作系统,则:
(1) 外界传给系统的热量 零;
(2) 外界对系统作的功 零;
(3) 系统的内能的增量 零。
(填大于、等于、小于) 3. 处于平衡态A 的热力学系统,若经准静态等容过程变到平衡
p
2 态B ,将从外界吸收热量416 J ;若经准静态等压过程变到与平衡态B 有相同的温度的平衡态C ,将从外界吸收热量582 J 。
所以,从平衡态A 变到平衡态C 的准静态等压过程中系统对外界所作的功为 。
4. 常温常压下,一定量的某种理想气体(可视为刚性分子自由度为i ),在等压过程中吸热为Q ,对外界作功为A ,内能增加为△E ,则Q A = ,Q
E ∆= 。
5. 刚性双原子分子的理想气体在等压下膨胀所作的功为A ,则传递给气体的热量为 。
6. 1 mol 的单原子理想气体,从状态),,(I 111T V p 变化至状态),,(I I 222T V p ,如图所示。
此过程气体对外界作功为 , 吸收热量为 。
三、计算题 1. 汽缸内有2 mol 氦气,初始温度为27℃,体积为20 L(升),
先将氦气等压膨胀,直至体积加倍,然后绝热膨涨,直至回复初温为止.把氦气视为理想气体.试求:
(1) 在p ―V 图上大致画出气体的状态变化过程. (2) 在这过程中氦气吸热多少?
(3) 氦气的内能变化多少?
(4) 氦气所作的总功是多少?
(普适气体常量R =8.31 1
1K mol J --⋅⋅)
2. 0.02 kg 的氦气(视为理想气体),温度由17℃升为27℃.若在升温过程中,(1) 体积保持不变;(2) 压强保持不变;(3) 不与外界交换热量;试分别求出气体内能的改变、吸收的热量、外界对气体所作的功.(普适气体常量R =8.31 11K mol J --⋅)
3. 一定量的理想气体在p ~V 图中的等温线与绝热线交点处两线的斜率之比为0.714,求其定容摩尔热容。
p 12。