最难初中几何题
- 格式:doc
- 大小:87.50 KB
- 文档页数:3

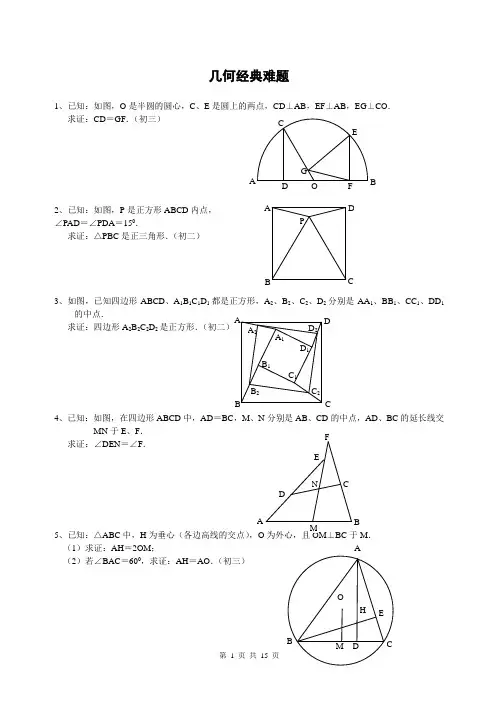
几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD=∠PDA=150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.求证:四边形A2B2C2D2是正方形.(初二)A P CDB4、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.5、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC 于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初三)6、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初三)7、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q.求证:AP=AQ.(初三)8、如图,分别以△ABC的AC和BC为一边,在△ABC的外侧作正方形ACDE和正方形CBFG,点P是EF的中点.求证:点P到边AB的距离等于AB的一半.(初二)9、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE=CF.(初二)10、如图,四边形ABCD为正方形,DE∥AC,且CE=CA,直线EC交DA延长线于F.求证:AE=AF.(初二)11、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.求证:PA=PF.(初二)12、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.(初三)13、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)14、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)15、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.(初三)16、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)17、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:≤L <2.18、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.19、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.20、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.解答1.如下图做GH⊥AB,连接EO。
几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点)(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E E P13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.AP C B PA D CB CB D AFPDECBA18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1.如下图做GH ⊥AB,连接EO 。
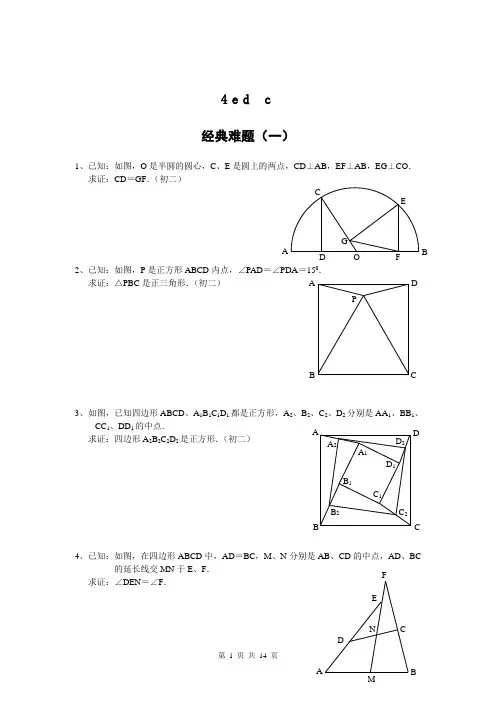
4e d c 经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CEBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典难1、已知:△ABC是正三角形,P求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二) 经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.FPDE CBAAPCBACBPDEDCA A CBPD经典难题(一)1.如下图做GH⊥AB,连接EO。
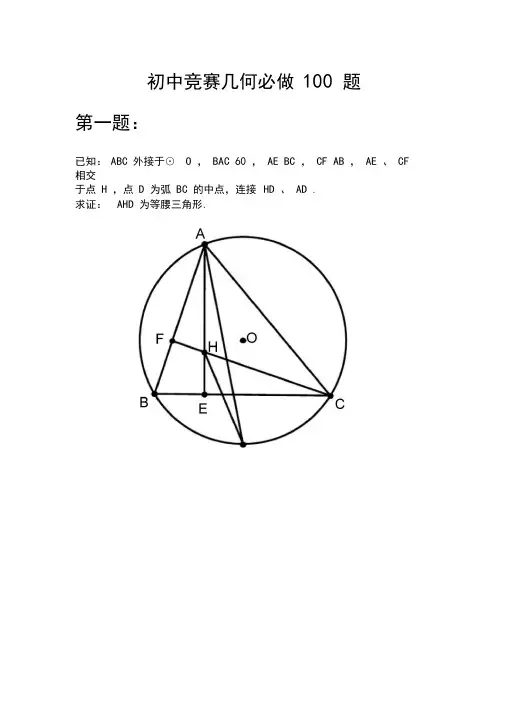
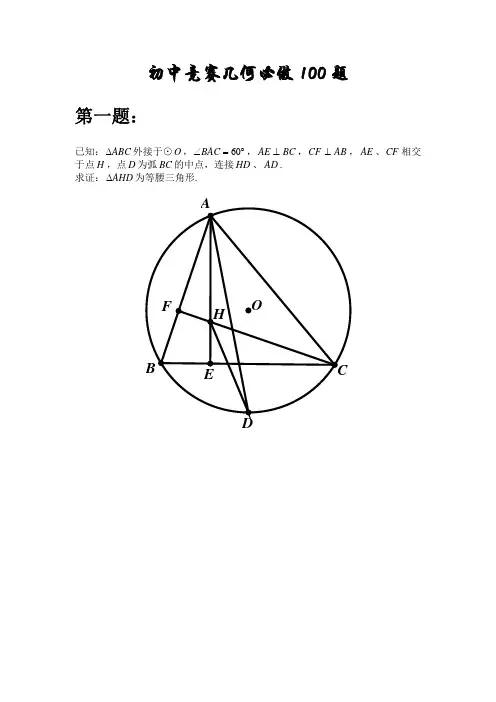
初中竞赛几何必做100 题第一题:已知:ABC 外接于⊙O ,BAC 60 ,AE BC ,CF AB ,AE 、CF 相交于点H ,点D 为弧BC 的中点,连接HD 、AD .求证:AHD 为等腰三角形.第二题:如图,F 为正方形ABCD 边CD 上一点,连接AC 、AF ,延长AF 交AC 的平行线DE 于点E ,连接CE ,且AC=AE.求证:CE CF .ABC 中, AB AC , BAC 20 , BDC AD BC .第三题: 已知30ABC 中, D 为 AC 边的中点, A 3 C , ADB 45 . AB BC .第四题: 已知第五题:如图,四边形ABCD 的两条对角线AC 、BD 交于点 E ,BAC 50 ,ABD 60 ,CBD 20 ,CAD 30 ,ADB 40 ,求ACD .AADC 60 , AD DC ,求证: AB 2 BC 2 BD 2.第六题: ABC 30 ,第七题:如图, PC 切 ⊙ O 于 C , AC 为圆的直径, PEF 为 ⊙ O 的割线,AE 、 AF 与直线 PO 相 交于 B 、 D .求证:四边形 ABCD 为平行四边形 . DE PB第八题:已知:在 求证:ABC 中, AB AC , A 80 , OBC 10 , OCA 20 . AB OB .第九题:ABCD 中,OAD ODA 15 ,求证:OBC 为正三角形.E 、F 为 AD 、 DC 的中点,连接 BE 、 AF ,相交于点 P ,连第十题: 已知:正方形 ABCD 中 , 接 PC .如图,ACB 与ADE 都是等腰直角三角形,交BE 于F ,求证:CFD 90 .A ADE ACB 90 ,CDF 45 ,DF第十一题:DF第十二题:已知:ABC 中,CBA 2 CAB ,CBA的角平分线BD 与CAB 的角平分线AD 相交于点D ,且BC AD .求证:ACB 60 .第十三题:ABC 中,AC BC , C 100 ,AD 平分CAB .求证:AD CD AB .第十四题:已知:ABC 中,AB BC ,D 是AC 的中点,过D 作DE BC 于E,连接A E ,取D E 中点F ,连接B F . 求证:A E B F .ABC 中, A 24 , C 30 , D 为 AC 上一点, AB CD ,连接 AB BC BD AC .第十五题: 已知BD .第十六题: 已知:的中点求证:ABCD 与 A 1B 1C 1D 1均为正方形, A 2 、 B 2 、 C 2 、 D 2 分别为 AA 1 、 BB 1 、 CC 1 、 DD 1 A 2 B 2C 2 D 2为正方形 .第十七题:45 ,如图,在ABC三边上,向外做三角形A BR 、BCP 、CAQ ,使CBP CAQBCP ACQ 30 ,ABR BAR 15 .求证:RQ 与RP 垂直且相等.第十八题:如图,已知AD 是⊙ O 的直径,D 是BC 中点,AB 、AC 交⊙ O 于点 E 、F ,EM 、FM 是⊙ O 的切线,EM 、FM 相交于点M ,连接DM .求证:DM BC .第十九题:如图,三角形ABC 内接于⊙O ,两条高AD 、BE 交于点H ,连接AO 、OH 。
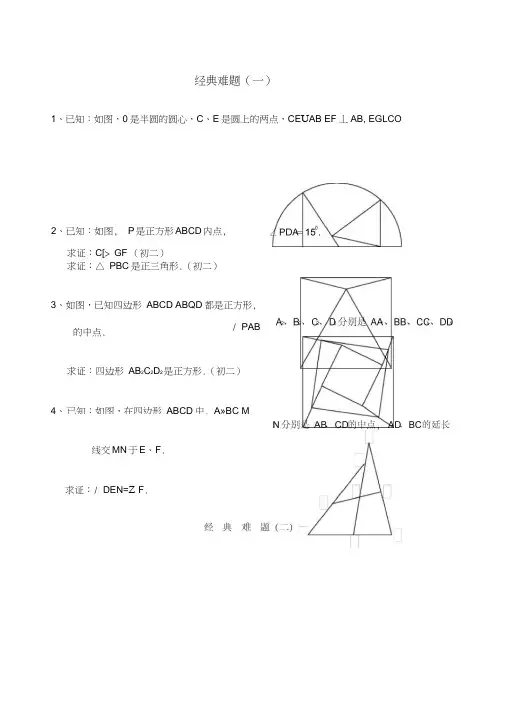
经典难题(一)1、已知:如图,0是半圆的圆心,C、E是圆上的两点,CE U AB EF丄AB, EGLCO2、已知:如图, P是正方形ABCD内点,求证:C[> GF (初二)求证:△ PBC是正三角形.(初二)3、如图,已知四边形ABCD ABQD都是正方形,/ PAB的中点.求证:四边形AB2C2D2是正方形.(初二)4、已知:如图,在四边形ABCD中, A»BC M线交MN于E、F.求证:/ DEN=Z F .1、已知:△ ABC中,H为垂心(各边高线的交点),0为外心,且OM L BC于M(1) 求证:AH= 20M经典难题(三)求证:CE= CF.(初二)求证:AE= AF.(初二) 3、设P 是正方形ABCD-边BC 上的任一点,PF 丄AP,求证:P 心PF.(初二)2、设MN 是圆0外一直线,过0作0A ±MN 于A ,自A 引圆的两条直线,交圆于 B 、C 及D E ,直线EB 及CD 分别交MN 于P 、Q.求证:A 吐AQ (初二)3、如果上题把直线 MN 由圆外平移至圆内,设MN 是圆0的弦,过 MN 的中点A 任作两弦BC DE 设CD EB 分别交MN 于P 、Q.求证:A 吐AQ (初二)4、如图,分别以厶ABC 的 AC 和BC 为一边,在△ ABC 的外侧作正方ACDE 和正方形CBFG 点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二1、如图,四边形ABC 助正方形,DE// AC ,AE= AC ,AE 与 CD 相交于 F .2、如图,四DE// AC ,且 CE= CA线EC 交DA 延长线,CEE4、如图,PC切圆0于C, AC为圆的直径,PEF为圆的割线,AE AF与直线PO相交于B、D.求求:/ APB的度数.(初二)2、设P是平行四边形ABCM部的一点,且/ PBA^Z求证:/ PAB=Z PCB (初二)3、设ABC助圆内接凸四边形,求证:AB- CM AD- BO AC- BD (初三)4、平行四边形ABC冲,设E、F分别是BC AB上的一点,AE与QF相交且AE= CF.求证:/ DPA F Z DPC (初二)经典难题(五)1、设P 是边长为1的正△ ABC 内任一点,L = PA + PB + PC ,求证:< L V 2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA + PB+ PC 的最小值.~C DB ADA / DCA CB GFHkZCAC B°,Z EBAC3、P 为正方形ABCD 内的一点,并且 PA = a , P 吐2a , PO 3a ,求正方形的边长.4、如图,△ ABC 中,/ ABC=ZACB= 80°, D E 分别是 AB =20°,求/ BED 勺度数. 经典难题(一)1.如下图做GH L AB,连接EQ 由于GOF 四点共圆,所以/ 即厶GHI ^A OGE 可得匹GQ =CO,又 CO=EQ 所以 CD=G 得证。
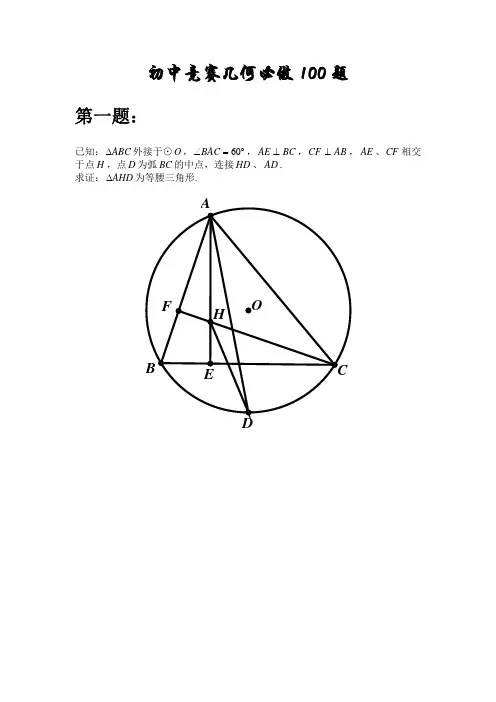
初中竞赛几何必做100题第一题:已知:ABCAE⊥,ABCF⊥,AE、CF相交BAC,BC∆外接于⊙O,︒=∠60于点H,点D为弧BC的中点,连接HD、AD.∆为等腰三角形.求证:AHD第二题:如图,F为正方形ABCD边CD上一点,连接AC、AF,延长AF交AC的平行线DE于点E,连接CE,且AC=AE.CE .求证:CFE第三题:已知:ABC ∆中,AC AB =,︒=∠20BAC ,︒=∠30BDC . 求证:BC AD =.B第四题:已知:ABC ∆中,D 为AC 边的中点,C A ∠=∠3,︒=∠45ADB . 求证:BC AB ⊥.AC第五题:如图,四边形ABCD 的两条对角线AC 、BD 交于点E ,︒=∠50BAC ,︒=∠60ABD ,︒=∠20CBD ,︒=∠30CAD ,︒=∠40ADB ,求ACD ∠.BD第六题:已知,︒=∠30ABC ,︒=∠60ADC ,DC AD =,求证:222BD BC AB =+.DB第七题:如图,PC切⊙O于C,AC为圆的直径,PEF为⊙O的割线,AE、AF与直线PO相交于B、D.求证:四边形ABCD为平行四边形.第八题:已知:在ABC ∆中,AC AB =,︒=∠80A ,︒=∠10OBC ,︒=∠20OCA . 求证:OB AB =.CB第九题:已知:正方形ABCD 中,︒=∠=∠15ODA OAD ,求证:OBC ∆为正三角形.第十题:已知:正方形ABCD中,E、F为AD、DC的中点,连接BE、AF,相交于点P,连接PC.PC .求证:BC第十一题:如图,ACB ∆与ADE ∆都是等腰直角三角形,︒=∠=∠90ACB ADE ,︒=∠45CDF ,DF 交BE 于F ,求证:︒=∠90CFD .EB第十二题:已知:ABC ∆中,CAB CBA ∠=∠2,CBA ∠的角平分线BD 与CAB ∠的角平分线AD 相交于点D ,且AD BC =. 求证:︒=∠60ACB .第十三题:已知:在ABC ∆中,BC AC =,︒=∠100C ,AD 平分CAB ∠. 求证:AB CD AD =+.AB第十四题:已知:ABC ∆中,BC AB =,D 是AC 的中点,过D 作BC DE ⊥于E ,连接AE ,取DE 中点F ,连接BF . 求证:BF AE ⊥.A第十五题:已知:ABC ∆中,︒=∠24A ,︒=∠30C ,D 为AC 上一点,CD AB =,连接BD . 求证:AC BD BC AB ⋅=⋅.A第十六题:已知:ABCD 与1111D C B A 均为正方形,2A 、2B 、2C 、2D 分别为1AA 、1BB 、1CC 、1DD 的中点.求证:2222D C B A 为正方形.A第十七题:如图,在ABC ∆三边上,向外做三角形ABR 、BCP 、CAQ ,使︒=∠=∠45CAQ CBP ,︒=∠=∠30ACQ BCP ,︒=∠=∠15BAR ABR .求证:RQ 与RP 垂直且相等.Q第十八题:如图,已知AD是⊙O的直径,D是BC中点,AB、AC交⊙O于点E、F,EM、FM 是⊙O的切线,EM、FM相交于点M,连接DM.DM .求证:BCB第十九题:如图,三角形ABC 内接于⊙O ,两条高AD 、BE 交于点H ,连接AO 、OH 。

几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点)(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E E P13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.AP C B PA D CB CB D AFPDECBA18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1.如下图做GH ⊥AB,连接EO 。
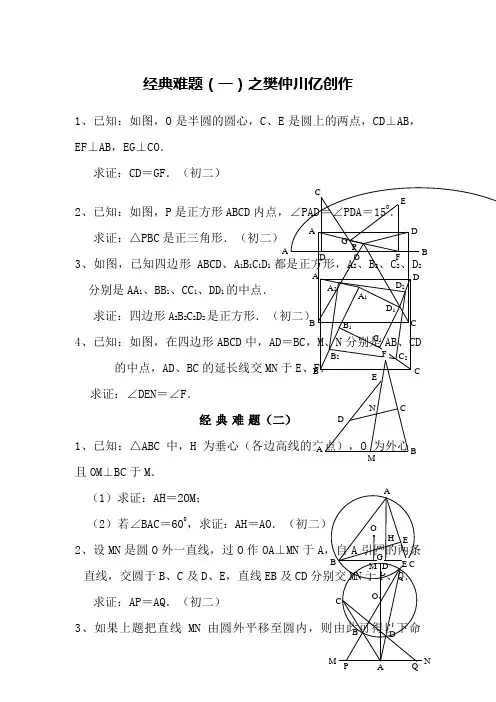
经典难题(一)之樊仲川亿创作1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C2D 24、已知:如图,在四边形ABCD 中,AD 的中点,AD 、BC 的延长线交MN 求证:∠DEN =∠F .经典难1、已知:△ABC 中,H 且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A 直线,交圆于B 、C 及D 、E ,直线EB 及CD 求证:AP =AQ .(初二)3、如果上题把直线MN题:设MN 是圆O 的弦,过MN CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 方形ACDE 和正方形CBFG ,点P 是EF求证:点P 到边AB 的距离等于AB经典难1、如图,四边形ABCD 为正方形,DE ∥交于F .求证:CE =CF 2、如图,四边形ABCD 交DA 延长线于F .求证:AE =AF 3、设P 是正方形ABCD DCE .求证:PA =PF 4、如图,PC 切圆O 于AF 与直线PO 相交于B 1、已知:△ABC 4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB+PC 的最小值.3、P 为正方形ABCD 内的一点,而且PA =a ,PB =正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E的点,∠DCA =300,∠EBA =200,求∠BED APC B P ADCBCBD A F PDE CBAAPC B经典难题(一)⊥AB,连接EO。

初二比较难的数学练习题在初二的数学学习中,遇到一些难题是很常见的。
这些题目需要我们掌握一定的数学知识和解题技巧才能顺利解答。
下面,我将为大家列举一些初二比较难的数学练习题。
一、立体几何题1. 某矩形纸片的长是宽的四倍,将该矩形剪成两个正方形,剪下的两个正方形面积之和是矩形面积的81%,求矩形的长和宽分别是多少?2. 下面的解析几何图形中,点A、B、C、D、E、F六点不在同一平面中,求ADE面与BCF面的夹角。
3. 设一条直线通过坐标轴上的点A(a, 0)和B(0, b),且直线与y轴交于点C(0, c),若三点A、B、C共线,求a、b、c之间的关系。
二、初中代数题4. 已知方程组:2x + 3y = 114x + ky = 15求k的值,使得方程组有唯一解。
5. 某数学题库有机试题100道,其中单选题每个题目的正确答案有4个选项,多选题每个题目的正确答案有5个选项,则这100道题中的选择题正确答案选项总数为多少?三、数列题6. 在等差数列{an}中,已知a1 = 3,a2 = 7,a4 = 17,则an的通项公式是什么?7. 若等比数列{bn}满足b1 = 2,b2 = 6,b4 = 90,则bn的通项公式是什么?四、概率题8. 一件商品的质量服从正态分布,已知其平均值为μ,标准差为σ。
若70%的商品质量在80kg到100kg之间,求μ和σ的值。
9. 一枚正六面体骰子有6个面,分别刻有1、2、3、4、5、6这6个数字。
现随机扔一枚骰子,连续扔5次,且每次都得到数字4的概率是多少?五、面积和体积题10. 在长方体中,一条对角线为18,长和宽的比为3:2,求长方体的体积和表面积。
以上是初二比较难的数学练习题,希望通过解题过程,能帮助大家加深对数学知识的理解和运用。
在解答这些题目时,我们要掌握相应的数学概念,并善于运用所学的数学方法和技巧进行推导和计算。
祝愿大家在数学学习中取得优异的成绩!。
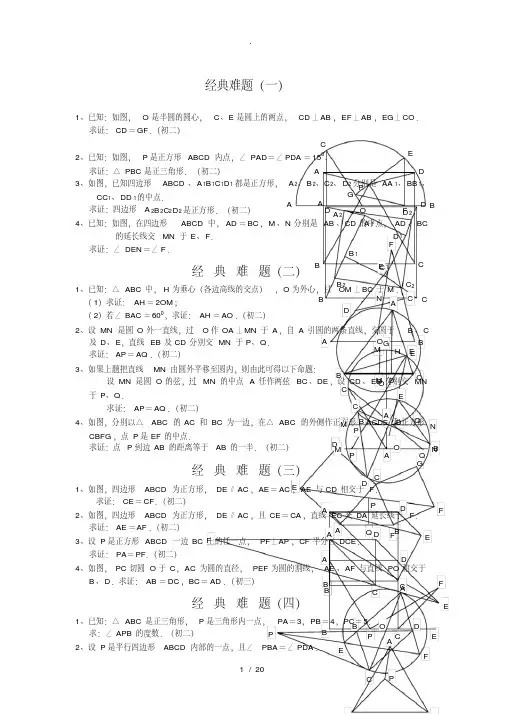
P C G FBQ A D E 经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C及D 、E ,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .APCDBAF G CE B O D D 2 C 2B 2 A 2 D 1C 1B 1C BD A A 1 A N FE C D MB · AD HE M C B O ·GAO D B E CQ P NM ·O Q PB DEC NM ·ADAFD EC BED ACBF F E P CB A ODB FAEP A求证:∠PAB=∠PCB.(初二)3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.(初三)4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:≤L<2.2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典难题(一)1.如下图做GH⊥AB,连接EO。
经典难题(一)之蔡仲巾千创作1、已知:如图, O 是半圆的圆心, C 、E 是圆上的两点, CD ⊥AB, EF ⊥AB, EG ⊥CO .求证:CD =GF .(初二)第1题图第2题图2、已知:如图, P 是正方形ABCD 内点, ∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图, 已知四边形ABCD 、A 1B 1C 1D 1都是正方形, A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)第3题图第4题图4、已知:如图, 在四边形ABCD 中, AD =BC, M 、N 分别是AB 、CD 的中点, AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)1、已知:△ABC 中, H 为垂心(各边高线的交点), O 为外心, 且OM ⊥BC 于M . (1)求证:AH =2OM ;AFGCEBODAPC DBD 2C 2B 2A 2D 1C 1B 1C BDAA 1B(2)若∠BAC =600, 求证:AH =AO .(初二)第1题图 第2题图2、设MN 是圆O 外一直线, 过O 作OA ⊥MN 于A, 自A 引圆的两条直线, 交圆于B 、C 及D 、E 直线EB 及CD分别交MN 于P 、Q .求证:AP =AQ .(初二) 3、如果上题把直线MN 由圆外平移至圆内, 则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE, 设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)第4题图4、如图, 分别以△ABC 的AC 和BC 为一边, 在△ABC 的外侧作正方形ACDE 和正方形CBFG, 点P 是EF 的中点.求证:点P 到边AB 的距离即是AB 的一半.(初二)经典难题(三)1、如图, 四边形ABCD 为正方形, DE ∥AC, AE =AC, AE 与CD 相交于F . 求证:CE =CF .(初二)NF第2题图2、如图, 四边形ABCD 为正方形, DE ∥AC,且CE =CA, 直线EC 交DA 延长线于F . 求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点, PF ⊥AP, CF 平分∠DCE . 求证:PA =PF .(初二)第3题图 4、如图, PC切圆O 于C, AC 为圆的直径, PEF 为圆的割线, AE 、AF 与直线PO 相交于B 、D . 求证:AB =DC, BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形, P 是三角形内一点, PA =3, PB =4, PC =5. 求:∠APB 的度数.(初二)第1题图 第2题图2、设P 是平行四边形ABCD 内部的一点, 且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)E3、设ABCD 为圆内接凸四边形, 求证:AB ·CD +AD ·BC =AC ·BD .(初三)第3题图 第4题图4、平行四边形ABCD 中, 设E 、F 分别是BC 、AB 上的一点, AE 与CF 相交于P, 且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点, L =PA +PB +PC, 求证:≤L <2.第1题图 第2题图2、P 是边长为1的正方形ABCD 内的一点, 求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点, 而且PA =a, PB =2a, PC =3a, 求正方形的边长.第3题图4、如图, △ABC 中, ∠ABC =∠ACB =800, D 、E 分别是AB 、AC 上的点, ∠DCA =300, ∠EBA =200, 求∠BED 的度数.C BDAFPDE CBAA PCBAC B PDEDCBAACBPD经典难题(一)1、已知:如图, O 是半圆的圆心, C 、E 是圆上的两点, CD ⊥AB, EF ⊥AB, EG ⊥CO .求证:CD =GF.(初二)证一:连接OE.∵EG ⊥CO , EF ⊥AB, ∴O 、G 、E 、F 四点共圆, 且OE 为直径.∴GF=OE ·sin ∠GOF.又△OCD 中, CD=OC ·sin ∠COD.∵∠GOF+∠COD=180°, OC= OE 为⊙O 半径, ∴CD =GF. 证二:连接OE, 过G 作GH ⊥AB 于H.∵EG ⊥CO , EF ⊥AB, ∴O 、G 、E 、F 四点共圆, 且OE 为直径.∴∠GEO=∠HFG.又∠EGO=∠FHG=Rt ∠, ∴△GEO ∽△HFG.∴GF:OE=GH:OG.又GH∥CD,∴GH:CD=OG:OC, 即GH:OG=CD:OC, ∴GF:OE=CD:OC, 而OE=OC, ∴CD =GF.2、已知:如图, P 是正方形ABCD 内点, ∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二) 证明:3、如图, 已知四边形ABCD 、A 1B 1C 1D 1都是正方形, A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)AFGCEBODAFG CEBO DAPCDB EH4、已知:如图, 在四边形ABCD 中, AD =BC, M 、N 分别是AB 、CD 的中点, AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)1、已知:△ABC 中, H 为垂心(各边高线的交点), O 为外心, 且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600, 求证:AH =AO .(初二)D 2C 2 B 2A 2D 1C 1B 1CBDAA 1B2、设MN 是圆O 外一直线, 过O 作OA ⊥MN 于A, 自A 引圆的两条直线, 交圆于B 、C 及D 、E 直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内, 则由此可得以下命题:设MN 是圆O 的弦, 过MN 的中点A 任作两弦BC 、DE, 设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图, 分别以△ABC 的AC 和BC 为一边, 在△ABC 的外侧作正方形ACDE 和正方形CBFG, 点P 是EF 的中点.求证:点P 到边AB 的距离即是AB 的一半.(初二)NF经典难题(三)1、如图, 四边形ABCD 为正方形, DE ∥AC, AE =AC, AE 与CD 相交于F . 求证:CE =CF .(初二)2、如图, 四边形ABCD 为正方形, DE ∥AC, 且CE =CA, 直线EC 交DA 延长线于F . 求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点, PF ⊥AP, CF 平分∠DCE . 求证:PA =PF .(初二)E4、如图, PC切圆O于C, AC为圆的直径, PEF为圆的割线, AE、AF与直线PO相交于B、D.求证:AB=DC, BC=AD.(初三)经典难题(四)1、已知:△ABC是正三角形, P是三角形内一点, PA=3, PB=4, PC=5.求:∠APB的度数.(初二)2、设P是平行四边形ABCD内部的一点, 且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD为圆内接凸四边形, 求证:AB·CD+AD·BC=AC·BD.(初三)4、平行四边形ABCD 中, 设E 、F 分别是BC 、AB 上的一点, AE 与CF 相交于P, 且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点, L =PA +PB +PC, 求证:≤L <2.CBDAFPDE CBA A PCB2、已知:P是边长为1的正方形ABCD内的一点, 求PA+PB+PC的最小值.3、P为正方形ABCD内的一点, 而且PA=a, PB=2a, PC=3a, 求正方形的边长.4、如图, △ABC中, ∠ABC=∠ACB=800, D、E分别是AB、AC上的点, ∠DCA=300,∠EBA=200, 求∠BED的度数.经典难题(一)⊥AB,连接EO.由于GOFE四点共圆, 所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO, 所以CD=GF得证.2. 如下图做△DGC使与△ADP全等, 可得△PDG为等边△, 从而可得△DGC≌△APD≌△CGP,得出PC=AD=DC,和∠DCG=∠PCG=150所以∠DCP=300 , 从而得出△PBC是正三角形3.如下图连接BC1和AB12F与A2E并延长相交于Q点,连接EB2并延长交C2Q于H点, 连接FB2并延长交A2Q于G点,由A2E=12A1B1=12B1C1= FB2 , EB2=12AB=12BC=F C1 , 又∠GFQ+∠Q=900和∠GE B2+∠Q=900,所以∠GE B2=∠GFQ又∠B2FC2=∠A2EB2 ,可得△B2FC2≌△A2EB2 , 所以A2B2=B2C2 ,又∠GFQ+∠HB2F=900和∠GFQ=∠EB2A2 ,从而可得∠A2B2 C2=900 ,同理可得其他边垂直且相等,从而得出四边形A2B2C2D2是正方形.4.如下图连接AC并取其中点Q, 连接QN和QM, 所以可得∠QMF=∠F, ∠QNM=∠DEN 和∠QMN=∠QNM, 从而得出∠DEN=∠F.经典难题(二)1.(1)延长AD到F连BF, 做OG⊥AF,又∠F=∠ACB=∠BHD,可得BH=BF,从而可得HD=DF,又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM (2)连接OB, OC,既得∠BOC=1200,从而可得∠BOM=600,所以可得OB=2OM=AH=AO,得证.⊥CD, OG⊥BE, 连接OP, OA, OF, AF, OG, AG, OQ.由于22AD AC CD FD FD AB AE BE BG BG,由此可得△ADF≌△ABG, 从而可得∠AFC=∠AGE.又因为PFOA与QGOA四点共圆, 可得∠AFC=∠AOP和∠AGE=∠AOQ, ∠AOP=∠AOQ, 从而可得AP=AQ.4.过E,C,F 点分别作AB 所在直线的高EG, CI, FH.可得PQ=2EGFH.由△EGA ≌△AIC, 可得EG=AI, 由△BFH ≌△CBI, 可得FH=BI.从而可得PQ=2AIBI =2AB, 从而得证.经典难题(三)△ADE, 到△ABG, 连接CG.由于∠ABG=∠ADE=900+450=1350从而可得B, G, D在一条直线上, 可得△AGB≌△CGB.推出AE=AG=AC=GC, 可得△AGC为等边三角形.∠AGB=300, 既得∠EAC=300, 从而可得∠A EC=750.又∠EFC=∠DFA=450+300=750.可证:CE=CF.⊥DE, 可得四边形CGDH是正方形.由AC=CE=2GC=2CH,可得∠CEH=300, 所以∠CAE=∠CEA=∠AED=150,又∠FAE=900+450+150=1500,从而可知道∠F=150, 从而得出AE=AF.⊥CD, FE⊥BE, 可以得出GFEC为正方形.令AB=Y , BP=X ,CE=Z ,可得PC=Y-X .tan∠BAP=tan∠EPF=XY=ZY X Z, 可得YZ=XY-X2+XZ,即Z(Y-X)=X(Y-X) , 既得X=Z , 得出△ABP≌△PEF , 获得PA=PF , 得证 .经典难题(四)1.顺时针旋转△ABP 600 , 连接PQ , 则△PBQ是正三角形. 可得△PQC是直角三角形.所以∠APB=1500 .2.作过P点平行于AD的直线, 并选一点E, 使AE∥DC, BE∥PC. 可以得出∠ABP=∠ADP=∠AEP, 可得:AEBP共圆(一边所对两角相等).可得∠BAP=∠BEP=∠BCP, 得证.3.在BD取一点E, 使∠BCE=∠ACD, 既得△BEC∽△ADC, 可得:BEBC=ADAC, 即AD•BC=BE•AC, ①又∠ACB=∠DCE, 可得△ABC∽△DEC, 既得ABAC =DEDC , 即AB •CD=DE •AC, ②由①+②可得: AB •CD+AD •BC=AC(BE+DE)= AC ·BD , 得证.⊥AE , AG ⊥CF , 由ADES=2ABCDS=DFCS, 可得:2AE PQ =2AE PQ , 由AE=FC.可得DQ=DG, 可得∠DPA =∠DPC (角平分线逆定理).经典难题(五)1.(1)顺时针旋转△BPC 600 , 可得△PBE为等边三角形.既得PA+PB+PC=AP++PE+EF要使最小只要AP, PE, EF在一条直线上, 即如下图:可得最小L=;(2)过P点作BC的平行线交AB,AC与点D, F.由于∠APD>∠ATP=∠ADP,推出AD>AP ①又BP+DP>BP ②和PF+FC>PC ③又DF=AF ④由①②③④可得:最年夜L< 2 ;由(1)和(2)既得:≤L<2 .△BPC 600 , 可得△PBE为等边三角形.既得PA+PB+PC=AP+PE+EF要使最小只要AP, PE, EF在一条直线上, 即如下图:可得最小PA+PB+PC=AF.既得AF=213(1)42=23=4232=2(31)2 =2(31)2=622 .△ABP 900 , 可得如下图:既得正方形边长L =2222(2)()22a=522a.4.在AB上找一点F, 使∠BCF=600 ,连接EF, DG, 既得△BGC为等边三角形,可得∠DCF=100 , ∠FCE=200 ,推出△ABE≌△ACF , 获得BE=CF , FG=GE .推出:△FGE为等边三角形 , 可得∠AFE=800 ,既得:∠DFG=400①又BD=BC=BG , 既得∠BGD=800 , 既得∠DGF=400②推得:DF=DG ,获得:△DFE≌△DGE ,从而推得:∠FED=∠BED=300 .经典难题(一)⊥AB,连接EO.由于GOFE四点共圆, 所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO, 所以CD=GF得证.2. 如下图做△DGC使与△ADP全等, 可得△PDG为等边△, 从而可得△DGC≌△APD≌△CGP,得出PC=AD=DC,和∠DCG=∠PCG=150所以∠DCP=300 , 从而得出△PBC是正三角形3.如下图连接BC1和AB12F与A2E并延长相交于Q点,连接EB2并延长交C2Q于H点, 连接FB2并延长交A2Q于G点,由A2E=12A1B1=12B1C1= FB2 , EB2=12AB=12BC=F C1 , 又∠GFQ+∠Q=900和∠GE B2+∠Q=900,所以∠GE B2=∠GFQ又∠B2FC2=∠A2EB2 , 可得△B2FC2≌△A2EB2 , 所以A2B2=B2C2 ,又∠GFQ+∠HB2F=900和∠GFQ=∠EB2A2 ,从而可得∠A2B2 C2=900 ,同理可得其他边垂直且相等,从而得出四边形A2B2C2D2是正方形.4.如下图连接AC并取其中点Q, 连接QN和QM, 所以可得∠QMF=∠F, ∠QNM=∠DEN 和∠QMN=∠QNM, 从而得出∠DEN=∠F.经典难题(二)1.(1)延长AD到F连BF, 做OG⊥AF,又∠F=∠ACB=∠BHD,可得BH=BF,从而可得HD=DF,又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM(2)连接OB, OC,既得∠BOC=1200,从而可得∠BOM=600,所以可得OB=2OM=AH=AO,得证.⊥CD, OG⊥BE, 连接OP, OA, OF, AF, OG, AG, OQ.由于22AD AC CD FD FD AB AE BE BG BG,由此可得△ADF≌△ABG, 从而可得∠AFC=∠AGE.又因为PFOA与QGOA四点共圆, 可得∠AFC=∠AOP和∠AGE=∠AOQ, ∠AOP=∠AOQ, 从而可得AP=AQ.4.过E,C,F 点分别作AB 所在直线的高EG, CI, FH.可得PQ=2EGFH.由△EGA ≌△AIC, 可得EG=AI, 由△BFH ≌△CBI, 可得FH=BI.从而可得PQ=2AIBI =2AB, 从而得证.经典难题(三)△ADE, 到△ABG, 连接CG.由于∠ABG=∠ADE=900+450=1350从而可得B, G, D在一条直线上, 可得△AGB≌△CGB.推出AE=AG=AC=GC, 可得△AGC为等边三角形.∠AGB=300, 既得∠EAC=300, 从而可得∠A EC=750.又∠EFC=∠DFA=450+300=750.可证:CE=CF.⊥DE, 可得四边形CGDH是正方形.由AC=CE=2GC=2CH,可得∠CEH=300, 所以∠CAE=∠CEA=∠AED=150,又∠FAE=900+450+150=1500,从而可知道∠F=150, 从而得出AE=AF.⊥CD, FE⊥BE, 可以得出GFEC为正方形.令AB=Y , BP=X ,CE=Z ,可得PC=Y-X .tan∠BAP=tan∠EPF=XY=ZY X Z, 可得YZ=XY-X2+XZ,即Z(Y-X)=X(Y-X) , 既得X=Z , 得出△ABP≌△PEF , 获得PA=PF , 得证 .经典难题(四)2.顺时针旋转△ABP 600 , 连接PQ , 则△PBQ是正三角形. 可得△PQC是直角三角形.所以∠APB=1500 .2.作过P点平行于AD的直线, 并选一点E, 使AE∥DC, BE∥PC. 可以得出∠ABP=∠ADP=∠AEP, 可得:AEBP共圆(一边所对两角相等).可得∠BAP=∠BEP=∠BCP, 得证.3.在BD取一点E, 使∠BCE=∠ACD, 既得△BEC∽△ADC, 可得:BEBC=ADAC, 即AD•BC=BE•AC, ①又∠ACB=∠DCE, 可得△ABC∽△DEC, 既得ABAC =DEDC , 即AB •CD=DE •AC, ②由①+②可得: AB •CD+AD •BC=AC(BE+DE)= AC ·BD , 得证.⊥AE , AG ⊥CF , 由ADES=2ABCDS=DFCS, 可得:2AE PQ =2AE PQ , 由AE=FC.可得DQ=DG, 可得∠DPA =∠DPC (角平分线逆定理).经典难题(五)1.(1)顺时针旋转△BPC 600 , 可得△PBE为等边三角形.既得PA+PB+PC=AP++PE+EF要使最小只要AP, PE, EF在一条直线上,即如下图:可得最小L=;(2)过P点作BC的平行线交AB,AC与点D, F.由于∠APD>∠ATP=∠ADP,推出AD>AP ①又BP+DP>BP ②和PF+FC>PC ③又DF=AF ④由①②③④可得:最年夜L< 2 ;由(1)和(2)既得:≤L<2 .△BPC 600 , 可得△PBE为等边三角形.既得PA+PB+PC=AP+PE+EF要使最小只要AP, PE, EF在一条直线上, 即如下图:可得最小PA+PB+PC=AF.既得AF=213(1)42=23=4232=2(31)2 =2(31)2=622 .△ABP 900 , 可得如下图:既得正方形边长L =2222(2)()22a=522a.4.在AB上找一点F, 使∠BCF=600 ,连接EF, DG, 既得△BGC为等边三角形,可得∠DCF=100 , ∠FCE=200 ,推出△ABE≌△ACF , 获得BE=CF , FG=GE .推出:△FGE为等边三角形 , 可得∠AFE=800 ,既得:∠DFG=400①又BD=BC=BG , 既得∠BGD=800 , 既得∠DGF=400②推得:DF=DG ,获得:△DFE≌△DGE ,从而推得:∠FED=∠BED=300 .创作时间:二零二一年六月三十日。
经典难题(一)1.已知:如图,O 是半圆的圆心,C.E 是圆上的两点,CD ⊥AB,EF ⊥AB,EG ⊥CO . 求证:CD =GF .(初二)2.已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3.如图,已知四边形ABCD.A 1B 1C 1D 1都是正方形,A 2.B 2.C 2.D 2分别是AA 1.BB 1.DD 1的中点. 求证:四边形A 2B 2C 2D 2是正方形.(初二)4.已知:如图,在四边形ABCD 中,AD =BC,M.N 分别是AB.CD 的中点,AD.BC 的延长线交MN 于E.F .求证:∠DEN =∠F .经典难题(二)A P C DB A F GC EBO D D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF 1.已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2.设MN 是圆O 外一直线,过O 作OA ⊥MN 于A,自A 引圆的两条直线,交圆于B.C 及D.E,直线EB 及CD 分别交MN 于P.Q . 求证:AP =AQ .(初二)3.如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC.DE,设CD.EB 求证:AP =AQ .(初二)4.如图,分别以△ABC 的AC 和BC 为一边,在△ABC 点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二经典难1.如图,四边形ABCD 为正方形,DE ∥AC,AE =AC,AE 与CD 相交于F . 求证:CE =CF .(初二)2.如图,四边形ABCD 为正方形,DE ∥AC,且CE =CA,直线EC 交DA 延长线于F . 求证:AE =AF .(初二)3.设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP,CF 平分∠DCE . 求证:PA =PF .(初二)4.如图,PC 切圆O 于C,AC 为圆的直径,PEF 为圆的割线,AE.AF 与直线PO 相交于B.D .求证:AB =DC,BC =AD .(初三)经典难题(四)1.已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2.设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3.设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4.平行四边形ABCD 中,设E.F 分别是BC.AB 上的一点,AE 与CF 相交于P,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1.设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC,求证:≤L <2.P A D CB CB DA F PDE CBAAPCB2.已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3.P 为正方形ABCD 内的一点,并且PA =a,PB =2a,PC =3a,求正方形的边长.4.如图,△ABC 中,∠ABC =∠ACB =800,D.E 分别是AB.AC 上的点,0=200,求∠BED 的度数.答案经典难题(一)1.如下图做GH ⊥AB,连接EO 。
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.AP CB ACBPDEDCB A A CBPD1.如下图做GH⊥AB,连接EO。
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)A P C DB A FG CE B O D D 2 C 2B 2 A 2 D 1C 1 B 1C B DA A 1BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC 求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,D .求证:AB =DC ,BC =AD .(初三)经典难1、已知:△ABC 是正三角形,P求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)1、设P是边长为1的正△ABC任一点,L=PA≤L<2.2、已知:P是边长为1的正方形ABCD的一点,求PA+PB+PC3、P为正方形ABCD的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC∠EBA=200,求∠BED的度数.经典难题(一)1.如下图做GH⊥AB,连接EO。
最难的几何数学题一、在三维空间中,给定一个正方体的一个顶点A和一个与之相对的顶点B,以及正方体表面上除A、B外任意一点C,求从C点出发沿表面到B点的最短路径与最长路径之比的可能取值范围。
A. (0,1)B. (1/√2, √2)C. (1, √3)D. (1/2, 2)(答案)B二、设有一个半径为R的圆内接于边长为a的正六边形中,现从圆上任意取一点P,求点P 到正六边形各边距离之和的最大值。
A. 3√3R/2B. 2√3RC. 3RD. (3+√3)R(答案)D三、在四面体ABCD中,已知AB=CD,AC=BD,且AD与BC垂直,若四面体的外接球半径为R,求四面体ABCD体积的最大值。
A. (4/3)πR3B. (8/9)√3πR3C. (2/3)√6πR3D. (1/3)√6πR3(答案)C四、考虑一个椭圆,其长轴为2a,短轴为2b,现有一条过椭圆中心的直线l,它与椭圆交于M、N两点,若MN的长度为定值d,求直线l的倾斜角α的取值范围。
A. [0, π/4]B. [π/6, π/3]C. 依赖于a, b, d的具体值D. [π/4, π/2](答案)C五、在直角坐标系中,给定三个点A(0,0),B(4,0),C(0,3),以及一个动点P(x,y),满足|PA|+|PB|+|PC|=10,求点P的轨迹所围成的图形面积。
A. 3πB. 4πC. 8πD. 12π(答案)B(注:点P的轨迹为椭圆,通过焦点和长轴短轴关系可求解)六、一个正n边形内接于一个半径为R的圆,其各边中点连接形成的多边形面积与原正n 边形面积之比为多少?A. 1/2B. 1/4C. 1/(n+1)D. 依赖于n的具体值(答案)B(对于任意正n边形,中点连接形成的多边形总是原多边形面积的1/4)七、在三维空间中,有一个边长为a的正方体,其内部有一个内切球,球心到正方体一个顶点的距离为d1,到正方体一条棱的中点的距离为d2,求d1/d2的值。
数学原创题 361.如果将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图①),此时,我们称△ABC向外扩展了一次,可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的若干倍.应用:某农户去年在面积为lO m2的△ABC空地上栽种了某种花卉,今年准备扩大种植规模,把△ABC向外进行两次扩展,第一次由△ABC扩展成△DEF,第二次由△DEF 扩展成△MGH(如图②).求这两次扩展的区域(即阴影部分)面积共为多少m2 ?A. 460 m2B. 480 m2C. 490 m2D. 530 m22.用大小相同的正六边形瓷砖按如图所示的方式来铺设广场,中间的正六边形瓷砖记为A,定义为第一组;在它的周围铺上6块同样大小的正六边形瓷砖,定义为第二组;在第二组的外围用同样大小的正六边形瓷砖来铺满,定义为第三组……按这种方式铺下去,用现有的2005块瓷砖最多能完整地铺满组;还剩块瓷砖.3.如图①,已知M (23,21),以M 为圆心,MO 为半径的⊙M 分别交x 轴、y 轴于B 、A 两点.若点C 是弧AO 的中点,点P 是弧AB 上一动点,连PA 、PB 、PC ,当P 在弧AB 上运动时,PCPOPA 的值是一个定值,这个定值为 .参考答案:1. 选B.扩展一次后得到的△DEF 的面积是原来△ABC 面积的7倍;扩展二次后得到的△MGH 的面积是原来△ABC 面积的72倍;所以拓展区域的面积应为: (72 – 1)×10=480 m 22. 26组,54块。
铺满n 组时,所用瓷砖总数为:1+6×1+6×2+…+6(n-1)=3n (n-1)+1.当n=26时,3n (n-1)+1=1951<2005,当n=27时,3n (n-1)+1=2107>2005,故最多能完整地铺满26组,还剩2005-1951=54(块)瓷砖.3.3.延长PO 至点D ,使OD=PA ,连结CD.可证得△ACP ≌△OCD ,所以PA+PO=PD.作CH ⊥PD ,则PH=21PD ,而=PC PH COS ∠CPO=COS300=23,所以3=PCPD,即PCPOPA +=3初中数学、科学原创题命题比赛双向细目表(样张)。
不准用三角函数,只能用初中几何的知识:全等三角形,相似三角形等,求出下面
两幅图中角 x 的大小。
此问题在网上流传的很广,所以不难搜到答案,但是如果你不知道答案的话,不妨
试一试自己的水平。
答案见下:
1.做CF⊥AB于F,做AH,使得∠BAH=60°,交CF于G,交CB于H,连接DH,
则△ABG是等边三角形,而∠ADB=∠BHA=40°,易得△ADB≌△BHA,故AH=BD,从而△DGH也是等边三角形,且∠DHE=∠ABC=80°.
而HA=HC=DC,∠DCG=∠HAE=10°,∠EHA=∠GDC=140°,故△DCG≌△HAE,故DG=HE,
而DG=DH,故HE=HD,故∠HED=∠HDE=(180°-80°)/2=50°,又∠AEH=30°,所以∠DEA=50°-30°=20°
2.在BC上取点F,使得∠BAF=20°,连接FA,FD,则AD=AB=AF,∠FAD=60°,故△FAD 为等边三角形,所以FA=FD,
又∠FEA=∠FAE=40°,故FA=FE,因此有FE=FD,又∠DFE=180°-60°-80°=40°,故∠FED=(180°-40°)/2=70°,故∠DEA=70°-40°=30°。