小学六年级数学总复习题库(组合图形)(1)
- 格式:doc
- 大小:2.00 MB
- 文档页数:4

期末总复习第二单元《图形与几何》一、选择题(5分)1.两根同样长的铁丝,一根铁丝做成长、宽、高分别是5cm、4cm、3cm的长方体框架(铁丝没有多余),另一根做成最大的正方体框架,这个正方体棱长是( )厘米。
A.3 B.4 C.5 D.62.把10厘米长的吸管剪两次,截成3段,首尾相接围成三角形,这三段长度可能是( )。
(单位:厘米)A.3,3,3 B.1,4,5 C.2,3,5 D.4,4,23.将如图沿折线围成一个正方体,这个正方体共顶点的三个面上的数字之积最大的是().A.120 B.90 C.72 D.604.底面积相等的圆柱和圆锥,它们的体积比是2∶1,圆锥的高是9厘米,圆柱的高是( )厘米。
A.3 B.6 C.8 D.25.在下面四句话中,正确的一句是()A.小于90度的角都是锐角,大于90度的角都是钝角B.在比例中,两个外项互为倒数,则两个内项成反比例C.一只热水瓶的容积是500毫升D.在c=πd中,c和π成正比例二、填空题(25分)6.一块平行四边形的草坪中有一条长8米、宽1米的小路,草坪的面积是________平方米.如果铺每平方米草坪的价格是16元,那么铺好这些草坪需要________元钱.7.要画一个周长是12.56厘米的圆,圆规两脚间的距离应定为(____)厘米,这个圆的面积是(____)平方厘米。
8.用三个完全一样的正方体,拼成一个长方体,长方体的表面积是70平方分米,原来一个正方体的表面积是(_____)平方分米。
9.大圆的直径是4厘米,小圆的直径是2厘米,大圆和小圆周长的最简整数比是________,大圆和小圆面积的最简整数比是________。
10.两个长、宽、高分别是5分米、4分米、3分米的长方体,拼成一个大的长方体,表面积至少要减少(_______)平方分米。
11.以学校为观测点,小红家在学校的南偏西30°方向,距离学校500米,那么以小红家为观测点,学校在小红家(_____)偏(_____)(_____)°的方向。
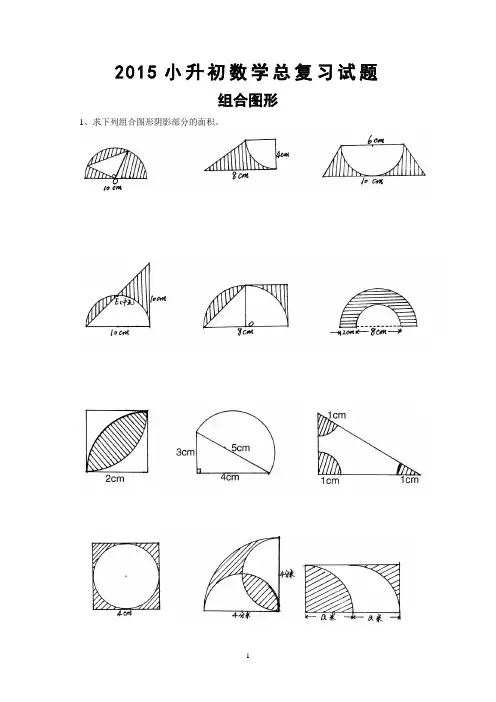
2015小升初数学总复习试题
组合图形
1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的
1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S 阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
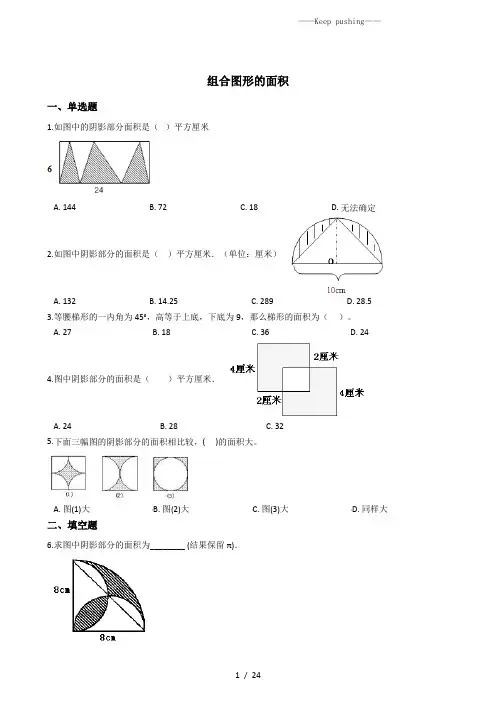
组合图形的面积一、单选题1.如图中的阴影部分面积是()平方厘米A. 144B. 72C. 18D. 无法确定2.如图中阴影部分的面积是()平方厘米.(单位:厘米)A. 132B. 14.25C. 289D. 28.53.等腰梯形的一内角为45°,高等于上底,下底为9,那么梯形的面积为()。
A. 27B. 18C. 36D. 244.图中阴影部分的面积是()平方厘米.A. 24B. 28C. 325.下面三幅图的阴影部分的面积相比较,( )的面积大。
A. 图(1)大B. 图(2)大C. 图(3)大D. 同样大二、填空题6.求图中阴影部分的面积为________ (结果保留π).7.已知如图中三角形的面积是10平方厘米,图中圆的面积是________平方厘米.8.看图计算(单位:厘米)组合图形的面积是________平方厘米9.求下列图形的面积是________dm2。
(单位:dm)10.图中正方形的面积是12平方厘米,圆的面积是________平方厘米.11.计算下面图形阴影部分的面积________.(单位:厘米)12.(202X•长沙)如图,两个正方形的边长分别是8厘米和4厘米,则阴影部分的面积是________平方厘米.13.先求右面图形中涂色部分的面积,再求小正方形的面积.涂色面积________平方分米,小正方形面积________平方分米.14.看图计算(单位:厘米)平行四边形AFEB的面积S=________平方厘米平行四边形CFED的面积S=________平方厘米15.下图表示的是一间房子侧面墙的形状.它的面积是________平方米.16.求下面各图阴影部分的面积(1)________(2)________17.计算下面图形的面积________.(单位:厘米)18.有一条引水渠穿过了一块麦地,这块地的总面积是引水渠占去的面积的________倍?19.把一个长12厘米,宽8厘米的长方形纸片剪下一个最大的正方形,剩下部分的面积是________平方厘米.20.求阴影部分的面积.________平方厘米21.大正方形边长为8厘米,小正方形边长为4厘米,阴影部分的面积是________平方厘米。


章节测试题1.【答题】在等腰三角形、平行四边形、长方形、正方形、梯形、圆这些图形中,一定是轴对称图形的有______个.【答案】4【分析】本题考查的是轴对称图形的辨识.【解答】等腰三角形是轴对称图形,只有1条对称轴;平行四边形不是轴对称图形;长方形是轴对称图形,有2条对称轴;正方形是轴对称图形;梯形中只有等腰梯形是轴对称图形;圆是轴对称图形,它有无数条对称轴;平行四边形不是轴对称图形,梯形中只有等腰梯形是轴对称图形.所以一定是轴对称图形的有4个.故本题的答案是4.2.【答题】分针从指向12转到下图所示的位置,经过了______分钟.【答案】20【分析】本题考查的是认识旋转.【解答】分针走1个大格,经过的时间是5分钟.分针从12旋转到4,走了4个大格,4×5=20(分钟),所以经过的时间是20分钟.故本题的答案是20.3.【答题】看图填空.(1)向______平移了______个方格;(2)向______平移了______个方格;(3)向______平移了______个方格.【答案】右,6,下,5,左,6【分析】本题考查的是确定平移的方向和距离.【解答】(1)观察图形不难发现:的三个顶点分别向右平移了6个方格;(2)图形的各个关键点分别向下平移了5个方格;(3)图形的各个关键点分别向左平移6个方格. 故本题的答案是右,6,下,5,左,6.4.【答题】等腰三角形有______条对称轴,等边三角形有______条对称轴,正方形有______条对称轴.(都填数字)【答案】1,3,4【分析】本题考查的是确认轴对称图形的对称轴条数.【解答】如下图,等腰三角形有1条对称轴,等边三角形有3条对称轴,正方形有4条对称轴.故本题的答案是1,3,4.5.【答题】下图的钟面是从镜子里看到的,实际钟面上的时刻是______:______.【答案】5,20【分析】镜面对称的特点是:上下前后方向一致,左右方向相反. 据此解答即可.【解答】图中镜子里看到的时间是,由镜面对称左右方向相反特点,镜中时针在6与7之间,实际是在5与6之间,是5时;镜中分针指向刻度8,实际是指向刻度4,即20分,所以实际钟面上的时刻是.故本题的答案是5,20.6.【答题】下图是围棋棋盘的一部分,在这个的方格图形中已经放置了5枚棋子.若要将它变为上下左右都对称的图形,则最少还要在棋盘上摆放______枚棋子.【答案】11【分析】根据轴对称图形的特点和性质,轴对称图形沿对称轴对折,对称轴两边的图形能够完全重合.由此作出图即可得出结论.【解答】如下图:所以最少还要在棋盘上摆放(枚)棋子.故本题的答案是11.7.【答题】下图中多边形的周长是______厘米.【答案】14【分析】要求多边形的周长是多少,只要把各边相加即可.由图可知,把上边的折线部分分成两部分,横着的部分相加正好是5厘米;竖着的部分相加是2厘米;于是多边形的周长是2个2厘米加上2个5厘米.【解答】(厘米),所以图中多边形的周长是14厘米.故本题的答案是14.8.【答题】下面图形的面积是______ cm².(图中每个小格的边长为1cm)【答案】12【分析】本题考查的是利用平移解决实际问题.【解答】将图中左端凸起的两块小三角形平移到右侧凹下处,则拼成一个长4cm、宽3cm的长方形,平移不改变图形的大小,则其面积为4×3=12(cm²).故本题的答案是12.9.【答题】下图是由3个小正方形组成的图形.若在图中补画一个小正方形,使补画后的图形为轴对称图形,则不同的补画方式有______种.【答案】4【分析】本题考查的是补画轴对称图形.【解答】如下图,不同的补画方式有4种.故本题的答案是4.10.【答题】下列英文字母,属于轴对称图形的是().A. NB. SC. LD. E【答案】D【分析】本题考查的是辨认轴对称图形.【解答】根据轴对称图形的特点可知,字母“E”是轴对称图形.选D.11.【答题】下列现象,是平移的是().A. 公路上行驶的汽车的车轮B. 大楼里的升降电梯C. 时针的运动【答案】B【分析】本题考查的是认识平移和旋转.【解答】公路上行驶的汽车的车轮和时针的运动都是旋转,大楼里的升降电梯的运动是平移.选B.12.【答题】如下图,图形从A处平移到B处,是().A. 向右平移了4个方格B. 向左平移了4个方格C. 向右平移了1个方格D. 向左平移了1个方格【答案】A【分析】本题考查的是图形的平移.【解答】由图可知,图形从A处平移到B处,是向右平移了4个方格.选A.13.【答题】下列各组中的两个数字,成轴对称的是().A. B. C.【答案】C【分析】如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.据此进行判断即可.【解答】根据轴对称图形的意义可知:、都不是轴对称图形,只有是轴对称图形.选C.14.【答题】下面的图形中,对称轴只有2条的是().A. B. C.【答案】C【分析】如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.据此依次进行判断即可.【解答】A选项有3条对称轴;B选项有3条对称轴;C选项有2条对称轴.选C. 15.【答题】由图①变为图②,下列方法错误的是().A. 图形①绕点A逆时针方向旋转90°得到图形②B. 图形①绕点A 顺时针方向旋转90°得到图形②C. 以直线AB为对称轴画图形①的对称图形得到图形②【答案】A【分析】根据图形旋转的方法可得:图形①绕点A顺时针旋转90°,即可得到图形②;或者以直线AB为对称轴画图形①的对称图形得到图形②;据此即可解答.【解答】观察图形可知,图形①绕点A顺时针旋转90°,即可得到图形②.又因为以直线AB为对称轴画图形①的对称图形得到图形②,所以由图①变为图②方法错误的是A. 选A.16.【答题】如图,旋转其中一个图形,能把两个图形组成一个长方形的是().A. 图形A绕点O顺时针旋转90°B. 图形B绕点O顺时针旋转90°C. 图形A绕点O逆时针旋转180°D. 图形B绕点O逆时针旋转90°【答案】B【分析】把一个图形绕着某一点转动一个角度的图形变换叫做旋转;把一个图形绕着一个点旋转一定的角度后,与原来的图形相吻合,旋转前后图形的大小和形状没有改变.据此进行解答即可.【解答】图形B绕点O顺时针旋转90°,或图形A绕点O逆时针旋转90°能把两个图形组成一个长方形.选B.17.【答题】如下图,把图甲通过变换得到图乙,方法不正确的是().A. 把图甲绕点B逆时针方向旋转180°B. 把图甲向下平移2格,再向右平移4格C. 把图甲向右平移4格,再以直线l为对称轴作对称图形【答案】B【分析】根据旋转和轴对称图形的定义即可判断.【解答】观察图形可知,图乙可以看作是图甲绕点B逆时针旋转180°后得到的;也可以看作是把图甲向右平移4格,再以直线l为对称轴作对称图形得到的.图乙不可能是图甲平移得到的.选B.18.【答题】两个圆组成的图形一定是轴对称图形.()【答案】✓【分析】两个圆无论半径相等,还是不相等,组成的图形都是轴对称图形,只是对称轴的条数多少而已.【解答】两个圆组成的图形一定是轴对称图形.故本题正确.19.【答题】在轴对称图形中,对称轴两侧的对称点到对称轴的距离相等. ()【答案】✓【分析】轴对称图形是指一个图形沿一条直线对折后直线两旁的部分能够完全重合,这条直线就是这个轴对称图形的对称轴.轴对称图形中,对称点到对称轴的距离相等.【解答】根据分析可知,在轴对称图形中,对称轴两侧的对称点到对称轴的距离相等.故本题正确.20.【答题】钟面上时针从12时到14时,时针绕中心点顺时针旋转了90°. ()【答案】×【分析】钟面上有12个数字,12个数字之间有12个大格,每两个数字之间是360÷12=30°,即时针转过1个大格是30°.【解答】从12时到14时,时针绕中心点顺时针旋转了2个大格,则旋转了30°×2=60°.故本题错误.。

新人教版六年级下册数学总复习专题五——空间与图形的试题及答案(个人整理)专题五——空间与图形(一) 一、填空。
(30分)1、一条10厘米长的线段,这条线段长()分米,是1米的()()。
2、经过两点可以画出()条直线;两条直线相交有()个交点。
3、如果等腰三角形的一个底角是53°,则它的顶角是().直角三角形的一个钝角是48°,另一个锐角是()。
4、上图是由()个棱长为1厘米的正方体搭成的。
将这个立体图形的表面涂上蓝色,其中只有三个面涂上蓝色的正方体有()个,只有四个面涂上蓝色正方体有()个。
5、在一块边长10cm的正方形硬纸板上剪下一个最大的圆,这个圆的面积是()cm2,剩下的边角料是()cm2。
6、一个长方形的周长是42cm,它的长与宽的比是4∶3,它的面积是()cm2。
7、用72cm长的铁丝焊成一个正方体框架(接口处不计),这个正方体框架的棱长是()cm,体积是()cm3,表面积是()cm2。
8、一个圆锥的体积是9.42立方分米,底面直径是6分米,它的高是()分米,和它等底等高的圆柱的体积是()立方分米。
9、从直线外一点到这条直线可以画无数条线段,其中最短的是和这条直线()的线段。
10、用百分数表示以下阴影部分是整个图形面积的百分之几。
11、把一个底面直径2分米的圆柱体截去一个高1分米的圆柱体,原来的圆柱体表面积减少()平方分米。
12、右图是由棱长1厘米的小正方体木块搭成的,这个几何体的表面积是()平方厘米。
至少还需要()块这样的小正方体才能搭成一个大正方体。
13、在一块边长是20厘米的正方形木板上锯下一个最大的圆,这个圆的面积是()平方厘米,剩下的边料是()平方厘米。
14、将一个大正方体切成大小相同的8个小正方体,每个小正方体的表面积是18平方厘米,原正方体的表面积是()平方厘米。
15、把一个棱长8cm的正方体切成棱长2cm的小正方体,可以得到()个小正方体,它们的表面积之和比原来增加了()c㎡。



北师大版小学六年级数学上册总复习整理及试题(1)第一单元圆1、圆心决定圆的位置,半径(直径)决定圆的大小。
在同圆或等圆中,所有的直径都相等,所有的半径都相等,直径是半径的2倍。
一个圆有无数条半径,有无数条直径。
2、连接圆心和圆上任意一点的线段叫半径,经过圆心并且两端都在圆上的线段叫直径。
3、圆是轴对称图形,有无数条对称轴,任意一条直径所在的直线都是圆的对称轴。
圆环也有无数条对称轴。
4、一个圆的周长总是它直径的兀倍,也就是3倍多一点,这就是圆周率。
圆周率是一个固定不变的数,不会随着圆的大小而改变,是一个无限不循环小数,一般取其近似值 3.14。
圆的周长与直径的比是兀:1,比值是兀。
我国古代数学家祖冲之首先算出圆周率的值在 3.1415926和 3.1415927之间。
5、周长相等的长方形、正方形和圆,圆的面积最大,正方形面积次之,长方形面积最小。
6、圆的周长=圆周率×直径 C=兀D D= C÷兀圆的面积=圆周率×半径2 S=兀r27、圆环的面积=圆周率×(大圆半径2-小圆半径2) S环=兀(R2-r2)8、圆的半径扩大a倍,则直径扩大a倍,周长也扩大a倍,则面积扩大a2倍。
周长相等的圆,则其半径、直径、面积一定相等,反之则不等。
圆典型题例1、一只挂钟的时针长4厘米,分针长5厘米,从上午8点到11点,分针针尖走过的路线长是多少厘米?时针扫过的面积是多少?2、在一张长10厘米宽8厘米的长方形内剪一个最大的圆,这个圆的面积是多少?3、在一个长30厘米,宽20厘米的长方形内画一个最大的半圆,这个半圆的周长和面积各是多少?4、在一个直径为8米的圆形花坛外修一条宽2米的环形小路,小路的面积是多少平方米?5、用37.68米的铁丝围成一个圆,这个圆的面积是多少平方米?6、一条线长15.7米,正好在一个圆形线圈上绕100圈,这个线圈的直径是多少?7、在一个周长80厘米的正方形内画一个最大的圆,这个圆的面积是多少?8、一张可折叠的圆桌,直径是1.2米,折叠后就成了正方形,折叠后的桌面面积是多少平方米?9、在一个直径4分米的半圆形钢板上取一个最大的三角形,这个三角形的面积是多少平方分米?10、甜甜骑自行车上学,自行车的外胎直径是60厘米,自行车每分钟转80圈,她从家骑车12分钟到学校,求学校和她家的距离。
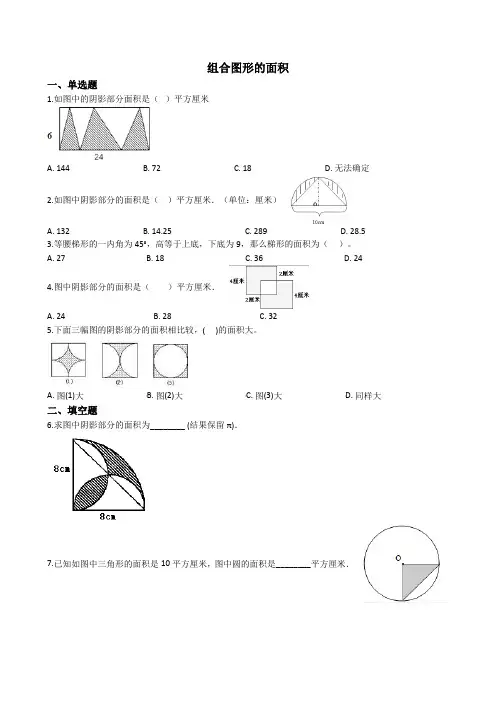
组合图形的面积一、单选题1.如图中的阴影部分面积是()平方厘米A. 144B. 72C. 18D. 无法确定2.如图中阴影部分的面积是()平方厘米.(单位:厘米)A. 132B. 14.25C. 289D. 28.53.等腰梯形的一内角为45°,高等于上底,下底为9,那么梯形的面积为()。
A. 27B. 18C. 36D. 244.图中阴影部分的面积是()平方厘米.A. 24B. 28C. 325.下面三幅图的阴影部分的面积相比较,( )的面积大。
A. 图(1)大B. 图(2)大C. 图(3)大D. 同样大二、填空题6.求图中阴影部分的面积为________ (结果保留π).7.已知如图中三角形的面积是10平方厘米,图中圆的面积是________平方厘米.组合图形的面积是________平方厘米9.求下列图形的面积是________dm2。
(单位:dm)10.图中正方形的面积是12平方厘米,圆的面积是________平方厘米.11.计算下面图形阴影部分的面积________.(单位:厘米)12.(2015•长沙)如图,两个正方形的边长分别是8厘米和4厘米,则阴影部分的面积是________平方厘米.13.先求右面图形中涂色部分的面积,再求小正方形的面积.涂色面积________平方分米,小正方形面积________平方分米.平行四边形AFEB的面积S=________平方厘米平行四边形CFED的面积S=________平方厘米15.下图表示的是一间房子侧面墙的形状.它的面积是________平方米.16.求下面各图阴影部分的面积(1)________(2)________17.计算下面图形的面积________.(单位:厘米)18.有一条引水渠穿过了一块麦地,这块地的总面积是引水渠占去的面积的________倍?19.把一个长12厘米,宽8厘米的长方形纸片剪下一个最大的正方形,剩下部分的面积是________平方厘米.20.求阴影部分的面积.________平方厘米21.大正方形边长为8厘米,小正方形边长为4厘米,阴影部分的面积是________平方厘米。

六年级下册图形和几何测试试卷一、填空题。
1、一个平行四边形的面积是1.2平方分米,它的高是0.6分米,底是()分米。
2、一个长方体的长、宽、高分别是3cm、2cm、4cm,这个长方体的棱长总和是( ),表面积是(),体积是()。
3、一个半圆的直径是6厘米,它的面积是()平方厘米,周长是()厘米。
4、6时整时,钟面上分针和时针所组成的角是( )°,它是一个()角;9时整时,分针和时针所组成的夹角是()°,它是一个()角,能形成这样的角的时刻还有()时整。
5、两个正方形的边长比是1∶2,它们的周长比是(),面积比是();两个圆的周长比是1∶3,则它们的半径比是(),面积比是()。
6、圆柱的体积一定,它的底面积和高成()比例关系。
7、把长为8cm,宽为6cm,高为4cm的长方体木块切成棱长是2cm的小正方体,能切出()块。
8、0.6dm3=( )cm3 3.02公顷=( )平方米530dm2=()m2二、选择题。
1、下面的图形中,不能折成正方体的是()C.2、一个正方体的棱长缩小到原来的21,表面积就会缩小到原来的( ),体积缩小到原来的( )。
A.21 B.41 C.81 3、小朋友喜欢玩的跷跷板的运动是( )。
A.旋转B.平移C.轴对称C.三、判断题。
1、在同一幅地图上,图上距离越大,实际距离也就越大。
( )2、长方体、正方体、圆柱和圆锥的体积计算公式可以统。
( )3、只有两个角是锐角的三角形一定是钝角三角形。
( )4、把一个长方形框架拉成一个平行四边形,它的周长不变,面积变大了。
( )5、甲在乙的东偏北30°方向,乙在甲的西偏南30°方向。
( )四、我会画。
(1)在下图中找出各点位置,并按顺序进行连线。
(5,1)(2,1)(2,4) (1,4)(3,6)(5,6)2、以图中的虚线为对称轴,画出图形的另一半。
五、解答题。
1、李叔叔家里要进行房屋装修,其中客厅长为5米,宽为4米,高为3米。
总复习测试卷(一)一、填空题。
(每题2分,共22分)1.一个数由8个百万,6个千,7个0.1和6个0.01组成,这个数写作( ),省略“万”位后面尾数约是( )。
2.45分:23时化成最简整数比是( ),比值是( )。
3.7.05吨=( )吨( )千克 35分=( )( )时 4.( )12=0.75=( )÷20=( )%=( ):24=( )折 5.57的分数单位是( ),再添上( )个这样的分数单位后是最小的质数。
6.三个连续奇数中间的数是m ,则m 的前面和后面的奇数分别是( )和( )。
7.如果a 和b 是不为0的两个连续自然数,那么a ,b 的最小公倍数是( ),最大公因数是( )。
8.57的后项加上21,要使比值不变,比的前项应加上( )。
9.根据规律填空。
12,23,35,58,813,( ),( )……10.今年植树节,六年级同学栽了180棵树,有20棵没有活,后来又补栽了20棵,全部成活。
六年级同学今年植树的成活率是( )。
11.40 kg 减少它的25后,再增加25 kg 是( )kg 。
二、判断题。
(每题1分,共6分)1.因为58>13,所以58的分数单位比13的分数单位大。
( ) 2.4900÷400=49÷4=12……1。
( ) 3.8和0.125互为倒数。
( ) 4.0.8和0.80大小相等,意义相同。
() 5.-2 ℃比-5 ℃的温度低。
() 6.把48%的百分号去掉,这个数就扩大为原来的100倍。
() 三、选择题。
(每题1分,共7分)1.下列分数中,不能化成有限小数的是( )。
A.720B.825C.712D.6152.六(1)班总人数一定,期中考试获得优秀的人数与优秀率()。
A .成正比例 B .成反比例C .不成比例D .无法确定3.两根同样长的绳子,甲绳用去14,乙绳用去14米,则两根绳子()。
A .甲剩下的长一些 B .乙剩下的长一些C .甲、乙剩下的一样长D .无法判断谁剩下的长4.在2.35·48·,2.3·548·,2.3548·,2.354·8·中,最小的数是( )。
小学数学总复习题库填 空1、一个数,它的亿位上是9,百万位上是7,十万位上和千位上都是5,其余各位都是0,这个数写作( ),读作( ),改写成以万作单位的数( ),省略万后面的尾数是( )万。
2、把4.87的小数点向左移动三位,再向右移动两位后,这个数是( )。
3、9.5607是( )位小数,保留一位小数约是( ),保留两位小数约是( )。
4、最小奇数是( ),最小素数( ),最小合数( ),既是素数又是偶数的是( ),20以内最大的素数是( )。
5、把36分解质因数是( )。
6、因为a=2×3×7,b=2×3×3×5,那么a 和b 的最大公约数是( ),最小公倍数是( )。
7、如果x 6 是假分数,x 7是真分数时,x=( )。
8、甲数扩大10倍等于乙数,甲、乙的和是22,则甲数是( )。
9、三个连续偶数的和是72,这三个偶数是( )、( )、( )。
10、x 和y 都是自然数,x ÷y=3(y ≠0),x 和y 的最大公约数是( ),最小公倍数是( )。
11、一个数,千位上是最小的质数,百位上是最小的自然数,个位上是最小的合数,百分位上是最大的数字,其余数位上的数字是0,这个数写作( ),读作( )。
12、三个连续奇数的和是129,其中最大的那个奇数是( ),将它分解质因数为( )。
13、两个数的最大公约数是1,最小公倍数是323,这两个数是( )和( ),或( )和( )。
14、用3、4或7去除都余2的数中,其中最小的是( )。
15、分数的单位是18的最大真分数是( ),它至少再添上( )个这样的分数单位就成了假分数。
16、0.045里面有45个( )。
17、把一根5米长的铁丝平均分成8段,每段的长度是这根铁丝的( ),每段长( )。
18、分数单位是111的最大真分数和最小假分数的和是( )。
19、a 与b 是互质数,它们的最大公约数是( ),[a 、b]=( )。
六年级数学总复习系列一(分类)一、填空。
1、一个数由二十九个亿,四百个万,五个千组成,这个数是(),读作()。
2、600600600中从左到右。
三个6依次表示()、()、()。
3、用三个8,两个0组成一个五位数,一个0也不读出来的是(),只读一个0的是(),两个0都读出来的是()。
4、最大的五位数与最小的三位数的和是(),最小的两位数与最大的三位数的积是(),最大两位数与最大一位数的差是()。
5、三个连续自然数的和是138,这三个连续自然数依次为()、()、()。
6、705300是()位数,最高位是()位,从个位向左第四位上的数字是(),它表示()。
7、上个月,爸爸领取工资1500元,记作+1500元,购买自行车用去588元,记作()元。
8、102分=()小时()分 1.5平方千米=()公顷 30公顷60平方米=()平方米9、一个数由9个百万。
5个十万,9个千,40个十,6个十分之一和5个0.01组成,这个数是(),四舍五入到万位是()。
10、八亿零四百七十万写作(),把它改写成用“万”作单位的数是()。
11、把3.400、0.1、7和15.1800改写成两位小数分别是()、()、()、()。
12、把5.12缩小10倍得(),把0.015扩大100倍得()。
()缩小100倍得0.035,()扩大1000倍得45.13、一个数小数点左边第九位是5,第六位上是4,第五位上是9,其余各位上都是0,这个数写作(),读作(),省略“万后面的尾数是()万,改成“亿”作单位的数是()亿。
一个小数由6个百,8个一,9个十分之一和8个百分之一组成,这个小数是(),保留到十分位记作()。
14、把一个小数的小数点先向右移动两位,在缩小1000倍后是4.02,原来的数是( )。
16、把5米长的绳子平均分成8份,每份是5米的( ),每份是1米的( )( ),每份是( )( )米。
17、78千克既可以看成是把1千克平均分成( )份,表示其中的( )份,也可以看成是把7千克平均分成( )份,表示其中的( )份。
六年级数学总复习系列一(分类)一、填空。
1、一个数由二十九个亿,四百个万,五个千组成,这个数是( ),读作( )。
2、600600600中从左到右。
三个6依次表示( )、( )、( )。
3、用三个8,两个0组成一个五位数,一个0也不读出来的是( ),只读一个0的是( ),两个0都读出来的是( )。
4、最大的五位数与最小的三位数的和是( ),最小的两位数与最大的三位数的积是( ),最大两位数与最大一位数的差是( )。
5、三个连续自然数的和是138,这三个连续自然数依次为( )、( )、( )。
6、705300是( )位数,最高位是( )位,从个位向左第四位上的数字是( ),它表示( )。
7、上个月,爸爸领取工资1500元,记作+1500元,购买自行车用去588元,记作( )元。
8、102分=( )小时( )分 1.5平方千米=( )公顷 30公顷60平方米=( )平方米9、一个数由9个百万。
5个十万,9个千,40个十,6个十分之一和5个0.01组成,这个数是( ),四舍五入到万位是( )。
10、八亿零四百七十万写作( ),把它改写成用“万”作单位的数是( )。
11、把3.400、0.1、7和15.1800改写成两位小数分别是( )、( )、( )、( )。
12、把5.12缩小10倍得( ),把0.015扩大100倍得( )。
( )缩小100倍得0.035,( )扩大1000倍得45.13、一个数小数点左边第九位是5,第六位上是4,第五位上是9,其余各位上都是0,这个数写作( ),读作( ),省略“万后面的尾数是( )万,改成“亿”作单位的数是( )亿。
一个小数由6个百,8个一,9个十分之一和8个百分之一组成,这个小数是( ),保留到十分位记作( )。
14、把一个小数的小数点先向右移动两位,在缩小1000倍后是4.02,原来的数是( )。
16、把5米长的绳子平均分成8份每份是5米的( ),每份是1米的( )( ),每份是( )( )米。
六年级数学总复习NO.1 数的认识练习一、填空。
1、一个数由二十九个亿,四百个万,五个千组成,这个数是(),读作()。
2、600600600中从左到右。
三个6依次表示()、()、()。
3、用三个8,两个0组成一个五位数,一个0也不读出来的是(),只读一个0的是(),两个0都读出来的是()。
4、最大的五位数与最小的三位数的和是(),最小的两位数与最大的三位数的积是(),最大两位数与最大一位数的差是()。
5、三个连续自然数的和是138,这三个连续自然数依次为()、()、()。
6、705300是()位数,最高位是()位,从个位向左第四位上的数字是(),它表示()。
7、上个月,爸爸领取工资1500元,记作+1500元,购买自行车用去588元,记作()元。
8、102分=()小时()分 1.5平方千米=()公顷 30公顷60平方米=()平方米9、一个数由9个百万。
5个十万,9个千,40个十,6个十分之一和5个0.01组成,这个数是(),四舍五入到万位是()。
10、八亿零四百七十万写作(),把它改写成用“万”作单位的数是()。
11、把3.400、0.1、7和15.1800改写成两位小数分别是()、()、()、()。
12、把5.12缩小10倍得(),把0.015扩大100倍得()。
()缩小100倍得0.035,()扩大1000倍得45.13、一个数小数点左边第九位是5,第六位上是4,第五位上是9,其余各位上都是0,这个数写作(),读作(),省略“万后面的尾数是()万,改成“亿”作单位的数是()亿。
一个小数由6个百,8个一,9个十分之一和8个百分之一组成,这个小数是(),保留到十分位记作()。
14、把一个小数的小数点先向右移动两位,在缩小1000倍后是4.02,原来的数是()。
15、16、把5米长的绳子平均分成8份,每份是5米的( ),每份是1米的( )( ),每份是( )( )米。
17、78千克既可以看成是把1千克平均分成( )份,表示其中的( )份,也可以看成是把7千克平均分成( )份,表示其中的( )份。
六年级小升初数学总复习【图形与几何】专题训练(解析卷)六年级小升初数学总复【图形与几何】专题训练【解析卷】直线型面积】1.在图中,平行四边形ABCD的边BC长10厘米,直角三角形ECB的直角边EC长8厘米。
已知阴影部分的总面积比三角形EFG的面积大10厘米2,求平行四边形ABCD的面积。
解答:因为阴影部分比三角形EFG的面积大10厘米2,都加上梯形FGCB后,根据差不变性质,所得的两个新图形的面积差不变,即平行四边形ABCD比直角三角形ECB的面积大10厘米2,所以平行四边形ABCD的面积等于10×8÷2+10=50(厘米2)。
2.图中,CA=AB=4厘米,三角形ABE比三角形CDE的面积大2厘米,求CD的长。
解答:连结CB。
三角形DCB的面积为4×4÷2-2=6(厘米2),CD=6÷4×2=3(厘米)。
3.有红、黄、绿三块同样大小的正方形纸片,放在一个正方形盒的底部,它们之间互相叠合。
已知露在外面的部分中,红色面积是20,黄色面积是14。
绿色面积是10,求正方形盒子底部的面积。
解答:把黄色正方形纸片向左移动并靠紧盒子的左边。
由于三个正方形纸片面积相等,所以原题图可以转化成下页右上图。
此时露出的黄、绿两部分的面积相等,都等于(14+10)÷2=12.因为绿:红=A∶黄,以是绿×黄=红×A,A=绿×XXX÷红12×12÷20=7.2.正方形盒子底部的面积是红+黄+绿+A=20+12+12+7.2=51.2.三角形的等积变换】:4.如左下图是两个相同的直角三角形叠在一起组成的,求阴影部分的面积。
单位:分米)谜底:32.5平方分米。
拓展:如图所示,已知正方形ABCD和正方形EFGC,且正方形EFGC的边长为6厘米,请问图中阴影部分面积是多少?答案:18平方厘米。
5.如图所示,在平行四边形ABCD中,DE=EF=FC,BG=GD.已知三角形GEF的面积是4平方厘米,求平行四边形的面积。
组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面
积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求
三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S 阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。