大学物理-守恒定律

大学物理—守恒定律
一、质点的动量定理
动量：质点质量与速度的乘积，可以表征质点瞬时运动的量，成为动量。

表达式：
由牛顿第二定律，得：
即：
这就是动量定理。

二、冲量定理，
有：
冲量：作用在质点上的某力对时间的累计，称为该力对质点的冲量。

冲量定理：即：合外力的冲量等于质点的动量增量
冲力：在冲击过程中，力一般是时间的函数。

冲击过程中任一时刻质点所受的合力称为此时刻质点上的冲力。

表达式：
平均冲力：当变化较快时，力的瞬时值能难确定，用一平均力代替该过程中的变力，这一等效力称为冲击过程的平均冲力。

【教材 p74 例3.1】
平均冲力与同段时间内变力等效。

在解题过程中，我们常常引入平均冲力的概念。

例如人从高处跳下、飞机与鸟相撞、小球撞击模板、打桩等碰撞事件中，作用时间很短，冲力很大。

【小球撞击木板】
例题：质量为2.5的乒乓球以10m/s的速率飞来，被板推挡后，又以20m/s 的速率飞出。

求：1）乒乓球的冲量；2）若撞击时间为0.01s，则板施于球的平均冲力的大小和方向。

解：由于作用时间很短，忽略重力影响。

设挡板对球的冲力为F
则（水平方向为x轴，垂直方向为y轴）
a为平均冲力与x方向的夹角
动量与冲量的区别
①动量是状态量；冲量是过程量；
②动量方向为物体运动方向；冲量方向为作用时间内动量变化的方向。

冲量定理的作用
①计算冲量时，无需确定各个外力，只需知道质点始末的动量即可。

②F为合外力，不是某一个外力。

③动量定理的分量式：
④平均冲量的计算：
⑤
三、质点系动量定理
因为内力，故
由于系统的内力成对出现，系统的内力矢量合为零。

推广到多质点系统，动量定理表达式为：
质点系的动量定理：
即：
质点系统总动量等于作用于该系统合外力的冲量
注意：只有外力才能引起质点系统总动量的改变，质点内力的矢量合为零，对系统总动量的改变毫无贡献，但内力会使系统内各质点的动量发生改变。

内力不会改变质点系的动量。

四、动量守恒定理【教材 p77 例3.2】
动量守恒定律：当系统所受合外力为零时，系统的动量守恒。

注意：
（1）质点所受合外力为零，每个质点的动量可能改变，系统内的动量可以相互转移，但他们的总合保持不变。

各质点的动量必相对于同一惯性参考系。

（2）若合外力不为零，但在某个方向上合外力分量为零，则在该方向上动量守恒。

（3）自然界中不受外力的物体是不存在的，但如果系统的外力<<内力，可近似认为动量守恒。

在碰撞、打击、爆炸等相互作用时间极短的过程中，往往可忽略外力。

（4）注意区别与，前者保证整个系统中动量守恒，后者说只说明始末时刻动量相同。

（5）动量守恒定律只适用于惯性系，在微观高速范围内仍使用，是自然界最普遍，最基本的定律之一。

讨论：
1.内力不会改变系统的动能，只有外力可改变系统的动能。

思考：在拔河时，如何判断哪儿队赢？
2.动量守恒是指总动量不变，各个质点的动量是可以变化的，通过内力的作用，动量在系统内的各个质点间进行转移。

3.动量守恒定律要求合外力为零的条件比较苛刻，如果内力远大于外力，或内力的冲量远大于外力的冲量时，可以当作合外力为零的近似情况。

4.动量定理与动量守恒定律都是矢量方程，在选取合适的坐标系后，可以写成相应各分量方程形式，则方程两端的物理含义表明了相应方向.上的合外力与动量变化之间的关系。

五、碰撞
碰撞过程分为完全弹性碰撞、弹性碰撞、完全非弹性碰撞。

（1）完全弹性碰撞
特点：机械能守恒、动量守恒
由机械能守恒：
由动量守恒：
2.完全非弹性碰撞
特点：机械能不守恒、动量守恒。

碰撞后两物体成为一个系统。

物体形变不能恢复。

例：质量为M=2.0kg的物体(不考虑体积)，用一根长1=1.0m为的细绳悬挂在天花板上，今有一质量为m=20g的子弹以v。

=600m/s的水平速度射穿物体,刚射出物体时子弹的速度大小v=30m/s,设穿透时间极短，求:
①子弹刚穿出时绳中张力的大小。

②子弹在穿透过程中所受的冲量。

解:
①因穿透时间极短,可认为物体未离开平衡位置,因此作用于子弹、物体
系统上的外力均在竖直方向，故系统在水平方向上动量守恒,设子弹穿出时物体的速度v则:
子弹射出瞬间，物体绕悬挂点做圆周运动：
③子弹冲量：
“-”表示冲量和速度方向相反，即水平向右。

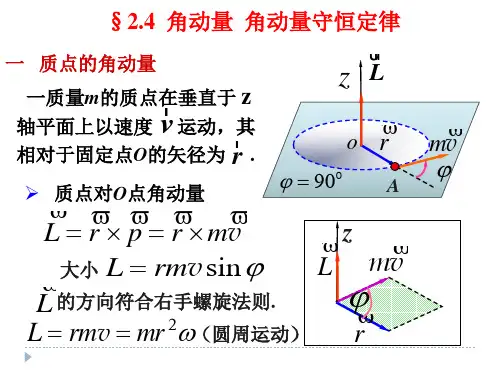
六、刚体的角动量
对于定轴转动而言：
定轴转动刚体的角动量定理：
微分形式：
积分形式：
或：
七、定轴轴转动刚体的角动量守恒
由定轴转动定理：
当M=0时
即：
刚体在定轴转动中，当对转轴的合外力矩为零时，刚体对转轴的角动量保持不变，这一规律就是定轴转动的角动量守恒定律。

讨论：
a．对于绕固定装轴转动的刚体，因J保持不变，当合外力矩力零吋，其角速度恒定。

当M=O时，J=恒量ω=恒量
b.若系统由若干个刚体构成,当合外力矩カ零肘,系统的角幼量依然守恒。

J大→の小,J小→の大。

当Mz=0吋，Lz=J1ω1+J2ω2=恒量
例如：花样滑冰运动员的“旋”动作、跳水运动员的“团身—展体”动作
c.若系统内既有平动也有转动现象发生,若对某一定轴的合外力矩为零,则系统对该轴的角动量守恒。

如：常平架上的回转仪
刚体的平动和定轴转动的一些重要公式
例：工程上，常用摩擦啮合器使两飞轮以相同的转速一起转动。

如图所示，A和B两飞轮的轴杆在同一中心线上，A轮的转动惯量为JA=10kg.m^2, B的转动惯量为JB=20kg.m^2。

开始时A轮的转速为600r/min,B轮静止。

C 为摩擦啮合器。

求两轮啮合后的转速;在啮合过程中，两轮的机械能有何变化?
解:
以飞轮A、B和啮合器C作为一系统来考虑，在啮合过程中，系统受到轴向的正压力和啮合器间的切向摩擦力，前者对转轴的力矩为零，后者对转轴有力矩，但为系统的内力矩。

系统没有受到其他外力矩，所以系统的角动量守恒。

按角动量守恒定律可得
ω为两齿轮齿和后共同转动的角速度，于是
各数值代入后得：
或共同转速为：
在啮合过程中，摩擦力矩作功，所以机械能不守恒，部分机械能将转化为热量，损失的机械能为
光电信息科学与工程2017级
信息学院朋辈导师王雨燕
质检组贾春虹。