2018年高考专题：曲线坐标图解题技法

图表曲线题解题技巧图表曲线题大多是以知识的获得过程为背景，或以知识的发现过程为背景来设计的，所获取的知识往往不是课本上现成的结论，有的还要求学生“现学现用”，这样的考查过程，实质上是在评价学生分析、归纳、推理的能力。

近几年的生物高考大纲相关能力要求部分均有：能用文字、图表等多种表达形式准确地描述生物学方面的内容。

读懂、读透图表、曲线等题中呈现的知识的过程也就是对知识再理解、再整合、再升华的过程。

针对不少学生看图、识表读图能力相对较差的特点，平时就得多加强这方面的评解和训练。

一．坐标曲线题坐标曲线题解题的一般思路和步骤：1．识图---关键是两看：一看纵横坐标所表示的生物学含义；二看曲线中的特殊点（起点、拐点、终点）和曲线的走势。

2．析图---图中为什么会出现特殊点，曲线为什么有这样的变化趋势和走向，分析曲线变化因果关系。

3．用图---通过联想、迁移等再现与图像曲线相关的知识点，生物学概念、原理、规律等。

例1．将盛有一定浓度蔗糖溶液的透析袋口扎紧后浸于蒸馏水中，下图表示透析袋中蔗糖溶液浓度与时间的关系，正确的是（）命题意图：本题考查的知识点是渗透作用的原理。

解析：渗透作用产生的2个必备条件是：一是具有半透膜；二是半透膜两侧溶液具有浓度差。

水分子能透过半透膜，从低浓度向高浓度扩散。

将盛有一定浓度的蔗糖溶液的透析袋放在蒸馏水中后，蒸馏水将不断向透析袋中扩散，蔗糖溶液浓度不断下降，但受到透析袋容积的限制，到一定时间后，水分子进出达到动态平衡，此时蔗糖溶液浓度下降到一定程度便保持相对稳定。

答案：B例2．下列各图中不正确的是（）命题意图：本题考查的知识点是杂合体连续自交后纯合体的比例、酵母菌呼吸作用产生的二氧化碳浓度、卵裂时细胞的体积、细胞有丝分裂中DNA的含量等方面的变化情况及识图分析的能力。

解析：据图分析可知，杂合体连续自交后产生的杂合子的比例为（1/2）n，自交次数无限增多时，则杂合体比例接近于0，而纯合体的比例接近于1，A项正确；卵裂时细胞进行有丝分裂，在卵裂期囊胚的总体积基本保持不变，但分裂产生的每个新细胞的体积是越来越小，C项正确；细胞有丝分裂过程中，间期DNA分子复制加倍，分裂期的前中后期中DNA的含量也是正常体细胞的2倍，末期复制的DNA分子随染色体平均分配到两个子细胞中，DNA含量恢复正常，D 选项正确；酵母菌的代谢类型是兼性厌氧型，在无氧条件下可进行无氧呼吸产生二氧化碳和酒精，在有氧条件下可进行有氧呼吸产生水和二氧化碳，因此，B选项错误。

图表曲线题的解题策略与技巧解题方法：坐标曲线题解题的一般思路和步骤：1、识图。

关键是两看：一看纵横坐标所表示 生物学含义；二看曲线中的特殊点（起点、拐点、终点）和曲线的走势。

2、析图。

图中为什么会出现特殊点，各特殊点表示的生物学意义，曲线为什么会有这样的趋势和走向，分析曲线变化的因果关系。

3、用图。

通过联想、迁移等再现与图像曲线相关的知识点，生物学概念、原理，规律等。

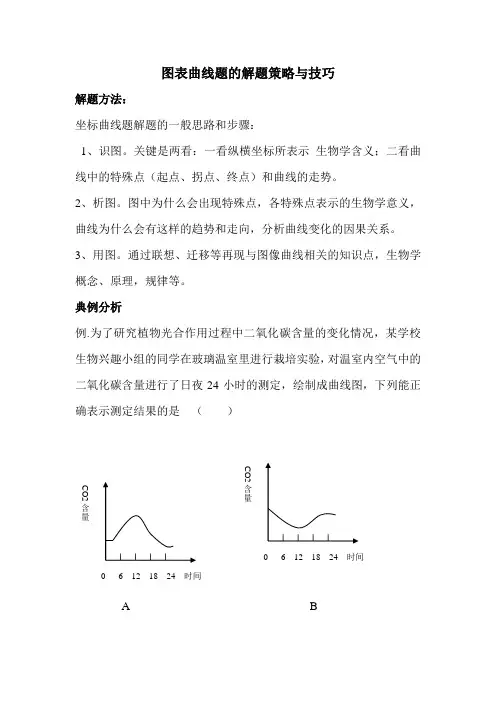
典例分析例.为了研究植物光合作用过程中二氧化碳含量的变化情况，某学校生物兴趣小组的同学在玻璃温室里进行栽培实验，对温室内空气中的二氧化碳含量进行了日夜24小时的测定，绘制成曲线图，下列能正确表示测定结果的是 （ ）AB0 6 12 18 24 时间 0 6 12 18 24 时间CD解析 此题首先要看清楚纵、横坐标所表示的生物学含义，再仔细观察曲线的走势（上升、下降、波动等变化）‘结合植物光合作用和呼吸作用的概念和原理，分析曲线变化的因果关系。

植物在0~6小时光线弱的条件下只能进行呼吸作用，吸收氧气，放出二氧化碳。

因此这段时间里温室内的二氧化碳是越来越多的。

在6~18小时光线较强的条件下既能进行光合作用，又能进行呼吸作用，但此时呼吸作用相对较弱，而植物在进行光合作用的过程中，不断的吸收二氧化碳，这样使温室内的二氧化碳越来越少。

植物在18~24小时光线暗的条件下也只能进行呼吸作用，吸收氧气，放出二氧化碳。

同样在这一段时间里温室中的二氧化碳越来越多。

故二氧化碳在温室内一天的变化是： 0~6小时二氧化碳的量是逐渐上升；6~18小时二氧化碳的量是逐渐下降18~24小时二氧化碳的量是逐渐上升。

答案：C 0 6 12 18 24 时间 0 6 12 18 24 时间。

2018届高三理科数学坐标系与参数方程解题方法规律技巧详细总结版【简介】坐标系与参数方程作为选做题，和不等式以二选一的形式出现，主要考查极坐标方程及应用，直线，圆和椭圆的参数方程的应用，难度一般不大，但是在做题过程有许多细节需要注意，例如审题时注意问的是参数方程还是极坐标方程，在应用上要从极坐标和参数方程中做出适合的选取，应用直线的参数方程解题时要理解参数t 的意义，如果理解不准极易出错，总之，对于本章的复习，要对概念要有准确的理解.【3年高考试题比较】坐标系与参数方程每年都以解答题的形式，和不等式以二选一的形式出现，在试卷中是最后一道题，但不是压轴题，属于解答题中的容易或比较容易的试题.内容主要涉及曲线与极坐标方程、参数方程、普通方程的关系，求曲线的轨迹、求曲线的交点，极坐标与直角坐标的转化等知识与方程，综合三年的高考题，对于极坐标的考察较多，不仅会极坐标与直角坐标转化，也要掌握极坐标的应用，同时椭圆、圆和直线的参数方程也要应用熟练，尤其是直线的参数方程易错点较多，复习时要引起重视. 【必备基础知识融合】1.平面直角坐标系中的坐标伸缩变换设点P (x ，y )是平面直角坐标系中的任意一点，在变换ϕ：⎩⎪⎨⎪⎧x ′＝λx （λ＞0），y ′＝μy （μ＞0）的作用下，点P (x ，y )对应到点P ′(x ′，y ′)，称φ为平面直角坐标系中的坐标伸缩变换. 2.极坐标系与点的极坐标(1)极坐标系：如图所示，在平面内取一个定点O (极点)；自极点O 引一条射线Ox (极轴)；再选定一个长度单位，一个角度单位(通常取弧度)及其正方向(通常取逆时针方向)，这样就建立了一个极坐标系. (2)极坐标：平面上任一点M 的位置可以由线段OM 的长度ρ和从Ox 到OM 的角度θ来刻画，这两个数组成的有序数对(ρ，θ)称为点M 的极坐标.其中ρ称为点M 的极径，θ称为点M 的极角. 3.极坐标与直角坐标的互化4.5.(1)直线l 过极点，且极轴到此直线的角为α，则直线l 的极坐标方程是θ＝α(ρ∈R ). (2)直线l 过点M (a ，0)且垂直于极轴，则直线l 的极坐标方程为ρcos__θ＝a .(3)直线过M ⎝⎛⎭⎪⎫b ，π2且平行于极轴，则直线l 的极坐标方程为ρsin__θ＝b . 6.曲线的参数方程一般地，在平面直角坐标系中，如果曲线上任意一点的坐标x ，y 都是某个变数t 的函数⎩⎪⎨⎪⎧x ＝f （t ），y ＝g （t ）并且对于t 的每一个允许值，由这个方程组所确定的点M (x ，y )都在这条曲线上，那么这个方程组就叫做这条曲线的参数方程，联系变数x ，y 的变数t 叫做参变数，简称参数. 7.参数方程与普通方程的互化通过消去参数从参数方程得到普通方程，如果知道变数x ，y 中的一个与参数t 的关系，例如x ＝f (t )，把它代入普通方程，求出另一个变数与参数的关系y ＝g (t )，那么⎩⎪⎨⎪⎧x ＝f （t ），y ＝g （t ）就是曲线的参数方程.在参数方程与普通方程的互化中，必须使用x ，y 的取值范围保持一致. 8.常见曲线的参数方程和普通方程(t 为参数)(θ为参数)(φ为参数)提醒一点M (x ，y )到M 0(x 0，y 0)的距离. 【解题方法规律技巧】典例1：将圆x 2＋y 2＝1上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C . (1)求曲线C 的标准方程；(2)设直线l ：2x ＋y －2＝0与C 的交点为P 1，P 2，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求过线段P 1P 2的中点且与l 垂直的直线的极坐标方程.典例2：在极坐标系中，已知极坐标方程C 1：ρcos θ－3ρsin θ－1＝0，C 2：ρ＝2cos θ. (1)求曲线C 1，C 2的直角坐标方程，并判断两曲线的形状； (2)若曲线C 1，C 2交于A ，B 两点，求两交点间的距离. 解 (1)由C 1：ρcos θ－3ρsin θ－1＝0， ∴x －3y －1＝0，表示一条直线. 由C 2：ρ＝2cos θ，得ρ2＝2ρcos θ. ∴x 2＋y 2＝2x ，即(x －1)2＋y 2＝1. 所以C 2是圆心为(1，0)，半径r ＝1的圆. (2)由(1)知，点(1，0)在直线x －3y －1＝0上， 所以直线C 1过圆C 2的圆心.因此两交点A ，B 的连线段是圆C 2的直径. 所以两交点A ，B 间的距离|AB |＝2r ＝2.典例3：在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝a cos t ，y ＝1＋a sin t (t 为参数，a >0).在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2：ρ＝4cos θ.(1)说明C 1是哪一种曲线，并将C 1的方程化为极坐标方程；(2)直线C 3的极坐标方程为θ＝α0，其中α0满足tan α0＝2，若曲线C 1与C 2的公共点都在C 3上，求a . 解 (1)消去t ，得C 1的普通方程x 2＋(y －1)2＝a 2， ∴曲线C 1表示以点(0，1)为圆心，a 为半径的圆.将x ＝ρcos θ，y ＝ρsin θ代入C 1的普通方程中，得到C 1的极坐标方程为ρ2－2ρsin θ＋1－a 2＝0. (2)曲线C 1，C 2的公共点的极坐标满足方程组⎩⎪⎨⎪⎧ρ2－2ρsin θ＋1－a 2＝0，ρ＝4cos θ. 若ρ≠0，由方程组得16cos 2θ－8sin θcos θ＋1－a 2＝0，由已知tan θ＝2，可得16cos 2θ－8sin θcos θ＝0，从而1－a 2＝0，解得a ＝－1(舍去)，a ＝1. 当a ＝1时，极点也为C 1，C 2的公共点，且在C 3上. 所以a ＝1.典例4：以直角坐标系中的原点O 为极点，x 轴正半轴为极轴的极坐标系中，已知曲线的极坐标方程为ρ＝21－sin θ.(1)将曲线的极坐标方程化为直角坐标方程；(2)过极点O 作直线l 交曲线于点P ，Q ，若|OP |＝3|OQ |，求直线l 的极坐标方程.典例5：在极坐标系中，已知圆C 的圆心C ⎝⎛⎭⎪⎫3，π3，半径r ＝3.(1)求圆C 的极坐标方程；(2)若点Q 在圆C 上运动，点P 在OQ 的延长线上，且OQ →＝2QP →，求动点P 的轨迹方程.解 (1)设M (ρ，θ)是圆C 上任意一点. 在△OCM 中，∠COM ＝⎪⎪⎪⎪⎪⎪θ－π3，由余弦定理得 |CM |2＝|OM |2＋|OC |2－2|OM |·|OC |cos ⎝ ⎛⎭⎪⎫θ－π3，化简得ρ＝6cos ⎝ ⎛⎭⎪⎫θ－π3.(2)设点Q (ρ1，θ1)，P (ρ，θ)， 由OQ →＝2QP →，得OQ →＝23OP →，∴ρ1＝23ρ，θ1＝θ，代入圆C 的方程，得23ρ＝6cos ⎝ ⎛⎭⎪⎫θ－π3，即ρ＝9cos ⎝⎛⎭⎪⎫θ－π3. 典例6：已知曲线C 1：x ＋3y ＝3和C 2：⎩⎨⎧x ＝6cos φ，y ＝2sin φ(φ为参数).以原点O 为极点，x 轴的正半轴为极轴，建立极坐标系，且两种坐标系中取相同的长度单位. (1)把曲线C 1和C 2的方程化为极坐标方程；(2)设C 1与x ，y 轴交于M ，N 两点，且线段MN 的中点为P .若射线OP 与C 1，C 2交于P ，Q 两点，求P ，Q 两点间的距离.典例7：已知曲线C ：x 24＋y 29＝1，直线l ：⎩⎪⎨⎪⎧x ＝2＋t ，y ＝2－2t (t 为参数).(1)写出曲线C 的参数方程，直线l 的普通方程；(2)过曲线C 上任意一点P 作与l 夹角为30°的直线，交l 于点A ，求|PA |的最大值与最小值. 解 (1)曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2cos θy ＝3sin θ(θ为参数).直线l 的普通方程为2x ＋y －6＝0.(2)曲线C 上任意一点P (2cos θ，3sin θ)到l 的距离为d ＝55|4cos θ＋3sin θ－6|， 则|PA |＝d sin 30°＝255|5sin(θ＋α)－6|，其中α为锐角，且tan α＝43.当sin(θ＋α)＝－1时，|PA |取得最大值，最大值为2255.当sin(θ＋α)＝1时，|PA |取得最小值，最小值为255.典例8：平面直角坐标系xOy 中，曲线C ：(x －1)2＋y 2＝1.直线l 经过点P (m ，0)，且倾斜角为π6.(1)求圆C 和直线l 的参数方程；(2)若直线l 与曲线C 相交于A ，B 两点，且|PA |·|PB |＝1，求实数m 的值.典例9：以直角坐标系的原点O 为极点，x 轴的正半轴为极轴，且两个坐标系取相等的长度单位.已知直线l的参数方程为⎩⎪⎨⎪⎧x ＝1＋t cos α，y ＝t sin α(t 为参数，0＜α＜π)，曲线C 的极坐标方程为ρsin 2θ＝4cos θ.(1)求曲线C 的直角坐标方程；(2)设直线l 与曲线C 相交于A ，B 两点，当α变化时，求|AB |的最小值. 解 (1)由ρsin 2θ＝4cos θ得(ρsin θ)2＝4ρcos θ， ∴曲线C 的直角坐标方程为y 2＝4x .(2)将直线l 的参数方程代入y 2＝4x 得到t 2sin 2α－4t cos α－4＝0. 设A ，B 两点对应的参数分别是t 1，t 2， 则t 1＋t 2＝4cos αsin 2 α，t 1t 2＝－4sin 2α. ∴|AB |＝|t 1－t 2|＝（t 1＋t 2）2－4t 1t 2＝4sin 2α≥4，当α＝π2时取到等号. ∴|AB |min ＝4，即|AB |的最小值为4.典例9:在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝3cos α，y ＝sin α(α为参数)，在以原点为极点，x 轴正半轴为极轴的极坐标系中，直线l 的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ－π4＝ 2.(1)求C 的普通方程和l 的倾斜角；(2)设点P (0，2)，l 和C 交于A ，B 两点，求|PA |＋|PB |的值.(2)由(1)知，点P (0，2)在直线l 上，可设直线l 的参数方程为⎩⎪⎨⎪⎧x ＝t cos π4，y ＝2＋t sin π4(t 为参数)，即⎩⎪⎨⎪⎧x ＝22t ，y ＝2＋22t(t 为参数)，代入x 29＋y 2＝1并化简，得5t 2＋182t ＋27＝0， Δ＝(182)2－4×5×27＝108＞0， 设A ，B 两点对应的参数分别为t 1，t 2，则t 1＋t 2＝－1825＜0，t 1t 2＝275＞0，所以t 1＜0，t 2＜0，所以|PA |＋|PB |＝|t 1|＋|t 2|＝－(t 1＋t 2)＝1825.典例10：在平面直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系．已知直线的参数方程为（为参数），曲线的极坐标方程为；（1）求直线的直角坐标系方程和曲线的直角坐标方程；（2）若直线与曲线交点分别为，，点，求的值．【答案】（1），曲线;(2) .【易错易混温馨提醒】一、直线参数方程的应用参数t解题时注意正负易错1：已知曲线的参数方程为（为参数），以平面直角坐标系的原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．（Ⅰ）求曲线的直角坐标方程及曲线上的动点到坐标原点的距离的最大值；（Ⅱ）若曲线与曲线相交于，两点，且与轴相交于点，求的值．【答案】（1），（2）二、注意直线与圆锥曲线联立时的判别式大于0易错2：在平面直角坐标系xOy 中，以坐标原点为极点， x 轴正半轴为极轴，取相同的长度单位建立极坐标系，曲线C 的极坐标方程为2sin ρθ=. (1)求曲线C 的直角坐标方程；(2)在平面直角坐标系中，将曲线C 的纵坐标不变，横坐标变为原来的2倍，得到曲线D ，过点()2,0M 作直线l ，交曲线D 于A B 、两点，若2MA MB ⋅=，求直线l 的斜率.【答案】（1）2220x y y +-=；（2）线l 的斜率为【解析】试题分析：（1）利用222,sin x y y ρρθ=+=把极坐标方程化为直角坐标方程；（2）设直线l 的参试题解析：(1)由2sin ρθ=，得22sin ρρθ=，将222,sin x y y ρρθ=+=，代入整理得2220x y y +-=. (2)把2220x y y +-=中的x 换成2x ，即得曲线D 的直角坐标方程2204x y y +-=. 设直线l 的参数方程为2,{x tcos y tsin φφ=+=（t 为参数， [)0,φπ∈）， 代入曲线D 的方程，整理得()()222cos 4sin 4cos 8sin 40t t φφφφ++-+=，()()2224cos 8sin 16cos 4sin 0φφφφ∆=--+>,cos sin 0φφ⇒<.设,A B 两点所对应的参数分别为12,t t ， 则12,t t 为上述方程的两个根. 由122240cos 4sin t t φφ=>+，得,MA MB 同向共线. 故由122242cos 4sin MA MB t t φφ⋅===21sin tan 3φφ⇒=⇒=.由cos sin 0φφ<，得tan 2φ=-即直线l 的斜率为2-..三、非标准形式的直线参数方程应用参数t 时要注意换为标准的参数. 易错3：在平面直角坐标系xOy 中，直线l的参数方程是1{x y ==（t 为参数），以O 为极点， x 轴的正半轴为极轴，建立极坐标系，曲线C 的极坐标方程为22223cos 4sin 12ρθρθ+=，且直线l 与曲线C 交于,P Q 两点.（Ⅰ）求直线l 的普通方程及曲线C 的直角坐标方程； （Ⅱ）把直线l 与x 轴的交点记为A ，求AP AQ ⋅的值. 【答案】(1)见解析；（2）18.7（II ）解法1：在10x y --=中，令0y =，得1x =，则()1,0A ． 由223412{10x y x y +=--=消去y 得27880x x --=.设()11,P x y ， ()22,Q x y ，其中12x x < ， 则有1287x x +=， 1287x x =-.故)1111AP x =-=-，)2211AQ x =-=-，所以AP AQ ⋅ ()()12211x x =--- ()121218217x x x x ⎡⎤=--++=⎣⎦.解法2：把()()112,{2,2x t y t =+=+==代入223412x y +=，整理得21490t +-=， 则12914t t =-， 所以AP AQ ⋅ ()()1212182247t t t t =-⋅=-=. 四、注意参数范围对于方程的影响易错4：在平面直角坐标系xOy 中，曲线1C 的参数方程为22,{32x cos y sin αα=+=+（α为参数， 2παπ≤≤），以原点O 为极点， x 轴正半轴为极轴，建立极坐标系，曲线2C的极坐标方程为sin 4πρθ⎛⎫-= ⎪⎝⎭． （1）求曲线1C 与2C 的直角坐标方程；（2）当1C 与2C 有两个公共点时，求实数t 的取值范围．【答案】（1）曲线2C 的直角坐标方程为0x y t -+=；（2）11t -<≤-.1C 有两个公共点，则当2C 与1C2=，整理得1t -=∴1t =-或1t =（舍去）， 当2C 过点()4,3时， 430t -+=，所以t=-1. ∴当1C 与2C 有两个公共点时，11t -<≤-．点睛：本题的易错点在把曲线1C 的参数方程化为直角坐标方程时，忽略了2παπ≤≤，得到曲线1C 是整个圆，那后面就会出错，所以在解题时，一定要注意认真审题，实行等价转化. 五、求轨迹方程时注意一些特殊点的取舍.易错5：在直角坐标系xOy 中，曲线1C 的参数方程为{x tcos y tsin αα== (t 为参数)，其中0απ<<，以坐标原点为极点， x 轴正半轴为极轴建立极坐标系，曲线2C 的极坐标方程是sin 5ρθ=， P 为曲线1C 与2C 的交点. (1)当3πα=时，求点P 的极径；(2)点Q 在线段OP 上，且满足20OP OQ ⋅=，求点Q 的轨迹的直角坐标方程.【答案】(2) ()()22240x y y +-=≠(2)在极坐标系中，设点(),Q ρθ， ()1,P ρθ，由题意可得， 1120[ 5sin ρρρθ==，进而可得4sin ρθ=，从而点Q 的轨迹的直角坐标方程为()()22240x y y +-=≠.六、参数方程化为普通方程时注意范围的变化在平面直角坐标系xOy 中，直线1l的参数方程为{x t y kt ==（t 为参数），直线2l的参数程为{3x mm y k==（m 为参数），设直线1l 与2l 的交点为P ,当k 变化时点P 的轨迹为曲线1C . （1）求出曲线1C 的普通方程； （2）以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，直线2C 的极坐标方程为sin 4πρθ⎛⎫+= ⎪⎝⎭，点Q 为曲线1C 的动点，求点Q 到直线2C 的距离的最小值. 【答案】（1）1C 的普通方程为()22103x y y +=≠;(2) d的最小值为由于1C的参数方程为{x y sina==（a 为参数， a k π≠， k Z ∈），所以曲线1C上的点)sin Qa a ，到直线80x y +-=的距离为d ==所以当sin 13a π⎛⎫+= ⎪⎝⎭时， d的最小值为。

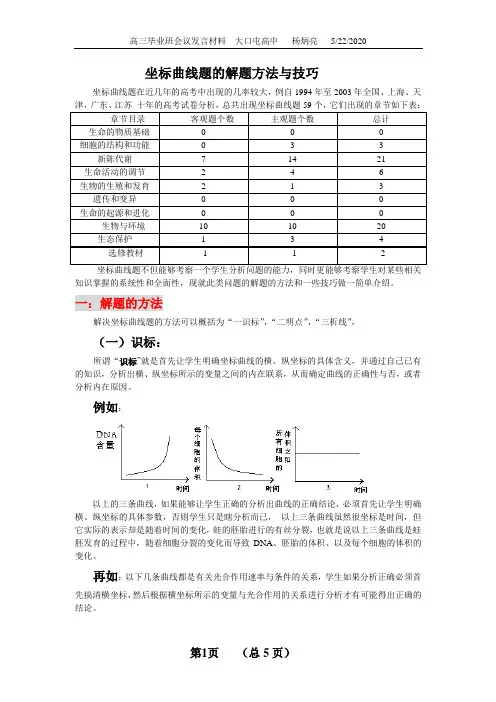
坐标曲线题的解题方法与技巧坐标曲线题在近几年的高考中出现的几率较大，例自1994年至2003年全国、上海、天津，广东、江苏十年的高考试卷分析，总共出现坐标曲线题59个，它们出现的章节如下表：坐标曲线题不但能够考察一个学生分析问题的能力，同时更能够考察学生对某些相关知识掌握的系统性和全面性，现就此类问题的解题的方法和一些技巧做一简单介绍。

一：解题的方法解决坐标曲线题的方法可以概括为“一识标”，“二明点”，“三析线”，（一）识标：所谓“识标”就是首先让学生明确坐标曲线的横、纵坐标的具体含义，并通过自己已有的知识，分析出横、纵坐标所示的变量之间的内在联系，从而确定曲线的正确性与否，或者分析内在原因。

例如：以上的三条曲线，如果能够让学生正确的分析出曲线的正确结论，必须首先让学生明确横、纵坐标的具体参数，否则学生只是瞎分析而已，以上三条曲线虽然很坐标是时间，但它实际的表示却是随着时间的变化，蛙的胚胎进行的有丝分裂，也就是说以上三条曲线是蛙胚发育的过程中，随着细胞分裂的变化而导致DNA、胚胎的体积、以及每个细胞的体积的变化。

再如：以下几条曲线都是有关光合作用速率与条件的关系，学生如果分析正确必须首先搞清横坐标，然后根据横坐标所示的变量与光合作用的关系进行分析才有可能得出正确的结论。

例三：以上两个曲线是叶绿体在不同的条件下有关有机物含量和生成率的曲线，如果学生没有明确纵坐标所问的是什么？光凭记忆去答题，有可能就弄错。

（二）：明点生物坐标的曲线是生物体某一生命活动，一种生理过程的反应，如果对某一生理过程有一个正确，全面的理解和掌握我们对曲线就要作全面地分析，例如：问：分析A 点表示_______________________________________。

分析AB 段表示_____________________________________。

分析B 点表示_________________________________________。

图表曲线题的解题策略与技巧解题方法：坐标曲线题解题的一般思路和步骤：1、识图。

关键是两看：一看纵横坐标所表示 生物学含义；二看曲线中的特殊点（起点、拐点、终点）和曲线的走势。

2、析图。

图中为什么会出现特殊点，各特殊点表示的生物学意义，曲线为什么会有这样的趋势和走向，分析曲线变化的因果关系。

3、用图。

通过联想、迁移等再现与图像曲线相关的知识点，生物学概念、原理，规律等。

典例分析例.为了研究植物光合作用过程中二氧化碳含量的变化情况，某学校生物兴趣小组的同学在玻璃温室里进行栽培实验，对温室内空气中的二氧化碳含量进行了日夜24小时的测定，绘制成曲线图，下列能正确表示测定结果的是 （ ）AB0 6 12 18 24 时间 0 6 12 18 24 时间CD解析 此题首先要看清楚纵、横坐标所表示的生物学含义，再仔细观察曲线的走势（上升、下降、波动等变化）‘结合植物光合作用和呼吸作用的概念和原理，分析曲线变化的因果关系。

植物在0~6小时光线弱的条件下只能进行呼吸作用，吸收氧气，放出二氧化碳。

因此这段时间里温室内的二氧化碳是越来越多的。

在6~18小时光线较强的条件下既能进行光合作用，又能进行呼吸作用，但此时呼吸作用相对较弱，而植物在进行光合作用的过程中，不断的吸收二氧化碳，这样使温室内的二氧化碳越来越少。

植物在18~24小时光线暗的条件下也只能进行呼吸作用，吸收氧气，放出二氧化碳。

同样在这一段时间里温室中的二氧化碳越来越多。

故二氧化碳在温室内一天的变化是： 0~6小时二氧化碳的量是逐渐上升；6~18小时二氧化碳的量是逐渐下降18~24小时二氧化碳的量是逐渐上升。

答案：C 0 6 12 18 24 时间 0 6 12 18 24 时间。

高中生物坐标曲线图解题技巧生物坐标曲线图题分为单一曲线图题和复合曲线图题，其解题步骤是：一是识图。

关键是三看，一看变量(x、y轴)表示的意义，找出两者之间的大致关系;二看曲线中的特殊点(起点、拐点、顶点、交叉点等)表示的意义;三看曲线的走向、变化趋势。

对有些曲线还要明白它的切线的斜率的含义。

分析图中为什么会有这种变化趋势。

如果同一坐标系中有多条曲线，做题时要明确每条曲线的含义、变化及其原因，与此曲线代表的生命现象相关的因素有哪些等;如果是复杂的生物图像题，可结合题意将图像拆分成若干个简单而直观的图像，先分析每一条曲线的变化规律，进而再分析不同曲线变化的因果关系、前后关系。

(类型题)拟南芥主根是研究细胞分裂和细胞生长的理想材料，生长素参与调节细胞的分裂、伸长和分化。

为探讨外施IAA、NAA、2，4-D 三种人工合成的生长素对拟南芥主根细胞分裂和伸长的影响，开展了以下研究。

生长素不直接参与细胞代谢，而向细胞传达一种调节代谢的_______。

取拟南芥的种子经过表面杀菌后，种在含有________的生长素的固体培养基上，培养8天后用直尺测量主根的长度，统计结果如图1统计时每组样本数为30株，实验重复3次的目的是________。

由图分析可知，三种生长素对主根的生长_______，且随着生长素浓度的增加_______。

为进一步探明此三种生长素对拟南芥主根影响的具体区域，用适宜浓度的三种生长素培养种子8天，对主根分生区和伸长区长度进行测量统计，结果如图2。

由图可知，IAA和NAA通过_______对拟南芥主根起作用。

2，4-D通过________对拟南芥主根起作用。

根尖分生区细胞的特点是_______。

研究人员将用三种激素培养的拟南芥幼苗根尖部分剪下，对分生区细胞数目进行观察统计。

发现与对照组相比，2，4-D处理后的分生区细胞数目减少，推断由分生区向伸长区转化的细胞数目________，最终影响到主根的生长。

微专题讲座1价格曲线坐标图题解题技巧价格曲线坐标图题2018年2017年2016年2015年2014年全国卷Ⅰ、Ⅱ全国卷Ⅰ、Ⅲ全国卷Ⅰ、Ⅱ经济曲线尤其是价格曲线试题具有直观性强、信息量大、新颖灵活等特点，因而受到命题人的青睐，近年来在高考中频频亮相。

它常以曲线图为载体，把数学的逻辑思维能力和函数知识应用到政治学科中，能全面地考查学生解读阐释信息、分析和解决问题的能力，是高考的常考题型。

解答曲线题要把握以下几个方面：①要观察坐标轴，明确谁是自变量(原因)，谁是因变量(结果)。

在政治学科中，一般情况下，纵轴是自变量，横轴是因变量。

特殊情况则是纵轴是自变量，横轴是因变量。

②明确两个量之间是正相关，还是负相关。

正相关的曲线是向上的，负相关的曲线是向下的。

③明确曲线的变化规律，是平行变动还是竖直变动，是平移变动还是沿曲线变动。

④根据曲线变动，对应材料信息，找出正确答案。

1.需求曲线和供给曲线典型例题1市场上某款运动鞋的价格上涨后，其供应量发生了相应的变化。

下列图示正确反映这一变化的是()A.①B.②C.③D.④解析价格与供应量之间是正相关关系，②是供给曲线，当选；①是需求曲线，应排除；③④反映的是价格不变，数量增加或减少的情况，不符合题意，因为题意指的是价格上涨。

答案 B方法总结解答需求曲线和供给曲线类试题，关键在于看方向。

价格与需求负相关，二者呈反方向变动。

价格与供给正相关，二者呈同方向变动。

跟踪训练1假设其他条件不变，下列图示能正确反映鸡蛋价格下跌带来的影响的是()A.①③B.①④C.②③D.②④解析鸡蛋属于生活必需品，它受价格变动影响比较小。

鸡蛋价格下跌，需求会略微增加，不会大幅增加，但供给会减少，因为获利减少，故①错误，②④正确；③表示的是高档耐用品，故排除。

答案 D2.需求曲线和供给曲线的变动典型例题2F市宣布，在2017年9月1日至2018年2月28日期间，对有当地户籍的农村户口居民，凡购买该市行政辖区内生产的小汽车，按汽车销售价格的6%给予补贴，最高补贴5 000元。