轮系的计算

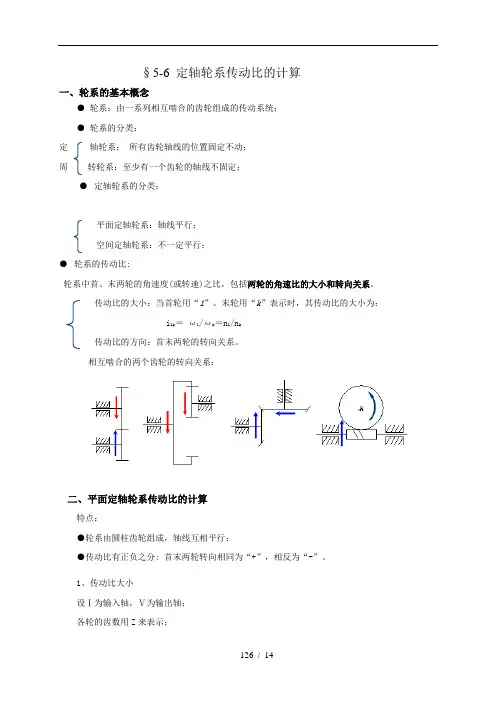
§5-6 定轴轮系传动比的计算一、轮系的基本概念●轮系：由一系列相互啮合的齿轮组成的传动系统；●轮系的分类：定轴轮系：所有齿轮轴线的位置固定不动；周转轮系：至少有一个齿轮的轴线不固定；●定轴轮系的分类：平面定轴轮系：轴线平行；空间定轴轮系：不一定平行；●轮系的传动比:轮系中首、末两轮的角速度(或转速)之比，包括两轮的角速比的大小和转向关系。

传动比的大小：当首轮用“1”、末轮用“k”表示时，其传动比的大小为： i1k＝ω1/ωk＝n1/n k传动比的方向：首末两轮的转向关系。

相互啮合的两个齿轮的转向关系：二、平面定轴轮系传动比的计算特点：●轮系由圆柱齿轮组成，轴线互相平行；●传动比有正负之分: 首末两轮转向相同为“+”，相反为“-”。

1、传动比大小设Ⅰ为输入轴，Ⅴ为输出轴；各轮的齿数用Z来表示；角速度用ω表示；首先计算各对齿轮的传动比：所以：结论：定轴轮系的传动比等于各对齿轮传动比的连乘积，其值等于各对齿轮的从动轮齿数的乘积与主动轮齿数的乘积之比；2、传动比方向在计算传动比时，应计入传动比的符号：首末两轮转向相同为“+”，相反为“-”。

（1）公式法式中：m为外啮合圆柱齿轮的对数举例：（2）箭头标注法采用直接在图中标注箭头的方法来确定首末两轮的转向，转向相同为“+”，相反为“-”。

举例：122112zzi==ωω32223332zizωωωω'''===33434443zizωωωω'''===455445zzi==ωω11211)1(--==kkmkk zzzziωω三、空间定轴轮系的传动比特点：●轮系中包含有空间齿轮（如锥齿轮、蜗轮蜗杆、螺旋齿轮等）； ●首末两轮的轴线不一定平行。

1 传动比的大小2 传动比的方向注意：只能采用箭头标注法，不能采用(-1)m 法判断。

分两种情况讨论：情况1：首、末两轮轴线平行传动比计算式前应加“+”、“-”号，表示两轮的转向关系。

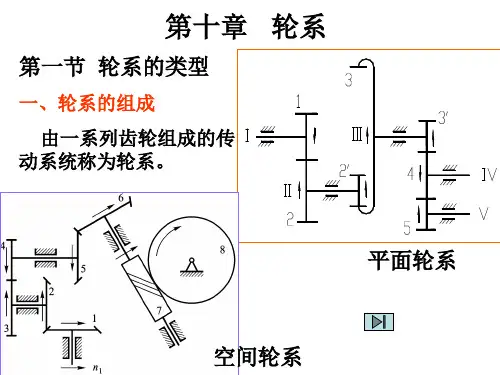
行星轮系自由度一、行星轮系简介行星轮系是一种常见的传动装置，由行星齿轮和太阳齿轮组成。

其具有许多独特的特点，其中之一就是自由度。

本文将详细探讨行星轮系的自由度问题。

1.1 行星轮系的构造行星轮系由一根轴和多个行星轮组成。

太阳齿轮位于行星轮系的中心，而行星轮则绕太阳齿轮旋转。

行星轮还与一个轮系（通常是外部环）相连，形成一个闭合的系统。

1.2 行星轮系的工作原理在行星轮系中，太阳齿轮是动力输入端，行星齿轮则是输出端。

当太阳齿轮旋转时，通过行星轮的转动，将动力传递到轮系上的外部环。

这种传动方式具有很高的效率和扭矩转动比。

二、行星轮系的自由度2.1 自由度的定义自由度是指系统可变动的自由度量。

在行星轮系中，自由度的定义与节点数和约束条件有关。

行星轮系的自由度可以用以下公式表示：自由度 = 节点数 - 约束条件在行星轮系中，节点数等于齿轮数+1，约束条件等于行星轮个数。

2.2 行星轮系的自由度计算方法行星轮系的自由度计算可以通过以下步骤完成：步骤1：确定齿轮数和行星轮个数。

步骤2：根据步骤1中的数据，计算节点数。

步骤3：根据行星轮个数，计算约束条件。

步骤4：应用自由度计算公式，得出行星轮系的自由度。

2.3 行星轮系的自由度举例例如，一个包含3个齿轮和2个行星轮的行星轮系，其计算过程如下：步骤1：齿轮数 = 3，行星轮个数 = 2步骤2：节点数 = 齿轮数 + 1 = 3 + 1 = 4步骤3：约束条件 = 行星轮个数 = 2步骤4：自由度 = 节点数 - 约束条件 = 4 - 2 = 2因此，该行星轮系的自由度为2。

三、行星轮系的自由度对传动性能的影响行星轮系的自由度对传动性能有着重要的影响。

自由度越大，系统的灵活性和可变性就越高，但也可能导致传动精度的下降。

下面将详细探讨自由度对传动性能的影响。

3.1 自由度与传动精度的关系自由度越大，行星轮系的误差累积越容易。

因为行星轮系的每个行星轮都可以自由运动，其位置误差会随着传动的进行而逐渐累积。

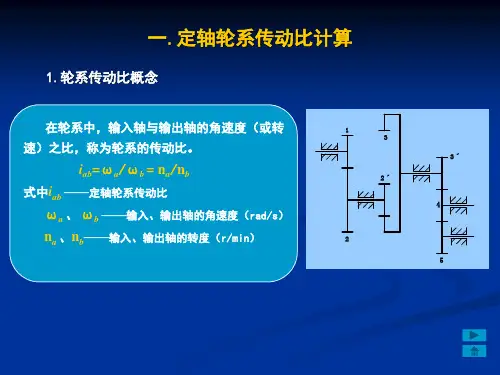
轮系及其传动比的计算详解轮系是由一组相互连接的轮齿组成的机械系统，用于传递动力和改变转速。

根据轮齿的不同数量和排列方式，轮系可以实现不同的传动比例，从而改变输入轮的转速和输出轮的转速。

在本文中，我们将详细介绍轮系的计算方法和传动比的计算方法。

首先，我们介绍一些与轮系计算相关的基本参数和概念。

1.轮齿数（Z）：每个轮齿的数量，通常用于计算轮齿的大小和分布。

2.模数（m）：轮齿的大小与分布的参数，表示每个轮齿的宽度与轮齿间距的比例。

3.齿轮比（i）：两个相邻轮齿的齿轮比为输出轮的齿数除以输入轮的齿数，用于表示输入轮与输出轮之间的转速比。

在轮系计算中，我们通常关注的是传动比（或齿轮比），它表示两个相邻轮齿之间的转速比。

传动比的计算方法取决于轮系的类型和轮齿的排列方式。

下面将介绍常见的轮系类型和它们的传动比计算方法。

1.平行轴齿轮传动：平行轴齿轮传动是最常见的轮系类型，用于将动力从一个轴传递到另一个轴上。

传动比的计算方法如下：- 整体齿轮比（i）=输出轮齿数（Z_out）/输入轮齿数（Z_in）- 输入轮输出转速（n_out）=输入轮输入转速（n_in）/整体齿轮比（i）2.平行轴齿轮传动（多级）：平行轴齿轮传动可以通过多级配置来实现更大的传动比。

在多级传动中，每个级别的传动比相乘，以得到整体的传动比。

3.内齿轮传动：内齿轮传动是一种特殊的齿轮传动，其中至少有一个轮齿是内部轮齿。

传动比的计算方法稍有不同：- 整体齿轮比（i）=输出轮齿数（Z_out）/（输入轮齿数（Z_in）+输出轮齿数（Z_out））- 输出轮输入转速（n_in）=输入轮输出转速（n_out）×整体齿轮比（i）4.锥齿轮传动：锥齿轮传动用于连接两个轴的交叉传动，其中两个轮齿是锥形的。

传动比的计算方法如下：- 整体齿轮比（i）=输出轮齿数（Z_out）/输入轮齿数（Z_in）- 输入轮输出转速（n_out）=输入轮输入转速（n_in）/整体齿轮比（i）最后，对于复杂的传动系统，传动比的计算可以通过将每个传动单元的传动比相乘来实现，从而得到整体的传动比。

针对你的问题有公式可参照分析：电机功率：P=1.732×U×I×cosφ电机转矩：T=9549×P/n ；电机功率转矩=9550*输出功率/输出转速转矩=9550*输出功率/输出转速P = T*n/9550公式推导电机功率，转矩，转速的关系功率=力*速度P=F*V---公式1转矩(T)=扭力(F)*作用半径(R) 推出F=T/R ---公式2线速度(V)=2πR*每秒转速(n秒) =2πR*每分转速(n分)/60 =πR*n分/30---公式3将公式2、3代入公式1得：P=F*V=T/R*πR*n分/30 =π/30*T*n分-----P=功率单位W，T=转矩单位Nm，n分=每分钟转速单位转/分钟如果将P的单位换成KW，那么就是如下公式：P*1000=π/30*T*n 30000/π*P=T*n 30000/3.1415926*P=T*n速比=电机输出转数÷减速机输出转数("速比"也称"传动比")1.知道电机功率和速比及使用系数，求减速机扭矩如下公式：减速机扭矩=9550×电机功率÷电机功率输入转数×速比×使用系数2.知道扭矩和减速机输出转数及使用系数，求减速机所需配电机功率如下公式：电机功率=扭矩÷9550×电机功率输入转数÷速比÷使用系数电动机扭距计算电机的“扭矩”，单位是N•m（牛米）计算公式是T=9549 * P / n 。

P是电机的额定（输出）功率单位是千瓦（KW）分母是额定转速n 单位是转每分(r/min)P和n可从电机铭牌中直接查到。

设：电机额定功率为P (kw)，转速为n1 (r/min)，减速器总传动比i，传动效率u。

则：输出转矩=9550*P*u*i/n1 (N.m)n=60f/p，p为极对数根据电机的同步转速n=60f/p计算同步转速：50HZ时：2极电机3000转/分；4极电机1500转/分；6极电机1000转/分60HZ时：2极电机3600转/分；4极电机1800转/分；6极电机1200转/分频率只差10HZ,极数少转速相差多，不知道你电机是几极的，除这个以外，因为上面的计算是同步转速，罩极电机也是异步电机，所以设法在电机设计中设法调整电机的转差率的大小也可以对转速进行控制依输出机构不同有不同算法以常见的机构,内齿圈固定,入力於中心的太阳齿,行星齿托架输出则为(内齿圈齿数/太阳齿齿数)+1,以一般伺服电机常用减速机为减速比1/10为例内齿圈齿数通常为108齿则太阳齿数为108/(10-1) = 12(齿)可得知减速比1/5 太阳齿为108/(5-1) = 27(齿)也就可以知道为甚麼这类机构减速比1/10 反而得不到最佳输出转矩原因就在此我查了一下，关于减速比是这样定义的。

《机械设计基础》试题库一、计算图示机构的自由度，并判断机构是否具有确定的运动。

（如有复合铰链、虚约束、局部自由度须指出）DEDCDDE二、轮系的计算1．在图示轮系中，已知各轮齿数为Z1=Z3=30，Z2=90，Z2’=40，Z3’=40，Z４=30，试求传动比i1H，并说明Ｉ、Ｈ轴的转向是否相同？2．在图示轮系中，已知各轮齿数为Z1 =15，Z2=20， Z2’ = Z3’= Z４=30， Z3=40，Z 5= 90，试求传动比IⅠⅡ，并说明Ｉ、Ⅱ轴的转向是否相同？3.在图示轮系中，已知各轮齿数为Z1=1（右旋蜗杆）， Z2=40 ，Z2’= 24，Z3=72，Z,3=18，Z4= 114.1、该轮系属于何种轮系2、求轮系的传动比i1H，并在图中标出系杆Ｈ的转向。

4.在图示轮系中，已知各轮齿数为Z1= 20，Z2=30，Z 2’= 50， Z3=80， n1=50r/min，方向如图所示，试求nH的大小和方向。

5.在图示轮系中，已知各轮齿数为Z1= Z4=20，Z 2= Z5=30，Z3= Z6=100，试求传动比i1H。

ⅠⅠⅡ6.在图示轮系中，已知各轮齿数为Z 1=100， Z 2=40，Z 2’=30， Z 3=90， Z ,3=50， Z 4=2(右旋)， n 1=200r/min ，n 4=1250r/min ，转向如图所示，试求n Ｈ的大小及方向。

7.在图示轮系中，已知各轮齿数为Z 1=15， Z 2=25，Z 2’=20， Z 3=20， Z 4=60，Z 4’= 55， n 1=110r/min ，转向如图所示，试求n h 的大小及转向。

8.某起重装置，其运动简图所图所示，已知各轮齿数为Z 1=Z 2=20，Z 3=60，Z 4=2(蜗杆)， Z 5=40，n 1的转向如图所示，试求 1、该轮系属于何种轮系？ 2、i 15的大小;3、此时重物Ｗ是上升还是下落？三、作图题（按作图规则作图，图线清晰） 1.凸轮为一偏心圆盘。

轮系自由度计算
轮系自由度是机器人运动学的基础，它表示机器人系统的空间运动自由度。

一般来讲，机器人的自由度是指机器人的运动轨迹受到的空间限制，以及机器人外形受到的关节约束所受到的限制。

常见的轮系自由度包括：
1. 直线移动的自由度：也称为X-Y自由度，指机器人可以在水平面内任意沿着X和Y方向进行移动的能力；
2. 转动自由度：也称为旋转自由度，指机器人可以在水平面内以指定的中心点为枢纽，任意沿着某个方向进行旋转的能力；
3. 高度调整自由度：也称为Z-轴自由度，指机器人可以在竖直面内任意沿着Z方向进行移动的能力；
4. 首部自由度：指机器人可以在指定的三维空间内任意沿着任意方向旋转的能力。

计算机器人的轮系自由度的方法是将机器人的每个关节的实际运动范围作为该关节的自由度，将它们加和起来，即为机器人的总自由度。

- 1 -。