(完整版)新课标高中数学微积分精选习题

高中微积分经典例题1. 函数求导- 例题1: 求函数 $f(x) = x^3 - 2x^2 + x$ 在点 $x=2$ 处的导数。

将函数 $f(x) = x^3 - 2x^2 + x$ 求导，得到 $f'(x) = 3x^2 - 4x + 1$。

将 $x=2$ 代入导数函数，得到 $f'(2) = 3(2)^2 - 4(2) + 1 = 9$。

所以函数 $f(x)$ 在点 $x=2$ 处的导数为 9。

- 例题2: 求函数 $g(x) = e^x \sin x$ 的导数。

使用链式法则，将函数 $g(x) = e^x \sin x$ 求导。

根据链式法则， $\frac{d}{dx} (e^x \sin x) = (e^x)' \sin x + e^x (\sin x)'$。

对于 $(e^x)'$，使用指数函数求导法则，得到 $(e^x)' = e^x$。

对于 $(\sin x)'$，使用三角函数求导法则，得到 $(\sin x)' = \cos x$。

将这些导数结果带入，得到 $\frac{d}{dx} (e^x \sin x) = e^x \sin x + e^x \cos x$。

所以函数 $g(x) = e^x \sin x$ 的导数为 $e^x \sin x + e^x \cos x$。

2. 积分计算- 例题1: 计算积分 $\int (3x^2 - 2x + 4) \, dx$。

根据积分的线性性质，将积分展开，得到 $\int (3x^2 - 2x + 4) \, dx = \int 3x^2 \, dx - \int 2x \, dx + \int 4 \, dx$。

对于每一项，根据幂函数积分法则，得到 $\int x^n \, dx =\frac{1}{n+1} x^{n+1}$。

将这些结果带入积分式，得到 $\int (3x^2 - 2x + 4) \, dx =\frac{1}{3} x^3 - x^2 + 4x + C$，其中 $C$ 为常数。

高一数学必修1微积分测试题及答案本文档为高一数学必修1微积分的测试题及答案，旨在帮助学生巩固和提高他们在微积分方面的知识和能力。

以下是题目及答案：题目一已知函数 f(x) 的导数 f'(x) = 2x + 3，求 f(x)。

答案：f(x) = x^2 + 3x + C （C为常数）题目二已知曲线 y = x^2 + 2x + 1，求曲线上任意点的切线方程。

答案：设曲线上某点的横坐标为 a，纵坐标为 b。

由题意可得，该点的切线斜率为曲线在该点的导数值。

曲线的导数为 f'(x) = 2x + 2。

将 a 代入 f'(x) 可得切线斜率 k = 2a + 2。

切线方程为 y - b = k(x - a)，将点的坐标代入可得切线方程。

题目三已知函数 f(x) = 2x^3 - 3x^2 + 2x，求函数 f(x) 的极值点和拐点。

答案：首先，求 f'(x)：f'(x) = 6x^2 - 6x + 2令 f'(x) = 0，求得极值点：x = (6 ± sqrt(36 - 48)) / 12，化简得 x = 0.5 或 x = 1将 x = 0.5 和 x = 1 代入 f(x) 可求得对应的 y 值。

其次，求 f''(x)：f''(x) = 12x - 6令 f''(x) = 0，求得拐点：x = 0.5将 x = 0.5 代入 f(x) 可求得对应的 y 值。

以上为高一数学必修1微积分的部分测试题及答案，希望对您有帮助。

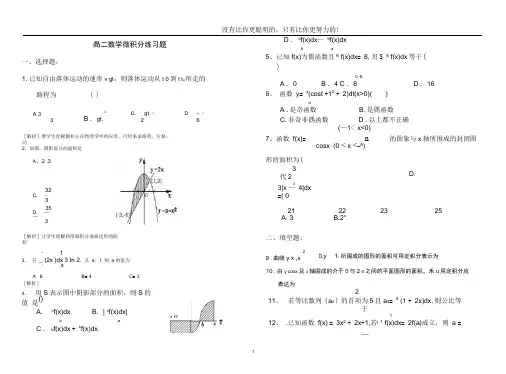
-1咼二数学微积分练习题一、选择题：1.已知自由落体运动的速率v gt ，则落体运动从t 0到t t o 所走的路程为( )A 33 2B .gt 。

c . gt 。

22 D .gt。

26［解析］要学生理解微积分在物理学中的应用，可用来求路程、位移、功D . c f(x)dx — b f(x)dxba5、 已知f(x)为偶函数且6 f(x)dx = 8,贝S 6 f(x)dx 等于()0 -6A . 0B . 4C . 8D . 166、 函数 y = x (cost +12 + 2)dt(x>0)()-xA .是奇函数B .是偶函数C .非奇非偶函数D .以上都不正确(—1< x<0)2、如图，阴影部分的面积是 A . 2 ,3 32 C. —335 D. —— 3 ［解析］让学生理解利用微积分求曲边形的面积 a1 3、 若 _ (2x )dx 3 In 2，且 a > 1,则 a 的值为1 x A . 6 B o 4 C o 3［解析］ 4、 用S 表示图中阴影部分的面积，则S 的值 是()A . c f(x)dxB . | c f(x)dx|a aC . b f(x)dx + c f(x)dx7、函数 f(x)= cosx n(0 < x <-^)的图象与x 轴所围成的封闭图a O形的面积为(3 代22D.3|x — 4|dx =( 0 21 A. 3 二、填空题:29 .曲线y x ,x0,y 22 B.2"23 251,所围成的图形的面积可用定积分表示为10 .由y cosx 及x 轴围成的介于0与2 n 之间的平面图形的面积，禾U 用定积分应表达为211、 若等比数列｛a n ｝的首项为5且a 4= 4 (1 + 2x)dx ,则公比等于112、 .已知函数 f(x) = 3x 2 + 2x +1,若 1 f(x)dx = 2f(a)成立，则 a = __14.求曲线y x3 x4 2x与x轴所围成的图形的面积. (2)若直线x= —t (O v t v 1=把y=f (x)的图象与两坐标轴所围成图形的面积二等分，求t的值.4求y=f (x)的图象与两坐标轴所围成图形的面积.15.已知f(a) = 1(2ax1 2—a2x)dx，求f(a)的最大值; 0一，选择题二、填空题9、10、三、解答题：.13.计算下列定积分的值11、12、16.设y=f (x)是二次函数，方程f (x) =0有两个相等的实根，且f'( x) =2x+2.cos2xdx2 5 (1) 1 (x 1) dx ；参考答案一、1. C; 2. C; 3. D; 4. D; 5 A 6 C 7. D 8; C二、9 o(1 X)dx 10. o Icosxdx ; 11、3 12、-1 或1/3 _2 1三、15、［解析］取F(x) = §ax3—2a3x2则F'(x) = 2ax2—a2x••• f (a) = 1(2 ax2—a2x)d x2 1 2=F(1) —F(0) = 3a—2a21 2 2 2一2a-3 + 91 1(2)依题意，有所求面积二l(x22x 1)dx (- x3x2x) |01 -.3 3t 2 0 2(3)依题意，有1(x 2x 1)dx t(x 2x 1)dx,•(£x3x2x)| - (3 x3x2x)|0t,3 3—1 t3+t2—t+1 = 1t3—t2+t,3 3 32t3—6t2+6t —仁0 ,1• 2 (t—1) 3= —1,于是t=1 —辽.评述：本题考查导数和积分的基本概念.(1) 求y=f (x)的表达式;3 2 ••当a= 3时,f (a)有最大值g.16.解：(1)设f (x) =ax2+bx+c,则f'( x) =2ax+b, 又已知f'( x) =2x+2• a=1, b=2.• f (x) =X2+2X+C又方程f (x) =0有两个相等实根，•判别式△=4 —4c=0,即c=1.故 f (x) =X2+2X+1.。

新课标高中数学微积分习题Document number【SA80SAB-SAA9SYT-SAATC-SA6UT-SA18】高二数学微积分练习题一、选择题：1．已知自由落体运动的速率gt v =，则落体运动从0=t 到0t t =所走的路程为 （ ）A ．320gtB ．20gt C ．220gt D ．620gt[解析]要学生理解微积分在物理学中的应用，可用来求路程、位移、功 2、如图，阴影部分的面积是A ．32B ．329-C ．332D ．335[解析]让学生理解利用微积分求曲边形的面积3、 若11(2)3ln 2ax dx x+=+⎰，且a ＞1，则a 的值为（ ）A ．6B 。

4C 。

3D 。

2 [解析]4、用S 表示图中阴影部分的面积，则S 的值是( )A ．⎠⎜⎛acf (x )d x B ．|⎠⎜⎛ac f (x )d x |C ．⎠⎜⎛a bf (x )d x ＋⎠⎜⎛bc f (x )d x D ．⎠⎜⎛b cf (x )d x －⎠⎜⎛ab f (x )d x 5、已知f (x )为偶函数且⎠⎜⎛6f (x )d x ＝8，则⎠⎜⎛-66f (x )d x 等于( )A ．0B ．4C ．8D ．166、函数y ＝⎠⎜⎛-xx(cos t ＋t 2＋2)d t (x >0)( ) A ．是奇函数B ．是偶函数C ．非奇非偶函数D ．以上都不正确 7、函数f(x)＝⎩⎪⎨⎪⎧x ＋1 (－1≤x<0)cosx (0≤x ≤π2)的图象与x 轴所围成的封闭图形的面积为( )B ． 1C ．28、⎠⎜⎛03|x 2－4|dx ＝( )二、填空题：9．曲线1,0,2===y x x y ，所围成的图形的面积可用定积分表示程f（x ＝；5 、-3－＝F (1)－F (0)＝23a －12a 2＝－12⎝⎛⎭⎪⎫a －232＋29∴当a ＝23时，f (a )有最大值29.16．解：（1）设f （x ）=ax 2+bx +c ，则f ′（x ）=2ax +b ， 又已知f ′（x ）=2x +2 ∴a =1，b =2. ∴f （x ）=x 2+2x +c又方程f （x ）=0有两个相等实根，∴判别式Δ=4－4c =0，即c =1. 故f （x ）=x 2+2x +1. （2）依题意，有所求面积=31|)31()12(0123201=++=++--⎰x x x dx x x .（3）依题意，有x x x x x x ttd )12(d )12(2021++=++⎰⎰---，∴023123|)31(|)31(t tx x x x x x ---++=++，－31t 3+t 2－t +31=31t 3－t 2+t ， 2t 3－6t 2+6t －1=0，∴2（t －1）3=－1，于是t =1－321. 评述：本题考查导数和积分的基本概念.。

微积分的应用专项练习60题(有答案)本文档包含60道微积分的应用专项练题目，每道题目均附有答案。

通过解答这些题目，您可以进一步巩固和应用微积分的知识，加深对微积分的理解。

以下是题目和答案的列表：1. 问题一（答案：A）2. 问题二（答案：B）3. 问题三（答案：C）4. 问题四（答案：D）5. 问题五（答案：A）6. 问题六（答案：B）7. 问题七（答案：C）8. 问题八（答案：D）9. 问题九（答案：A）10. 问题十（答案：B）11. 问题十一（答案：C）12. 问题十二（答案：D）13. 问题十三（答案：A）14. 问题十四（答案：B）15. 问题十五（答案：C）16. 问题十六（答案：D）17. 问题十七（答案：A）18. 问题十八（答案：B）19. 问题十九（答案：C）20. 问题二十（答案：D）21. 问题二十一（答案：A）22. 问题二十二（答案：B）23. 问题二十三（答案：C）24. 问题二十四（答案：D）25. 问题二十五（答案：A）26. 问题二十六（答案：B）27. 问题二十七（答案：C）28. 问题二十八（答案：D）29. 问题二十九（答案：A）30. 问题三十（答案：B）31. 问题三十一（答案：C）32. 问题三十二（答案：D）33. 问题三十三（答案：A）34. 问题三十四（答案：B）35. 问题三十五（答案：C）36. 问题三十六（答案：D）37. 问题三十七（答案：A）38. 问题三十八（答案：B）39. 问题三十九（答案：C）40. 问题四十（答案：D）41. 问题四十一（答案：A）42. 问题四十二（答案：B）43. 问题四十三（答案：C）44. 问题四十四（答案：D）45. 问题四十五（答案：A）46. 问题四十六（答案：B）47. 问题四十七（答案：C）48. 问题四十八（答案：D）49. 问题四十九（答案：A）50. 问题五十（答案：B）51. 问题五十一（答案：C）52. 问题五十二（答案：D）53. 问题五十三（答案：A）54. 问题五十四（答案：B）55. 问题五十五（答案：C）56. 问题五十六（答案：D）57. 问题五十七（答案：A）58. 问题五十八（答案：B）59. 问题五十九（答案：C）60. 问题六十（答案：D）这些题目的难度各不相同，涵盖了微积分应用的不同方面，包括导数、积分、微分方程等内容。

微积分练习题带答案微积分是数学的分支之一，它研究的是函数的变化规律。

在微积分中，经常会出现各种各样的练习题，这些练习题有助于我们加深对微积分概念和原理的理解。

在这篇文章中，我们将分享一些微积分练习题，并附带答案，希望对你的学习有所帮助。

1. 求函数f(x) = 2x^3 - x^2 + 3x - 5的导数。

答案：f'(x) = 6x^2 - 2x + 32. 求函数g(x) = e^x * sin(x)的导数。

答案：g'(x) = e^x * sin(x) + e^x * cos(x)3. 求函数h(x) = ln(x^2)的导数。

答案：h'(x) = 2/x4. 求函数i(x) = ∫(0到x) t^2 dt的导数。

答案：i'(x) = x^25. 求函数j(x) = ∫(x到1) t^2 dt的导数。

答案：j'(x) = -x^26. 求函数k(x) = ∫(0到x) e^t * sin(t) dt的导数。

答案：k'(x) = e^x * sin(x)7. 求函数l(x) = e^(-x)的不定积分。

答案：∫ e^(-x) dx = -e^(-x) + C (C为常数)8. 求函数m(x) = 1/(x^2+1)的不定积分。

答案：∫ 1/(x^2+1) dx = arctan(x) + C (C为常数)9. 求函数n(x) = 2x * cos(x^2)的不定积分。

答案：∫ 2x * cos(x^2) dx = sin(x^2) + C (C为常数)10. 求函数o(x) = ∫(1到x) e^(t^2) dt的原函数。

答案：o(x) = ∫(1到x) e^(t^2) dt + C (C为常数)以上是一些微积分练习题及其答案。

通过解答这些题目，我们可以巩固对微积分概念和原理的理解，并提升解题能力。

微积分是应用广泛的数学工具，在物理、工程、经济等领域都有重要的应用，掌握微积分对于进一步深入学习这些领域十分必要。

微积分练习题及答案微积分练习题及答案微积分是数学中的一门重要学科，它研究的是函数的变化规律和求解各种问题的方法。

在学习微积分的过程中，练习题是非常重要的，它能够帮助我们巩固知识、提高技能。

下面，我将为大家提供一些微积分的练习题及其答案，希望能够对大家的学习有所帮助。

一、求导练习题1. 求函数f(x) = x^3 + 2x^2 - 3x + 1的导数。

答案：f'(x) = 3x^2 + 4x - 32. 求函数g(x) = e^x * sin(x)的导数。

答案：g'(x) = e^x * sin(x) + e^x * cos(x)3. 求函数h(x) = ln(x^2 + 1)的导数。

答案：h'(x) = (2x) / (x^2 + 1)二、定积分练习题1. 计算定积分∫[0, 1] (x^2 + 1) dx。

答案：∫[0, 1] (x^2 + 1) dx = (1/3)x^3 + x ∣[0, 1] = (1/3) + 1 - 0 = 4/32. 计算定积分∫[1, 2] (2x + 1) dx。

答案：∫[1, 2] (2x + 1) dx = x^2 + x ∣[1, 2] = 4 + 2 - 1 - 1 = 43. 计算定积分∫[0, π/2] sin(x) dx。

答案：∫[0, π/2] sin(x) dx = -cos(x) ∣[0, π/2] = -cos(π/2) + cos(0) = 1三、微分方程练习题1. 求解微分方程dy/dx = 2x。

答案：对方程两边同时积分，得到y = x^2 + C，其中C为常数。

2. 求解微分方程dy/dx = e^x。

答案：对方程两边同时积分，得到y = e^x + C，其中C为常数。

3. 求解微分方程d^2y/dx^2 + 2dy/dx + y = 0。

答案：设y = e^(mx)，代入方程得到m^2 + 2m + 1 = 0，解得m = -1。

高三数学微积分专项练习题及答案1. 求函数f(x)=x^3-3x^2+2x的极值点。

解：首先，我们需要求出函数f(x)的导函数f'(x)，然后令f'(x)=0，解得的x值就是函数的极值点。

求导得到f'(x) = 3x^2 - 6x + 2。

令f'(x) = 0，解方程得到3x^2 - 6x + 2 = 0。

使用求根公式，我们得到x = (6 ± √(6^2 - 4*3*2))/(2*3)。

化简得到x = (6 ± √12)/(6) = (2 ± √3)/(2)。

所以，函数f(x)的极值点为x = (2 + √3)/(2)和x = (2 - √3)/(2)。

2. 求函数f(x)=sin(x)在区间[0, π]上的最大值和最小值。

解：首先，我们需要求出函数f(x)在区间[0, π]上的导函数f'(x)，然后找到导函数f'(x)=0的所有解，用这些解以及区间端点来确定最大值和最小值。

求导得到f'(x) = cos(x)。

找出f'(x)=0的解，即cos(x) = 0，解方程得到x = π/2。

此外，观察区间端点，当x = 0和x = π时，函数f(x)的值分别为sin(0) = 0和sin(π) = 0。

所以，在区间[0, π]上，函数f(x)的最大值为1（当x=π/2时），最小值为-1（当x=π/2时）。

3. 求函数f(x)=e^x * ln(x)的图像的渐近线。

解：函数f(x)的渐近线可以分为水平渐近线和垂直渐近线。

首先，我们来找水平渐近线。

当x趋向于负无穷或正无穷时，e^x趋向于0或正无穷，而ln(x)函数的定义域为(0,正无穷)，所以e^x * ln(x)的值趋向于0或正无穷。

因此，y = 0是函数f(x)的水平渐近线。

接下来，我们来找垂直渐近线。

垂直渐近线出现的位置取决于ln(x)的定义域。

ln(x)的定义域为(0,正无穷)，所以垂直渐近线会出现在x=0的位置。

高二数学微积分练习题一、选择题：1．已知自由落体运动的速率gt v =，则落体运动从0=t 到0t t =所走的路程为（ ）A ．320gtB ．20gtC ．220gt D ．620gt [解析]要学生理解微积分在物理学中的应用，可用来求路程、位移、功 2、如图，阴影部分的面积是A ．32B ．329-C ．332D ．335[解析]让学生理解利用微积分求曲边形的面积 3、 若11(2)3ln 2ax dx x+=+⎰，且a ＞1，则a 的值为 （ ）A ．6B 。

4C 。

3D 。

2[解析]4、用S 表示图中阴影部分的面积，则S 的值是( )A ．⎠⎛acf (x )d xB ．|⎠⎛ac f (x )d x |C ．⎠⎛ab f (x )d x ＋⎠⎛bcf (x )d xD ．⎠⎛bc f (x )d x －⎠⎛ab f (x )d x5、已知f (x )为偶函数且⎠⎛06 f (x )d x＝8，则⎠⎛-66f (x )d x 等于( )A ．0B ．4C ．8D ．166、函数y ＝⎠⎛-xx (cos t ＋t 2＋2)d t (x >0)( )A ．是奇函数B ．是偶函数C ．非奇非偶函数D ．以上都不正确 7、函数f(x)＝⎩⎨⎧x ＋1 (－1≤x<0)cosx (0≤x ≤π2)的图象与x轴所围成的封闭图形的面积为( )B ．1C ．2 8、⎠⎛03|x 2－4|dx ＝( )二、填空题：9．曲线1,0,2===y x x y ，所围成的图形的面积可用定积分表示为 ．f′（x）y=f.5 A dx|；3－1 2有最大值2 9 .16．解：（1）设f （x ）=ax 2+bx +c ，则f ′（x ）=2ax +b ， 又已知f ′（x ）=2x +2 ∴a =1，b =2. ∴f （x ）=x 2+2x +c又方程f （x ）=0有两个相等实根， ∴判别式Δ=4－4c =0，即c =1. 故f （x ）=x 2+2x +1.（2）依题意，有所求面积=31|)31()12(0123201=++=++--⎰x x x dx x x . （3）依题意，有x x x x x x ttd )12(d )12(2021++=++⎰⎰---，∴023123|)31(|)31(t tx x x x x x ---++=++，－31t 3+t 2－t +31=31t 3－t 2+t ， 2t 3－6t 2+6t －1=0，∴2（t －1）3=－1，于是t =1－321. 评述：本题考查导数和积分的基本概念.。

x 0 t x
2
1
x2
．
1
解： lim x e
x 0
2
1
lim
x2
et ． t t
17．求极限： lim sin x ln x ．
x 0
解： lim sin x ln x lim
x 0 x 0
1 ln x tan x sin x x lim lim 0． x 0 csc x x 0 csc x cot x x 1 x 2 1 x ． 1 x2 lim x 1 1 x tan 2 1 x x
cos 2x 1 2 sin 2x lim 2 x 0 sin x 2 x sin 2 x x cos 2 x 2 sin 2x 6x cos 2x 2x2 sin 2x ； 2 sin 2x 1 2 x lim x 0 2 sin 2x 3 4 cos 2 x x sin 2 x 2x lim


2．求极限： lim
e x e sin x ． x 0 x sin x
( x 0) ，∴ lim
解：∵ e x 1 ~ x
e x e sin x e x sin x 1 lim e sin x 1． x 0 x sin x x0 x sin x
x 0
2
13．求极限： lim
x1
1 1 ． 1 x ln x
1 1 1 1 ln x 1 x x lim lim lim x 1 1 x x 1 x 1 1 x ln x (1 x) ln x ln x ； 解： x 1 x 1 1 lim lim x 1 1 x x ln x x 1 1 ln x 1 2

高中数学微积分练习题目集一、函数与导数1. 求函数 $f(x) = x^2 + 3x + 2$ 在 $x=2$ 处的导数。

2. 求函数 $g(x) = \frac{1}{2}x^3 - 4x$ 的增减性和极值。

3. 已知函数 $h(x) = 3x^4 - 2x^3 + 5x^2 + 1$，求函数 $h(x)$ 的拐点。

二、极限的计算1. 计算 $\lim_{x \to 2} \frac{x^2 - 4}{x - 2}$。

2. 计算 $\lim_{x \to 0} \frac{\sin 3x}{\sin 5x}$。

3. 求 $\lim_{x \to \infty} \left(1 + \frac{1}{x}\right)^x$。

三、定积分1. 计算 $\int_0^1 (2x + 1) \ dx$。

2. 求 $\int_1^2 (3x^2 + 2x + 1) \ dx$。

3. 计算 $\int_0^{\pi/2} \cos x \ dx$。

四、微分方程1. 求解微分方程 $\frac{dy}{dx} + y = \sin x$。

2. 求解微分方程 $\frac{dy}{dx} = -\frac{y}{x}$。

3. 已知微分方程 $\frac{dy}{dx} = ky$，其中 $k$ 为常数，求其一阶线性齐次微分方程的通解。

五、数列与级数1. 求等差数列 $a_n = 2n - 1$ 的前 $n$ 项和。

2. 求等比数列 $b_n = 3 \cdot 2^{n-1}$ 的前 $n$ 项和。

3. 计算级数 $\sum_{n=1}^{\infty} \frac{1}{2^n}$。

六、多元函数1. 求函数 $f(x, y) = x^2 + y^2$ 的偏导数。

2. 已知函数 $g(x, y) = x^2 + 3xy + y^2$，求函数 $g(x, y)$ 在点 $(1, -2)$ 处的梯度。

3. 求函数 $h(x, y) = \sqrt{x^2 + y^2}$ 的方向导数，在点 $(3, 4)$ 朝斜率为 $-2$ 的方向上的方向导数。

新课标高中数学微积分习题修订版IBMT standardization office【IBMT5AB-IBMT08-IBMT2C-ZZT18】高二数学微积分练习题一、选择题：1．已知自由落体运动的速率gt v =，则落体运动从0=t 到0t t =所走的路程为（ ）A ．320gt B ．20gtC ．220gtD ．620gt[解析]要学生理解微积分在物理学中的应用，可用来求路程、位移、功2、如图，阴影部分的面积是A ．32B ．329-C ．332D ．335 [解析]让学生理解利用微积分求曲边形的面积3、 若11(2)3ln 2ax dx x+=+⎰，且a ＞1，则a 的值为（A ．6B 。

4C 。

3[解析]4、用S 表示图中阴影部分的面积，则S的值是( ) A．⎠⎛acf (x )d xB ．|⎠⎛ac f (x )d x |C ．⎠⎛a b f (x )d x ＋⎠⎛bc f (x )d x D ．⎠⎛bc f (x )d x －⎠⎛ab f (x )d x5、已知f (x )为偶函数且⎠⎛06 f (x )d x ＝8，则⎠⎛-66f (x )d x 等于( )A ．0B ．4C ．8D ．166、函数y ＝⎠⎛-xx (cos t ＋t 2＋2)d t (x >0)( )A ．是奇函数B ．是偶函数C ．非奇非偶函数D ．以上都不正确7、函数f(x)＝⎩⎨⎧x ＋1 (－1≤x<0)cosx (0≤x ≤π2)的图象与x 轴所围成的封闭图形的面积为( )A.32B ． 1C ．2 D.128、⎠⎛03|x 2－4|dx ＝( ) A.213 B.223 C.233D.253二、填空题： 9．曲线1,0,2===y x x y ，所围成的图形的面积可用定积分表示为 ．10．由x y cos =及x 轴围成的介于0与2π之间的平面图形的面积，利用定积分应表达为 ．11、若等比数列{a n }的首项为23，且a 4＝⎠⎛14(1＋2x )d x ，则公比等于____． 12、.已知函数f (x )＝3x 2＋2x ＋1，若⎠⎛-11f (x )d x ＝2f (a )成立，则a ＝________一，选择题 二、填空题9、 10、11、 12、 三、解答题：．13．计算下列定积分的值参考答案一、1．C ；dx |；－12a2x2有最大值2 9 .16．解：（1）设f （x ）=ax 2+bx +c ，则f ′（x ）=2ax +b ， 又已知f ′（x ）=2x +2∴a =1，b =2.∴f （x ）=x 2+2x +c又方程f （x ）=0有两个相等实根，∴判别式Δ=4－4c =0，即c =1.故f （x ）=x 2+2x +1.（2）依题意，有所求面积=31|)31()12(0123201=++=++--⎰x x x dx x x .（3）依题意，有x x x x x x ttd )12(d )12(2021++=++⎰⎰---，∴023123|)31(|)31(t tx x x x x x ---++=++，－31t 3+t 2－t +31=31t 3－t 2+t ，2t 3－6t 2+6t －1=0，∴2（t －1）3=－1，于是t =1－321. 评述：本题考查导数和积分的基本概念.。

高等数学微积分练习题集2(含答案)1．求抛物线2x y =与直线02=--y x 之间的最短距离。

2．求点)8,2(到抛物线x y 42=的最短距离。

3．求过点31,1,2(的平面，使它与三个坐标面在第一卦限内所围成的立体体积最小。

4．计算二重积分dxdy xy I D ⎰⎰=2，其中D 是由直线2,==x x y 及双曲线1=xy 所围成的区域。

5．计算二重积分dxdy e I D y ⎰⎰-=2，其中区域D 由y 轴，直线x y y ==,1所围成。

6．求dxdy y xy I D ⎰⎰+=31，其中D 由2,1,0x y y x ===所围成。

7．求dy e dx x I x y ⎰⎰-=11022。

8．求dxdy y x I D ⎰⎰+=)(，其中D 为224,x y xy ==及1=y 所围成的区域。

9．求σd y x I D⎰⎰+=)|(|，其中D 为：1||||≤+y x 。

10．求dxdy y x I D⎰⎰--=221，其中D ：y y x ≤+22。

11．求dxdy y x x I D ⎰⎰--=)2(22，其中D ：1)1(22≤+-y x 。

12．设{}x y x y x D ≤+=22),(，求dxdy x D ⎰⎰。

13．计算二重积分dxdy yx y x D ⎰⎰++--222211，其中D 是由圆周122=+y x 及坐标轴所围成的在第一卦限内的闭区域。

14．求ds y x c ⎰+)(，其中c 是以)0,0(O ，)0,1(A ，)1,0(B 为顶点的三角形边界。

15．设L 是半圆周24y x -=上由点)2,0(A 到点)2,0(-B 之间的一段弧。

计算⎰++L ds y x )1(。

16．计算ds y x L ⎰+22，其中L 为圆周222a y x =+（0>a ）。

17．计算曲线积分⎰+L ds y x 22，其中L 为圆周x y x =+22。

18．计算曲线积分：dy y x dx y x I L )653()42(-++--=⎰，其中L 是从点)0,0(O 到点)2,3(A 再到点)0,4(B 的折线段。

新课标高中数学微积分习题SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#高二数学微积分练习题一、选择题：1．已知自由落体运动的速率gt v =，则落体运动从0=t 到0t t =所走的路程为（ ）A ．32gt B ．20gt C ．220gtD ．620gt[解析]要学生理解微积分在物理学中的应用，可用来求路程、位移、功 2、如图，阴影部分的面积是A ．32B ．329-C ．332D ．335[解析]让学生理解利用微积分求曲边形的面积3、 若11(2)3ln 2ax dx x+=+⎰，且a ＞1，则a 的值为（ ）A ．6B 。

4C 。

3 D 。

2[解析]4、用S 表示图中阴影部分的面积，则S 的值是( )A ．⎠⎜⎛acf (x )d x B ．|⎠⎜⎛acf (x )d x |C ．⎠⎜⎛a bf (x )d x ＋⎠⎜⎛bc f (x )d xD ．⎠⎜⎛bcf (x )d x －⎠⎜⎛ab f (x )d x 5、已知f (x )为偶函数且⎠⎜⎛6f (x )d x ＝8，则⎠⎜⎛-66f (x )d x 等于( )A ．0B ．4C ．8D ．166、函数y ＝⎠⎜⎛-xx(cos t ＋t 2＋2)d t (x >0)( )A ．是奇函数B ．是偶函数C ．非奇非偶函数D ．以上都不正确 7、函数f(x)＝⎩⎪⎨⎪⎧x ＋1 (－1≤x<0)cosx (0≤x ≤π2)的图象与x轴所围成的封闭图形的面积为( )B ．1C ．2 8、⎠⎜⎛03|x 2－4|dx ＝( )二、填空题：9．曲线1,0,2===y x x y ，所围成的图形的面积可用定积分表示为 ．16．解：（1）设f （x ）=ax 2+bx +c ，则f ′（x ）=2ax +b ， 又已知f ′（x ）=2x +2 ∴a =1，b =2. ∴f （x ）=x 2+2x +c又方程f （x ）=0有两个相等实根， ∴判别式Δ=4－4c =0，即c =1. 故f （x ）=x 2+2x +1. （2）依题意，有所求面积=31|)31()12(0123201=++=++--⎰x x x dx x x . （3）依题意，有x x x x x x ttd )12(d )12(2021++=++⎰⎰---，∴023123|)31(|)31(t tx x x x x x ---++=++，－31t 3+t 2－t +31=31t 3－t 2+t ， 2t 3－6t 2+6t －1=0，∴2（t －1）3=－1，于是t =1－321. 评述：本题考查导数和积分的基本概念.。

高二数学微积分练习题一、选择题：1．已知自由落体运动的速率gt v =，则落体运动从0=t 到0t t =所走的路程为（ ）A ．320gt B ．20gtC ．220gt D ．620gt[解析]要学生理解微积分在物理学中的应用，可用来求路程、位移、功 2、如图，阴影部分的面积是A ．32B ．329-C ．332D ．335[解析]让学生理解利用微积分求曲边形的面积3、 若11(2)3ln 2ax dx x+=+⎰，且a ＞1，则a 的值为（ ）A ．6B 。

4C 。

3D 。

2 [解析] 4、用S 表示图中阴影部分的面积，则S 的值是( )A ．⎠⎛a c f (x )d xB ．|⎠⎛ac f (x )d x |C ．⎠⎛a b f (x )d x ＋⎠⎛bc f (x )d xD ．⎠⎛b c f (x )d x －⎠⎛ab f (x )d x5、已知f (x )为偶函数且⎠⎛06 f (x )d x ＝8，则⎠⎛-66f (x )d x等于( )A ．0B ．4C ．8D ．16 6、函数y ＝⎠⎛-xx (cos t ＋t 2＋2)d t (x >0)( )A ．是奇函数B ．是偶函数C ．非奇非偶函数D ．以上都不正确7、函数f(x)＝⎩⎨⎧x ＋1 (－1≤x<0)cosx (0≤x ≤π2)的图象与x 轴所围成的封闭图形的面积为( )A.32 B ．1 C ．2 D.128、⎠⎛03|x 2－4|dx ＝( ) A.213 B.223 C.233D.253二、填空题：9．曲线1,0,2===y x x y ，所围成的图形的面积可用定积分表示为 ．10．由x y cos =及x 轴围成的介于0与2π之间的平面图形的面积，利用定积分应表达为 ．11、若等比数列{a n }的首项为23，且a 4＝⎠⎛14 (1＋2x )d x ，则公比等于____．12、.已知函数f (x )＝3x 2＋2x ＋1，若⎠⎛-11f (x )d x ＝2f (a )成立，则a ＝________二、填空题9、 10、11、 12、三、解答题：．13．计算下列定积分的值（1）⎰-215)1(dx x ；（2）dx x ⎰-222cos ππ14．求曲线x x x y 223++-=与x 轴所围成的图形的面积．15．已知f(a)＝1(2ax2－a2x)dx，求f(a)的最大值；⎠⎛016．设y=f（x）是二次函数,方程f（x）=0有两个相等的实根，且f′（x）=2x+2.（1）求y=f（x）的表达式；（2）求y=f（x）的图象与两坐标轴所围成图形的面积.（2）若直线x=－t（0＜t＜1＝把y=f（x）的图象与两坐标轴所围成图形的面积二等分，求t的值.参考答案一、1．C ；2．C ；3．D ；4．D ；5 A 6 C 7．D 8；C 二、9dx x ⎰-12)1( 10．dx x ⎰π20|cos |；11、3 12、-1或1/3三、15、[解析] 取F (x )＝23ax 3－12a 2x 2则F ′(x )＝2ax 2－a 2x ∴f (a )＝⎠⎛01(2ax 2－a 2x )d x＝F (1)－F (0)＝23a －12a 2＝－12⎝⎛⎭⎪⎫a －232＋29∴当a ＝23时，f (a )有最大值29.16．解：（1）设f （x ）=ax 2+bx +c ，则f ′（x ）=2ax +b ，又已知f ′（x ）=2x +2 ∴a =1，b =2.∴f （x ）=x 2+2x +c又方程f （x ）=0有两个相等实根， ∴判别式Δ=4－4c =0，即c =1. 故f （x ）=x 2+2x +1.（2）依题意，有所求面积=31|)31()12(0123201=++=++--⎰x x x dx x x .（3）依题意，有x x x x x x ttd )12(d )12(2021++=++⎰⎰---， ∴023123|)31(|)31(t t x x x x x x ---++=++， －31t 3+t 2－t +31=31t 3－t 2+t ， 2t 3－6t 2+6t －1=0，∴2（t －1）3=－1，于是t =1－321. 评述：本题考查导数和积分的基本概念.。

高中数学练习题微积分与解析几何高中数学练习题 -- 微积分与解析几何（正文内容开始）题目一：已知曲线C的参数方程为：x = t³ - 3t² + 3t, y = t² - 2t + 1.求曲线C的切向量和法向量，并求曲线C在t=1处的切线和法线方程。

解答：首先，我们需要求曲线C的切向量和法向量。

曲线C的切向量可以通过对参数方程求导得到，即：dx/dt = 3t² - 6t + 3, dy/dt = 2t - 2.所以，曲线C的切向量为 (dx/dt, dy/dt) = (3t² - 6t + 3, 2t - 2).接下来，我们需要求曲线C在t=1处的切线和法线方程。

将t=1代入切向量表达式中，可得曲线C在t=1处的切向量为 (0, 0).由于切线的方向与切向量平行，切线方程的斜率为0，即切线方程为x = 1.同时，我们知道切线与曲线C相切于同一点，并且切线的法向量与曲线的切向量垂直。

所以，曲线C在t=1处的法向量与切向量垂直，即 (3t² - 6t + 3, 2t - 2)·(x-1, y) = 0.将曲线C的参数方程代入，可得曲线C在t=1处的法线方程为 (t³ - 3t² + 3t - 1)(x-1) + (t² - 2t + 1)(y) = 0.题目二：已知直线L1过点A(1, 2, 3)和点B(-2, 1, 4)，直线L2过点C(-1, 0, 1)且与L1平行，求直线L2的解析式。

解答：首先，我们可以通过点A和点B来确定直线L1的方向向量d1，即d1 = AB = (1 - (-2), 2 - 1, 3 - 4) = (3, 1, -1).由于直线L2与L1平行，所以直线L2与直线L1具有相同的方向向量d1。

因此，直线L2的方向向量为d2 = (3, 1, -1).接下来，我们可以通过已知点C和L2的方向向量d2来确定直线L2的解析式。

微积分练习题一、极限与连续(1) lim(x→0) (sin x / x)(2) lim(x→1) (x^2 1) / (x 1)(3) lim(x→∞) (1 + 1/x)^x(1) f(x) = |x| 1，在x = 0处(2) f(x) = (x^2 1) / (x 1)，在x = 1处(3) f(x) = sqrt(x + 2) 2，在x = 1处二、导数与微分(1) f(x) = x^3 3x + 2(2) f(x) = e^x sin x(3) f(x) = ln(sqrt(1 + x^2))(1) f(x) = x^2 + 3x 5(2) f(x) = cos(2x)(3) f(x) = 1 / (1 x)三、高阶导数与微分方程(1) f(x) = x^4 2x^2 + 1(2) f(x) = e^x cos x(3) f(x) = ln(x^2 + 1)(1) y' = 2x + y(2) y'' 2y' + y = e^x(3) (1 + x^2) y'' + 2x y' = 0四、不定积分与定积分(1) ∫(x^2 + 1) dx(2) ∫(e^x x) dx(3) ∫(1 / (x^2 + 1)) dx(1) ∫_{0}^{1} (3x^2 2x + 1) dx(2) ∫_{π}^{π} (sin x) dx(3) ∫_{1}^{e} (1 / x) dx五、多元函数微分学(1) f(x, y) = x^2 + y^2(2) f(x, y) = e^(x + y) sin(x y)(3) f(x, y) = ln(x^2 + y^2)(1) f(x, y) = x^3 + y^3(2) f(x, y) = sin(x + y)(3) f(x, y) = sqrt(x^2 + y^2)六、重积分(1) ∬_D (x^2 + y^2) dxdy，其中D为圆心在原点，半径为1的圆(2) ∬_D (x y) dxdy，其中D为矩形区域0 ≤ x ≤ 1，0 ≤ y ≤ 2(3) ∬_D (e^(x + y)) dxdy，其中D为三角形区域0 ≤ x ≤ 1，0 ≤ y ≤ x(1) ∭_E (x^2 + y^2 + z^2) dxdydz，其中E为立方体区域0 ≤ x ≤ 1，0 ≤ y ≤ 1，0 ≤ z ≤ 1(2) ∭_E (xyz) dxdydz，其中E为长方体区域0 ≤ x ≤ 2，0 ≤ y ≤ 3，0 ≤ z ≤ 4七、级数(1) Σ (1/n^2)，n从1到∞(2) Σ (n/(n+1)^2)，n从1到∞(3) Σ ( (1)^n / n )，n从1到∞(1) Σ (x^n / n)，n从1到∞(2) Σ (n! x^n)，n从0到∞(3) Σ ( (n^2 + 1)^n x^n )，n从0到∞八、微分方程的应用(1) 物体在空气中自由下落，其速度v与时间t的关系，已知阻力与速度成正比。