云南省三校生高考复习——集合

“集合”单元测试题班级： 姓名： 得分：一、选择题（每小题4分，共80分）1、①“全体著名文学家”构成一个集合；②集合{0}中不含元素；③{1，2}，{2，1}是不同的集合；上面三个叙述中，正确的个数是（ ）A 、0B 、1C 、2D 、32、已知集合{|21}M x x =-<<，则下列关系式正确的是（）M A 、∈5B.0M ∉C.1M ∈D.2M π-∈3、在下列式子中，①}210{1，，∈ ②}210{}1{，，∈ ③}210{}210{，，，，⊆ ④{0,1,2}⊂∅≠⑤{0，1，2}={2，1，0}，其中错误的个数是（ ） A 、1个B 、2个C 、3个D 、4个4、}3,2,1,0{}1,0{⊆⊆A ，则集合A 的个数有（ ）A 、2个B 、3个C 、4个D 、5个5、下列各式中，不正确的是（ ）A 、A A =B 、A A ⊆C 、A A ⊂≠D 、A A ⊇6、已知集合*{|2}A x x x N =≥∈且，*{|6}B x x x N =≤∈且，则B A ⋂等于（ ）A 、{1，2，3，4，5，6}B 、{2，3，4，5，6}C 、{2，6}D 、{|26}x x ≤≤7、集合A={0，1，2，3，4，5}，B={2，3，4}，A B ⋃=（ ）A 、{0，1，2，3，4，5}B 、{2，3，4}C 、{0，1，2，2，3，3，4，4，5}D 、{1，2，3，4}8、设{|A x x a =≤=（ ）A 、{}a A ∉B 、{}a A ∈C 、a A ∉D 、a A ∈9、设{}()M 1{1,2},{1,2,3},S P M S P ===⋃⋂，则等于（ ）A 、{1，2，3}B 、{1，2}C 、{1}D 、{3}10、满足条件{}M 1{1,2,3}⋃=的集合M 的个数是（ ）A 、4B 、3C 、2D 、111、设全集{0,123456}U =，，，，，，集合{3456}A =，，，，则U C A =（ ） A 、{0，3，4，5，6}B 、{3，4，5，6}C 、∅D 、{0，1，2}12、225x =的充分必要条件是（ ） A 、55x x ==-且B 、55x x ==-或C 、5x =D 、5x =-13、设3{|23},{|},2A x xB x x =-≤<=≥则A B ⋃=（ ）A 、{|2}x x <-B 、{|23}x x x <-≤或C 、{|23}x x x <->或D 、}2|{-≥x x14、下列集合是无限集的是（ ） A 、{|01}x x ≤≤B 、2{|10}x x +=C 、2{|60}x x x --=D 、{|(1),}n x x n N =-∈15、下列四个推理：①()a A B a A ∈⋃⇒∈ ； ② ()()a A B a A B ∈⋂⇒∈⋃； ③A B A B B ⊆⇒⋃=； ④A B A A B B ⋃=⇒⋂=。

高考关于集合的知识点总结在高考数学考试中，集合是一个重要的数学概念，也是考试中常常出现的题型。

本文将从一些基本概念和运算法则入手，总结高考中关于集合的知识点。

一、基本概念集合是由一些确定的对象组成的整体。

在集合中，对象称为元素，记作x∈A，表示x是集合A的一个元素。

如果集合A中的某个元素x没有特定的性质，只要它属于集合A，都可以被接受。

集合的表示方法有两种：列举法和描述法。

列举法是把集合中的元素一一列出来，用大括号括起来表示，如A={1, 2, 3}。

描述法是通过一定的条件描述集合中的元素，用大括号括起来表示，如A={x|x>0}，表示集合A中的元素x满足x大于0。

二、集合的关系1. 相等关系：当两个集合A和B中的元素完全相同，记作A=B。

2. 包含关系：当集合A中的所有元素都是集合B的元素时，称集合A是集合B的子集，记作A⊆B。

3. 真包含关系：当集合A是集合B的子集，并且集合B中还有集合A没有的元素时，称集合A是集合B的真子集，记作A⊂B。

4. 并集：将两个集合A和B中所有的元素都放在一起构成的集合，记作A∪B。

5. 交集：集合A和集合B中都有的公共元素构成的集合，记作A∩B。

6. 差集：集合A中去掉与集合B相同的元素所剩下的元素构成的集合，记作A-B。

三、集合的运算法则1. 交换律：A∪B=B∪A，A∩B=B∩A2. 结合律：(A∪B)∪C=A∪(B∪C)，(A∩B)∩C=A∩(B∩C)3. 分配律：A∪(B∩C)=(A∪B)∩(A∪C)，A∩(B∪C)=(A∩B)∪(A∩C)4. 吸收律：A∪(A∩B)=A，A∩(A∪B)=A5. 互补律：A∪A' = U（全集），A∩A' = φ（空集）6. De Morgan定律：(A∪B)'=A'∩B'，(A∩B)'=A'∪B'四、应用题解析在高考中，常常出现一些应用题考查集合的知识点。

集合知识点高三复习笔记一、集合的定义和表示方法在数学中，集合是由一些确定的对象组成的特定的整体。

集合通常用大写字母表示，元素用小写字母表示，并且用花括号 {} 表示。

例如，集合 A 可以表示为 A = {a, b, c}，其中 a、b、c 是集合A 的元素。

二、集合的基本运算1. 并集：两个集合的并集是包含这两个集合所有元素的集合。

表示为 A ∪ B。

例如，如果 A = {1, 2, 3}，B = {3, 4}，则 A ∪ B = {1, 2, 3, 4}。

2. 交集：两个集合的交集是同时包含在这两个集合中的元素的集合。

表示为A ∩ B。

例如，如果 A = {1, 2, 3}，B = {3, 4}，则 A ∩ B = {3}。

3. 差集：两个集合的差集是除去两个集合共有元素之外的元素所构成的集合。

表示为 A - B。

例如，如果 A = {1, 2, 3}，B = {3, 4}，则 A - B = {1, 2}。

4. 互斥：如果两个集合没有共同的元素，则称它们为互斥的。

例如，如果 A = {1, 2}，B = {3, 4}，则 A 和 B 是互斥的。

三、集合的特性和性质1. 空集：不包含任何元素的集合称为空集，用符号∅表示。

2. 子集：如果一个集合的所有元素都属于另一个集合，则称该集合为另一个集合的子集。

表示为 A ⊆ B。

例如，如果 A = {1, 2}，B = {1, 2, 3}，则 A ⊆ B。

3. 互为子集：如果集合 A 是集合 B 的子集，同时集合 B 也是集合 A 的子集，则称集合 A 和集合 B 为互为子集。

4. 幂集：一个集合的所有子集所构成的集合称为该集合的幂集。

例如，如果 A = {1, 2}，则 A 的幂集为 P(A) = {{}, {1}, {2}, {1, 2}}。

5. 交换律：并集和交集的运算满足交换律，即 A ∪ B = B ∪ A，A ∩B = B ∩ A。

6. 结合律：并集和交集的运算满足结合律，即 (A ∪ B) ∪ C =A ∪ (B ∪ C)，(A ∩ B) ∩C = A ∩ (B ∩ C)。

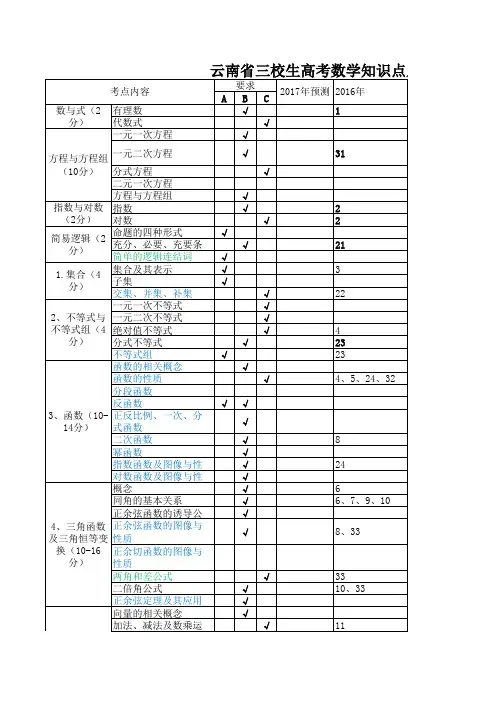
高考复习科目：数学高中数学总复习(一)I. 基础知识要点1. 集合中元素具有确定性、无序性、互异性.2. 集合的性质：①任何一个集合是它本身的子集，记为；②空集是任何集合的子集，记为；③空集是任何非空集合的真子集；如果，同时，那么A = B.如果.[注]：①Z= {整数}（√）Z ={全体整数} （×）②已知集合S中A的补集是一个有限集，则集合A也是有限集.（×）（例：S=N； A=，则C sA= {0}）③空集的补集是全集.④若集合A=集合B，则C B A = ，C A B = C S（C A B）= D（注：C A B = ）.3. ①{（x，y）|xy =0，x∈R，y∈R}坐标轴上的点集.②{（x，y）|xy＜0，x∈R，y∈R二、四象限的点集.③{（x，y）|xy＞0，x∈R，y∈R} 一、三象限的点集.[注]：①对方程组解的集合应是点集.例：解的集合{(2，1)}.②点集与数集的交集是. （例：A ={(x，y)| y =x+1} B={y|y =x2+1} 则A∩B =）4. ①n个元素的子集有2n个. ②n个元素的真子集有2n－1个. ③n个元素的非空真子集有2n－2个.5. ⑴①一个命题的否命题为真，它的逆命题一定为真. 否命题逆命题.②一个命题为真，则它的逆否命题一定为真. 原命题逆否命题.例：①若应是真命题.解：逆否：a = 2且b = 3，则a+b = 5，成立，所以此命题为真.②.解：逆否：x + y =3x = 1或y = 2.,故是的既不是充分，又不是必要条件. ⑵小范围推出大范围；大范围推不出小范围.例：若.II. 竞赛知识要点1. 集合的运算.De Morgan公式C u A∩C u B= C u（A∪B）C u A∪C u B = C u（A∩B）2. 容斥原理：对任意集合AB有..。

高考数学基础知识复习：集合一、知识清单：1.元素与集合的关系:用∈或∉表示；2.集合中元素具有确定性、无序性、互异性.3.集合的分类：①按元素个数分：有限集，无限集；②按元素特征分；数集，点集。

如数集{y |y =x 2},表示非负实数集，点集{(x ，y )|y =x 2}表示开口向上，以y 轴为对称轴的抛物线； 4.集合的表示法：①列举法：用来表示有限集或具有显著规律的无限集，如N +={0，1，2，3，…}； ②描述法③字母表示法:常用数集的符号：自然数集N ；正整数集*N N +或；整数集Z ；有理数集Q 、实数集R;5．集合与集合的关系:用⊆，≠⊂，=表示;A 是B 的子集记为A ⊆B ；A 是B 的真子集记为A ≠⊂B 。

①任何一个集合是它本身的子集，记为A A ⊆；②空集是任何集合的子集，记为A ⊆φ；空集是任何非空集合的真子集；③如果B A ⊆，同时A B ⊆，那么A = B ；如果A B ⊆，B C ⊆，A C ⊆那么.④n 个元素的子集有2n 个；n 个元素的真子集有2n －1个；n 个元素的非空真子集有2n －2个.6．交集A∩B={x |x ∈A 且x ∈B};并集A ∪B={x |x ∈A ，或x ∈B};补集C U A=｛x |x ∈U ，且x ∉A ｝，集合U 表示全集. 7.集合运算中常用结论: ①;A B AB A ⊆⇔=A B A B B ⊆⇔=②()()();U U U A B A B =()()()UU U A B A B =③()()card A B card A =+()()card B card A B - 二、课前预习1．下列关系式中正确的是（ ）(A){}Φ⊆Φ (B){}0∈Φ (C)0{}Φ= (D)0{}⊆Φ 2． 3231x y x y +=⎧⎨-=⎩解集为______.3．设{}{}24,21,,9,5,1A a a B a a =--=--,已知{}9AB =,求实数a 的值.4．设{}220,M x x x x R =++=∈，a =lg(lg10)，则{a }与M 的关系是( ) (A){a }=M (B)M{a } (C){a }M (D)M ⊇{a }5．集合A={x |x =3k -2，k ∈Z}，B={y |y=3n +1，n ∈Z}，S={y |y =6m +1，m ∈Z}之间的关系是( ) (A)SBA (B)S=BA (C)SB=A (D)SB=A6．用适当的符号()∈∉、、=、、填空： ①π___Q ; ②{3.14}____Q ;③-R ∪R +_____R; ④{x |x =2k +1, k ∈Z}___{x |x =2k －1, k ∈Z}。

高中集合专题复习一、集合有关概念1.集合的含义2.集合的中元素的三个特性：确定性、互异性、无序性。

(1)元素的确定性如：世界上最高的山(2)元素的互异性如：由HAPPY 的字母组成的集合{H,A,P,Y}(3)元素的无序性: 如：{a,b,c}和{a,c,b}是表示同一个集合3.集合的表示：{ … } 如：{我校的篮球队员}，{太平洋,大西洋,印度洋,北冰洋}(1)用拉丁字母表示集合：A={我校的篮球队员},B={1,2,3,4,5}(2)集合的表示方法：列举法与描述法。

注意：常用数集及其记法：非负整数集（即自然数集） 记作：N正整数集：N*或 N+ 整数集Z 有理数集Q 实数集R1）列举法：{a,b,c ……}2）描述法：将集合中的元素的公共属性描述出来，写在大括号内表示集合的方法。

{x ∈R|x-3>2} ,{x|x-3>2}3）语言描述法：例：{不是直角三角形的三角形}4）Venn 图:4、集合的分类：(1)有限集：含有有限个元素的集合(2)无限集：含有无限个元素的集合(3)空集：不含任何元素的集合 例：{x|x2=－5｝二、集合间的基本关系1.“包含”关系—子集注意：B A ⊆有两种可能（1）A 是B 的一部分；（2）A 与B 是同一集合。

反之: 集合A 不包含于集合B,或集合B 不包含集合A,记作B A ⊄或A B ⊄2．“相等”关系：A=B (5≥5，且5≤5，则5=5)实例：设A={x|x2-1=0} B={-1,1} “元素相同则两集合相等”即：① 任何一个集合是它本身的子集。

A A ⊆②真子集:如果A 属于B,且A ≠B 那就说集合A 是集合B 的真子集，记作B A ⊆(或A B ⊆) ③如果 B A ⊂,C B ⊂ ,那么 C A ⊂④ 如果B A ⊂ 同时A B ⊂,那么A=B3. 不含任何元素的集合叫做空集，记为Φ规定: 空集是任何集合的子集， 空集是任何非空集合的真子集。

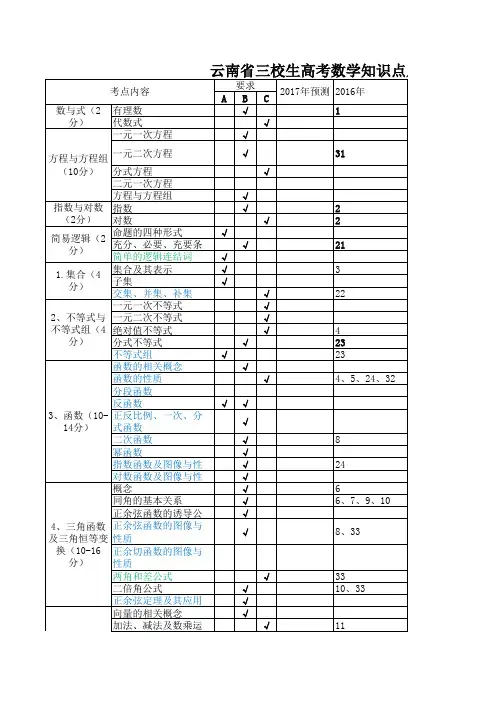
高考复习专题：集合与不等式1、下列四个关系中，正确的是（ ）A 、{}a ∈φB 、{}a a ⊆C 、{}{}b a a ,∈D 、{}b a a ,∈2、若01>-x ，则（ ）A 、1±≥xB 、1>xC 、11<<-xD 、11>-<x x 或3、已知b a ,是空间的两条直线，那么的相交是","""b a b a ⊥（ ）A 、充分非必要条件B 、必要非充分条件C 、充要条件D 、既非充分又非必要条件4、若集合{}3,2,1=P 、{}6,4,2=S ，则下列命题不正确的是（ ）A 、P ∈2B 、{}1,2,3,6P S =C 、{}2=S PD 、P ⊆Φ5、“022=+y x ”是“0=xy ”的（ ）A 、充要条件B 、充分但不必要条件C 、必要但不充分条件D 、既不充分又不必要条件6、下列关于不等式的命题为真命题的是（ ）A 、b a b a >⇒>22B 、b a b a 11>⇒>C 、111>⇒<a a D 、c b c a b a +<+⇒<7、某股票第一天上涨10%，第二天又下降10%，则两天后的股价与原来股价的关系是（）A 、相等B 、上涨1%C 、下降1%D 、是原股价的90%8、不等式02≤-x x的解集为（ ）（A ） ∅ （B ）{}20<≤x x（C ） {}20≤≤x x （D ）{}20>≤x x x 或9、如果0<<b a ,则（ ）（A ）22b a < （B ）33b a <（C ） b a < （D ）1<b a10、“x = y ”是“sin x = sin y ”的（ ）A 、充分但非必要条件B 、必要但非充分条件C 、充分且必要条件D 、既不充分也不必要条件11、如果+∈Ｒb a 、，且a + b = 1，那么ab 有（ ）A 、最小值41 B 、最大值41 C 、最小值21 D 、C 、最大值21 12、已知22,32x x x >++-则的最小值是 。

《高考数学集合复习知识点全攻略》引言：高考，是千军万马过独木桥的征程，而数学作为其中的重要科目，往往起着关键作用。

在高考数学中，集合是一个基础且重要的知识点，它贯穿于整个高中数学的学习。

掌握好集合的相关知识，不仅有助于我们在高考中取得优异成绩，更能为后续的数学学习奠定坚实的基础。

那么，让我们一同深入探索高考数学集合复习的知识点吧。

一、集合的概念1. 集合的定义集合是由一些确定的、不同的对象所组成的整体。

这些对象称为集合的元素。

例如，“所有小于 10 的正整数”就可以组成一个集合。

2. 集合的表示方法（1）列举法：将集合中的元素一一列举出来，用花括号括起来。

例如，{1,2,3,4,5}。

（2）描述法：用集合中元素的共同特征来表示集合。

例如，{x|x 是小于 10 的正整数}。

二、集合的关系1. 子集如果集合 A 中的所有元素都属于集合 B，那么称集合 A 是集合 B 的子集，记作 A⊆B。

特别地，任何集合都是它自身的子集。

2. 真子集如果集合 A 是集合 B 的子集，且存在元素属于集合 B 但不属于集合 A，那么称集合 A 是集合 B 的真子集，记作 A⊂B。

3. 相等如果集合 A 和集合 B 的元素完全相同，那么称集合 A 与集合B 相等，记作 A=B。

三、集合的运算1. 交集由既属于集合 A 又属于集合 B 的所有元素组成的集合，称为集合 A 与集合 B 的交集，记作A∩B。

例如，设 A={1,2,3,4}，B={3,4,5,6}，则A∩B={3,4}。

2. 并集由属于集合 A 或属于集合 B 的所有元素组成的集合，称为集合 A 与集合 B 的并集，记作A∪B。

例如，对于上述集合 A 和 B，A∪B={1,2,3,4,5,6}。

3. 补集设全集为 U，集合 A 是 U 的子集，由 U 中所有不属于集合 A 的元素组成的集合，称为集合 A 在全集 U 中的补集，记作∁UA。

四、集合中元素的性质1. 确定性对于一个给定的集合，它的元素是确定的。

2020年云南省高等职业技术教育招生考试数学复习提纲（基础知识梳理版）2019.12目录第一章基础知识 (01)第二章集合、不等式与不等式组14 第三章函数 (27)第四章三角函数 (47)第五章平面向量 (51)第六章直线、二次曲线 (53)第七章多面体和旋转体 (57)第八章数列 (63)第九章复数 (64)附录Ⅰ关于反函数 (71)附录Ⅱ关于复合函数 (73)2020年云南省高等职业技术教育招生考试 数学复习提纲第一章 基础知识一. 实数的概念及分类(1)实数的分类正有理数有理数 零 有限小数和无限循环小数实数 负有理数正无理数无理数 无限不循环小数负无理数整数包括正整数、零、负整数;正整数又叫自然数;正整数、零、负整数、正分数、负分数统称为有理数。

(2)无理数在理解无理数时，要抓住“无限不循环”这一点，归纳起来有四类：（1）开方开不尽的数，如32,7等；（2）有特定意义的数，如圆周率π)14159.3(≈π e 71828.2≈或化简后含有π或e 的数，如3π+8等； （3）有特定结构的数，如0.1010010001…等；（4）某些三角函数，如sin60o 等二. 实数的倒数、相反数和绝对值1、相反数实数与它的相反数是一对数（只有符号不同的两个数叫做互为相反数，零的相反数是零），从数轴上看，互为相反数的两个数所对应的点关于原点对称，如果a 与b 互为相反数，则有a+b=0，a=-b ，反之亦成立。

2、绝对值一个数的绝对值就是表示这个数的点与原点的距离，|a|≥0。

零的绝对值是它本身，若|a|=a ，则a ≥0；若|a|=-a ，则a ≤0。

正数大于零，负数小于零，正数大于一切负数，两个负数，绝对值大的反而小。

3、倒数如果a 与b 互为倒数，则有ab=1，反之亦成立。

倒数等于本身的数是1和-1。

零没有倒数。

三、平方根、算数平方根和立方根1、平方根如果一个数的平方等于a ，那么这个数就叫做a 的平方根（或二次方跟）。

集合高考必考知识点总结高考是中国学生人生中最重要的考试之一，集合作为数学必考的重要知识点，在高考中占据着很大的比重。

本文将对高考数学中集合的必考知识点进行总结。

一、集合的基本概念集合是一个由确定的对象所构成的整体。

常用大写字母A、B、C 等表示集合，小写字母a、b、c等表示集合中的元素。

例如，集合A={1, 2, 3, 4}，其中的元素1、2、3和4都属于集合A。

二、集合的运算1. 交集运算：集合A和集合B的交集，表示为A∩B，表示A和B 共有的元素组成的集合。

例如，集合A={1, 2, 3}，集合B={2, 3, 4}，则A∩B={2, 3}。

2. 并集运算：集合A和集合B的并集，表示为A∪B，表示A和B 所有的元素组成的集合。

例如，集合A={1, 2, 3}，集合B={2, 3, 4}，则A∪B={1, 2, 3, 4}。

3. 补集运算：集合A相对于集合B的补集，表示为A-B，表示A 中除去B中的所有元素所组成的集合。

例如，集合A={1, 2, 3}，集合B={2, 3, 4}，则A-B={1}。

4. 包含关系：集合A包含集合B的情况，即A⊇B，表示A中的所有元素都属于B。

例如，集合A={1, 2, 3}，集合B={2, 3}，则A⊇B。

5. 空集与全集：空集是不包含任何元素的集合，用符号∅表示；全集是指讨论问题所涉及的全部元素组成的集合。

三、集合的性质1. 交换律：集合的交集和并集满足交换律。

即A∩B=B∩A，A∪B=B∪A。

2. 结合律：集合的交集和并集满足结合律。

即A∩(B∩C)=(A∩B)∩C，A∪(B∪C)=(A∪B)∪C。

3. 分配律：集合的交集和并集满足分配律。

即A∩(B∪C)=(A∩B)∪(A∩C)，A∪(B∩C)=(A∪B)∩(A∪C)。

四、集合的表示方法1. 列举法：将集合中的元素一一列举出来。

例如，集合A={1, 2, 3, 4}。

2. 描述法：根据元素的性质进行描述。

高三集合知识点在高三的数学学习中，集合是一个重要的基础概念，它贯穿于整个数学体系之中。

理解和掌握集合的相关知识，对于后续的数学学习有着至关重要的作用。

集合，简单来说，就是把一些确定的、不同的对象放在一起组成的一个整体。

这些对象被称为集合的元素。

集合通常用大写字母来表示，比如 A、B、C 等，而元素则用小写字母表示，比如 a、b、c 等。

如果一个元素 a 属于集合 A，我们记作a∈A；如果元素 b 不属于集合 A，就记作 b∉A。

集合有多种表示方法。

列举法就是将集合中的元素一一列举出来，用花括号括起来。

比如，由数字 1、2、3 组成的集合，可以表示为{1, 2, 3}。

描述法呢，则是通过描述元素所具有的共同特征来表示集合。

例如，所有大于 0 小于 5 的整数组成的集合，可以表示为{x ｜ 0 ＜ x＜ 5, x∈Z}，其中 Z 表示整数集。

集合之间有着不同的关系。

如果集合 A 中的所有元素都属于集合 B，那么集合 A 就是集合 B 的子集，记作 A⊆B。

如果集合 A 是集合 B 的子集，并且集合 B 中存在元素不属于集合 A，那么集合 A 就是集合 B的真子集，记作 A⊂B。

当两个集合 A 和 B 的元素完全相同，我们就说集合 A 和集合 B 相等，记作 A ＝ B。

集合的运算也是集合知识中的重要部分。

交集就是两个集合共有的元素组成的集合。

如果集合 A 和集合 B 的交集记作A∩B，那么A∩B ＝｛x ｜ x∈A 且 x∈B}。

并集则是把两个集合的所有元素放在一起组成的新集合，如果集合 A 和集合 B 的并集记作 A∪B，那么 A∪B ＝｛x ｜ x∈A 或 x∈B}。

补集是在一个给定的全集 U 中，集合 A 的补集就是由全集中不属于集合 A 的元素组成的集合，记作∁UA ＝｛x ｜x∈U 且 x∉A}。

在解决集合相关的问题时，一定要注意集合中元素的性质。

首先，集合中的元素具有确定性，也就是说，对于一个给定的集合，某个元素是否属于这个集合是明确的，不能模棱两可。

云南省高等职业技术教育招生考试模拟试题 数学第二章（集合、不等式与不等式组）田应雄命题一、选择题(本大题共20小题，每小题2分，满分40分，在每小题给出的四个选项中，选出一个符合题目要求的，并且2B 铅笔在答题卡上将该项涂黑)1、下列选项能组成集合的是 （ ）A.学校篮球水平较高的学生B.校园中长的高大的树木C.2007年所有的欧盟国家D.中国经济发达的城市2、不等式组⎩⎨⎧<>bx a x 的解集为{}21|<<x x ，则a ，b 的值为（ ）A ．1,2 B.1,1 C.2,1 D. 2,23、下列表述正确的是 （ ）A.}0{=∅B. }0{⊆∅C. }0{⊇∅D. }0{∈∅4、已知集合M={*,4|N n n x x ∈=}则下列各数属于集合M 的是（ ）A.0B.2007C.2008D.20095、集合{a ，b ，c }的真子集共有 个.（ ）A ．7B ．8C ．9D ．106、设集合{}{}1,1,1,0,1-=-=N M ，则（ ）A.N M ⊆B.N M ⊂C.N M =D.M N ⊂7、已知{}2<=x x A ，则下列写法正确的是（ ）A.A ⊆0B.{}A ∈0C.A ∈φD.{}A ⊆08、设全集{}6,5,4,3,2,1,0=U ，集合{}6,5,4,3=A ，则=A C U （ ）A ．{}6,2,1,0 B. ∅ C. {}5,4,3 D. {}2,1,09、已知集合{}3,2,1=A ，集合{}7,5,3,1=B ，则=B A （ ）A ．{}5,3,1 B.{}3,2,1 C.{}3,1 D. ∅10、已知集合{}2,=+=y x y x A ）（，集合{}4,=-=y x y x B ）（，则=⋂B A （）A ．3，-1 B. {}13-， C. {})13(-， D. {})31(，-11、已知集合{}3,2,1=A ，集合{}765,4，，=B ，则=B A （ ） A ．{}3,2 B.{}3,2,1 C.{}765,4,3,2,1，， D. ∅ 12、设集合M = {x │x+1＞0}，N = {x │－x+3＞0}，则M ∩N =（ ）A 、{x │x ＞－1}B 、{x │x ＜－3}C 、{x │－1＜x ＜3}D 、{x │x ＞－1或x ＜3}13.下列各式错误的是( ). A.{}3|2<⊂-x x B.{}3|1<∈-x x C.{}{}3|2<⊂-x x D.∅{}3|<⊂x x14.设全集为N ，集合M={},8|*N x x x ∈≥，则集合M C N 中元素的个数为（ ）A.7个B.8个C.9个D.无数多个16.已知集合P={1，2}，那么满足Q ⊆P 的集合Q 的个数为（ ）A ．1 B.2 C.3 D. 417.若{}023|2=+-x ax x 有2个子集，则a=( ).A. -1或1B. 0或89C. 1或0D. 98或0 18、设集合M={}{}00|),(,0|),(>>=>y x y x N xy y x 且则正确的是（ ）.A.M N M =⋃B.N N M =⋃C.M N M =⋂D.=⋂N M ∅.19. 已知集合{}20<<=x x A ，集合{}31≤<=x x B ，则=B A （ ）A ．{}30<<=x x A B. {}30≤<=x xB C. {}21<<=x x B D. {}21≤<=x x B20.设{}{}共有则满足条件的集合M M ,4,3,2,12,1⊆⊂( ). A.1个 B.2个 C.3个 D.4个二、填空题（本大题共10小题，每小题2分，满分20分，请将答案写在答题卡相应题号后）21、)13(2)1(32+++-a x a x 在实数范围内分解因式为____________.22、以x 、y 为未知数的方程组⎩⎨⎧=-=+k y x y x 1622有实数解，那么k 的取值范围是_____. 23、已知集合A={}R x x x ∈≤,1|，B={}Z x x x ∈>+,02|则=⋂B A ___________.24、已知A={}02|2<-x x x ，B={}31|<<x x ，则=⋂B A _____________.25、已知A={}12,3,1-m ，B={}2,3m ，若A B ⊆,则实数m=___________. 26、若A={}2log |2≤x x ，B={}a ,∞-，B A ⊆,实数a 取值范围为{}+∞,c ，则c=_____________.27、若nm --⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛3131，则m 与n 的大小关系是_____________. 28、不等式7253<-≤x 的解集_____________ .29、不等式12141log log +<x x 的解集_____________. .30、用列举法表示{}=∈<--=Z x x x x D ,043|2____________.三、解答题（本大题共5小题，每小题8分，满分40分，请将答案填写在答题卡上相应题号后，解答时应写出推理、演算步骤）31、解不等式1032<+x x .32、设全集U=R ，集合{}21≤<-=x x A ，{}30<<=x x B ，求B A ，B A 和U C (A B)。

三校生高考常考知识点高考是每年中国学生所面临的一项重要考试，对于学生们而言，高考成绩往往决定了他们能否进入心仪的大学以及未来的发展方向。

为了能够在高考中取得好成绩，学生们不得不花费大量的时间和精力来备考，掌握一些高考常考的知识点是非常必要的。

本文将就三校生高考常考的知识点进行探讨。

一、语言文学篇在语言文学篇中，常考的知识点主要包括诗歌、散文和小说的理解与鉴赏，古诗文的背诵和注释，以及现代作家的作品解读。

其中，对于古诗文的理解与鉴赏是考生常常感到困扰的部分。

因此，在备考过程中，应该多读一些古代文学作品，了解古代文学的特点、主题以及意蕴等，通过理解与鉴赏的能力来提高阅读理解的水平。

二、数学篇数学是高考科目中的重中之重，也是许多学生感到头疼的一门科目。

在数学中，常考的知识点包括集合与函数、数列与数学归纳法、平面向量、立体几何等。

这些知识点都要求学生掌握基本的概念和定理，能够熟练运用各种解题方法和技巧。

为了应对这些考点，学生们应该注重基础知识的打牢，多做一些相关的习题和真题，通过反复训练来提高解题的技巧。

三、外语篇外语是高考科目中的另一大难点，尤其是英语。

在英语中，常考的知识点主要包括阅读理解、写作和听力部分。

针对这些知识点，学生们应该注重平时的课外阅读，提高自己的阅读理解能力；积累一些写作素材，提高自己的写作水平；并且多听一些英语材料，提高自己的听力能力。

此外，还可以通过刷一些真题来熟悉考试形式和题型，为高考做好充分准备。

四、理综篇理综是高考中另一门较为重要的科目，其中包括物理、化学和生物三个子学科。

在理综中，常考的知识点主要涵盖了每个学科的基本概念和常见实验方法。

为了能够应对这些考点，学生们需要掌握每个学科的基本理论，了解一些实际应用，还要熟悉一些实验操作和实验结果的分析。

此外，还可以通过做一些实验、实践和习题来加深对知识点的理解和应用。

通过对以上几个科目的分析，我们可以看出，高考常考的知识点虽然众多，但只要学生们能够在备考过程中注重基础知识的打牢，提高解题的技巧，加大对重点知识的理解和应用，相信高考成绩一定会有所提升。

云南高三数学知识点总结在高三数学学习中，云南的学生需要掌握各个数学知识点，以应对高考数学科目的考试。

本文将对云南高三数学知识点进行总结，帮助学生加深对数学内容的理解与记忆。

一、集合与函数1. 集合的表示与运算在集合的表示中，我们可以使用集合的列举法、描述法以及通用集合符号。

集合的运算包括并、交、差、补等。

2. 函数及其性质函数是数学中重要的概念，包括定义域、值域、单射、满射、一一对应等性质。

二、数与式1. 实数的性质实数包括有理数和无理数。

有理数可以表示为分数形式或小数形式，无理数表示为无限不循环小数。

2. 数与式的计算数与式的计算包括四则运算、整式的加减乘除、分式的加减乘除等。

三、平面坐标系与图形1. 平面坐标系平面坐标系由横轴（x轴）和纵轴（y轴）组成，用以表示点的位置。

2. 图形的性质图形的性质包括点、线、面的定义与性质，如线段、射线、角、平行线、垂直线等。

四、函数的基本性质1. 基本初等函数及其图像基本初等函数包括常数函数、幂函数、指数函数、对数函数和三角函数等。

了解这些函数的定义、性质以及图像特点至关重要。

2. 函数的运算与复合函数函数的运算包括加、减、乘、除以及复合运算。

复合函数是指将一个函数的输出作为另一个函数的输入，了解复合函数的性质和计算方法。

五、数列与数学归纳法1. 数列的概念与表示数列是指按照一定规律排列的一组数，可以用通项公式、递推公式或递归定义表示。

2. 数列的计算数列的计算包括求和、求通项、求极限等。

六、概率与统计1. 概率基本概念概率是指某一事件发生的可能性或程度，包括样本空间、随机事件、必然事件和不可能事件等概念。

2. 统计与统计图表统计是指根据抽样调查得到的数据，对总体的特征进行推断。

统计图表包括频数表、频率表、直方图、折线图等。

七、解析几何1. 直线与圆的方程直线的方程包括点斜式、一般式、两点式等表示方法；圆的方程包括标准方程、一般方程等表示方法。

2. 直线与圆的位置关系直线与圆的位置关系包括相离、相切、相交等情况的分析与判断。