小学数学数学故事数学猜想系列四色猜想
- 格式:doc
- 大小:12.50 KB
- 文档页数:1

四色猜想四色图猜想是什么?各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢四色猜想四色猜想此猜想已被证明不再是猜想是定理了四色原理世界近代三大数学难题之一.四色猜想的提出来自英国.1852年,毕业于伦敦大学的弗南西斯·格思里(Francis Guthrie)来到一家科研单位搞地图着色工作时,发现了一种有趣的现象:“看来,每幅地图都可以用四种颜色着色,使得有共同边界的国家着上不同的颜色.”这个结论能不能从数学上加以严格证明呢?他和在大学读书的弟弟格里斯决心试一试.兄弟二人为证明这一问题而使用的稿纸已经堆了一大叠,可是研究工作没有进展.1852年10月23日,他的弟弟就这个问题的证明请教他的老师、著名数学家德·摩尔根,摩尔根也没有能找到解决这个问题的途径,于是写信向自己的好友、著名数学家哈密尔顿爵士请教.哈密尔顿接到摩尔根的信后,对四色问题进行论证.但直到1865年哈密尔顿逝世为止,问题也没有能够解决.1872年,英国当时最著名的数学家凯利正式向伦敦数学学会提出了这个问题,于是四色猜想成了世界数学界关注的问题.世界上许多一流的数学家都纷纷参加了四色猜想的大会战.1878~1880年两年间,著名的律师兼数学家肯普和泰勒两人分别提交了证明四色猜想的论文,宣布证明了四色定理,大家都认为四色猜想从此也就解决了.11年后,即1890年,数学家赫伍德以自己的精确计算指出肯普的证明是错误的.不久,泰勒的证明也被人们否定了.后来,越来越多的数学家虽然对此绞尽脑汁,但一无所获.于是,人们开始认识到,这个貌似容易的题目,其实是一个可与费马猜想相媲美的难题:先辈数学大师们的努力,为后世的数学家揭示四色猜想之谜铺平了道路.进入20世纪以来,科学家们对四色猜想的证明基本上是按照肯普的想法在进行.1913年,伯克霍夫在肯普的基础上引进了一些新技巧,美国数学家富兰克林于1939年证明了22国以下的地图都可以用四色着色.1950年,有人从22国推进到35国.1960年,有人又证明了39国以下的地图可以只用四种颜色着色;随后又推进到了50国.看来这种推进仍然十分缓慢.电子计算机问世以后,由于演算速度迅速提高,加之人机对话的出现,大大加快了对四色猜想证明的进程.1976年,在J. Koch的算法的支持下,美国数学家阿佩尔(Kenneth Appel)与哈肯(Wolfgang Haken)在美国伊利诺斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿判断,终于完成了四色定理的证明.四色猜想的计算机证明,轰动了世界,当时中国科学家也有在研究这原理.它不仅解决了一个历时100多年的难题,而且有可能成为数学史上一系列新思维的起点.证明方法将地图上的无限种可能情况减少为1,936种状态,这些状态由计算机一个挨一个的进行检查.这一工作由不同的程序和计算机独立的进行了复检.在1996年,Neil Robertson、Daniel Sanders、Paul Seymour和Robin Thomas使用了一种类似的证明方法,检查了633种特殊的情况.这一新证明也使用了计算机,如果由人工来检查的话是不切实际的.四色定理是第一个主要由计算机证明的理论,这一证明并不被所有的数学家接受,因为它不能由人工直接验证.最终,人们必须对计算机编译的正确性以及运行这一程序的硬件设备充分信任.德·摩尔根:地图四色定理德·摩尔根致哈密顿的信我的一位学生今天请我解释一个我过去不知道,现在仍不甚了了的事实.他说如果任意划分一个图形并给各部分着上颜色,使任何具有公共边界的部分颜色不同,那么需要且仅需要四种颜色就够了.下图是需要四种颜色的例子.现在的问题是是否会出现需要五种或更多种颜色的情形.就我目前的理解,若四个不订分割的区域两两具有公共边界线,则其中三个必包围第四个而使其不与任何第五个区域相毗邻.这事实若能成立,那么用四种颜色即可为任何可能的地图着色,使除了在公共点外同种颜色不会.现画出三个两两具有公共边界的区域ABC,那么似乎不可能再画第四个区域与其他三个区域的每一个都有公共边界,除非它包围了其中一个区域.但要证明这一点却很棘手,我也不能确定问题复杂的程度一对此您的意见如何呢?并且此事如果当真,难道从未有人注意过吗?我的学生说这是在给一幅英国地图着色时提出的猜测.我越想越觉得这是显然的事情.如果您能举出一个简单的反例来,说明我像一头蠢驴,那我只好重蹈史芬克斯①的复辙了…….各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢。


四色猜想的数学模型李传学四色猜想的数学语言定义:将平面任意地细分为不相重叠的区域,每一区域总可以用1、2、3、4这四个数字之一来进行标记,且不会使相邻的两个区域得到相同的数字(网络“科普中国”)。
本文利用“1+3、3+1”链锁重组三角形,给予地球四色猜想数学方法与应用方法两种模型证明。
一、数学方法依据。
1、三角形定义,对顶△定义,平角定义。
2、平面公理。
公理一(推论一、推论二)、公理二、公理三。
3、排列组合Pn m或P(n,m)、Cnm或C(n,m)4、拓扑等价。
5、数理统计、个体与总体概念。
6、射线定义。
二、数学方法证明。
将给定的四色猜想数学语言定义,用数学作图法转换成相应的已知△ABC条件。
以起始△ABC的边AB、BC、CA为底边,分别作△ABD、△BCE、△CAF,组成DEF平面△图形。
这里将△ABD、△BCE、△CAF作为相邻面,△ABC作为起始单元面,并分别标记为1、2、3、4。
即任意色为起始△ABC“1”单元面,李传学:《人亦大的史前史》,香港:文化研究出版社(修订版),2020年。
其他三色则为“3”相邻面。
简称“1单元、3相邻”面。
令起始△ABC 的“1面、3线(点)”为已知条件。
(一)起始△ABC的“1+3”“3+1”概念。
在△DEF中,当△ABD两底外角等于180º时,则三边同时重合在△ABC的AB边线段上;当△BCE两底外角等于180º时,则三边同时重合在△ABC的BC边线段上;当△CAF两底外角等于180º时,则三边同时重合在△ABC的CA边线段上。
这样△ABC“1单元、3相邻”面,便有了“1面、3线(点)”(记作“1+3”或“3+1”)组成的起始△ABC单元区域特征。
单元,是指每个△面位置;单元区域,是指△“1面、3线”C (4,3)组合位置;区域,是指位置整(总)体。
根据平面几何三角形定义与平面公理二,四色猜想使用的“1面、3线”与“1面、3点”概念是一致的。

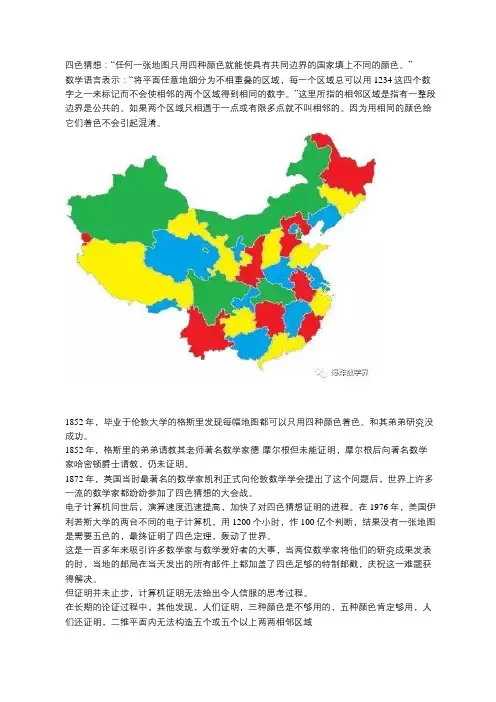
四色猜想:“任何一张地图只用四种颜色就能使具有共同边界的国家填上不同的颜色。
”
数学语言表示:“将平面任意地细分为不相重叠的区域,每一个区域总可以用1234这四个数字之一来标记而不会使相邻的两个区域得到相同的数字。
”这里所指的相邻区域是指有一整段边界是公共的。
如果两个区域只相遇于一点或有限多点就不叫相邻的。
因为用相同的颜色给它们着色不会引起混淆。
1852年,毕业于伦敦大学的格斯里发现每幅地图都可以只用四种颜色着色。
和其弟弟研究没成功。
1852年,格斯里的弟弟请教其老师著名数学家德·摩尔根但未能证明,摩尔根后向著名数学家哈密顿爵士请教,仍未证明。
1872年,英国当时最著名的数学家凯利正式向伦敦数学学会提出了这个问题后,世界上许多一流的数学家都纷纷参加了四色猜想的大会战。
电子计算机问世后,演算速度迅速提高,加快了对四色猜想证明的进程。
在1976年,美国伊利若斯大学的两台不同的电子计算机,用1200个小时,作100亿个判断,结果没有一张地图是需要五色的,最终证明了四色定理,轰动了世界。
这是一百多年来吸引许多数学家与数学爱好者的大事,当两位数学家将他们的研究成果发表的时,当地的邮局在当天发出的所有邮件上都加盖了四色足够的特制邮戳,庆祝这一难题获得解决。
但证明并未止步,计算机证明无法给出令人信服的思考过程。
在长期的论证过程中,其他发现,人们证明,三种颜色是不够用的,五种颜色肯定够用,人们还证明,二维平面内无法构造五个或五个以上两两相邻区域。

数学经典问题·四色猜想世界近代三大数学难题之一――四色猜想的提出来自英国。
1852年,毕业于伦敦大学的弗南西斯·格思里来到一家科研单位搞地图着色工作时,发现了一种有趣的现象:“看来,每幅地图都可以用四种颜色着色,使得有共同边界的国家着上不同的颜色。
”这个结论能不能从数学上加以严格证明呢?他和在大学读书的弟弟格里斯决心试一试。
兄弟二人为证明这一问题而使用的稿纸已经堆了一大叠,可是研究工作没有进展。
1852年10月23日,他的弟弟就这个问题的证明请教他的老师、著名数学家德.摩尔根,摩尔根也没有能找到解决这个问题的途径,于是写信向自己的好友、著名数学家哈密尔顿爵士请教。
哈密尔顿接到摩尔根的信后,对四色问题进行论证。
但直到1865年哈密尔顿逝世为止,问题也没有能够解决。
1872年,英国当时最著名的数学家凯利正式向伦敦数学学会提出了这个问题,于是四色猜想成了世界数学界关注的问题。
世界上许多一流的数学家都纷纷参加了四色猜想的大会战。
1878~1880年两年间,著名的律师兼数学家肯普和泰勒两人分别提交了证明四色猜想的论文,宣布证明了四色定理,大家都认为四色猜想从此也就解决了。
11年后,即1890年,数学家赫伍德以自己的精确计算指出肯普的证明是错误的。
不久,泰勒的证明也被人们否定了。
后来,越来越多的数学家虽然对此绞尽脑汁,但一无所获。
于是,人们开始认识到,这个貌似容易的题目,其实是一个可与费马猜想相媲美的难题:先辈数学大师们的努力,为后世的数学家揭示四色猜想之谜铺平了道路。
进入20世纪以来,科学家们对四色猜想的证明基本上是按照肯普的想法在进行。
1913年,伯克霍夫在肯普的基础上引进了一些新技巧,美国数学家富兰克林于1939年证明了22国以下的地图都可以用四色着色。
1950年,有人从22国推进到35国。
1960年,有人又证明了39国以下的地图可以只用四种颜色着色;随后又推进到了50国。
看来这种推进仍然十分缓慢。

四色猜想定义的微分解析
1 什么是四色猜想?
四色猜想是指,任何地图都可以用四种或更少颜色着色,使得相邻区域颜色不同。
这个猜想是由英国人弗朗西斯·伯克(Francis Guthrie)在1852年提出来的。
2 什么是微分解析?
微分解析是一种用微积分方法将函数进行分析的方法。
微分就是对函数进行微小的变化,从而研究函数的性质。
解析就是指用公式和函数进行计算和分析。
3 四色猜想的微分解析
研究“四色猜想”是一个十分复杂的问题,需要用到许多数学工具,其中包括微分解析。
具体来说,解决“四色猜想”问题的方法是在平面上建立一个图形模型,然后对这个模型进行数学分析,最终得出结论。
在模型分析中,微分解析的主要作用是通过微分几何方法,建立各个区域与相邻区域之间的关系,从而进一步推断出各个区域颜色的分布情况。
例如,可以用微分方程模拟着色过程中的颜色变化,然后利用微积分方法计算出各个区域的颜色分布方式。
这样就可以避免色彩混淆,使得每个区域的颜色都可以清晰明了地呈现出来。
除了微分解析外,还要借助其他数学工具,如图论、拓扑等方法,才能完整地解决这个问题。
因此,“四色猜想”一直是数学家们努力
探究的难题,也是一个充满挑战和创新的领域。
4 结论
在数学研究中,微分解析是一个十分重要的工具,尤其是在解决
如“四色猜想”这样的难题中发挥着至关重要的作用。
通过对微积分
方法的应用,可以对函数进行精细的分析,并从中获得有关函数性质
的重要信息。
未来,如果能够进一步发展微分解析技术,也许我们将
有更多机会解决更加复杂、深奥的数学问题。


四色猜想 -四色猜想四色定理地图四色定理(Four color theorem) 最初是由一位叫古德里 Francis Guthrie 的英国大学生提出来的。
四色问题的内容是“任何一张地图只用四种颜色就能使拥有共同界限的国家着上不一样的颜色。
”用数学语言表示即“将平面任意地细分为不相重叠的地区每一个地区总能够用 1234 这四个数字之一来标志而不会使相邻的两个地区获得相同的数字。
”这里所指的相邻地区是指有一整段界限是公共的。
假如两个地区只相遇于一点或有限多点就不叫相邻的。
由于用相同的颜色给它们着色不会惹起混杂。
四色问题的内容是“任何一张地图只用四种颜色就能使拥有共同界限的国家着上不一样的颜色。
”也就是说在不惹起混杂的状况下一张地图只要四种颜色来标志就行发展历史可是状况也不是过分消极。
数学家希奇早在 1936年就以为议论的状况是有限的可是特别之大大到可能有 10000种。
关于巨大而有限的数,最好由谁去对付?今日的人都理解:计算机。
从 1950年起希奇就与其学生丢莱研究如何用计算机去考证各样种类的图形。
这时计算机才刚才发明。
两人的思想堪称十分超前。
1972 年起黑肯与阿佩尔开始对希奇的方法作重要改良。
到 1976 年他们以为问题已经压缩到能够用计算机证明的地步了。
于是从 1 月份起他们就在伊利诺伊大学的 IBM360 机上分 1482 种状况检查历时 1200 个小时,作了 100 亿个判断最后证了然四色定理。
在当地的信封上盖“Fourcolorssutfice 四色”,足够了的邮戳就是他们想到的一种流传这一惊人消息的新奇的方法。
人类破天荒运用计算机证明有名数学猜想应当说是十分惊动的。
欣赏者有之,思疑者也许多,由于真实确性一时不可以一定。
以后也确实有人指出其错误。
1989 年,黑肯与阿佩尔发布文章声称错误已被改正。
1998 年托马斯简化了黑肯与阿佩尔的计算程序但仍依靠于计算机。
不论如何四色问题的计算机解决给数学研究带来了很多重要的新思想。


四色猜想的证明四色猜想的内容是:如果把地图上有共同边界的国家涂成不同颜色,那么只需要4种颜色就足够了。
要证明四色猜想,首先需要定义一些新的概念:1、国家的表示法——点由于该猜想的内容中不涉及与国家形状有关的问题,而只涉及国与国之间的相邻关系,因此任何一个国家都用点来表示。
2、相邻与不相邻在叙述时,用符号“=”表示相邻,用“#”表示不相邻,如果用图示法表示相邻与不相邻则要复杂一些,先看下图:(a)(b) (c)图1在图1(a)与(b)中,分别用了直线和曲线连接两个国家A和B,表示国家A与B相邻,为了简便起见,这里只用直线表示相邻,图1(c)中是已知A与B相邻,叫你判断C 与D能否相邻,连接CD、CD与AB相交,相交是否就是不相邻呢?我们先看一组图:图2图2是把图进行等分后的结果,从三等分开始,如果每一份代表一个国家,这表示等分后的所有国家相聚于一点,从四等分后的国家A 、B、C、D可知,如果国家之间点的接触算是相邻,则A与B,C与D都为相邻,显然这时的A与B,C与D是交叉相邻,与图1(c)中的情况相同,此时A与B,C与D的交点表示接触点。
若点的接触不算相邻,那么连接A与B的直线可以看作一道墙,在这中间不能有任何直线通过。
因此,由于C与D的连线与AB相交,据此判断出C与D不能相邻。
但是当相邻用曲线进行表示,C与D却能够相邻,这是否说明用直线表示相邻有问题呢?当然不是,仔细分析就可以发现,用曲线表示相邻同样不能有相交的情况出现,因此,用直线表示相邻时,适当移动C或D的位置就可以使C与D相邻。
3、完全相邻这是一个关键问题,可以这么说,没有这一概念的证明都是伪证明,现在给出完全相邻的定义:在一个面上(可以是平面也可以是曲面)给定N个国家,如果这N个国家两相邻,那么我们就称这N个国家完全相邻。
由于1个国家没有相邻关系,因此上面的N要求要大于1。
如果是3个国家完全相邻,它们的相邻关系为:(这三个国家分别设为1、2、3)1=2,1=3,2=3有了以上这些概念之后,就有了证明四色猜想的基础。
轰动全球的四色问题1、“四色猜想”的由来1852年,刚从大学毕业的学生弗南西斯·葛斯里,在对英国地图着色的时候,发现一个很有趣的现象。
对无论多么复杂的地图,只消用四种色调就足以将相邻区域分开。
弗南西斯感到这绝不是一个偶然现象,其中说不定隐藏着某种深刻的科学道理哩。
他把自己的想法告诉胞兄弗德雷克·葛斯里,请他解决。
后者是著名数学家德·摩根教授的学生。
他对弟弟提出的问题很感兴趣,并敏锐地感到,这个地图着色问题很可能是个数学问题,于是准备给出数学证明。
尽管他绞尽脑汁,却百思不得其解。
当年10月23日,弗德雷克第一次用数学的形式作为“四色定理”请求德·摩根给以证明。
摩根教授对自己的学生所提出的定理有着浓厚的兴趣,当即写信将这事告诉了他在三一学院时的学友、著名数学家和物理学家哈密尔顿爵士: “我的一个学生今天要我为他提供一个充分的理由,来说明一件我自己还无法判明究竟是对的还是错的事实。
他说,如果画一张图,图上任意分成许多部分,凡是有共同边界线的两部分要涂上不同的颜色。
那么,大概需要四种颜色,而不需要更多的颜色就可以了。
请问:难道不能够构造出一个需要五种或者更多种颜色的图么?图1摩根教授期望这位智慧超人的超复数的缔造者能够给出答案。
哈密尔顿爵士根本没有想到,一个学生提出的这样一个简简单单的问题,居然会如此意想不到的困难。
他经过长达13年的冥思苦索,直到1865年逝世为止,对此染色定理,始终一筹莫展,毫无结果。
哈氏死后13年,1878年6月13日,一位当时很有名望的数学家凯莱,在数学年会上宣读他曾在伦敦数学会会刊上发表过的一篇文章时,将上述问题归纳为“四色猜想”。
并在 1879年英国皇家地理会创办的第一期会刊上,再次提及这个“猜想”,征求对这一“猜想”的正确解答。
川凯莱的文章和讲话,引起了很大的反响,吸引了一大批很有才华的有志之士去探索这一难题的奥秘。
值得一提的是,在这群有志之士中,有的人并不是以数学为专业的,而仅仅是对“四色猜想”着了迷而改攻数学的。
四色猜想定义的微分解析
四色猜想是一个著名的数学问题,它的定义是:任何一个地图都可以用四种颜色来涂色,使得相邻的区域颜色不同。
这个问题在数学界引起了广泛的关注和研究,直到1976年才被证明是正确的。
微分解析是数学中的一个重要分支,它研究的是函数的微分和积分。
微分解析的研究对象是连续可微的函数,它通过求导和积分来研究函数的性质和变化规律。
将四色猜想和微分解析联系起来,可以得到一个有趣的问题:如何用微分解析的方法来证明四色猜想?
我们可以将地图看作是一个函数,它将每个区域映射到一个颜色。
我们可以用微分解析的方法来研究这个函数的性质,比如它的导数和积分。
通过对函数的导数和积分的研究,我们可以得到一些关于函数的性质和变化规律的结论。
我们可以将四色猜想看作是一个约束条件,它要求相邻的区域颜色不同。
我们可以用微分解析的方法来研究这个约束条件对函数的影响。
通过对约束条件的研究,我们可以得到一些关于函数的限制条件和约束条件的结论。
我们可以将微分解析和约束条件结合起来,来研究四色猜想。
通过对函数的性质、限制条件和约束条件的综合研究,我们可以得到一些关于四色猜想的结论。
这些结论可以用来证明四色猜想的正确性。
将四色猜想和微分解析联系起来,可以得到一个有趣的问题。
通过对函数的性质、限制条件和约束条件的综合研究,我们可以得到一些关于四色猜想的结论,从而证明它的正确性。
这个问题不仅有理论意义,还有实际应用价值,比如在地图着色、电路布线等领域。
世界近代三大数学难题之一。
四色猜想的提出来自英国。
1852年,毕业于伦敦大学的弗南西斯·格思里(Francis Guthrie)来到一家科研单位搞地图着色工作时,发现了一种有趣的现象:“看来,每幅地图都可以用四种颜色着色,使得有共同边界的国家着上不同的颜色。
”这个结论能不能从数学上加以严格证明呢?他和在大学读书的弟弟格里斯决心试一试。
兄弟二人为证明这一问题而使用的稿纸已经堆了一大叠,可是研究工作没有进展。
1852年10月23日,他的弟弟就这个问题的证明请教他的老师、著名数学家德·摩尔根,摩尔根也没有能找到解决这个问题的途径,于是写信向自己的好友、著名数学家哈密尔顿爵士请教。
哈密尔顿接到摩尔根的信后,对四色问题进行论证。
但直到1865年哈密尔顿逝世为止,问题也没有能够解决。
1872年,英国当时最著名的数学家凯利正式向伦敦数学学会提出了这个问题,于是四色猜想成了世界数学界关注的问题。
世界上许多一流的数学家都纷纷参加了四色猜想的大会战。
1878~1880年两年间,著名的律师兼数学家肯普和泰勒两人分别提交了证明四色猜想的论文,宣布证明了四色定理,大家都认为四色猜想从此也就解决了。
11年后,即1890年,数学家赫伍德以自己的精确计算指出肯普的证明是错误的。
不久,泰勒的证明也被人们否定了。
后来,越来越多的数学家虽然对此绞尽脑汁,但一无所获。
于是,人们开始认识到,这个貌似容易的题目,其实是一个可与费马猜想相媲美的难题:先辈数学大师们的努力,为后世的数学家揭示四色猜想之谜铺平了道路。
进入20世纪以来,科学家们对四色猜想的证明基本上是按照肯普的想法在进行。
1913年,伯克霍夫在肯普的基础上引进了一些新技巧,美国数学家富兰克林于1939年证明了22国以下的地图都可以用四色着色。
1950年,有人从22国推进到35国。
1960年,有人又证明了39国以下的地图可以只用四种颜色着色;随后又推进到了50国。
小学数学数学故事数学猜想系列四色猜想
世界近代三大数学难题之一。
四色猜想的提出来自英国。
1852年,毕业于伦敦大学的弗南西斯.格思里来到一家科研单位搞地图着色工作时,发现了一种有趣的现象:“看来,每幅地图都可以用四种颜色着色,使得有共同边界的国家着上不同的颜色。
”这个结论能不能从数学上加以严格证明呢?他和在大学读书的弟弟格里斯决心试一试。
兄弟二人为证明这一问题而使用的稿纸已经堆了一大叠,可是研究工作没有进展。
1852年10月23日,他的弟弟就这个问题的证明请教他的老师、著名数学家德.摩尔根,摩尔根也没有能找到解决这个问题的途径,于是写信向自己的好友、著名数学家哈密尔顿爵士请教。
哈密尔顿接到摩尔根的信后,对四色问题进行论证。
但直到1865年哈密尔顿逝世为止,问题也没有能够解决。
1872年,英国当时最著名的数学家凯利正式向伦敦数学学会提出了这个问题,于是四色猜想成了世界数学界关注的问题。
世界上许多一流的数学家都纷纷参加了四色猜想的大会战。
1878~1880年两年间,著名的律师兼数学家肯普和泰勒两人分别提交了证明四色猜想的论文,宣布证明了四色定理,大家都认为四色猜想从此也就解决了。
11年后,即1890年,数学家赫伍德以自己的精确计算指出肯普的证明是错误的。
不久,泰勒的证明也被人们否定了。
后来,越来越多的数学家虽然对此绞尽脑汁,但一无所获。
于是,人们开始认识到,这个貌似容易的题目,其实是一个可与费马猜想相媲美的难题:先辈数学大师们的努力,为后世的数学家揭示四色猜想之谜铺平了道路。
进入20世纪以来,科学家们对四色猜想的证明基本上是按照肯普的想法在进行。
1913年,伯克霍夫在肯普的基础上引进了一些新技巧,美国数学家富兰克林于1939年证明了22国以下的地图都可以用四色着色。
1950年,有人从22国推进到35国。
1960年,有人又证明了39国以下的地图可以只用四种颜色着色;随后又推进到了50国。
看来这种推进仍然十分缓慢。
电子计算机问世以后,由于演算速度迅速提高,加之人机对话的出现,大大加快了对四色猜想证明的进程。
1976年,美国数学家阿佩尔与哈肯在美国伊利诺斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿判断,终于完成了四色定理的证明。
四色猜想的计算机证明,轰动了世界。
它不仅解决了一个历时100多年的难题,而且有可能成为数学史上一系列新思维的起点。
不过也有不少数学家并不满足于计算机取得的成就,他们还在寻找一种简捷明快的书面证明方法。