北师大版八年级数学上册 第一章 勾股定理 单元练习试题 含答案

第一章勾股定理数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题，共计45分)1、若，，为的三边长，则下列条件中不能判定是直角三角形的是（）A. ，，B.C.D.2、如图，矩形ABCD的两条对角线相交于点O，∠ACB=30°,AB=2，则矩形的面积为（）A. B.2 C.4 D.3、如图，小明将一张长为20cm，宽为15cm的长方形纸（AE＞DE）剪去了一角，量得AB=3cm，CD=4cm，则剪去的直角三角形的斜边长为（）A.5cmB.12cmC.16cmD.20cm4、如图，O是正内一点，，，，将线段BO以点B为旋转中心逆时针旋转得到线段，下列五个结论中，其中正确的结论是（）可以由绕点B逆时针旋转得到；点O与的距离为4；；；．A. B. C. D.5、如图：图形A的面积是（）A.225B.144C.81D.无法确定6、如图，一个小球沿倾斜角为的斜坡向下滚动，经过5秒时，测得小球的平均速度为米秒.已知，则小球下降的高度是（）A.1米B.1.5米C.2米D.2.5米7、用圆心角为120°，半径为3 cm的扇形纸片卷成一个圆锥形无底纸冒（如图所示），则这个纸冒的高是（）A.3 cmB.2 cmC.3 cmD.4 cm8、在Rt△ABC中，∠C=90°，AB=15，AC：BC=3：4，则这个直角三角形的面积是（）A.24B.48C.54D.1089、如图，在△ABC中，AB=AC=5，P是BC边上除B、C点外的任意一点，则代数式AP2+PB•PC等于（）A.25B.15C.20D.3010、如图，AB是⊙O的弦，AB=5，点C是⊙O上的一个动点，且∠ACB=45°，点M，N分别是AB，AC的中点，则线段MN长的最大值为（）A.5B.C.5D.11、在直角坐标系中，点P(-2，3)到原点的距离是( )A. B. C. D.212、如图所示，点B，D在数轴上，OB=3，OD=BC=1，∠OBC=90°，以D为圆心，DC长为半径画弧，与数轴正半轴交于点A，则点A表示的实数是（）A. B. 1 C. 1 D.不能确定13、如图，将一边长为a的正方形（最中间的小正方形）与四块边长为b的正方形（其中b＞a）拼接在一起，则四边形ABCD的面积为（）A.b 2+（b﹣a）2B.b 2+a 2C.（b+a）2D.a 2+2ab14、如图，在矩形中，，，过对角线交点作交于点，交于点，则的长是( )A.1B.C.2D.15、如图，将等腰直角三角形（）沿折叠，使点落在边的中点处，，那么线段的长度为（）A.5B.4C.4. 25D.二、填空题(共10题，共计30分)16、如图，等边的边与轴交于点，点是反比例函数图像上一点，若为边的三等分点时，则等边的边长为________．17、如图，在△ABC中，AB＝BC＝6，AO＝BO，P是射线CO上在AB下方的一个动点，∠AOC ＝45°．则当△PAB为直角三角形时，AP的长为________．18、如图，巳知AB是⊙O的一条直径，延长AB至C点，使得AC=3BC，CD与⊙O相切，切点为D．若CD= ，则线段BC的长度等于________．19、《九章算术》中有一个“折竹抵地”问题：“今有竹高九尺，末折抵地，去本三尺，问折者高几何？”意思是：现有竹子高9尺，折后竹尖抵地与竹子底部的距离为3尺，问折处高几尺？即：如图，AB＋AC＝9尺，BC＝3尺，则AC=________尺.20、已知△ABC中，AB=5，AC=3，BC=4，P为边AB上一点，且△APC为等腰三角形，则CP 的长为________21、如图，已知菱形ABCD的周长为16，面积为8 ，E为AB的中点，若P为对角线BD 上一动点，则EP+AP的最小值为________．22、如图，长方体的底面边长分别为1cm和3cm，高为6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要________cm．23、如图，线段AB=2，过点B作BD⊥AB，使BD= AB，连接AD，在AD上截取DE=DB．在AB上截取AC=AE．那么线段AC的长为________．24、在⊙O中，弦AB＝24cm，圆心O到弦AB的距离为5cm，则⊙O的半径为________cm．25、如图，在等腰Rt△OAA1中，∠OAA1＝90°，OA＝1，以OA1为直角边作等腰Rt△OA1A2，以OA2为直角边作等腰Rt△OA2A3，…则OA8的长度为________.三、解答题(共5题，共计25分)26、如图，已知在△ABC中，CD⊥AB于D，AC＝20，BC＝15，DB＝9.求AB的长.27、如图，在平面直角坐标系xOy中，点A、B坐标分别为（4，2）、（0，2），线段CD 在于x轴上，CD＝，点C从原点出发沿x轴正方向以每秒1个单位长度向右平移，点D随着点C同时同速同方向运动，过点D作x轴的垂线交线段AB于点E、交OA于点G，连结CE交OA于点F．设运动时间为t，当E点到达A点时，停止所有运动．（1）求线段CE的长；（2）记S为RtΔCDE与ΔABO的重叠部分面积，试写出S关于t的函数关系式及t的取值范围；（3）连结DF，①当t取何值时，有DF=CD?②直接写出ΔCDF的外接圆与OA相切时t的值.28、在Rt△ABC中，∠ACB=90°，AC=BC，D为AB边的中点，点P为BC边上一点，把△PBD沿PD翻折，点B落在点E处，设PE交AC于F，连接CD(1)求证：△PCF的周长=CD；(2)设DE交AC于G，若， CD=6，求FG的长29、将一个直角三角形纸片ABO，放置在平面直角坐标系中，点A（，0），点B （0，1），点0（0，0）．过边OA上的动点M（点M不与点O，A重合）作MN丄AB于点N，沿着MN折叠该纸片，得顶点A的对应点A′，设OM=m，折叠后的△AM′N与四边形OMNB重叠部分的面积为S．（Ⅰ）如图①，当点A′与顶点B重合时，求点M的坐标；（Ⅱ）如图②，当点A′，落在第二象限时，A′M与OB相交于点C，试用含m的式子表示S；（Ⅲ）当S= 时，求点M的坐标（直接写出结果即可）．30、如图，AB是的直径，弦于点E，若，，求的长．参考答案一、单选题(共15题，共计45分)1、D2、A3、D4、C5、C6、B7、B8、C9、A10、D11、B12、C13、A14、B15、D二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)28、29、30、。

第一章勾股定理数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题，共计45分)1、分别以下列四组数为一个三角形的边长：（1）6,8,10,；（2）5,12,13；（3）8,15,17；（4）4，5，6，其中能构成直角三角形的有 ( )A.4组B.3组C.2组D.1组2、下列判断中正确的有（）个①直角三角形的两边为3和4，则第三边长为5②有一个内角等于其它两个内角和的三角形是直角三角形③若三角形的三边满足b2＝a2﹣c2，则△ABC是直角三角形④若△ABC中，∠A：∠B：∠C＝8：15：17，则△ABC是直角三角形A.1B.2C.3D.43、如图，等边三角形OAB的顶点O在坐标原点，顶点A在x轴上，OA=2，将等边三角形OAB绕原点顺时针旋转105°至OA′B′的位置，则点B′的坐标为（）A.（，- ）B.（- ，）C.（- , ）D.（，- ）4、四边形中，，则的值为（）A.15B.C.D.205、如图，点C是线段AB上一点，分别以AC，BC为边在线段AB的同侧作等边△ACD和等边△BCE，连结DE，点F为DE的中点，连结CF.若AB＝2a（a为常数，a＞0），当点C在线段AB上运动时，线段CF的长度l的取值范围是（）A. B. C. D.6、如图，平面直角坐标系中，与轴分别交于、两点，点的坐标为，．将沿着与轴平行的方向平移多少距离时与轴相切（）A.1B.2C.3D.1或37、一个直角三角形中，两直角边长分别为3和4，下列说法正确的是（）A.斜边长为25B.三角形周长为25C.斜边长为5D.三角形面积为208、如图，已知在4 4的网格中，每个小正方形的边长都是1，△ABC的顶点都在这些小正方形的顶点上，则cos∠CAB的值为（）A. B. C. D.9、一直角三角形的斜边长比一直角边长大2，另一直角边长为6，则斜边长为（）A.4B.8C.10D.1210、在中，若，，，则下列结论正确的是（）A. B. C. D. 不是直角三角形11、直角三角形三边的长分别为3、4、x，则x可能取的值为（）A.5B.C.5或D.不能确定12、如图，将半径为4cm的圆折叠后圆弧正好经过圆心，问折痕长（）A. cmB. cmC. cmD. cm13、如图，有一块直角三角形纸片，两直角边分别为AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于( )A.2cmB.3cmC.4cmD.5cm14、⊙O的直径为10，圆心O到弦AB的距离OM的长为3，则弦AB的长是（）A.4B.6C.7D.815、如图，正方形ABCD的边长为2，其面积标记为S1，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S2，…，按照此规律继续下去，则S9的值为（）A.（）6B.（）7C.（）6D.（）7二、填空题(共10题，共计30分)16、如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=2，CE=6，H是AF的中点，那么CH的长是________．17、如图为某楼梯的侧面，测得楼梯的斜长AB为5米，高BC为3米，计划在楼梯表面铺地毯，地毯的长度至少需要________米．18、如图，在矩形纸片ABCD中，AB=6，BC=10，点E在CD上，将△BCE沿BE折叠，点C 恰落在边AD上的点F处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H 处，有下列结论：①∠EBG=45°；②△DEF∽△ABG；③S△ABG= S△FGH；④AG+DF=FG．其中正确的是________．（把所有正确结论的序号都选上）19、如图，已知A为⊙O外一点，连结OA交⊙O于P，AB为⊙O的切线，B为切点，AP＝5㎝，AB＝㎝，则劣弧与AB，AP所围成的阴影的面积是________.20、已知的三边长分别是，则的面积是________．21、如图，已知菱形ABCD中，∠BAD=120°，AD=8，则这个菱形的面积为________。

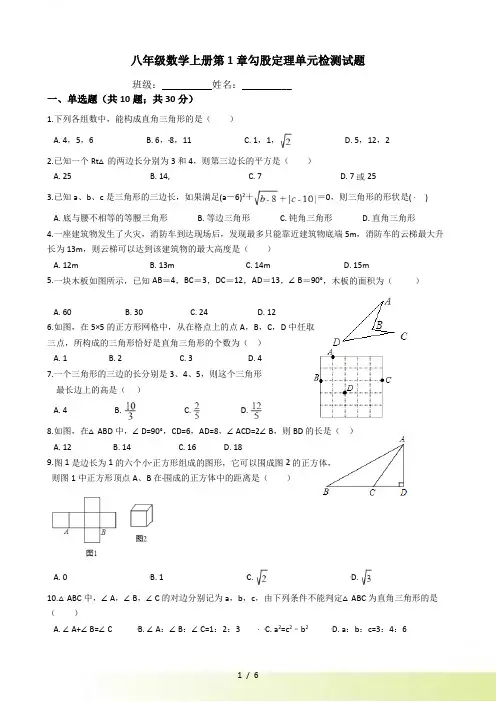
八年级数学上册第1章勾股定理单元检测试题班级：__________姓名：__________一、单选题（共10题；共30分）1.下列各组数中，能构成直角三角形的是（）A. 4，5，6B. 6，8，11C. 1，1，D. 5，12，22.已知一个Rt△的两边长分别为3和4，则第三边长的平方是（）A. 25B. 14,C. 7D. 7或253.已知a、b、c是三角形的三边长，如果满足(a－6)2＋＝0，则三角形的形状是( )A. 底与腰不相等的等腰三角形B. 等边三角形C. 钝角三角形D. 直角三角形4.一座建筑物发生了火灾，消防车到达现场后，发现最多只能靠近建筑物底端5m，消防车的云梯最大升长为13m，则云梯可以达到该建筑物的最大高度是（）A. 12mB. 13mC. 14mD. 15m5.一块木板如图所示，已知AB＝4，BC＝3，DC＝12，AD＝13，∠B＝90°，木板的面积为（）A. 60B. 30C. 24D. 126.如图，在5×5的正方形网格中，从在格点上的点A，B，C，D中任取三点，所构成的三角形恰好是直角三角形的个数为（）A. 1B. 2C. 3D. 47.一个三角形的三边的长分别是3、4、5，则这个三角形最长边上的高是（）A. 4B.C.D.8.如图，在△ABD中，∠D=90°，CD=6，AD=8，∠ACD=2∠B，则BD的长是（）A. 12B. 14C. 16D. 189.图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体，则图1中正方形顶点A、B在围成的正方体中的距离是（）A. 0B. 1C.D.10.△ABC中，∠A，∠B，∠C的对边分别记为a，b，c，由下列条件不能判定△ABC为直角三角形的是（）A. ∠A+∠B=∠CB. ∠A：∠B：∠C=1：2：3C. a2=c2﹣b2D. a：b：c=3：4：6二、填空题（共8题；共24分）11.如图为某楼梯的侧面，测得楼梯的斜长AB为13米，高BC为5米，计划在楼梯表面铺地毯，地毯的长度至少需要________米．12.在直角三角形ABC中，斜边AB=2，则AB2+AC2+BC2=________．13.一直角三角形的一条斜边和一直角边的长度分别是4和3，则它的另一直角边长是________.14.已知直角三角形的两边的长分别是3和4，则第三边长为________．15.将一根24cm的筷子，置于底面直径为15cm，高8cm的圆柱形水杯中，如图所示，设筷子露在杯子外面的长度为hcm，则h的取值范围是________ ．16.在直线l上依次摆放着七个正方形（如图所示）．已知斜放置的三个正方形的面积分别是1，2，3，正放置的四个正方形的面积依次是S1，S2，S3，S4，则S1+S2+S3+S4=________17.要在一个长方体中放入一细直木条，现知长方体的长为2，宽为，高为，则放入木盒的细木条最大长度为________ ．18.如图，一根旗杆在离地面9米处断裂，旗杆顶部落在离旗杆底部12米处，则旗杆折断之前有________米．三、解答题（共66分）19.已知：如图，在△ABC 中，∠C=90°，D 是BC 的中点，AB=10，A C=6．求AD 的长度．20.求如图的Rt△ABC的面积．21.如图，∠AOB=90°，OA=90cm，OB=30cm，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少?22.一个25米长的梯子AB，斜靠在一竖直的墙AO上，这时的AO距离为24米，如果梯子的顶端A沿墙下滑4米，那么梯子底端B也外移4米，对吗？为什么？23.铁路上A，B两站（视为直线上的两点）相距50km，C，D为两村庄（视为两个点），DA⊥AB于点A，CB⊥AB于点B（如图）.已知DA=20km，CB=10km，现在要在铁路AB上建一个土特产收购站E，使得C，D 两村庄到收购站E的直线距离相等，请你设计出收购站的位置，并计算出收购站E到A站的距离.24.如图，南北向MN为我国领海线，即MN以西为我国领海，以东为公海，上午9时50分，我国反走私A艇发现正东方有一走私艇以13海里/时的速度偷偷向我领海开来，便立即通知正在MN线上巡逻的我国反走私艇B密切注意．反走私艇A和走私艇C的距离是13海里，A、B两艇的距离是5海里；反走私艇B 测得距离C艇12海里，若走私艇C的速度不变，最早会在什么时候进入我国领海？25.已知在中，，，．（1）判断△ABC的形状，并说明理由；（2）试在下面的方格纸上补全△ABC，使它的顶点都在方格的顶点上。

第一章勾股定理数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题，共计45分)1、如图，数轴上的点A表示的数是-1，点B表示的数是1，CB⊥AB于点B，且BC=2，以点A为圆心，AC为半径画弧交数轴于点D，则点D表示的数为（）A.2.8B. -C.D.2、如图，在Rt△ABC中，∠ACB=90°，以点A为圆心，AC长为半径作圆弧交边AB于点D．若 AC=3，BC=4．则BD的长是（）A.2B.3C.4D.53、如图，在四边形ABCD中，，，，.分别以点A，C为圆心，大于长为半径作弧，两弧交于点E，作射线BE交AD于点F，交AC于点O.若点O是AC的中点，则CD的长为（）4、如图是一圆柱形输水管的横截面，阴影部分为有水部分，如果水面AB宽为8cm，水面最深地方的高度为2cm，则该输水管的半径为（）A.3cmB.4cmC.5cmD.6cm5、如图，在平行四边形中，对角线与相交于点，则的长为（）A.8B.4C.3D.56、如图，小正方形的边长均为1，则下列图中的三角形(阴影部分)与△ABC相似的是( )A. B. C. D.7、如图，已知正方形ABCD的边长为3，E为CD上一点，DE=1，以点A为中心，把△ADE 顺时针旋转90°得△ABE'，连接EE'，则EE'的长度为( )8、如图，O是正△ABC内一点，OA=3，OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：①△BO′A可以由△BOC绕点B逆时针旋转60°得到；②点O与O′的距离为4；③∠AOB=150°；④S四边形AOBO′=6+3；⑤S△AOC+S△=6+．其中正确的结论是（）AOBA.①②③⑤B.①②③④C.①②③④⑤D.①②③9、下列四组数中，不能构成直角三角形边长的一组是( )A. B. C. D.10、如图，在ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG=，则ΔCEF的周长等于A.8B.9.5C.10D.11.511、满足下列条件的，不是直角三角形的是（）A. B. C.D.12、图1为一个长方体，AD=AB=10，AE=6，M，N为所在棱的中点，图2为图1的表面展开图，则图2中MN的长度为（）A.11B.10C.10D.813、已知：如图在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE．以下四个结论：①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④BE2=2（AD2+AB2）﹣CD2，其中结论正确的个数是（）A.1B.2C.3D.414、将矩形纸片ABCD 按如图所示的方式折叠，得到菱形AECF．若AB＝3，则BC 的长为（）A. B.2 C.1.5 D.15、在直角三角形中，自锐角顶点引的两条中线为和，则这个直角三角形的斜边长是( )A.3B.2C.2D.6二、填空题(共10题，共计30分)16、《九章算术》是我国古代重要的数学著作之一，在“勾股”中记载了一道“折竹抵地”问题：“今有竹高一丈，未折抵地，去本三尺，问折者高几何？”翻译成数学问题是：如图所示，△ABC中，∠ACB＝90°，AC+AB＝10，BC＝3，求AC的长，如果设AC＝x，则可列方程求出AC的长为________.17、如图，正方形ABCD中，AB=2，对角线AC，BD相交于点O，将△OBC绕点B逆时针旋转得到△O′BC′，当射线O′C′经过点D时，线段DC′的长为________．18、在中，若，，，则________.19、如图，在矩形中，，，对角线相交于点O，点P为边上一动点，连接，以为折痕，将折叠，点A的对应点为点E，线段与相交于点F.若为直角三角形，则的长________.20、如图，Rt△ABC中，∠ACB＝90°，AC＝4，BC＝6，D为线段AC上一动点，连接BD，过点C作CH⊥BD于H，连接AH，则AH的最小值为________.21、在△ABC中，AB=4，AC=3，BC=5，则△ABC的面积是________．22、如图，平面直角坐标系内有一点A（3，4），O为坐标原点.点B在x轴上，若△AOB 为等腰三角形，则点B的坐标为________.23、如图，长方形ABCD中，AB＝3，BC＝4，点E是BC边上任一点，连接AE，把∠B沿AE 折叠，使点B落在点B′处，当CE的长为________时，△CEB′恰好为直角三角形.24、在《九章算术》中有一个问题（如图)：今有竹高一丈，末折抵地，去本三尺，问折者高几何?它的意思是：一根竹子原高一丈（尺)，中部一处折断，竹梢触地面处离竹根尺，试问折断处离地面________尺．25、在直角三角形ABC中，∠C=90º，如果c=13，a=5，那么b=________．三、解答题(共5题，共计25分)26、如图，在Rt△ABC中，∠C=90°，BC=8，tanB= ，点D在BC上，且BD=AD，求AC 的长和cos∠ADC的值．27、如图，在四边形ABCD中，AB＝BC＝2，CD＝3，AD＝1，且∠ABC＝90°，试求∠A的度数．28、已知：如图，在四边形ABCD中，∠B＝90°，AB＝BC＝2，CD＝3，AD＝1，求∠DAB的度数．29、如图，学校有一块空地ABCD，准备种草皮绿化已知∠ADC＝90°，AD＝4米，CD＝3米，AB＝13米，BC＝12米，求这块地的面积．30、如图，校园内有一棵与地面垂直的树，数学兴趣小组两次测量它在地面上的影子，第一次是阳光与地面成60°角时，第二次是阳光与地面成30°角时，两次测量的影长相差8米，求树高AB多少米．（结果保留根号）参考答案一、单选题(共15题，共计45分)1、B2、A3、A4、C5、B6、B7、A8、A9、B10、A11、C12、A13、D14、D15、D二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、27、29、。

北师大版八年级数学上册第一章勾股定理单元测试题一、选择题(每小题4分，共40分)1．下列各组数分别为三角形三边的长，其中不能构成直角三角形的一组是(B) A．3，4，5 B．4，5，6C.34，54，1 D．9，12，152．如图，以数轴的单位长线段为边作一个正方形，以数轴的原点为圆心，以正方形的对角线为半径画弧交数轴正半轴于点A，则点A表示的数是(B)A.32B. 2C. 3 D．1.43．两只小鼹鼠在地下打洞，一只朝前方挖，每分钟挖8 cm，另一只朝左挖，每分钟挖6 cm，10分钟后，两只小鼹鼠相距(B)A．50 cm B．100 cmC．140 cm D．80 cm4．如图，在Rt△ABC中，∠ACB＝90°，以点A为圆心，AC长为半径作圆弧交边AB于点D.若AC＝6，BC＝8，则BD的长是(A)A．4B．5C．6D．75．如果将长为6 cm，宽为5 cm的长方形纸片折叠一次，那么这条折痕的长不可能是(A) A．8 cm B．5 2 cmC．5.5 cm D．1 cm6．如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为(C)A．4 B．6 C．16 D．557．如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案．已知大正方形面积为49，小正方形面积为4，若用x，y表示直角三角形的两直角边(x＞y)，下列四个说法：①x2＋y2＝49；②x－y＝2；③x＋y＝9；④2xy＋4＝49；其中说法正确的是(C)A．①② B．①②③C．①②④ D．①②③④8．小明准备测量一段河水的深度，他把一根竹竿竖直插到离岸边1.5 m远的水底，竹竿高出水面0.5 m，把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，则河水的深度为(A)A．2 m B．2.5 mC．2.25 m D．3 m9．如图，将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起，其中点A′与点A 重合，点C′落在边AB上，连接B′C.若∠ACB＝∠AC′B′＝90°，AC＝BC＝3，则B′C 的长为(A)A．3 3 B．6 C．3 2 D.2110．(钦州中考)如图，6个边长为1的小正方形及其部分对角线所构成的图形中，如果从A 点到B点只能沿图中的线段走，那么从A点到B点的最短距离的走法共有(C)A．1种 B．2种 C．3种 D．4种二、填空题(每小题4分，共20分)11．在平面直角坐标系中，点A的坐标是(0，9)，点B的坐标是(－12，0)，则A，B两点间的距离是15.12．在Rt△ABC中，∠C＝90°，周长为60 cm，且两直角边BC∶AC＝5∶12，则△ABC的面积为120cm2.13．如图，在网格中，小正方形边长为a，则图中是直角三角形的是△ABC与△DEF．14．将一根长为25 cm的筷子置于底面直径为5 cm，高为12 cm的圆柱形水杯中，设筷子露在杯子外面的长为h cm，则h的取值范围是12≤h≤13．15．在△ABC中，AB＝10，AC＝210，BC边上的高AD＝6，则另一边BC等于6或10．三、解答题(共40分)16．(8分)如图，在3×4正方形网格中，每个小正方形的边长都是1.(1)分别求出线段AB，CD的长度；(2)在图中画线段EF，使得EF的长为5，AB，CD，EF三条线段能否构成直角三角形，并说明理由．解：(1)AB＝32＋22＝13；CD＝22＋22＝2 2.(2)如图，EF ＝22＋12＝5， ∵CD 2＋EF 2＝8＋5＝13，AB 2＝13， ∴CD 2＋EF 2＝AB 2.∴AB ，CD ，EF 三条线段可以组成直角三角形．17．(10分)如图，四边形ABCD 中，AB ＝1，BC ＝2，CD ＝2，AD ＝3，且AB ⊥BC.求证：AC ⊥CD.证明：由AB ＝1，BC ＝2，且AB ⊥BC ，得AC 2＝AB 2＋BC 2＝5. 在△ACD 中，AD 2＝32＝9，AC 2＋CD 2＝5＋22＝9， ∴AC 2＋CD 2＝AD 2.∴△ACD 为直角三角形，∠ACD ＝90°. ∴AC ⊥CD. 18.(10分)如图，圆柱的底面周长为6 cm ，AC 是底面圆的直径，高BC ＝6 cm ，点P 是BC 上一点，且PC ＝23BC.一只蚂蚁从点A 出发沿着圆柱体的表面爬行到点P 的最短距离是多少？解：画侧面展开图，如图，因为圆柱的底面周长为6 cm ， 所以展开图中AC ＝3 cm. 又因为PC ＝23BC ，所以PC ＝23×6＝4(cm)．在Rt △ACP 中，AP 2＝AC 2＋CP 2，得AP ＝5 cm. 所以蚂蚁爬行的最短距离是5 cm.19．(10分)如图，△ACB 和△ECD 都是等腰直角三角形，∠ACB ＝∠ECD ＝90°，D 为AB 边上一点，试证明：(1)△ACE ≌△BCD ； (2)AD 2＋DB 2＝DE 2.证明：(1)∵∠ACB ＝∠ECD ＝90°， ∴∠ACD ＋∠BCD ＝∠ACD ＋∠ACE ， 即∠BCD ＝∠ACE.∵△ACB 和△ECD 都是等腰直角三角形， ∴BC ＝AC ，DC ＝EC. ∴△ACE ≌△BCD(SAS)． (2)∵△ACB 是等腰直角三角形， ∴∠B ＝∠BAC ＝45°. ∵△ACE ≌△BCD ， ∴∠CAE ＝∠B ＝45°.∴∠DAE＝∠CAE＋∠BAC＝45°＋45°＝90°.∴AD2＋AE2＝DE2.∵△ACE≌△BCD，∴AE＝DB.∴AD2＋DB2＝DE2.20.(10分)如图，在正方形ABCD纸片上有一点P，PA＝1，PD＝2，PC＝3.现将△PCD剪下，并将它拼到如图所示位置(C与A重合，P与G重合，D与D重合)．求：(1)线段PG的长；(2)∠APD的度数．【解答】(1)根据题意可得△AGD≌△CPD，∴∠GDA＝∠PDC.∵∠ADC＝90°，∴∠GDP＝90°.又∵GD＝PD＝2，∴PG＝2 2.(2)∵AG＝3，AP＝1，(22)2＋12＝32，∴∠APG＝90°.又由(1)可知△PDG是等腰直角三角形，∴∠GPD＝45°，∴∠APD＝135°.21、(12分)如图，在正方形ABCD中，E是BC中点，F在AB上，且AF∶FB＝3∶1.(1)请判断EF与DE的位置关系，并说明理由；(2)若此正方形的面积为16，求DF的长．解：(1)EF 与DE 垂直，即EF ⊥DE.理由：设正方形边长为a ， 则AD ＝DC ＝a ，AF ＝34a ，FB ＝14a ，BE ＝EC ＝12a.在Rt △DAF 中，DF 2＝AD 2＋AF 2＝2516a 2.在Rt △CDE 中，DE 2＝CD 2＋CE 2＝54a 2.在Rt △EFB 中，EF 2＝FB 2＋BE 2＝516a 2.∵DE 2＋EF 2＝54a 2＋516a 2＝2516a 2＝DF 2，∴△DFE 为直角三角形，∠DEF ＝90°.∴EF ⊥DE. (2)∵正方形的面积为16，∴a 2＝16. ∵DF 2＝2516a 2＝2516×16＝25，∴DF ＝5.。

第一章勾股定理单元测试卷一．选择题（共12小题）1．如图，四边形ABCD的对角线AC与BD互相垂直，若AB=3，BC=4，CD=5，则AD的长为（）A．3B．4 C．2D．4(第1题) (第4题) (第5题)2．△ABC中，∠A，∠B，∠C的对边分别记为a，b，c，由下列条件不能判定△ABC为直角三角形的是（）A．∠A+∠B=∠C B．∠A：∠B：∠C=1：2：3C．a2=c2﹣b2D．a：b：c=3：4：63．三角形的三边长a，b，c满足2ab=（a+b）2﹣c2，则此三角形是（）A．钝角三角形B．锐角三角形C．直角三角形D．等边三角形4．如图，在△ABC中，∠C=90°，AC=2，点D在BC上，∠ADC=2∠B，AD=，则BC 的长为（）A．﹣1 B．+1 C．﹣1 D．+15．如图所示，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D，则BD的长为（）A．B．C．D．6．以下列各组线段为边长，能构成直角三角形的是（）A．1，1，B．3，4，5 C．5，10，13 D．2，3，47．如图，一轮船以16海里/时的速度从港口A出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A出发向东南方向航行，离开港口2小时后，则两船相距（）A．25海里B．30海里C．40海里D．50海里(第7题) (第9题) (第10题)8．△ABC中，边AB=15，AC=13，高AD=12，则△ABC的周长是（）A．42 B．32 C．42或32 D．不能确定9．如图，在Rt△ABC中，∠ACB=90°，AB=，BC=2，则这个直角三角形的面积为（）A．3 B．6 C．D．10．如图，有4个相同的直角三角形与中间的小正方形拼成一个大正方形，若大正方形面积是17，小正方形面积是5，直角三角形较长直角边为a，较短直角边为b，则ab的值是（）A．4 B．6 C．8 D．1011．如图①所示，有一个由传感器A控制的灯，要装在门上方离地高4、5m的墙上，任何东西只要移至该灯5m及5m以内时，灯就会自动发光．请问一个身高1、5m的学生要走到离墙多远的地方灯刚好发光？（）A．4米B．3米C．5米D．7米(第11题) (第12题)12．如图表示的是一个十字路口，O是两条公路的交点，点A、B、C、D表示的是公路上的四辆车，若OC=8cm，AC=17cm，AB=5cm，BD=10m，则C，D两辆车之间的距离为（）A．5m B．4m C．3m D．2m二．填空题（共5小题）13．如图，在△ABC中，AB=AC=4，AO=BO，P是射线CO上的一个动点，∠AOC=120°，则当△P AB为直角三角形时，AP的长为．(第13题) (第14题) (第15题) 14．如图，一架10米长的梯子斜靠在墙上，刚好梯顶抵达8米高的路灯．当电工师傅沿梯上去修路灯时，梯子下滑到了B′处，下滑后，两次梯脚间的距离为2米，则梯顶离路灯米．15．如图，将一根长24cm的筷子，置于底面直径为5cm，高为12cm的圆柱形茶杯中，设筷子露在杯子外面的长为acm（茶杯装满水），则a的取值范围是．16．如图，四边形ABCD中，AD=3，CD=4，∠ABC=∠ACB=∠ADC=45°，则BD的长为．17．如果矩形的周长是14cm，相邻两边长之比为3：4，那么对角线长为cm．三．解答题（共5小题）18．一架梯子长25米，斜靠在一面墙上，梯子底端离墙7米，（1）这个梯子的顶端距地面有多高？（2）如果梯子的顶端下滑了4米到A′，那么梯子的底端在水平方向滑动了几米？19．在△ABC中，CD是AB边上的高，AC=4，BC=3，DB=求：（1）求AD的长；（2）△ABC是直角三角形吗？为什么？20．如图，AB=BC=CD=DE=1，且BC⊥AB，CD⊥AC，DE⊥AD，求线段AE的长．21．如图，在Rt△ABC中，∠A=90°，边BC的垂直平分线DE交AB于点E，连接CE．求证：BE2=AC2+AE2．22．（1）如图（1），分别以Rt△ABC三边为直径向外作三个正方形，其面积分别用S1，S2，S3表示，写出S1，S2，S3之间关系．（不必证明）（2）如图（2），分别以Rt△ABC三边为边向外作三个半圆，其面积分别用S1，S2，S3表示，确定它们的关系证明；（3）如图（3），分别以Rt△ABC三边为边向外作正三角形，其面积分别用S1，S2，S3表示，确定它们的关系并证明．参考答案一．选择题（共12小题）1．如图，四边形ABCD的对角线AC与BD互相垂直，若AB=3，BC=4，CD=5，则AD的长为（）A．3B．4 C．2D．4【解答】解：在Rt△AOB中，AO2=AB2﹣BO2；Rt△DOC中可得：DO2=DC2﹣CO2；∴可得AD2=AO2+DO2=AB2﹣BO2+DC2﹣CO2=18，即可得AD==3．故选A．2．△ABC中，∠A，∠B，∠C的对边分别记为a，b，c，由下列条件不能判定△ABC为直角三角形的是（）A．∠A+∠B=∠C B．∠A：∠B：∠C=1：2：3C．a2=c2﹣b2D．a：b：c=3：4：6【解答】解：A、∠A+∠B=∠C，又∠A+∠B+∠C=180°，则∠C=90°，是直角三角形；B、∠A：∠B：∠C=1：2：3，又∠A+∠B+∠C=180°，则∠C=90°，是直角三角形；C、由a2=c2﹣b2，得a2+b2=c2，符合勾股定理的逆定理，是直角三角形；D、32+42≠62，不符合勾股定理的逆定理，不是直角三角形．故选D．3．三角形的三边长a，b，c满足2ab=（a+b）2﹣c2，则此三角形是（）A．钝角三角形B．锐角三角形C．直角三角形D．等边三角形【解答】解：∵原式可化为a2+b2=c2，∴此三角形是直角三角形．故选：C．http://www、czsx、com、cn4．如图，在△ABC中，∠C=90°，AC=2，点D在BC上，∠ADC=2∠B，AD=，则BC 的长为（）A．﹣1 B．+1 C．﹣1 D．+1【解答】解：∵∠ADC=2∠B，∠ADC=∠B+∠BAD，∴∠B=∠DAB，∴DB=DA=5，在Rt△ADC中，DC===1，∴BC=+1．故选D．5．如图所示，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D，则BD的长为（）A．B．C． D．【解答】解：△ABC的面积=×BC×AE=2，由勾股定理得，AC==，则××BD=2，解得BD=，故选：A．6．以下列各组线段为边长，能构成直角三角形的是（）A．1，1，B．3，4，5 C．5，10，13 D．2，3，4【解答】解：A、12+12≠（）2，不能构成直角三角形，故此选项错误；B、32+42=52，能构成直角三角形，故此选项正确；C、52+102≠132，不能构成直角三角形，故此选项错误；D、22+32≠42，不能构成直角三角形，故此选项错误．故选B．7．如图，一轮船以16海里/时的速度从港口A出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A出发向东南方向航行，离开港口2小时后，则两船相距（）A．25海里B．30海里C．40海里D．50海里【解答】解：连接BC，由题意得：AC=16×2=32（海里），AB=12×2=24（海里），CB==40（海里），故选：C．8．△ABC中，边AB=15，AC=13，高AD=12，则△ABC的周长是（）A．42 B．32 C．42或32 D．不能确定【解答】解：此题应分两种情况说明：（1）当△ABC为锐角三角形时，在Rt△ABD中，BD===9，在Rt△ACD中，CD===5∴BC=5+9=14∴△ABC的周长为：15+13+14=42；（2）当△ABC为钝角三角形时，在Rt△ABD中，BD===9，在Rt△ACD中，CD===5，∴BC=9﹣5=4．∴△ABC的周长为：15+13+4=32∴当△ABC为锐角三角形时，△ABC的周长为42；当△ABC为钝角三角形时，△ABC的周长为32．综上所述，△ABC的周长是42或32．故选：C．9．如图，在Rt△ABC中，∠ACB=90°，AB=，BC=2，则这个直角三角形的面积为（）A．3 B．6 C．D．【解答】解：∵在Rt△ABC中，∠ACB=90°，AB=，BC=2，∴AC==3，∴这个直角三角形的面积=AC•BC=3，故选A．10．如图，有4个相同的直角三角形与中间的小正方形拼成一个大正方形，若大正方形面积是17，小正方形面积是5，直角三角形较长直角边为a，较短直角边为b，则ab的值是（）A．4 B．6 C．8 D．10【解答】解：根据勾股定理可得a2+b2=17，四个直角三角形的面积是：ab×4=17﹣5=12，即：ab=6．故选：B．11．如图①所示，有一个由传感器A控制的灯，要装在门上方离地高4、5m的墙上，任何东西只要移至该灯5m及5m以内时，灯就会自动发光．请问一个身高1、5m的学生要走到离墙多远的地方灯刚好发光？（）A．4米B．3米C．5米D．7米【解答】解：由题意可知．BE=CD=1、5m，AE=AB﹣BE=4、5﹣1、5=3m，BD=5m由勾股定理得CE==4m故离门4米远的地方，灯刚好打开，故选A．12．如图表示的是一个十字路口，O是两条公路的交点，点A、B、C、D表示的是公路上的四辆车，若OC=8cm，AC=17cm，AB=5cm，BD=10m，则C，D两辆车之间的距离为（）A．5m B．4m C．3m D．2m【解答】解：在RT△AOC中，∵OA2+OC2=AC2，∴OA===15（m），∴OB=0A+AB=20m，在RT△BOD中，∵BD2=OB2+OD2，∴OD===10（m），∴CD=OD﹣OC=2m，故选：D．二．填空题（共5小题）13．如图，在△ABC中，AB=AC=4，AO=BO，P是射线CO上的一个动点，∠AOC=120°，则当△P AB为直角三角形时，AP的长为2或2．【解答】解：当∠APB=90°时，分两种情况讨论，情况一：如图1，∵AO=BO，∴PO=BO，∵∠AOC=120°，∴∠AOP=60°，∴△AOP为等边三角形，∴∠OAP=60°，∴∠∠PBA=30°，∴AP=AB=2；情况二：如图2，∵AO=BO，∠APB=90°，∴PO=BO，∵∠AOC=120°，∴∠BOP=60°，∴△BOP为等边三角形，∴∠OBP=60°，∴AP=AB•sin60°=4×=2；当∠BAP=90°时，如图3，∵∠AOC=120°，∴∠AOP=60°，∴AP=OA•tan∠AOP=2×=2．故答案为：2或2．14．如图，一架10米长的梯子斜靠在墙上，刚好梯顶抵达8米高的路灯．当电工师傅沿梯上去修路灯时，梯子下滑到了B′处，下滑后，两次梯脚间的距离为2米，则梯顶离路灯2米．【解答】解：在直角三角形AOB中，根据勾股定理，得：OB=6m，根据题意，得：OB′=6+2=8m．又∵梯子的长度不变，在Rt△A′OB′中，根据勾股定理，得：OA′=6m．则AA′=8﹣6=2m．15．如图，将一根长24cm的筷子，置于底面直径为5cm，高为12cm的圆柱形茶杯中，设筷子露在杯子外面的长为acm（茶杯装满水），则a的取值范围是11cm≤a≤12cm．【解答】解：当筷子与杯底垂直时h最大，h最大=24﹣12=12cm．当筷子与杯底及杯高构成直角三角形时a最小，如图所示：此时，AB===13cm，故a=24﹣13=11cm．所以a的取值范围是：11cm≤a≤12cm．故答案是：11cm≤a≤12cm．16．如图，四边形ABCD中，AD=3，CD=4，∠ABC=∠ACB=∠ADC=45°，则BD的长为．【解答】解：作AD′⊥AD，AD′=AD，连接CD′，DD′，如图：∵∠BAC+∠CAD=∠DAD′+∠CAD，即∠BAD=∠CAD′，在△BAD与△CAD′中，，∴△BAD≌△CAD′（SAS），∴BD=CD′．∠DAD′=90°由勾股定理得DD′==3，∠D′DA+∠ADC=90°由勾股定理得CD′==，∴BD=CD′=，故答案为：．17．如果矩形的周长是14cm，相邻两边长之比为3：4，那么对角线长为5cm．【解答】解：设矩形的相邻两边的长度分别为3acm，4acm，由题意3a+4a=7，a=1，所以矩形的相邻两边分别为3cm，4cm，所以对角线长==5cm，故答案为5．三．解答题（共5小题）18．一架梯子长25米，斜靠在一面墙上，梯子底端离墙7米，（1）这个梯子的顶端距地面有多高？（2）如果梯子的顶端下滑了4米到A′，那么梯子的底端在水平方向滑动了几米？【解答】解：（1）由题意得：AC=25米，BC=7米，AB==24（米），答：这个梯子的顶端距地面有24米；（2）由题意得：BA′=20米，BC′==15（米），则：CC′=15﹣7=8（米），答：梯子的底端在水平方向滑动了8米．19．在△ABC中，CD是AB边上的高，AC=4，BC=3，DB=求：（1）求AD的长；（2）△ABC是直角三角形吗？为什么？【解答】解：（1）∵CD⊥AB，∴∠CDB=∠CDA=90°，在Rt△BCD中，BC=3，DB=，根据勾股定理得：CD==，在Rt△ACD中，AC=4，CD=，根据勾股定理得：AD==；（2）△ABC为直角三角形，理由为：∵AB=BD+AD=+=5，∴AC2+BC2=AB2，∴△ABC为直角三角形．20．如图，AB=BC=CD=DE=1，且BC⊥AB，CD⊥AC，DE⊥AD，求线段AE的长．【解答】解：∵BC⊥AB，CD⊥AC，AC⊥DE，∴∠B=∠ACD=∠ADE=90°，∵AB=BC=CD=DE=1，∴在Rt△ACB中，AC═==，∴在Rt△ACD中，AD===，在Rt△ADE中，AE===2．21．如图，在Rt△ABC中，∠A=90°，边BC的垂直平分线DE交AB于点E，连接CE．求证：BE2=AC2+AE2．【解答】证明：∵如图，边BC的垂直平分线DE交AB于点E，∴CE=BE．∵在Rt△ABC中，∠A=90°，∴由勾股定理得到：CE2=AC2+AE2∴BE2=AC2+AE2．22．（1）如图（1），分别以Rt△ABC三边为直径向外作三个正方形，其面积分别用S1，S2，S3表示，写出S1，S2，S3之间关系．（不必证明）（2）如图（2），分别以Rt△ABC三边为边向外作三个半圆，其面积分别用S1，S2，S3表示，确定它们的关系证明；（3）如图（3），分别以Rt△ABC三边为边向外作正三角形，其面积分别用S1，S2，S3表示，确定它们的关系并证明．【解答】解：（1）S2+S3=S1，由三个四边形都是正方形则：∵S3=AC2，S2=BC2，S1=AB2，∵三角形ABC是直角三角形，∴AC2+BC2=AB2，∴S2+S3=S1．（2）∵S3=AC2，S2=BC2，S1=AB2，∵三角形ABC是直角三角形，∴AC2+BC2=AB2，∴S2+S3=S1．（3）∵S1=AB2，S2=BC2，S3=AC2，∵三角形ABC是直角三角形，∴AC2+BC2=AB2，∴S2+S3=S1．。

第1章勾股定理一．选择题（共12小题）1．下列为勾股数的是（）A．2，3，4 B．，，C．6，7，8 D．5，12，132．已知a，b，c是△ABC的三边，且满足（a﹣b）（a2﹣b2﹣c2）＝0，则△ABC是（）A．直角三角形B．等边三角形C．等腰直角三角形D．等腰三角形或直角三角形3．在△ABC中，AB＝10，AC＝2，BC边上的高AD＝6，则另一边BC等于（）A．10 B．8 C．6或10 D．8或104．已知x、y为正数，且|x2﹣4|+（y2﹣3）2＝0，如果以x、y的长为直角边作一个直角三角形，那么以这个直角三角形的斜边为边长的正方形的面积为（）A．5 B．25 C．7 D．155．△ABC中，∠A，∠B，∠C的对边分别记为a，b，c，由下列条件不能判定△ABC为直角三角形的是（）A．∠A+∠B＝∠C B．∠A：∠B：∠C＝1：2：3C．a2＝c2﹣b2D．a：b：c＝3：4：66．下列各组线段中的三个长度：①9，12，15；②7，24，25；③32，42，52；④3a，4a，5a （a＞0）；⑤m2﹣n2，2mn，m2+n2（m，n为正整数，且m＞n）其中可以构成直角三角形的有（）A．5组B．4组C．3组D．2组7．△ABC中，AB＝7，BC＝24，AC＝25．在△ABC内有一点P到各边的距离相等，则这个距离为（）A．1 B．2 C．3 D．48．如图，由4个相同的直角三角形与中间的小正方形拼成一个大正方形，若大正方形面积是9，小正方形面积是1，直角三角形较长直角边为a，较短直角边为b，则ab的值是（）A．4 B．6 C．8 D．109．如图，两个较大正方形的面积分别为225、289，则字母A所代表的正方形的面积为（）A．4 B．8 C．16 D．6410．如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若最大正方形G的边长是6cm，则正方形A，B，C，D，E，F，G的面积之和是（）A．18cm2 B．36cm2C．72cm2D．108cm211．如图，长方体的底面边长分别为2cm和4cm，高为5cm．若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点，则蚂蚁爬行的最短路径长为（）A．13cm B．12cm C．10cm D．8cm12．如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，已知一条到达底部的直吸管在罐内部分的长度为a，若直吸管在罐外部分还剩余3，则吸管的总长度b（罐壁的厚度和小圆孔的大小忽略不计）范围是（）A．12≤b≤13 B．12≤b≤15 C．13≤b≤16 D．15≤b≤16 二．填空题（共6小题）13．如图，BD为△ABC的中线，AB＝10，AD＝6，BD＝8，△ABC的周长是．14．直角三角形两条边的长度分别为3cm，4cm，那么第三条边的长度是cm．15．如图，点A、B、C分别是正方体展开图的小正方形的顶点，则∠BAC的大小为．16．如图，矩形ABCD中，AB＝8，BC＝4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为．17．已知△ABC的三边长为a、b、c，满足a+b＝10，ab＝18，c＝8，则此三角形为三角形．三．解答题（共10小题）18．如图为一个广告牌支架的示意图，其中AB＝13m，AD＝12m，BD＝5m，AC＝15m，求图中△ABC的周长和面积．19．如图，一根竹子高10米，折断后竹子顶端C落在竹子底端A的4米处，折断处B离地面的高度AB是多少？20．如图，在△ABD中，∠D＝90°，C是BD上一点，已知BC＝9，AB＝17，AC＝10，求AD 的长．21．已知：如图，四边形ABCD，AB＝1，BC＝2，CD＝2，AD＝3，且AB⊥BC．求四边形ABCD 的面积．22．长方形纸片ABCD中，AD＝4cm，AB＝10cm，按如图方式折叠，使点B与点D重合，折痕为EF，求DE的长．23．如图，在Rt△ABC中，∠C＝90°，BC＝6，AC＝8，AB的垂直平分线DE交AB于点D，交AC于点E，连接BE．（1）求AD的长；（2）求AE的长．24．如图，一个放置在地面上的长方体，长为15cm，宽为10cm，高为20cm，点B与点C 的距离为5cm，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是多少？25．如图，是一个三级台阶，它的每一级的长、宽、高分别为20dm、3dm、2dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点的最短路程是多少？26．（1）如图1，长方体的长为4cm，宽为3cm，高为12cm．求该长方体中能放入木棒的最大长度；（2）如图2，长方体的长为4cm，宽为3cm，高为12cm．现有一只蚂蚁从点A处沿长方体的表面爬到点G处，求它爬行的最短路程．（3）若将题中的长方体换成透明圆柱形容器（容器厚度忽略不计）的高为12cm，底面周长为10cm，在容器内壁离底部3cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处．求蚂蚁吃到饭粒需要爬行的最短路程是多少？参考答案一．选择题（共12小题）1．【解答】解：A、22+32≠42，不能构成勾股数，故错误；B、（）2+（）2≠（）2，不能构成勾股数，故错误；C、62+72≠82，不能构成勾股数，故错误；D、52+122＝132，能构成勾股数，故正确．故选：D．2．【解答】解：∵（a﹣b）（a2﹣b2﹣c2）＝0，∴a﹣b＝0，或a2﹣b2﹣c2＝0，即a＝b或a2＝b2+c2，∴△ABC的形状为等腰三角形或直角三角形．故选：D．3．【解答】解：根据题意画出图形，如图所示，如图1所示，AB＝10，AC＝2，AD＝6，在Rt△ABD和Rt△ACD中，根据勾股定理得：BD＝＝8，CD＝＝2，此时BC＝BD+CD＝8+2＝10；如图2所示，AB＝10，AC＝2，AD＝6，在Rt△ABD和Rt△ACD中，根据勾股定理得：BD＝＝8，CD＝＝2，此时BC＝BD﹣CD＝8﹣2＝6，则BC的长为6或10．故选：C．4．【解答】解：依题意得：x2﹣4＝0，y2﹣3＝0，∴x＝2，y＝，斜边长＝＝，所以正方形的面积＝（）2＝7．故选：C．5．【解答】解：A、∠A+∠B＝∠C，又∠A+∠B+∠C＝180°，则∠C＝90°，是直角三角形；B、∠A：∠B：∠C＝1：2：3，又∠A+∠B+∠C＝180°，则∠C＝90°，是直角三角形；C、由a2＝c2﹣b2，得a2+b2＝c2，符合勾股定理的逆定理，是直角三角形；D、32+42≠62，不符合勾股定理的逆定理，不是直角三角形．故选：D．6．【解答】解：①中有92+122＝152；②中有72+242＝252；③（32）2+（42）2≠（52）2；④中有（3a）2+（4a）2＝（5a）2；⑤中有（m2﹣n2）2+（2mn）2＝（m2+n2）2，所以可以构成4组直角三角形．故选：B．7．【解答】解：∵△ABC中，AB＝7，BC＝24，AC＝25，∴AB2+BC2＝72+242＝252＝AC2，∴∠ABC＝90°，连接AP，BP，CP．设PE＝PF＝PG＝xS△ABC＝×AB×CB＝84，S△ABC＝AB×x+AC×x+BC×x＝（AB+BC+AC）•x＝×56x＝28x，则28x＝84，x＝3．故选：C．8．【解答】解：由题意得：大正方形的面积是9，小正方形的面积是1，直角三角形的较长直角边为a，较短直角边为b，即a2+b2＝9，a﹣b＝1，解得a＝，b＝，则ab＝4．解法2，4个三角形的面积和为9﹣1＝8；每个三角形的面积为2；则ab＝2；所以ab＝4故选：A．9．【解答】解：∵正方形PQED的面积等于225，∴即PQ2＝225，∵正方形PRGF的面积为289，∴PR2＝289，又△PQR为直角三角形，根据勾股定理得：PR2＝PQ2+QR2，∴QR2＝PR2﹣PQ2＝289﹣225＝64，则正方形QMNR的面积为64．故选：D．10．【解答】解：由图可得，A与B的面积的和是E的面积；C与D的面积的和是F的面积；而E，F的面积的和是G的面积．即A、B、C、D、E、F、G的面积之和为3个G的面积．∵G的面积是62＝36cm2，∴A、B、C、D、E、F、G的面积之和为36×3＝108cm2．故选：D．11．【解答】解：如下图所示：∵长方体的底面边长分别为2cm和4cm，高为5cm．∴PA＝4+2+4+2＝12（cm），QA＝5cm，∴PQ＝＝13cm．故选：A．12．【解答】解：如图，连接BO，AO，当吸管底部在O点时吸管在罐内部分a最短，此时a就是圆柱形的高，即a＝12；当吸管底部在A点时吸管在罐内部分a最长，即线段AB的长，在Rt△ABO中，AB＝＝＝13，故此时a＝13，所以12≤a≤13，则吸管的总长度b（罐壁的厚度和小圆孔的大小忽略不计）范围是：15≤b≤16．故选：D．二．填空题（共6小题）13．【解答】解：∵AB＝10，AD＝6，BD＝8，∴AB2＝AD2+BD2＝100，∴△ABD是直角三角形且AD⊥BD．又BD为△ABC的中线，∴AB＝BC＝10，AD＝CD＝6．∴，△ABC的周长＝AB+BC+AD＝2AB+2AD＝20+12＝32．故答案是：32．14．【解答】解：当这个直角三角形的两直角边分别为3cm，4cm时，则该三角形的斜边的长为：＝5（cm）．当这个直角三角形的一条直角边为3cm，斜边为4cm时，则该三角形的另一条直角边的长为：＝（cm）．故答案为：5或．15．【解答】解：连接BC．根据勾股定理可以得到：AB＝BC＝，AC＝2，∵（）2+（）2＝（2）2，即AB2+BC2＝AC2，∴△ABC是等腰直角三角形．∴∠BAC＝45°．故答案为：45°．16．【解答】解：易证△AFD′≌△CFB，∴D′F＝BF，设D′F＝x，则AF＝8﹣x，在Rt△AFD′中，（8﹣x）2＝x2+42，解之得：x＝3，∴AF＝AB﹣FB＝8﹣3＝5，∴S△AFC＝•AF•BC＝10．故答案为：10．17．【解答】解：∵a+b＝10，ab＝18，c＝8，∴（a+b）2﹣2ab＝100﹣36＝64，c2＝64，∴a2+b2＝c2，∴此三角形是直角三角形．故答案为：直角．三．解答题（共10小题）18．【解答】解：在△ABD中，∵AB＝13m，AD＝12m，BD＝5m，∴AB2＝AD2+BD2，∴AD⊥BC，在Rt△ADC中，∵AD＝12m，AC＝15m，∴DC＝＝9（m），∴△ABC的周长为42m，△ABC的面积为84m2．19．【解答】解：设竹子折断处离地面x米，则斜边为（10﹣x）米，根据勾股定理得：x2+42＝（10﹣x）2解得：x＝4.2．答：折断处离地面的高度是4.2米．20．【解答】解：设CD＝x，则BD＝BC+CD＝9+x．在△ACD中，∵∠D＝90°，∴AD2＝AC2﹣CD2，在△ABD中，∵∠D＝90°，∴AD2＝AB2﹣BD2，∴AC2﹣CD2＝AB2﹣BD2，即102﹣x2＝172﹣（9+x）2，解得x＝6，∴AD2＝102﹣62＝64，∴AD＝8．故AD的长为8．21．【解答】解：连接AC．∵∠ABC＝90°，AB＝1，BC＝2，∴AC＝，在△ACD中，AC2+CD2＝5+4＝9＝AD2，∴△ACD是直角三角形，∴S四边形ABCD＝AB•BC+AC•CD，＝×1×2+××2，＝1+．故四边形ABCD的面积为1+．22．【解答】解：设DE＝xcm，则BE＝DE＝x，AE＝AB﹣BE＝10﹣x，△ADE中，DE2＝AE2+AD2，即x2＝（10﹣x）2+16．∴x＝（cm）．23．【解答】解：（1）如图所示：∵在Rt△ABC中，∠C＝90°，BC＝6，AC＝8，∴AB＝10，∵DE垂直平分AB，∴AD＝BD＝5．（2）∵DE垂直平分AB，∴BE＝AE，设EC＝x，则AE＝BE＝8﹣x，故62+x2＝（8﹣x）2，解得：x＝，∴AE＝8﹣＝．24．【解答】解：如图所示，根据勾股定理得，AB＝＝25cm．答：需要爬行的最短距离是25cm．25．【解答】解：三级台阶平面展开图为长方形，长为20dm，宽为（2+3）×3dm，则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长．可设蚂蚁沿台阶面爬行到B点最短路程为xdm，由勾股定理得：x2＝202+[（2+3）×3]2＝252，解得：x＝25．答：蚂蚁沿着台阶面爬到B点的最短路程是25dm．26．【解答】解：（1）由题意得：该长方体中能放入木棒的最大长度是：（cm）．（2）分三种情况可得：AG＝cm＞AG＝cm ＞AG＝cm，所以最短路程为cm；（3）∵高为12cm，底面周长为10cm，在容器内壁离容器底部3cm的点B处有一饭粒，此时蚂蚁正好在容器外壁，离容器上沿3cm与饭粒相对的点A处，∴A′D＝5cm，BD＝12﹣3+AE＝12cm，∴将容器侧面展开，作A关于EF的对称点A′，连接A′B，则A′B即为最短距离，A′B＝＝13（Cm）．。

第一章勾股定理数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题，共计45分)1、在直角三角形中，两条直角边的长分别为12和5，则斜边上的中线长是（）A.6.5B.8.5C.13D.2、等腰三角形的腰长为，底长为，则其底边上的中线长为（）．A. B. C. D.3、如图，在平面直角坐标系中，将矩形AOCD沿直线AE折叠，折叠后顶点D恰好落在边OC上的点F处.若点D的坐标为，则点E的坐标为（）A. B. C. D.4、如图，A、B、C分别是小正方形的三个顶点，且每个小正方形的边长均为1，则sin∠BAC的值为（）A. B. C.1 D.5、如图，在▱OABC中C（2，0），AC⊥OC，反比例函数y= （k＞0）在第一象限内的图象过点A，且与BC交于点D，点D的横坐标为3，连接AD，△ABD的面积为，则k的值为（）A.4B.5C.D.6、小明量得家中的彩电屏幕的长为58厘米，宽为46厘米，你能判断这是一台多少英寸的电视机。

（）A.9英寸（23厘米）B.21英寸（54厘米）C.29英寸（74厘米） D.34英寸（87厘米）7、下列各组数据中，不能构成直角三角形的一组数是（）A.9，12，15B.0.2，0.3，0.4C. ，1，D.40，41，98、直角三角形的两条直角边的长分别为5，12，则斜边上的高线的长为（）A. cmB.13cmC. cmD. cm9、如图，是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（）A.5≤a≤12B.5≤a≤13C.12≤a≤13D.12≤a≤1510、如图，在平行四边形ABCD中，AC与BD相交于点O，AB⊥AC，∠DAC=45°，AC=2，则BD的长为（）A.6B.2C.D.311、如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，下列说法中正确的个数是（）①AC•BC=AB•CD ②AC2=AD•DB ③BC2=BD•BA ④CD2=AD•DB．A.1个B.2个C.3个D.4个12、下列各数为边不能组成直角三角形的一组是（）A.15，12，9B. ，2，C.8，15，17D. ，2，13、如图，已知一商场自动扶梯的长l为13米，高度h为5米，自动扶梯与地面所成的夹角为θ，则tanθ的值等于（）A. B. C. D.14、如图是由5个正方形和5个等腰直角三角形组成的图形，已知③号正方形的面积是1，那么①号正方形的面积是（）A.4B.8C.16D.3215、如图，⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，则⊙O的半径长为（）A.3cmB.4cmC.5cmD.6cm二、填空题(共10题，共计30分)16、如图，已知中，为直径，平分，弦，则半径的为________ .17、如图，已知点A（0，3），B（4，0），点C在第一象限，且AC=5 ，BC=10，则直线OC的函数表达式为________．18、如图，A、B两地之间有一座山，汽车原来从A地到B地经过C地沿折线A→C→B行驶，现开通隧道后，汽车直接沿直线AB行驶．已知AC=10千米，∠B=45°，则隧道开通后，汽车从A地到B地比原来少走________千米．19、如图，在长方形ABCD中，DC＝6cm，在DC上存在一点E，沿直线AE把△ADE折叠，使点D恰好落在BC边上的点F处，若△ABF的面积为24cm2，那么折叠的△ADE的面积为________.20、Rt△ABC中，∠ACB=90°，CD是高，AC=4cm，BC=3cm，则CD=________．21、一直角三角形的两条直角边长分别为12、5,则斜边上的中线长是________22、如图，△ABC内接于⊙O，半径为5，BC=6，CD⊥AB于D点，则tan∠ACD的值为________．23、如图,在Rt△ABC中，∠C=90°，BC=3，AC=4，D、E分别是AC、BC上的一点，且DE=3，若以DE为直径的圆与斜边AB相交于M、N，则MN的最大值为________．24、如图，在平面直角坐标系中，点A，A1， A2，……在工轴上，点P，P1 ， P2 ，在直线l：y=kx+ (k>0)上，∠OPA=90°，点P(1，1) ，A(2，0)，且AP1，A1P2，……均与OP平行，A1P1， A2P2，……均与AP平行，则有下列结论：①直线AP1的函数解析式为y=x-2；②点P2的纵坐标是；③点P2021的纵坐标为( )2021。

八（上）第一章 勾股定理单元检测班级_______ 姓名_______ 分数________一、填空题（每题3分，共24分）1．三角形的三边长分别为 a 2＋b 2、2ab 、a 2－b 2（a 、b 都是正整数），则这个三角形是（ ）A.直角三角形B.钝角三角形C.锐角三角形D.不能确定2．若△ABC 的三边a 、b 、c 满足a 2＋b 2＋c 2十338＝10a ＋24b ＋26c ，则△ABC 的面积是（ ）A.338B.24C.26D.303．若等腰△ABC 的腰长AB ＝2，顶角∠BAC ＝120°，以 BC 为边的正方形面积为（ ） A.3 B.12 C.427 D.3164．△ABC 中，AB ＝15，AC ＝13，高AD ＝12，则△ABC 的周长为（ ） A.42 B.32 C.42 或32 D.37 或 335．直角三角形三条边的比是3∶4∶5.则这个三角形三条边上的高的比是（ ）A.15∶12∶8B. 15∶20∶12C. 12∶15∶20D.20∶15∶126．在△ABC 中，∠C ＝90°，BC ＝3，AC ＝4.以斜边AB 为直径作半圆，则这个半圆的面积等于（ ）A.258π B. 254π C. 2516πD.25π 7．如图1，有一块直角三角形纸片，两直角边AC ＝6cm ，BC ＝8cm ，现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，则CD 等于（ ）A.2cmB.3 cmC.4 cmD.5 cm图1D 18cm图2B8．如图2，一个圆桶儿，底面直径为16cm，高为18cm，则一只小虫底部点A爬到上底B处，则小虫所爬的最短路径长是（π取3）（）A.20cmB.30cmC.40cmD.50cm二、填空题（每小题3分，共24分）9．在△ABC中，若其三条边的长度分别为9、12、15，则以两个这样的三角形所拼成的长方形的面积是＿＿＿．10．一个长方体同一顶点的三条棱长分别是3、4、12，则这个长方体内能容下的最长的木棒为＿＿＿.11．在△ABC中，∠C＝90°，BC＝60cm，CA＝80cm，一只蜗牛从C点出发，以每分20cm的速度沿CA→AB→BC的路径再回到C点，需要＿＿＿分的时间．12．如图3，一艘船由岛A正南30海里的B处向东以每小时20海里的速度航行2小时后到达C处.则AC间的距离是＿＿＿．13．在△ABC中，∠B＝90°，两直角边AB＝7，BC＝24，三角形内有一点P到各边的距离相等，则这个距离是＿＿＿．14．已知两条线段长分别为5cm、12cm，当第三条线段长为＿＿＿时，这三条线段可以组成一个直角三角形，其面积是＿＿＿．15．观察下列一组数：列举：3、4、5，猜想：32＝4+5；列举：5、12、13，猜想：52＝12+13；图3 列举：7、24、25，猜想：72＝24+25；…………列举：13、b、c，猜想：132＝b+c；请你分析上述数据的规律，结合相关知识求得b＝＿＿＿，c＝＿＿＿.16．已知：正方形的边长为1.（1）如图4（a ），可以计算出正方形的对角线长为2；如图（b），两个并排成的矩形的对角线的长为＿＿＿；n个并排成的矩形的对角线的长为＿＿＿.（2）若把（c）（d）两图拼成如图5“L”形，过C作直线交DE于A，交DF于B .若DB ＝53，则 DA 的长度为＿＿＿．三、解答题（共58分）17．如图6，折叠长方形一边AD ，点D 落在BC 边的点F 处，BC ＝10cm ，AB ＝8cm ，求：(1)FC 的长；(2)EF 的长．18．为了丰富少年儿童的业余生活，某社区要在如图7所示AB 所在的直线建一图书室，本社区有两所学校所在的位置在点C 和点D 处，CA ⊥AB 于A ，DB ⊥AB 于B ，已知AB ＝25km ，CA ＝15km ，DB ＝10km ，试问：图书室E 应该建在距点A 多少km 处，才能使它到两所学校的距离相等?19．一艘渔船正以30海里／时的速度由西向东追赶渔群，在A 处看见小岛C 在船北偏东 60°.40分钟后，渔船行至 B 处，此时看见小岛 C 在船的北偏东30°，已知小岛C 为中心周围10海里以内为我军导弹部队军事演习的着弹危险区，问这艘渔船继续航行（追赶鱼群），是否有进入危险区的可能？图5EF BCAD图4（a ） （b ） （c ） （d ）图6图7E DCBA20．在Rt△ABC中，AC＝BC，∠C＝90°，P、Q在AB上，且∠PCQ＝45°试猜想分别以线段AP、BQ、PQ为边能组成一个三角形吗？若能试判断这个三角形的形状．21．如图8，有一块塑料矩形模板ABCD，长为10cm，宽为4cm，将你手中足够大的直角三角板PHF的直角顶点P落在AD边上(不与A、D重合)，在AD上适当移动三角板顶点P：图8①能否使你的三角板两直角边分别通过点B与点C？若能，请你求出这时AP的长；若不能，请说明理由．②再次移动三角板位置，使三角板顶点P在AD上移动，直角边PH始终通过点B，另一直角边PF与DC的延长线交于点Q，与BC交于点E，能否使CE＝2cm？若能，请你求出这时AP的长；若不能，请你说明理由．参考答案一、1．A 2．D 3．B 4．C 5．D.提示：由三角形面积公式，可得12·AB ·CD ＝12·BC ·AC .设BC ＝3k ，AC ＝4k ，AB ＝5k ，则5k ·CD ＝2k ·4k .所以CD ＝135k .所以AC ∶BC ∶CD ＝4k ∶3k ∶125k ＝20∶15∶12；6．A.提示：在Rt △ABC 中，由勾股定理可以得到AB 2＝42+32＝25，所以AB ＝5.所以半圆的面积S ＝12π252⎛⎫ ⎪⎝⎭＝258π；7．B 8．B.二、9．108 10．13 11．12 12．由勾股定理，可以得到AB 2+BC 2＝AC 2，因为AB＝30，BC ＝20×2＝40，所以302+202＝AC 2，所以AC ＝50，即AC 间的距离为50海里；13．314．13cm ，30cm 2或522 15．84、85 16、52. 三、17．(1)在Rt △ABC 中，由勾股定理可以得到AF 2＝AB 2+BF 2，也就是 102＝82+BF 2.所以BF ＝6，FC ＝4(cm) (2)在Rt △ABC 中，由勾股定理，可以得到EF 2＝FC 2+(8－EF )2.也就是EF 2＝42+(8－EF )2.所以EF ＝5(cm)18．10米；19．设小岛C 与AB 的垂直距离为a ，则易求得a 2＝300＞102，所以这艘渔船继续航行不会进入危险区；20．能组成一个三角形，且是一个以PQ 为斜边的直角三角形.理由是：可将△CBQ 绕点C 顺时针旋转90°，则CB 与CA 重合，Q 点变换到Q ′点，此时，AQ ′＝BQ ，△APQ ′是直角三角形，即AP 2＋AQ ′2＝PQ ′2，另一方面，可证得△CPQ ′≌△CPQ （SAS ），于是，PQ ′＝PQ ，则AP 2＋BQ 2＝PQ 2.21．①能.设AP ＝x 米，由于BP 2＝16+x 2，CP 2＝16+(10－x )2，而在Rt △PBC 中，有BP 2+ CP 2＝BC 2，即16+x 2+16+(10－x )2＝100，所以x 2－10x +16＝0，即(x －5)2＝9，所以x －5＝±3，所以x ＝8，x ＝2，即AP ＝8或2，②能.仿照①可求得AP ＝4.第一章勾股定理单元检测题班级_____ 姓名_____ 分数_____一、选择题（每小题3分，共30分）1．如果下列各组数是三角形的三边，那么不能组成直角三角形的一组数是( ) A ．7，24，25 B ．321，421，521 C ．3，4，5 D ．4，721，821 2．如果把直角三角形的两条直角边同时扩大到原来的2倍，那么斜边扩大到原来的( ) A ．1倍 B ．2倍 C ．3倍 D ．4倍 3．在下列说法中是错误的（ ）A ．在△ABC 中，∠C ＝∠A 一∠B ，则△ABC 为直角三角形B ．在△ABC 中，若∠A ∶∠B ∶∠C ＝5∶2∶3则△ABC 为直角三角形 C ．在△ABC 中，若a ＝53c ，b ＝54c ，则△ABC 为直角三角形 D ．在△ABC 中，若a ∶b ∶c ＝2∶2∶4，则△ABC 为直角三角形4．四组数:①9，12，15；②7，24，25；③32，42，52；④3a ，4a ，5a (a ＞0)中，可以构成直角三角形的边长的有( )A ．4组B ．3组C ．2组D ．1组5．三个正方形的面积如图1，正方形A 的面积为（ ） A ． 6 B ． 36 C ． 64 D ． 86．一块木板如图2所示，已知AB ＝4，BC ＝3，DC ＝12，AD ＝13，∠B ＝90°，木板的面积为( )A ．60B ．30C ．24D ．127．直角三角形的两直角边分别为5cm ，12cm ，其中斜边上的高为（ ） A ．6cm B ．8．5cm C ．1330cm D ．1360cm8．两只小鼹鼠在地下打洞，一只朝前方挖，每分钟挖8cm ，另一只朝左挖，每分钟挖6cm ，10分钟之后两只小鼹鼠相距（ ）A ．50cmB ．100cmC ．140cmD ．80cm9．小明想知道学校旗杆的高，他发现旗杆上的绳子垂到地面还多1m ，当它把绳子的下端拉开5m 后，发现下端刚好接触地面，则旗杆的高为 （ ）A ．8cmB ．10cmC ．12cmD ．14cm10．在△ABC 中，∠ACB ＝90°，AC ＝40，CB ＝9，M 、N 在AB 上且AM ＝AC ，BN ＝BC ，则MN 的长为（ ）A ．6B ．7C ．8D ．9 二、填空题（每小题3分，共30分）A DBC图211．在△ABC中，∠C＝90°，若a＝5，b＝12，则c＝＿＿＿．12．在△ABC中，∠C＝90°，若c＝10，a∶b＝3∶4，则ab＝．13．等腰△ABC的面积为12cm2，底上的高AD＝3cm，则它的周长为＿＿＿．14．等边△ABC的高为3cm，以AB为边的正方形面积为＿＿＿．15．直角三角形三边是连续整数，则这三角形的各边分别为＿＿＿．16．在Rt△ABC中，斜边AB＝2，则AB2+BC2+CA2＝＿＿＿．17．有两棵树，一棵高6米，另一棵高3米，两树相距4米．一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少飞了＿＿＿米．18．一座桥横跨一江，桥长12m，一般小船自桥北头出发，向正南方驶去，因水流原因到达南岸以后，发现已偏离桥南头5m，则小船实际行驶＿＿＿m．19．一个三角形的三边的比为5∶12∶13，它的周长为60cm，则它的面积是＿＿＿．20．在Rt△ABC中，∠C＝90°，中线BE＝13，另一条中线AD2＝331，则AB＝＿＿＿．三、解答题（每小题8分，共40分）21．某车间的人字形屋架为等腰△ABC，跨度AB＝24m，上弦AC＝13m．求中柱CD （D为底AB的中点）．22．有一个小朋友拿着一根竹竿要通过一个长方形的门，如果把竹竿竖放就比门高出1尺，斜放就恰好等于门的对角线长，已知门宽4尺．求竹竿高与门高．23．如图3，台风过后，一希望小学的旗杆在离地某处断裂，旗杆顶部落在离旗杆底部8m处，已知旗杆原长16m，你能求出旗杆在离底部什么位置断裂的吗？请你试一试．图3OB′图4BAA′24．如图4所示，梯子AB靠在墙上，梯子的底端A到墙根O的距离为2m，梯子的顶端B到地面的距离为7m．现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离为3m，同时梯子的顶端B下降到B′，那么BB′也等于1m吗?25．在△ABC中，三条边的长分别为a，b，c，a＝n2－1，b＝2n，c＝n2+1(n＞1，且n 为整数)，这个三角形是直角三角形吗？若是，哪个角是直角？与同伴一起研究．参考答案：A卷：一、1．B2．B3．D4．B5．B6．C7．D8．B9．C10．C二、11．1312．4813．1814．1215．3、4、516．817．518．1319．2400 20．20三、21．5米22．设门高为x尺，则竹杆长为(x+1)尺，依题意由勾股定理，得x2+42＝(x+1)2，解得x＝7．5，所以门高为7．5尺，则竹杆长为8．5尺．23．设旗杆在离底部x m位置断裂，则根据题意，得(x+1)2－x2＝64，解得x＝6，即旗杆在离底部6m位置断裂．cb a cba ED CBACABcb a24．在Rt △ABO 中，梯子AB 2＝AO 2+BO 2＝22+72＝53．在Rt △A ′B ′O 中，梯子A ′B ′2＝53＝A ′O 2+B ′O 2＝32+B ′O 2，所以，B ′O＞2×3＝6．所以BB ′＝OB －OB ′＜1．25．因为a 2＝n 4－2n 2+1，b 2＝4n ，c 2＝n 4+2n 2+1，a 2+b 2＝c 2，所以△ABC 是直角三角形，∠C 为直角．北师大版八年级数学上册第一章 勾股定理 提高培优讲义：勾股定理、逆定理及应用 基础知识梳理模块一：勾股定理及证明 1．勾股定理：如果直角三角形的两直角边分别是a ，b ，斜边为c ，那么222a b c +=． 即直角三角形中两直角边的平方和等于斜边的平方． 注：勾——较短的边、股——较长的直角边、弦——斜边． 2．勾股定理的证明： （1）弦图证明DC BAGF E H内弦图 外弦图221()42ABCD S a b c ab =-=+⨯正方形 221()42EFGH S c a b ab ==-+⨯正方形∴222a b c += ∴222a b c += （2）“总统”法（半弦图）如图所示将两个直角三角形拼成直角梯形：2()()112222ABCD a b a b S ab c +-==⨯+梯形∴222a b c += 3．勾股数：满足222a b c +=的三个正整数，称为勾股数．（1）3、4、5；6、8、10；9、12、15；12、16、20；15、20、25等．（2）(,,)a b c 是组勾股数，则(,,)ka kb kc （k 为正整数）也是一组勾股数. （3）3、4、5；5、12、13；7、24、25；9、40、41；11、60、61等 （4）21a n =+，222b n n =+，2221c n n =++（n 为大于1的自然数） （5）22a m n =-，2b mn =，22c m n =+（m n >，且m 和n 均为正整数） 模块二：勾股定理逆定理及应用 1．勾股定理的逆定理：如果三角形中两边的平方和等于第三边的平方，那么前两边的夹角一定是直角．即在ABC △中，如果222AC BC AC +=，那么ABC △是直角三角形．2．勾股定理的常见题型． 模块三：例题精讲（1）勾股证明的方法成百上千种，其中《几何原本》中的证法非常经典，是在一个我们非常熟悉的几何图形中实现的（如图所示），如果直角三角形ABC 的三边长为a ，b ，c （c 为斜边），以这三边向外作三个正方形，试利用此图证明222a b c +=．cbaNMHFE DCBAABCEFHMNP（2）如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm ，则正方形A ，B ，C ，D 的面积之和为__________．【解析】（1）如上图可知：ACF ADB △△≌，2ACED ADB S S =正方形△，2AFGP ACF S S =矩形△，∴2AFGP b S =矩形，同理2GHBP a S =矩形，∴222a b c +=． （2）49cm 2．（1）若把直角三角形的两条直角边同时扩大到原来的2倍，则斜边扩大到原来的（ ）． A ．1倍 B ．2倍 C ．3倍 D ．4倍（2）若一个直角三角形三边的长分别是三个连续的自然数，则这个三角形的周长为________．（3）下面几组数：①7，8，9；②12，9，15；③22m n +，22m n -,2mn （m ，n 均为正整数，m n >）；④2a ，21a +，22a +．其中能组成直角三角形的三边长的是（ ）．A ．①②B ．②③C ．①③D ．③④【解析】（1）B ；（2）可知三边为3，4，5，所以周长为12； （3）B ；容易知道①错误②正确，对于③，由2224224()2m n m m n n -=-+，222(2)4mn m n =，2224224()2m n m m n n +=++所以2222422422222()(2)(2)4()m n mn m m n n m n m n -+=-++=+． 所以，以这三条线段的长为边的三角形是直角三角形．答案选B ．ABC △中，BC a =，AC b =，AB c =．若90C ∠=︒，如图3-1，根据勾股定理，则222a b c +=．若ABC △不是直角三角形，如图3-2，90C ∠<︒；如图3-3，90C ∠<︒．请你类比勾股定理，试猜想22a b +与2c 的关系，并证明你的结论．图1a b c a b c cb a A BCA B C C B Aa bca bcA ABC C Ba bcABC B图3-1 图3-2 图3-3【解析】图2猜想：222a b c +>．证明：过点A 作AD BC ⊥于D ，设CD x =，222AD b x =-， 22222222()()2c a x b x a ax x b x =-+-=-++-， 即22220a b c ax +-=>，故222a b c +>． 图3猜想：222a b c +<．证明：过B 作BD AC ⊥，交AC 的延长线于D ． 设CD 为x ，则有222BD a x =-．根据勾股定理，得2222()b x a x c ++-=． 即2222a b bx c ++=，∵0b >，0x >，∴20bx >，∴222a b c +<．（1）如果直角三角形的两边长为4、5，则第三边长为________．（2）如果直角三角形的三边长为10、6、x ，则最短边上的高为________．（3）若|1|0a b --=，则以a 、b 为边的直角三角形的第三边为________．在ABC △中，15AB =，13AC =，高12AD =，则三角形的周长是_________．【解析】32或42．DabcACBDa bcABC【提示】题型：已知三角形的两边及第三边高求第三边，B 卷填空必考题，一般题目无图，为易错题，切记要分类讨论,分形内高和形外高．（1）如图6-1，四边形ABCD 中，AB BC ⊥，1AB =，2BC =，2CD =，3AD =，求四边形ABCD 的面积．（2）如图6-2，在四边形ABDC 中，BD CD ⊥，6BD =，8CD =，24AB =，26AC =，求该四边形面积．ABC DDCB A图6-1 图6-2（2）96．四边形ABDC 的面积为96． 连接BC ，根据勾股定理可得10BC =，因为222BC AB AC +=，所以ABC △为直角三角形，故四边形ABDC 的面积1202496ABC BCD S S S =-=-=△△．（1）如图，梯子AB 长2.5米，顶端A 靠在墙AC 上，这时梯子下端B 与墙角C 距离为1.5米，梯子滑动后停在DE 位置，BD 长0.5米，则梯子顶端A 下落了________米．（2）梯子靠在墙上，梯子的底端A 到墙根O 的距离2米，梯子的顶端B 到地面的距离为7米，现将梯子的底端向外移动到C ，使梯子底端C 到墙根O 的距离等于3米，同时梯子的顶端B 下降至D ，那么BD （ ）A ．等于1米B ．大于1米C ．小于1米D ．以上结果都不对（3）如图，梯子AB 斜靠在墙面上，AC BC ⊥，AC BC =，当梯子的顶端A 沿AC 方向下滑x 米时，梯子B 沿CB 方向滑动y 米，则x 与y 的大小关系是（ ） A ．x y = B ．x y >C ．x y <D ．不确定【解析】（1）0.5；（2）C ；（3）选B ，设AC BC a==米，化简得222()0a x y x y -=+>，x y >．EAB CD（1）若直角三角形斜边长为4，周长为432+，则三角形面积等于________．（2）如图，ABC △中，90BAC ∠=︒，AD BC ⊥于点D ，若455AD =，25BC =，请求出ABC △的周长．【解析】（1）12； （2）222(25)45255AB AC AB AC ⎧+=⎪⎨⨯=⨯⎪⎩，解得6AB BC +=，625ABC C =+△．（1）已知9-1，如图所示，折叠长方形的一边AD ，使点D 落在BC 边的点F 处，如果8cm AB =，10cm BC =，求EC 的长．（2）如图9-2，已知矩形ABCD 沿着直线BD 折叠，使点C 落在'C 处，'BC 交AD 于E ，16AD =，8AB =，则DE 的长度为________．（3）如图9-3，矩形纸片ABCD 的长9cm AD =，宽3cm AB =，沿EF 将其折叠，使点D 与点B 重合，则折痕EF 的长为________cm ．EDC'C BA图9-1 图9-2 图9-3【解析】（1）由题意得，10cm AF AD ==．在ABF △中，应用勾股定理得，6cm BF =． 所以1064FC BC BF cm =-=-=．在CEF △中，应用勾股定理，设cm EC x =， 得222(8)4x x -=+．解得3x =，即3cm EC =． （2）设ED x =，因为CBD EBD EDB ∠=∠=∠， 则EB ED x ==，16AE AD ED x =-=-， 在Rt E AB △中，由勾股定理可得：222(16)8x x +=-，∴10x =，即10DE =．（3）设AE x =，因为BEF DEF BFE ∠=∠=∠， 则9BE DE B x F ===-，根据勾股定理得：222AB AE BE +=，即222239(9)x x x +=+=-，解得：4x =；∴4AE =，∴5DE BF ==，∴4CF DM ==，∴1EM =，根据勾股定理得：EF ==；若0x >，0y >且12x y +=【解析】如下图，不妨设12AB =，AC AB ⊥，BD AB ⊥，2AC =，3BD =，y 2+9x 2+432y xPDC B AD CA P为线段AB 上的动点，AP x =，于是PB y =，PC，PD 问题转化为求点C ，D 之间距离的最小值．当P ，C ，D 三点不共线时，有PC PDCD +>；当P ，C ，D 共线时，PC PD CD +=． 于是点C ，D 13．【教提示】数形结合，几何构造，将军饮马．模块四：课后作业设计1、如图1-1，分别以直角三角形A 、B、C 三边为边向外作三个正方形，其面积分别用1S 、2S 、3S 表示，则不难证明123S S S =+．） （1）如图1-2，分别以直角三角形ABC 三边为直径向外作三个半圆，其面积分别用1S 、2S 、3S 表示，那么1S 、2S 、3S 之间有什么关系？（不必证明）（2）如图1-3，分别以直角三角形A 、B 、C 三边为边向外作三个正三角形，其面积分别用1S 、2S 、S 表示，请你确定S 、S 、S 之间的关系并加以证明．B C S 1S 2图图图1A B C S 1S 3S 2图图2A BCS 1S 3S 2图3图1-1图1-2图1-3【解析】（1）设BC 、CA 、AB 长分别为a 、b 、c ，则222c a b =+，123S S S =+；（2）123S S S =+．证明如下：显然，21S =，22S =，23S ，AB D C∴22223133()44S S a b c S +=+==． 【点评】分别以直角三角形ABC 三边为一边向外作“相似形”，其面积对应用1S 、2S 、3S 表示，则123S S S =+（设斜边所做图形面积为1S ）．2、已知a ，b ，c 是三角形的三边长，222a n n =+，21b n =+，2221c n n =++（n 为大于1的自然数），试说明ABC △为直角三角形．【解析】因为222212221n n n n n ++>+>+，222222(221)(22)441(21)n n n n n n n ++-+=++=+．所以22222(21)(22)(221)n n n n n +++=++，所以ABC △为直角三角形．3、如图，四边形ABCD 中，6cm AB =，8cm BC =，24cm CD =，26cm DA =，且90ABC ∠=︒，则四边形ABCD 的面积是（ ）cm 2．A ．336B ．144C ．102D ．无法确定【解析】答案：B ．连接AC ，运用勾股定理逆定理．4、如图，一根长5米的竹篙AB 斜靠在与地面垂直的墙上，顶端A 距离墙根4米，若竹篙顶端A 下滑1米，则底端B 向外滑行了多少米？【解析】设竹篙顶端下滑1米到1A 点，底端向外滑行到1B 点．由题意得AA 1=1m ，113m AC AC AA =-=， 在11Rt ACB △中：2211114m B C A B AC -， 在Rt ABC △中：223m BC AB AC =-=， 111BB B C BC m =-=，即竹篙顶端A 下滑1米，则底端B 向外滑行了1米．5、（1）（在ABC △中15AB =，13AC =，高12AD =，则ABC S =△_______．（2）如图，ABC △中，90BAC ∠=︒，AD BC ⊥于点D ，若3AD =，23BC =ABC △的周长为________．【解析】（1）24或84（分类讨论：行外高和行内高，对应例5）ABC（2）423+．（对应例8考查直角三角形与知二推二综合）．6、（1）如图6-1，已知ABC △是直角边长为1的等腰直角三角形，以Rt ABC △的斜边AC 为直角边，画第二个等腰Rt ACD △，再以Rt ACD △的斜边AD 为直角边，画第三个等腰Rt ADE △，……，依此类推，第n 个等腰直角三角形的斜边长是________．（2）如图6-2，矩形ABCD 中，5cm AB =，3cm BC =，如图所示折叠矩形纸片ABCD ，使D 点落在边AB 上一点E 处，折痕端点G 、F 分别在边AD 、DC 上，则当折痕端点F 恰好与C 点重合时，AE 的长为________cm ．GFED CB A图6-1 图6-2（3）若0x >，0y >且15x y +=2264144x y ++________．【解析】（1）由题意可得：第1个等腰直角三角形，ABC △中，斜边长1AB BC ==，22112AC+＝＝； 第2个等腰直角三角形，ACD △中，斜边长2222(2)AD AC CD =+==； 第3个等腰直角三角形，ADE △中，斜边长22322(2)AE AD DE =+=； 依此类推，……第n 个等腰直角三角形中，斜边长为(2)n ． （2）F 点与C 点重合时（如图），∵在矩形ABCD 中，5AB =，3BC =， ∴5CD AB ==，90B ∠=︒，由折叠的性质可得：5CE CD ==， ∴224CE BE BC -=， ∴1AE AB BE =-=．（3）答案：25（对应例题10，几何构造）．北师大版八年级数学上册 第一章 勾股定理 章末培优卷一、选择题：（共30分）1、一个圆柱形铁桶的底面半径为12cm ，高为32cm ，则桶内所能容下的木棒最长为（ ）A ．20cmB ．50cmC ．40cmD ．45cm2、已知直角三角形的两条边长分别是3和5，那么这个三角形的第三条边的长为A. 4B. 16C.D. 4或3、如图，正方形ABCD 的边长为10，AG=CH=8，BG=DH=6，连接GH ，则线段GH 的平方为（ ）A 2524 B. 8 C. 25196 D.5 4、如图，一棵大树被大风刮断后，折断处离地面8m ，树的顶端离树根6m ，则这棵树在折断之前的高度是（ ） A．18mB ．10mC ．14mD ．24m5、如图，在4×4方格中作以AB 为一边的Rt △ABC ，要求点C 也在格点上，这样的Rt △ABC 能作出（ ） A ．2个 B ．3个 C ．4个D ．6个二、填空题（共24分）11、ABC ∆的三边长c b a ,,满足：03018)602(2=-+-+-+c b b a ，则ABC ∆是 三角形；12、如图，在平行四边形A BCD 中，C A ⊥A B ，若A B=3，BC=5，则平行四边形A BCD 的面积为 。

第一章勾股定理数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题，共计45分)1、△ABC中，如果两条直角边分别为3，4，则斜边上的高线是（）A. B. C.5 D.不能确定2、如图是一个古代车轮的碎片，小明为求其外圆半径，连接外圆上的两点A、B，并使AB 与车轮内圆相切于点D，半径为OC⊥AB交外圆于点C．测得CD=10cm，AB=60cm，则这个车轮的外圆半径是（）A.10cmB.30cmC.60cmD.50cm3、已知直角三角形两边长x、y满足，则第三边长为（）A.5B.C.5或D. 或4、如图，将两个大小、形状完全相同的△ABC 和△A′B′C′拼在一起，其中点 A′与点A 重合，点 C′落在边 AB 上，连接 B′C．若∠ACB=∠AC′B′=90°，AC=BC=3，则 B′C 的长为( )A. B.6 C. D.5、已知圆锥的底面的半径为3cm，高为4cm，则它的侧面积为（）A.15πcm 2B.16πcm 2C.19πcm 2D.24πcm 26、下列长度的三条线段能组成直角三角形的是( )A.2，3，4B.4，6，8C.6，8，10D.5，11，127、如图，点E在正方形ABCD内，满足∠AEB=90°，AE=6，BE=8，则阴影部分的面积是（）A.48B.60C.76D.808、如图，点E在正方形ABCD内，满足∠AEB=90°，AE=3，BE=4，则阴影部分的面积是（）A.12B.15C.19D.209、下列各组线段中，能够组成直角三角形的是（）．A.6，7，8B.5，6，7C.4，5，6D.3，4，510、如图所示，一场暴雨过后，垂直于地面的一棵树在距地面1米处折断，树尖B 恰好碰到地面，经测量AB=2米，则树高为（）A. 米B. 米C.( 米D.3 米11、平面直角坐标系中，直线y=(2m-3)x-2m+5与以坐标原点为圆心的⊙O交于A、B两点，⊙O的半径为3，则AB最小值为（）A. B.3 C.4 D.12、在Rt中，∠B＝90°，AC＝5，AB＝3，则的值为（）.A. B. C. D.13、如图，AB是⊙O的直径，弦CD⊥AB于点E．若AB=8，AE=1，则弦CD的长是（）A. B.2 C.6 D.814、如图所示，四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH……,如此下去，则第2017个正方形的边长是（）A. B. C. D.15、下列四组数据表示三角形的三边长,其中不能构成直角三角形的一组数据是( )A.1 cm, cm, 4cmB.5cm, 12cm, 13cm:C.3cm, 4cm,5cm: D.7cm, 24cm, 25 cm二、填空题(共10题，共计30分)16、如图，为正方形的对角线，延长到，使，以为一边作菱形，若菱形的面积为，则正方形边长________．17、⊙O的半径为1，弦AB= ,点C是圆上异于A、B的一动点，则∠ACB=________.18、如图为一个半径为5m的圆形广场，其中放有六个宽为m的长方形临时摊位，这些摊位均有两个顶点在广场边上，另两个顶点紧靠相邻摊位的顶点，则每个长方形摊位的长为________m.19、如图，等边△ABC的边长为8，D、E分别是BC、AC边的中点，过点D作DF⊥AB于F，连接EF，则EF的长为________.20、如图，已知两正方形的面积分别是25和169，则字母B所代表的正方形的边长是________。

第一章《勾股定理》单元测试卷班别：姓名：__________一、选择题（本题共10小题，每小题3分，满分30分）1．一直角三角形的斜边长比一直角边长大2，另一直角边长为6，则斜边长为（）A．4 B．8 C．10 D．122．已知a=3，b=4，若a，b，c能组成直角三角形，则c=（）A.5B.7C.5或7D.5或63．如图中字母A所代表的正方形的面积为（）A．4 B．8 C．16 D．644．将直角三角形的三条边长同时扩大同一倍数，得到的三角形是（）A．钝角三角形B．锐角三角形C．直角三角形D．等腰三角形5．直角三角形的一直角边长是7cm，另一直角边与斜边长的和是49cm，则斜边的长（）A．18cm B．20cm C．24cm D．25cm6．适合下列条件的△ABC中，直角三角形的个数为（）①a=，b=，c=②a=6，∠A=45°；③∠A=32°，∠B=58°；④a=7，b=24，c=25 ⑤a=2，b=2，c=4A．2个B．3个C．4个D．5个7．在△ABC中，若a=n2﹣1，b=2n，c=n2+1，则△ABC是（）A．锐角三角形B．钝角三角形C．等腰三角形D．直角三角形8．直角三角形斜边的平方等于两条直角边乘积的2倍，这个三角形有一个锐角是（）A．15°B．30°C．45°D．60°9．已知，如图长方形ABCD 中，AB=3cm ，AD=9cm ，将此长方形折叠，使点B 与点D 重合，折痕为EF ，则△ABE 的面积为（ ）A ．3cm 2B ．4cm 2C ．6cm 2 D.12cm 210．已知，如图，一轮船以16海里/时的速度从港口A 出发向东北方向航行，另一轮船以12海里/时的速度同时从港 口A 出发向东南方向航行，离开港口2小时后，则两船相距（ ）A ．25海里B ．30海里C ．35海里D ． 40海里二、填空题（本题共8小题，每小题3分，满分24分）11．一个三角形三边长度之比为1∶2∶3 ，则这个三角形的最大角为_______度．12．如图，等腰△ABC 的底边BC 为16，底边上的高AD 为6，则腰长AB 的长为 ．13．如图，某人欲横渡一条河，由于水流的影响，实际上岸地点C 偏离欲到达点B200m ，结果他在水中实际游了520m ，求该河流的宽度为 m ．14．小华和小红都从同一点O 出发，小华向北走了9米到A 点，小红向东走到B 点时,当两人相距为15米，则小红向东走了 米．15．一个三角形三边满足22()2a b c ab +-=,则这个三角形是 三角形．16．木工做一个长方形桌面，量得桌面的长为60cm ，宽为32cm ，对角线为68cm ，这个桌面 （填”合格”或”不合格”）．17．直角三角形一直角边为12cm，斜边长为13cm，则它的面积为cm2．18．如图，一个三级台阶，它的每一级的长宽和高分别为20、3、2，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是．三、解答题（共46分）19．在RtΔABC中，∠A CB=90°，AB=5，AC=3，CD⊥AB于D，求CD的长．21．（7分）如图，在△ABC中，AD⊥BC于D，AB=3，BD=2，DC=1，求AC 的值．22．（8分）如图，一个牧童在小河的南4km的A处牧马，而他正位于他的小屋B的西8km北7km处，他想把他的马牵到小河边去饮水，然后回家.他要完成这件事情所走的最短路程是多少？小河23．如图，A城气象台测得台风中心在A城正西方向320km的B处，以每小时40km的速度向北偏东60°的BF方向移动，距离台风中心200km的范围内是受台风影响的区域．（1）A城是否受到这次台风的影响？为什么？（2）若A城受到这次台风影响，那么A城遭受这次台风影响有多长时间？《勾股定理》单元测试卷答案一、选择题（共10小题，每小题3分，满分30分）1． C ．2． C ．3． D ．4． C ．5． D ．6． A ．7． D ．8． C ．9． C ．10． D ．二、填空题（共8小题，每小题3分，满分24分）11． 900 ． 12． 10 ． 13． 480 m ． 14． 12 米．15． 直角 ． 16． 合格 ． 17． 30 cm 2． 18． 25 ．三、解答题（共46分）19．略20．解：∵∠ACB=90°，AB=5，AC=3，∴BC 2 = AB 2 -AC 2 =42，∴BC=4，∵CD ⊥AB ，∴21AB·CD=21AC·BC，∴5CD=12，∴CD=512． ．21．解：∵AD ⊥BC 于D ，∴∠ADB=∠ADC=90°∵AB=3，BD=2∴AD 2=AB 2﹣BD 2=5∵DC=1，∴AC 2=AD 2+DC 2=5+1=6．∴AC= 22．解：设矩形的长是a ，宽是b ，根据题意，得：， （2）+（1）×2，得（a+b ）2=196，即a+b=14，所以矩形的周长是14×2=28m ．23. 如图，作出A点关于MN的对称点A′，则A′A=8 km,连接A′B交MN 于点P，则A′B就是最短路线.在Rt△A′DB中，A′D=15 km,BD=8 km由勾股定理得A′B2= A′D 2+BD2=289∴A′D =17km24．解：（1）由A点向BF作垂线，垂足为C，在Rt△ABC中，∠ABC=30°，AB=320km，则AC=160km，因为160＜200，所以A城要受台风影响；（2）设BF上点D，DA=200千米，则还有一点G，。

第一章勾股定理一、选择题1. 若a，b，c为△ABC的三边长，则下列条件中不能判定△ABC是直角三角形的是( )A．a=1.5，b=2，c=2.5B．a:b:c=3:4:5C．∠A+∠B=∠C D．∠A:∠B:∠C=3:4:52. 在Rt△ABC中，若∠C=90∘，AC=3，BC=4，则点C到直线AB的距离为( )A．3B．4C．5D．2.43. 如图，四边形ABCD中，∠B=90∘，且AB=BC=2，CD=3，DA=1，则∠DAB的度数为( )A．90∘B．120∘C．135∘D．150∘4. 如图，在高为5 m，坡面长为13 m的楼梯表面铺地毯，地毯的长度至少需要( )A．17 m B．18 m C．25 m D．26 m5. 如图是一株美丽的勾股树，其中所有四边形都是正方形，所有的三角形都是直角三角形．若正方形A，B，C，D的面积分别为3，5，2，3，则最大正方形E的面积是( )A．47B．13C．11D．86. 如图，将一根长度为8 cm，自然伸直的弹性皮筋AB两端固定在水平的桌面上，然后把皮筋中点C竖直向上拉升3 cm到点D，则此时该弹性皮筋被拉长了( )A．6 cm B．5 cm C．4 cm D．2 cm7. 如图，为了测得湖两岸A点和B点之间的距离，一个观测者在C点设桩，使∠ABC=90∘，并测得BC长为16 m，若已知AC比AB长8 m，则A点和B点之间的距离为( )A．25 m B．12 m C．13 m D．43 m8. 如图，在三角形纸片ABC中，∠ACB=90∘，AC=4，BC=3，点D，E分别在AB，AC上，连接DE，将△ADE沿DE翻折，使点A的对应点F落在BC的延长线上．若FD平分∠EFB，则AD的长为( )A．259B．258C．157D．207二、填空题9. 在△ABC中，∠C=90∘．（1）已知a=10，b=24，那么c=．（2）已知b:c=4:5，a=9，那么b=，c=．10. 如图是“赵爽弦图”，△ABH，△BCG，△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形，如果AH=6，EF=2，那么AB等于．11. 《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去根六尺．问折高者几何？意思是：一根竹子，原高一丈（一丈=10尺），一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部6尺远，问折断处离地面的高度是多少？设折断处离地面的高度为x尺，则可列方程为．12. 如图，一个长方体长4 cm，宽3 cm，高12 cm，则它上下两底面的对角线MN的长为cm．13. 已知a，b，c为△ABC的三边，且满足a2+b2+c2+338=10a+24b+26c，则可以判断△ABC的形状为．14. 如图所示的网格是正方形网格，则∠PAB+∠PBA=∘（点A，B，P是网格线的交点）．15. 对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD，对角线AC，BD交于点O．若AD=2，BC=4，则AB2+CD2=．三、解答题16. 在Rt△ABC中，∠C=90∘．(1) 已知a=8，c=17，求b．(2) 已知b=40，c=41，求a．17. 如图，在四边形ABCD中，∠DBC=90∘，AB=9，AD=12，BC=8，DC=17，求四边形ABCD的面积．18. 如图，滑竿在机械槽内运动，∠C=90∘，AB=2.5 m，BC=1.5 m，当底端B向右移动0.5 m时，顶端A下滑了多少米？19. 假期中，王强和同学到某海岛上去旅游．他们按照如图所示路线．在点A登陆后租借了自行车，骑车往东走8千米，又往北走2千米；遇到障碍后往西走3千米，再折向北走到6千米处往东拐，走了1千米到达景点B．登陆点A到景点B的直线距离是多少千米？20. 若正整数a，b，c（a<b<c）满足a2+b2=c2，则称（a，b，c）为一组“勾股数”．观察下列两类“勾股数”：第一类（a是奇数）：(3,4,5)，(5,12,13)，(7,24,25)，⋯⋯第二类（a是偶数）：(6,8,10)，(8,15,17)，(10,24,26)，⋯⋯(1) 请再写出两组勾股数，每类各写一组；(2) 分别就a为奇数、偶数两种情形，用a表示b和c，并选择其中一种情形证明(a,b,c)是“勾股数”．答案一、选择题1. D2. D3. C4. A5. B6. D7. B8. D二、填空题9. 26；12；1510. 1011. x2+62=(10−x)212. 1313. 直角三角形14. 4515. 20三、解答题16.(1) 15．(2) 9．17. ∵∠DBC=90∘，DC=17，BC=8，∴BD2=CD2−BC2=172−82=225=152，∴BD=15．∵AD2+AB2=122+92=144+81=225，BD 2=225， ∴AD 2+AB 2=BD 2，∴△ABD 是直角三角形，且 ∠A =90∘，∴ 四边形 ABCD 的面积 =△ABD 的面积 +∠CBD 的面积 =12×9×12+12×15×8=54+60=114．18. 依题意得 AB =DE =2.5 m ，BC =1.5 m ，∠C =90∘，∴AC 2+BC 2=AB 2，即 AC 2+1.52=2.52，解得 AC =2 m ． ∵BD =0.5 m ， ∴CD =2 m ．在 Rt △ECD 中，CE 2+CD 2=DE 2， ∴CE =1.5 m ， ∴AE =0.5 m ．答：顶端 A 下滑了 0.5 m ．19. 10 千米．20.(1) 第一组（a 是奇数）：9,40,41（答案不唯一）；第二组（a 是偶数）：12,35,37（答案不唯一）．(2) 当 a 为奇数时，b =a 2−12，c =a 2+12；当 a 为偶数时，b =a 24−1，c =a 24+1．证明：当 a 为奇数时，a 2+b 2=a 2+(a 2−12)2=(a 2+12)2=c 2，∴(a,b,c ) 是“勾股数”．当 a 为偶数时，a 2+b 2=a 2+(a 24−1)2=(a 24+1)2=c 2，∴(a,b,c ) 是“勾股数”．。

第一章勾股定理一、选择题(每题3分，共30分)1．下列由线段a，b，c组成的三角形是直角三角形的是()A．a＝1，b＝2，c＝3B．a＝2，b＝3，c＝4C．a＝3，b＝4，c＝5D．a＝4，b＝5，c＝62．如图1所示，∠AOC＝∠BOC，点P在OC上，PD⊥OA于点D，PE⊥OB于点E.若OD＝8，OP＝10，则PE的长为()图1A．5B．6C．7D．83．下列结论中，错误的有()①在Rt△ABC中，已知两边长分别为3和4，则第三边的长为5；②△ABC的三边长分别为a，b，c，若a2＋b2＝c2，则∠A＝90°；③在△ABC中，若∠A∶∠B∶∠C＝1∶5∶6，则△ABC是直角三角形；④若三角形的三边长之比为3∶4∶5，则该三角形是直角三角形．A．0个B．1个C．2个D．3个4．如图2，将长为8cm的橡皮筋放置在地面上，固定两端点A和B，然后把中点C向上拉升3cm至点D，则橡皮筋被拉长了()图2A．2cm B．3cm C．4cm D．5cm5．将面积为8π的半圆与两个正方形按图3所示的方式摆放，则这两个正方形面积的和为()图3A．16B．32C．8πD．646．若△ABC 的三边长a ，b ，c 满足(a －b )2＋|b －2|＋(c 2－8)2＝0，则下列对此三角形的形状描述最确切的是()A．等边三角形B．等腰三角形C．等腰直角三角形D．直角三角形7．如图4所示，AC ⊥BD ，O 为垂足，设m ＝AB 2＋CD 2，n ＝AD 2＋BC 2，则m ，n 的大小关系为()图4A．m ＜n B．m ＝n C．m ＞nD．不确定8．如图5，点D 在△ABC 的边AC 上，将△ABC 沿BD 翻折后，点A 恰好与点C 重合．若BC ＝5，CD ＝3，则BD 的长为()图5A．1B．2C．3D．49．如图6，设正方体ABCD －A 1B 1C 1D 1的棱长为1，黑甲壳虫从点A 出发，白甲壳虫从点C 1出发，它们以相同的速度分别沿棱向前爬行．黑甲壳虫爬行的路线是：AA 1→A 1D 1→D 1C 1→C 1C →CB →BA →AA 1→A 1D 1…，白甲壳虫爬行的路线是：C 1C →CB →BB 1→B 1C 1→C 1C →CB …，那么当黑、白两个甲壳虫各爬行完第2018条棱分别停止在所到的正方体顶点处时，它们之间的最短路程的平方是()图6A．2B．3C．4D．510．如图7所示，在长方形纸片ABCD中，已知AD＝8，折叠纸片使AB边与对角线AC 重合，点B落在点F处，折痕为AE，且EF＝3，则AB的长为()图7A．3B．4C．5D．6二、填空题(每题3分，共18分)11．在△ABC中，若AC2＋BC2＝AB2，∠A∶∠B＝1∶2，则∠B的度数是________．12．古希腊的哲学家柏拉图曾指出：如果m表示大于1的整数，a＝2m，b＝m2－1，c＝m2＋1，那么a，b，c为勾股数．请你利用这个结论得出一组勾股数是____________．13．木工师傅做了一个桌面，要求桌面为长方形，现量得桌面的长为60cm，宽为32cm，对角线的长为68cm，则这个桌面________．(填“合格”或“不合格”)14．一座垂直于两岸的桥长27米，一艘小船自桥北头出发，向正南方向驶去，因水流原因，到达南岸后，发现已偏离桥南头36米，则小船实际行驶了________米．15．如图8所示，把长方形纸片ABCD沿EF，GH同时折叠，B，C两点恰好都落在AD边上的点P处，若∠FPH＝90°，PF＝8，PH＝6，则BC边的长为________．图816．我国数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”．如图9，它是用八个全等的直角三角形拼接而成的，记图中正方形ABCD，正方形EFGH，正方形MNKT 的面积分别为S 1，S 2，S 3，若S 1＋S 2＋S 3＝15，则S 2的值是________．图9三、解答题(共52分)17．(6分)如图10，△ABC 中，D 是BC 上的一点，AB＝10，BD＝6，AD＝8，AC＝17.(1)判断AD 与BC 的位置关系，并说明理由；(2)求△ABC 的面积．图1018．(6分)如图11所示，在长方形ABCD 中，AB＝CD＝24，AD＝BC＝50，E 是AD 上一点，且AE∶DE＝9∶16，判断△BEC 的形状．图1119．(6分)如图12是某同学设计的机器人比赛时行走的路径，机器人从A处先往东走4 m，又往北走1.5m，遇到障碍后又往西走2m，再转向北走4.5m处往东一拐，仅走0.5m 就到达了B处，则点A，B之间的距离是多少？图1220．(6分)如图13所示，有两根长杆隔河相对，一杆高3m，另一杆高2m，两杆相距5m．两根长杆都与地面垂直，现两杆顶部各有一只鱼鹰，它们同时看到两杆之间的河面上E处浮出一条小鱼，于是同时以同样的速度飞下来夺鱼，结果两只鱼鹰同时叼住小鱼．求两杆底部距小鱼的距离各是多少米．(假设小鱼在此过程中保持不动)图1321．(6分)如图14，河边有A，B两个村庄，A村距河边10m，B村距河边30m，两村平行于河边方向的水平距离为30m，现要在河边建一抽水站，需铺设管道抽水到A村和B 村．(1)求铺设管道的最短长度是多少，请画图说明；(2)若铺设管道每米需要500元，则最低费用为多少？图1422.(6分)有一个如图15所示的长方体的透明鱼缸，假设其长AD＝80cm，高AB＝60cm，水深AE＝40cm，在水面上紧贴内壁G处有一鱼饵，G在水面线EF上，且EG＝60cm.一小虫想从鱼缸外的点A处沿缸壁爬到鱼缸内G处吃鱼饵．(1)小虫应该走怎样的路线才可使爬行的路程最短？请画出它的爬行路线，并用箭头标注；(2)试求小虫爬行的最短路程．图1523．(8分)如图16，在由6个大小相同的小正方形组成的方格中，设每个小正方形的边长均为1.(1)如图①，A，B，C是三个格点(即小正方形的顶点)，判断AB与BC的位置关系，并说明理由；(2)如图②，连接三格和两格的对角线，求∠α＋∠β的度数(要求：画出示意图，并说明理由)．图1624．(8分)八年级(3)班开展了手工制作竞赛，每名同学都需在规定时间内完成一件手工作品．陈莉同学在制作手工作品时的第一、二个步骤是：①如图17，先裁下一张长BC＝20cm ，宽AB＝16cm 的长方形纸片ABCD；②将纸片沿着直线AE 折叠，点D 恰好落在BC 边上的点F 处．请你根据步骤①②解答下列问题：(1)找出图中∠FEC 的余角；(2)求EC 的长．图17答案1．C2．B3．C4．A5．D6．C7．B8．D9.D10．D11．60°12．答案不唯一，如20，99，10113．合格14．4515．2416．517．解：(1)AD ⊥BC .理由如下：因为BD 2＋AD 2＝62＋82＝102＝AB 2，所以△ABD 是直角三角形，且∠ADB ＝90°，所以AD ⊥BC .(2)在Rt△ACD 中，因为CD 2＝AC 2－AD 2＝172－82＝152，所以CD ＝15，所以S △ABC ＝12BC ·AD ＝12(BD ＋CD )·AD ＝12×21×8＝84.18．解：因为AD ＝50，AE ∶DE ＝9∶16，所以AE ＝18，DE ＝32.在Rt△ABE 中，由勾股定理，得BE 2＝AB 2＋AE 2＝242＋182＝900.在Rt△CDE 中，由勾股定理，得CE 2＝DE 2＋CD 2＝322＋242＝1600.在△BCE 中，因为BE 2＋CE 2＝900＋1600＝2500＝502＝BC 2，所以△BEC 是直角三角形．19．解：如图，过点B 作BC ⊥AD 于点C ，由图可知AC ＝4－2＋0.5＝2.5(m)，BC ＝4.5＋1.5＝6(m)．在Rt△ABC 中，AB 2＝AC 2＋BC 2＝2.52＋62＝42.25，所以AB ＝6.5(m)，即点A ，B 之间的距离是6.5m.20．解：由题意可知AB ＝2m，CD ＝3m，BC ＝5m，AE ＝DE .设BE＝x m，则EC＝(5－x)m.在Rt△ABE中，由勾股定理，得AE2＝AB2＋BE2.在Rt△DCE中，由勾股定理，得DE2＝CD2＋EC2.所以AB2＋BE2＝CD2＋EC2，即22＋x2＝32＋(5－x)2，解得x＝3，则5－x＝2.所以杆AB底部距小鱼3m，杆CD底部距小鱼2m.21．解：(1)如图，过点A作AC⊥CE于点C，延长AC至点D，使CD＝AC，连接BD，交河边于点E，连接AE，则抽水站应建在点E处，可使铺设的管道最短，最短长度为AE＋BE，即BD的长．过点B作BF⊥AC于点F，由题意得：AC＝10m，CF＝30m，BF＝30m，所以CD＝AC＝10m，所以DF＝10＋30＝40(m)．在Rt△BDF中，BD2＝302＋402＝502，所以BD＝50(m)．即铺设管道的最短长度是50m.(2)最低费用为50×500＝25000(元)．22．解：(1)如图所示，AQ→QG为最短路线．(2)因为AE＝40cm，AA′＝120cm，所以A′E＝120－40＝80(cm)．因为EG＝60cm，所以A′G2＝A′E2＋EG2＝802＋602＝10000，所以A′G＝100cm，所以AQ＋QG＝A′Q＋QG＝A′G＝100cm，所以小虫爬行的最短路程为100cm.23．解：(1)AB⊥BC.理由：如图①，连接AC.由勾股定理可得AB2＝12＋22＝5，BC2＝12＋22＝5，AC2＝12＋32＝10，所以AB2＋BC2＝AC2，所以△ABC是直角三角形且∠ABC＝90°，所以AB⊥BC.(2)∠α＋∠β＝45°.理由：如图②，由勾股定理得AB2＝12＋22＝5，BC2＝12＋22＝5，AC2＝12＋32＝10，所以AB2＋BC2＝AC2，所以△ABC是直角三角形且∠ABC＝90°.又因为AB＝BC，所以△ABC是等腰直角三角形，所以∠BAC＝45°，即∠α＋∠γ＝45°.由图可知∠β＝∠γ，所以∠α＋∠β＝45°.24．解：(1)∠CFE，∠BAF.(2)由折叠的性质，得AF＝AD＝20cm，EF＝DE.设EC＝x cm，则EF＝DE＝(16－x)cm.在Rt△ABF中，BF2＝AF2－AB2＝202－162＝144，所以BF＝12(cm)，所以FC＝BC－BF＝20－12＝8(cm)．在Rt△EFC中，由勾股定理，得EF2＝FC2＋EC2，即(16－x)2＝82＋x2，解得x＝6，所以EC的长为6cm.。

北师大版八年级上册《第一章勾股定理》单元测试（含答案）八年级数学勾股定理单元测试（时间：100分钟总分：120分）班级学号姓名得分一、相信你一定能选对！（每小题4分，共32分）1. 三角形的三边长分别为6,8,10，它的最短边上的高为( )A . 6B . 4.5C . 2.4D . 82. 下面几组数:①7,8,9；②12,9,15；③m 2 + n 2, m 2–n 2, 2mn （m ，n 均为正整数,m >n ）；④2a ,12+a ,22+a .其中能组成直角三角形的三边长的是( ) A . ①② B . ②③ C .①③ D . ③④3. 三角形的三边为a 、b 、c ，由下列条件不能判断它是直角三角形的是（）A ．a :b :c=8∶16∶17B ． a 2-b 2=c 2C ．a 2=(b+c)(b-c)D ．a :b :c =13∶5∶12 4. 三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( )A . 等边三角形B . 钝角三角形C . 直角三角形D . 锐角三角形. 5．已知一个直角三角形的两边长分别为3和4，则第三边长是（） A ．5 B ．25 C ．7 D ．5或76．已知Rt △ABC 中，∠C =90°，若a +b =14cm ，c =10cm ，则Rt △ABC 的面积是（）A. 24cm 2B. 36cm 2C. 48cm 2D. 60cm27．直角三角形中一直角边的长为9，另两边为连续自然数，则直角三角形的周长为（）A ．121B ．120C ．90D ．不能确定8. 放学以后，小红和小颖从学校分手，分别沿东南方向和西南方向回家，若小红和小颖行走的速度都是40米/分，小红用15分钟到家，小颖20分钟到家，小红和小颖家的直线距离为（）A ．600米B . 800米C . 1000米D. 不能确定二、你能填得又快又对吗？（每小题4分，共32分）9. 在△ABC 中，∠C=90°， AB ＝5，则2AB +2AC +2BC =_______．10. 如图，是2002年8月北京第24届国际数学家大会会标，由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4，那么一个直角三角形的两直角边的和等于．11．直角三角形两直角边长分别为5和12，则它斜边上的高为_______．12．直角三角形的三边长为连续偶数，则这三个数分别为__________．13．如图，一根树在离地面9米处断裂，树的顶部落在离底部12米处．树折断之前有______第10题图第13题图第14题图第15题图米.14．如图所示，是一个外轮廓为矩形的机器零件平面示意图，根据图中标出尺寸（单位：mm）计算两圆孔中心A和B的距离为．15．如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为2米，梯子的顶端B到地面的距离为7米．现将梯子的底端A向外移动到A’，使梯子的底端A’到墙根O的距离等于3米，同时梯子的顶端B下降至B’，那么BB’的值：①等于1米；②大于1米5；③小于1米.其中正确结论的序号是．16.小刚准备测量河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,河水的深度为 .三、认真解答，一定要细心哟！（共72分）17．（5分）右图是由16个边长为1的小正方形拼成的，任意连结这些小正方形的若干个顶点，可得到一些线段，试分别画出一条长度是有理数的线段和一条长度是无理数的线段．18．（6分）已知a、b、c是三角形的三边长，a＝2n2＋2n，b ＝2n＋1，c＝2n2＋2n＋1（n为大于1的自然数）,试说明△ABC为直角三角形.19．（6分）小东拿着一根长竹竿进一个宽为3米的城门，他先横着拿不进去，又竖起来拿，结果竿比城门高1米，当他把竿斜着时，两端刚好顶着城门的对角，问竿长多少米？20.（6分）如图所示,某人到岛上去探宝，从A处登陆后先往东走4km，又往北走1.5km，遇到障碍后又往西走2km ，再折回向北走到4.5km 处往东一拐，仅走0.5km 就找到宝藏。

第一章勾股定理数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题，共计45分)1、如图，AB是⊙O的直径，弦CD交AB于点P，AP=2，BP=6，∠APC=30°，则CD的长为（）A. B.2 C.2 D.82、满足下列条件的三角形是直角三角形的有（）个．⑴在△ABC中，∠A=15°，∠B=75°；⑵在△ABC中，AB=12，BC=16，AC=20；⑶一个三角形三边长之比为5：12：13；⑷一个三角形三边长a、b、c满足a2﹣b2=c2．A.1B.2C.3D.43、以下各组数为边长的三角形中，能组成直角三角形的是（）A.1，2，3B.2，3，4C.4，5，6D.5，12，134、在△ABC中，∠A，∠B，∠C的对边分别是a，b，c，满足下列条件的△ABC 不是直角三角形的是（）A.∠A∶∠B∶∠C = 1∶1∶2B.a∶b∶c =1∶1∶C.D.∠A+∠B=2∠C5、如图，四边形是菱形，对角线，相交于点O，，，点E是上一点，连接，若，则的长是（）A.2B.C.3D.46、如图，△ABC中AD⊥BC于D，AB=3，BD=2，DC=1，则AC等于（）A.6B.C.D.47、如图,将置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A'OB'.已知∠AOB=30°,∠B=90°,AB=1,则B'点的坐标为 ( )A. B. C. D.8、如图，在△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥AB于E，若AB=6cm，则△DBE的周长是（）A.6 cmB.7 cmC.8 cmD.9 cm9、如图，矩形ABCD中，对角线AC、BD相交于点O，∠AOB=600， AB=5，则AD的长是（）A.5B.5C.5D.1010、在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到斜边AB的距离是（）A. B. C.9 D.611、如图，把矩形ABCD绕点A顺时针旋转，使点B的对应点B落在DA的延长线上，若AB ＝2，BC＝4，则点C与其对应点C的距离为（）A.6B.8C.2D.212、如图，根据图中的标注和作图痕迹可知，在数轴上的点所表示的数为（）A. B. C. D.13、下列各组数中，能作为直角三角形的三边长的是（）A.1，2，3B. ，，C.3，3，5D.6，8，914、如图，在直角三角形ABC中，∠C=90°，AB=10，AC=8，点E、F分别为AC和AB的中点，则EF=（）A.3B.4C.5D.615、如图所示，已知在三角形纸片中，，，，在边上取一点，以为折痕，使的一部分与重合，与延长线上的点重合，则的长度为（）A. B. C. D.二、填空题(共10题，共计30分)16、如图所示，矩形纸片ABCD中，AB=6cm，BC=8cm，现将其沿EF对折，使得点C与点A 重合，则EF长为________cm．17、如图，在周长为16，面积为6的矩形纸片中，是的中点. 是上一动点，将沿直线折叠，点落在点处.在上任取一点，连接，，则的最小值为________.18、如图，过圆外一点P作⊙O的切线PC，切点为B，连结OP交圆于点A.若AP＝0A＝1，则该切线长为________.19、如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅少走了________步路（假设2步为1米），却踩伤了花草．20、如图四边形中，，，，，则的长为________．21、如图，方格纸上有一个格点三角形和一条格点线段AB．在这个格点纸上找一点C，使得△ABC与这个格点三角形全等，这样的C点可以找到________个．22、如图，点A（2，a）在直线y＝x上，AB⊥x轴于点B，若点C在△AOB的内部，到点O、B的距离相等且CA＝AB，则点C的坐标为________.23、四个全等的直角三角形按图示方式围成正方形ABCD，过各较长直角边的中点作垂线，围成面积为2的小正方形EFGH.已知AM为Rt△ABM较长直角边，AM＝4 EF，则正方形ABCD的面积为________24、如图，在边长为4的菱形ABCD中，∠A=60°，M是AD边的中点，点N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，则线段A′C长度的最小值是________．25、如图，矩形ABCD中，AB＝12，AD＝15，E是CD上的点，将△ADE沿折痕AE折叠，使点D落在BC边上点F处，点P是线段CB延长线上的动点，连接PA，若△PAF是等腰三角形，则PB的长为________.三、解答题(共5题，共计25分)26、已知，在△ABC中，∠ACB=90°，CD⊥AB垂足为D，BC=6，AC=8，求AB与CD的长．27、如图，在梯形ABCD中, ,，求DC的长．28、如图在中，，点E，F分别在上，求证：.29、在右图的正方形网格中，每个小正方形的边长为1．请在图中画一个面积为10的正方形，并写出其边长．（要求：正方形的顶点都在格点上）30、生活表明，靠墙摆放梯子时，若梯子底端离墙距离为梯子长度的，则梯子比较稳定.现有一长度为6米的梯子，当梯子稳定摆放时，它的顶端能达到5.7米高的墙头吗？参考答案一、单选题(共15题，共计45分)1、C2、D3、D4、D5、B6、B7、A8、A9、A11、D12、A13、B14、A15、A二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、三、解答题(共5题，共计25分)26、27、28、29、30、。

第一章勾股定理数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题，共计45分)1、如图，在中，于点D，且是的中点，若则的长等于（）A.5B.6C.7D.82、如图，⊙M与x轴相交于点A（2，0）、B（8，0），与y轴相切于点C，则圆心M的坐标是（）A.（3，5）B.（5，3）C.（4，5）D.（5，4）3、如图，由4个相同的直角三角形与中间的小正方形拼成一个大正方形，若大正方形面积是17，小正方形面积是5，直角三角形较长直角边为b，则ab的值是（）A.4B.6C.8D.104、如图，在4×3的长方形网格中，已知A，B两点为格点（网格线的交点称为格点），若C也为该网格中的格点，且△ABC为等腰直角三角形，则格点C的个数为（）A.5B.6C.3D.45、如图，圆锥侧面展开得到扇形，此扇形半径，圆心角，则此圆锥高的长度是（）A.2B.C.D.6、下列说法中正确的个数为（）①如果三角形的三边长a，b，c满足，那么这个三角形是直角三角形；②对角线相等的平行四边形是菱形；③如果一个一元二次方程有实数根，那么；④三个角相等的四边形是矩形．A.1个B.2个C.3个D.4个7、一根高9m的旗杆在离地4m高处折断，折断处仍相连，此时在3.9m远处耍的身高为1m 的小明（）A.没有危险B.有危险C.可能有危险D.无法判断8、四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”（如图）．如果小正方形面积为49，大正方形面积为169，直角三角形中较小的锐角为θ，那么sinθ的值（）A. B. C. D.9、如图，网格中每个小正方形的边长均为1，点，，都在格点上，以为圆心，为半径画弧，交最上方的网格线于点，则的长为（）A. B.0.8 C. D.10、如图，在△ABC中，∠ACB=90º，AC=BC=1，E、F为线段AB上两动点，且∠ECF=45°，过点E、F分别作BC、AC的垂线相交于点M，垂足分别为H、G.现有以下结论：①AB= ；②AF+BE=EF；③当点E与点B重合时，MH= ；其中正确结论的个数是( )A.0B.1C.2D.311、如图，在平面直角坐标系中，⊙M与x轴相切于点A（8，0），与y轴分别交于点B （0，4）和点C（0，16），则圆心M到坐标原点O的距离是（）A.10&nbsp;B.8C.4D.212、如图所示，在正方形中，边长为2的等边三角形的顶点，分别在和上.下列结论：①；②；③；④.其中结论正确的序号是（）A.①②③B.①②④C.①③④D.②③④13、已知：如图，菱形ABCD的两条对角线相交于O，若AC=8，BD=6，则菱形ABCD的周长是（）A.20B.16C.12D.1014、如图，在矩形ABCD中，AB=6，AD=8，以BC为斜边在矩形所在平面作直角三角形BEC，F为CD的中点，则EF的最小值为（）A. B. C. D.15、如图，A，B是直线l同侧的两点，作点A关于直线l的对称点A′，连结A′B．若点A，B到直线l的距离分别为2和3，则线段AB与A′B之间的数量关系是（）A.A′B 2﹣AB 2=13B.A′B 2﹣AB 2=24C.A′B 2+AB2=25 D.A′B 2+AB 2=26二、填空题(共10题，共计30分)16、如图，点G是正方形ABCD的AB边的中点，点E、F在对角线AC上，并且AE=EF=FC，如果AB=2，则BF+GE=________．</p>17、如图，四边形ABCD中，AB=BC=2，CD=1，DA=3，AC为一条对角线，若∠ABC=90°，则四边形ABCD的面积为________．18、读诗求解：“出水三尺一红莲，风吹花朵齐水面，水平移动有六尺，水深几何请你算？”请你写出水的深度为________尺．19、如图，矩形ABCD中，AB=8，点E是AD上的一点，有AE=4，BE的垂直平分线交BC的延长线于点F，连结EF交CD于点G．若G是CD的中点，则BC的长是________．20、已知|x﹣12|+（y﹣13）2与z2﹣10z+25互为相反数，则以x，y，z为边的三角形是________ 三角形．21、如图，已知四边形ABCD是平行四边形，BC＝3AB，A、B两点的坐标分别是（1，0），（0，2），C、D两点在反比例函数y＝（k＞0，x＞0）的图象上，则k的值等于________.22、如图，在矩形ABCD中，对角线AC， BD交于点O，已知∠AOD=120°， AB=1，则BC的长为________23、如图，在边长为的正方形中，点Q是边的中点，点P是边上的一点，连接，，且，则线段的长为________ ．24、如图，将矩形ABCD沿对角线AC折叠，E是点D的对称点，CE交AB于点F．若AB=16，BC=8，则BF的长为________．25、如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作⊙P．当⊙P与正方形ABCD的边相切时，BP的长为________．三、解答题(共5题，共计25分)26、在 Rt△ABC 中，∠C＝90°，∠A、∠B、∠C 的对边分别为a、b、c．若a∶c＝15∶17，b＝24，求a.27、如图，在笔直的铁路上A、B两点相距25km，C、D为两村庄，DA=10km，CB=15km，DA ⊥AB于A，CB⊥AB于B，现要在AB上建一个中转站E，使得C、D两村到E站的距离相等．求E应建在距A多远处？28、在由6个大小相同的小正方形组成的方格中；如图，A、B、C是三个格点（即小正方形的顶点）．判断AB与BC的关系，并说明理由．29、如图，是等腰直角三角形，，D是斜边的中点，分别是边上的点，且，若，，求线段的长．30、如图，△ABC中，，且AD=AC．若∠ABC=45°，D是BC边上一点，BD-DC=1．求DC的长.参考答案一、单选题(共15题，共计45分)1、D2、D3、B5、C6、A7、B8、D9、A10、C11、D12、B13、A14、B15、B二、填空题(共10题，共计30分)16、17、18、19、20、22、23、24、25、三、解答题(共5题，共计25分)28、。

第一章勾股定理数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题，共计45分)1、一直角三角形的两直角边长为3和4，则第三边长为（）A. B.5 C. 或5 D.72、如图，点A在双曲线y=上，且OA=4，过A作AC⊥x轴，垂足为C，OA的垂直平分线交OC于B，则△ABC的周长为（）A.2B.4C.D.53、小明搬来一架 3.5 米长的木梯，准备把拉花挂在 2.8 米高的墙上，则梯脚与墙脚的距离为( )A.2.7 米B.2.5 米C.2.1 米D.1.5 米4、如图，在半径为4的⊙O中，弦AB=6，点C是优弧上一点（不与A，B重合），则cosC的值为（）A. B. C. D.5、一艘轮船以16n mile/h的速度从港口A出发向东北方向航行，另一轮船以12n mile/h 的速度从港口A出发向东南方向航行，则3h后两船相距（）A.36n mileB.48n mileC.60n mileD.54n mile6、已知⊙O的直径AB=8cm，点C在⊙O上，且∠B0C=60°，则AC的长为（）A.4cmB.4 cmC.5cmD.2．5cm7、如图，在Rt△ABC中，∠ACB=90°，以点A为圆心，AC长为半径作圆弧交边AB于点D．若 AC=3，BC=4．则BD的长是（）A.2B.3C.4D.58、已知下列三角形的各边长：①3、4、5，②5、12、13，③3、4、6，④5、11、12其中直角三角形有（）A.4个B.3个C.2个D.1个9、以下列各组数作为三角形的三边长，其中不能构成直角三角形的是（）A.1，1，B.12，16，20C.1，，D.1，2，210、下列各组数，可以作为直角三角形的三边长的是（）A.8，12，20B.2，3，4C.8，10，6D.5，13，1511、图1为一个长方体，AD=AB=10，AE=6，M，N为所在棱的中点，图2为图1的表面展开图，则图2中MN的长度为（）A.11B.10C.10D.812、如图，正方形ABCD的边长为1，E、F分别是BC，CD上的点，且△AEF是等边三角形，则BE的长为（）A. B. C. D.13、如图有两棵树，一棵高6米，另一棵高3米，两树相距4米。