《线性代数A》教学大纲

《线性代数（A）类（2）》课程大纲一、课程简介教学目标：线性代数是数学专业乃至所有理工科专业本科教学的最基础课程之一，基本内容为线性空间与线性变换（矩阵）等，具有广泛应用性。

在讲授基本理论、基本方法的同时，我们也强调对学生数学素养及数学能力的培养。

希望学生在学习这门课的同时能体会到数学理论的美妙与数学思维的乐趣。

我们同时也希望学生了解该课程在其它学科的应用以及与后续课程的联系。

主要内容：《线性代数（A）类（2）》是《线性代数（A）类（1）》的延续，主要内容包括：相似标准型及其应用、矩阵函数，实二次型、复二次型及Hermite型的分类，实内积空间、酉空间及其各种应用广泛的线性变换、矩阵的分解、双线性型等。

二、教学内容第一章相似标准型主要内容：多项式矩阵的相抵，矩阵的相似，Jordan标准型与有理标准型及其几何意义。

相似标准型的证明及应用，矩阵函数。

重点与难点：矩阵的相似标准型的证明和计算。

第二章二次型主要内容：数域K上二次型的化简，实二次型的惯性定理，正定二次型与正定矩阵，Hermite型。

重点与难点：惯性定理、正定二次型、Hermite型。

第三章内积空间主要内容：实和复内积空间，Schmidt正交化过程，正规算子及其性质，正交变换及酉变换，矩阵的分解。

重点与难点：内积空间的理解，内积空间中的各种变换。

第四章：双线性型主要内容：双线性型，对偶空间，交错型与辛几何，对称型与正交几何。

重点与难点：对偶的概念，交错型与对称型及其应用。

三、教学进度安排三、课程考核及说明30%为平时成绩（大作业等）70%为考试成绩四、教材与参考书1. 姚慕生、吴泉水，《高等代数学》，复旦大学出版社；2. 张贤科，许莆华，《高等代数学》，清华大学出版社，2004；3. 许以超，《线性代数与矩阵论》，高等教育出版社，2008；4. 龚升，《线性代数五讲》，科学出版社，2005；5. 蓝以中，《高等代数简明教程》（上、下），第二版，北京大学出版社，20106 S K. Berberian, Linear algebra. Oxford, USA:Oxford Univ.Press,1992.7. S. Lipschutz, Theory and problems o linear algebra, New York:McGraw-Hill,1991;8. W C. Bwown, A second course in linear algebra, New York: J. Wiley& Sons, 19889. D H. Griffel, Linear algebra and its applications, New York: MarceiDekker, 1985.10.S. Maclane and G. Birkhoff, Algebra, New York:Macmillan,1979.。

《线性代数A》课程教学大纲课程代码：090011050课程英文名称：Linear Algebra, Level A课程总学时：40 讲课：40 实验：0 上机：0适用专业：经济、管理类本科专业大纲编写（修订）时间：2017.11一、大纲使用说明（一）课程的地位及教学目标线性代数是经济、管理类本科各专业的一门重要基础课。

它是讨论有限维空间中线性关系经典理论的课程，具有较强的抽象性与逻辑性。

线性代数这一数学工具在经济、管理科学中有着广泛的应用，著名的投入产出模型就是以线性代数理论为基础的。

学好这一门课程不仅对学习后继课程是必不可少的，而且对掌握现代经济理论并应用于实际也是很有必要的，尤其是在计算机日益普及和广泛应用的今天，该课程的地位与作用更显重要。

通过本课程的学习，可以使学生获得线性代数的基本知识和基本方法，培养学生的抽象思维能力、逻辑推理能力、熟练运算能力及利用矩阵方法解决问题的能力，为学习后继课程概率论与数理统计等数学类课程以及经济、管理类的一些专业课程奠定必要的数学基础。

（二）知识、能力及技能方面的基本要求1.基本知识：掌握行列式的计算，矩阵的各种运算及其运算律，利用矩阵的初等变换求矩阵的秩、解线性方程组、判别向量组的线性相关性以及求最大无关组，利用正交矩阵化对称矩阵为对角阵等有关基础知识。

2. 基本能力：培养学生抽象思维能力、逻辑推理能力、基本运算能力、自学能力与科学创新能力以及运用线性代数方法分析和解决实际问题的能力等。

3.基本技能:使学生具有矩阵运算、利用矩阵方法解决一些实际问题的基本技能等。

（三）实施说明1．教学方法：课堂讲授中要重点对基本概念、基本方法和解题思路的讲解；采用启发式教学，培养学生思考问题、分析问题和解决问题的能力；引导和鼓励学生通过实践和自学获取知识，培养学生的自学能力；课堂讲授中，可增加问题的讨论环节，以调动学生学习的主观能动性；注意培养学生利用矩阵方法解决一些实际问题的能力。

《线性代数A》教学大纲4学分 64学时一、课程的地位、作用和任务线性代数是讨论有限维空间中线性关系经典理论的课程，它具有较强的抽象性和逻辑性，是高等学校工科本科各专业的一门重要的基础理论课。

由于线性问题广泛存在在于科学技术的各个领域，而某些非线性问题在一定条件下可以转化为线性问题，因此本课程所介绍的方法广泛地应用于各个学科。

随着计算技术和计算手段的发展和提高，本课程的地位和作用也更为重要。

通过本课程的学习，使学生掌握线性代数的基本概念，基本理论和方法。

培养学生的抽象思维和逻辑思维能力，运用线性代数的基本理论分析典型的数学问题的能力，会选用恰当的线性代数方法进行计算的能力，并为学习相关课程奠定必要的数学基础。

二、课程内容与教学基本要求（一）行列式（7学时）1. 理解n阶行列式的定义和性质。

熟悉代数余子式的定义和性质。

2. 掌握二阶、三阶行列式的计算方法。

3. 熟悉行列式按某行（列）展开的方法。

4. 会计算简单的n阶行列式。

了解行列式计算的常用方法。

5. 了解行列式的Laplace展开定理。

6. 熟悉Cramer法则，理解齐次线性方程组有非零解的条件。

（二）三维空间的直线与平面（6学时）1. 理解空间直角坐标系和R3中向量的坐标表示。

2. 掌握单位向量、方向余弦、向量的投影等概念3. 掌握向量的数量积与矢量积的运算，了解向量的混合积及其运算。

4. 掌握向量的线性运算和两向量垂直、平行的条件。

5. 熟悉R3中平面的方程和直线的方程及其求法。

6. 会利用平面、直线的相互关系解决简单问题。

（三）矩阵（7学时）1．理解矩阵的概念，熟悉常见的特殊矩阵的基本性质。

2．掌握矩阵的简单代数运算（线性运算、乘法、转置）及其运算法则。

3．理解线性变换的概念，了解线性变换与矩阵运算的联系。

4．理解逆矩阵的概念。

掌握逆矩阵存在的条件，熟悉矩阵求逆的方法。

5．掌握矩阵的初等变换。

了解初等方阵。

6．会用初等变换方法求逆矩阵。

7．理解矩阵秩的概念并掌握其求法。

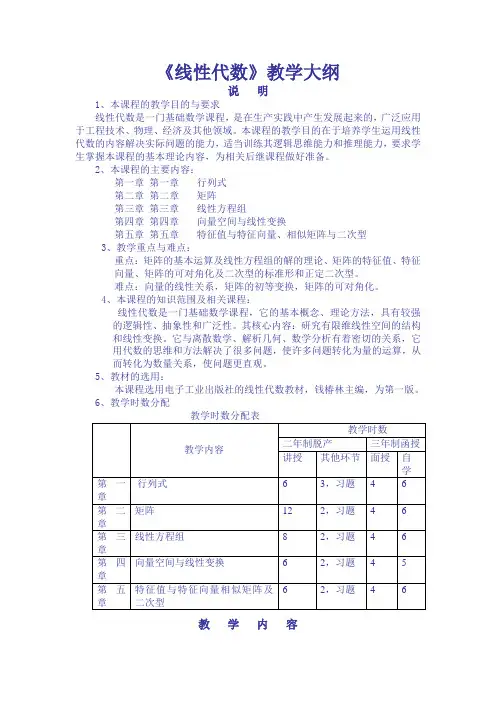
《线性代数》教学大纲说明1、本课程的教学目的与要求线性代数是一门基础数学课程，是在生产实践中产生发展起来的，广泛应用于工程技术、物理、经济及其他领域。

本课程的教学目的在于培养学生运用线性代数的内容解决实际问题的能力，适当训练其逻辑思维能力和推理能力，要求学生掌握本课程的基本理论内容，为相关后继课程做好准备。

2、本课程的主要内容：第一章第一章行列式第二章第二章矩阵第三章第三章线性方程组第四章第四章向量空间与线性变换第五章第五章特征值与特征向量、相似矩阵与二次型3、教学重点与难点：重点：矩阵的基本运算及线性方程组的解的理论、矩阵的特征值、特征向量、矩阵的可对角化及二次型的标准形和正定二次型。

难点：向量的线性关系，矩阵的初等变换，矩阵的可对角化。

4、本课程的知识范围及相关课程：线性代数是一门基础数学课程，它的基本概念、理论方法，具有较强的逻辑性、抽象性和广泛性。

其核心内容：研究有限维线性空间的结构和线性变换。

它与离散数学、解析几何、数学分析有着密切的关系，它用代数的思维和方法解决了很多问题，使许多问题转化为量的运算，从而转化为数量关系，使问题更直观。

5、教材的选用：本课程选用电子工业出版社的线性代数教材，钱椿林主编，为第一版。

6、教学时数分配教学内容第一章第一章行列式（讲授6学时，习题2学时）1．1．教学内容及进度安排：§1 行列式的定义及性质（3学时）（1）（1）行列式的定义（2）（2）行列式的计算性质§2 行列式的计算（1学时）（1）（1）利用行列式的性质计算行列式（2）（2）利用行列式的按某一行展开计算行列式§3 克莱姆法则（2学时）（1）（1）克莱姆法则（2）（2）克莱姆法则的应用及意义2．教学目的与要求：目的：通过引入行列式的定义，为讨论矩阵的一般理论打下基础，并为讨论线性方程组提供工具。

要求：掌握行列式的定义、计算性质，会利用克莱姆法则解决问题。

3．教学重点：行列式的计算及克莱姆法则4．教学难点：行列式的计算5．主要教学环节的组织：由低阶行列式对方程组的作用，启发一般阶的行列式对一般阶的方程组的作用即：克莱姆法则第二章第二章矩阵（讲授12学时，习题2学时）1．1．教学内容及进度安排：§1 高斯消元法（2学时）（1）（1）矩阵的定义（2）（2）矩阵的初等行变换（3）（3）线性方程组的解的情况§2 矩阵的加法、数量乘法、乘法（3学时）（1）（1）三种运算的定义（2）（2）三种运算满足的运算性质（3）（3）矩阵的行列式及运算性质§3 矩阵的转置、对称矩阵（1学时）（1）（1）矩阵的转置及转置的性质（2）（2）对称矩阵的定义及性质§4 可逆矩阵的逆矩阵（2学时）（1）（1）可逆矩阵、逆矩阵的定义（2）（2）矩阵可逆的充要条件（3）（3）逆运算及其运算性质§5 矩阵的初等变换和初等矩阵（2学时）（1）（1）初等变换和初等矩阵的定义（2）（2）利用初等变换求逆矩阵的方法§6 分块矩阵（2学时）（1）（1）分块矩阵的定义（2）（2）分块矩阵的运算2．2．教学目的与要求：目的：通过消元法引入矩阵，从而进一步讨论方程组解的情况，为研究其解的结构打下理论基础。

《线性代数》教学大纲教学内容及要求《线性代数》教学内容及要求1．行列式二阶和三阶行列式，n阶行列式的定义，行列式的性质，行列式按行(列)展开，克拉默法则。

2．矩阵矩阵，矩阵的运算，逆矩阵，分块矩阵，矩阵的初等矩阵和初等变换，矩阵的秩。

目的要求：理解矩阵的概念，掌握几种特殊矩阵(单位矩阵，对角矩阵，数量矩阵，三角矩阵，对称矩阵，反对称矩阵)的定义与性质。

熟练掌握矩阵运算(加、减、数乘、乘法)及其运算，掌握矩阵转置的性质，掌握行列式运算规律，了解方阵的幂。

理解逆矩阵的概念，掌握矩阵可逆的充要条件，掌握可逆矩阵的性质。

理解伴随矩阵的概念，会用伴随矩阵求矩阵的逆。

理解分块矩阵的概念，会用矩阵分块法进行矩阵运算。

理解矩阵的初等变换，初等矩阵的概念。

理解矩阵秩的概念，会用初等变换求矩阵的逆和秩。

3．线性方程组高斯消元法，向量组的线性相关性，向量组的秩和极大线性无关组，线性方程组解的结构。

目的要求：理解线性方程组的概念，掌握用矩阵的秩讨论齐次线性方程组有非零解的主要条件和非齐次线性方程组有解的主要条件。

熟练掌握用初等行变换求线性方程组的通解的方法（高斯消元法），理解向量组线性相关和线性无关的概念，理解向量组的秩的概念，掌握向量组秩与矩阵秩之间的关系，并用矩阵秩研究向量组线性相关与线性无关的判定方法。

了解线性方程组的解的结构，会求齐次线性方程组的基础解系以及非齐次线性方程组的通解。

4．相似矩阵方阵的特征值与特征向量，相似矩阵，对称矩阵的相似矩阵。

目的要求：理解矩阵的特征值，特征向量的概念，掌握矩阵特征值的性质，掌握求矩阵特征值和特征向量的方法。

理解矩阵相似的概念，掌握相似矩阵的性质，了解矩阵可对角化的主要条件．掌握将矩阵化为相似对角矩阵的方法，掌握实对称矩阵的特征值和特征向量的性质。

5．相似矩阵与二次型向量的内积，二次型及其标准形，用正交变换法化二次型为标准形，正定二次型。

目的要求：了解二次型的概念，会用矩阵形式表示二次型，理解二次型秩的概念，理解二次型及其标准形等概念以及惯性定理的条件和结论，会用正交变换化二次型为标准形．理解正定二次型，正定矩阵的概念，掌握正定矩阵的性质。

线性代数与解析几何(A)教学大纲（课程编号：07011270；课程类型：必修；总学分：4；总上课学时：64；上机时数：0）东南大学数学系一．课程的性质与目的本课程是(吴健雄学院)工科电类专业学生本科阶段关于几何及离散量数学重要的数学基础课程。

本课程的目的是使学生熟悉空间解析几何与线性代数基本概念，掌握用坐标及向量的方法讨论几何图形的方法，熟悉空间中简单的几何图形的方程及其特点，掌握线性代数的基本理论和基本方法，熟悉矩阵运算的基本规律和基本技巧，熟悉矩阵在等价关系、相似关系、合同关系下的标准形，提高其空间想象能力、抽象思维和逻辑思维的能力，为后继课程的学习做好准备，并为用线性代数的理论解决实际问题打下基础。

二．课程内容的教学要求1．向量代数平面与直线（1）理解几何向量的概念及其加法、数乘运算，熟悉运算规律，了解两个向量共线和三个向量共面的充分必要条件；（2）理解空间直角坐标系的概念，理解仿射坐标系的概念，掌握向量的坐标表示；（3）理解向量的数量积、向量积和混合积的概念，理解它们的几何意义，了解相关的运算性质，掌握利用坐标进行计算的方法；（4）理解平面的法向量的概念，熟练掌握平面的方程的确定方法，熟悉特殊位置的平面方程的形式；（5）理解直线的方向向量的概念，熟练掌握直线的对称方程、一般方程及参数方程的确定方法；（6）了解直线、平面间的夹角的定义，了解点与直线、平面间的距离的定义，并掌握相关的计算；（7）了解平面束的概念，并会用平面束处理相关几何问题。

2．矩阵和行列式（1）理解矩阵和n维向量的概念；（2）理解矩阵和向量的加法、数乘、乘法运算及矩阵的转置及相关的运算性质，熟练掌握上述运算；（3）理解零矩阵、单位矩阵、数量矩阵、对角阵、三角阵、对称矩阵、反对称矩阵的定义及其运算性质；（4）理解二阶、三阶行列式的定义，熟练掌握它们的计算；（5）知道全排列及全排列的逆序数的定义，会计算排列的逆序数，知道对换及对换对于排列的奇偶性的影响；（6）了解n阶行列式的定义，会用行列式的定义计算简单的n阶行列式；（7）掌握行列式的性质，熟练掌握行列式按行、列展开公式，了解行列式的乘法定理；（8）掌握利用行列式的性质计算行列式的方法；（9）理解矩阵的可逆性的概念，掌握矩阵可逆的判别方法，掌握逆矩阵的性质；（10）理解伴随矩阵的概念，熟练掌握伴随矩阵的性质，掌握利用伴随矩阵计算矩阵的逆矩阵；（11）理解Cramer法则，掌握用Cramer法则求方程组的解的方法；（12）掌握分块矩阵的运算规则，掌握典型的分块方法。

《线性代数》教学大纲一、课程概述1。

课程研究对象和研究内容《线性代数》是数学中的一个重要分支，是高等工科院校的重要基础理论课.其不仅在数学、力学、物理学和技术学科中有各种重要应用，而且在计算机图形学、计算机辅助设计、密码学、虚拟现实等技术中无不是理论和算法的基础内容。

本课程教学内容主要有：行列式;矩阵;n维向量空间；线性方程组;特征值与特征向量；二次型。

通过本课程的学习,能够培养学生对研究对象进行有序化、代数化、可解化的处理方法，并且为其他后续课程打好基础。

因此，本课程对学生今后专业的发展具有非常重要的意义。

2. 课程在整个课程体系中的地位《线性代数》是计算机专业的基础课。

《线性代数》的后续课是《离散数学》，《计算方法》等。

二、课程目标1．知道《线性代数》这门学科的理论和方法及其在专业教育体系中的位置；2．理解这门学科的基本概念、基本定理和基本方法；3．熟练掌握行列式、矩阵的运算；会用行列式与矩阵的方法求解齐次线性方程组、非齐次线性方程组的解；学会矩阵的特征值、特征向量及二次型的相关应用；4．突出计算能力的培养，引导学生进行归纳、对比和思考，培养学生的创造性能力;5．学会用线性代数的方法处理离散对象；6．培养运用本学科的基本知识与基本技能分析问题、解决问题的能力；逐步培养学生抽象思维和逻辑推理的能力;7．通过本课程的学习,协助学生逐步树立辩证唯物主义的观点。

三、课程内容和要求这门学科的知识与技能要求分为知道、理解、掌握、学会四个层次。

这四个层次的一般涵义表述如下：知道——-是指对这门学科和教学现象的认知。

理解—--是指对这门学科涉及到的概念、原理、策略与技术的说明和解释，能提示所涉及到的教学现象演变过程的特征、形成原因以及教学要素之间的相互关系。

掌握—-—是指运用已理解的教学概念和原理说明、解释、类推同类教学事件和现象。

学会-——是指能模仿或在教师指导下独立地完成某些教学知识和技能的操作任务，或能识别操作中的一般差错.教学内容和要求表中的“√”号表示教学知识和技能的教学要求层次.本标准中打“＊”号的内容可作为自学，教师可根据实际情况确定要求或不布置要求。

《线性代数》课程教学大纲课程名称：线性代数课程代码：课程性质: 必修总学分：2 总学时： 32* 其中理论教学学时：32*适用专业和对象：理（非数学类专业）、工、经、管各专业**使用教材：注：（1）大部分高校开设本课程的教学学时数约为32—48学时，为兼顾少学时高校开展教学工作，本大纲以最低学时数32学时（约2学分）进行教学安排，有多余学时的学校或专业可对需要加强的内容适当拓展教学学时。

（2）对线性代数课程而言，理工类与经管类专业的教学基本要求几乎一致，所以这里所列教学内容及要求对这两类专业均适合。

一、课程简介《线性代数》是高等学校理（非数学类专业）、工、经、管各专业的一门公共基础课，其研究对象是向量，向量空间（或称线性空间），线性变换和有限维的线性方程组。

该课程具有理论上的抽象性、逻辑推理的严密性和工程应用的广泛性。

主要内容是学习科学技术中常用的矩阵方法、线性方程组及其有关的基本计算方法，使学生具有熟练的矩阵运算能力并能用矩阵方法解决一些实际问题。

通过本课程的学习，使学生理解和掌握行列式、矩阵的基本概念、主要性质和基本运算，理解向量空间的概念、向量的线性关系、线性变换、了解欧氏空间的线性结构，掌握线性方程组的求解方法和理论，掌握二次型的标准化和正定性判定。

线性代数的数学思想和数学方法深刻地体现辩证唯物主义的世界观和方法论，线性代数的发展历史也充分展示数学家们开拓创新、追求真理的科学精神，展现古今中外数学家们忠诚爱国、献身事业的高尚情怀。

思想政治教育元素融入线性代数的教学实践之中，可以培养学生用哲学思辨立场、观点和方法分析解决问题，能够提高学生的创新能力和应用意识，培养学生的爱国主义情怀、爱岗敬业精神和开拓创新精神，帮助学生在人生道路上形成良好的人格，树立正确的世界观、人生观、价值观。

线性代数理论不仅渗透到了数学的许多分支中，而且在物理、化学、生物、航天、经济、工程等领域中都有着广泛的应用。

同时，线性代数课程注重培养学生逻辑思维和抽象思维能力、空间直观和想象能力，提高学生分析问题解决问题的能力。