第6章(6.1.4)移动信道的模型(多径衰落信道)

移动通信信道模型归纳报告13信息 XXXXXXX摘要移动通信中，无线电波传播特性非常复杂，在传播过程中信号收到各种干扰。

对无线通信信道的建模研究可以在理论上抑制部分干扰，因此信道模型的研究作为推动整个移动通信发展的关键技术之一，国内外都对它做了大量的研究，并得到了一些成果。

本文将对现有的移动通信信道模型进行分类，并举例对典型的移动通信信道模型进行详细介绍。

关键词：移动通信，信道模型1.简介移动通信的迅猛发展使移动信道无线电波传播预测成为移动通信领域的研究热点。

移动信道与其它信道相比是稳定性最差的一种，由于电波在移动信道中传输时在时域和空域上都会有较大随机性的波动和起伏，要对其进行控制和测量都比较困难，且实地设站检测费用极高。

如果能建噪声立一些模型，通过数值计算就可以较好地预知信道特性，那它们将比实地测量方法更可取。

近年来国内外都有不少相关论文发表，建立了一些较实用的电波传播预测模型，本文根据已有的研究成果进行归纳展示。

移动通信信道是多径衰落信道，数字信号在信道中传输时，容易发生突发性误码和严重的码间串扰。

对于多径衰落的信道，根据不同的标准有不同的分类方法。

根据尺度不同，可以分为大尺度模型（数米范围内的均值）和小尺度模型（在波长范围内的测量值）。

根据环境特征不同，可分为室内、室外、陆地、海洋、空间等等。

根据应用区域不同，可分为宏蜂窝（2km）、微蜂窝（500m）、微微蜂窝。

根据建模方式可分为统计性模型 (经验模型 )、半经验或半确定性模型和确定性模型[1]。

统计性模型 (经验模型 )是根据大量的测量结果统计分析后得出的图表和公式 ,不需要相关环境的详细信息。

确定性模型是对具体的现场环境直接应用电磁理论计算的方法。

半经验或半确定性模型是基于把确定性方法用于一般的市区或室内环境中导出的等式 ,有时为改善它们和实验结果的一致性，则根据实验结果对等式进行修正[2]。

本文将以建模方式为分类标准，从原理、特点、用途等方面剖析不同信道模型的特点。

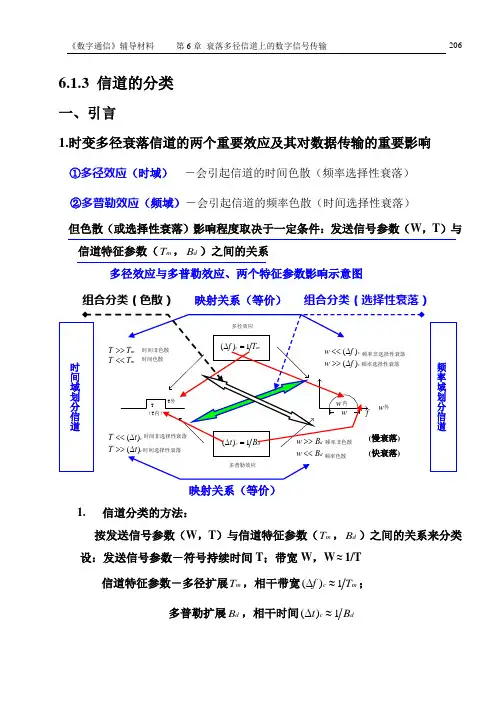
6.1.3 信道的分类一、引言1.时变多径衰落信道的两个重要效应及其对数据传输的重要影响①多径效应（时域） －会引起信道的时间色散（频率选择性衰落）②多普勒效应（频域）－会引起信道的频率色散（时间选择性衰落） 但色散（或选择性衰落）影响程度取决于一定条件：发送信号参数（W ，T ）与信道特征参数（m T ，d B ）之间的关系多径效应与多普勒效应、两个特征参数影响示意图映射关系（等价）1.信道分类的方法：按发送信号参数（W ，T ）与信道特征参数（m T ，d B ）之间的关系来分类设：发送信号参数－符号持续时间T ；带宽W ，W ≈1/T 信道特征参数－多径扩展m T ，相干带宽m c T f 1)(≈∆； 多普勒扩展d B ，相干时间d c B t 1)(≈∆二、分类1.非色散信道－或时间/频率（双重）非选择性衰落信道。

条件：m ,)(T T f W c >>∆<<∙或扩展因子1B d m <<T （欠扩展） d c B W t T >>∆<<∙或,)(2.时间色散信道－或频率选择性衰落信道。

条件：m ,)(T T f W c <<∆>>∙或 时间色散，频率选择性衰落 d c B W t T >>∆<<∙或,)( 时间非选择性衰落，频率非色散3.频率色散信道－或时间选择性衰落信道。

条件：m ,)(T T f W c >>∆<<∙或 频率非选择性衰落，时间非色散 d c B W t T <<∆>>∙或,)( 频率色散，时间选择性衰落4.双重色散信道－时间/频率（双重）选择性衰落信道。

条件：m ,)(T T f W c <<∆>>∙或 时间色散，频率选择性衰落 d c B W t T <<∆>>∙或,)( 频率色散，时间选择性衰落另外，频率非色散条件：d B W >>与“慢衰落”条件：（符号速率）d f T>>1（衰落频率）相当 按数据速率和车速不同划分信道： 1()c d t B ∆≈大，慢衰落 1()c dt B ∆≈小，快衰落T慢衰落快衰落C T B ≈C B ≈频率非选择性率选择性()C f ∆ ()C t ∆多径衰落信道的分类示意图三、关于非色散（非选择性衰落）信道的进一步说明上述非色散信道的第二个条件：T1B W B d TW d <<−−→−<<≈所以1 因为d B 和d f (衰落频率)λv∝，所以T1f d <<(符号速率)－时间慢衰落(相对符号速率）即：接收的衰落信号的包络衰落频率（d f ）远低于符号速率。

简单模型2种：常量（Constant ）模型和纯多普勒模型1. 常量（Constant ）模型：常量模型既没有衰落，也没有多普勒频移，适用于可预测的固定业务无线信道。

其幅度分布的概率密度函数（PDF ）为：0(r)A (r r )p δ=-式中r 为信道响应的幅度，A 为概率常数。

常量模型的多普勒谱为： ()db d f P B f δ=式中fd 为最大多普勒频移，f 为基带频率，B 为常数。

2. 纯多普勒模型：纯多普勒模型无衰落，但有多普勒频移，适用于可预测的移动业务无线信道。

其幅度分布与常量模型相同，多普勒谱为：()x db d df f P C f f δ=-，C 为常数。

由于移动通信中移动台的移动性，无线信道中存在多普勒效应。

在移动通信中，当移动台移向基站时，频率变高，远离基站时，频率变低。

我们在移动通信中要充分考虑“多普勒效应”。

虽然，由于日常生活中，我们移动速度的局限，不可能会带来十分大的频率偏移，但是这不可否认地会给移动通信带来影响，为了避免这种影响造成我们通信中的问题，我们不得不在技术上加以各种考虑。

也加大了移动通信的复杂性。

3. 瑞利模型：瑞利衰落信道（Rayleigh fading channel）是一种无线电信号传播环境的统计模型。

这种模型假设信号通过无线信道之后，其信号幅度是随机的，即“衰落”，并且其包络服从瑞利分布。

这一信道模型能够描述由电离层和对流层反射的短波信道，以及建筑物密集的城市环境。

瑞利衰落只适用于从发射机到接收机不存在直射信号（LoS，Line of Sight）的情况，否则应使用莱斯衰落信道作为信道模型。

在无线通信信道环境中，电磁波经过反射折射散射等多条路径传播到达接收机后，总信号的强度服从瑞利分布。

同时由于接收机的移动及其他原因，信号强度和相位等特性又在起伏变化，故称为瑞利衰落。

瑞利分布是一个均值为0，方差为σ2的平稳窄带高斯过程，其包络的一维分布是瑞利瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性的一种分布类型。

移动通信网络中的信道模型建立在移动通信网络中，无线信道是连接移动用户设备与基站之间的重要媒介，它的好坏程度直接影响着通信质量、用户体验以及网络容量等方面。

作为无线通信领域的重要问题之一，“信道建模”在无线通信的研究中也显得格外重要。

本文将深入探讨移动通信网络中的信道模型建立，包括基本概念、分类、常用模型以及建立方法等方面。

一、基本概念1. 信道信道是指无线通信中传递信息的物理链路，它包括了传播介质、传播方式、利用频段以及信号传输方法等几个方面。

比如说，无线电波穿过空气传递到地面上的基站接收机，实现了信息的传递。

2. 信噪比信噪比是指有用信号和干扰和噪声信号的比值，也就是传输信号中有用信号的功率与噪声功率之比。

在无线通信中，信号的传输受到各种噪声和干扰的干扰，信号强度和噪声强度之间的比值越大，表明信号的质量越好。

3. 衰落衰落是指无线信号在传输过程中衰减失真的现象，也称为衰减。

衰落的原因是由于信号受到多径信号干扰、空气介质介电常数和导电率的波动、障碍物阻碍以及信号频率等因素所引起的。

二、分类移动通信网络中的信道模型可分为以下几类：1. 静态信道模型静态信道模型是指信道特性变化缓慢，信道状态可以假设不随时间变化或者随时间变化缓慢的信道模型。

静态信道模型最常用的就是大尺度衰落模型，通常可以用标准的理论模型进行描述。

这种信道模型适用于城市和农村等人口密度较低的区域。

2. 动态信道模型动态信道模型是指信道特性变化快，信道状态需要随时间变化而变化的信道模型。

动态信道模型适合于城市中的通信环境，尤其是在高速移动环境下。

三、常用模型1. 经典模型经典信道模型是根据充分的场强测量数据进行建模，通常需要进行大量的实地数据采集和处理。

在实际应用中，常用如大尺度衰落模型、多径衰落模型、特定场合衰落模型、生产无回波地形衰落模型等经典模型。

2. 统计模型统计信道模型是用概率统计方法处理信道随机性的模型。

常见的统计模型包括如Rayleigh分布模型和Rice分布模型等。

第6章衰落多径信道上的数字信号传输引言：着重讨论陆地移动通信中的信道及数字信号传输问题本章内容：6.1移动无线信道（课本14.1和14.2节）6.2在频率非选择性慢衰落信道上二进制数字信号传输（14.3节）6.3 多径衰落信道的分集技术（课本14.4节）6.4 在频率选择性慢衰落信道中数字信号传输（课本14.5节）6.1移动无线信道本节讨论：1.移动无线信道的特性(6.1.1)2.信道的数学描述（6.1.2）3.信道的分类（6.1.3）4.移动信道的模型（6.1.4）6.1.1 移动无线信道的特性（物理信道）引言：1.物理描述—①侧重于定性、概念性描述②侧重于说明信道对信号传输的影响（衰落）2.移动通信媒质（电磁波传播环境）移动无线通信所传送的信息是通过电磁波承载在空中传播来实现的。

电磁波传播的途径就是无线信道，这种信道是一种开放性信道。

电磁波的传播特性就决定了无线信道的特性。

而电磁波的传播特性与电磁波的传播机制有密切关系。

1.电磁波的传播机制▲最简单的情况－自由空间传播，即视距传播。

这是一种直射的传播机制。

例：卫星通信系统和微波通信系统的无线视距链路中。

电磁波在自由空间中22df传播路径损耗。

根据自由空间的路径损耗可以对视距无线链路进行设计。

▲移动通信系统中电磁波的传播环境（或通信媒质）比较复杂：基站天线：30～100米，移动台天线1～4米通信媒质：大气，地形，自然物，建筑物，天气等在移动通信系统中，电磁波的传播会遇到各种障碍物，同时移动台运动过程中电磁波的传播环境也在不断变化。

因此，在移动通信系统中，电磁波的传播机制通常不是自由空间的视距传播，而是反射(reflection)、绕射(diffraction)和散射(scattering)等三种基本的传播机制。

反射—当电磁波传播时遇到尺寸比波长λ大得多的物体表面时，会发生反射现象。

如地球表面、建筑物和墙壁表面都绘引起电磁波的反射。

绕射—当发射天线与接收天线之间存在密度比较大且尺寸比波长λ大的物体，就会在阻挡物的后面产生次级波，也就是说电磁波“绕过”障碍物继续传播，这种现象称为绕射。

6.1.4 移动信道的模型（多径衰落信道）一、时变线性滤波器模型及其响应1.带通系统分析 （1）离散多径信道：信道系数()n t α，即(,)n t ατ，时延()n t τ响应：()()(())(,)(())n n nn n nx t t s t t t s t t αταττ=-=-∑∑ （14-1-2）（2）连续多径信道：)(),,(t t ττα，即(,)t ατ表示在0时刻的冲激在τ时刻的响应。

响应：()(,)()x t t s t d ατττ∞-∞=-⎰ （14-1-6）2.等效低通分析 （1）离散多径由带通信道模型：其中()(,)n n t t αατ=为实函数，所以有 即得到等效低通模型为 所以得到：信道系数：2()()c n j f t n t e πτα-或2()(;)c n j f t n t e πτατ- （14-1-5） 响应：2()()()(())c n j f t l n l n nr t t e s t t πτατ-=-∑ （14-1-4）其中()(;)n n t t αατ@。

若令2()(;)()(())c n j f t n n nc t t e t πτταδττ-=-∑，则可见(;)c t τ是0时刻的冲激通过信道后在τ时刻上的响应。

（2）连续多径信道： 2()(;)(;)c j f t c t t eπττατ-= （14-1-8）响应：2()()(;)()(;)()c j f t l l l r t c t s t d t e s t d πττττατττ∞∞--∞-∞=-=-⎰⎰二、多径衰落信道的统计特性1.等效低通信道论冲激响应：即0时刻的冲激通过信道后在τ时刻上的响应。

离散多径：()(;)()(())n j t nn nc t t e t θταδττ-=-∑ 其中()2()n c n t f t θπτ= 连续多径：()(;)(;)j t c t t e θτατ-= 其中()2()c t f t θπτ=2.分析：(;)c t τ由许多时变随机向量组成幅度系数()n t α－随移动台运动而随机变化；相位偏移()n t θ－在[0,2π)内随机变化。

多径衰落模型多径衰落模型是用来描述无线信道中信号传播过程中的一种现象和特性的数学模型。

在无线通信中，信号会经过多个路径传播到接收端，每条路径上的信号会受到传播过程中的各种影响，导致信号强度的变化。

多径衰落模型通过考虑这些影响因素来模拟信号衰减过程，从而更准确地描述信号传播的特性。

首先，多径衰落模型考虑了信号传播过程中的多径效应。

在无线信道中，信号不仅会直接从发射端传播到接收端，还会通过其他路径进行反射、绕射、散射等传播方式到达接收端。

每个路径上的信号在传播过程中会受到不同的路径损耗和多普勒效应的影响，导致信号的衰减和频率偏移。

多径衰落模型通过考虑这些路径的存在，将信号传播过程中的影响因素进行建模，从而更准确地描述信号传播的过程。

其次，多径衰落模型考虑了信号的相关性。

在无线信道中，由于路径的不同长度和传播时间不同，不同路径上的信号会存在时延和相位差等差异。

因此，在接收端的时间域和频域上，信号的叠加和干扰会导致信号功率的变化。

多径衰落模型通过引入相关性参数来描述信号之间的相关性，从而能更准确地模拟信号衰减过程，使接收端能够更好地处理多个路径上的信号。

此外，多径衰落模型还考虑了信道中的噪声和干扰。

在无线信道中，由于天线的位置、环境的复杂性等因素，信道中常常存在信号的噪声和干扰。

这些噪声和干扰会对信号的衰减和传输质量产生影响。

多径衰落模型通过考虑噪声和干扰的统计特性，将其加入到信号传播的模型中，从而更准确地描述信号的传播过程和受到的影响。

最后，多径衰落模型还可以通过不同的数学方法和模拟技术来实现。

例如，常用的多径衰落模型有瑞利衰落模型和莱斯衰落模型。

瑞利衰落模型假设信道中不存在直达路径，并且路径衰落服从瑞利分布。

莱斯衰落模型则假设信道中存在直达路径，并且路径衰落服从莱斯分布。

这些模型通过数学方法和模拟技术将路径损耗、多普勒效应、相关性、噪声和干扰等因素进行建模，从而更真实地描述信号的传播过程。

总之，多径衰落模型是用来描述无线信道中信号传播过程中的一种现象和特性的数学模型。

信道频率损耗模型阴影模型衰落模型本文主要介绍无线通信中常用的四个模型：信道频率模型、损耗模型、阴影模型和衰落模型。

这些模型是对无线信号传输的描述，可用于无线电路设计、无线网络规划、信号覆盖预测等领域。

一、信道频率模型信道频率模型是描述无线信道频率特性的模型。

由于每个频率都有不同的传播特性，因此，无线信道的频率响应是需要建模的一个方面。

信道频率模型主要用于预测在不同频率（即不同带宽）上信道的性能和损失。

其中，常见的信道频率模型有两种：理想无限平坦频率响应模型和实际的有限频带响应模型。

理想的无限平坦频率响应模型假定无线信道对所有频率的信号响应相同，并无任何滚降和干扰。

这种模型主要用于在不同频谱范围内比较不同的无线网络方案，例如Wi-Fi和蜂窝无线电连接。

实际的有限带宽响应模型基于实际信道的复杂特性，由于加性白噪声和多径反射等，信号的响应会随着信号频率而发生变化。

这种模型更加接近实际情况，但是比起理想模型更加复杂。

二、损耗模型在无线通信系统中，有很多因素能够影响信号的传输质量，如空气介质、障碍物、雨雪、建筑物等。

而这些环境因素会因传输距离的不同而导致信号衰减，这就是所谓的信号损耗。

损耗模型主要被用来描述这种随距离而发生变化的信号弱化。

由于信号损耗涉及到多个因素，因此建立一个准确的信号损耗模型是必须的。

普遍采用的损耗模型包括路径损耗模型和自由空间传输损耗模型。

路径损耗模型考虑了多种影响信号强度的因素，包括距离、传播介质、障碍物、频率、传输功率等。

该模型描绘了信号强度沿着直线传输路径的弱化过程，并使用密集度函数表示环境因素对信号传输的影响。

自由空间传输损耗模型是另一种常见的损耗模型，它假定空气介质是完全透明的，没有任何干扰。

这种模型假设无线信号在没有障碍物的情况下沿着一条直线传播，其信号强度随着传输距离的平方根而减弱。

三、阴影模型阴影模型是一种经验模型，用于描述障碍物阻挡无线信号的效果。

在真实环境中，无线信号发射器和接收器之间存在很多干扰，包括建筑物、植被、地形等障碍物，因此阴影模型非常重要。

信道模型1. 引言信道模型是无线通信领域中的一个重要概念，它描述了信号在传输过程中受到的各种干扰和衰落情况。

了解信道模型可以帮助我们分析和设计无线通信系统，提高通信质量和可靠性。

本文将介绍信道模型的基本概念、常见类型以及相关应用。

2. 信道模型的基本概念信道模型是对无线通信中信号传输过程进行抽象和描述的数学模型。

在信道模型中，我们假设信号是在一定时间和空间上传播的，受到各种干扰和衰落影响。

2.1 信道衰落信道衰落是指信号在传输过程中功率的减小。

常见的原因包括自由空间路径损耗、多径效应、阴影衰落等。

衰落的强度可以通过信号的损失因子或路径损耗指数来描述。

2.2 信号干扰信号在传输过程中可能会受到外部干扰。

干扰可以分为同频干扰和异频干扰两种类型。

同频干扰是指接收信号受到同一频率其他信号的影响，而异频干扰是指接收信号受到其他频率信号的影响。

2.3 信噪比信噪比（Signal-to-Noise Ratio，SNR）是指接收信号与噪声信号的比值。

信噪比描述了信号与噪声的对比情况，是衡量信号质量的重要指标。

信噪比越大，表示噪声对信号的影响越小。

3. 常见的信道模型类型根据信道模型的特点和应用场景，可以将信道模型分为多径衰落信道模型、杂波信道模型和衰落信道模型等。

3.1 多径衰落信道模型多径衰落信道模型是描述由于多径效应引起的信号衰落的模型。

多径效应是指信号在传播过程中经历多个路径，每个路径的传播时间和损失不同，导致接收信号叠加和衰落。

3.2 杂波信道模型杂波信道模型是描述无线通信中受到底噪、窄带干扰和宽带干扰等影响的模型。

底噪是常态存在的背景噪声，干扰源包括其他系统的信号和自然界的噪声。

3.3 衰落信道模型衰落信道模型是描述信号受到大尺度和小尺度衰落的模型。

大尺度衰落由于信号传输距离、遮挡和反射等因素引起，而小尺度衰落由于多径效应引起。

4. 信道模型的应用信道模型在无线通信系统设计和性能评估中起着重要作用。

通过对信道模型的建模和仿真，可以评估系统的容量、覆盖范围和连接质量等性能指标。

3.1 单状态模型3.1.1 Rayleigh 模型在移动无线信道中，瑞利模型是常见的用于描述平坦衰落信号或独立多径分量接收包络统计时变特性的一种经典模型。

众所周知，两个正交的正态分布的随机过程之和的包络服从瑞利分布，即设X 和Y 为正态随机过程，则R=X+jY 的包络r =|R |则服从瑞利分布。

瑞利分布的概率密度函数（pdf ）为[24,27,28]：⎪⎩⎪⎨⎧<≥⎪⎪⎭⎫⎝⎛-=0,00,2exp )(222r r r r r p σσ (3-1)其中，][22r E =σ是包络检波之前的接收信号包络的时间平均功率。

R 的相位θ服从0到2π之间的均匀分布，即⎪⎩⎪⎨⎧≤≤=其他，020,21)(πθπθp (3-2)则接收信号包络不超过某特定值R 的累计概率分布函数（CDF ）为⎰⎪⎪⎭⎫⎝⎛--==≤=RR dr r p R r p R F 0222exp 1)()()(σ (3-3)图3-1所示为瑞利模型的概率密度函数曲线图。

1234567891000.10.20.30.40.50.60.7接收信号包络rp d f瑞利分布包络的概率密度曲线图图3-1 瑞利模型的概率密度函数曲线图3.1.2 Ricean 模型当接收端存在一个主要的静态（非衰落）信号时，如LOS 分量（在郊区和农村等开阔区域中，接收端经常会接收到的）等，此时接收端接收的信号的包络就服从莱斯分布。

在这种情况下，从不同角度随机到达的多径分量迭加在静态的主要信号上，即包络检波器的输出端就会在随机的多径分量上迭加一个直流分量。

当主要信号分量减弱后，莱斯分布就转变为瑞利分布。

莱斯分布的概率密度函数为：⎪⎩⎪⎨⎧<≥≥⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛+-=0,00,0,2exp )(202222r r C Cr I C r r r p σσσ （3-4）其中C 是指主要信号分量的幅度峰值，()0I 是0阶第一类修正贝赛尔函数。

156第六章小尺度衰落信道前面已经介绍无线信道的传播模型可分为大尺度（Large-Scale）传播模型和小尺度（Small-Scale）衰落两种[2]，三、四、五章已经介绍了大尺度传播。

所谓小尺度是描述短距离（几个波长）或短时间（秒级）内接收信号强度快速变化的；而移动无线信道的主要特征是多径，由于这些多径使得接收信号的幅度急剧变化，产生了衰落，因此，本章将介绍小尺度衰落信道，这对我们移动通信研究中传输技术的选择和数字接收机的设计尤为重要。

本章将先介绍小尺度的衰落和多径的物理模型和数学模型，使读者从概念上清楚地认识移动无线信道的主要特点，并建立一个统一的数学模型，为以后讨论各种模型奠定基础；接着将介绍移动多径信道的三组色散参数——时间色散参数(时延扩展，相关带宽)、频率色散参数(多普勒扩展，相关时间)、角度色散参数(角度扩展，相关距离)，为之后的信道分类奠定了基础；接下来介绍衰落信道的一阶包络统计特性、二阶统计特性，大量的实测数据表明，在没有直达路径的情况下（如市区），信道的包络服从瑞利分布，在有直达路径的情况下（如郊区），信号包络服从莱斯分布，因此，一阶包络统计特性主要介绍瑞利衰落分布和莱斯衰落分布，二阶统计特性主要介绍一组对偶参数——时间电平交叉率和平均衰落持续时间，简要介绍其他两组对偶参数——频域电平交叉率和平均衰落持续带宽，空间电平交叉率和平均衰落持续距离；在已经介绍了多径信道的三组色散参数之后，将介绍小尺度衰落信道相对应的不同分类。

6.1 衰落和多径6.1.1 衰落和多径的物理模型陆地移动信道的主要特征是多径传播。

传播过程中会遇到很多建筑物，树木以及起伏的地形，会引起能量的吸收和穿透以及电波的反射，散射及绕射等，这样，移动信道是充满了反射波的传播环境。

到达移动台天线的信号不是单一路径来的，而是许多路径来的众多反射波的合成。

由于电波通过各个路径的距离不同，因而各路径来的反射波到达时间不同，相位也就不同。

信道模型1. 介绍在通信系统中，信道模型是描述信号传递路径和信号传输过程中各种噪音和干扰影响的数学模型。

信道模型是通信系统设计和性能分析的基础之一，它能够帮助我们理解信号在传输过程中的变化和损耗，并确定合适的调制和解调方式以及信号处理策略。

2. 信道类型根据信道传输介质和信号传输方式的不同，信道可以分为以下几种类型：2.1 有线信道有线信道是通过铜线、光纤等有线介质传输信号的信道。

有线信道通常具有较低的信号损耗和较小的干扰，适用于高可靠性和高带宽要求的通信系统。

常见的有线信道模型包括直线模型、电缆模型和光纤模型等。

2.2 无线信道无线信道是通过空间传播信号的信道。

无线信道的特点是传播距离较远、传输速率较慢、受干扰和衰落影响较大。

无线信道的建模常常使用统计方法和几何方法，包括多径衰落模型、高斯白噪声模型、瑞利衰落模型等。

2.3 多径信道多径信道是指信号在传输路径上经历多次反射、折射和散射，导致多个信号在接收端同时到达的信道。

多径效应会导致信号的时延扩展和功率衰落，从而对通信系统的性能产生重大影响。

常见的多径信道模型有莱斯衰落模型、瑞利衰落模型和尼克尔森信道模型等。

2.4 补偿信道补偿信道是通过对信号进行加权、反向补偿等处理来消除信道传输中的干扰和失真的信道。

补偿信道主要用于降低信道带宽限制、抑制多径干扰和抵消非线性失真等。

常见的补偿信道模型有等化器模型、预编码模型和干扰对消模型等。

3. 信道建模方法信道建模的目的是通过数学模型描述信道的特性，以便进一步分析和优化通信系统。

信道建模方法通常可分为物理建模方法和统计建模方法两种。

3.1 物理建模方法物理建模方法是通过研究信道的物理过程和传输机制来建立信道模型。

物理建模方法需要考虑信号的传播路径、干扰噪声来源以及信道参数等因素，它可以提供较为准确的信道模型，但计算复杂度较高。

常用的物理建模方法包括环境建模、波动方程建模和传输线建模等。

3.2 统计建模方法统计建模方法是通过统计分析和概率模型来描述信道的随机特性。

6.1.4 移动信道的模型（多径衰落信道）一、时变线性滤波器模型及其响应1.带通系统分析2()Re[()c l j f t s t s t e π=2()Re[()]c l j f t t r t e π=（1）离散多径）（t 1α）（t 2α）（t 3α）（t 4α）（t 1τ）（t 2τ）（t 3τ）（t 4ττ信道：信道系数()n t α，即(,)n t ατ，时延()n t τ响应：()()(())(,)(())n n nn n nx t t s t t t s t t αταττ=-=-∑∑ （14-1-2）（2）连续多径信道：)(),,(t t ττα，即(,)t ατ表示在0时刻的冲激在τ时刻的响应。

响应：()(,)()x t t s t d ατττ∞-∞=-⎰ （14-1-6）2.等效低通分析(l s t ()l t );(t c τ（1）离散多径由带通信道模型：()()(())(,)(())n n n n nnx t t s t t t s t t αταττ=-=-∑∑其中()(,)n n t t αατ=为实函数，所以有22(())Re ()e Re ()(())e c c n j f t j f t t n n l l nr t t s t t ππτατ-⎡⎤⎡⎤=-⎣⎦⎣⎦∑即得到等效低通模型为2()()()e (())c n j f t n n l l nr t t s t t πτατ-=-∑所以得到：信道系数：2()()c n j f t n t e πτα-或2()(;)c n j f t n t e πτατ- （14-1-5）响应：2()()()(())c n j f t l n l n nr t t e s t t πτατ-=-∑ （14-1-4）其中()(;)n n t t αατ 。

若令2()(;)()(())c n j f t n n nc t t e t πτταδττ-=-∑，则()(;)()l l r t c t s t d τττ∞-∞=-⎰2()()(())()c n j f t nn l nt e t s t d πταδττττ∞--∞=--∑⎰2()()(())c n j f t n l n nt e s t t πτατ-=-∑可见(;)c t τ是0时刻的冲激通过信道后在τ时刻上的响应。

6.3 多径衰落信道的分集技术（课本14.4节）6.3.1 分集技术及其性能本节讨论：1、分集的必要性2、分集的原理与方法3、合并的方法4、分集性能的评价一、引言—分集的必要性必要性：抗信道的快衰落1.●大尺度衰落●小尺度衰落●噪声与干扰瑞利衰落信道：接收信号电平（或SNR）波动范围达30～40 dB。

在该信道上的二进制数字传输性能远劣于与其平均SNR相同而无衰落时的性能。

（可参见p.313图14-3-2中m=1瑞利衰落与m=∞无衰落的平均误比特率比较）2. 抗（快）衰落的办法发端：抗衰落的调制技术、编码技术、提高发送电平等收端：分集接收技术二、分集的原理与方法1.分集的原理发送：同样的信息信道：划分为L个相互统计独立的衰落信道（按频率、时间、空间等划分）接收：合并技术（最大比合并，等增益合并，选择性合并）接收机对L的信道的接收信号进行合并，可提高接收信号电平(SNR)。

（注：分集与复用是相反的技术：1）分集重在提高可靠性，复用关注有效性；2）分集是各个信道上发同样的信号，产生复本，复用是各个子信道上传不同的信号。

）分集技术抗衰落的原理可从两个方面解释：●衰落概率解释—。

（注：设每个信道衰落的概率为p, 则L个信道同时衰落的概率为L p p这里衰落指的是信道衰减很大的意思。

） 衰落信噪比解释—从瑞利衰落的信噪比形式看：1()exp b b b b p γγγγ⎛⎫- ⎪⎝⎭= (0max (b b γγ==当时）小的概率大） （指数衰减函数）分集的作用是：通过分集合并技术，修正无分集时()b p γ，使()b p γ↓小，而()b p γ↑大。

)(b p γ b γ2.分集的方法（划分不同独立信道的方法）有三种基本方法：空间分集，频率分集，时间分集。

（1） 空间分集不相关衰落所要求的空间间隔距离为：D λθ=其中，λ为载波波长，θ为天线波束张角（扩散角）。

【例1】短波通信：15θ=o o～，则10~100D λ≥。