昌平区2016-2017学年第一学期高三年级期末考试质量检测数学试卷(文科)

昌平区2015－2016学年第一学期高三年级期末质量抽测 数学试卷（理科）（满分150分，考试时间 120分钟）2016.1考生须知：1． 本试卷共6页，分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分.2． 答题前考生务必将答题卡上的学校、班级、姓名、考试编号用黑色字迹的签字笔填写. 3．答题卡上第I 卷(选择题)必须用2B 铅笔作答，第II 卷(非选择题)必须用黑色字迹的签字笔作答，作图时可以使用2B 铅笔.请按照题号顺序在各题目的答题区内作答，未在对应的答题区域内作答或超出答题区域作答的均不得分.4． 修改时，选择题部分用塑料橡皮擦涂干净，不得使用涂改液.保持答题卡整洁，不要折叠、折皱、破损.不得在答题卡上做任何标记.5． 考试结束后，考生务必将答题卡交监考老师收回，试卷自己妥善保存.第Ⅰ卷（选择题 共40分）一、选择题(本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．)（1）若集合{}2,1,0,1,2Α=--，{}2|1Βx x =>，则=ΑΒA ．{|11}x x x <->或B ．{}2,2-C ．{}2D ．{0}(2) 下列函数中，在区间(0,)+∞上为增函数的是A ．y = B. 1y x =C. 1()2xy = D. 12log y x = (3) 已知两点(0,0),(2,0)O A -，以线段OA 为直径的圆的方程是 A ．22(1)4x y -+= B ．22(1)4x y ++= C ．22(1)1x y -+= D ．22(1)1x y ++= (4) 在ABC ∆中，3,2,3ac B π===，则b =A ．19B ．7C ． D俯视图侧（左）视图正（主）视图⑸ 某三棱锥的三视图如图所示，则该三 棱锥四个面的面积中最大的是A.B. 3C.D.（6）已知函数f (x ) 的部分对应值如表所示. 数列{}n a 满足11,a =且对任意*n ∈N ，点1(,)n n a a +都在函数()f x 的图象上，则2016a 的值为A . 1 B.2 C. 3 D. 4⑺ 若,x y 满足0,30,30,y x y kx y ≥⎧⎪-+≥⎨⎪-+≥⎩且2z x y =+的最大值为4，则k 的值为A ．32-B ． 32C ．23-D ．23（8）某大学进行自主招生时，需要进行逻辑思维和阅读表达两项能力的测试.学校对参加测试的200名学生的逻辑思维成绩、阅读表达成绩以及这两项的总成绩进行了排名.其中甲、乙、丙三位同学的排名情况如下图所示：逻辑思维成绩排名200200阅读表达成绩排名O 丙逻辑思维成绩排名总成绩排名200200O 甲乙下列叙述一定正确的是A ．甲同学的阅读表达成绩排名比他的逻辑思维成绩排名更靠前B ．乙同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前C ．甲、乙、丙三位同学的逻辑思维成绩排名中，甲同学更靠前D ．乙同学的总成绩排名比丙同学的总成绩排名更靠前第Ⅱ卷（非选择题 共110分）二、填空题（本大题共6小题，每小题5分，共30分）（9）在261(2)x x-的展开式中，常数项是 （用数字作答）.（10）双曲线22:1916x y C -=的渐近线方程为__________________；某抛物线的焦点与双曲线C 的右焦点重合，则此抛物线的标准方程为____________. （11）执行如图所示的程序框图， 输出的S 值为_______.PDCBA 步数(千步)（12）将序号为1，2，3，4的四张电影票全部分给3人，每人至少一张. 要求分给同一人的两张电影票连号，那么不同的分法种数为________________.（用数字作答）（13）如图，在矩形ABCD 中，3DP PC =，若,PB mAB nAD =+则m =______;n =_________.（14）已知函数2()|3|,.f x x x x =-∈R 若方程()|1|0f x a x -+=恰有4个互异的实数根，则实数a 的取值范围是_____________________．三、解答题(本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．)（15）（本小题满分13分）已知函数2()3sin(π)cos cos f x x x x --．（I ） 求函数()f x 的最小正周期； （II ）求函数()f x 的单调递减区间．(16)（本小题满分13分）小王为了锻炼身体，每天坚持“健步走”, 并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图（图1）及相应的消耗能量数据表（表1）如下.图1 表1（Ⅰ）求小王这8天 “健步走”步数的平均数；（Ⅱ）从步数为16千步，17千步，18千步的几天中任选2天，设小王这2天通过健步走消耗的“能量和”为X ，求X 的分布列.P MD CBA（17）（本小题满分14分）在四棱锥P ABCD -中，平面PAD ⊥平面ABCD ，PAD ∆为等边三角形,12AB AD CD ==,AB AD ⊥,//AB CD ,点M 是PC 的中点． （I ）求证://MB 平面PAD ； （II ）求二面角P BC D --的余弦值； （III ）在线段PB 上是否存在点N ，使得DN ⊥平面PBC ？若存在,请求出PNPB的值；若不存在,请说明理由.（18）（本小题满分13分）已知函数()()2ln 1f x x =+.（Ⅰ）若函数()f x 在点()()00P x f x ，处的切线方程为2y x =，求切点P 的坐标；（Ⅱ）求证：当[0,e 1]x ∈-时，()22f x x x ≥-；（其中e 2.71828=⋅⋅⋅） （Ⅲ）确定非负实数．．．．a 的取值范围，使得()()220,x f x x a x ∀≥≥-成立.（19）（本小题满分13分）已知椭圆C 2222:1(0)x y a b a b +=>>点1)2在椭圆C 上．直线l 过点(1,1)，且与椭圆C 交于A ，B 两点，线段AB 的中点为M ．（I ）求椭圆C 的方程；（Ⅱ）点O 为坐标原点，延长线段OM 与椭圆C 交于点P ，四边形OAPB 能否为平行四边形？若能，求出此时直线l 的方程，若不能，说明理由．（20）（本小题满分14分）对于任意的*n ∈N ，记集合{1,2,3,,}n E n =⋅⋅⋅，,n n n P x x a E b E ⎧⎫==∈∈⎨⎬⎩⎭.若集合A 满足下列条件：①n A P ⊆；②12,x x A ∀∈，且12x x ≠，不存在*k ∈N ，使212x x k +=，则称A 具有性质Ω.如当2n =时，2{1,2}E =，2{1,P =.122,x x P ∀∈，且12x x ≠，不存在*k ∈N ，使212x x k +=，所以2P 具有性质Ω. (Ⅰ) 写出集合35,P P 中的元素个数，并判断3P 是否具有性质Ω. （Ⅱ）证明：不存在,A B 具有性质Ω，且A B =∅，使15E A B =．（Ⅲ）若存在,A B 具有性质Ω，且AB =∅，使n P A B =，求n 的最大值.昌平区2015－2016学年第一学期高三年级期末质量抽测数学试卷参考答案及评分标准 （理科） 2016.1二、选择题(本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合二、填空题（本大题共6小题，每小题5分，共30分）（9）60 （10）24;203y x y x =±= （11） 52（12）18 （13）1;14- （14） (0,1)(9,)+∞ 三、解答题(本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．) (15)（本小题满分13分） 解：（I ）2()3sin cos cos f x x x x-311sin 2cos 2222x x -- π1sin(2)62x --所以 最小正周期2π2ππ.2T ω …………………………..7分(II) 由ππ3π2π22π,,262k x k k ≤≤∈Z得π5πππ,.36k x k k ≤≤∈Z ………………………11分所以函数()f x 的单调递减区间是π5π[π,π],.36k k k ∈Z ……………13分(16)（本小题满分13分）解: (I) 小王这8天 “健步走”步数的平均数为16317218119217.258⨯+⨯+⨯+⨯=（千步）. …………………………..4分（II ）X 的各种取值可能为800，840，880，920.23261(800)5C P X C ===,1132262(840),5C C P X C ===112312264(880),15C C C P X C +=== 1121262(920),15C C P X C === X 的分布列为：…………………………..13分 （17）（本小题满分14分）C（Ⅰ）证明:取PD 中点H ,连结,MH AH . 因为 M 为PC 中点 ,所以 1//,2HM CD HM CD =.因为1//,2AB CD AB CD =. 所以//AB HM 且AB HM =. 所以四边形ABMH 为平行四边形,所以 //BM AH .因为 BM PAD ⊄平面,AH ⊂平面PAD ,所以//BM 平面PAD . …………………………..4分（Ⅱ） 取AD 中点O ,连结.PO因为 PA PD =, 所以PO AD ⊥.因为 平面PAD ⊥平面ABCD , 平面PAD 平面ABCD AD =,PO ⊂平面PAD ,所以PO ABCD ⊥平面.取BC 中点K ,连结OK ,则//.OK AB 以O 为原点,如图建立空间直角坐标系, 设2,AB =则(1,0,0),(1,2,0),(1,4,0),(1,0,0),A B C D P --(2,2,0),(1,2,BC PB =-=.平面BCD的法向量OP =, 设平面PBC 的法向量(,,)n x y z =,由0,0,BC n PB n ⎧⋅=⎪⎨⋅=⎪⎩得220,20.x y x y -+=⎧⎪⎨+=⎪⎩令1x =，则n =.15cos ,5||||OP n OP n OP n ⋅<>==. 由图可知，二面角P BCD --是锐二面角， 所以二面角P BC D --. …………………………..9分 （Ⅲ） 不存在. 设点(,,)N x y z ,且,[0,1]PNPBλλ=∈ ,则,PN PB λ=所以(,,(1,2,x y z λ=.则,2,.x y z λλ⎧=⎪=⎨⎪=⎩所以(,2)N λλ, (1,2)DN λλ=+.若 DN PBC ⊥平面,则//DN n , 即12λλ+==，此方程无解, 所以在线段PB 上不存在点N ,使得DN PBC ⊥平面. …………………………..14分（18）（本小题满分13分）（Ⅰ）解：定义域为(1,)-+∞，()2'1f x x =+. 由题意，()0'2f x =，所以()00,00x f ==，即切点P 的坐标为(0,0). ………3分 （Ⅱ）证明：当[0,e 1]x ∈-时，()22f x x x ≥-，可转化为 当[0,e 1]x ∈-时，()220f x x x -+≥恒成立.设()2()2g x f x x x =-+，所以原问题转化为当[0,e 1]x ∈-时，()min 0g x ≥恒成立.所以2242'()2211x g x x x x -=-+=++.令'()0g x =，则1x =（舍），2x 所以()g x ，'()g x 变化如下：因为()(0)000g f =-=，2(e 1)2(e 1)2(e 1)2(e 1)(3e)0g -=--+-=+-->， 所以min ()0g x =.当[0,e 1]x ∈-时，()22f x x x ≥-成立. ………………..8分 （Ⅲ）解：()()20,2x f x a x x ∀≥≥-，可转化为当0x ≥时，()()220f x a x x--≥恒成立.设()()2()2h x f x a x x =--，所以222(1)'()2211ax a h x a ax x x +-=-+=++. ⑴当0a =时，对于任意的0x ≥，2'()01h x x =>+， 所以()h x 在[0,)+∞上为增函数，所以()min ()00h x h ==， 所以命题成立.当0a >时，令'()0h x =，则210ax a +-=，⑵当10a -≥，即01a <≤时，对于任意的0x ≥，'()0h x >， 所以()h x 在[0,)+∞上为增函数，所以()min ()00h x h ==， 所以命题成立.⑶当10a -<，即1a >时，则1x =20x ==. 所以()h x ，'()h x 变化如下：因为()min 2()()00h x h x h =<=， 所以，当0x ≥时，命题不成立.综上，非负实数a 的取值范围为[0,1]. …………………………..13分（19）（本小题满分13分）解：（I ）由题意得22222311,4.c e a ab a bc ⎧==⎪⎪⎪+=⎨⎪⎪=+⎪⎩解得224,1a b ==. 所以椭圆C 的方程为22 1.4x y += …………………………..5分 （Ⅱ）四边形OAPB 能为平行四边形．法一：（1）当直线l 与x 轴垂直时，直线l 的方程为1x = 满足题意；（2）当直线l 与x 轴不垂直时，设直线:l y kx m =+，显然0,0k m ≠≠.11(,)A x y ，22(,)B x y ，(,)M M M x y ．将y kx m =+代入22 1.4x y +=得222(41)8440k x kmx m +++-=， 2221228(8)4(41)(44)0,.41km km k m x x k -=-+->+=+ 故1224241M x x km x k +==-+， 241M M m y kx m k =+=+．于是直线OM 的斜率14M OM M y k x k==-，即14OM k k ⋅=-． 由直线:l y kx m =+(0,0)k m ≠≠，过点(1,1)，得1m k =-，因此24(1)41M k k x k -=+． OM 的方程为14y x k=-．设点P 的横坐标为P x ．由221,41,4y x k x y ⎧=-⎪⎪⎨⎪+=⎪⎩得2221641P k x k =+，即P x =． 四边形OAPB 为平行四边形当且仅当线段AB 与线段OP 互相平分，即2P M x x =．于是24(1)241k k k -=⨯+．由0k ≠，得35,.88k m ==满足0.> 所以直线l 的方程为3588y x =+时，四边形OAPB 为平行四边形． 综上所述：直线l 的方程为3588y x =+或1x = . ………………………….13分 法二：（1）当直线l 与x 轴垂直时，直线l 的方程为1x = 满足题意；（2）当直线l 与x 轴不垂直时，设直线:l y kx m =+，显然0,0k m ≠≠，11(,)A x y ，22(,)B x y ，(,)M M M x y ．将y kx m =+代入22 1.4x y +=得222(41)8440k x kmx m +++-=， 2221228(8)4(41)(44)0,.41km km k m x x k -=-+->+=+ 故1224241M x x km x k +==-+， 241M M m y kx m k =+=+. 四边形OAPB 为平行四边形当且仅当线段AB 与线段OP 互相平分，即2,2.P M P Mx x y y =⎧⎨=⎩． 则2222()()82114441km m k k -++=+. 由直线:l y kx m =+(0,0)k m ≠≠，过点(1,1)，得1m k =-. 则2222(164)(1))1(41k k k +-+=， 则2(41)(83)0k k +-= .则35,.88k m == 满足0.> 所以直线l 的方程为3588y x =+时，四边形OAPB 为平行四边形． 综上所述：直线l 的方程为3588y x =+或1x = . …………………………..13分（20）（本小题满分14分）(Ⅰ) 解：集合35,P P 中的元素个数分别为9，23，3P 不具有性质Ω. ……………..6分 （Ⅱ）证明：假设存在,A B 具有性质Ω，且AB =∅，使15E A B =．其中15{1,2,3,,15}E =⋅⋅⋅. 因为151E ∈，所以1A B ∈，不妨设1A ∈．因为2132+=，所以3A ∉，3B ∈．同理6A ∈，10B ∈，15A ∈．因为21154+=，这与A 具有性质Ω矛盾．所以假设不成立，即不存在,A B 具有性质Ω，且A B =∅，使15E A B =.…..10分（Ⅲ）因为当15n ≥时，15n E P ⊆，由（Ⅱ）知，不存在,A B 具有性质Ω，且A B =∅，使n P A B =．若14,n =当1b =时，1414x x a E E ⎧⎫=∈=⎨⎬⎩⎭，取{}11,2,4,6,9,11,13A =，{}13,5,7,8,10,12,14B =，则11,A B 具有性质Ω，且11A B =∅，使1411E A B =． 当4b =时，集合14x x a E ⎧⎫=∈⎨⎬⎩⎭中除整数外，其余的数组成集合为13513{,,,,}2222⋅⋅⋅，令215911{,,,}2222A =，23713{,,}222B =，则22,A B 具有性质Ω，且22A B =∅，使2213513{,,,,}2222A B ⋅⋅⋅=． 当9b =时，集14x x a E ⎧⎫=∈⎨⎬⎩⎭中除整数外，其余的数组成集合12457810111314{,,,,,,,,,}3333333333，令31451013{,,,,}33333A =，32781114{,,,,}33333B =．则33,A B 具有性质Ω，且33A B =∅，使3312457810111314{,,,,,,,,,}3333333333A B =．集合1414,,1,4,9C x x a E b E b ⎧⎫==∈∈≠⎨⎬⎩⎭中的数均为无理数，它与14P 中的任何其他数之和都不是整数，因此，令123A A A A C =，123B B B B =，则A B =∅，且14P A B =． 综上，所求n 的最大值为14. ……………..14分。

2017昌平区高三（上）期末数学（文科）一、选择题（本大题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.）1．（5分）设全集U={1，2，3，4，5，6}，A={3，4}，B={2，4，5}，则（∁U A）∩B=（）A．{1，2，4，5，6}B．{2，3，4，5}C．{2，5}D．{1，6}2．（5分）已知直线3x+（1﹣a）y+1=0与直线x﹣y+2=0平行，则a的值为（）A．4 B．﹣4 C．2 D．﹣23．（5分）执行如图所示的程序框图，若输入的x值为1，则输出的k值为（）A．3 B．4 C．5 D．64．（5分）下列四个函数中，在其定义域上既是奇函数又是单调递增函数的是（）A．y=e x B．y=log2x C．y=sinx D．y=x35．（5分）在平行四边形ABCD中，若，则平行四边形ABCD是（）A．矩形B．梯形C．正方形D．菱形6．（5分）一个几何体的三视图如图所示，则这个几何体的直观图为（）A．B．C．D．7．（5分）已知直线m，n和平面α，且m⊥α．则“n⊥m”是“n∥α”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件8．（5分）甲袋中有16个白球和17个黑球，乙袋中有31个白球，现每次任意从甲袋中摸出两个球，如果两球同色，则将这两球放进丙袋，并从乙袋中拿出一白球放回甲袋；如果两球不同色，则将白球放进丙袋，并把黑球放回甲袋．那么这样拿次后，甲袋中只剩一个球，这个球的颜色是（）A．16，黑色B．16，白色或黑色C．32，黑色D．32，白色二、填空题（本大题共6小题，每小题5分，共30分.）9．（5分）已知i为虚数单位，则复数i（1﹣i）=．10．（5分）已知数列{a n}的前n项和为S n，且，则a3=．11．（5分）三个数中最大的数是．12．（5分）在△ABC中，，则∠A=．13．（5分）已知双曲线的一条渐近线的倾斜角为，则双曲线的渐近线的方程为；该双曲线的离心率为．14．（5分）若函数①当a=2时，若f（x）=1，则x=；②若f（x）的值域为[0，2]，则a的取值范围是．三、解答题（本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.）15．（13分）已知函数f（x）=sin2x+2cos2x﹣1．（Ⅰ）求f（x）的最小正周期：（Ⅱ）求f（x）在区间[﹣，]上的最大值和最小值．16．（13分）已知{a n}是等差数列，{b n}是正项的等比数列，且a1=b1=2，a5=14，b3=a3．（Ⅰ）求{a n}、{b n}的通项公式；（Ⅱ）求数列{a n}中满足b4＜a n＜b6的各项的和．17．（14分）昌平区在滨河公园举办中学生冬季越野赛．按年龄段将参赛学生分为A，B，C三个组，各组人数如下表所示．组委会用分层抽样的方法从三个组中选出6名代表．（I）求A，B，C三个组各选出代表的个数；（II）若从选出的6名代表中随机抽出2人在越野赛闭幕式上发言，求这两人来自同一组的概率P1；（III）若从所有参赛的300名学生中随机抽取2人在越野赛闭幕式上发言，设这两人来自同一组的概率为P2，试判断P1与P2的大小关系（不要求证明）．18．（13分）在三棱锥P﹣ABC中，PA⊥平面ABC，AB=AC=2，BC=2，M，N分别为BC，AB中点．（I）求证：MN∥平面PAC（II）求证：平面PBC⊥平面PAM（III）在AC上是否存在点E，使得ME⊥平面PAC，若存在，求出ME的长，若不存在，请说明理由．19．（13分）已知函数f（x）=lnx﹣mx（m＞0）．（I）若m=1，求曲线y=f（x）在点（1，f（1））处的切线方程；（II）求函数f（x）的最大值g（m），并求使g（m）＞m﹣2成立的m取值范围．20．（14分）已知椭圆C：=1（a＞b＞0）的左右焦点分别为F1，F2，且经过点P（0，），离心率为，过点F1的直线l与直线x=4交于点A（I）求椭圆C的方程；（II）当线段F1A的垂直平分线经过点F2时，求直线l的方程；（III）点B在椭圆C上，当OA⊥OB，求线段AB长度的最小值．参考答案与试题解析一、选择题（本大题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.）1．【解答】∵U={1，2，3，4，5，6}，A={3，4}，B={2，4，5}，∴∁U A={1，2，5，6}，则（∁U A）∩B={2，5}，故选：C2．【解答】可得直线x﹣y+2=0的斜率为1，由于直线平行，故有斜率相等，故可得=1，解得a=4故选：A3．【解答】若输入x=1．则第一次，x=1+5=6，不满足条件，x＞23，k=1，第二次，x=6+5=11，不满足条件，x＞23，k=2，第三次，x=11+5=16，不满足条件，x＞23，k=3，第四次，x=16+5=21，不满足条件，x＞23，k=4，第五次，x=21+5=26，满足条件，x＞23，程序终止，输出k=4，故选：B4．【解答】A．y=e x是非奇非偶函数，不满足条件．B．y=log2x是非奇非偶函数，不满足条件．C．y=sinx是奇函数，在定义域上不是单调函数，不满足条件．D．y=x3是奇函数，定义域上单调递增，满足条件．故选：D5．【解答】由，平方得2﹣2•+2=2+2•+2，得得•=0，即得⊥，则平行四边形ABCD是矩形，故选：A6．【解答】由已知的三视图可得：该几何体是一个以俯视图为底面的四棱锥，而且有一侧棱垂直与底面，结合俯视图，可知B满足，故选B．7．【解答】当m⊥α时，若n⊥m，则n∥α或n⊂α，即充分性不成立，若n∥α，则n⊥m成立，即“n⊥m”是“n∥α”的必要不充分条件，故选：B8．【解答】由题意知，每摸球一次后，甲袋中的球减少一个，∵甲袋中原有16个白球和17个黑球，∴当甲袋中只剩一个球时，摸球次数为32．当每次取走两个黑球时，甲袋中黑球减少2个，白球个数增加1个，当每次取走两个球中有白球时，甲袋中黑球个数不变，白球个数减少一个，由此循环，当摸球31次后，甲袋中还剩两个球，且这两球不同色，∴当摸球32次后甲袋中只剩一个黑球．故选：C．二、填空题（本大题共6小题，每小题5分，共30分.）9．【解答】复数i（1﹣i）=i+1，故答案为：1+i．10．【解答】∵数列{a n}的前n项和为S n，且，∴a3=S3﹣S2=（9+3）﹣（4+2）=6．故答案为：6．11．【解答】∵e﹣2∈（0，1），＞1，ln2∈（0，1），因此三个数中最大的数是．故答案为：．12．【解答】由题意：已知，由正弦定理=，则有sinC=∵0°＜C＜135°∴C=30°则A=180°﹣30°﹣45°=105°故答案为：105°13．【解答】∵一条渐近线的倾斜角为，∴渐近线的斜率为k=tan=，∴双曲线的渐近线的方程为y=±x，∴=，∴e===，故答案为：，．14．【解答】函数y=2﹣x （﹣1≤x＜1）的值域为（，2]，函数y=lnx （1≤x≤a）的值域为：[0，lna]①当a=2时，若f（x）=1，即2﹣x =1，则x=0②若f（x）的值域为[0，2]，≤lna≤2，则a的取值范围是．故答案为：0，．三、解答题（本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.）15．【解答】（Ⅰ）∵f（x）===，∴ω=2，∴f（x）的最小正周期为．（Ⅱ）∵，∴．于是，当时，；当，．16．【解答】（Ⅰ）设等差数列{a n}的公差为d．因为a1=2，a5=14，所以a1+4d=14．所以d=3．所以a n=3n﹣1．所以b3=a3=8．因为b1=2，因为，所以q2=4．因为b n＞0，所以q=2．所以．…（6分）（Ⅱ）因为b4＜a n＜b6，即24＜3n﹣1＜26，所以，n∈N*．即n=6，7，8， (21)所以满足b4＜a n＜b6的各项的和为a6+a7+…+a21=S21﹣S5== =632．…（13分）17．【解答】（I）因为样本容量与总体容量的比是，所以A，B，C三个组各选出的代表的数量分别为：．所以A，B，C三个组各选出的代表的个数分别为2，3，1．…（4分）（II）设来自A，B，C三个组的代表分别为a1，a2，b1，b2，b3，c．则从6名代表中任意取出两人的所有结果所构成的基本事件空间：Ω={（a1，a2），（a1，b1），（a1，b2），（a1，b3），（a1，c），（a2，b1），（a2，b2），（a2，b3），（a2，c），（b1，b2），（b1，b3），（b1，c），（b2，b3），（b2，c），（b3，c）}，共15个基本事件．记事件D=“抽出的两个代表来自同一组”．则D={（a1，a2），（b1，b2），（b1，b3），（b2，b3）}，共4个基本事件．所以这两名代表来自同一组的概率．…（11分）（III）P2＞P1．…（14分）18．【解答】（I）证明：因为M，N分别为BC，AB中点，所以MN∥AC．因为MN⊄平面PAC，AC⊂平面PAC，所以MN∥平面PAC．…（4分）（II）证明：因为PA⊥平面ABC，BC⊂平面ABC，所以PA⊥BC．因为AB=AC=2，M为BC的中点，所以AM⊥BC．因为AM∩PA=A，所以BC⊥平面PAM．因为BC⊂平面PBC，所以平面PBC⊥平面PAM．…（8分）（III）解：存在．过点M作ME⊥AC，交AC于点E，因为PA⊥平面ABC，BC⊂平面ABC，所以PA⊥ME．因为ME⊥AC，AC∩PA=A，所以ME⊥平面PAC．因为在△ABC中，AB=AC=2，BC=2，M为BC的中点，所以ME=．…（13分）19．【解答】（I）若m=1，则f（x）=lnx﹣x．所以．所以f'（1）=0，f（1）=﹣1．所以曲线y=f（x）在点（1，f（1））处的切线方程为y=﹣1．…（5分）（II）因为，当时，f'（x）＞0；时，f'（x）＜0．所以f（x）在上单调递增；在上单调递减．所以f（x）的最大值．g（m）＞m﹣2，即g（m）﹣（m﹣2）＞0．．设h（m）=g（m）﹣（m﹣2）=﹣lnm﹣m+1．因为，所以h（m）在（0，+∞）上单调递减．又因为h（1）=0所以当0＜m＜1时，h（m）＞h（1）=0．所以m取值范围为（0，1）．…（13分）20．【解答】（I）由解得所以椭圆C的方程为+=1．（II）法一：设A（4，y），F1（﹣2，0），因为线段F1A的垂直平分线经过点F2，所以|F1F2|=|F2A|．由2c=4=，解得y=±2．所以直线l的方程为y=±（x+2）．（II）法二设过点F1（﹣2，0）的直线l的斜率为k，显然k存在．则直线l的方程为y=k（x+2）．所以A（4，6k）．设AF1的中点P（x0，y0）．则．所以P（1，3k）．因为PF2⊥F1A，所以．所以．所以直线l的方程为y=±（x+2）．（III）点B在椭圆C上，设B（m，n），n∈[﹣，0）∪（0，]，A（4，y）．因为OA⊥OB，所以，即4m+ny=0．因为点B在椭圆C上，所以+=1，所以|AB|2=（m﹣4）2+（n﹣y）2=m2﹣8m+16+n2﹣2ny+y2=m2﹣8m+16+n2+8m+y2，=m2+16+n2+y2=m2+16+n2+（）2，=9（1﹣）+16+n2+，=﹣﹣设t=n2，t∈（0，5]设．因为，所以g（t）在（0，5]上单调递减．所以当t=5，即时，|AB|min=．第11页共11 页。

昌平区第一学期高三期末考试数学参考答案（文科）二、填空题(本大题共6小题，每小题5分，共30分．)（9）（0，3±） (10) 600,32 (11) 4,10(12) 3 (13) ①和④ (14) [3,)+∞三、解答题(本大题共6小题，共80分)（1５）(本小题满分13分)解：(I),ABC ∆在中由正弦定理得：2sin ,2sin ,2sin a R A b R B c R C ===代入 (2)cos cos a c B b C -=整理得：2sin cos sin cos sin cos A B B C C B =+..…3分 即：2sin cos sin()sin A B B C A =+=，在三角形中，sin 0A >，2cos 1B =，∵∠Ｂ是三角形的内角，∴B=60°. ……………………………………………… 6分(II),ABC ∆在中由余弦定理得：2222cos b a c ac B =+-⋅2()22cos a c ac ac B =+--⋅4b a c =+=将代入整理得3ac = …………………………………………10分故13sin sin 6022ABC S ac B ∆==︒= …………………………………………… 13分 （16）(本小题满分14分)解：(I)设数列{}n a 的公差为d ，则3410a a d d =-=-，642102a a d d =+=+， 1046106a a d d =+=+ ……2分由3610a a a ，，成等比数列得23106a a a =，……………………………………………… 4分即2(10)(106)(102)d d d -+=+，整理得210100d d -=， 解得0d =或1d =． ∵0d ≠,∴1d = ……………………………………………… 6分141310317,(1)6n a a d a a n d n =-=-⨯==+-=+， 于是2012019202S a d ⨯=+207190330=⨯+=．…………………………………… 9分 (II) 11111(6)(7)(6)(7)n n a a n n n n +==-++++ ……………………………………11分 111111()()...()788967n T n n =-+-++-++=1177n -+ ……………………14分 （17）(本小题满分14分)解:(I)证明：由已知D 在平面ABC 上的射影O 恰好在AB 上, ∴DO ⊥平面ABC ，∴AO 是AD 在平面ABC 上的射影． …………………………………… 2分 又∵BC ⊥AB ，∴BC ⊥AD ． …………………………………… 4分 (II)解：由(1)得AD ⊥BC ，又AD ⊥DC又BC ∩DC=C ，∴AD ⊥平面BDC又∵BD 平面ADB ，∴AD ⊥BD ， ……………………………………6分 在R T ⊿ABD 中，由已知AC = 2，得2=AB ，AD = 1，∴BD = 1, ∴BD = AD,∴O 是AB 的中点. ……………………………………8分 (III)解：过D 作DE ⊥AC 于E ，连结OE ，∵DO ⊥平面ABC ，∴O E 是DE 在平面ABC 上的射影．∴OE ⊥AC∴∠DEO 是二面角D －AC －B 的平面角， …………………………………11分22=DO 且36sin 23AD DC DO DE DEO AC DE ==∴∠==g 即二面角D －AC －B 的正弦值为63 ……………………………………14分 （18）(本小题满分13分)解：(I)2'()663f x x ax b =++ ……………………………………2分 ()12f x x x ==由函数在及时取得极值,得'(1)0,'(2)0,f f ==即6630,3, 4.241230,a b a b a b ++=⎧=-=⎨++=⎩解得 ……………………………………5分 (II)由(1)知322()29128,'()618126(1)(2).f x x x x c f x x x x x =-++=-+=--(0,1)'()0;(1,2)'()0;(2,3)'()0.x f x x f x x f x ∈>∈<∈>当时,当时,当时, …………8分 1()(1)58.(0)8,(3)98,[0,3]()(3)98.x f x f c f c f c x f x f c ==+==+∈=+当时,取得极大值又则当时,的最大值为11分 22[0,3],(),19,(,1)(9,).x f x c c c c c c ∈<<<->-∞-⋃+∞因为对任意的有恒成立所以9+8,解得或即的取值范围是13分（19）(本小题满分13分)解（I ）设“设抛掷一颗骰子掷出的点数为3的倍数”为事件Ａ。

昌平区2017年高三第二次统一练习数学试卷（文科）（满分150分，考试时间120分钟）2017.5考生须知：1． 本试卷共6页，分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分。

2． 答题前考生务必将答题卡上的学校、班级、姓名、考试编号用黑色字迹的签字笔填写。

3．答题卡上第I 卷(选择题)必须用2B 铅笔作答，第II 卷(非选择题)必须用黑色字迹的签字笔作答，作图时可以使用2B 铅笔。

请按照题号顺序在各题目的答题区内作答，未在对应的答题区域内作答或超出答题区域作答的均不得分。

4． 修改时，选择题部分用塑料橡皮擦涂干净，不得使用涂改液。

保持答题卡整洁，不要折叠、折皱、破损。

不得在答题卡上做任何标记。

5．考试结束后，考生务必将答题卡交监考老师收回，试卷自己妥善保存。

第Ⅰ卷（选择题共40分）一、选择题（本大题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.）(1)设全集U =R ,集合{20}A x x =->，则U A =ð (A)(2,)+∞(B )[2,)+∞(C)(,2)-∞(D)(,2]-∞(2)已知==)k a b ，若//a b ，则k = （A ）1-（B ）1（C ）3-（D ）3（3）若实数,x y 满足10,0,0,x y x y x -+≥⎧⎪+≥⎨⎪≤⎩则2x y +的最小值为（A ）12-（B ）0（C ）1（D ）32(4)已知直线,m n 和平面α，满足,m n αα⊄⊂.则“//m n ”是“//m α”的 （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件(5)执行如图所示的程序框图，输出的S 值为(A)14 (B)310(C )13(D)514(6)给定函数①12y x =，②1y x =，③1y x =-，④cos()2y x π=-，其中既是奇函数又在区间(0,1)上是增函数的是 （A ）①（B ）②（C ）③（D ）④(7)已知函数22,0,(),0xx f x x x ⎧≤⎪=⎨>⎪⎩，若函数()()(1)g x f x k x =--恰有两个零点，则实数k 的取值范围是（A ）(,1)(4,)-∞-+∞U （B ）(,1][4,)-∞-+∞U （C ）[1,0)(4,)-+∞U （D ）[1,0)[4,)-+∞U(8)已知圆22(2)4x y -+=的圆心为C ，过原点O 的直线l 与圆交于,A B 两点.若ABC ∆的面积为1,则满足条件的直线l 有 （A ）2条（B ）4条（C ）8条（D ）无数条正（主）视图第二卷（非选择题共110分）二、填空题（本大题共6小题，每小题5分，共30分.）(9)设a∈R，若(1+i)(i)=2ia--，则a=______ .(10)某校从高三年级中随机选取200名学生，将他们的一模数学成绩绘制成频率分布直方图（如图）.由图中数据可知a=_____.若要从成绩在[ 120 , 130），[130 ，140) , [140 , 150]三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从成绩在[130 ，140) 内的学生中选取的人数应为__________ .(11)某三棱锥的三视图如图所示，则该三棱锥的最长棱的棱长为_____________ .(12)双曲线22:13yC x-=的渐近线方程为；若双曲线C的右焦点恰是抛物线2:2(0)N y p x p=>的焦点，则抛物线N的准线方程为.(13)某校高三年级5个班进行拔河比赛，每两个班都要比赛一场.到现在为止，1班已经比了4场，2班已经比了3场，3班已经比了2场，4班已经比了1场，则5班已经比了场.(14)设函数()sin()f x A xωϕ=+（,,Aωϕ是常数，0,0Aω>>）.若()f x在区间(1,3)上具有单调性，且(1)(3)(5)f f f=-=-，则ω=_______________.DCBA 三、解答题（本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.）(15)(本小题满分13分)已知公差不为0的等差数列{}n a 的前三项和为12，且248,,a a a 成等比数列. （I ）求数列{}n a 的通项公式；（II ）设2n a n b =，求数列{}n b 的前n 项和n S .(16)(本小题满分13分)学校组织学生参加某项比赛，参赛选手必须有很好的语言表达能力和文字组织能力.学校对10位已入围的学生进行语言表达能力和文字组织能力的测试，测试成绩分为A ，B ，C能力或文字组织能力为C 的学生的概率为310. （I ）求a ，b 的值；（II ）从测试成绩均为A 或 B 的学生中任意抽取2位，求其中至少有一位语言表达能力或文字组织能力为A 的学生的概率．(17)(本小题满分13分)在ABC ∆中，A ∠的角平分线AD 与边BC 相交于点D ，且2,3,AC AB ==60BAC ∠=︒.(Ⅰ)求BC 的长及sin B 的值；（Ⅱ）求AD 的长．DBAP(18)(本小题满分14分)在四棱锥P ABCD -中，PAD ∆为正三角形，平面PAD ⊥平面ABCD ，//AB CD ，AB AD ⊥，224CD AB AD ===.（Ⅰ）求证：平面PCD ⊥平面PAD ； （Ⅱ）求三棱锥P ABC -的体积；（Ⅲ）在棱PC 上是否存在点E ，使得//BE 平面PAD ? 若存在，请确定点E 的位置并证明；若不存在，说明理由．(19)(本小题满分13分)已知椭圆经过点(2,0)A -，(0,1)B -，点P 是椭圆上在第一象限的点，直线PA 交y 轴于点M ，直线PB 交x 轴于点N . （Ⅰ）求椭圆的标准方程和离心率；（Ⅱ）是否存在点P ，使得直线MN 与直线AB 平行？若存在，求出点P 的坐标，若不存在，请说明理由．(20)(本小题满分14分) 已知函数()(1)ln (0)af x x a x a x=++-<． （Ⅰ）若2a =-，求曲线()y f x =在点(1,(1))f 处的切线方程； （Ⅱ）求函数()f x 的单调区间； （Ⅲ）设函数()ag x x=．若对于任意(1,e]x ∈，都有()()f x g x >成立，求实数a 的取值范围．。

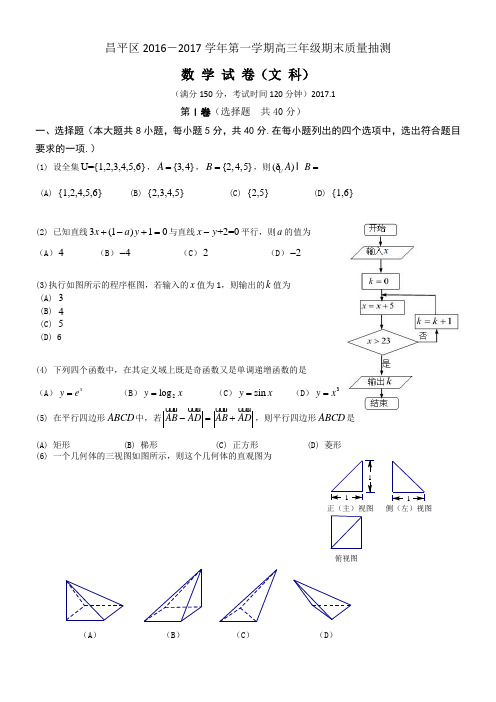
俯视图1侧（左）视图正（主）视图昌平区2016－2017学年第一学期高三年级期末质量抽测数学试卷（文科）（满分150分，考试时间120分钟）2017.1第Ⅰ卷（选择题共40分）一、选择题（本大题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.）(1) 设全集U={1,2,3,4,5,6}，{3,4}A=，{2,4,5}B=，则()UA B=Ið(A) {1,2,4,5,6} (B) {2,3,4,5} (C) {2,5} (D) {1,6}(2) 已知直线3(1)10x a y+-+=与直线+2=0x y-平行，则a的值为（A）4（B）4-（C）2（D）2-(3)执行如图所示的程序框图，若输入的x值为1，则输出的k值为(A) 3(B) 4(C) 5(D) 6(4) 下列四个函数中，在其定义域上既是奇函数又是单调递增函数的是（A）xy e=（B）2logy x=（C）siny x=（D）3y x=(5) 在平行四边形ABCD中，若AB AD AB AD-=+uu u r uuu r uu u r uuu r，则平行四边形ABCD是(A)矩形 (B)梯形 (C)正方形 (D)菱形(6)一个几何体的三视图如图所示，则这个几何体的直观图为（A）（B）（C）（D）(7) 已知直线,m n 和平面α，且m α⊥.则“n m ⊥”是“//n α”的（A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件(8) 甲袋中有16个白球和17个黑球，乙袋中有31个白球，现每次任意从甲袋中摸出两个球，如果两球同色，则将这两球放进丙袋，并从乙袋中拿出一白球放回甲袋；如果两球不同色，则将白球放进丙袋，并把黑球放回甲袋.那么这样拿 次后，甲袋中只剩一个球，这个球的颜色是（A ）16，黑色 （B ）16，白色或黑色 （C ）32，黑色（D ）32，白色第二卷（非选择题 共110分）二、填空题（本大题共6小题，每小题5分，共30分.）(9) 已知i 为虚数单位,则复数i(1i)-=__________ .(10) 已知数列{}n a 的前n 项和为n S ，且2n S n n =+，则3a =__________ . (11) 12,2,ln2ee -三个数中最大的数是_________ .(12) 在ABC ∆中，,24C B b π=∠==，则A ∠=__________ .(13) 已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线的倾斜角为6π，则双曲线的渐近线的方程为________ ；该双曲线的离心率为________ .(14) 若函数2,11,()ln ,1.x x f x x x a -⎧-≤<=⎨≤≤⎩①当2a =时，若()1f x =，则x =___________；②若()f x 的值域为[0,2]，则a 的取值范围是________ .三、解答题（本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.）(15)(本小题满分13分)已知函数2()22cos 1f x x x +- (Ⅰ)求函数()f x 的最小正周期； （Ⅱ）求函数()f x 在64ππ⎡⎤-⎢⎥⎣⎦，上的最大值和最小值．(16)(本小题满分13分)已知{}n a 是等差数列，{}n b 是正项的等比数列，且115332,14,a b a b a ====. (Ⅰ)求{}n a 、{}n b 的通项公式；(Ⅱ)求数列{}n a 中满足46n b a b <<的各项的和.MNCBA P(17)(本小题满分14分)昌平区在滨河公园举办中学生冬季越野赛.按年龄段将参赛学生分为A,B,C 三个组,各组人数如下表所示.组委会用分层抽样的方法从三个组中选出6名代表.(I) 求A,B,C 三个组各选出代表的个数；(II) 若从选出的6名代表中随机抽出2人在越野赛闭幕式上发言，求这两人来自同一组的概率1P ；(III)若从所有参赛的300名学生中随机抽取2人在越野赛闭幕式上发言，设这两人来自同一组的概率为2P ，试判断1P 与2P 的大小关系(不要求证明).(18)(本小题满分13分)在三棱锥ABC P -中，ABC PA 平面⊥，32,2===BC AC AB ，N M ,分别为AB BC ,中点. （I ）求证：PAC MN 平面//； （II ）求证：PAM PBC 平面平面⊥；（III ）在AC 上是否存在点E ，使得PAC ME 平面⊥，若存在，求出ME 的长，若不存在，请说明理由.(19)(本小题满分13分)已知函数()ln (0)f x x mx m =->.(I) 若1=m ，求曲线)(x f y =在点))1(,1(f 处的切线方程；(II)求函数)(x f 的最大值()g m ，并求使()g m >2-m 成立的m 取值范围.(20)(本小题满分14分)已知椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别为21,F F ，且经过点)5,0(P ，离心率为32，过点1F 的直线l 与直线4=x 交于点A . （I ） 求椭圆C 的方程；（II ） 当线段A F 1的垂直平分线经过点2F 时，求直线l 的方程； （III ）点B 在椭圆C 上，当OB OA ⊥，求线段AB 长度的最小值..昌平区2016－2017学年第一学期高三年级期末质量抽测数学试卷（文科）参考答案及评分标准 2017.1一、选择题共10小题，每小题5分，共50分。

昌平区2016－2017学年第一学期高三年级期末质量抽测数 学 试 卷（文 科）（满分150分，考试时间120分钟）2017．1考生须知：1． 本试卷共6页，分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分．2． 答题前考生务必将答题卡上的学校、班级、姓名、考试编号用黑色字迹的签字笔填写．3．答题卡上第I 卷（选择题）必须用2B 铅笔作答，第II 卷（非选择题）必须用黑色字迹的签字笔作答，作图时可以使用2B 铅笔．请按照题号顺序在各题目的答题区内作答，未在对应的答题区域内作答或超出答题区域作答的均不得分．4． 修改时，选择题部分用塑料橡皮擦涂干净，不得使用涂改液．保持答题卡整洁，不要折叠、折皱、破损．不得在答题卡上做任何标记．5．考试结束后，考生务必将答题卡交监考老师收回，试卷自己妥善保存．第Ⅰ卷（选择题 共40分）一、选择题（本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．）（1） 设全集U={1,2,3,4,5,6}，{3,4}A =，{2,4,5}B =，则()UA B =（ ）．A ． {1,2,4,5,6}B ． {2,3,4,5}C ． {2,5}D ． {1,6} 解析：{1,2,5,6}UA =，所以(){2,5}U A B =，故选C ．（2） 已知直线3(1)10x a y +-+=与直线+2=0x y -平行，则a 的值为（ ）．A ．4B ．4-C ．2D ．2- 解析：由题意有3(1)(1)1a ⨯-=-⨯解得4a =，故选A ．（3） 执行如图所示的程序框图，若输入的x 值为1，则输出的k 值为（ ）． A ．3 B ．4 C ．5 D ．6 解析：0k =，6x =，23x <； 1k =，11x =，23x <； 2k =，16x =，23x <； 3k =，21x =，23x <； 4k =，26x =，23x >； 所以输出为4k =，故选B ．（4） 下列四个函数中，在其定义域上既是奇函数又是单调递增函数的是（ ）． A ．e x y = B ．sin y x = C ．y x =D ．3y x =俯视图侧（左）视图正（主）视图解析：AC项不是奇函数，B项不是在定义域内单调增，由幂函数的性质易知3y x=在其定义域上既是奇函数又是单调递增函数，故选D．（5）在平行四边形ABCD中，若AB AD AB AD-=+，则平行四边形ABCD是（）．A．矩形B．梯形C．正方形D．菱形解析：由题意可知||||BD AC=，对角线相等的平行四边形是矩形，故选A．（6）一个几何体的三视图如图所示，则这个几何体的直观图是（）．A．B．C．D．解析：由三视图的性质可知B正确．（7）已知直线m，n和平面α，且mα⊥．则“n m⊥”是“//nα”的（）．A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件解析：mα⊥，若//nα，必然有m n⊥；若mα⊥，若m n⊥，当nα⊂时没有nα∥；所以“n m⊥”是“//nα”的必要不充分条件；故选B．（8）甲袋中有16个白球和17个黑球，乙袋中有31个白球，现每次任意从甲袋中摸出两个球，如果两球同色，则将这两球放进丙袋，并从乙袋中拿出一白球放回甲袋；如果两球不同色，则将白球放进丙袋，并把黑球放回甲袋．那么这样拿次后，甲袋中只剩一个球，这个球的颜色是A．16，黑色B．16，白色或黑色C．32，黑色D．32，白色解析：由题意可知每次甲袋中少一个球，所以需要拿32次才能使甲袋中只剩一个球；不论怎么拿，每次黑球要么少2个，要么一个不少，所以最终黑球一定只剩奇数个，所以最后剩下的一定是黑球；故选C．第二卷（非选择题共110分）二、填空题（本大题共6小题，每小题5分，共30分．）（9）已知i为虚数单位，则复数i(1i)-=__________ ．解析：由题意有i(1i)i11i-=+=+．（10）已知数列{}n a的前n项和为n S，且2nS n n=+，则3a=__________ ．解析：312S=，26S=，3321266a S S=-=-=．（11） 2e -，1e2，ln 2三个数中最大的数是_________ ．解析：由题意有12e 10e ln 2122-<<<<<，即最大的数为1e 2．（12） 在ABC △中，2c =，π4B ∠=，2b =，则A ∠=__________ ．解：由题意有sin 1sin 2c B C b ⋅==， 因为c b <，所以C B <，所以π6B =，则7ππ12A B C =--=．（13） 已知双曲线22221(0x y a a b -=>，0)b >的一条渐近线的倾斜角为π6，则双曲线的渐近线的方程为________ ；该双曲线的离心率为________ ． 解析：由题意可知渐近线斜率k =3tan θ=，所以渐近线方程为3y x =±； 即3b a =，即3a b =，所以离心率2223e 33c a b a a b+====． （14） 若函数2,11()ln ,1x x f x x x a-⎧-≤<=⎨≤≤⎩．①当2a =时，若()1f x =，则x =___________；②若()f x 的值域为[0,2]，则a 的取值范围是________ ． 解析：做出函数的图像，如右图所示；①当2a =时，()1f x =，解得0x =或e x =（舍去）．②若()f x 的值域为[0,2]，显然1ln 22a ≤≤，解得122e e a ≤≤．三、解答题（本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．）（15）（本小题满分13分） 已知函数2()3sin 22cos 1f x x x =+-．（Ⅰ）求函数()f x 的最小正周期． （Ⅱ）求函数()f x 在ππ64⎡⎤-⎢⎥⎣⎦,上的最大值和最小值．（16）（本小题满分13分）已知{}n a 是等差数列，{}n b 是正项的等比数列，且112a b ==，514a =，33b a =．MNCBAP（Ⅰ）求{}n a 、{}n b 的通项公式．（Ⅱ）求数列{}n a 中满足46n b a b <<的各项的和．（17）（本小题满分14分）昌平区在滨河公园举办中学生冬季越野赛．按年龄段将参赛学生分为A ，B ，C 三个组，各组人数如下表所示．组委会用分层抽样的方法从三个组中选出名代表．（I ） 求，，三个组各选出代表的个数．（II ） 若从选出的6名代表中随机抽出2人在越野赛闭幕式上发言，求这两人来自同一组的概率1P ．（III ）若从所有参赛的300名学生中随机抽取2人在越野赛闭幕式上发言，设这两人来自同一组的概率为2P ，试判断1P 与2P 的大小关系（不要求证明）． （18）（本小题满分13分）在三棱锥P ABC -中，PA ⊥平面ABC ，2AB AC ==，BC =M ，N 分别为BC ，AB 中点．（I ）求证：MN ∥平面PAC ．（II ）求证：平面PBC ⊥平面PAM ．（III ）在AC 上是否存在点E ，使得ME ⊥平面PAC ，若存在，求出ME 的长，若不存在，请说明理由．（19）（本小题满分13分） 已知函数()ln (0)f x x mx m =->．（I ） 若1=m ，求曲线)(x f y =在点))1(,1(f 处的切线方程．（II ）求函数)(x f 的最大值()g m ，并求使()2g m m >-成立的m 取值范围．（20）（本小题满分14分）已知椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别为1F ，2F ，且经过点P ，离心率为23，过点1F 的直线l 与直线4x =交于点A ． （I ）求椭圆C 的方程．（II ）当线段1F A 的垂直平分线经过点2F 时，求直线l 的方程． （III ）点B 在椭圆C 上，当OA OB ⊥，求线段AB 长度的最小值．昌平区2016－2017学年第一学期高三年级期末质量抽测 数学试卷（文科）参考答案及评分标准 2017．1一、选择题共10小题，每小题5分，共50分．在每小题列出的四个选项中，二、填空题共6小题，每小题5分，共30分． （9）1i + （10）6（11）1e2 （12）7π12（13）3y x =± ，3； （14）0；122e ,e ⎡⎤⎢⎥⎣⎦（第一空2分，第二空3分）三、解答题（本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．）（15）（本小题满分13分）解：（Ⅰ） 因为2()22cos 1f x x x =+-2+cos2x x π2sin(2)6x =+，所以2π2πT=π2ω==． （Ⅱ）因为ππ64x -≤≤， 所以ππ2π2663x -≤+≤．即 1πsin(2)126x -≤+≤， 所以π12sin(2)26x -≤+≤． 所以当ππ262x +=，即π6x =时，()f x 的最大值为2； 当ππ266x +=-，即π6x =-时，()f x 的最小值为1-． （16）（本小题满分13分）解：（Ⅰ）设等差数列{}n a 的公差为d ．因为12a =，514a =，所以1414a d +=，所以3d =，所以31n a n =-， 所以338b a ==．因为12b =，因为231b b q =，所以24q =．因为0n b >，所以2q =，所以1222n nn b -=⋅=．（Ⅱ）因为46n b a b <<，即462312n <-<，所以176533n <<，*n ∈N ． 即6n =，7，8， (21)所以满足46n b a b <<的各项的和为1512167212155()21()21(262)5(214)6322222a a a a a a a S S +++++++=-=-=-=．（17）（本小题满分14分）解：（I ）因为样本容量与总体容量的比是501501501006=++， 所以A ，B ，C 三个组各选出的代表的数量分别为：1100250⨯=，1150350⨯=，150150⨯=．所以A ，B ，C 三个组各选出的代表的个数分别为2，3，1．（II ）设来自A ，B ，C 三个组的代表分别为1a ，2a ，1b ，2b ，3b ，c ．则从6名代表中任意取出两人的所有结果所构成的基本事件空间：121112*********{(,),(,),(,),(,),(,),(,),(,),(,),a a a b a b a b a c a b a b a b Ω= 2121312323(,),(,),(,),(,),(,),(,),(,)}a c b b b b b c b b b c b c ，共15个基本事件．记事件D =“抽出的两个代表来自同一组”．则12121323{(,),(,),(,),(,)}D a a b b b b b b = ，共4个基本事件．所以这两名代表来自同一组的概率1415P =． （III ）21P P >．（18）（本小题满分13分） 证明：（I ）因为M ，N 分别为BC ，AB 中点， 所以MN AC ∥．因为MN ⊄平面PAC AC ⊂平面PAC ，所以MN ∥平行PAC ．（II ）因为PA ⊥平面ABC ，BC ⊂平面ABC ， 所以PA BC ⊥．因为2AB AC ==，M 为BC 的中点，所以AM BC ⊥． 因为AM PA A =，所以BC ⊥平面PAM ． 因为BC ⊂平面PBC ，所以平面PBC ⊥平面PAM ．（III ）存在．过点M 作ME AC ⊥，交AC 于点E ， 因为PA ⊥平面ABC ，BC ⊂平面ABC ，所以PA ME ⊥．因为ME AC ⊥，AC PA A =，所以ME ⊥平面PAC ．因为在ABC △中，2AB AC ==，BC =M 为BC 的中点，所以2ME =． （19）（本小题满分13分）解：（I ）若1=m ，则x x x f -=ln )(．所以1()1(0)f x x x'=->．所以(1)0f '=，1)1(-=f ．所以曲线)(x f y =在点))1(,1(f 处的切线方程为1-=y ．（II ） 因为1()(0)f x m x x'=->，当)1,0(m x ∈时， ()0f x '>；),1(+∞∈mx 时，()0f x '<． 所以)(x f 在)1,0(m 上单调递增；在),1(+∞m上单调递减．所以)(x f 的最大值1()()ln 1g m f m m ==--．()2g m m >-，即()(2)0g m m -->．设()()(2)ln 1h m g m m m m =--=--+． 因为1()10h x m'=--<， 所以()h m 在(0,)+∞上单调递减．又因为(1)0h =，所以当01m <<时，()(1)0h m h >=． 所以m 取值范围为()0,1．（20）（本小题满分14分）解:（I）由2222e 3b c a a b c ⎧=⎪⎪==⎨⎪⎪=+⎩，解得32a c =⎧⎨=⎩．所以椭圆C 的方程为22195x y +=． （II ）法一：设(4,)A y ，1(2,0)F -，因为线段1F A 的垂直平分线经过点2F ， 所以122||||F F F A =．由24c ==y =±． 所以直线l的方程为2)3y x =±+． 法二：设过点1(2,0)F -的直线l 的斜率为k ，显然k 存在．则直线l 的方程为(2)y k x =+． 所以(4,6)A k ．设1AF 的中点00(,)P x y ． 则02412x -+==，00632ky k +==．所以(1,3)P k ． 因为21PF F A ⊥，所以30112k k -⋅=--．所以k =． 所以直线l的方程为2)y x =+． （III ）点B 在椭圆C 上，设(,)B m n，[(0,5]n ∈，(4,)A y ．因为OA OB ⊥，所以0OA OB ⋅=，即40m ny +=．因为点B 在椭圆C 上，所以22195m n +=．||AB =======设2t n=，(0,5]t∈设144419()55tg tt=--．因为21444()05g tt-'=-<，所以()g t在(0,5]上单调递减．所以当5t=，即n=min||AB=【各题若有其它解法，请酌情给分】。

昌平区2008－2009学年第一学期高三期末考试数学参考答案（文科） 2009.1二、（9）（0，3±） (10) 600,32 (11) 4,10(12) 3 (13) ①和④ (14) [3,)+∞三、解答题(本大题共6小题，共80分)（1５）(本小题满分13分)解：(I),ABC ∆在中由正弦定理得：2sin ,2sin ,2sin a R A b R B c R C ===代入 (2)cos cos a c B b C -=整理得：2sin cos sin cos sin cos A B B C C B =+..…3分 即：2sin cos sin()sin A B B C A =+=，在三角形中，sin 0A >，2cos 1B =，∵∠Ｂ是三角形的内角，∴B=60°. ……………………………………………… 6分 (II),ABC ∆在中由余弦定理得：2222cos b a c ac B =+-⋅2()22cos a c ac ac B =+--⋅4b a c =+=将代入整理得3ac = …………………………………………10分故13sin sin 60224ABC S ac B ∆==︒=． …………………………………………… 13分 （16）(本小题满分14分)解：(I)设数列{}n a 的公差为d ，则3410a a d d =-=-，642102a a d d =+=+， 1046106a a d d =+=+ ……2分由3610a a a ，，成等比数列得23106a a a =，……………………………………………… 4分即2(10)(106)(102)d d d -+=+，整理得210100d d -=， 解得0d =或1d =． ∵0d ≠,∴1d = ……………………………………………… 6分 141310317,(1)6n a a d a a n d n =-=-⨯==+-=+，于是2012019202S a d ⨯=+207190330=⨯+=．…………………………………… 9分(II)11111(6)(7)(6)(7)n n a a n n n n +==-++++ ……………………………………11分 111111()()...()788967n T n n =-+-++-++=1177n -+ ……………………14分 （17）(本小题满分14分) 解:(I)证明：由已知D 在平面ABC 上的射影O 恰好在AB 上, ∴DO ⊥平面ABC ，∴AO 是AD 在平面ABC 上的射影． …………………………………… 2分 又∵BC ⊥AB ，∴BC ⊥AD ． …………………………………… 4分 (II)解：由(1)得AD ⊥BC ，又AD ⊥DC又BC ∩DC=C ，∴AD ⊥平面BDC又∵BD ⊂平面ADB ，∴AD ⊥BD ， ……………………………………6分 在R T ⊿ABD 中，由已知AC = 2，得2=AB ，AD = 1，∴BD = 1, ∴BD = AD, ∴O 是AB 的中点. ……………………………………8分 (III)解：过D 作DE ⊥AC 于E ，连结OE ，∵DO ⊥平面ABC ，∴O E 是DE 在平面ABC 上的射影．∴OE ⊥AC∴∠DEO 是二面角D －AC －B 的平面角， …………………………………11分 22=DO且3sin AD DC DO DE DEO AC DE ==∴∠==即二面角D －AC －B ……………………………………14分 （18）(本小题满分13分)解：(I)2'()663f x x ax b =++ ……………………………………2分 ()12f x x x ==由函数在及时取得极值,得'(1)0,'(2)0,f f ==即6630,3, 4.241230,a b a b a b ++=⎧=-=⎨++=⎩解得 ……………………………………5分 (II)由(1)知322()29128,'()618126(1)(2).f x x x x c f x x x x x =-++=-+=-- (0,1)'()0;(1,2)'()0;(2,3)'()0.x f x x f x x f x ∈>∈<∈>当时,当时,当时, …………8分 1()(1)58.(0)8,(3)98,[0,3]()(3)98.x f x f c f c f c x f x f c ==+==+∈=+当时,取得极大值又则当时,的最大值为11分22[0,3],(),19,(,1)(9,).x f x c c c c c c ∈<<<->-∞-⋃+∞因为对任意的有恒成立所以9+8,解得或即的取值范围是13分（19）(本小题满分13分)解（I ）设“设抛掷一颗骰子掷出的点数为3的倍数”为事件Ａ。

2016－2017学年度第一学期期末考试试题一、细心选一选.（每小题3分，共30分）1．在下列各式的计算中，正确的是 （ ）．A ．5x 3·（-2x 2）=-10x 5B ．4m 2n-5mn 2 = -m 2nC ．(-a)3÷(-a) =-a 2D ．3a+2b=5ab2．点M 1（a-1，5）和M 2(2,b-1)关于x 轴对称,则a,b 的值分别为（ ）．A ．3，－2B ．－3，2C ．4，－3D ．3，－4 3．下列图案是轴对称图形的有 （ ）．A. 1个 B ．2个 C ．3个 D ．4个4．下列说法正确的是( )．A ．等腰三角形任意一边的高、中线、角平分线互相重合B ．顶角相等的两个等腰三角形全等C ．等腰三角形的一边不可以是另一边的两倍D ．等腰三角形的两底角相等5．如图所示,下列图中具有稳定性的是( )．6．下列各组线段中，能组成三角形的是（ ）．A ． a=2，b=3，c=8B ．a=7，b=6，c=13C ． a=12，b=14，c=18D ．a=4，b=5，c=67．下列多项式中，能直接用完全平方公式因式分解的是（ ）．A. x 2+2xy- y 2B. -x 2+2xy+ y 2C. x 2+xy+ y 2D. 42x -xy+y 28．在△ABC 和△DEF 中，给出下列四组条件：（1） AB=DE, BC=EF, AC=DF（2） AB=DE, ∠B=∠E, BC=EF （3）∠B=∠E , BC=EF, ∠C=∠FDC B A（4） AB=DE, AC=DF, ∠B=∠E 其中能使△ABC ≌△DEF 的条件共有 ( ).A.1组B.2组C.3组D.4组9．已知 a=833， b=1625, c=3219, 则有（ ）.A ．a ＜b ＜cB ．c ＜b ＜aC ．c ＜a ＜bD ．a ＜c ＜b10．如图，在直角△ABC 中，∠ACB=90°，∠A 的平分线交BC 于D ．过C 点作CG ⊥AB 于G, 交AD 于E, 过D 点作DF ⊥AB 于F.下列结论：（1）∠CED=∠CDE （2）∠ADF=2∠FDB （3）CE=DF （4）△AEC 的面积与△AEG 的面积比等于AC:AG其中正确的结论是（ ）.A ．（1）（3）（4）B ．（2）（3）C ．(2) (3)（4）D ．(1)(2)(3)(4)二、耐心填一填.（每小题3分，共30分）11．实验表明，人体内某种细胞的形状可近似地看作球体，它的直径约为0.00000156m ，这个数用科学记数法表示为__________ m. 12. 如果把分式yx x＋2中的x 和y 都扩大5倍，那么分式的值 ． 13.已知ab=1，m =a ＋11+b＋11 ,则m 2016的值是 . 14．如果一个多边形的边数增加一条，其内角和变为1260°，那么这个多 边形为 边形．15．如图，若△ACD 的周长为19cm , DE为AB 边的垂直平分线,则 AC+BC= cm.16．若（x-1）0-2(3x-6)-2有意义，则x 的取值范围是 .17．如图，在直角△ABC 中，∠BAC=90°，AD ⊥BC 于D ，将AB 边沿AD 折叠， 发现B 的对应点E 正好在AC 的垂 直平分线上，则∠C= .18．如图，在△ABC 中,∠A=50°，点D 、E 分别在AB ，AC 上，EF 平分∠CED ，DF 平分∠BDE ，则 ∠F = ．19．已知等腰△ABC ，AB=AC,现将△ABC 折叠，使A 、B 两点重合，折痕所在的直 线与直线AC 的夹角为40°，则∠B 的 度数为 ．E DCBAGFEDCBAF EDC BA EDCBA20．如图，在△ABC 中，AB=AC,点D 在AB 上，过点D 作DE ⊥AC 于E ，在BC 上取一点F ， 且点F 在DE 的垂直平分线上，连接DF ， 若∠C=2∠BFD ，BD=5，CE=11，则BC 的 长为 ． 三、用心答一答.（60分） 21．（9分）(1) 分解因式： 8xy+ (2x-y)2（2）先化简，再求值：(a+b)2- b(2a+b)- 4b ，其中a=-2， b=-43；（3）先化简，再求值：（4482＋－＋x x x -x －21）÷xx x 232－＋，其中 x=-222．（6分）图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长为1，点A 、点B 和点C 在小正方形的顶点上， 请在图1、图2中各画一个四边形，满足以下要求：（1）在图1中画出以A 、B 、C 和D 为顶点的四边形，此四边形为轴 对称图形，并画出一条直线将此四边形分割为两个等腰三角形；（2）在图2中画出以A 、B 、C 和E 为顶点的四边形，此四边形为 轴对称图形，并画出此四边形的对称轴； （3）两个轴对称图形不全等．FEDCB A图1图223．（9分）已知关于x 的方程21＋＋x x - 1-x x = ）（＋1-)2(x x a的解是正数， 求a 的取值范围.24．(6分) 如图，△ABC 与△ABD 都是等边三角形，点E 、F 分别在BC ，AC 上，BE=CF,AE 与BF 交于点G.（1）求∠AGB 的度数；（2）连接DG,求证：DG=AG+BG.25．（10分）百姓果品店在批发市场购买某种水果销售，第一次用1200元购进若干千克，并以每千克8元出售，很快售完；由于水果畅销，第二次购买时，每千克进价比第一次提高10%，用1452元所购买的数量比第一次多20kg ，以每千克9元出售100千克后，因出现高温天气，水果不易保鲜，为减少损失，便降价50%售完剩余的水果. （1）求第一次水果的进价是每千克多少元？（2）该果品店在这次销售中，总体是盈利还是亏损？盈利或亏损了多少元？G F E DC B A26．（10分）（1）已知3x =4y =5z ，求yx y z 5332＋－的值．（2）已知6122－－－x x x =2＋x A +3－x B，其中A 、B 为常数， 求2A+5B 的值．（3）已知 x+y+z ≠0，a 、b 、c 均不为0，且zy x＋=a, x z y ＋=b ， yx z ＋=c 求证：a a ＋1+b b ＋1+cc ＋1=127．（10分）如图1，AD//BC,AB ⊥BC 于B ，∠DCB=75°，以CD 为边的等边△DCE 的另一顶点E在线段AB 上.（1）求∠ADE 的度数； （2）求证：AB=BC ；（3）如图2，若F 为线段CD 上一点，∠FBC=30°，求DF:FC 的值.D图1E CBA D图2FE CBA。

昌平区2010届高三上学期期末质量抽测数学试卷（文科）（满分150分，考试时间 120分钟）考生须知：1． 本试卷共6页，分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分。

2． 答题前考生务必将答题卡上的学校、姓名、考试编号用黑色字迹的签字笔填写，并认真核对条形码上的考试编号、姓名。

3．答题卡上第一部分(选择题)必须用2B 铅笔作答，第二部分(非选择题)必须用黑色字迹的签字笔作答，作图时可以使用2B 铅笔。

请按照题号顺序在各题目的答题区内作答，未在对应的答题区域内作答或超出答题区域作答的均不得分。

4． 修改时，选择题部分用塑料橡皮擦涂干净，不得使用涂改液。

保持答题卡整洁，不要折叠、折皱、破损。

不得在答题卡上做任何标记。

5．考试结束后，考生务必将答题卡交监考老师收回，试卷自己妥善保存。

参考公式：柱体的体积公式V=Sh ，其中S 是柱体的底面积，h 是柱体的高。

锥体的体积公式V=13Sh ，其中S 是锥体的底面积，h 是锥体的高第Ⅰ卷（选择题 共40分）一、选择题(本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．)(1) 已知全集U={1，2，3，4，5，6}，集合A={x|x 2-7x+10=0},B={2，3，6},则集合(U A)∩B =A ．{1，3，4，6}B ．{3，6}C ．{2}D ．{2，3，5，6} (2) 若复数ii z -=1（i 是虚数单位），则=|z |A ．21 B ．22C ．1D ．2 （3）已知直线12:210:(1)10l x my l x m y -+=+--=与,则“m =2”是“1l ⊥2l ”的 A ．充分不必要条件 B ．必要不充分条件C ．充分且必要条件D ．既不充分又不必要条件(4)下列函数中,周期为π的偶函数是A.cos y x =B.sin 2y x =C. tan y x = D . sin(2)2y x π=+（5）数列{n a }的前n 项和223(N*)n S n n n =-∈，则4a = A. 11 B. 15 C. 17 D.20（6）如果一个几何体的三视图如图所示（单位长度：cm ）， 则此几何体的体积是（ ）A ．396cmB ．380cm C．(380cm + D ．3224cm 3（7）已知点（,m n ）在直线52200x y +-=上, 其中0m n >、,则lg lg m n + A.有最大值为2 B.有最小值为2 C ．有最大值为1 D. 有最小值为1（8）已知函数),3[)(+∞-的定义域为x f ，且2)3()6(=-=f f . )()(x f x f 为'的导函数，函数 '()f x 的图像如右图所示.则平面区域0,0,(2)2,a b f a b ≥⎧⎪≥⎨⎪+≤⎩所围成的面积是（ ）A ．10B ．4C ．9D ．18第Ⅱ卷（非选择题 共110分）二、填空题（本大题共6小题，每小题5分，共30分．）（9） 已知函数()(0,1)xf x a a a =>≠过点（2，4），则a =________. （10）为了测算如右图阴影部分的面积，做一个边长为6的 正方形将其包含在内，并向正方形内随机投掷800个点。

昌平区2016—2017学年第一学期高三年级期末质量抽测语文试卷 2017.1本试卷共10页，共150分。

考试时长150分钟。

考生务必将答案答在答题卡上。

在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

一、本大题共8小题，共24分。

阅读下面材料，完成1-8题。

材料一里约奥运会不乏中国元素，从地铁、空调到安检设备，从毛绒玩具、各国国旗到专业运动装备，你总能看到熟悉的品牌名字。

在奥运会开幕前一周，里约地铁四号线终于宣布通车。

它全长16公里，共设5站，全程用时13分钟。

这条线路比从里约南部市中心驱车到奥林匹克公园所在巴哈区的耗时缩短了半小时，它也被称作“奥运地铁”。

据估计，它每天能运送30万人次，被视为“里约奥运会留给里约的最大财富”，对提升里约民众的生活舒适度和便利度发挥着重要作用。

据报道，车体的纵向载荷．．为363吨，该数值是欧洲城铁设计标准的2.5倍。

针对治安环境问题，列车设计方特别为它安装了防爆聚酯玻璃。

由于里约常年高温，设计师还贴心地为其加装了空调，保证车厢内温度保持在20到23摄氏度之间。

中国公司“同方威视”为奥运会提供了260多台手提行李和大型货物的X射线扫描设备。

而且，这些设备在奥运会结束后，将继续为巴西司法部所辖的各个监狱提供安检服务。

据介绍，本次奥运会上，“同方威视”的两款安检机，都拿出了高科技。

它们采用低能X射线成像系统，该系统具备更加优化的X射线发生器、高分辨率探测器和更高级别的图像计算方法，还拥有基于人体工程原理的用户界面和多样的网络程序，可以帮助安检员实现高效操作。

里约奥运会还对安检设备提出了一些特殊要求。

比如沙滩排球比赛场地设在科帕卡巴纳海滩，安检设备需要安装在松软的沙滩上，它还可能遭受海水腐蚀，供电也可能出现问题。

为了保证设备能顺畅运行，“同方威视”为奥运会成立了一支16人的技术保障队伍。

马拉卡纳赛区和德奥多鲁赛区使用的安检设备全部由“同方威视”提供。

所以，进入这些赛区之前，你一定能碰到“中国制造”。