§1.4 命题的四种形式及等价关系

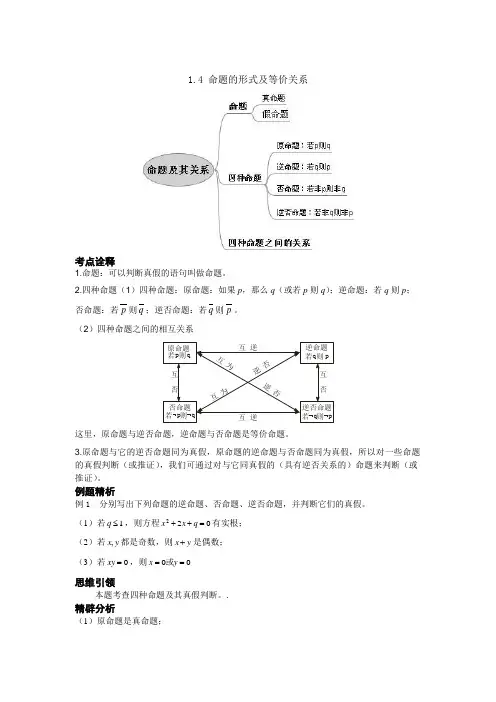
1.4 命题的形式及等价关系考点诠释1.命题：可以判断真假的语句叫做命题。

2.四种命题（1）四种命题：原命题：如果p ，那么q （或若p 则q ）；逆命题：若q 则p ； 否命题：若p 则q ；逆否命题：若q 则p 。

（2）四种命题之间的相互关系若 则否命题原命题若 则若 则逆否命题互 逆互 逆互 为互为逆 否逆否互 否互 否q p 若 则逆命题q p q p q p这里，原命题与逆否命题，逆命题与否命题是等价命题。

3.原命题与它的逆否命题同为真假，原命题的逆命题与否命题同为真假，所以对一些命题的真假判断（或推证），我们可通过对与它同真假的（具有逆否关系的）命题来判断（或推证）。

例题精析例1 分别写出下列命题的逆命题、否命题、逆否命题，并判断它们的真假。

（1）若1≤q ，则方程022=++q x x 有实根； （2）若y x ,都是奇数，则y x +是偶数； （3）若0=xy ，则00==y x 或思维引领本题考查四种命题及其真假判断。

.精辟分析（1）原命题是真命题；逆命题：若方程022=++q x x 有实根，则1≤q 是真命题； 否命题：若1>q ，则方程022=++q x x 无实根，是真命题； 逆否命题：若方程022=++q x x 无实根，则1>q 是真命题； （2）原命题是真命题；逆命题：若y x +是偶数，则y x ,都是奇数，是假命题； 否命题：若y x ,不都是奇数，则y x +不是偶数，是假命题； 逆否命题：若y x +不是偶数，则y x ,不都是奇数，是真命题； （3）原命题为真命题；逆命题：若00==y x 或，则0=xy ，是真命题； 否命题：若0≠xy ，则00≠≠y x 且，是真命题； 逆否命题：若00≠≠y x 且，则0≠xy ，是真命题；方法规律总结（1）“原命题”与“逆否命题”同真同假．．．．，“逆命题”与“否命题”同真同假．．．．，但“互逆”或“互否”的命题真假性未必相同。

高考数学四种命题及其相互关系学问点汇总数学课本中毁灭的四种命题的内容经常在高考选择题中考察，下面是学习啦我给大家带来的高考数学四种命题及其相互关系学问点汇总，期望对你有关怀。

高考数学四种命题及其相互关系学问点(一)1、四种命题：一般地，用p和q分别表示原命题的条件和结论，用或分别表示p和q的否认，四种命题的形式是：(1)原命题：若p则q;(2)逆命题：若q则p;(3)否命题：若则;(4)逆否命题：若则。

2、四种命题的真假关系：一个命题与它的逆否命题是等价的，其逆命题与它的否命题也是等价的;3、四种命题的相互关系：留意：1、区分"否命题'与"命题的否认'，若原命题是"若p则q'，则这个命题的否认是"若p则非q'，而它的否命题是"若非p则非q'。

2、互为逆否命题同真假，即"等价'高考数学四种命题及其相互关系学问点(二)【若则命题】命题的常见形式为"若p则q'，其中p叫做命题的条件，q叫做命题的结论.【逆命题】对于两个命题，假如一个命题的条件和结论分别是另一个命题的结论和条件，那么这两个命题称为互逆命题.其中一个命题称为原命题(originalproposition)，另一个称为原命题的逆命题(inverseproposition).也就是说，假如原命题为"若p，则q'，那么它的逆命题为"若q，则p'.【否命题】对于两个命题，假如一个命题的条件和结论分别是另一个命题的条件的否认和结论的否认，那么这两个命题称为互否命题.其中一个命题称为原命题，另一个称为原命题的否命题(negativeproposition).也就是说，假如原命题为"若p，则q'，那么它的否命题为"若，则'.【逆否命题】对于两个命题，假如一个命题的条件和结论恰好是另一个命题的结论的否认和条件的否认，那么这两个命题称为互为逆否命题.其中一个命题称为原命题，另一个称为原命题的逆否命题(inverseandnegativeproposition).也就是说，假如原命题为"若p，则q'，那么它的逆否命题为"若，则'.。

二、四种命题的形式§1.4.1命题的形式及等价关系（1） —命题与推出关系、四种命题形式1．了解命题、推出关系及命题证明的意义；2．知道常见数学命题的结构，掌握证明一些简单命题的真假的方法； 3．理解四种命题的形式及互相关系；4．能写出一些简单命题的逆命题、否命题及逆否命题.问1 什么是命题？如何判断命题的真假？[练习]（P14例1）下列语句哪些是命题，哪些不是命题？如果是命题，那么它们是真命题还是假命题？为什么？（1）个位数是5的自然数能被5整除； （2）凡直角三角形都相似； （3）上课请不要讲话；（4）互为补角的两个角不相等；（5）如果两个三角形的三条边对应相等，那么这两个三角形全等； （6）你是高一学生吗？ （7）210x x ++>； （8）210x +>.问2 通常一个命题由哪两个部分组成？[例如]（1）对顶角相等. .（2）等腰梯形的两条对角线相等. 如果一个梯形的两腰相等，那么它的两条对角线相等.[练习] 将下列命题改写为“如果p ，那么q ”的形式.（1）个位是5的整数能被5整除；_________________________________________________.（2）空集是任何集合的真子集； _________________________________________________. （3）凡直角三角形都相似. _________________________________________________.问3 什么是推出关系（αβ⇒）？ 什么是等价关系？什么是推出关系的传递性？问4 写出四种命题形式，指出四种命题的真假关系？ 1、四种命题的构成形式[例][练习] 写出下列命题的逆命题、否命题、和逆否命题，并判断其真假.（1）如果0a =，那么0ab =；（2）如果两个角是对顶角，那么这两个角相等.2、四种命题的相互关系图及真假性问5 写出下列常用词语的否定词语：例1 判断下列命题的真假，并给出证明（1）对顶角相等；（2）两个无理数的和一定是无理数；（3）如果集合A 、B 、C 满足A B A C =，那么B C =；（4）如果一元二次方程20ax bx c ++=满足0ac <，那么这个方程有两个不相等的实数根.例2 写出下列语句的否定形式（1）a 、b 都是正数；（2）a 、b 、c 中至少有两个是负数； （3）a 、b 、c 中至多有两个是负数； （4）0a >或0b <；（5）对任意实数x ，都有2220x x -+>.[举一反三] 写出“存在实数x ，使得210x x -+=”的否定形式.例3 （1）写出命题“已知a 、b 、c 、d 是实数，若a b =，c d =，则ac bd =”的逆命题、否命题、逆否命题；（2）判断上述四个命题的真假并说明理由.例4 在下列命题中，用符号“⇒”、“⇐”，或“⇔”把α、β这两件事联系起来（1）α：实数x 满足92=x ，__________β：3=x 或3-=x ；（2）α：A B =∅，__________β：A =∅或B =∅； （3）α：B A ⊆，__________β：A B A = ； （4）α：0=ab ，__________β：0=a ； （5）α：a b +是偶数，β：33a b +是偶数.1. 用推出符号“⇒”、“⇐”，或“⇔”把α、β这两件事联系起来： （1）α：x N ∈__________β：2x N ∈； （2）α：0ab =__________β：0a =或0b =；（3）α：四边形ABCD 是平行四边形__________β：四边形ABCD 是矩形； （4）α：4a <-__________β：方程240x ax ++=有实数解. 2. 判断下列命题的真假：（1）互为子集的两个集合相等；（ ） （2）曲线231y kx x =+-与x 轴至少有一个交点； （ ） （3）若0a b +>且0ab >，则0a >或0b >；（ ） （4）无理数不都是无限小数.（ ）3. 写出下列语句的否定：（1）a b >____________________；（2）a 、b 、c 不都是无理数_____________________.4. 命题：如果0c =，那么抛物线2(0)y ax bx c a =++≠的图像过原点的逆否命题是_________________________________________________________________________________. 5. 命题：“两个有理数的和是有理数”的否命题是_________________________________________. 6. 命题“设a 、b 、c ∈*N ，如果ab 是c 的倍数，那么a 、b 中至少有一个是c 的倍数”是___________ 命题（填“真”或“假”），理由是_____________________________________________________. 7. 与命题“x 、y 、z 不全是负数”等价的命题（ ） A ．x 、y 、z 中至少有一个是正数； B ．x 、y 、z 全不是负数；C ．x 、y 、z 中只有一个负数；D ．x 、y 、z 中至少有一个是非负数. 8. 有下列命题：① 210x +=不是方程；② 若a R ∈，则01a =，；③ 若2xa a =，则2x =； ④ 关于x 的不等式20ax a ->的解集是2()x a R >∈，其中假命题的个数是 （ ）A ．1；B ．2；C ．3；D ．4.9. 命题：“如果1x ≥，那么1x >”的逆否命题是 （ ） A ．如果1x >，那么1x ≥； B ．如果1x ≤，那么1x <； C ．如果1x <，那么1x ≤；D ．如果1x ≤，那么1x <.10. 命题:()M ax b cx d a b c d R +=+∈、、、，命题:d bN x a c-=-，则命题M 与N 的推出关系是（ ）A ．M N ⇐；B ．M N ⇒；C ．M N ⇔；D ．以上都不对. 11. 判断命题“两个奇数的平方差是8的倍数”的真假，并给出证明.12. 写出命题“非空集合A 、B 是全集U 的子集，若A B Ü，则U AB =∅ð”的逆命题、否命题、逆否命题，并指出是真命题还是假命题.13. 写出命题：“如果一元二次方程20ax bx c ++=有一正根和一负根，那么0ca<”的逆命题，判断真假并给出证明.。

1.4 命题的形式及等价关系基础热身：(1)命题“若21x <，则11x -<<”的逆否命题是（ ） .A 若2x ≥1，则x ≥1或x ≤1-.B 若11x -<<，则21x < .C 若1x >或1x <-，则21x > .D 若x ≥1或x ≤1-，则2x ≥1(2)命题“若函数()log (0,1)a f x x a a =>≠在定义域内是减函数,则log 20a <”的逆否命题是（ ）A 、若log 20a ≥，则函数()log (0,1)a f x x a a =>≠在其定义域内不是减函数B 、若log 20a <，则函数()log (0,1)a f x x a a =>≠在其定义域内不是减函数C 、若log 20a ≥，则函数()log (0,1)a f x x a a =>≠在其定义域内是减函数D 、若log 20a <，则函数()log (0,1)a f x x a a =>≠在其定义域内是减函数知识梳理：1.命题：可以判断真假的语句叫做命题。

说明:(1)命题通常用陈述句表述。

数学中的定义、公理、定理等, 都是数学命题。

在数学中，一般只研究数学命题。

(2)命题一般地由条件、结论两部分组成。

命题常写成“如果α，那么β”的形式。

对于这样的命题，用“如果”开始的部分是条件，用“那么”开始的部分是结论。

注意:α、β也都是命题，可能是简单命题，也可能是复合命题。

简单命题：不含逻辑联结词的命题。

复合命题：由简单命题与逻辑联结词构成的命题。

逻辑联结词：“或”、“且”、“非”这些词叫做逻辑联结词。

如：(1)3是12的约数.(2)3是12的约数且3是15的约数.2．判断命题的真假：正确的命题叫做真命题，错误的命题叫做假命题。

（1） 确定一个命题是真命题必须作出证明；①直接证明；②间接证明（同一法、反证法）直接法：即从已知条件出发，依据所学过的公理，定理，公式进行逐步推理，从而得出结论。

1.4 命题的形式及等价关系1.命题与推出关系在初中，我们已经知道，可以判断真假的语句叫做命题，命题常用陈述句表述.正确的命题叫做真命题，错误的命题叫做假命题.【例题】判断下列语句哪些不是命题，哪些是命题？如果是命题，那么它们是真命题还是假命题？为什么？（1）个位数是5的自然数都能被5整除；（2）凡直角三角形都相似；（3）上课请不要讲话；（4）互为补角的两个角不相等；（5）如果两个三角形的三条边对应相等，那么这两个三角形全等；（6）你是高一学生吗？在数学中常见的命题由条件与结论两部分组成.要确定一个命题是假命题，只要举出一个满足命题条件，而不满足命题结论的例子就可以了，这在数学中称为举反例.如果命题α成立可以退出命题β也成立，那么就说由α可以退出β，并用记号α⟹β表示，读作“α推出β”.换言之，α⟹β表示以α为条件、β为结论的命题是真命题.如果α成立不能推出β成立，可记作α⇏β.换言之，α⇏β表示以α为条件，β为结论的命题是一个假命题.如果α⟹β，并且β⟹α，那么记作α⟺β，叫做α与β等价.推出关系具有传递性【例题】用符号⇒、⇐、⟺表示下列事件的推出关系；（1）α：△ABC是等边三角形，β：△ABC是轴对称图形，αβ；（2）α：一次函数y=kx+b的图像经过第一、二、三象限，β：一次函数y=kx+b中，k>0，b>0,αβ；（3）α：实数x适合x2=1，β：x=1，αβ.2. 四种命题形式逆命题：“如果α，那么β”把结论与条件互换，就得到一个新命题“如果β，那么α”，我们把这个命题叫做原命题的逆命题.例如：平行四边形的对角线互相平分→对角线互相平分的四边形是平行四边形否命题：把原命题的条件和结论都换成它们的否定形式，那么另一个命题就叫做原命题的否命题.例如：平行四边形的对角线互相平分→如果四边形不是平行四边形，那么它的对角线不互相平分【例题】请写出下列命题的逆命题和否命题，并判断其真假.命题A：如果两个三角形全等，那么它们的面积相等；命题B：如果一个三角形两边相等，那么这两边所对的角也相等.逆否命题：如果把原命题“如果α，那么β”结论的否定作条件，把条件的否定作结论，那么就可得到原命题的逆否命题.例如：平行四边形的对角线互相平分→如果一个四边形的对角线不互相平分，那么这个四边形不是平行四边形.3.等价命题逆命题与否命题互为逆否命题互为逆否命题的两个命题是同真同假的【例题】原命题、逆命题、否命题、逆否命题，这四种命题中真命题的个数可能是【例题】证明：若a2−4b2−2a+1≠0，则a≠2b+1..【例题】已知a，b，c∈R，证明：若a+b+c<1，则a，b，c中至少有一个小于13当我们证明某个命题有困难时，就可尝试用证明它的逆否命题来代替证明原命题.1.5 充分条件，必要条件“三角形有两个内角相等”“三角形是等腰三角形”“某个整数能够被4整除”“某个整数是偶数”一般地，用α、β分别表示两个命题，如果命题α成立，可以推出命题β也成立，即α⟹β，那么α叫做β的充分条件，β叫做α的必要条件.对于α、β两件事而言，α与β之间不一定有充分条件或者必要条件的关系，例如a+b>0与ab>0，是非充分非必要条件【例题】已知四边形ABCD是凸四边形，那么“AC=BD”是“四边形ABCD是矩形”的什么条件？为什么？如果α⟹β，那么α是β的充分条件；如果β⟹α，那么α是β的必要条件.如果既有α⟹β，又有β⟹α，即α⟺β，那么α既是β的充分条件，又是β的必要条件.这时我们就说α是β的充分必要条件，简称充要条件.“三角形两个内角相等”“三角形是等腰三角形”思考：x,y不都为0x,y都不为0的充分条件1.6 子集与推出关系设A、B是非空集合，A={a|a具有性质α}，B={b|b具有性质β}，则A⊆B与α⟹β等价。

1.4 （2）命题的形式及等价关系【教学目标】（1）理解四种命题的概念；（2）理解四种命题之间的相互关系，能由原命题写出其他三种形式；（3）理解一个命题的真假与其他三个命题真假间的关系；（4）初步掌握反证法的概念，进一步领会分类、判断、推理的思想方法。

【教学重点】理解四种命题的关系；【教学难点】体会反证法的理论依据。

【教学过程】一．复习提问： （1）什么是命题？什么是真命题 ？什么是假命题？ （2）语句“内接于圆的四边形对角互补”是否是命题？ （3）命题 “内接于圆的四边形对角互补”的条件与结论各是什么？ 二．讲授新课： 关于四种命题 1、概念引入 在命题“内接于圆的四边形对角互补”中，条件是“内接于圆的四边形”，结论是“四边形的对角互补”。

如果我们把以上命题作以下变化：（1）如果把命题中的结论“四边形的对角互补”作为条件，把命题中的条件“内接于圆的四边形” 作为结论，则得到了新命题“对角互补的四边形内接于圆”。

我们把原来命题中的结论作为条件，原来命题中的条件作为结论所组成的新命题叫做原来命题的逆命题。

并且它们互为逆命题。

（2）如果将命题的条件和结论都换成它们的否定形式，即条件是“四边形不内接于圆”，结论是“四边形对角不互补”，那么就可得到一个新命题：“不内接于圆四边形对角不互补”。

像这种将命题的条件与结论同时否定而得到的新命题叫做原来命题的否命题。

并且新命题与原来的命题互为否命题。

（3）如果将命题的条件和结论互换并取原来的否定形式，即条件是“四边形对角不互补”，结论是“四边形不内接于圆”，那么就可得到一个新命题：“对角不互补的四边形不内接于圆”。

像这种将命题的条件与结论互换并同时否定而得到的新命题叫做原来命题的否命题。

并且新命题与原来的命题互为否命题。

2、概念形成由以上例子归纳出四个命题的一般形式：原命题： βα，那么如果逆命题： αβ，那么如果否命题： βα，那么如果逆否命题：αβ，那么如果并在四种命题之间的相互关系如下：3、概念运用（例题分析） 例1：试写出下列命题的逆命题、否命题和逆否命题，并判断其真假。

命题的四种形式及关系1. 什么是命题？在逻辑学中，命题是一个陈述句，它可以被判断为真或假。

命题是逻辑推理的基本单位，通过对命题的分析和组合，我们可以进行有效的推理和论证。

2. 命题的四种形式2.1 简单命题简单命题是最基本的命题形式，它不能再被分解为更小的命题。

简单命题通常用一个字母或一个词来表示，例如：P、Q、R等。

简单命题可以是真（True）或假（False）。

例如，“太阳从东方升起”这个陈述就是一个简单命题，它可以被判断为真。

2.2 复合命题复合命题由多个简单命题通过逻辑运算符连接而成。

常见的逻辑运算符有：•否定（Negation）：表示取反关系，用符号”¬“表示。

•合取（Conjunction）：表示与关系，用符号”∧“表示。

•析取（Disjunction）：表示或关系，用符号”∨“表示。

•条件（Implication）：表示蕴含关系，用符号”→“表示。

•双条件（Biconditional）：表示等价关系，用符号”↔“表示。

例如，命题”P并且Q”可以表示为P∧Q，命题”P或者Q”可以表示为P∨Q。

2.3 合取范式合取范式是一种复合命题的标准形式，它由多个简单命题的合取构成。

合取范式通常用括号和逻辑运算符来表示。

例如，命题”(P∨Q)并且(¬R)“就是一个合取范式。

在合取范式中，每个简单命题都是一个子命题，并通过逻辑运算符连接起来。

2.4 析取范式析取范式是另一种复合命题的标准形式，它由多个简单命题的析取构成。

析取范式通常用括号和逻辑运算符来表示。

例如，命题”(P∧¬Q)或者R”就是一个析取范式。

在析取范式中，每个简单命题都是一个子命题，并通过逻辑运算符连接起来。

3. 命题的关系3.1 等价关系两个命题被称为等价关系，如果它们具有相同的真值表。

换句话说，两个等价的命题在所有情况下都具有相同的真假值。

等价关系可以用双条件符号”↔“来表示。

例如，命题”P并且Q”和命题”Q并且P”是等价命题，可以表示为P∧Q ↔ Q∧P。

四种命题的形式•概念命题：可以判断真假的语句叫做命题，命题通常用陈述句表示真命题：正确的命题叫做真命题假命题：错误的命题叫做假命题在数学中，常见的命题由条件和结论两部分组成（如：如果三角形的三条边相等，那么这两个三角形全等）命题的证明：1、要确定一个命题是假命题，只要举出一个满足命题条件，而不满足命题结论的例子就可以了，这在数学中称为举反例2、确定一个命题是真命题，就必须做出证明，证明若满足命题条件就一定能推出命题的结论一般来说，如果命题α成立可以推出命题β也成立，那么久说由α可以推出β，并用记号“α=>β”表示，读作“α推出β”，换言之，α=>β表示以α为条件，β为结论的命题是真命题；同理，α≠＞β表示以α为条件，β为结论的命题是一个假命题等价命题：如果A 、B 是两个命题，A=>B ，B=>A ，那么A 、B 叫做等价命题，记作A<=>B 。

称A 与B 等价四种命题：（参见下图）若把一个已知命题定义为原命题（由条件和结论组成）把原命题的条件和结论交换，所得到的命题叫做原命题的逆命题把原命题的条件和结论都换成它们的否定形式，所得到的命题是原命题的否命题 （且α的否命题记为 ）把原命题的结论的否定作条件，把条件的否定作结论，所得到的命题是原命题的逆否命题 （值得注意的是，否命题和逆命题也互为逆否命题）四种命题之间的相互关系：（参见上图）一般来说，原命题与逆否命题是同真或同假的，即，原命题与逆否问题是等价命题 （当我们证明某个命题有困难时，就可尝试用证明它的逆否命题来代替证明原命题） Eg.结合初中证明：已知BD 、CE 分别是△ABC 的∠B 、∠C 的角平分线，BD ≠CE 。

求证：AB ≠AC四种命题的真假常用结论：1．原命题为真，它的逆命题不一定为真。

例如：原命题为真：逆命题为假2．原命题为真，它的否命题不一定为真。

例如：原命题为真：否命题为假：3．原命题为真，它的逆否命题一定为真。

二、四种命题形式1.4命题的形式及等价关系知识点1命题的判定及证明1.命题的有关概念:(1)判断真假的语句叫命题,命题常用陈述句表述.(2)正确的命题叫真命题.错误的命题叫假命题.(3)若α这件事成立可以推出β这件事成立,那么就说由α可推出β,记作α⇒β,读作“α推出β”.(4)要证明一个命题是假命题，只要举出满足条件而不满足命题结论的例子就可以了，也就是说，通常使用举一反例的方法来证明一个命题是假命题。

2.真命题的证明方法:(1)从已知的条件出发,根据已学的公理、定理、公式等应用推出关系,得出要证明的结论.(2)反证法用反证法证明命题的一般步骤：①假设命题的结论不成立,即假设结论的反面成立;②从这个假设出发,经过推理论证,得出矛盾;③由矛盾判定假设不正确,从而肯定命题的结论正确.【例1】判断下列命题的真假,并给出证明(1)两个三角形两边一对角对应相等,则这两个三角形全等.(2)如果一元二次方程ax2+bx+c=0满足ac＜0，那么这个方程有两个不相等的实根.(3)如果集合A、B、C满足A∩B=A∩C,那么B=C.(4)已知集合A、B、C,如果A⊆B,那么A∩C⊆B∩C.知识点2推出关系1.定义:一般地,如果事件α成立可以推出事件β也成立,那么就称α推出β,记作α⇒β.2.性质:(1)推出关系具有传递性.即若α→β,β→γ,就有α→γ.(2)如果命题的条件、结论有推出关系,则这个命题是真命题.【例2】用符号“⇒、⇐、⇔”连接事件α与β.(1)α:x2=4,β:x=2,则αβ.(2)α:实数x适合x＞1,β:x≥0,则αβ.(3)A、B是两集合,α:A⊆B,β:A∩B=A,则αβ.(4)a、b是两整数,α:a与b奇偶性相同,β:a+b是偶数,则αβ.(5)α:x+2≥3y,β:x-3y-1≥0,则αβ.知识点3命题的四种形式及其相互关系1.命题的四种形式:当把α⇒β称为原命题时,则称β⇒α为原命题的逆命题,α⇒β为原命题的否命题,β⇒α为原命题的逆否命题.2.命题的四种形式相互具有互逆、逆否的关系,其关系如图所示:3.根据原命题写逆命题、否命题、逆否命题给定一个原命题,总可以写出其逆命题、否命题、逆否命题.分清原命题的条件与结论,改写成“若α,则β”的形式,是写出其余三个命题的关键.【例3】设原命题为“已知a、b、c、d是实数,若a=b,c=d,则ac=bd”,请分别写出它的逆命题、否命题和逆否命题.逆命题：否命题：逆否命题：【思维误区点拨】命题P:若a、b都是奇数,则a+b是偶数.试写出命题P的逆否命题.【点拨】要掌握四种命题的结构形式,注意“且”与“或”在否定中的转换.【例4】写出下列命题的逆命题、否命题和逆否命题,并判断真假.(1)若一个整数的末位数字是0,则这个整数能被5整除;逆命题：（）否命题：（）逆否命题：（）(2)等腰三角形的底角相等.逆命题：（）否命题：（）逆否命题：（）知识点4等价命题如果两个命题A、B,A⇒B且B⇒A,那么A、B叫等价命题.【注意】等价命题同真同假.原命题与其逆否命题,逆命题与否命题分别互为逆否命题,为等价命题,同真同假,所以有时在证明一个命题有困难,可以证其等价命题,通常证明其逆否命题来代替证明原命题.【例5】下列各组中两个命题是否互为等价命题.(1)“A⊆B”与“A∪B=B”.(2)“x∈A”与“x∈A∪B”.(3)“a∈A∩B”与“a∈B”.(4)“m∈A∩B”与“m∈A∪B”.【解析】是否互为等价命题,要看能否互相推出.【点拨】本题都是与集合运算有关的问题,可以借助文氏图来解.课后练习【例1】写出下列命题的逆命题、否命题、逆否命题,并判断真假;(1)若x+y≤0,则x≤0或y≤0;逆命题：（）否命题：（）逆否命题：（）(2)已知x、y、z∈Z,如果x、y、z中至少有一个是偶数,那么xyz能被2整除.逆命题：（）否命题：（）逆否命题：（）【点拨】命题改写若不方便,可先将命题写成三段式,大前提、条件、结论,一般情况下,四种命题的大前提是一致的,然后将条件、结论写成“如果……那么……”.【例2】(1)已知A∩B≠∅,B⊆C,证明A∩C≠∅.(2)已知a 与b 均为正有理数,且b a 与都是无理数,证明b a +也是无理数. 【点拨】对基础定义、定理的熟练应用及推理的严密性是证明命题的基础,这一点要求较高.【例3】求证:对角线不互相平分的四边形不是平行四边形.【例4】已知BD 、CE 分别是△ABC 的AC 、AB 边上的中线，且BD ≠CE ，求证：AB ≠AC.自我检测1.在原命题“若A ∪B ≠B ，则A ∩B ≠A ”及它的逆命题、否命题、逆否命题中，真命题的个数是.2.命题“A ⇒B ”为真，那么下列命题中真命题是（ ）（A ）A ⇒B （B ）A ⇒B （C ）B ⇒A （D ）B ⇒A3.写出命题“若A=∅或B=∅，则A ∩B=∅”的逆命题、否命题、逆否命题.逆命题：否命题：逆否命题：4.已知命题：“如果两个数同为有理数或同为无理数，那么这两个数之和是有理数.”写出它的否命题，判断否命题的真假，并说明理由.5.判断命题“如果△ABC 为锐角三角形，则A+B ＞2π”的真假，并证明.。

说明：本系列教案,学案，经多次使用，修改，其中有部分来自网络，它山之石可以攻玉，希望谅解。

为了一个课件，我们仔细研磨；为了一个习题，我们精挑细选；为了一点进步，我们竭尽全力；没有最好，只有更好！制作水平有限，错误难免，请多指教：28275061@【教学内容的课时安排】本章总共15课时，其中§1.4 (1)命题的形式及等价关系一、教学目标设计理解四种命题之间的相互关系，能由原命题写出其他三种形式；知道推出关系的概念，理解一个命题的真假与其他三个命题真假间的关系；掌握等价关系的概念.二、教学重点及难点了解命题的构成；会用举反例法说明一个命题为假命题；知道真命题需要证明.三、教学用具准备多媒体四、学过程设计(一)、复习回顾在初中，我们已学过命题，真命题，假命题.命题：表示判断的语句.真命题：正确的命题.假命题：错误的命题.命题“全等三角形的面积相等”的条件与结论各是什么？本节将进一步研究命题与其有关的命题的概念.[说明]通过学生回顾以前的知识，唤起他们原有认知结构中的知识结点，从而为下面的要学习的一些下位概念的同化和顺应提供最近发展区.(二)、讲授新课1．命题例1：下列语句哪些不是命题，哪些是命题？如果是命题，那么它们是真命题还是假命题？为什么？（1）个位数是5的自然数能被5整除；（2）凡直角三角形都相似；（3）上课请不要讲话；（4）互为补角的两个角不相等；（5）你是高一学生吗？结论：①命题必定由条件与结论两部分组成.②假命题的确定：举反例（举出一个满足条件，不满足结论的例子，一个即可）.③真命题必须证明.2、推出关系：一般地，如果α这件事成立可以推出β这件事也成立，那么就说由α可以推出β，并用记号α⇒β表示，读作“α推出β”.换言之，α⇒β表示以α为条件，β为结论的命题是真命题.例2：设α表示“两个角是对顶角”，β表示为“两个角相等”，问能用“⇒”表示α、β之间关系吗？例3：在下列各题中，用符号“⇒”或“⇔”把α、β这两件事联系起来.(1).α：实数x 满足92=x ，β：3=x 或3-=x ；(2).α：U B A = ，β：U B U A ==或（U 为全集）； (3).α：B A ⊆，β：A B A = ； (4).α：0=ab ，β：0=a3、α与β等价：如果α⇒β，β⇒α，那么记作βα⇔，叫做α与β等价4、传递性：α⇒β，β⇒γ，则α⇒γ（类比推出关系的传递性，你能再举一些具有传递关系的关系吗？说说看）三、巩固练习：课本P/17 练习1.4（1）——1，2，3四、课堂小结：本节课主要介绍了真假命题判断的方法及命题的推出关系.五、教学反思（1）命题的有关概念在初中平面几何中已经学过,因此可以通过具体的例子帮助学生回顾旧知,为以后进一步研究命题做好铺垫.在推出关系的教学中,要强调命题的条件和结论,要结合并集的概念强调“或”的三层含义.（2）理解推出关系具有传递性，为以后学习充要条件做好准备. （3）要明确有关数学符号、记号的意义，正确加以使用.本单元中引进的数学符号、记号比较多，初学者往往不善于使用，对此教学中必须在每一符号引进时，说明其意义，配备适当的例题、习题，逐步让学生熟悉这些符号，正确地运用这些符号.导学案§1.4 (1)命题的形式及等价关系学习目标⒈知道“命题”、“推出”的意义；知道命题的结构“如果α，那么β”．⒉．掌握真假命题判断的方法及命题的推出关系；理解“证明“的意义学习重点：学会找一个命题的条件和结论，了解推出关系的定义.学习难点：判断命题的真假并说明理由学习过程：一、知识回顾1、_________________语句叫做命题，命题通常用_______________表述._________________叫做真命题._________________假命题.2、在数学中常见的命题由_______与________两部分组成.二、新知导学1、推出关系：一般地，如果α这件事成立可以推出β这件事也成立，那么就说由α可以推出β，并用记号_______表示，读作“_______”.换言之，α⇒β表示以____为条件，____为结论的命题是真命题.2、α与β等价：如果α⇒β，β⇒α，那么记作________ ___，叫做α与β.3、传递性：α⇒β，β⇒γ，则_____________.三、问题探究例1：下列语句哪些不是命题，哪些是命题？如果是命题，请写出命题的条件与结论（1）如果两直线平行，那么同位角相等（2）全等三角形的面积相等（3）上课请不要讲话（4）你主动学习了吗？反思：命题必定由条件与结论两部分组成.例2：判断下列命题是真命题还是假命题，并说明理由.(1).个位数是5的自然数能被5整除；(2).凡直角三角形都相似；(3).互为补角的两个角不相等；说明：举反例，即：举出一个满足条件，不满足结论的例子.例3：设α表示“两个角是对顶角”，β表示为“两个角相等”，问能用“⇒”表示α、β之间关系吗？例4：在下列各题中，用符号“⇒”或“⇔”把α、β这两件事联系起来.(1). α：实数x 满足92=x ，β：3=x 或3-=x . __________(2). α：B A ⊆，β：A B A = .__________ (3). α：0=ab ，β：0=a .__________四、学习小结1. 用“或”、“且”、“非”填空：⑴ 若()()130x x -+=，则1x =_______3x =-； ⑵ 若0ab ≠，则0a ≠_______0b ≠； ⑶ 若0x ≥，则x 是_______负实数．2. 判断下列命题的真假（在题后括号中填“真”或“假”）：（1） 如果b a ,都是奇数，那么b a +是偶数……………………………（ ） （2） 一组对边平行且两对对角线相等的四边形是平行四边形…………（ ） （3） 如果2<a ，那么2<a ……………………………………………（ ） （4） 如果A B A = ，那么B B A = …………………………………（ ）3. 在下列各题中，用符号“⇒”或“⇐”或“⇔”把命题α与β联系起来．⑴ α：x 是方程2320x x -+=的根 β：2x =⑵ α：5x =- β：||5x =⑶ α：A B ⊆ β：A B A =（4）α：x 适合方程0652=+-x x ， β：3x 2==或x ；（5）α：B A ⊆， β：B B A = ；。