力学第三四章习题课

理论力学习题答案(总26页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2第一章 静力学公理和物体的受力分析一、是非判断题在任何情况下，体内任意两点距离保持不变的物体称为刚体。

( ∨ ) 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反，沿同一直线。

( × ) 加减平衡力系公理不但适用于刚体，而且也适用于变形体。

( × ) 力的可传性只适用于刚体，不适用于变形体。

( ∨ ) 两点受力的构件都是二力杆。

( × ) 只要作用于刚体上的三个力汇交于一点，该刚体一定平衡。

( × ) 力的平行四边形法则只适用于刚体。

( × ) 凡矢量都可以应用平行四边形法则合成。

( ∨ ) 只要物体平衡，都能应用加减平衡力系公理。

( × ) 凡是平衡力系，它的作用效果都等于零。

( × ) 合力总是比分力大。

( × ) 只要两个力大小相等，方向相同，则它们对物体的作用效果相同。

( × )若物体相对于地面保持静止或匀速直线运动状态，则物体处于平衡。

( ∨ )当软绳受两个等值反向的压力时，可以平衡。

( × )静力学公理中，二力平衡公理和加减平衡力系公理适用于刚体。

( ∨ )静力学公理中，作用力与反作用力公理和力的平行四边形公理适用于任何物体。

( ∨ )凡是两端用铰链连接的直杆都是二力杆。

( × )如图所示三铰拱，受力F ，F 1作用，其中F 作用于铰C 的销子上，则AC 、BC 构件都不是二力构件。

( × )图3二、填空题力对物体的作用效应一般分为 外 效应和 内 效应。

对非自由体的运动所预加的限制条件称为 约束 ；约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ；约束力由 主动 力引起，且随 主动 力的改变而改变。

第一章练习题1、物质能以液态形式存在的最高温度为（A）沸腾温度Tb （B）玻义耳温度TB （C）临界温度Tc2、当压缩因子Z<1时，表示该实际气体（A）易压缩（B）不易压缩（C）无法确定3、下列何种条件下真实气体可以液化（）（A）Tr>1,Pr>1 （B）Tr>1,Pr<1 （C）Tr=1,Pr<1 （D）Tr<1,Pr=14、对理想气体，压缩因子Z=1。

能否说当气体的Z=1 时，该气体必定是理想气体。

答案：（不能，因为在实际气体的等温线与理想气体的等温线交点处，Z＝1）5、当温度足够低时，任何实际气体的Z～P 曲线与理想气体的Z～P 曲线均交于两点。

试解释这种现象。

答案：（这是因为当温度足够低时，气体的玻义耳温度高于体系温度，Z～p 曲线出现极小值。

）6、从范德华方程出发并结合玻义耳温度定义，证明(1)在足够高的温度，实际气体的压缩因子Z>1 。

(2)在低温，低压下，Z<1 。

答案：（当T＜＝TB，Z＞1）(3)当a=0 ，Z 随压力p 的增加而线性增加。

答案：（当a＝0，Z＝1+bp/RT，恒温时，p 增加，Z 增大。

）7、下列说法何者正确？(1)临界压力是气体可被液化的最低压力。

(2)气体被液化的必要条件是气体温度小于波义耳温度(3)在临界点，饱和液体与饱和蒸气的密度相同。

(4)气体的临界状态与气体的性质无关。

答案：（3）8、气体A、B、C 都服从范德华方程，其范德华常数a和b的大小顺序为a(A)=a(B)>a(C);b(C)>b(B)>b(A)。

问三种气体临界温度的大小顺序。

答案：（T c(A)>T c(B)>T c(C)）9、某气体的状态方程为，式中b为常数，n为物质的量。

若该气体经一等温过程，压力自p1变至p2，则下列状态函数的变化，何者为零？（ΔU）第二章练习题1、指出下列说法的错误。

(1)因Qp =ΔH，Qv=ΔU，所以Qp 和Qv 都是状态函数。

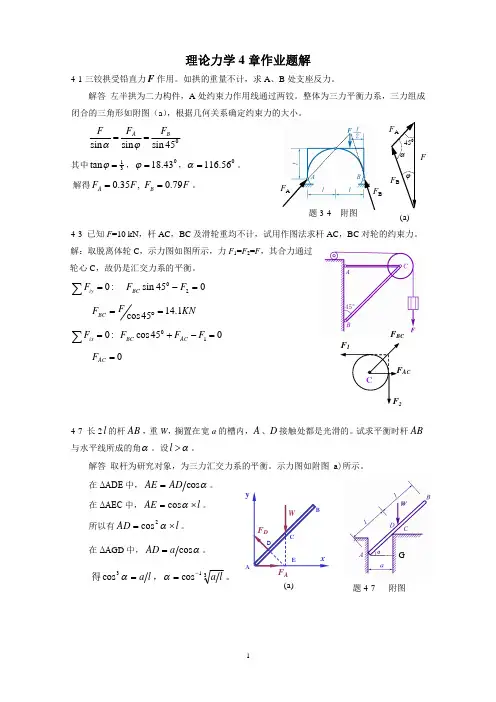
理论力学4章作业题解4-1三铰拱受铅直力F 作用。

如拱的重量不计，求A 、B 处支座反力。

解答 左半拱为二力构件，A 处约束力作用线通过两铰。

整体为三力平衡力系，三力组成闭合的三角形如附图（a ），根据几何关系确定约束力的大小。

45sin sin sin B A F F F ==j a其中31tan =j ，043.18=j ，056.116=a 。

解得F F F F B A 79.0 ,35.0==。

4-3 已知F =10 kN ，杆AC ，BC 及滑轮重均不计，试用作图法求杆AC ，BC 对轮的约束力。

解：取脱离体轮C ，示力图如图所示，力F 1=F 2=F ，其合力通过轮心C ，故仍是汇交力系的平衡。

:0=åiyF 045sin 20=-F F BCKN FF BC 1.1445cos =°=045cos :010=-+=åF F F FAC BC ix0=AC F4-7 长2l 的杆AB ，重W ，搁置在宽a 的槽内，A 、D 接触处都是光滑的。

试求平衡时杆AB 与水平线所成的角a 。

设a >l 。

解答 取杆为研究对象，为三力汇交力系的平衡。

示力图如附图(a)所示。

在ΔADE 中，a cos AD AE =。

在ΔAEC 中，l AE ´=a cos 。

所以有l AD ´=a 2cos 。

在ΔA GD 中，a cos a AD =。

得a =a 3cos ，31cosl a -=a 。

F BCAC题3-4 附图F BF AF BF AFa45j(a)A (a)题4-7 附图G4-9 AB ，AC ，AD 三连杆支撑一重物，如图所示。

已知W=10kN ，AB =4m ，AC =3 m ，且ABEC 在同一水平面内，试求三连杆所受的力。

解：取铰A 研究，示力图如图示，为汇交力系的平衡。

0=åix F ： 05430sin =´°+AD AB F F 0=åiy F ： 05330sin =´°+AD AC F F 0=åiZF： 030cos =-°W F AD联立求解KNF KNF KN F AD AC AB 5.115.36.4=-=-=4-8 图示结构上作用一水平力F 。

材料力学性能课后习题答案第一章单向静拉伸力学性能1、解释下列名词。

1弹性比功：金属材料吸收弹性变形功的能力，一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。

2．滞弹性：金属材料在弹性范围内快速加载或卸载后，随时间延长产生附加弹性应变的现象称为滞弹性，也就是应变落后于应力的现象。

3．循环韧性：金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。

4．包申格效应：金属材料经过预先加载产生少量塑性变形，卸载后再同向加载，规定残余伸长应力增加；反向加载，规定残余伸长应力降低的现象。

5．解理刻面：这种大致以晶粒大小为单位的解理面称为解理刻面。

6．塑性：金属材料断裂前发生不可逆永久（塑性）变形的能力。

脆性：指金属材料受力时没有发生塑性变形而直接断裂的能力韧性：指金属材料断裂前吸收塑性变形功和断裂功的能力。

7.解理台阶：当解理裂纹与螺型位错相遇时，便形成一个高度为b的台阶。

8.河流花样：解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。

是解理台阶的一种标志。

9.解理面：是金属材料在一定条件下，当外加正应力达到一定数值后，以极快速率沿一定晶体学平面产生的穿晶断裂，因与大理石断裂类似，故称此种晶体学平面为解理面。

10.穿晶断裂：穿晶断裂的裂纹穿过晶内，可以是韧性断裂，也可以是脆性断裂。

沿晶断裂：裂纹沿晶界扩展，多数是脆性断裂。

11.韧脆转变：具有一定韧性的金属材料当低于某一温度点时，冲击吸收功明显下降，断裂方式由原来的韧性断裂变为脆性断裂，这种现象称为韧脆转变2、说明下列力学性能指标的意义。

答：E 弹性模量 G 切变模量 r σ规定残余伸长应力 2.0σ屈服强度 gt δ金属材料拉伸时最大应力下的总伸长率 n 应变硬化指数 P15 3、 金属的弹性模量主要取决于什么因素？为什么说它是一个对组织不敏感的力学性能指标？答：主要决定于原子本性和晶格类型。

合金化、热处理、冷塑性变形等能够改变金属材料的组织形态和晶粒大小，但是不改变金属原子的本性和晶格类型。

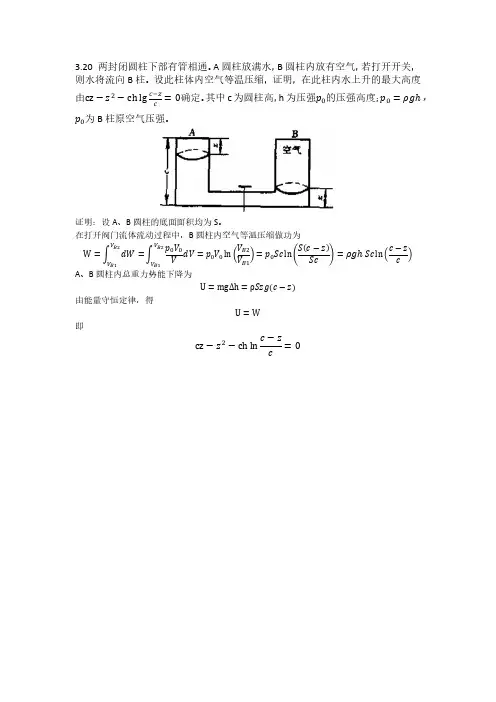
第三、四章 习题及答案3-8已知流速场u x =xy 2, 313yuy=-, u z =xy, 试求：（1）点（1，2，3）的加速度；（2）是几维流动；（3）是恒定流还是非恒定流；（4）是均匀流还是非均匀流？ 解：（1）411633x x x x x xyzu u u u a u u u xy txyz∂∂∂∂=+++==∂∂∂∂2533321331323331216 3 . 06m /sy y z x y a y u y a yu xu xy xy xy a =-===+=-====（2）二元流动 （3）恒定流 （4）非均匀流41xy33-11已知平面流动速度分布为xy 2222cx uu x ycy x y=-=++，， 其中c 为常数。

求流线方程并画出若干条流线。

解：2222-x d x =yd yxyd x d y d x d y c y c x u u xyxy=⇒-=⇒++积分得流线方程：x 2+y 2=c方向由流场中的u x 、u y 确定——逆时针3-17下列两个流动，哪个有旋？哪个无旋？哪个有角变形？哪个无角变形？(1)u x =－ay,u y =ax,u z =0 （2）z2222,,0,a c xycy cxu u u x y x y =-==++式中的、为常数。

z 2222,,0,a c x y cy cx u u u x yx y=-==++式中的、为常数。

解：（1）110 ()()22y xx y z u u a a ax y ωωω∂∂===-=+=∂∂有旋流动xy 11()()0 22y x xy zx u u a a x y εεε∂∂=+=-==∂∂ 无角变形(2)222222222222222222211()2()2()22()()12()2()0 0 2()y x z x y u u x y c cx x y c cy x y x y x y c x y c x y x y ωωω∂⎡⎤∂+-+-=-=+⎢⎥∂∂++⎣⎦⎡⎤+-+====⎢⎥+⎣⎦无旋流动2222xy22222112()()()022()()y x u u c x y c x y x y x y x y ε∂⎡⎤∂---=+==-≠⎢⎥∂∂++⎣⎦ 有角变形4—7变直径管段AB ，d A =0.2m,d B =0.4m ，高差△h=1.5m ，测得p A =30kPa ，p B =40kPa ，B 点处断面平均流速v B =1.5m/s ，试判断水在管中的流动方向。

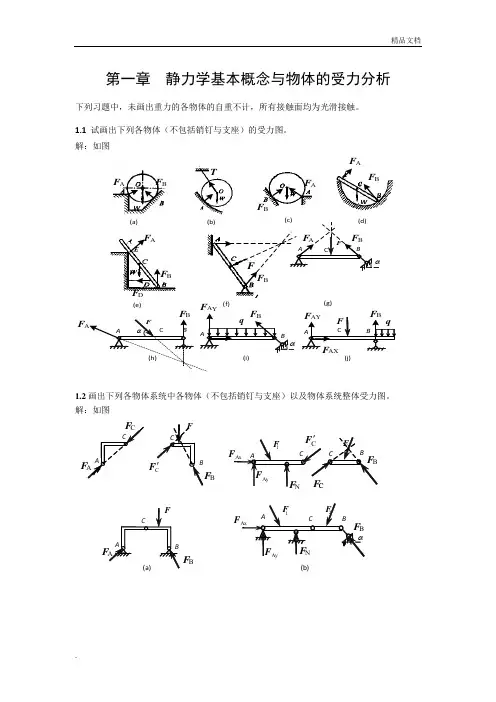
第一章 静力学基本概念与物体的受力分析下列习题中，未画出重力的各物体的自重不计，所有接触面均为光滑接触。

1.1 试画出下列各物体（不包括销钉与支座）的受力图。

解：如图(g)(j)P (a)(e)(f)WWF F A BF DF BF AF ATF BA1.2画出下列各物体系统中各物体（不包括销钉与支座）以及物体系统整体受力图。

解：如图F BB(b)(c)C(d)CF D(e)AFD(f)FD(g)(h)EOBO E F O(i)(j) BYFB XBFXE(k)1.3铰链支架由两根杆AB、CD和滑轮、绳索等组成，如题1.3图所示。

在定滑轮上吊有重为W的物体H。

试分别画出定滑轮、杆CD、杆AB和整个支架的受力图。

解：如图'D1.4题1.4图示齿轮传动系统，O1为主动轮，旋转方向如图所示。

试分别画出两齿轮的受力图。

解：1o xF2o xF2o yF o yFFF'1.5结构如题1.5图所示，试画出各个部分的受力图。

解：第二章 汇交力系2.1 在刚体的A 点作用有四个平面汇交力。

其中F 1＝2kN ，F 2=3kN ，F 3=lkN ， F 4=2.5kN ，方向如题2.1图所示。

用解析法求该力系的合成结果。

解 00001423cos30cos45cos60cos45 1.29Rx F X F F F F KN ==+--=∑ 00001423sin30cos45sin60cos45 2.54Ry F Y F F F F KN ==-+-=∑2.85R F KN ==0(,)tan63.07Ry R RxF F X arc F ∠==2.2 题2.2图所示固定环受三条绳的作用，已知F 1＝1kN ，F 2=2kN ，F 3=l.5kN 。

求该力系的合成结果。

解：2.2图示可简化为如右图所示023cos60 2.75Rx F X F F KN ==+=∑013sin600.3Ry F Y F F KN ==-=-∑2.77R F KN ==0(,)tan6.2Ry R RxF F X arc F ∠==-2.3 力系如题2.3图所示。

第二章 习题与思考题17、在邓肯-张的非线性双曲线模型中，参数a 、b 、i E 、t E 、13-ult σσ（）以及f R 各代表什么意思？答：参数i E 代表三轴试验中的起始变形模量，a 代表i E 的倒数；ult )(31σσ-代表双曲线的渐近线对应的极限偏差应力，b 代表ult )(31σσ-的倒数；t E 为切线变形模量；f R 为破坏比。

18、饱和粘土的常规三轴固结不排水实验的应力应变关系可以用双曲线模拟，是否可以用这种实验确定邓肯-张模型的参数？这时泊松比ν为多少？这种模型用于什么情况的土工数值分析？答：可以，这时ν=0.49，,用以确定总应力分析时候的邓肯-张模型的参数。

19、是否可以用饱和粘土的常规三轴固结不排水试验来直接确定用有效应力表示的邓肯-张模型的参数？对于有效应力，上述的131()/d d σσε-是否就是土的切线模量t E ？用有效应力的广义胡克定律来推导131()/d d σσε-的表达式。

答：不能用饱和粘土的常规三轴固结不排水试验来直接确定用有效应力表示的邓肯-张模型的参数；在有效应力分析时，邓肯-张模型中的131()/d d σσε-不再是土的切线模量，而需做以下修正：131()/=1-(1-2)t t E d d A σσευ- 具体推导如下：'''11231231231231=[-(d +d )]1=[(-du)-(d +d -2du)]1=[(-du)-(d +d )-2du)]1=[-(d +d )-(1-2)du)]d d Ed E d Ed Eεσυσσσυσσσυσσυσυσσυ 又由于23=d =0d σσ；且B=1.0时，13=(-)u A σσ∆，则：13=(-)du Ad σσ，代入上式，可得：1313131=[d(-)-(1-2)Ad(-)]1=[1-(1-2)A]d(-)d E Eεσσυσσυσσ 可知131(-)=1-(1-2)t t d E d A σσευ 20、土的3σ为常数的平面应变试验及平均主应力为常数的三轴压缩试验〔1σ增加的同时，3σ相应的减少，保持平均主应力p 不变〕、减压的三轴伸长试验〔围压1σ保持不变，轴向应力3σ不断减少〕的应力应变关系曲线都接近双曲线，是否可以用这些曲线的切线斜率131(-)/d d σσε直接确定切线模量t E ？用广义胡克定律推导这些试验的131(-)/d d σσε表达式。

第三章 平面问题的直角坐标解答【3-4】试考察应力函数ay 3在图3-8所示的矩形板和坐标系中能解决什么问题（体力不计）？【解答】⑴相容条件：不论系数a 取何值，应力函数 a y 3总能满足应 力函数表示的相容方程，式（2-25）.⑵求应力分量当体力不计时，将应力函数代入公式（2-24），得⑶考察边界条件上下边界上应力分量均为零，故上下边界上无面力 左右边界上；主矢的中心在矩下边界位置。

即本题情况下，可解决各种偏心拉伸问题 偏心距e ：e ：P因为在A 点的应力为零。

设板宽为b ，集中荷载p 的偏心距e ：同理可知，当a <0时，可以解决偏心压缩问题x6ay, y 0, xyyx应力分布如图所示，当 主矢，主矩l? h 时应用圣维南原理可以将分布的面力，等效为右端:f xx xl6ay (0 y h)h _l当a>0时，考察x 分布情况，注意到 0，故 y 向无面力左端:f x ( x )x 0 6ayxyx 0(x )A P pebh bh 2/6e h/6 图3-■xxyh(xy )x l 0Oyf②在x=0 , x=l的次要边界上，面力分别为:12FIy -3 , f yh因此，各边界上的面力分布如图所示:③在x=0，x=l的次要边界上，面力可写成主矢、主矩形式:x=0上x=l上【3-6】试考察应力函数一xy（3h24y2），能满足相容方程，并求出应2h力分量（不计体力），画出图3-9所示矩形体边界上的面力分布（在小边界上画出面力的主矢量和主矩），指出该应力函数能解决的问题。

h/2h/2| l【解答】（1）将应力函数代入相容方程（2-25）4 4 4石2 2 2 40，显然满足x x y y（2）将代入式（2-24），得应力分量表达式12Fxy 0x 厂3 , y 0, xy yxh3h（i 帶（3）由边界形状及应力分量反推边界上的面力：号，应精确满足应力边界条件式①在主要边界上（上下边界）上，y (2-15),应力y y h/2 0,yxyh/2 0因此，在主要边界yh h2上，无任何面力，即f x y 20, f y y x 0: f x0f y 3Fy2h3Fi2h4y2h2xO(I?h)图3-（a ） （b ） 因此，该应力函数可解决悬臂梁在自由端受集中力F 作用的问题【3-8】设有矩形截面的长竖柱，密度为 p,在一边侧面上受 【解答】采用半逆法求解。

1页第三章 力系的平衡习题解[习题3－1] 三铰拱受铅直力F 作用，如拱的重量不计，求A 、B 处支座反力。

[解]:（1）画受力图如图所示。

（2）因为BC 平衡，所以①0=∑ixF ②0=∑iyF（3）由AC 的平衡可知：P P C A F F R R 35.079.051'=⨯==[习题3－2] 弧形闸门自重W ＝150ｋＮ，试求提起闸门所需的拉力F 和铰支座处的反力。

解：)(761.565.0522.113kN R Ax =⨯= （←）)(690.51866.0522.11315060sin 0kN F W R Ax =⨯-=-= （↑）[习题3－3] 已知F ＝10ｋＮ，杆AC 、BC 及滑轮重均不计，试用作图法求杆AC 、BC 对轮的约束力。

解： 作力三角形图如图所示。

)(142.14102kN R B =⨯=，0=A R[习题3－4] 直径相等的两均质混凝土圆柱放在斜面与之间，柱重kN W W 4021==。

设圆柱与斜面接触处是光滑的，试用作图法求圆柱对斜面D 、E 、G 处的压力。

解：（1）以上柱为研究对象，其受力图与力三角形图如图所示。

由力三角形图上读得：)(20405.0212kN W N G =⨯==，方向如图所示。

（2）以下柱为研究对象，其受力图与力多边形如图所示。

[习题3－5] 图示一履带式起重机，起吊重量W ＝100ｋＮ，在图示位置平衡。

如不计吊臂AB 自重及滑轮半径和摩擦，求吊臂AB 及缆绳AC 所受的力。

解：以轮A 为研究对象，其受力图如图所示。

由轮A 的平衡条件可得：6.869397.07071.0=-AC AB T R .............................(1) 150342.07071.0=-AC AB T R .. (2)(2)-(1)得：[习题3－6] 压路机碾子重W ＝20ｋＮ，半径R ＝400ｍｍ，若用水平力F 拉碾子越过高ｈ＝2页N80ｍｍ的石坎，问F应多大?若要使F为最小，力F与水平线的夹角α应为多大?此时F等于多少?解：碾子走越过石坎时，22)()(hRRWhRF--=-当F倾斜时，令0)sin3cos4()cos3sin4(602=++--=αααααddF，得：3775.0arctan==α，此时，[习题3－7] 长２l的杆AB，重Ｗ，搁置在宽α的槽内。

工程力学第四版课后习题答案工程力学第四版课后习题答案工程力学是一门研究物体静力学和动力学的学科，是工程学的基础课程之一。

通过学习工程力学，可以帮助我们理解和解决各种工程问题。

而课后习题则是巩固和应用所学知识的重要方式。

本文将为读者提供工程力学第四版课后习题的答案，希望能够帮助大家更好地掌握这门学科。

第一章：力的基本概念1. 一个物体的质量是5kg，重力加速度为9.8m/s²，求其重力。

答案：重力 = 质量× 重力加速度= 5kg × 9.8m/s² = 49N2. 一个力的大小为20N，方向与x轴夹角为30°，求其在x轴上的分力。

答案：在x轴上的分力 = 力的大小× cos(夹角) = 20N × cos(30°) ≈ 17.32N第二章：力的作用效果1. 一个物体受到两个力的作用，一个力的大小为10N，方向与x轴正向夹角为30°；另一个力的大小为15N，方向与x轴正向夹角为60°。

求物体所受合力的大小和方向。

答案：合力的x分力= 10N × cos(30°) + 15N × cos(60°) ≈ 17.32N合力的y分力= 10N × sin(30°) + 15N × sin(60°) ≈ 23.09N合力的大小= √(合力的x分力² + 合力的y分力²) ≈ 28.35N合力的方向 = arctan(合力的y分力 / 合力的x分力) ≈ 53.13°第三章：力的分解与合成1. 一个力的大小为30N，方向与x轴夹角为45°，求其在x轴和y轴上的分力。

答案：在x轴上的分力 = 力的大小× cos(夹角) = 30N × cos(45°) ≈ 21.21N在y轴上的分力 = 力的大小× sin(夹角) = 30N × sin(45°) ≈ 21.21N2. 一个物体受到两个力的作用，一个力的大小为20N，方向与x轴正向夹角为60°；另一个力的大小为15N，方向与x轴正向夹角为45°。

页脚内容第一章第二章第三章 绪论思 考 题1) 现代力学有哪些重要的特征？2) 力是物体间的相互作用。

按其是否直接接触如何分类？试举例说明。

3) 工程静力学的基本研究内容和主线是什么？ 4) 试述工程力学研究问题的一般方法。

第二章 刚体静力学基本概念与理论习 题2-1 求图中作用在托架上的合力F R 。

习题2-1图12030200NN页脚内容2-2 已知F 1=7kN ，F 2=5kN, 求图中作用在耳环上的合力F R 。

2-3 求图中汇交力系的合力F R 。

2-4 求图中力F 2的大小和其方向角。

使 a )合力F R =1.5kN, 方向沿x 轴。

b)合力为零。

2-5 二力作用如图，F 1=500N 。

为提起木桩，欲使垂直向上的合力为F R =750N ，且F 2力尽量小，试求力F 2的大小和角。

24560F 1习题2-2图)xy4530F 1=30N F 2=20NF 3=40N Axy4560F 1=600NF 2=700NF 3=500N A 习题2-3图()x70F 2F 1=1.25kNA习题2-4图30F 1=500NAF 2页脚内容2-6 画出图中各物体的受力图。

(b )(a )A (c)(d )DACDB页脚内容2-7 画出图中各物体的受力图。

2-8 试计算图中各种情况下F 力对o 点之矩。

习题2-6图)(d )习题2-7图(a )DDAB CBABC页脚内容2-9 求图中力系的合力F R 及其作用位置。

习题2-8图P (d )PF)( a )NF 3NNM =6kN m F 3NF 2N页脚内容2-10 求图中作用在梁上的分布载荷的合力F R 及其作用位置。

( a )q 1=600N/mq=4kN/m( b )q A =3kN/ 习题2-9图( c )NF Nm F 3N页脚内容2-11 图示悬臂梁AB 上作用着分布载荷，q 1=400N/m ，q 2=900N/m, 若欲使作用在梁上的合力为零，求尺寸a 、b 的大小。