惯性参照系
- 格式:doc
- 大小:242.00 KB
- 文档页数:2

惯性与参照系的关系一切物体总保持匀速直线运动状态或静止状态,直到有外力迫使它改变这种状态为止。
这就是牛顿第一定律,又叫做惯性定律。
物体的这种保持原来的匀速直线运动或静止状态的性质叫做惯性。
假如这里脱离了任何天体的引力,飞船在靠惯性飞行。
那么飞船里的人和一切物体都处于失重状态,可以飘在空中,从手里松开的任何东西也不会往下落。
如果飞船又开动了火箭,以一定的加速度向前飞行,那么飞船里的人又感到有了重量,原来在空中漂浮的东西又纷纷加速下落。
如果飞船的加速度等于g=9.8米/秒2,那么这些现象就跟飞船停在地面时发生的一样。
假定飞船里的乘客完cuan听不到飞船的火箭工作的声音,他又看不到飞船外的任何物体,他就无法区分飞船是静止在地面或是在没有任何引力的空间做加速飞行。
在描述一个物体的运动时,选另外的物体作为标准。
描写物体的运动,可以考虑研究问题的方便,而任意选择参照系。
在某参照系看来,物体具有惯性,保持惯性运动,在另一参照系看来物体却在加速运动。
那么相对于某参照系,物体以一定的加速度加速运动时,相对于另一参照系看来,物体有可能具有惯性,在保持惯性运动。
物体具有惯性,在加速系(非惯性系)看来,物体以一定的加速度加速运动。
在非惯性系看来,以一定的加速度加速运动的物体,在惯性系看来,物体具有惯性。
在惯性系中加速运动的物体,在非惯性系看来,物体具有惯性。
例如自由落体运动在自由落体系看来处于惯性状态。
物体相对于参照系表现为惯性时,相对于另一参照系(有可能)表现为不是惯性。
相对于另一参照系,物体表现为不是惯性时;相对于参照系(有可能)表现为惯性。
如果物体相对于参照系表现为惯性时,把此时的参照系叫为惯性系,相对于另一参照系(有可能)表现为不是惯性时的参照系叫为非惯性系;,那么在惯性系中物体具有惯性,在非惯性系看来(加速系)物体受到惯性力加速运动;在非惯性系中受惯性力加速运动时,在惯性系看来,物体具有惯性。
那么在非惯性系(加速系)看来物体具有惯性时,在惯性系中,物体受到力加速运动。

惯性参考系的认识惯性系的定义对一切运动的描述,都是相对于某个参考系的。
参考系选取的不同,对运动的描述,或者说运动方程的形式,也随之不同。
人类从经验中发现,总可以找到这样的参考系:其时间是均匀流逝的,空间是均匀和各向同性的;在这样的参考系内,描述运动的方程有着最简单的形式。
这样的参考系就是惯性系。
朗道《场论》(主要是相对论电动力学)给出的定义:牛顿第一定律成立的参照系叫做惯性系。
(原文没有用牛顿第一定律,而是直接说在这样的参照系中,一个不受相互作用的粒子将保持静止或匀速直线运动)。
这个定义在牛顿力学和狭义相对论中均适用。
这样①牛顿第一定律定义了惯性系②牛顿力学在惯性系中成立。
(在相对论中,第二条只要修正为麦可斯韦方程组和相对论力学在其中成立即可)这样就不存在逻辑循环的问题,同时也可以说明,牛顿第一定律不是牛顿第二定律在F=0时的特殊情况。
在空间内,相对于任何参考点(静止中或移动中),一个运动中的粒子的位移、速度、和加速度都可以测量计算而求得。
虽然如此,经典力学假定有一组特别的参考系。
在这组特别的参考系内,大自然的力学定律呈现出比较简易的形式。
称这些特别的参考系为惯性参考系。
惯性参考系有个特性:两个惯性参考系之间的相对速度必是常数;相对于一个惯性参考系,任何非惯性参考系必定呈加速度运动。
所以,一个净外力是零的点粒子在任何惯性参考系内测量出的速度必定是常数;只有在净外力非零的状况下,才会有点粒子加速度运动。
问题是,因为万有引力的存在,并无任何方法能够保证找到净外力为零的惯性参考系。
实际而言,相对于遥远星体呈现常速度运动的参考系应是优良的选择。
惯性系判定一个参考系是不是惯性系,只能由试验确定。
最基本的判据就是牛顿运动定律成立与否。
根据伽利略相对性原理,和一个惯性系保持相对静止或相对匀速直线运动状态的参考系也是惯性系。
在实践中,人们总是根据实际需要选取近似的惯性参考系。
比如,在研究地面上物体小范围内的运动时,地球是一个很好的惯性系。




惯性参照系与非惯性参照系凡是牛顿运动定律能够适用的参考系称为惯性参照系(惯性系),反之,牛顿运动定律不适用的参考系称为非惯性参考系(非惯性系)。
摘自360百科《非惯性参照系》。
牛顿力学的基础就是惯性认识,惯性参照系是研究物体、星体运动规律的关键,可以说宇宙中的一切物体运动都是受制于物理环境的,因此不同的物理环境就是不同的惯性参照系,特别是选择惯性参照系的过程中此前的认识根本就不太考虑物理环境对相关研究对象的影响,有些认识甚至认为运动是相对的就可以互为运动的参照,而事实上,运动的参照系是不可以互选的,甚至根本就不能以研究对象作为运动的参照。
研究物体、星体、星系运动必须以产生各种物理环境的主要物体、星体、星系作为运动的参照,只有以产生相关的物理环境作为运动的参照才能正确认识自然的运动,因此宇宙中根本就不存在什么“非惯性参照系”,“牛顿运动定律不适用的参考系称为非惯性参考系(非惯性系)。
”之说显然不成立,因为宇宙中根本就不存在非物理环境,也就是说物理的宇宙根本就没有什么非惯性参考系,非惯性参考系只在在于一些人的幻想中,惯性是物体在物理环境中的基本现象,无论离其它物质物体多远其惯性强度可以发生改变而永远大于零。
惯性强度与牛顿力学或经典力学中的物体的“惯性质量”是成正比的,但是并不与牛顿力学或经典力学中的“引力质量”成正比。
在物理世界中有惯性强度的不同,因此也就要惯性参照系的不同,研究物体运动必须选择正确有效的惯性参照系,惯性参照系选择不当,其研究结果必然走偏。
而且特别要注意的是,不同的物理环境是很难等效的,因此《相对论》中的相对性原理研究不同空间的物体运动是不科学的,得到的结论必然也经不起检验。
不同宇宙空间中物质物体、星体星系间的任何相互作用都会或多或少受到不同空间环境其它物质物体、星体星系的影响,而且各种物质物体、星体星系随时都是运动和变化着的,绝对的等效几乎不存在。
所以真正不适应研究物理环境运动规律的是《相对论》、《量子力学》。

牛顿第一定律惯性与惯性参考系牛顿第一定律是经典力学中的基础原理之一,也被称为惯性定律。
它表明一个物体如果不受到外力的作用,将会保持静止或匀速直线运动。
惯性参考系是指观察者观测物体运动时所处的参考系。
本文将探讨牛顿第一定律的概念以及如何确定惯性参考系。
1. 牛顿第一定律的概念牛顿第一定律简称为惯性定律或惯性法则,由英国物理学家艾萨克·牛顿在1687年提出。
它表明在没有外力作用的情况下,物体将保持其运动状态,即静止或匀速直线运动。
这意味着物体具有惯性,即一种抵抗状态改变的性质。
2. 惯性参考系的定义惯性参考系是指一个观测者进行物体运动观察时所选择的参考系。
在这个参考系中,牛顿第一定律适用,物体如果不受到外力,则保持静止或匀速直线运动。
这样的参考系被认为是惯性参考系。
3. 如何确定惯性参考系确定惯性参考系的关键在于排除非惯性力的影响。
非惯性力是指不是由物体自身作用力引起的力,而是由其他物体或参考系的加速度引起的力。
当存在非惯性力时,物体将会受到额外的力的作用,从而使牛顿第一定律失效。
为了确定惯性参考系,可以采取以下步骤:3.1 观察是否存在可见的力在选定的参考系中观察物体的运动,如果物体在不受外力作用下保持静止或匀速直线运动,则说明该参考系是惯性参考系。
如果观察到物体的运动状态发生变化,可能存在非惯性力的作用。
3.2 排除外力的干扰如果在观测中发现物体的运动状态发生改变,需要仔细检查是否有外力的作用。
外力可以通过实验设计、测量仪器等方式进行确定和排除。
只有排除了外力的作用,才能得到准确的惯性参考系。
3.3 持续观测运动状态通过持续观测物体的运动状态,可以进一步验证所选参考系是否为惯性参考系。
如果运动状态始终保持不变,则说明该参考系是惯性参考系。
4. 惯性参考系的意义惯性参考系的确立对于研究物体的运动规律和力学定律具有重要意义。
只有在惯性参考系中,牛顿力学定律才能得到准确应用。
通过确定惯性参考系,我们可以研究物体在不受外力作用下的自由运动规律,揭示自然界中的普遍定律。

惯性,惯性定律和惯性参照系
惯性是维护物体运动力学运行状态的重要基础,因此我们都了解到它的重要性。
不仅行星、电影明星,而且连我们每日生活中也有惯性的体现。
惯性是物体本质上在没有外力作用时保持其内力和运动状态的能力。
这一能力
是“惯性定律”的基础。
它的基本原理是,只有物体力学行为受到外界力的作用,才能使物体有变速运动的状态。
在没有力的作用下,物体应当保持该状态不变。
谈到惯性的作用,就不得不提到“惯性参考系”。
惯性参考系可以理解为物体
在处于恒定运动状态时,参照物体之间的运动关系及物体运动变化量。
惯性参考系能够更全面、更准确地反映物体之间的运动关系。
在我们的日常生活中,一举一动都会受到惯性的影响。
比如运动员在沾上冰球
的冰面打球的时候必须考虑惯性的影响,街舞表演者跳舞的时候也要掌握视觉惯性;赛车手要掌握障碍赛车时的惯性,并准确控制车辆;乐队演奏乐曲时,它们也必须充分考虑乐器之间的惯性,这样才能使音乐更加协调。
举着小米手机打游戏也受到惯性的影响,因为当我们手中弄着手机,如果不考虑手机惯性,就无法及时准确的操作,也无法获得好的成绩。
总之,我们的日常生活中没有不受惯性的物体,惯性的作用体现在我们的每个
角落。
只有对惯性有深入的理解,我们才能得到更优秀的结果。


浅议惯性与参照系的关系文/姚黎豪摘要:对在运动进行描述时,需要选取一定的参照系,所选择的参照系不同,那么对物体运动的描述就会不同。
要判断一个参照系是否为惯性参照系,需要通过实验来验证。
而在对牛顿第一定律进行表述时,我认为要判断所选取的参照系是否为惯性系,其判断的依据就是牛顿第一定律是否成立。
关键词:惯性参照系关系|基础教育|惯性系是一种十分理想化的参照系,引力不会对其起到任何作用,且其自身不存在加速度,是一种较为自由的参照系。
在牛顿第一定律中,对惯性系进行定义,因此,我认为对惯性与参照系的关系进行研究非常有必要。
一、惯性与参照系惯性是指物体保持静止或者匀速直线运动状态的性质,其是物体的一种固有属性。
我认为,物体都有其自身的运动状态,而惯性所表现的就是物体对这一状态变化的阻抗程度,而对惯性大小进行衡量时,衡量的标准便是物体的质量。
比如,在物体不受外力时,惯性表现为物体的状态维持不变;当其受到外力的作用且外力不为0时,其状态就会发生改变。
参照系是在对物体运动情形进行研究时,所选定的具有参照作用的物体,或者彼此之间不存在相对运动的物体系。
将牛顿定律作为判断依据,如果其在参照系中成立,那么就认为其是惯性参照性;如果牛顿定律在参照系中不成立,那么则认为此参照系是非惯性参照系。
我认为参照系具有以下特点:首先,可被作为参照系的物体都是假设处于绝对静止状态的,而被研究物体的运动状态是相对于参照系来说的。
其次,任何物体都可作为参照系,因此,可根据研究需要,进行合理选择。
最后,在不同的运动进行比较时,应在同一参照系中进行。
二、惯性参照系的判断依据是牛顿第一定律动力学问题是高中物理研究的重点问题,而在解决此类问题时,比较常用的是牛顿第一定律和牛顿第二定律。
在运用牛顿定律时,我认为最重要的就是要确定惯性参照系。
我们都知道,在经典力学中,绝对静止的参照系是不存在的,因此只能假设存在这样的参照系,能够利用此参照系对牛顿定律进行表述,而惯性参照系是相对于绝对静止的参照系而言的,相对于其做匀速运动的参照系便被定义为惯性参照系。
惯性、力、惯性参照系
惯性、力、惯性参照系是物理学中的重要概念,它们在我们的日常生
活中也有着重要的作用。
惯性是指物体在没有外力作用的情况下,保持原有运动状态的能力。
它是物体运动的基本特性,也是物体运动的基础。
比如,当我们把一
个物体放在桌子上,它就会保持原有的位置,这就是惯性的作用。
力是指物体运动的基本原因,它可以改变物体的运动状态。
比如,当
我们用力把一个物体推动时,它就会发生运动,这就是力的作用。
惯性参照系是指在物体运动时,参照物的位置和运动状态。
比如,当
我们把一个物体放在桌子上,桌子就是参照物,它的位置和运动状态
就是惯性参照系。
惯性、力、惯性参照系在我们的日常生活中也有着重要的作用。
比如,当我们开车时,惯性参照系就是路面,它可以帮助我们更好地控制车
辆的运动方向;当我们拿起一个物体时,力就是我们的手,它可以帮
助我们把物体拿起来;当我们跳舞时,惯性就是我们身体的惯性,它
可以帮助我们更好地控制身体的运动方向。
总之,惯性、力、惯性参照系是物理学中的重要概念,它们在我们的
日常生活中也有着重要的作用,可以帮助我们更好地控制物体的运动
方向,更好地完成我们的日常活动。
惯性参照系名词解释惯性参照系是指以物体为参考系的非惯性系。
其实它就是一种坐标系,但它与常规坐标系有很大的区别,常规坐标系只有x、y、 z三个坐标轴,而惯性系则有四个坐标轴,即x、 y、 z、 r (惯性坐标轴),同时还有惯性原点,可见其独特之处。
下面来给你介绍几个惯性参照系: 1、地球静止系。
由于地球自转,故地球上的任何点都有一个固定的正北点,即地轴通过的地方,这个地方称为地轴。
地轴不是一条直线,而是一个极小的圆,叫做黄赤交角,这个角度随时间和地点而变化。
惯性参照系是在惯性系中不同点的位置相同的参考系。
那么除了惯性系之外,还有没有非惯性参照系呢?当然有!其特点如下:2、天文静止系。
3、非惯性系的特点。
①点的坐标与其在该参照系中的坐标不同;②不同点的时间间隔不同;③物理量的单位不同;④在不同参照系中,时间的流逝速率不同,或方向不同。
现举例说明,其目的是使同学们更好地掌握此概念。
( 1)水星的公转周期约为88.7d,故运动轨道是椭圆,太阳在椭圆轨道的长轴上,近日点时角速度达到最大,称为水星近日点进动。
它的椭圆形轨道与太阳的平均距离约为165.5日地距离,平均运行速度约为186km/s。
( 2)对地飞行物的水平飞行的航线,假设为一条抛物线,其末端落在两个焦点之内,称为极轨道。
运动的情况有四种:①落在一个焦点之内;②落在两个焦点之内;③落在焦点之外;④落在极点。
4、什么是动力学基本方程?其主要内容是:牛顿第二定律f=ma式中A为质量; m为物体的质量; G为牛顿第二定律; f为物体所受合外力的冲量; a为物体质心至质点的距离。
将物体作为惯性系,在基本方程的表述中,引入坐标、时间,而且引入力、加速度等变量。
总之,牛顿第二定律表示为物体具有惯性力,力的冲量就是物体受到的力,因此,引入动量变量,就是为了研究物体运动时所产生的惯性力和惯性力的冲量。
同时,引入动量变量也是为了研究物体间的相互作用。
当然,通过引入加速度和力、质量等变量,可以求解力学问题,从而进行研究,达到我们的目的。
惯性参照系
惯性参照系是物理学的基本概念,是衡量物体在宇宙中的运动的重要参照系。
它的基本定义是,“相对于某一个参照系,不受任何外力的作用,而具有
恒定运行速度和方向的物体,就称为惯性系。
”惯性参照系可以用于描述物体
的运动方向和物体运动的速度。
惯性参照系是一个虚拟的概念,它不存在于外
部的物理环境中,而是一个抽象的概念。
惯性参照系也是宇宙中运动的最基本的准则。
它指的是,对于一个坐标系
而言,当它以一个固定的速度运动时,在这一参考系中,它会一直保持这样的
运动,而不会被任何外力所影响。
惯性参照系可以让我们清楚地理解物体运动
以及外力在物体运动中所产生的影响。
此外,在实际应用中,惯性参照系也非常重要。
它可以用来对导航、飞行
和航海中的物体实现定位和运动的控制。
它在其它运动学问题的应用中也能发
挥重要作用,如研究基于惯性参照系的物体运动,从而制定出有效的控制策略。
总之,惯性参照系是一个非常重要的概念,它是许多物理问题的基础,同
时也在实际应用中发挥着重要作用。
参照系的名词解释参照系参照系(Reference Frame)是指研究一个物体或系统运动状态时所选择的一个参考标准或坐标系。
在物理学中,参照系是描述运动的基本工具之一。
以下是关于参照系的相关名词和其解释。
惯性参照系•惯性参照系(Inertial Reference Frame),是指一个不存在外力作用下,自由运动的物体的参照系。
在惯性参照系中,物体沿直线运动或保持静止。
例如,地球上的车厢内的物体在不受到摩擦力等外力作用下,沿直线匀速运动。
非惯性参照系•非惯性参照系(Non-inertial Reference Frame),是指在非惯性参照系中,物体受到惯性力的影响,出现了相对加速度。
非惯性参照系的例子包括旋转的车厢、加速的自动车辆等。
在非惯性参照系中,物体可能沿曲线运动,速度和方向都会改变。
固连参照系•固连参照系(Attached Reference Frame),是指参照系随着物体的运动一起移动的参照系。
例如,一个固连参照系可以是一个位于飞行器上的坐标系。
这种参照系能够以参照物为基准来描述物体的运动状态。
绝对参照系•绝对参照系(Absolute Reference Frame),是指一个无关联其他物体或系统而存在的参照系。
在绝对参照系中,物体的运动状态不会受到其他物体的影响。
然而,绝对参照系在现实中很难实现,通常是理论假设。
牛顿力学中的绝对时间和绝对空间就是绝对参照系的例子。
相对参照系•相对参照系(Relative Reference Frame),是指一个相对于其他物体或系统而存在的参照系。
在相对参照系中,物体的运动状态是相对于其他物体或系统来描述的。
例如,一个驾驶摩托车的人可以使用地面作为参照系来描述自己的速度和方向。
非相对论参照系•非相对论参照系(Non-relativistic Reference Frame),是指在经典力学中使用的参照系。
在非相对论参照系中,时间是绝对的,物体的速度远小于光速,不考虑相对论效应。
[科普知识]惯性参考系与非惯性参考系我们知道,任何物体的位置及变动,只有相对于事先选定的视为不动的物体而言才有明确的意义。
这种被选定的作为物体运动依据的物体称为“参考物”。
与参考物固连的三维空间称为“参考空间”。
参考空间和与之固连的钟的组合称为“参考系”。
那么什么是惯性参考系呢?牛顿在《自然哲学的数学原理》一书中,把运动规律总结为三条我们熟知的牛顿运动定律。
那么问题来了,第一定律中所谓不受力作用的物体保持静止或作匀速直线运动,是相对什么参考系而言的?也就是说,第一定律在什么参考系中成立?显然,第一定律不可能相对任何一个参考系都成立。
比如两列并列同向行进的火车A和B,A相对地面作匀速直线运动,B相对地面作加速直线运动,那么A相对于B就不可能作匀速直线运动。
牛顿自己解释第一定律在“绝对空间”中成立,但脱离物质的绝对空间是没有意义的,至少是无法判定的。
而在承认第一定律正确的前提下,我们总能找到这样一个参考系满足第一定律。
从这个意义上来说:尽管第一定律定义了惯性系,并断言了惯性系的存在,但实际的惯性系究竟在哪里?如果我们能找到一个物体C,它不受任何其他物体的作用,那么若存在另一物体D,C相对D静止或作匀速直线运动,那么我们就可以说这个物体C是一个惯性参考系。
显然,物体D也应该是一个远离其他物体的物体。
但完全不受其他物体作用的孤立物体(群)是不存在的,也就是说理想惯性系并不存在。
习惯上把某些星体(群)作为惯性系,但真正孤立的星体(群)是不存在的,所以这种惯性系只是近似的惯性系。
而非惯性系,即:严格来说,现实中的参考系都是非惯性系。
比如相对加速行驶着的火车,或相对转动着的离心机的运动等等。
但在应用牛顿运动定律解决具体问题的时候,常视实际情况把地面等作为为惯性系,以便牛顿三定律能够成立。
这种近似在研究某些精度要求不太高的问题时是合理的。
而且在非惯性系引入适当的“惯性力”之后,牛顿运动定律依然适用。
地球是最常用的惯性系。
惯性参照系
在第一单元中,我们提到过,运用运动学规律来讨论物体间的相对运动并计算物体的相遇时间时,参照系可以任意选择,视研究问题方便而定。
运动独立性原理的应用所涉及的,就是这一类问题。
但是,在研究运动与力的关系时,即涉及到运动学的问题时,参照系就不能任意选择了。
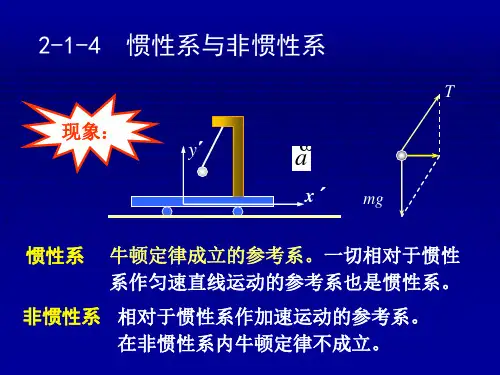
下面两个例子中,我们可以看到,牛顿运动定律只能对某些特定的参照系才成立,而对于正在做加速运动的参照系不再成立。
如图所示,甲球从高h 处开始自由下落。
在甲出发的同时,在地面上正对甲
球有乙球正以初速0v 做竖直上抛运动。
如果我们讨论的问题是:两球何时相遇,则参照系的选择是任意的。
如果选地面为参照系,甲做自由落体运动,乙做竖直上抛运动。
设甲向下的位移为1s ,乙向上的位移为2s ,则
t v gt t v gt s s h 020221)2
1(21=-+=+= 得 0v h t = 若改选甲为参照系,则乙相对于甲做匀速直线运动,相对位移为h ,相遇时间为0v h t =,可见,两个参照系所得出的结论是一致的。
如果我们分析运动和力的关系。
若选地球做参照系,甲做自由落体运动,乙做竖直上抛运动,二者都仅受重力,加速度都是g ,而g m G m F a ===,符合牛顿第二定律。
但如果选甲为参照系,则两物皆受重力而加速度为零(在这个参照系中观察不到重力加速度),显然牛顿第二定律不再成立。
再如图所示,平直轨道上有列车,正以速度v 做匀速运动,突然它以大小为a 的加速度刹车。
车厢内高h 的货架上有一光滑小球B 飞出并落在车厢地板上。
如果我们仅研究小球的运动,计算由于刹车,小球相对于车厢水平飞行多大距离。
若选地面为参照系,车厢做匀减速运动,向前位移为1s 。
小球在水平方向不受外力,做匀速运动,位移为2s ,在竖直方向上做自由落体运动,合运动为平抛运动。
2s 与1s 之差就是刹车过程中小球相对于车厢水平飞行的距离。
2200122
1)21(at at t v t v s s x =--=-= g h t 2=
若改选小球做参照系,水平速度v 观察不到,车厢相对于小球做大小为a ,方向向车前进反方向的,初速为零的匀加速运动。
直接可以写出22
1at x -=',两种方法得出相同的结论。
如果我们对小球研究运动和力的关系。
选地球为参照系时,小球具有向前的初速v ,仅受重力,做平抛运动,加速度为g ,符合牛顿第二定律。
若选车厢做参照系,小球在水平方向相对于车厢将附加一个加速度为a -,由于速度v 观察不到。
小球相对于车厢仅具有一个大小为22)(a g -+,方向斜向前下方的加速度,做初速为零的匀加速运动。
显然m G g a g a =≠-+=22)(,牛顿第二定律不再成立。
人们把牛顿运动定律能在其中成立的参照系叫做惯性系。
在研究问题精度要求不太高的情况下,地球可以看作惯性系。
而相对于地球做匀速直线运动的参照系都可以作为惯性系。
在中学范围内讨论动力学问题时所选取的坐标系,都必须是惯性系,计算力时,代入公式的速度和加速度,都必须是相对于地球的。
有时,为了研究问题方便,讨论动力学问题时,需选取做加速运动的物体做参照系(非惯性系)。
为了使牛顿定律在这一坐标系中成立,必须引入一个虚拟的力(它没有施力者),叫做“惯性力”。
它的大小等于ma ,方向与所选定的非惯性系的加速度的方向相反。
在上例中,引入“惯性力”后,小球所受合外力为重力与“惯性力”(ma -)的合力,其大小
2222)()(g a m ma mg F +=-+= 它所产生的加速度大小为22g a +,正好与在车厢中观察的加速度一致。
牛顿定律又重新成立了。