用EXCEL计算卡方统计量时x2
- 格式:xls
- 大小:17.00 KB
- 文档页数:1

如何在Excel中使用CHIDIST函数计算卡方分布的累积概率在Excel中,使用CHIDIST函数可以计算卡方分布的累积概率。
卡方分布是一种常见的统计分布,用于判断随机变量的观察值与理论值之间的偏差程度。
本文将向您介绍如何使用CHIDIST函数进行卡方分布的累积概率计算。
首先,我们需要了解CHIDIST函数的语法。
CHIDIST函数的参数有两个,分别为x和自由度(deg_freedom)。
其中,x代表要计算的值,自由度代表卡方分布的自由度。
在Excel中,我们可以通过以下步骤来计算卡方分布的累积概率:1. 打开Excel,并创建一个新的工作表。
2. 在A1单元格中输入标题"卡方分布累积概率计算"。
3. 在A3单元格中输入标题"观察值",在A4单元格中输入标题"自由度"。
4. 在B3单元格中输入要计算的观察值,例如5。
在B4单元格中输入卡方分布的自由度,例如3。
5. 在C3单元格中输入标题"累积概率"。
6. 在C4单元格中输入CHIDIST函数的公式,即"=CHIDIST(B3,B4)"。
7. 按下Enter键,即可得到卡方分布的累积概率值。
通过上述步骤,我们就可以在Excel中使用CHIDIST函数计算卡方分布的累积概率了。
下面,我们将通过一个示例来进一步说明。
假设我们要计算观察值为5,自由度为3的卡方分布的累积概率。
按照上述步骤,在B3单元格中输入5,在B4单元格中输入3。
然后按下Enter键,我们可以得到C4单元格中的卡方分布的累积概率值。
需要注意的是,CHIDIST函数计算的是右尾概率,即大于等于给定值的概率。
如果需要计算左尾概率(小于等于给定值的概率),可以使用CHIINV函数。
在使用CHIDIST函数计算卡方分布的累积概率时,我们还可以使用Excel提供的其他功能,如填充函数、自动计算等,以提高效率和准确性。


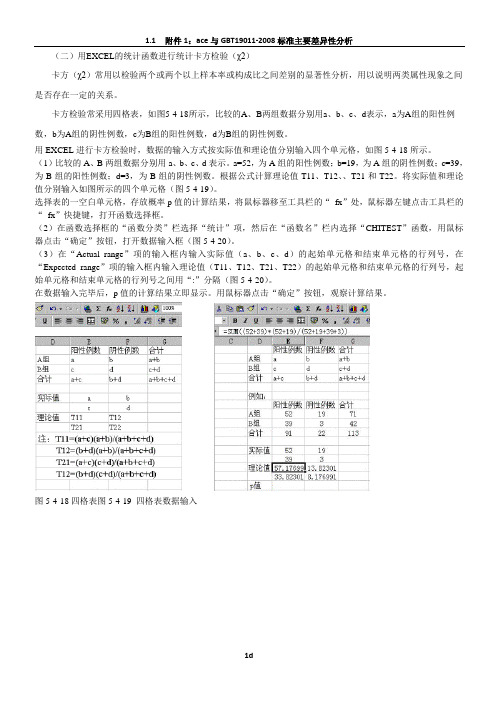
(二)用EXCEL的统计函数进行统计卡方检验(χ2)卡方(χ2)常用以检验两个或两个以上样本率或构成比之间差别的显著性分析,用以说明两类属性现象之间是否存在一定的关系。
卡方检验常采用四格表,如图5-4-18所示,比较的A、B两组数据分别用a、b、c、d表示,a为A组的阳性例数,b为A组的阴性例数,c为B组的阳性例数,d为B组的阴性例数。
用EXCEL进行卡方检验时,数据的输入方式按实际值和理论值分别输入四个单元格,如图5-4-18所示。
(1)比较的A、B两组数据分别用a、b、c、d表示。
a=52,为A组的阳性例数;b=19,为A组的阴性例数;c=39,为B组的阳性例数;d=3,为B组的阴性例数。
根据公式计算理论值T11、T12、、T21和T22。
将实际值和理论值分别输入如图所示的四个单元格(图5-4-19)。
选择表的一空白单元格,存放概率p值的计算结果,将鼠标器移至工具栏的“fx”处,鼠标器左键点击工具栏的“fx”快捷键,打开函数选择框。
(2)在函数选择框的“函数分类”栏选择“统计”项,然后在“函数名”栏内选择“CHITEST”函数,用鼠标器点击“确定”按钮,打开数据输入框(图5-4-20)。
(3)在“Actual_range”项的输入框内输入实际值(a、b、c、d)的起始单元格和结束单元格的行列号,在“Expected_range”项的输入框内输入理论值(T11、T12、T21、T22)的起始单元格和结束单元格的行列号,起始单元格和结束单元格的行列号之间用“:”分隔(图5-4-20)。
在数据输入完毕后,p值的计算结果立即显示。
用鼠标器点击“确定”按钮,观察计算结果。
图5-4-18四格表图5-4-19 四格表数据输入图5-4-20 计算选择框图5-4-21 p值计算结果4.在表存放概率p 值的空白单元格处显示p 值的计算结果。
在“编辑”栏处显示χ2检验的函数“CHITEST”及两组比较数据的起始与结束单元格的行列号(图5-4-21)。

卡方检验医学统计EXCEL模板卡方检验是一种用来判断两个分类变量之间是否存在显著关联的统计方法,常应用于医学研究中,比如判断其中一种疾病是否与其中一种风险因素相关等。
在进行卡方检验时,我们需要计算一个卡方值,并根据卡方分布表得到相应的P值,进而判断两个变量之间的关联性。
下面我们介绍如何使用Excel来进行卡方检验,并给出一个模板供参考。
首先,我们需要准备两个分类变量的数据,假设我们研究其中一种疾病与性别的关系,将性别分为男和女两个分类。
假设我们有100个样本数据,其中男性有60人,女性有40人。
我们想要判断性别是否与患该种疾病的风险相关。
接下来,我们使用Excel来计算卡方值。
首先,将数据按照以下表格形式输入到Excel中:```疾病男性女性患病ab未患病cd```在Excel中,我们可以将上述数据输入到A1:D3单元格范围中。
然后,我们需要计算每个单元格的期望频数。
期望频数是指根据两个变量的边际分布计算得到的理论上的预期频数。
在E1单元格中输入以下公式:"=SUM($B$2:$B$3)*SUM($C$2:$D$2)/SUM($B$2:$D$3)",在F1单元格中输入公式:"=SUM($B$2:$B$3)*SUM($D$2:$D$3)/SUM($B$2:$D$3)",在E2单元格中输入公式:"=SUM($C$2:$D$3)*SUM($C$2:$D$2)/SUM($B$2:$D$3)",在F2单元格中输入公式:"=SUM($C$2:$D$3)*SUM($D$2:$D$3)/SUM($B$2:$D$3)"。
然后,我们需要计算每个单元格的卡方值。
在G2单元格中输入公式:"=((B2-E2)^2)/E2",在H2单元格中输入公式:"=((B2-F2)^2)/F2",在G3单元格中输入公式:"=((C3-E3)^2)/E3",在H3单元格中输入公式:"=((C3-F3)^2)/F3"。

excel卡方分布函数公式卡方分布是一种常用的概率分布函数,在统计学和数据分析中经常被使用。
Excel提供了相应的函数来计算卡方分布的概率值。
本文将介绍Excel中的卡方分布函数公式以及如何使用卡方分布函数进行计算。
在Excel中,卡方分布函数的语法如下:CHISQ.DIST(x,df,cumulative)其中,x代表一个实数,表示要计算概率值的点;df代表自由度,是卡方分布的参数;cumulative是一个逻辑值,用于指定求解累积分布函数或概率密度函数。
下面将详细解释参数的含义以及如何使用卡方分布函数。
- x:代表要计算概率值的点。
通常情况下,x应该为非负数。
如果x小于0,则卡方分布函数的结果将为错误值#NUM!。
- df:表示卡方分布的自由度。
在卡方分布中,自由度是一个重要的参数,决定了卡方分布的形状。
较大的自由度意味着卡方分布趋于正态分布。
- cumulative:是一个逻辑值,用于确定是计算累积分布函数还是概率密度函数。
如果cumulative为TRUE,则计算累积分布函数;如果cumulative为FALSE,则计算概率密度函数。
下面举例说明如何使用Excel的卡方分布函数。
假设我们有一组样本数据,我们想要计算这组数据的卡方分布的概率值。
首先,我们需要输入样本数据。
假设我们的数据位于A1到A10单元格中。
我们可以使用CHISQ.DIST函数来计算卡方分布的概率。
在B1单元格中,输入以下公式:=CHISQ.DIST(A1, 9, FALSE)上述公式表示计算x为A1单元格的值,自由度为9的卡方分布的概率密度函数值。
然后,拖动鼠标选择B1单元格,直到B10单元格,以复制该公式到B列的其余单元格中。
这样,我们就可以同时计算这组数据对应的卡方分布的概率密度函数值。
接下来,我们可以在另一个单元格中使用CHISQ.DIST函数来计算累积分布函数值。
假设我们想要计算累积分布函数值,可以在C1单元格中输入以下公式:=CHISQ.DIST(A1, 9, TRUE)与之前相同,我们拖动鼠标选择C1单元格,直到C10单元格,以将该公式复制到C列的其他单元格中。
(二)用EXCEL的统计函数进行统计4.卡方检验(χ2)卡方(χ2)常用以检验两个或两个以上样本率或构成比之间差别的显著性分析,用以说明两类属性现象之间是否存在一定的关系。
卡方检验常采用四格表,如图5-4-18所示,比较的A、B两组数据分别用a、b、c、d表示,a 为A组的阳性例数,b为A组的阴性例数,c为B组的阳性例数,d为B组的阴性例数。
用EXCEL进行卡方检验时,数据的输入方式按实际值和理论值分别输入四个单元格,如图5-4-18所示。
(1)比较的A、B两组数据分别用a、b、c、d表示。
a=52,为A组的阳性例数;b=19,为A 组的阴性例数;c=39,为B组的阳性例数;d=3,为B组的阴性例数。
根据公式计算理论值T11、T12、、T21和T22。
将实际值和理论值分别输入如图所示的四个单元格(图5-4-19)。
选择表的一空白单元格,存放概率p值的计算结果,将鼠标器移至工具栏的“fx”处,鼠标器左键点击工具栏的“fx”快捷键,打开函数选择框。
(2)在函数选择框的“函数分类”栏选择“统计”项,然后在“函数名”栏内选择“CHITEST”函数,用鼠标器点击“确定”按钮,打开数据输入框(图5-4-20)。
(3)在“Actual_rang e”项的输入框内输入实际值(a、b、c、d)的起始单元格和结束单元格的行列号,在“Expected_ra nge”项的输入框内输入理论值(T11、T12、T21、T22)的起始单元格和结束单元格的行列号,起始单元格和结束单元格的行列号之间用“:”分隔(图5-4-20)。
在数据输入完毕后,p值的计算结果立即显示。
用鼠标器点击“确定”按钮,观察计算结果。
图5-4-18 四格表图5-4-19 四格表数据输入图5-4-20 计算选择框图5-4-21 p值计算结果4.在表存放概率p 值的空白单元格处显示 p值的计算结果。
如何用EXCEL的统计函数进行统计卡方检验(χ2)卡方(χ2)常用以检验两个或两个以上样本率或构成比之间差别的显著性分析,用以说明两类属性现象之间是否存在一定的关系。
卡方检验常采用四格表,如图5-4-18所示,比较的A、B两组数据分别用a、b、c、d表示,a为A组的阳性例数,b为A组的阴性例数,c为B组的阳性例数,d为B组的阴性例数。
用EXCEL进行卡方检验时,数据的输入方式按实际值和理论值分别输入四个单元格,如图5-4-18所示。
(1)比较的A、B两组数据分别用a、b、c、d表示。
a=52,为A组的阳性例数;b=19,为A组的阴性例数;c=39,为B组的阳性例数;d=3,为B组的阴性例数。
根据公式计算理论值T11、T12、、T21和T22。
将实际值和理论值分别输入如图所示的四个单元格(图5-4-19)。
选择表的一空白单元格,存放概率p值的计算结果,将鼠标器移至工具栏的“fx”处,鼠标器左键点击工具栏的“fx”快捷键,打开函数选择框。
(2)在函数选择框的“函数分类”栏选择“统计”项,然后在“函数名”栏内选择“CHITEST”函数,用鼠标器点击“确定”按钮,打开数据输入框(图5-4-20)。
(3)在“Actual_range”项的输入框内输入实际值(a、b、c、d)的起始单元格和结束单元格的行列号,在“Expected_range”项的输入框内输入理论值(T11、T12、T21、T22)的起始单元格和结束单元格的行列号,起始单元格和结束单元格的行列号之间用“:”分隔(图5-4-20)。
在数据输入完毕后,p值的计算结果立即显示。
用鼠标器点击“确定”按钮,观察计算结果。
图5-4-18四格表图5-4-19四格表数据输入图5-4-20计算选择框图5-4-21p值计算结果4.在表存放概率p值的空白单元格处显示p值的计算结果。
在“编辑”栏处显示χ2检验的函数“CHITEST”及两组比较数据的起始与结束单元格的行列号(图5-4-21)。
(二)用EXCEL的统计函数进行统计卡方检验(χ2)之杨若古兰创作卡方(χ2)经常使用以检验两个或两个以上样本率或构成比之间差此外明显性分析,用以说明两类属性景象之间是否存在必定的关系.卡方检验常采取四格表,如图5-4-18所示,比较的A、B两组数据分别用a、b、c、d暗示,a为A组的阳性例数,b为A组的阴性例数,c为B组的阳性例数,d为B组的阴性例数.用EXCEL进行卡方检验时,数据的输入方式按实际值和理论值分别输入四个单元格,如图5-4-18所示.(1)比较的A、B两组数据分别用a、b、c、d暗示.a=52,为A组的阳性例数;b=19,为A组的阴性例数;c=39,为B组的阳性例数;d=3,为B组的阴性例数.根据公式计算理论值T11、T12、、T21和T22.将实际值和理论值分别输入如图所示的四个单元格(图5-4-19).选择表的一空白单元格,存放概率p值的计算结果,将鼠标器移至工具栏的“ fx”处,鼠标器左键点击工具栏的“ fx”快捷键,打开函数选择框.(2)在函数选择框的“函数分类”栏选择“统计”项,然后在“函数名”栏内选择“CHITEST”函数,用鼠标器点击“确定”按钮,打开数据输入框(图5-4-20).(3)在“Actual_range”项的输入框内输入实际值(a、b、c、d)的起始单元格和结束单元格的行列号,在“Expected_range”项的输入框内输入理论值(T11、T12、T21、T22)的起始单元格和结束单元格的行列号,起始单元格和结束单元格的行列号之间用“:”分隔(图5-4-20).在数据输入终了后,p值的计算结果立即显示.用鼠标器点击“确定”按钮,观察计算结果.图5-4-18四格表图5-4-19 四格表数据输入图5-4-20 计算选择框图5-4-21 p值计算结果4.在表存放概率 p 值的空白单元格处显示 p 值的计算结果.在“编辑”栏处显示χ2检验的函数“CHITEST”及两组比较数据的起始与结束单元格的行列号(图5-4-21).。
利用Excel的CHIINV函数编制卡方分布表董大钧卡方分布(Chi-square Distribution)是常用的一种概率分布。
若n个独立的随机变量均服从标准正态分布,则这n个随机变量的平方和构成一新的随机变量,其分布规律称为服从自由度为ν的χ2分布。
卡方分布常用于假设检验和置信区间的计算。
χ2分布具有可加性:若有K个服从χ2分布且相互独立的随机变量,则它们之和仍是χ2分布,新的χ2分布的自由度为原来K个χ2分布自由度之和。
卡方分布可以用来测试随机变量之间是否相互独立,也可用来检测统计模型是否符合实际要求。
卡方分布的概率密度曲线如图1所示:图1 卡方分布的概率密度曲线在对实验数据进行卡方分析时,需要查找卡方分布表,在大多数涉及卡方分布的书中都会提供它的累积分布的概率值表。
然而查表很不方便,使用Excel的CHIINV函数可以获得卡方分布的概率值。
函数格式:CHIINV(概率,自由度)在Excel中,可以利用CHIINV函数生成卡方分布表。
在下面的Excel表格中,第3行为显著性水平α,如B3、C3、D3、E3分别为0.1、0.05、0.025、0.01;A列为自由度,A4为1,A5为2,选定A4、A5,向下拉动填充柄,得到连续的整数。
B4单元格中公式为= CHIINV(B$3, $A4 )这里,B4单元格公式中地址引用使用了混合地址,B$3锚定了第3行,以保证不管公式复制到那一行的单元格,都使用该列第3行的值;$A4锚定了A列相应的行(自由度)。
回车后显示为2.705544。
选中B3单元格,向右拖动填充柄,复制公式至E列,再向下拖动填充柄,到需要的行。
选中B4:E18整块区域,设定小数位为6位小数。
以保证所有的函数值都为6位小数,结果如图2所示。
这样就可得到卡方分布表。
实际应用中,可根据α与ν,使用CHIINV(α,ν)得到需要的卡方值,不必再查表,方便了数据处理分析。
图2卡方分布表。