下载文档原格式
实验⼋粉体⼒学特性测定实验⼋粉体⼒学特性测定⼀、实验⽬的了解DSJ-3型电动四联等应变直剪仪与BT-1000型粉体综合特性测试仪的结构与⼯作原理，通过实验掌握粉体摩擦⾓与休⽌⾓的测定⽅法，并了解上述粉体特性在粉体输送与储存等单元操作中的意义。
⼆、实验装置DSJ-3型电动四联等应变直剪仪的结构如图1，可同时采⽤四个试样，分别在不同的垂直压⼒下施加⽔平剪切⼒进⾏剪切，求得粉体样破坏时的剪应⼒，然后根据库仑定律确定粉体的摩擦⾓。
图1 DJS-3型电动四联等应变直剪仪1⼿轮 2推动座 3 固定盒 4 滑动盒 5 量⼒环 6 测微表 7 加压装置8 量⼒环⽀架 9 杠杠 10 吊盘部件 11 传动装置 12 换档⼿柄DSJ-3型电动四联等应变直剪仪可分为推动、剪切、杠杆加荷、测⼒四部分。
推动部分1 910 283 4 6 5 7 1211的推动轴的⽔平推进速率分为2.4、0.8、0.1、0.02mm/min 四档；剪切盒分上盒和下盒，上盒剪切过程中固定不动，下盒可沿底部导轨移动，盒内物料⾯积为30cm 2，⾼2cm ，；杠杆⽐例为1：12；仪器附有砝码多块，其中1.275公⽄4块，2.55公⽄12块。
可使物料表⾯加上垂直应⼒数值为50、100、200、400KPa 等四级。
测⼒环置于剪切盒与后档之间，测量⽔平剪切⼒。
BT-1000型粉体综合特性测试仪是⼀种主要⽤于评价粉体流动特性的仪器，其测试项⽬包括休⽌⾓、动态休⽌⾓、平板⾓、分散度、松装密度及振实密度等参数，其结构如图2，本实验主要⽤于测试休⽌⾓及动态休⽌⾓。
图2 BT-1000型粉体综合特性测试仪正⾯图1 定时器开关2 照明灯开关3 出料⼝4 透明套筒管5 松、实密度6 休⽌⾓试样7 接料盘8 减振器9 电源开关 10 分散度料仓 11 ⾓度尺12 照明灯 13 分散度筒 14 振动电机开关 15 振动筛开关 16 定时器三、实验原理休⽌⾓(⽤符号?r 表⽰)是指物料的⾃由表⾯与⽔平⾯所形成的最⼤⾓度。
粉尘爆炸：悬浮于空气中的可燃粉尘颗粒与空气中氧气充分接触，在特定的条件下瞬间完成的氧化反应，反应中放出大量的热，进而产生高温、高压现象。
粉尘爆炸的6个阶段：1、（未反应带）颗粒表面的初期燃烧，温度尚未上升，氧化反应尚未开始。
2、（发泡带）外形无变化，随着粉体内的温度上升，粉体开始分解及放出挥发性成分，粉体起泡3、（流运带）粉体温度继续上升，挥发性成分也在空气中广泛流动，但还未发生燃烧。
4、（反应带）挥发性成分流速增快5、（燃烧带）燃烧反应加剧，发出旺盛火焰6、（炽热带）处于火焰温度，光亮闪耀。
除重力外颗粒不再受任何外力的作用，此时的流动状态称为：自由流动粉体自由流动型式：1、全仓流（整体流）：整个粉体层在料仓内能够大致均匀地下降以至流出，其特点是：‘先进先出’。
（流动性优良的粉体或细粒散体一般可实现全仓流）2、核仓流（漏斗流）料仓内粉体层的流动区域呈漏斗形，粉体在储存设备的中心区域是流动的，但在边缘或壁面附近是静止不动的，造成部分先加入的物料后流出的结果，即‘后进先出’（锥角较大或粉体流动性能差时可见核仓流）配位数：粉体堆积中与某颗粒接触的颗粒的个数。
球形度：与颗粒体积相等的球表面积与实际颗粒的表面积之比。
（球）当量径：往往以球为基准，把不规则形状的颗粒看作是某当量球。
等球径就是与颗粒某几何量或物理量相当的球体直径。
视密度（粉体视在密度，堆积密度）：单位堆积体积V所含粉体质量m 。
填充的粉体质量/粉体的填充体积。
破坏包络线：粉体开始滑移时滑移面上的切应力、正应力用坐标曲线来表示，并称这样的曲线为该粉体的破坏包络线。
破坏包络线的切线与正应力轴的夹角称为内摩擦角。
破坏角：说明破坏面方位的角度。
三轴压缩：给定水平压力（围压），然后用活塞单向压缩，变动铅锤压力，直至粉体破坏，记录下此时的铅锤压力的极限值。
分数维：维数是几何对象的一个重要特征量，它是几何对象中一个点的位置所需的独立坐标数目。
在欧氏空间中，人们习惯把空间看成三维的，平面或球面看成二维，而把直线或曲线看成一维。
颗粒:人工或天然制成的粒状物。
一般指固体颗粒。
粉体:大量具有相互作用的微小固体颗粒的集合体。
粉体的特点：1、具有固体的抗变形能力；2、具有与液体相类似的流动性；3、粉体不是连续体，受压后体积缩小类似气体性质。
粉体的种类：按成因分类：自然粒体、工业粉尘、人工粒体；按粒度大小分类：粗粒、细化学活性。
可塑性能好：没有固定的外形。
流动性好：便于输送、储存、混合、成型等单元操作。
物化性质：电、磁、光、声、热；吸附、湿润；溶解；燃烧。
粉粒体：颗粒（＞100 μm）；粉体（1～100μm）；超细粉体（0.1～1μm）；纳米粉体（＜0.1μm）。
粉体的粒子学特性包括粉体粒径、粒径分布、粒子形状、密度、流动性、堆积密度、比表面积等。
尺寸分布的概念：原因：粉体是有不连续的微粒组成，属于多分散系统。
因此粉体颗粒的粒径不是单一的，通常会在一定范围内连续取值。
即颗粒的大小服从统计学规律。
粉体的力学性能，不仅与其平均粒径的大小有关，还与各种粒径的颗粒在粉体中所占的比例有关。
为了表示粉体中颗粒大小组成情况，必须要用粒度分布的概念。
定义及意义：描述粒径分布的状态。
通常是指某一粒径的颗粒在整个粉体中所占的比例。
有了粒度分布的数据，就不难求出这种粉体的某些特征值，如平均粒径等从而可以对成品粒度进行评价。
尺寸分布的基准：1．作为分散系统的粉体，其颗粒的大小服从统计学规律。
单个颗粒的粒径是在某一范围内随机取值，对整个粉体，可以用采样分析的方法来测量粒度分布。
（频率分布与累积分布）2．尺寸分布可以取个数、长度、面积、体积（或质量）等4个参数中的一个作为基准。
粒度分布的基准取决于粒度分布的测定方法。
如用显微镜法测定粒径分布时常用个数基准；用沉降法时用质量基准。
测量/描述方法：将连续的粒度分布范围分成多个离散的粒级，测出各粒级中颗粒的个数或质量百分数。
显微镜法；计数器法：个数分布数据。
筛分析法；沉降法：个数分布数据；数学函数法：概率理论或近似函数的经验法寻求数学函数，以描述粒度分布。
中位粒径D50：粉体物料的样品中，把样品的个数（或质量）分成相等两部分的颗粒粒径。
最频粒径Dmod：频率分布坐标图中，纵坐标最大值对应的粒径。
即在颗粒群中个数或质量出现概率最大的颗粒粒径。
若f(Dp)已知，令f(Dp)的一阶导数为零，可求出Dmod。
若D(Dp)或R(Dp)已知，其二阶导数为零，可求出Dmod。
标准偏差：分布的标准偏差，即粒径Di对平均粒径的二次矩的平方根。
它反映分布对D平的分散程度。
分布函数中的两个参数D平和 完全决定了粒度分布。
粉体密度的概念：粉体的密度系指单位体积粉体的质量。
由于粉体的颗粒内部和颗粒间存在空隙，粉体的体积具有不同的含义。
粉体的密度根据所指的体积不同分为真密度、表观密度、松密度三种。
ρ真=ρ表/(1-e)概述：由于颗粒的形状多为不规则体，因此用一个数值去描述一个三维几何体的大小是不可能的。
对于一个形状极其复杂的颗粒来说，用一个数值去直接描述它们的大小就更不可能了。
那么，怎样仅用一个数值描述一个颗粒的大小？这是粒度测试的基本问题。
取样方法测试方法的种类：筛分法；显微镜法；库尔特计数法；沉降法；空气透过法，气体吸附法。
形状系数：粒径相同的颗粒，形状不相同，其表面积、体积也相同，因此，颗粒的表面积、体积与其粒径之间的数量关系，在一定的程度上可以反映颗粒的形状。
另外，颗粒的表面积、体积是与某一特征尺寸（粒径）的平方、立方成正比的，这个比例系数就可定义为颗粒的形状系数。
注意：①粒径的定义和粒径的测量方法②单个颗粒的形状系数与整个颗粒群的形状系数的区别。
③形状系数为一个修正系数，用来衡量实际颗粒与球形颗粒不一致的程度。
形状指数：利用颗粒本身的各种粒径以及表面积等数据进行各种无因次的组合，或与球形颗粒进行比较而定义的表示颗粒形状的各种指标称为形状指数，其本身并不具有特定的物理意义。
根据不同的使用目的，可选择相应的形状指数来表示颗粒的形状。
常用的形状指数有：自由沉降与沉降速度：颗粒-流体体系一定，ut一定，与之对应的Rep 也一定。
根据对应的Rep，可得到不同Rep范围内ut 的计算式：()218p p tgd u ρρμ-=()0.60.27p pp t g d Re u ρρρ-=⨯()1.74p p t gd u ρρρ-=⨯(1) Rep <2，层流区(斯托克斯公式) (2) 2<Rep <500，过渡区(阿仑公式) (3) 500<Rep <1×105，湍流区(牛顿公式) 因Rep 中包含 ut ，故需通过假设检验法确定计算公式。
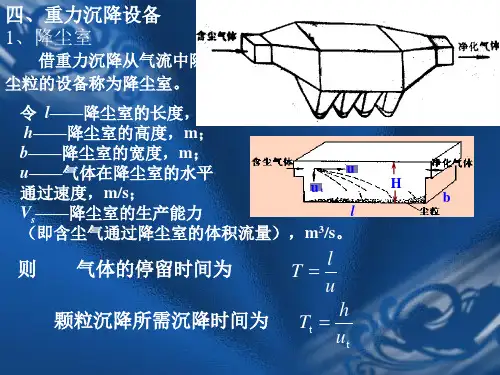
沉降分离满足的基本条件为 T ≥T t 或 降尘室的生产能力为 理论上降尘室的生产能力只与其沉降面积bl 及颗粒的沉降速度ut 有关，而与降尘室高度无关。
故降尘室应设计成扁平形，或在室内均匀设置多层水平隔板，构成多层降尘室。
多层降尘室生产能力：VS ≤(n+1)ut ·lb )(1取整-≥∴t S blu V n 1+=n Hh 隔板间距： 沉降速度ut 应按需要分离下来的最小颗粒计算；气流速度u 不应太高，以免干扰颗粒的沉降或把已经沉降下来的颗粒重新卷起。
为此，应保证气体流动的雷诺准数处于滞流范围之内；降尘室结构简单，流动阻力小，但体积庞大，分离效率低，通常仅适用于分离直径大于50μm 的颗粒，用于过程的预除尘。
多层降尘室虽能分离细小的颗粒，并节省地面，但出灰麻烦。
降尘室的计算：设计型：已知气体处理量和除尘要求，求降尘室的大小；操作型：用已知尺寸的降尘室处理一定量含尘气体时，计算可以完全除掉的最小颗粒的尺寸，或者计算要求完全除去直径dp 的尘粒时所能处理的气体流量。
固体颗粒容易聚集在一起，尤其是细颗粒——颗粒之间存在附着力；粉体的摩擦特性、流动性、分散性、可压缩性等分子间的范德华力、颗粒间的范德华力、附着水分的毛细管力、颗粒间的静电力、磁性力、颗粒表面不平引起的机械咬合力。
颗粒间 液相状态摆动状态 链索状态 毛细管状态 浸渍状态摆动状态：颗粒接触点上存在透镜状或环状的液相，液相互不连续；链索状态：随着液体量增多，环张大，颗粒空隙中的液相相互连结成网状，空气分布其中；毛细管状态：颗粒间的所有空隙被液体充满，仅在粉体层表面存在气液界面；浸渍状态：颗粒群浸在液体中，存在自由液面空气中颗粒团聚的主要原因是什么？什么作用力起主要作用？非常干燥条件下又是什么作用力其主要作用？团聚：颗粒在气相或液相中，颗粒间的作用力远大于颗粒的重力而形成聚合状态。
在空气中，颗粒的团聚主要是毛细力造成的。
在干燥条件下由范德华力引起的。
颗粒在空气中和液体中分散的主要途径有哪些？颗粒在空气中分散：机械分散、干燥分散、表面改性、静电分散。
颗粒在液体中的分散：介质调控、分散剂调控、超声调控和机械调控。
粉体流动所形成的角度，是表征粉体力学行为和流动状况的重要参数。
由于颗粒间的摩擦力和内聚力形成的角度统称为摩擦角。
根据颗粒群运动状态的不同，分为安息角/休止角：安息角越小，粉体的流动性越好。
内摩擦角、壁面摩擦角、运动摩擦角。
内摩擦角：库仑定律 µC －粉体的摩擦系数（内摩擦系数）； c －初抗剪强度；c = 0 时，为“简单库仑粉体”。
t u hu l ≥ts blu V =C c τμσ=+0 στCA B AByσxσxyOθ σx τxy σyn σθ τ剪切盒试验Molerus 按照粉体的摩擦行为将粉体分成三类： 初抗剪强度C=0的粉体为Molerus I 类粉体 初抗剪强度C ≠0，与预压缩应力无关的粉体为 Molerus II 类粉体初抗剪强度C ≠0，与预压缩应力有关的粉体为 Molerus III 类粉体由式得：Molerus I 类粉体的开放屈服强度为0，即Molerus I 类粉体不结拱； Molerus II 类粉体的开放屈服强度为常数，与预压缩应力无关；Molerus III 类粉体的开放屈服强度随预压缩应力的增加而增加，即拱的强度随预压缩应力的增加而增加。
W.Jenlike 粉体流动函数：0σ：预压缩应力；c f ：水泥粉体的开发屈服强度莫尔应力圆：粉体的应力规定：粉体内部的滑动可沿任何一个面发生，只要该面上的 剪应力达到其抗剪强度。
用摩尔应力圆表示斜面上的应力由前两式平方并相加，整理得 在στ坐标平面内，粉体单元体的应力状态的轨迹 是一个圆，圆心落在σ轴上，与坐标原点的距离为(σ1+ σ3)/2,半径为(σ1- σ3)/2, 该圆就称为莫尔应力圆。
莫尔应力圆圆周上的任意点，都代表着单元粉体中相应面上的应力状态。
应力圆的画法：（1）在σq 轴上作出A0(σx ,0), B0(σy ,0)；（2） A0, B0的中点为圆心C（3）过A0垂直向上取τxy 得A ， CA 为半径；（4）以C 为圆心、CA 为半径画圆 第二种画法（1）坐标系内画出点A (σ x ，τxy ) B (σy ，τyx ) （2） AB 与sq 轴的交点C 是圆心（3） 以 C 为圆心，以AC表：剪切试验测定例垂直应力s （*105Pa ） 0.253 0.505 0.755 1.01 剪应力t （*105Pa ） 0.450 0.537 0.629 0.718 流动函数FF ≤22< FF ≤4 4< FF ≤10 FF >10流动性 差，流不动 不易流动 容易流动 自由流动 A (σx ,τxy ) c f FF /0σ=判据：2221313()()22σσσσστ+--+=OστC B (σy ,τyx )2nD ( σθ , τθ)库仑粉体：符合库仑定律的粉体 粉体流动和临界流动的充要条件，临界流动条件在（σ，τ）坐标中是直线：IYF莫尔-库仑定律：粉体内任一点的莫尔应力圆在IYF 的下方时，粉体将处于静止状态；粉体内某一点的莫尔应力圆与IYF 相切时，粉体处于临界流动或流动状态 根据莫尔-库仑定律，当单元体到极限平衡状态时，莫尔应力圆恰好与库仑抗剪强度线相切。
朗肯应力状态：Walters 转换应力：Walters 提出当粉体从上向下流动时，粉体的应力状态从朗肯主动态转变为朗肯被动态。
排料时转换应力发生在柱体与锥体的交接处，则柱体部分为朗肯主动态，锥体部分为朗肯被动态两种流动模式的比较：整体流仓内没有死角，避免了物料的不稳定流动、沟流和溢流；能把粒度分离的物料重新混合，形成了先进先出的流动，最大限度地减少了存储期间的结块、变质或偏析问题；颗粒料的密度在卸料时是常数，料位差对它没有影响，可用容积式供料装置很好地控制物料；可制流量，因此任意截面上的压力可以预测且相对均匀；物料的密实程度和透气性能是均匀的，流动的边界可以预测，可用静态流动条件进行分析；整体流需要增加料仓高度，增加仓壁的磨损。
