第17讲 统计与统计案例-2021届高考数学(理)培优专题提升训练(解析版)

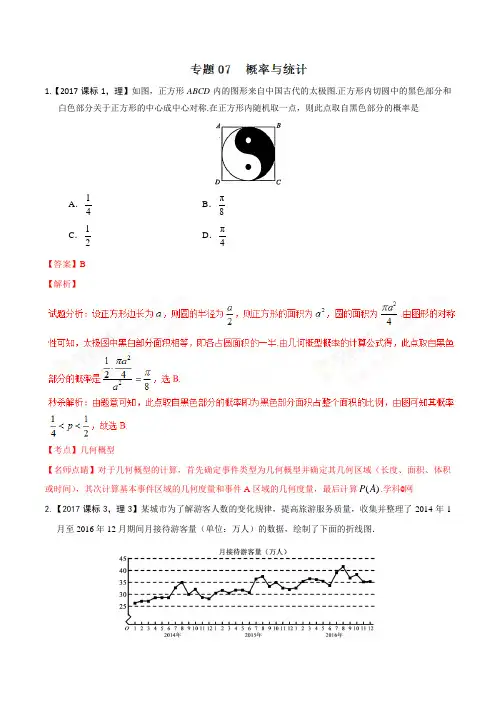
1.【2017课标1，理】如图，正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是A．14B．π8C．12D．π4【答案】B【解析】【考点】几何概型【名师点睛】对于几何概型的计算，首先确定事件类型为几何概型并确定其几何区域（长度、面积、体积或时间），其次计算基本事件区域的几何度量和事件A区域的几何度量，最后计算()P A.学科@网2.【2017课标3，理3】某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是 A ．月接待游客量逐月增加 B ．年接待游客量逐年增加C ．各年的月接待游客量高峰期大致在7,8月D ．各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳 【答案】A 【解析】【考点】 折线图【名师点睛】将频率分布直方图中相邻的矩形的上底边的中点顺次连结起来，就得到一条折线，我们称这条折线为本组数据的频率折线图，频率分布折线图的的首、尾两端取值区间两端点须分别向外延伸半个组距，即折线图是频率分布直方图的近似，他们比频率分布表更直观、形象地反映了样本的分布规律.A ．1E()ξ<2E()ξ，1D()ξ<2D()ξB ．1E()ξ<2E()ξ，1D()ξ>2D()ξC ．1E()ξ>2E()ξ，1D()ξ<2D()ξD ．1E()ξ>2E()ξ，1D()ξ>2D()ξ【答案】A 【解析】 试题分析：112212(),(),()()E p E p E E ξξξξ==∴<111222121212()(1),()(1),()()()(1)0D p p D p p D D p p p p ξξξξ=-=-∴-=---<，选A ．【考点】 两点分布【名师点睛】求离散型随机变量的分布列，首先要根据具体情况确定X 的取值情况，然后利用排列，组合与概率知识求出X 取各个值时的概率．对于服从某些特殊分布的随机变量，其分布列可以直接应用公式给出，其中超几何分布描述的是不放回抽样问题，随机变量为抽到的某类个体的个数．由已知本题随机变量i ξ服从两点分布，由两点分布均值与方差公式可得A 正确．4.【2017山东，理5】为了研究某班学生的脚长x （单位：厘米）和身高y （单位：厘米）的关系，从该班随机抽取10名学生，根据测量数据的散点图可以看出y 与x 之间有线性相关关系，设其回归直线方程为ˆˆˆybx a =+．已知101225i i x ==∑，1011600i i y ==∑，ˆ4b =．该班某学生的脚长为24，据此估计其身高为 （A ）160 （B ）163 （C ）166 （D ）170 【答案】C【解析】试题分析：由已知22.5,160,160422.570,42470166x y a y ==∴=-⨯==⨯+= ,选C. 【考点】线性相关与线性回归方程的求法与应用．【名师点睛】（1）判断两个变量是否线性相关及相关程度通常有两种方法：（1）利用散点图直观判断；（2）将相关数据代入相关系数r 公式求出r ，然后根据r 的大小进行判断．求线性回归方程时在严格按照公式求解时，一定要注意计算的准确性．5.【2017山东，理8】从分别标有1，2，⋅⋅⋅，9的9张卡片中不放回地随机抽取2次，每次抽取1张．则抽到的2张卡片上的数奇偶性不同的概率是 （A ）518 （B ）49 （C ）59（D ）79 【答案】C【考点】古典概型【名师点睛】概率问题的考查，侧重于对古典概型和对立事件的概率考查，属于简单题.江苏对古典概型概率考查，注重事件本身的理解，淡化计数方法.因此先明确所求事件本身的含义，然后一般利用枚举法、树形图解决计数问题，而当正面问题比较复杂时，往往采取计数其对立事件. 学科@网6.【2017课标II ，理13】一批产品的二等品率为0.02，从这批产品中每次随机取一件，有放回地抽取100次，X 表示抽到的二等品件数，则D X = 。

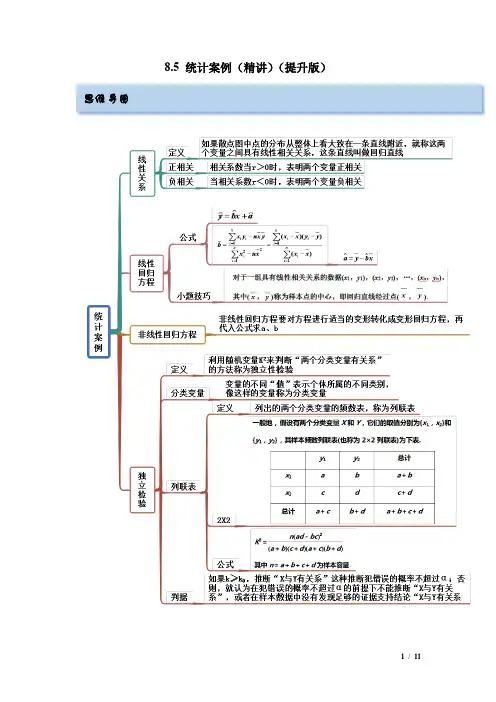
8.5 统计案例（精讲）（提升版）思维导图考点一独立性检验【例1】（2022·吉林·梅河口市第五中学高三开学考试）某中学准备组建“文科”兴趣特长社团，由课外活动小组对高一学生进行了问卷调查，问卷共100道题，每题1分，总分100分，该课外活动小组随机抽取了100名学生的问卷成绩（单位：分）进行统计，将数据按照[0,20),[20,40),[40,60),[60,80),[80,100]分成5组，绘制的频率分布直方图如图所示，若将不低于60分的称为“文科方向”学生，低于60分的称为“理科方向”学生.(1)根据已知条件完成下面2×2列联表，并据此判断是否有99.5%的把握认为“文科方向”与性别有关？理科方向文科方向总计男40女45考点呈现例题剖析总计 1001人，共抽取4次，记被抽取的4人中“文科方向”的人数为X ，若每次抽取的结果是相互独立的，求X 的分布列和数学期望.参考公式：()()()()22()n ad bc a b c d a c b d χ-=++++，其中n a b c d =+++.参考临界值：()2P k αχ=0.10 0.05 0.025 0.010 0.005 0.001k2.7063.841 5.024 6.635 7.879 10.828【一隅三反】1．（2022·白山模拟）十三届全国人大四次会议表决通过了关于国民经济和社会发展第十四个五年规划和2035年远景目标纲要的决议，决定批准这个规划纲要，纲要指出：“加强原创性引领性科技攻关”．某企业集中科研骨干，攻克系列“卡脖子”技术，已成功实现离子注入机全谱系产品国产化，包括中束流、大束流、高能、特种应用及第三代半导体等离子注入机，工艺段覆盖至28nm，为我国芯片制造产业链补上重要一环，为全球芯片制造企业提供离子注入机一站式解决方案．此次技术的突破可以说为国产芯片的制造做出了重大贡献．该企业使用新技术对某款芯片进行试生产，在试产初期，生产一件该款芯片有三道工序，每道工序的生产互不影响，这三道工序的次品率分别为118，119，120．附：()()()()()22n ad bcKa b c d a c b d-=++++，n a b c d=+++．()2P K k≥0.0500.0100.0050.001 k 3.841 6.6357.87910.828（①P①100X（2）某手机生产厂商将该款芯片投入到某新款手机上使用，并对部分芯片做了技术改良，推出了两种型号的手机，甲型号手机采用没有改良的芯片，乙型号手机采用改良了的芯片，现对使用这两种型号的手机用户进行回访，就他们对开机速度进行满意度调查．据统计，回访的100名用户中，使用甲型号手机的有30人，其中对开机速度满意的有15人；使用乙型号手机的有70人，其中对开机速度满意的有55人．完成下列22⨯列联表，并判断是否有99.5%的把握认为该项技术改良与用户对开机速度的满意度有关．甲型号乙型号合计满意不满意合计2．（2022·陕西咸阳·三模（理））2022年北京冬奥组委发布的《北京2022年冬奥会和冬残奥会经济遗产报告（2022）》显示，北京冬奥会已签约45家赞助企业，冬奥会赞助成为一项跨度时间较长的营销方式．为了解该45家赞助企业每天销售额与每天线上销售时间之间的相关关系，某平台对45家赞助企业进行跟踪调查，其中每天线上销售时间不少于8小时的企业有20家，余下的企业中，每天的销售额不足30万元的企业占35，统计后得到如下22⨯列联表：销售额不少于30万元销售额不足30万元合计线上销售时间不少于8小时 17 20 线上销售时间不足8小时合计45售时间有关？(2)按销售额在上述赞助企业中采用分层抽样方法抽取5家企业．在销售额不足30万元的企业中抽取时，记“抽到线上销售时间不少于8小时的企业数”为X ，求X 的分布列和数学期望． 附： ()20P K k ≥0.050 0.010 0.001 0k3.841 6.635 10.828参考公式：()()()()2 n ad bc K a b c d a c b d -=++++，其中n a b c d =+++．考点二 线性回归方程【例2-1】（2022·齐齐哈尔模拟）某单位为了解夏季用电量与月份的关系，对本单位2021年5月份到8月份的日平均用电量y （单位：千度）进行了统计分析，得出下表数据：月份（x ）5 6 7 8 日平均用电量（y ）1.93.4t7.11.7877ˆ.0y x =-t 的值为（ ）A ．5.8B ．5.6C ．5.4D ．5.2【例2-2】（2022·湖南模拟）《中共中央国务院关于全面推进乡村振兴加快农业农村现代化的意见》，这是21世纪以来第18个指导“三农”工作的中央一号文件.文件指出，民族要复兴，乡村必振兴.为助力乡村振兴，某电商平台为某地的农副特色产品开设直播带货专场.为了对该产品进行合理定价，用不同的单价在平台试销，得到如下数据：单价x （元/件） 8 8.2 8.4 8.6 8.8 9 销量y （万件）908483807568附：参考公式：回归方程ˆˆˆybx a =+，其中()()()iii ii 1i 1222iii 1i 1ˆnnx x y y x y nxyb x x xnx ====---==--∑∑∑∑，ˆˆay bx =-. 参考数据：614066i ii x y==∑，621434.2i i x ==∑.（1）（i ）根据以上数据，求y 关于x 的线性回归方程；（ii ）若该产品成本是7元/件，假设该产品全部卖出，预测把单价定为多少时，工厂获得最大利润.（2）为了解该产品的价格是否合理，在试销平台上购买了该产品的顾客中随机抽了400人，阅读“购买后的评价”得知：对价格满意的有300人，基本满意的有50人，不满意的有50人.为进一步了解顾客对该产品价格满意度形成的原因，在购买该产品的顾客中随机抽取4人进行电话回访，记抽取的4人中对价格满意的人数为随机变量X ，求随机变量X 的分布列和数学期望.（视频率为相应事件发生的概率）【一隅三反】1．（2022·安徽三模）对某位同学5次体育测试的成绩（单位：分）进行统计得到如下表格：第x 次 1 2 3 4 5 测试成绩y3940484850根据上表，可得关于的线性回归方程为ˆ3ˆy x a =+，下列结论不正确的是（ ）A ．ˆ36a= B ．这5次测试成绩的方差为20.8 C ．y 与x 的线性相关系数0r < D ．预测第6次体育测试的成绩约为542．（2022·安徽模拟）新冠疫情期间，口罩的消耗量日益增加，某药店出于口罩进货量的考虑，连续9天统计了第i (i 1239)x =，，，，天的口罩的销售量i y （百件），得到的数据如下：99i i i=1i=145171x y ==∑∑，，()99922ii i i i=1i=1i=1312528510953x x y y y ==-=∑∑∑，，． 参考公式：相关系数()()()()iii=122iii=1i=1nnnx x y y r x x y y --=--∑∑∑数据()i i ()i 123x y n =，，，，，，其回归直线ˆˆˆy bx a =+的斜率和截距的最小二乘估计分别为()()()iii i1222i i11ˆˆˆnn i inni i x x y y x y nxybay bx x x xnx ===---===---∑∑∑∑， （1）若用线性回归模型ˆˆˆybx a =+拟合y 与x 之间的关系，求该回归直线的方程； （2）统计学家甲认为用（1）中的线性回归模型（下面简称模型1）进行拟合，不够精确，于是尝试使用非线性模型（下面简称模型2）得到i x 与i y 之间的关系，且模型2的相关系数20989r =．，试通过计算说明模型1，2中，哪一个模型的拟合效果更好． 3．（2022·湖南模拟）《中共中央国务院关于全面推进乡村振兴加快农业农村现代化的意见》，这是21世纪以来第18个指导“三农”工作的中央一号文件.文件指出，民族要复兴，乡村必振兴.为助力乡村振兴，某电商平台为某地的农副特色产品开设直播带货专场.为了对该产品进行合理定价，用不同的单价在平台试销，得到如下数据：单价x （元/件） 8 8.2 8.4 8.6 8.8 9 销量y （万件）908483807568附：参考公式：回归方程ˆˆˆybx a =+，其中()()()iiiii 1i 1222iii 1i 1ˆnnx x y y x y nxyb x x xnx ====---==--∑∑∑∑，ˆˆay bx =-. 参考数据：614066i ii x y==∑，621434.2i i x ==∑.（1）（i ）根据以上数据，求y 关于x 的线性回归方程；（ii ）若该产品成本是7元/件，假设该产品全部卖出，预测把单价定为多少时，工厂获得最大利润.（2）为了解该产品的价格是否合理，在试销平台上购买了该产品的顾客中随机抽了400人，阅读“购买后的评价”得知：对价格满意的有300人，基本满意的有50人，不满意的有50人.为进一步了解顾客对该产品价格满意度形成的原因，在购买该产品的顾客中随机抽取4人进行电话回访，记抽取的4人中对价格满意的人数为随机变量X，求随机变量X的分布列和数学期望.（视频率为相应事件发生的概率）考点三非线性回归方程【例3】（2022·福建·三明一中模拟预测）当前，新一轮科技革命和产业变革蓬勃兴起，以区块链为代表的新一代信息技术迅猛发展，现收集某地近5年区块链企业总数量相关数据，如下表年份20172018201920202021编号x12345企业总数量y（单位：千个） 2.156 3.7278.30524.27936.224(1)根据表中数据判断，y a bx=+与e dxy c=（其中 2.71828e=…为自然对数的底数），哪一个回归方程类型适宜预测未来几年我国区块链企业总数量？（给出结果即可，不必说明理由），并根据你的判断结果求y关于x的回归方程；(2)为了促进公司间的合作与发展，区块链联合总部决定进行一次信息化技术比赛，邀请甲、乙、丙三家区块链公司参赛．比赛规则如下：①每场比赛有两个公司参加，并决出胜负；①每场比赛获胜的公司与未参加此场比赛的公司进行下一场的比赛；①在比赛中，若有一个公司首先获胜两场，则本次比赛结束，该公司获得此次信息化比赛的“优胜公司”．已知在每场比赛中，甲胜乙的概率为12，甲胜丙的概率为13，乙胜丙的概率为35，若首场由甲乙比赛，求甲公司获得“优胜公司”的概率．参考数据：5174.691i i y ==∑，51312.761i i i x y ==∑，5110.980i i z ==∑，5140.457i i i x z ==∑（其中ln z y =）． 附：样本(),(1,2,,)i i x y i n =的最小二乘法估计公式为1221ˆni ii nii x y nx ybxnx==-=-∑∑，ˆa y bx=-．【一隅三反】1．（2022·山西二模）数据显示，中国在线直播用户规模及在线直播购物规模近几年都保持高速增长态势，下表为2017－2021年中国在线直播用户规模（单位：亿人），其中2017年－2021年对应的代码依次为1－5．年份代码x 1 2 3 4 5 市场规模y3.984.565.045.866.36参考数据： 5.16y =， 1.68v =，145.10i ii v y==∑，其中i i v x =．参考公式：对于一组数据()11v y ，，()22v y ，，…，()n n v y ，，其回归直线ˆˆˆybv a =+的斜率和截距的最小二乘估计公式分别为1221ˆni ii ni i v y nvybv nv ==-=-∑∑，ˆˆay bv =-． （1）由上表数据可知，可用函数模型ˆˆyx a =拟合y 与x 的关系，请建立y 关于x 的回归方程（ˆa ，ˆb 的值精确到0.01）；（2）已知中国在线直播购物用户选择在品牌官方直播间购物的概率为p ，现从中国在线直播购物用户中随机抽取4人，记这4人中选择在品牌官方直播间购物的人数为X ，若()()34P X P X ===，求X 的分布列与期望．2．（2022·广东广州·一模）人们用大数据来描述和定义信息时代产生的海量数据，并利用这些数据处理事务和做出决策，某公司通过大数据收集到该公司销售的某电子产品1月至5月的销售量如下表. 月份x1 2 3 4 5 销售量y （万件）4.95.86.88.310.2该公司为了预测未来几个月的销售量，建立了y 关于x 的回归模型：ˆv . (1)根据所给数据与回归模型，求y 关于x 的回归方程（ˆu 的值精确到0.1）；(2)已知该公司的月利润z （单位：万元）与x ，y 的关系为z x x=，根据（1）的结果，问该公司哪一个月的月利润预报值最大？ 参考公式：对于一组数据()()()1122,,,,,,n n x y x y x y ，其回归直线ˆˆˆy bx a =+的斜率和截距的最小二乘估计公式分别为()()()121ˆniii nii x x y y bx x ==--=-∑∑，ˆˆay bx =-.11 / 113．（2022·广东肇庆·二模）下表是我国从2016年到2020年能源消费总量近似值y （单位：千万吨标准煤）的数据表格： 年份2016 2017 2018 2019 2020 年份代号x1 2 3 4 5 能源消费总量近似值y （单位：千万吨标准煤） 442 456 472 488 498以x 为解释变量，y 为预报变量，若以11为回归方程，则相关指数210.9946R ≈，若以22ˆln ya b x =+为回归方程，则相关指数220.9568R ≈． (1)判断11ˆyb x a =+与22ˆln y a b x =+哪一个更适宜作为能源消费总量近似值y 关于年份代号x 的回归方程，并说明理由；(2)根据（1）的判断结果及表中数据，求出y 关于年份代号x 的回归方程．参考数据：512356i i y ==∑，517212i i i x y ==∑．参考公式：回归方程ˆˆˆybx a =+中斜率和截距的最小二乘估计公式分别为：()()()1122211ˆn ni i i ii i n n ii i i x x y y x y nxy b x x x nx ====---==--∑∑∑∑，ˆˆa y bx =-．。

培优点17 概率与统计的创新题型概率统计问题在近几年的高考中背景取自现实，题型新颖，综合性增强，难度加深，掌握此类问题的解题策略在高考中就显得非常重要．【典例】 (2020·青岛模拟)某网络购物平台每年11月11日举行“双十一”购物节，当天有多项优惠活动，深受广大消费者喜爱．(1)已知该网络购物平台近5年“双十一”购物节当天成交额如表所示：求成交额y (百亿元)与时间变量x (记2016年为x ＝1,2017年为x ＝2，…依次类推)的线性回归方程，并预测2021年该平台“双十一”购物节当天的成交额(百亿元)；(2)在2021年“双十一”购物节前，某同学的爸爸、妈妈计划在该网络购物平台上分别参加A ，B 两店各一个订单的“秒杀”抢购，若该同学的爸爸、妈妈在A ，B 两店订单“秒杀”成功的概率分别为p ，q ，记该同学的爸爸和妈妈抢购到的订单总数量为X . ①求X 的分布列及E (X )；②已知每个订单由k (k ≥2，k ∈N *)件商品W 构成，记该同学的爸爸和妈妈抢购到商品W 的总数量为Y ，假设p ＝7sin πk 4k －πk 2，q ＝sinπk4k，求E (Y )取最大值时正整数k 的值．【拓展训练】一种掷骰子走跳棋的游戏：棋盘上标有第0站、第1站、第2站…第100站，共101站，设棋子跳到第n站的概率为P n，一枚棋子开始在第0站，棋手每掷一次骰子，棋子向前跳动一次．若掷出奇数点，棋子向前跳一站；若掷出偶数点，棋子向前跳两站，直到棋子跳到第99站(获胜)或第100站(失败)时，游戏结束(骰子是用一种均匀材料做成的立方体形状的游戏玩具，它的六个面分别标有点数1,2,3,4,5,6)．(1)求P0，P1，P2，并根据棋子跳到第n站的情况，试用P n－2和P n－1表示P n；(2)求证：{P n－P n－1}(n＝1,2，…，99)为等比数列；(3)求玩该游戏获胜的概率．培优点17 概率与统计的创新题型概率统计问题在近几年的高考中背景取自现实，题型新颖，综合性增强，难度加深，掌握此类问题的解题策略在高考中就显得非常重要．【典例】 (2020·青岛模拟)某网络购物平台每年11月11日举行“双十一”购物节，当天有多项优惠活动，深受广大消费者喜爱．(1)已知该网络购物平台近5年“双十一”购物节当天成交额如表所示：求成交额y (百亿元)与时间变量x (记2016年为x ＝1,2017年为x ＝2，…依次类推)的线性回归方程，并预测2021年该平台“双十一”购物节当天的成交额(百亿元)；(2)在2021年“双十一”购物节前，某同学的爸爸、妈妈计划在该网络购物平台上分别参加A ，B 两店各一个订单的“秒杀”抢购，若该同学的爸爸、妈妈在A ，B 两店订单“秒杀”成功的概率分别为p ，q ，记该同学的爸爸和妈妈抢购到的订单总数量为X . ①求X 的分布列及E (X )；②已知每个订单由k (k ≥2，k ∈N *)件商品W 构成，记该同学的爸爸和妈妈抢购到商品W 的总数量为Y ，假设p ＝7sin πk 4k －πk 2，q ＝sinπk4k ，求E (Y )取最大值时正整数k 的值．【解析】解 (1)由已知可得 x ＝1＋2＋3＋4＋55＝3，y ＝9＋12＋17＋21＋275＝17.2，i y i ＝1×9＋2×12＋3×17＋4×21＋5×27＝303， 2i＝12＋22＋32＋42＋52＝55. 所以b ^＝303－5×3×17.255－5×32＝4510＝4.5，所以a ^＝y －b ^x ＝17.2－4.5×3＝3.7， 所以y ^＝4.5x ＋3.7.当x ＝6时，y ^＝4.5×6＋3.7＝30.7(百亿元)，所以预测2021年该平台“双十一”购物节当天的成交额为30.7百亿元．(2)①由题意知，X 的所有可能取值为0,1,2. P (X ＝0)＝(1－p )(1－q )， P (X ＝1)＝(1－p )q ＋(1－q )p ， P (X ＝2)＝pq . 所以X 的分布列为E (X )＝0×(1－p )(1－q )＋(p ＋q －2pq )＋2pq ＝p ＋q . ②因为Y ＝kX ，所以E (Y )＝kE (X )＝k (p ＋q ) ＝k ⎝ ⎛⎭⎪⎫7sin πk 4k －πk 2＋sin πk 4k ＝2sin πk －πk . 令t ＝1k ∈⎝⎛⎦⎤0，12， 设f (t )＝2sin πt －πt ，则E (Y )＝f (t )．因为f ′(t )＝2πcos πt －π＝2π⎝⎛⎭⎫cos πt －12，且πt ∈⎝⎛⎦⎤0，π2，所以，当t ∈⎝⎛⎭⎫0，13时，f ′(t )>0， 所以f (t )在区间⎝⎛⎭⎫0，13上单调递增； 当t ∈⎝⎛⎭⎫13，12时，f ′(t )<0， 所以f (t )在区间⎝⎛⎭⎫13，12上单调递减， 所以，当t ＝13时，f (t )max ＝3－π3，即E (Y )取最大值时，正整数k 的值为3.【方法总结】概率统计问题考查学生的数据分析能力，要从已知数表中经过阅读分析判断获取关键信息，搞清各数据、各事件间的关系，建立适当的数学模型．【拓展训练】一种掷骰子走跳棋的游戏：棋盘上标有第0站、第1站、第2站…第100站，共101站，设棋子跳到第n 站的概率为P n ，一枚棋子开始在第0站，棋手每掷一次骰子，棋子向前跳动一次．若掷出奇数点，棋子向前跳一站；若掷出偶数点，棋子向前跳两站，直到棋子跳到第99站(获胜)或第100站(失败)时，游戏结束(骰子是用一种均匀材料做成的立方体形状的游戏玩具，它的六个面分别标有点数1,2,3,4,5,6)．(1)求P 0，P 1，P 2，并根据棋子跳到第n 站的情况，试用P n －2和P n －1表示P n ； (2)求证：{P n －P n －1}(n ＝1,2，…，99)为等比数列；(3)求玩该游戏获胜的概率．【解析】(1)解 棋子开始在第0站是必然事件，所以P 0＝1.棋子跳到第1站，只有一种情形，第一次掷骰子出现奇数点，其概率为12，所以P 1＝12.棋子跳到第2站，包括两种情形，①第一次掷骰子出现偶数点，其概率为12；②前两次掷骰子都出现奇数点，其概率为14，所以P 2＝12＋14＝34.棋子跳到第n (2≤n ≤99)站，包括两种情形，①棋子先跳到第n －2站，又掷骰子出现偶数点，其概率为12P n －2；②棋子先跳到第n －1站，又掷骰子出现奇数点，其概率为12P n －1.故P n ＝12P n －2＋12P n －1(2≤n ≤99，n ∈N *)．棋子跳到100站只有一种情况，棋子先跳到第98站，又掷骰子出现偶数点，其概率为12P 98，所以P 100＝12P 98.(2)证明 由(1)知，当2≤n ≤99时， P n ＝12P n －2＋12P n －1，所以P n －P n －1＝－12(P n －1－P n －2)．又因为P 1－P 0＝－12，所以{P n －P n －1}(n ＝1,2，…，99)是首项为－12，公比为－12的等比数列．(3)解 由(2)知，P n －P n －1＝－12⎝⎛⎭⎫－12n －1＝⎝⎛⎭⎫－12n. 所以P 99＝(P 99－P 98)＋(P 98－P 97)＋…＋(P 1－P 0)＋P 0 ＝⎝⎛⎭⎫－1299＋⎝⎛⎭⎫－1298＋…＋⎝⎛⎭⎫－12＋1 ＝⎝⎛⎭⎫－12⎣⎡⎦⎤1－⎝⎛⎭⎫－12991－⎝⎛⎭⎫－12＋1＝23⎝⎛⎭⎫1－12100. 所以玩该游戏获胜的概率为23⎝⎛⎭⎫1－12100.。

高考数学二轮复习专题突破—统计与统计案例1.某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y 的频数分布表.(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01) 附:√74≈8.602.2.(2021·江西赣州二模改编)遵守交通规则,人人有责.“礼让行人”是我国《道路交通安全法》的明文规定,也是全国文明城市测评中的重要内容.《道路交通安全法》第47条明确规定:“机动车行经人行横道时,应当减速行驶;遇行人正在通过人行横道,应当停车让行.机动车行经没有交通信号的道路时,遇行人横过道路,应当避让.否则扣3分罚200元”.下表是2021年1至4月份我市某主干路口监控设备抓拍到的驾驶员不“礼让行人”行为统计数据:(1)请利用所给数据求不“礼让行人”驾驶员人数y 与月份x 之间的经验回归方程y ^=b ^x+a ^,并预测该路口2021年10月不“礼让行人”驾驶员的大约人数(四舍五入);(2)交警从这4个月内通过该路口的驾驶员中随机抽查50人,调查驾驶员不“礼让行人”行为与驾龄的关系,得到下表:依据小概率值α=0.10的独立性检验,分析“礼让行人”行为是否与驾龄有关.参考公式:b ^=∑i=1nx i y i -nx y ∑i=1nx i 2-nx2=∑i=1n(x i -x)(y i -y)∑i=1n(x i -x)2.χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d),其中n=a+b+c+d.3.(2021·河北石家庄二模改编)某地区在2020年底全面建成小康社会,随着实施乡村振兴战略规划,该地区农村居民的收入逐渐增加,可支配消费支出也逐年增加.该地区统计了2016~2020年农村居民人均消费支出情况,对有关数据处理后,制作如图1的折线图[其中变量y (单位:万元)表示该地区农村居民人均年消费支出,年份用变量t 表示,其取值依次为1,2,3,…].(1)由图1可知,变量y与t具有很强的线性相关关系,求y关于t的经验回归方程,并预测2021年该地区农村居民人均消费支出;2016~2020年该地区农村居民人均消费支出图1(2)在国际上,常用恩格尔系数(其含义是指食品类支出总额占个人消费支出总额的比重)来衡量一个国家和地区人民生活水平的状况.根据联合国粮农组织的标准:恩格尔系数在40%~50%为小康,30%~40%为富裕.已知2020年该地区农村居民平均消费支出构成如图2所示,预测2021年该地区农村居民食品类支出比2020年增长3%,从恩格尔系数判断2021年底该地区农村居民生活水平能否达到富裕生活标准.2020年该地区农村居民人均消费支出构成图2参考公式:经验回归方程y ^=b ^x+a ^中斜率和截距的最小二乘估计分别为:b ^=∑i=1n(x i -x)(y i -y)∑i=1n(x i -x)2=∑i=1nx i y i -nx y∑i=1nx i 2-nx 2,a ^=y −b ^x .4.(2021·山东潍坊一模)在对人体的脂肪含量和年龄之间的关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机样本数据(x i ,y i )(i=1,2,…,20,25<x i <65),其中x i 表示年龄,y i 表示脂肪含量,并计算得到∑i=120x i 2=48 280,∑i=120y i 2=15 480,∑i=120x i y i =27 220,x =48,y =27,√22≈4.7.(1)请用样本相关系数说明该组数据中y 与x 之间的关系可用线性回归模型进行拟合,并求y 关于x的经验回归方程y ^=a ^+b ^x (a ^,b ^的计算结果保留两位小数);(2)科学健身能降低人体脂肪含量,下表是甲、乙两款健身器材的使用年限(整年)统计表:某健身机构准备购进其中一款健身器材,以使用年限的频率估计概率,请根据以上数据估计,该机构选择购买哪一款健身器材,才能使用更长久?参考公式:样本相关系数r=∑i=1n(x i -x)(y i -y)√∑i=1n (x i -x)2√∑i=1n(y i -y)2=∑i=1nx i y i -nx y√∑i=1nx i 2-nx 2√∑i=1ny i 2-ny 2;对于一组具有线性相关关系的数据(x i ,y i )(i=1,2,…,n ),其经验回归直线y ^=b ^x+a ^的斜率和截距的最小二乘估计分别为:b ^=∑i=1n(x i -x)(y i -y)∑i=1n(x i -x)2,a ^=y −b ^x .答案及解析1.解 (1)根据产值增长率频数分布表得,所调查的100个企业中产值增长率不低于40%的企业频率为14+7100=0.21.产值负增长的企业频率为2100=0.02.用样本频率分布估计总体分布得这类企业中产值增长率不低于40%的企业比例为21%,产值负增长的企业比例为2%.(2)y =1100(-0.10×2+0.10×24+0.30×53+0.50×14+0.70×7)=0.30, s 2=1100[(-0.40)2×2+(-0.20)2×24+02×53+0.202×14+0.402×7]=0.029 6, s=√0.029 6=0.02×√74≈0.17.所以,这类企业产值增长率的平均数与标准差的估计值分别为0.30,0.17. 2.解 (1)由表中数据易知:x =1+2+3+44=52,y =125+105+100+904=105,则b ^=∑i=14x i y i -4x y∑i=14x i 2-4x2=995−1 05030−25=-11,a ^=y −b ^ x =105-(-11)×52=132.5,故所求经验回归方程为y ^=-11x+132.5.令x=10,则y ^=-11×10+132.5=22.5≈23(人),预测该路口10月份不“礼让行人”的驾驶员大约人数为23. (2)零假设为H 0:“礼让行人”行为与驾龄无关.由表中数据可得χ2=50×(10×12−20×8)218×32×30×20≈0.23<2.706=x 0.10,依据小概率值α=0.10的独立性检验,没有充分证据推断H 0不成立,可以认为H 0成立,即认为“礼让行人”行为与驾龄无关.3.解 (1)由已知数据可求t =1+2+3+4+55=3, y =1.01+1.10+1.21+1.33+1.405=1.21,∑i=15t i 2=12+22+32+42+52=55,∑i=15t i y i =1×1.01+2×1.10+3×1.21+4×1.33+5×1.40=19.16,b ^=19.16−5×3×1.2155−5×32=1.0110=0.101,a ^=1.21-0.101×3=0.907,所求经验回归方程为y ^=0.101t+0.907. 当t=6时,y ^=0.101×6+0.907=1.513(万元),故2021年该地区农村居民人均消费支出约为1.513万元.(2)已知2021年该地区农村居民平均消费支出1.513万元,由图2可知,2020年该地区农村居民食品类支出为4 451元,则预测2021年该地区食品类支出为4 451×(1+3%)=4 584.53元,恩格尔系数=4 584.5315 130×100%≈30.3%∈(30%,40%),所以,2021年底该地区农村居民生活水平能达到富裕生活标准.4.解 (1)x 2=2 304,y2=729,∑i=120x i y i -20x y =1 300,∑i=120x i 2-20x 2=2 200,∑i=1ny i 2-20y 2=900,r=∑i=120x i y i -20x y√∑i=120x i 2-20x 2√∑i=1ny i 2-20y2≈0.92,因为y 与x 的样本相关系数接近1,所以y 与x 之间具有较强的线性相关关系,可用线性回归模型进行拟合.由题可得,b ^=∑i=120(x i -x)(y i -y)∑i=120(x i -x)2=∑i=120x i y i -20x y∑i=120x i 2-20x2=1322≈0.591,a ^=y −b ^ x =27-0.591×48≈-1.37,所以y ^=0.59x-1.37.(2)以频率估计概率,设甲款健身器材使用年限为X (单位:年).E (X )=5×0.1+6×0.4+7×0.3+8×0.2=6.6. 设乙款健身器材使用年限为Y (单位:年).E (Y )=5×0.3+6×0.4+7×0.2+8×0.1=6.1.因为E (X )>E (Y ),所以该健身机构购买甲款健身器材更划算.。

高中数学【统计与统计案例】专题练习1.(多选)下列统计量中，能度量样本x 1，x 2，…，x n 的离散程度的是( ) A.样本x 1，x 2，…，x n 的标准差 B.样本x 1，x 2，…，x n 的中位数 C.样本x 1，x 2，…，x n 的极差 D.样本x 1，x 2，…，x n 的平均数 答案 AC解析 由标准差的定义可知，标准差考查的是数据的离散程度；由中位数的定义可知，中位数考查的是数据的集中趋势；由极差的定义可知，极差考查的是数据的离散程度；由平均数的定义可知，平均数考查的是数据的集中趋势；故选AC.2.某厂研制了一种生产高精产品的设备，为检验新设备生产产品的某项指标有无提高，用一台旧设备和一台新设备各生产了10件产品，得到各件产品该项指标数据如下： 旧设备 9.8 10.3 10.0 10.2 9.9 9.8 10.0 10.1 10.2 9.7 新设备10.110.410.110.010.110.310.610.510.410.5旧设备和新设备生产产品的该项指标的样本平均数分别记为x －和y －，样本方差分别记为s 21和s 22. (1)求x －，y －，s 21，s 22；(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果y －－x －≥2s 21＋s 2210，则认为新设备生产产品的该项指标的均值较旧设备有显著提高，否则不认为有显著提高).解 (1)x －＝9.8＋10.3＋10.0＋10.2＋9.9＋9.8＋10.0＋10.1＋10.2＋9.710＝10，y －＝10.1＋10.4＋10.1＋10.0＋10.1＋10.3＋10.6＋10.5＋10.4＋10.510＝10.3，s 21＝0.22＋0.32＋0＋0.22＋0.12＋0.22＋0＋0.12＋0.22＋0.3210＝0.036，s 22＝0.22＋0.12＋0.22＋0.32＋0.22＋0＋0.32＋0.22＋0.12＋0.2210＝0.04. (2)由(1)知，y －－x －＝0.3； 2s 21＋s 2210＝20.036＋0.0410＝20.007 6.又(y －－x －)2＝0.09>(20.007 6)2＝0.030 4，则y －－x －>2s 21＋s 2210，所以新设备生产产品的该项指标的均值较旧设备有显著提高.3.某沙漠地区经过治理，生态系统得到很大改善，野生动物数量有所增加.为调查该地区某种野生动物的数量，将其分成面积相近的200个地块，从这些地块中用简单随机抽样的方法抽取20个作为样区，调查得到样本数据(x i ，y i )(i ＝1，2，…，20)，其中x i 和y i 分别表示第i 个样区的植物覆盖面积(单位：公顷)和这种野生动物的数量，并计算得∑20i ＝1x i ＝60，∑20i ＝1y i ＝1 200，∑20i ＝1(x i －x －)2＝80，∑20i ＝1(y i－y －)2＝9 000，∑20i ＝1(x i －x －)(y i －y －)＝800.(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数)；(2)求样本(x i ，y i )(i ＝1，2，…，20)的相关系数(精确到0.01)；(3)根据现有统计资料，各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计，请给出一种你认为更合理的抽样方法，并说明理由.附：相关系数r ＝∑ni ＝1 （x i －x －）（y i －y －）∑n i ＝1（x i －x －）2∑n i ＝1 （y i －y －）2，2≈1.414.解 (1)由已知得样本平均数y －＝120∑20i ＝1y i ＝60，从而该地区这种野生动物数量的估计值为60×200＝12 000.(2)样本(x i ，y i )(i ＝1，2，…，20)的相关系数r ＝∑20i ＝1 （x i －x －）（y i －y －）∑20i ＝1（x i －x －）2∑20i ＝1（y i －y －）2＝80080×9 000＝223≈0.94.(3)分层随机抽样：根据植物覆盖面积的大小对地块分层，再对200个地块进行分层随机抽样.理由如下：由(2)知各样区的这种野生动物数量与植物覆盖面积有很强的正相关性.由于各地块间植物覆盖面积差异很大，从而各地块间这种野生动物数量差异也很大，采用分层随机抽样的方法较好地保持了样本结构与总体结构的一致性，提高了样本的代表性，从而可以获得该地区这种野生动物数量更准确的估计.1.抽样方法抽样方法包括简单随机抽样、分层随机抽样，两种抽样方法都是等概率抽样，体现了抽样的公平性，但又各有其特点和适用范围. 2.统计中的五个数据特征(1)众数：在样本数据中，出现次数最多的那个数据.(2)中位数：在样本数据中，将数据按大小顺序排列，位于最中间的数据.如果数据的个数为偶数，就取中间两个数据的平均数作为中位数. (3)平均数：样本数据的算术平均数，即x －＝1n (x 1＋x 2＋…＋x n ).(4)第p 百分位数：将一组数据(共n 个)按从小到大排列，计算i ＝n ×p %，若i 不是整数，而大于i 的比邻整数为j ，则第p 百分位数为第j 项数据；若i 是整数，则第p 百分位数为第i 项与第(i ＋1)项数据的平均数.(5)方差与标准差.s 2＝1n [(x 1－x －)2＋(x 2－x －)2＋…＋(x n －x －)2]，s ＝1n [（x 1－x －）2＋（x 2－x －）2＋…＋（x n －x －）2].3.频率分布直方图的两个结论 (1)小长方形的面积＝组距×频率组距＝频率. (2)各小长方形的面积之和等于1. 4.回归分析与独立性检验(1)回归直线y ^＝b ^x ＋a ^经过样本点的中心(x －，y －)，若x 取某一个值代入回归直线方程y ^＝b ^x ＋a ^中，可求出y 的估计值. (2)独立性检验对于取值分别是{x 1，x 2}和{y 1，y 2}的分类变量X 和Y ，其样本频数列联表是：X Y 合计 y 1 y 2 x 1 a b a ＋b x 2 c d c ＋d 合计a ＋cb ＋dn则χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ）(其中n ＝a ＋b ＋c ＋d 为样本容量).热点一 用样本估计总体考向1 数字特征与统计图表的应用【例1】 (1)空气质量指数分为六级，指数越大说明污染的情况越严重，对人体危害越大，其中指数范围[0，50]，[51，100]，[101，150]，[151，200]，[201，300]分别对应“优”“良”“轻度污染”“中度污染”“重度污染”五个等级.如图是某市连续14天的空气质量指数趋势图，下列说法不正确的是( )A.这14天中有4天空气质量为“良”B.这14天中空气质量指数的中位数是103C.从2日到5日空气质量越来越差D.连续三天中空气质量指数方差最小的是9日到11日(2)2020年我国突发新冠肺炎疫情，疫情期间中小学生“停课不停学”.已知某地区中小学生人数情况如甲图所示，各学段学生在疫情期间“家务劳动”的参与率如乙图所示.为了进一步了解该地区中小学生参与“家务劳动”的情况，现用分层随机抽样的方法抽取4%的学生进行调查，则抽取的样本容量、抽取的高中生中参与“家务劳动”的人数分别为()A.2 750，200B.2 750，110C.1 120，110D.1 120，200答案(1)B(2)C解析(1)在这14天中，1日、3日、12日、13日的空气质量为良，共4天，故A正确.14天中空气质量指数的中位数为86＋1212＝103.5，故B错误.从2日到5日，空气质量指数越来越高，故空气质量越来越差，C正确.观察题图可得，9日至11日空气质量指数偏差最小，因此方差最小，D正确.综上知，说法不正确的是B.(2)学生总数为15 500＋5 000＋7 500＝28 000(人)，由于抽取4%的学生进行调查，则抽取的样本容量为28 000×4%＝1 120.故高中生应抽取的人数为5 000×4%＝200，而抽取的高中生中参与“家务劳动”的比率为0.55，故抽取的高中生中参与“家务劳动”的人数为200×0.55＝110.探究提高 1.解题的关键是理解统计图表的含义，从中提取数字信息，平均数、众数、中位数描述数据的集中趋势，方差与标准差描述数据的波动大小，标准差、方差越小，数据的离散程度越小，越稳定.2.进行分层随机抽样的相关计算时，常用到的两个关系：(1)样本容量n总体的个数N＝该层抽取的个体数该层的个体数；(2)总体中某两层的个体数之比等于样本中这两层抽取的个体数之比.【训练1】(1)以下数据为参加数学竞赛决赛的15人的成绩：(单位：分)78，70，72，86，88，79，80，81，94，84，56，98，83，90，91，则这15人成绩的第80百分位数是()A.90B.90.5C.91D.91.5(2)(多选) 2020年上半年，中国养猪企业受猪价高位的利好影响，大多收获史上最佳半年报业绩，部分企业半年报营业收入同比增长超过1倍.某养猪场抓住机遇，加大了生猪养殖规模，为了检测生猪的养殖情况，该养猪场对2 000头生猪的体重(单位：kg)进行了统计，得到如图所示的频率分布直方图，则下列说法正确的是()A.这2 000头生猪体重的众数为160 kgB.这2 000头生猪中体重不低于200 kg的有80头C.这2 000头生猪体重的中位数落在区间[140，160)内D.这2 000头生猪体重的平均数为152.8 kg答案(1)B(2)BCD解析(1)把成绩按从小到大的顺序排列为：56，70，72，78，79，80，81，83，84，86，88，90，91，94，98，因为15×80%＝12，所以这15人成绩的第80百分位数是90＋912＝90.5.(2)由频率分布直方图可知，[140，160)这一组的数据对应的小长方形最高，所以这2 000头生猪的体重的众数为150 kg，A错误；这2 000头生猪中体重不低于200 kg的有0.002×20×2 000＝80(头)，B正确；因为生猪的体重在[80，140)内的频率为(0.001＋0.004＋0.01)×20＝0.3，在[140，160)内的频率为0.016×20＝0.32，且0.3＋0.32＝0.62>0.5，所以这2 000头生猪体重的中位数落在区间[140，160)内，C正确；这2 000头生猪体重的平均数为(0.001×90＋0.004×110＋0.01×130＋0.016×150＋0.012×170＋0.005×190＋0.002×210)×20＝152.8(kg)，D正确.考向2用样本的频率分布估计总体分布【例2】为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成A，B两组，每组100只，其中A组小鼠给服甲离子溶液，B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图：记C为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到P(C)的估计值为0.70.(1)求乙离子残留百分比直方图中a，b的值；(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).解(1)由已知得0.70＝a＋0.20＋0.15，故a＝0.35，b＝1－0.05－0.15－0.70＝0.10.(2)甲离子残留百分比的平均值的估计值为2×0.15＋3×0.20＋4×0.30＋5×0.20＋6×0.10＋7×0.05＝4.05.乙离子残留百分比的平均值的估计值为3×0.05＋4×0.10＋5×0.15＋6×0.35＋7×0.20＋8×0.15＝6.00.探究提高 1.平均数与方差都是重要的数字特征，是对数据的一种简明描述，它们所反映的情况有着重要的实际意义.2.在例2中，抓住频率分布直方图各小长方形的面积之和为1，这是求解的关键；本题易混淆频率分布条形图和频率分布直方图，误把频率分布直方图纵轴的几何意义当成频率，导致样本数据的频率求错.【训练2】(多选)为了更好地支持中小型企业的发展，某市决定对部分企业的税收进行适当的减免，现调查了当地100家中小型企业年收入(单位：万元)情况，并根据所得数据画出了如图所示的频率分布直方图，则下列结论正确的是()A.样本在区间[500，700]内的频数为18B.如果规定年收入在300万元以内的企业才能享受减免税收政策，估计有30%的当地中小型企业能享受到减免税收政策C.样本的中位数大于350万元D.可估计当地中小型企业年收入的平均数超过400万元(同一组中的数据用该组区间的中点值作代表)答案ABC解析依题意，(0.001＋0.002＋0.002 6×2＋a＋0.000 4)×100＝1，所以a＝0.001 4.对于A，样本在[500，700]内的频率为(0.001 4＋0.000 4)×100＝0.18，故频数为0.18×100＝18，故A正确.对于B，年收入在300万元以内的频率为(0.001＋0.002)×100＝0.3，故B正确. 对于C，设样本的中位数为x，易知中位数位于[300，400]内，则0.3＋(x－300)×0.002 6＝0.5，解得x≈376.9，376.9>350，故C正确.因为样本的平均数为150×0.1＋250×0.2＋350×0.26＋450×0.26＋550×0.14＋650×0.04＝376<400，所以估计当地中小型企业年收入的平均数小于400万元，故D 错误. 热点二 回归分析【例3】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x (单位：千元)对年销售量y (单位：t)和年利润z (单位：千元)的影响，对近8年的年宣传费x i 和年销售量y i (i ＝1，2，…，8)数据进行了初步处理，得到如图所示散点图及一些统计量的值.x －y －w －∑8i ＝1(x i －x －)2∑8i ＝1(w i －w －)2∑8i ＝1(x i －x －)·(y i －y －) ∑8i ＝1(w i －w －)·(y i －y －) 46.65636.8289.8 1.61 469108.8表中w i ＝x i ，w －＝18∑8i ＝1w i .(1)根据散点图判断，y ＝a ＋bx 与y ＝c ＋d x 哪一个更适宜作为年销售量y 关于年宣传费x 的回归方程？(给出判断即可，不必说明理由) (2)根据(1)的判断结果及表中数据，建立y 关于x 的回归方程.(3)已知这种产品的年利润z 与x ，y 的关系为z ＝0.2y －x .根据(2)的结果回答下列问题：①年宣传费x ＝49时，年销售量及年利润的预报值是多少？ ②年宣传费x 为何值时，年利润的预报值最大？附：对于一组数据(u 1，v 1)，(u 2，v 2)，…，(u n ，v n )，其回归直线v ＝α＋βu 的斜率和截距的最小二乘估计分别为：β^＝∑ni ＝1（u i －u －）（v i －v －）∑n i ＝1（u i －u －）2，α^＝v －－β^u －.解 (1)由散点图可以判断，y ＝c ＋d x 更适宜作为年销售量y 关于年宣传费x 的回归方程.(2)易知w ＝x ，则y ^＝d ^w ＋c ^.由题意得d ^＝∑8i ＝1（w i －w －）（y i －y －）∑8i ＝1（w i －w －）2＝108.81.6＝68，所以c ^＝y －－d ^w －＝563－68×6.8＝100.6.所以y 关于w 的线性回归方程为y ^＝100.6＋68w ， 所以y 关于x 的回归方程为y ^＝100.6＋68x .(3)①由(2)知，当x ＝49时，年销售量y 的预报值为y ^＝100.6＋6849＝576.6，年利润z 的预报值为z ^＝576.6×0.2－49＝66.32.②根据(2)的结果知，年利润z 的预报值z ^＝0.2(100.6＋68x )－x ＝－x ＋13.6x ＋20.12，所以当x ＝13.62＝6.8，即x ＝46.24时，z ^取得最大值.故年宣传费为46.24千元时，年利润的预报值最大. 探究提高 1.求回归直线方程的关键及实际应用 (1)关键：正确理解b ^，a ^的计算公式并准确地计算.(2)实际应用：在分析实际中两个变量的相关关系时，可根据样本数据作出散点图来确定两个变量之间是否具有相关关系，若具有线性相关关系，则可通过线性回归方程估计和预测变量的值. 2.相关系数(1)当r >0时，表明两个变量正相关；当r <0时，表明两个变量负相关. (2)当|r |>0.75时，认为两个变量具有较强的线性相关关系.【训练3】 (多选)我国5G 技术研发试验在2016～2018年进行，分为5G 关键技术试验、5G 技术方案验证和5G 系统验证三个阶段.2020年初以来，5G 技术在我国已经进入高速发展的阶段，5G 手机的销量也逐渐上升.某手机商城统计了2021年5个月5G 手机的实际销量，如下表所示：若y 与x 线性相关，且求得线性回归方程为y ^＝45x ＋5，则下列说法正确的是( ) A.a ＝142 B.y 与x 正相关C.y 与x 的相关系数为负数D.2021年7月该手机商城的5G 手机销量约为365部 答案 AB解析 x －＝1＋2＋3＋4＋55＝3，y －＝50＋96＋a ＋185＋2275＝558＋a 5，因为点(x －，y －)在回归直线上，所以558＋a5＝45×3＋5，解得a ＝142，所以选项A 正确；从表格数据看，y 随x 的增大而增大，所以y 与x 正相关，所以选项B 正确；因为y 与x 正相关，所以y 与x 的相关系数为正数，所以选项C 错误；2021年7月对应的月份编号x ＝7，当x ＝7时，y ^＝45×7＋5＝320，所以2021年7月该手机商城的5G 手机销量约为320部，所以选项D 错误.故选AB.热点三 独立性检验【例4】 为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了100天空气中的PM2.5和SO 2浓度(单位：μg/m 3)，得下表：(1)估计事件“该市一天空气中PM2.5浓度不超过75，且SO 2浓度不超过150”的概率；(2)根据所给数据，完成下面的2×2列联表：(3)根据(2)中的列联表，依据小概率值α＝0.01的χ2独立性检验，能否认为该市一天空气中PM2.5浓度与SO 2浓度有关？ 附：χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ），解 (1)根据抽查数据，该市100天的空气中PM2.5浓度不超过75，且SO 2浓度不超过150的天数为32＋18＋6＋8＝64，因此，该市一天空气中PM2.5浓度不超过75，且SO 2浓度不超过150的概率的估计值为64100＝0.64. (2)根据抽查数据，可得2×2列联表：(3)零假设为H 0：该市一天空气中PM2.5浓度与SO 2浓度无关．根据(2)的列联表得χ2＝100×（64×10－16×10）280×20×74×26≈7.484>6.635＝x 0.01.根据小概率值α＝0.01的χ2独立性检验，我们推断H 0不成立，即认为该市一天空气中PM2.5浓度与SO 2浓度有关，此推断犯错误的概率不超过0.01. 探究提高 1.独立性检验的一般步骤 (1)根据样本数据列成2×2列联表； (2)根据公式χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ），计算χ2的值；(3)查表比较χ2与临界值的大小关系，作统计判断．2．χ2的值越大，对应假设事件H 0成立(两类变量相互独立)的概率越小，H 0不成立的概率越大．【训练4】 甲、乙两台机床生产同种产品，产品按质量分为一级品和二级品，为了比较两台机床产品的质量，分别用两台机床各生产了200件产品，产品的质量情况统计如下表：(1)甲机床、乙机床生产的产品中一级品的频率分别是多少？(2)依据小概率值α＝0.01的χ2独立性检验，能否认为甲机床的产品质量与乙机床的产品质量有差异？附：χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ），α 0.050 0.010 0.001 x α3.8416.63510.828解 (1)根据2×2列联表知：甲机床生产的产品中一级品的频率为150200＝75%， 乙机床生产的产品中一级品的频率为120200＝60%.(2)零假设为H 0：甲机床的产品质量与乙机床的产品质量没有差异．由2×2列联表，得χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ）＝400×（150×80－120×50）2270×130×200×200＝40039≈10.256>6.635＝x 0.01.根据小概率值α＝0.01的χ2独立性检验，我们推断H 0不成立，即认为甲机床的产品质量与乙机床的产品质量有差异，此推断犯错误的概率不超过0.01.一、选择题1.设一组样本数据x 1，x 2，…，x n 的方差为0.01，则数据10x 1，10x 2，…，10x n 的方差为( ) A.0.01 B.0.1 C.1 D.10答案 C解析 10x 1，10x 2，…，10x n 的方差为102×0.01＝1.2.为了研究某班学生的脚长x (单位：厘米)和身高y (单位：厘米)的关系，从该班随机抽取10名学生，根据测量数据的散点图可以看出y 与x 之间有线性相关关系，设其回归直线方程为y ^＝b ^x ＋a ^.已知∑10i ＝1x i ＝225，∑10i ＝1y i ＝1 600，b ^＝4.该班某学生的脚长为24，据此估计其身高为( ) A.160 B.163 C.166 D.170答案 C解析 ∵x －＝110∑10i ＝1x i ＝110×225＝22.5，y －＝110∑10i ＝1y i＝160， ∴a ^＝y －－b ^x －＝160－4×22.5＝70， ∴回归直线方程为y ^＝4x ＋70. 因此估计其身高y ^＝4×24＋70＝166.3.从一批零件中抽取80个，测量其直径(单位：mm)，将所得数据分为9组：[5.31，5.33)，[5.33，5.35)，…，[5.45，5.47)，[5.47，5.49]，并整理得到如下频率分布直方图，则在被抽取的零件中，直径落在区间[5.43，5.47)内的个数为( )A.10B.18C.20D.36答案 B解析 因为直径落在区间[5.43，5.47)内的频率为0.02×(6.25＋5.00)＝0.225，所以零件的个数为0.225×80＝18.4.某旅游城市为向游客介绍本地的气温情况，绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A 点表示十月的平均最高气温约为15 ℃，B 点表示四月的平均最低气温约为5 ℃.下面叙述不正确的是()A.各月的平均最低气温都在0 ℃以上B.七月的平均温差比一月的平均温差大C.三月和十一月的平均最高气温基本相同D.平均最高气温高于20 ℃的月份有5个答案 D解析由雷达图易知A，C正确；七月的平均最高气温超过20 ℃，平均最低气温约为12 ℃，一月的平均最高气温约为6 ℃，平均最低气温约为2 ℃，所以七月的平均温差比一月的平均温差大，B正确；由雷达图知平均最高气温超过20 ℃的月份有3个月，D错误.5.(多选) 5G时代已经到来，5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展，进而对GDP增长产生直接贡献，并通过产业间的关联效应，间接带动国民经济各行业的发展，创造出更多的经济增加值.如图，某单位结合近年数据，对今后几年的5G经济产出作出预测.由上图提供的信息可知()A.运营商的经济产出逐年增加B.设备制造商的经济产出前期增长较快，后期放缓C.设备制造商在各年的总经济产出中一直处于领先地位D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势 答案 ABD解析 对于A ，由图知，运营商的经济产出逐年增加，故A 正确；对于B ，由图知，设备制造商的经济产出在2020～2023年间增长较快，后几年增长逐渐趋于平缓，故B 正确；对于C ，由图可知，设备制造商在各年的总经济产出中在前期处于领先地位，而后期是信息服务商处于领先地位，故C 错误；对于D ，由图知，在2020～2025年间信息服务商与运营商的经济产出的差距不大，后几年中信息服务商的经济产出增长速度明显高于运营商的经济产出增长速度，两者间的差距有逐步拉大的趋势，故D 正确.综上所述，选ABD.6.已知某7个数的平均数为4，方差为2，现加入一个新数据4，此时这8个数的平均数为x －，方差为s 2，则( )A.x －＝4，s 2<2B.x －＝4，s 2>2 C.x －>4，s 2<2 D.x －>4，s 2>2答案 A解析 ∵某7个数的平均数为4，∴这7个数的和为4×7＝28.∵加入一个新数据4，∴x －＝28＋48＝4.又∵这7个数的方差为2，且加入一个新数据4，∴这8个数的方差s 2＝7×2＋（4－4）28＝74<2，故选A.二、填空题 7．给出如下列联表非 30 50 80 合计5060110根据独立性检验，__________在犯错误的概率不超过0.01的前提下认为“高血压与患心脏病有关”(填“能”或“不能”)． 答案 能解析 零假设为H 0：高血压与患心脏病无关． 由列联表中的数据可得 χ2＝110×（20×50－10×30）230×80×50×60≈7.486＞6.635＝x 0.01，根据小概率值α＝0.01的χ2独立性检验，我们推断H 0不成立，即认为高血压与患心脏病有关，此推断犯错误的概率不超过0.01，即能在犯错误的概率不超过0.01的前提下，认为高血压与患心脏病有关．8.为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，测试成绩(单位：分)如图所示，假设得分值的中位数为m e ，众数为m 0，平均值为x －，则m e ，m 0与x －的大小关系是________.答案 m 0<m e <x －解析 由图可知，30名学生的得分情况依次为得3分的有2人，得4分的有3人，得5分的有10人，得6分的有6人，得7分的有3人，得8分的有2人，得9分的有2人，得10分的有2人.中位数为第15、16个数(分别为5、6)的平均数，即m e ＝5.5.5出现的次数最多，故m 0＝5，x －＝2×3＋3×4＋10×5＋6×6＋3×7＋2×8＋2×9＋2×1030≈5.97.于是得m 0<m e <x －.9.下面的折线图给出的是甲、乙两只股票在某年中每月的收盘价格，已知股票甲的极差是6.88元，标准差为2.04元；股票乙的极差为27.47元，标准差为9.63元，根据这两只股票在这一年中的波动程度，给出下列结论：①股票甲在这一年中波动相对较小，表现的更加稳定；②购买股票乙风险高但可能获得高回报；③股票甲的走势相对平稳，股票乙的收盘价格波动较大；④两只股票在全年都处于上升趋势.其中正确的结论是________(填序号).答案 ①②③解析 由题意可知，甲的标准差为2.04元，乙的标准差为9.63元，可知股票甲在这一年中波动相对较小，表现的更加稳定，故①正确；甲的极差是6.88元，乙的极差为27.47元，可知购买股票乙风险高但可能获得高回报，故②正确；通过折线图可知股票甲的走势相对平稳，股票乙的收盘价格波动较大，故③正确；通过折线图可得乙在6月到8月明显是下降趋势，故④错误. 三、解答题10．某商场为提高服务质量，随机调查了50名男顾客和50名女顾客，每位顾客对该商场的服务给出满意或不满意的评价，得到下面列联表：性别对该商场的服务 合计满意不满意(1)分别估计男、女顾客对该商场服务满意的概率；(2)依据小概率值α＝0.05的χ2独立性检验，能否认为男、女顾客对该商场服务的评价有差异？附：χ2＝n （ad －bc ）2（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ）.解 (1)由调查数据，男顾客中对该商场服务满意的比率为4050＝0.8，因此男顾客对该商场服务满意的概率的估计值为0.8.女顾客中对该商场服务满意的比率为3050＝0.6，因此女顾客对该商场服务满意的概率的估计值为0.6. (2)零假设为H 0：男、女顾客对该商场服务的评价没有差异． 由列联表中的数据，得 χ2＝100×（40×20－30×10）250×50×70×30≈4.762>3.841＝x 0.05.根据小概率值α＝0.05的χ2独立性检验，我们推 断H 0不成立，即认为男、女顾客对商场服务的评价有差异，此推断犯错误的概率不大于0.05.11.某互联网公司为了确定下季度的前期广告投入计划，收集了近6个月广告投入量x (单位：万元)和收益y (单位：万元)的数据如表：他们分别用两种模型①y ＝bx ＋a ，②y ＝a e bx 进行拟合，得到相应的回归方程并进行残差分析，得到如图所示的残差图及一些统计量的值.x －y －∑6i ＝1x i y i∑6i ＝1x 2i7301 464.24 364(1)根据残差图，比较模型①，②的拟合效果，应选择哪个模型？并说明理由； (2)残差绝对值大于2的数据被认为是异常数据，需要剔除. (ⅰ)剔除异常数据后，求出(1)中所选模型的回归方程； (ⅱ)若广告投入量x ＝18，则该模型收益的预报值是多少？附：对于一组数据(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )，其回归直线y ^＝b ^x ＋a ^的斜率和截距的最小二乘估计分别为：b ^＝∑n i ＝1（x i －x －）（y i －y －）∑n i ＝1（x i －x －）2＝∑ni ＝1x i y i －nx －·y －∑n i ＝1x 2i －n ·x －2，a ^＝y －－b ^x －. 解 (1)由于模型①残差波动小，应该选择模型①. (2)(ⅰ)剔除异常数据，即3月份的数据， 剩下数据的平均数为x －＝15×(7×6－6)＝7.2，y －＝15×(30×6－31.8)＝29.64，∑5i ＝1x i y i －5x －·y －＝206.4，∑5i ＝1x 2i －5·x －2＝68.8. ∴b ^＝206.468.8＝3，a ^＝y －－b ^x －＝29.64－3×7.2＝8.04.∴所选模型的回归方程为y ^＝3x ＋8.04. (ⅱ)若广告投入量x ＝18，则该模型收益的预报值是3×18＋8.04＝62.04(万元).12.(多选)2020年7月国家统计局发布了我国2020年上半年国内经济数据，图1为国内三大产业生产总值的比重，图2为第三产业中各行业生产总值的比重.以下关于我国2020年上半年经济数据的说法正确的是()A.在第三产业中，“批发和零售业”与“金融业”的生产总值之和同“其他服务业”的生产总值基本持平B.若“租赁和商务服务业”生产总值为15 000亿元，则“房地产业”生产总值为32 500亿元C.若“金融业”的生产总值为42 000亿元，则第三产业生产总值为262 500亿元D.若“金融业”的生产总值为42 000亿元，则第一产业生产总值为45 000亿元答案ABC解析对于选项A，在第三产业中，“批发和零售业”与“金融业”的生产总值之和占比为16%＋16%＝32%，“其他服务业”的生产总值占比为32%，所以“批发和零售业”与“金融业”的生产总值之和同“其他服务业”的生产总值基本持平，故选项A正确.对于选项B，若“租赁和商务服务业”生产总值为15 000亿元，在第三产业中，因为“租赁和商务服务业”生产总值占比为6%，所以第三产业生产总值为15 000＝250 000(亿元)，又“房地产业”生产总值占比为13%，所以“房地产6%业”生产总值为13%×250 000＝32 500(亿元)，故选项B正确.对于选项C ，在第三产业中，若“金融业”的生产总值为42 000亿元，因为“金融业”生产总值占比为16%，所以第三产业生产总值为42 00016%＝262 500(亿元)，故选项C 正确.对于选项D ，第三产业生产总值在三大产业中占比为57%，第一产业生产总值在三大产业中占比为6%，由C 选项知第三产业生产总值为262 500亿元，所以第一产业生产总值为262 50057%×6%≈27 632(亿元)，所以选项D 错误.13.由于受到网络电商的冲击，某品牌的洗衣机在线下的销售受到影响，承受了一定的经济损失，现将A 地区200家实体店该品牌洗衣机的月经济损失统计如图所示，估算月经济损失的平均数为m ，中位数为n ，则m －n ＝________.答案 360解析 第一块小矩形的面积S 1＝0.3，第二块小矩形的面积S 2＝0.4，故n ＝2 000＋0.5－0.30.000 2＝3 000；又第四、五块小矩形的面积均为S ＝0.06，故a ＝12 000[1－(0.3＋0.4＋0.06×2)]＝0.000 09，所以m ＝1 000×0.3＋3 000×0.4＋5 000×0.18＋(7 000＋9 000)×0.06＝3 360，故m －n ＝360.14.某公司为了预测下月产品销售情况，找出了近7个月的产品销售量y (单位：万件)的统计表：月份代码t 1 2 3 4 5 6 7 销售量y (万件)y 1y 2y 3y 4y 5y 6y 7但其中数据污损不清，经查证∑7i ＝1y i ＝9.32，∑7i ＝1t i y i ＝40.17，∑7i ＝1（y i －y －）2＝0.55.。

专题升级训练17　概率、统计与统计案例 (时间：60分钟　满分：100分)一、选择题(本大题共6小题，每小题6分，共36分) 1．从2 007名学生中选取50名学生参加全国数学联赛，若采用下面的方法选取：先用简单随机抽样从2 007人中剔除7人，剩下的2 000人再按系统抽样的方法抽取，则每人入选的概率( )． A．不全相等 B．均不相等 C．都相等，且为 D．都相等，且为 2．已知x与y之间的一组数据： x0123y1357则y与x的线性回归方程＝＋x必过点( )． A．(2,2) B．(1.5,0) C．(1,2) D．(1.5,4) 3．向假设的三座相互毗邻的军火库投掷一颗炸弹，只要炸中其中任何一座，另外两座也要发生爆炸．已知炸中第一座军火库的概率为0.2，炸中第二座军火库的概率为0.3，炸中第三座军火库的概率为0.1，则军火库发生爆炸的概率是( )． A．0.006 B．0.4 C．0.5 D．0.6 4．在区间[－2,2]内任取两数a，b，使函数f(x)＝x2＋2bx＋a2有两相异零点的概率是( )． A． B． C． D． 5．在样本的频率分布直方图中，共有11个小长方形，若中间一个长方形的面积等于其他10个小长方形面积和的，且样本容量为160，则中间一组的频数为( )． A．32 B．0.2 C．40 D．0.25 6．从标有1,2,3，…，7的7个小球中取出一球，记下它上面的数字，放回后再取出一球，记下它上面的数字，然后把两数相加得和，则取得的两球上的数字之和大于11或者能被4整除的概率是( )． A． B． C． D． 二、填空题(本大题共3小题，每小题6分，共18分) 7．某校有高一学生400人，高二学生302人，高三学生250人，现在按年级分层抽样，从所有学生中抽取一个容量为190人的样本，应该从高______学生中剔除______人，高一、高二、高三抽取的人数依次是________． 8．现有10个数，它们能构成一个以1为首项，－3为公比的等比数列，若从这10个数中随机抽取一个数，则它小于8的概率是__________． 9．已知实数x∈[－1,1]，y∈[0,2]，则点P(x，y)落在区域内的概率为__________． 三、解答题(本大题共3小题，共46分．解答应写出必要的文字说明、证明过程或演算步骤) 10．(本小题满分15分)(2012·江西八校联考，理17)某公司举办一次募捐爱心演出，有1 000人参加，每人一张门票，每张100元．在演出过程中穿插抽奖活动，第一轮抽奖从这1 000张票根中随机抽取10张，其持有者获得价值1000元的奖品，并参加第二轮抽奖活动．第二轮抽奖由第一轮获奖者独立操作按钮，电脑随机产生两个数x，y(x，y∈{0,1,2,3})，满足|x－1|＋|y－2|≥3电脑显示“中奖”，且抽奖者获得9 000元奖金；否则电脑显示“谢谢”，则不中奖． (1)已知小明在第一轮抽奖中被抽中，求小明在第二轮抽奖中获奖的概率； (2)若小白参加了此次活动，求小白参加此次活动收益的期望． 11．(本小题满分15分)设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ＝0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ＝1. (1)求概率P(ξ＝0)； (2)求ξ的分布列，并求其数学期望E(ξ)． 12．(本小题满分16分)某单位招聘面试，每次从试题库中随机调用一道试题．若调用的是A类型试题，则使用后该试题回库，并增补一道A类型试题和一道B类型试题入库，此次调题工作结束；若调用的是B类型试题，则使用后该试题回库，此次调题工作结束．试题库中现有n＋m道试题，其中有n道A类型试题和m道B类型试题．以X表示两次调题工作完成后，试题库中A类型试题的数量． (1)求X＝n＋2的概率； (2)设m＝n，求X的分布列和均值(数学期望)．一、选择题 1．C　2．D 3．D　解析：设A，B，C分别表示炸中第一、第二、第三座军火库这三个事件，则P(A)＝0.2，P(B)＝0.3，P(C)＝0.1.设D表示“军火库爆炸”，则D＝A∪B∪C.又∵A，B，C彼此互斥，∴P(D)＝P(A∪B∪C)＝P(A)＋P(B)＋P(C)＝0.2＋0.3＋0.1＝0.6. 4．D 5．A　解析：设中间的长方形面积为x，则其他的10个小长方形的面积为4x，所以可得x＋4x＝1，得x＝0.2；又因为样本容量为160，所以中间一组的频数为160×0.2＝32，故选A. 6．A 二、填空题 7．二　2　80,60,50　解析：总体人数为400＋302＋250＝952(人)，∵＝5……2，＝80，＝60，＝50，∴从高二年级中剔除2人．从高一，高二，高三年级中分别抽取80人、60人、50人． 8．　解析：∵以1为首项，－3为公比的等比数列的10个数为1，－3,9，－27，…，其中有5个负数，1个正数一共6个数小于8，∴从这10个数中随机抽取一个数，它小于8的概率是＝. 9．　解析：如图所示，(x，y)在矩形ABCD内取值，不等式组所表示的区域为△AEF，由几何概型的概率公式，得所求概率为. 三、解答题 10．解：(1)从0,1,2,3四个数字中(可重复)任取2个数字，其基本事件有(0,0)，(0,1)，(0,2)，(0,3)，(1,0)，(1,1)，(1,2)，(1,3)，(2,0)，(2,1)，(2,2)，(2,3)，(3,0)，(3,1)，(3,2)，(3,3)，共16个． 设“小明在第二轮抽奖中获奖”为事件A，且事件A所包含的基本事件有(0,0)，(2,0)，(3,0)，(3,1)，(3,3)，共5个． ∴P(A)＝. (2)设小白参加此次活动的收益为ξ，ξ的可能取值为－100,900，9 900. 则P(ξ＝－100)＝，P(ξ＝900)＝×＝，P(ξ＝9 900)＝×＝. ∴ξ的分布列为 ξ－1009009 900P∴E(ξ)＝－100×＋900×＋9 900×＝－. 11．解：(1)若两条棱相交，则交点必为正方体8个顶点中的1个，过任意1个顶点恰有3条棱，所以共有8对相交棱，因此P(ξ＝0)＝＝＝. (2)若两条棱平行，则它们的距离为1或，其中距离为的共有6对，故P(ξ＝)＝＝， 于是P(ξ＝1)＝1－P(ξ＝0)－P(ξ＝)＝1－－＝， 所以随机变量ξ的分布列是 ξ01P(ξ)因此E(ξ)＝1×＋×＝. 12．解：以Ai表示第i次调题调用到A类型试题，i＝1,2. (1)P(X＝n＋2)＝P(A1A2)＝·＝. (2)X的可能取值为n，n＋1，n＋2. P(X＝n)＝P()＝·＝. P(X＝n＋1)＝P(A1)＋P(A2)＝·＋·＝， P(X＝n＋2)＝P(A1A2)＝·＝， 从而X的分布列是 Xnn＋1n＋2PE(X)＝n×＋(n＋1)×＋(n＋2)×＝n＋1.。

第17讲统计与统计案例统计与现实生活联系较为紧密，应用性非常强，理论要求低，难度不大，在复习中要深入课本，牢牢把握统计的基本思想和统计方法，掌握随机抽样、用样本估计总体、线性回归分析的方法．对于统计案例，知道回归分析、独立性检验的基本思想、方法及简单应用，会解决简单独立性检验问题．1．把握统计的基本思想．通过复习课本，从中提炼出统计的基本思想，即用样本估计总体，它主要研究两个主要问题，一是如何从总体中抽取样本，二是如何通过对所抽取的样本进行数据处理、分析，对总体的情况作出判断和分析．把握了统计的基本思想，就抓住了统计方法的主线．2．能根据样本的特点正确抽样．明确简单随机抽样、分层抽样与系统抽样的共同点，各自特点，适用范围，清楚它们之间的相互联系，用表格的形式把它们作一对比．3．掌握用样本估计总体的方法．利用图表分析数据是统计的基本要求，频率分布表、频数分布表、2×2列联表是统计数据的数字体现，频率分布直方图、茎叶图、散点图是统计数据的直观体现．会用样本的频率分布直方图、茎叶图估计总体分布，会用样本的数字特征估计总体的数字特征，会根据散点图判断两组变量的相关关系．4．了解回归分析、独立性检验的原理．对于回归分析、独立性检验，了解其基本思想、方法及简单应用即可，知道独立性检验的步骤，会按照公式计算，能和临界值表对照得出正确结论．例1某单位有840名职工，现采用系统抽样方法，抽取42人做问卷调查，将840人按1，2，…，840随机编号，则抽取的42人中，编号落入区间[481，720]的人数为()A．11 B．12 C．13 D．14解后反思利用简单随机抽样抽取出的样本号码没有规律性；分层抽样中，在每一层抽取的号码个数m等于该层所含个体数目与抽样比的积，并且应该恰有m个号码在该层的号码段内；利用系统抽样取出的样本号码有规律性，其号码按从小到大的顺序排列，则所抽取的号码是：l，l＋k，l＋2k，…，l＋(n－1)k.其中，n为样本容量，l是第一组中的号码，k为分段间隔＝总体容量/样本容量．例2某市2013年4月1日～4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物)：61，76，70，56，81，91，92，91，75，81，88，67，101，103，95，91，77，86，81，83，82，82，64，79，86，85，75，71，49，45.(1)完成频率分布表．(2)作出频率分布直方图．(3)根据国家标准，污染指数在0～50之间时，空气质量为优；在51～100之间时，为良；在101～150之间时，为轻微污染；在151～200之间时，为轻度污染．请你依据所给数据和上述标准，对该市的空气质量给出一个简短评价．解后反思1．用样本估计总体是统计的基本思想，当样本容量较大时，将样本数据恰当分组，通过频率分布表或频率分布直方图，用各组的频率分布描述总体的分布．2．在频率分布直方图中，各小长方形的面积等于相应各组的频率，小长方形的高与频数成正比，各组频数之和等于样本容量，频率之和等于1.例3从某居民区随机抽取10个家庭，获得第i个家庭的月收入x i(单位：千元)与月储蓄y i(单位：千元)的数据资料，算得（1）求家庭的月储蓄y对月收入x的线性回归方程y=bx+a；（2）判断变量x与y（3）若该居民区某家庭月收入为7千元，预测该家庭的月储蓄.解后反思2．在分析两个变量的相关关系时，可根据样本数据作出散点图来确定两个变量之间是否具有相关关系，若具有线性相关关系，则可通过线性回归方程估计和预测变量的值．例4某高校共有学生15 000人，其中男生10 500人，女生4 500人，为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据(单位：小时)．(1)应收集多少位女生的样本数据？(2)根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图(如图所示)，其中样本数据的分组区间为：[0，2]，(2，4]，(4，6]，(6，8]，(8，10]，(10，12]，估计该校学生每周平均体育运动时间超过4小时的概率．(3)在样本数据中，有60位女生的每周平均体育运动时间超过4小时，请完成每周平均体育运动时间与性别列联表，并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”..附：K2＝（a＋b）（c＋d）（a＋c）（b＋d）解后反思独立性检验是一种假设检验(先假设，再推翻假设)，其基本思想类似反证法：(1)提出假设：即假设两个分类变量没有关系；(2)在此假设下随机变量K2应该很小，如果由观测数据计算得到K2的观测值k很大，则在一定程度上说明假设不合理．然后根据随机变量K2的含义，评价该假设不合理的程度，继而得出在多大程度上认为两个分类变量有关系．总结感悟1．用样本估计总体是统计的基本思想，科学的统计方法是保证．一要合理抽样，使样本更具有代表性，二要对所抽取的样本进行数据处理、分析，对总体的情况作出判断．2．利用图表分析数据是统计的基本方法，能熟练作频率分布表、频数分布表、2×2列联表，它们是作图、计算的基础，频率分布直方图、茎叶图、散点图，是统计数据的直观体现，是识图和用图的基础．3．独立性检验是一种假设检验(先假设，再推翻假设)，其基本思想类似反证法．A级1．为了解某地区的中小学生视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大，在下面的抽样方法中，最合理的抽样方法是()A．简单随机抽样B．按性别分层抽样C．按学段分层抽样D．系统抽样2．某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分成6组：[40，50)，[50，60)，[60，70)，[70，80)，[80，90)，[90，100]加以统计，得到如图所示的频率分布直方图．已知高一年级共有学生600名，据此估计，该模块测试成绩不少于60分的学生人数为()A．588 B．480C．450 D．1203．设某大学的女生体重y(单位：kg)与身高x(单位：cm)具有线性相关关系，根据一组样本数据(x i，y i)(i＝1，2，…，n)，用最小二乘法建立的回归方程为y^＝0.85x－85.71，则下列结论中不正确．．．的是()A．y与x具有正的线性相关关系B．回归直线过样本点的中心(x，y)C．若该大学某女生身高增加1 cm，则其体重约增加0.85 kgD．若该大学某女生身高为170 cm，则可断定其体重必为58.79 kg4．下图是某公司10个销售店某月销售某产品数量(单位：台)的茎叶图，则数据落在区间[22，30)内的频率为()A.0.2 B．0.4 C．0.5 D．0.65．一个容量为20的样本，数据的分组及各组的频数如下：[10，20)，2；[20，30)，3；[30，40)，x；[40，50)，5；[50，60)，4；[60，70)，2；则x＝________；根据样本的频率分布估计，数据落在[10，50)的概率约为________．6．200名职工年龄分布如图所示，从中随机抽取40名职工作样本，采用系统抽样方法，按1～200编号，分为40组，分别为1～5，6～10，…，196～200，第5组抽取号码为22，第8组抽取号码为________．若采用分层抽样，40岁以下年龄段应抽取________人．7．下面茎叶图表示的是甲、乙两人在5次综合测评中的成绩，其中一个数字被污损，若乙的平均分是89，求被污损的数字．B级8．已知变量x与y正相关，且由观测数据算得样本平均数x＝3，y＝3.5，则由该观测数据算得的线性回归方程可能是()A．y＝0.4x＋2.3 B．y＝2x－2.4C．y＝－2x＋9.5 D．y＝－0.3x＋4.49．为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分(十分制)如图所示，假设得分值的中位数为m e，众数为m o，平均值为x，则()A．m e＝m o＝x B．m e＝m o<xC．m e<m o<x D．m o<m e<x10．(2015·全国Ⅱ)根据下面给出的2004年至2013年我国二氧化硫年排放量(单位：万吨)柱形图．以下结论中不正确的是()A．逐年比较，2008年减少二氧化硫排放量的效果最显著B．2007年我国治理二氧化硫排放显现成效C．2006年以来我国二氧化硫年排放量呈减少趋势D．2006年以来我国二氧化硫年排放量与年份正相关11．某中学为了解学生数学课程的学习情况，在 3 000名学生中随机抽取200名，并统计这200名学生的某次数学考试成绩，得到了样本的频率分布直方图(如图)．根据频率分布直方图推测这3 000名学生在该次数学考试中成绩小于60分的学生数是________．12．下表是某数学老师及他的爷爷、父亲和儿子的身高数据：身高为________．13．某公路设计院有工程师6人，技术员12人，技工18人，要从这些人中抽取n个人参加市里召开的科学技术大会．如果采用系统抽样和分层抽样的方法抽取，不用剔除个体，如果参会人数增加1个，则在采用系统抽样时，需要在总体中先剔除1个个体，求n.14.为了了解一个小水库中养殖的鱼的有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量(单位：kg)，并将所得数据分组，画出频率分布直方图(如图所示)．(1)在下面表格中填写相应的频率；(2)估计数据落在[1.15，1.30中的概率为多少；(3)将上面捕捞的100条鱼分别作一记号后再放回水库，几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条．请根据这一情况来估计该水库中鱼的总条数．第17讲 统计与统计案例题型分析例1 B [由84042＝20，即每20人抽取1人，所以抽取编号落入区间[481，720]的人数为720－48020＝24020＝12(人)．] 例2 解 (1)频率分布表：(2)频率分布直方图如图所示．(3)答对下述两条中的一条即可：①该市有一个月中空气污染指数有2天处于优的水平，占当月天数的115；有26天处于良的水平，占当月天数的1315；处于优或良的天数为28，占当月天数的1415.说明该市空气质量基本良好．②轻微污染有2天，占当月天数的115；污染指数在80以上的接近轻微污染的天数15，加上处于轻微污染的天数2，共有17天，占当月天数的1730，超过50%；说明该市空气质量有待进一步改善．例3 解 (1)由题意知n ＝10，x ＝1n ∑i ＝1n x i ＝8010＝8，y ＝1n ∑i ＝1n y i ＝2010＝2，又l xx ＝错误!i y i －n x y ＝184－10×8×2＝24，由此得b＝l xyl xx＝2480＝0.3，a＝y－b x＝2－0.3×8＝－0.4，故所求线性回归方程为y＝0.3x－0.4.(2)由于变量y的值随x值的增加而增加(b＝0.3>0)，故x与y之间是正相关．(3)将x＝7代入回归方程可以预测该家庭的月储蓄为y＝0.3×7－0.4＝1.7(千元)．例4解(1)300×4 50015 000＝90，所以应收集90位女生的样本数据．(2)由频率分布直方图得1－2×(0.025＋0.100)＝0.75，所以该校学生每周平均体育运动时间超过4小时的概率的估计值为0.75.(3)由(2)知，300位学生中有300×0.75＝225(人)的每周平均体育运动时间超过4小时，75人的每周平均体育运动时间不超过4小时．又因为样本数据中有210份是关于男生的，90份是关于女生，所以每周平均体育运动时间与性别列联表如下：每周平均体育运动时间与性别列联表结合列联可算得K 2＝300×（45×60－165×30）275×225×210×90＝10021≈4.762>3.841.所以，有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”． 线下作业1．C [不同的学段在视力状况上有所差异，所以应该按照学段分层抽样．] 2．B [少于60分的学生人数600×(0.05＋0.15)＝120(人)， ∴不少于60分的学生人数为480人．]3．D [根据线性回归方程中各系数的意义求解． 由于线性回归方程中x 的系数为0.85，因此y 与x 具有正的线性相关关系，故A 正确． 又线性回归方程必过样本点的中心(x ，y )，因此B 正确．由线性回归方程中系数的意义知，x 每增加1 cm ，其体重约增加0.85 kg ，故C 正确．当某女生的身高为170 cm 时，其体重估计值是58.79 kg ，而不是具体值，因此D 不正确．]4．B [10个数据落在区间[22，30)内的数据有22，22，27，29，共4个，因此，所求的频率为410＝0.4.故选B.] 5．4 0.7解析 x ＝20－(2＋3＋5＋4＋2)＝4， P ＝2＋3＋4＋520＝0.7或P ＝1－4＋220＝0.7.6．37 20解析 将1～200编号分为40组，则每组的间隔为5，其中第5组抽取号码为22，则第8组抽取的号码应为22＋3×5＝37；由已知条件200名职工中40岁以下的职工人数为200×50%＝100，设在40岁以下年龄段中应抽取x 人，则40200＝x100，解得x ＝20.7．解 设污损的数字对应的成绩是x ，由茎叶图可得89×5＝83＋83＋87＋x ＋99，所以x ＝93，故污损的数字是3.8．A [因为变量x 和y 正相关，则回归直线的斜率为正，故可以排除选项C 和D.因为样本点的中心在回归直线上，把点(3，3.5)分别代入选项A 和B 中的直线方程进行检验，可以排除B ，故选A.]9．D [由题目所给的统计图示可知，30个得分中，按大小顺序排好后，中间的两个得分为5，6，故中位数m e ＝6＋52＝5.5， 又众数m o ＝5，平均值x ＝3×2＋4×3＋5×10＋6×6＋7×3＋8×2＋9×2＋10×230＝17930，∴m o <m e <x .]10．D [从2006年起，将每年的二氧化硫排放量与前一年作差比较，得到2008年二氧化硫排放量与2007年排放量的差最大，A 选项正确； 2007年二氧化硫排放量较2006年降低了很多，B 选项正确；虽然2011年二氧化硫排放量较2010年多一些，但自2006年以来，整体呈递减趋势，即C 选项正确；自2006年以来我国二氧化硫年排放量与年份负相关，D 选项错误，故选D.] 11．600解析 由频率分布直方图易得，成绩低于60分的频率为0.002×10＋0.006×10＋0.012×10＝0.2，故3 000名学生中成绩低于60分的学生数为：3 000×0.2＝600(人)．12．185 cm13．解总体容量为6＋12＋18＝36.当样本容量是n时，由题意知，系统抽样的间隔为36n，分层抽样的比例是n36，抽取的工程师人数为n36×6＝n6，技术员人数为n36×12＝n3，技工人数为n36×18＝n2，所以n应是6的倍数，36的约数，即n＝6，12，18.当样本容量为(n＋1)时，总体容量是35人，系统抽样的间隔为35n＋1，因为35n＋1必须是整数，所以n只能取6.即样本容量n＝6.14．解(1)根据频率分布直方图可知，频率＝组距×(频率/组距)，故可得下表：(2)0.30＋0.15＋0.02＝0.47，所以数据落在[1.15，1.30)中的概率约为0.47.(3)120×1006＝2 000，所以水库中鱼的总条数约为2 000.。

高考数学统计与统计案例专题卷（附答案）一、单选题1.新高考改革后，某校2000名学生参加物理学考，该校学生物理成绩的频率分布直方图如图所示，若规定分数达到90分以上为A级，则该校学生物理成绩达到A级的人数是（）A. 600B. 300C. 60D. 302.国庆70周年庆典磅礴而又欢快的场景，仍历历在目.已知庆典中某省的游行花车需要用到某类花卉，而该类花卉有甲、乙两个品种，花车的设计团队对这两个品种进行了检测.现从两个品种中各抽测了10株的高度，得到如下茎叶图.下列描述正确的是（）A. 甲品种的平均高度大于乙品种的平均高度，且甲品种比乙品种长的整齐B. 甲品种的平均高度大于乙品种的平均高度，但乙品种比甲品种长的整齐C. 乙品种的平均高度大于甲品种的平均高度，且乙品种比甲品种长的整齐D. 乙品种的平均高度大于甲品种的平均高度，但甲品种比乙品种长的整齐3.某次歌唱比赛中，7位评委为某选手打出的分数分别为83，91，91，94，94，95，96，去掉一个最高分和一个最低分后，所剩数据的平均数为（）A. 94B. 93C. 92D. 914.为了解某市居民用水情况，通过抽样，获得了100位居民某年的月均用水量(单位：吨).将数据按照，…，分成9组，绘制了如图所示的频率分布直方图.政府要试行居民用水定额管理，制定一个用水量标准.使的居民用水量不超过，按平价收水费，超出的部分按议价收费，则以下比较适合做为标准的是（）A. 2.5吨B. 3吨C. 3.5吨D. 4吨5.某校高三年级有男生220人，学籍编号为1，2，...，220；女生380人，学籍编号为221，222， (600)为了解学生学习的心理状态，按学籍编号采用系统抽样的方法从这600名学生中抽取10人进行问卷调查(第一组采用简单随机抽样，抽到的号码为10)，再从这10名学生中随机抽取3人进行座谈，则这3人中既有男生又有女生的概率是（）A. B. C. D.6.如图的折线图是某超市2018年一月份至五月份的营业额与成本数据，根据该折线图，下列说法正确的是（）A. 该超市2018年的前五个月中三月份的利润最高B. 该超市2018年的前五个月的利润一直呈增长趋势C. 该超市2018年的前五个月的利润的中位数为0.8万元D. 该超市2018年前五个月的总利润为3.5万元7.为了从甲、乙两组学生中选一组参加“喜迎祖国七十华诞，共建全国文明城市”知识竞赛活动，班主任老师将这两组学生最近6次的测试成绩进行统计，得到如图所示的茎叶图．若甲、乙两组的平均成绩分别是，则下列说法正确的是（）A. ，乙组比甲组成绩稳定，应选乙组参加竞赛B. ，甲组比乙组成绩稳定，应选甲组参加竞赛C. ，甲组比乙组成绩稳定，应选甲组参加竞赛D. ，乙组比甲组成绩稳定，应选乙组参加竞赛8.为了节能减排，发展低碳经济，我国政府从2001年起就通过相关政策推动新能源汽车产业发展.下面的图表反映了该产业发展的相关信息:根据上述图表信息，下列结论错误的是（）A. 2017年3月份我国新能源汽车的产量不超过万辆B. 2017年我国新能源汽车总销量超过万辆C. 2018年8月份我国新能源汽车的销量高于产量D. 2019年1月份我国插电式混合动力汽车的销量低于万辆9.某学校运动会的立定跳远和秒跳绳两个单项比赛分成预赛和决赛两个阶段．下表为名学生的预赛成绩，其中有三个数据模糊．秒跳绳（单位：次）在这名学生中，进入立定跳远决赛的有人，同时进入立定跳远决赛和30秒跳绳决赛的有6人，则（）A. 号学生进入秒跳绳决赛B. 号学生进入秒跳绳决赛C. 号学生进入秒跳绳决赛D. 号学生进入秒跳绳决赛10.2010-2018年之间，受益于基础设施建设对光纤产品的需求，以及个人计算机及智能手机的下一代规格升级，电动汽车及物联网等新机遇，连接器行业增长呈现加速状态．根据该折线图，下列结论正确的个数为（）①每年市场规模量逐年增加；②增长最快的一年为2013～2014；③这8年的增长率约为40％；④2014年至2018年每年的市场规模相对于2010年至2014年每年的市场规模，数据方差更小，变化比较平稳A. 1B. 2C. 3D. 4二、填空题（共7题；共7分）11.己知随机变量与有相关关系，当时，的预报值为________.12.若数据的方差为，则________．13.某学校高一、高二、高三年级的学生人数成等差数列，现用分层抽样的方法从这三个年级中抽取90人，则应从高二年级抽取的学生人数为________.14.某班的全体学生参加数学测试，成绩的频率分布直方图如图，数据的分组依次为：、、、，若低于分的人数是，则成绩不低于分的学生人数是________.15.已知样本7，8，9，的平均数是9，且，则此样本的方差是________.16.某中学采用系统抽样方法，从该校高三年级全体800名学生中抽50名学生做牙齿健康检查．现将800名学生从1到800进行编号．已知从33～48这16个数中取的数是42，则在第1小组1～16中随机抽到的数是________．17.2020年年初，新冠肺炎疫情袭击全国.口罩成为重要的抗疫物资，为了确保口罩供应，某工厂口罩生产线高速运转，工人加班加点生产.设该工厂连续5天生产的口罩数依次为，，，，（单位：十万只），若这组数据，，，，的方差为1.44，且，，，，的平均数为4，则该工厂这5天平均每天生产口罩________十万只.三、解答题（共6题；共60分）18.每年的12月4日为我国“法制宣传日”.天津市某高中团委在2019年12月4日开展了以“学法、遵法、守法”为主题的学习活动.已知该学校高一、高二、高三的学生人数分别是480人、360人、360人.为检查该学校组织学生学习的效果，现采用分层抽样的方法从该校全体学生中选取10名学生进行问卷测试.具体要求：每位被选中的学生要从10个有关法律、法规的问题中随机抽出4个问题进行作答，所抽取的4个问题全部答对的学生将在全校给予表彰.（1）求各个年级应选取的学生人数；（2）若从被选取的10名学生中任选3人，求这3名学生分别来自三个年级的概率；（3）若被选取的10人中的某学生能答对10道题中的7道题，另外3道题回答不对，记表示该名学生答对问题的个数，求随机变量的分布列及数学期望.19.清华大学自主招生考试题中要求考生从A，B，C三道题中任选一题作答，考试结束后，统计数据显示共有600名学生参加测试，选择A，B，C三题答卷数如下表：（Ⅰ）负责招生的教授为了解参加测试的学生答卷情况，现用分层抽样的方法从600份答案中抽出若干份答卷，其中从选择A题作答的答卷中抽出了3份，则应分别从选择B，C题作答的答卷中各抽出多少份？（Ⅱ）测试后的统计数据显示，A题的答卷得优的有60份，若以频率作为概率，在（Ⅰ）问中被抽出的选择A题作答的答卷中，记其中得优的份数为，求的分布列及其数学期望．20.近年来，国资委.党委高度重视扶贫开发工作，坚决贯彻落实中央扶贫工作重大决策部署，在各个贫困县全力推进定点扶贫各项工作，取得了积极成效，某贫困县为了响应国家精准扶贫的号召，特地承包了一块土地，已知土地的使用面积以及相应的管理时间的关系如下表所示：土地使用面积（单位：亩） 1 2管理时间（单位：月）并调查了某村300名村民参与管理的意愿，得到的部分数据如下表所示:参考公式：其中．临界值表：0.100 0.050 0.025 0.010 0.001参考数据：（1）求出相关系数的大小，并判断管理时间与土地使用面积是否线性相关？（2）是否有99.9%的把握认为村民的性别与参与管理的意愿具有相关性？（3）若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况，则从该贫困县中任取3人，记取到不愿意参与管理的男性村民的人数为,求的分布列及数学期望．21.出版商为了解某科普书一个季度的销售量y（单位：千本）和利润x（单位：元/本）之间的关系，对近年来几次调价之后的季销售量进行统计分析，得到如下的10组数据.根据上述数据画出如图所示的散点图：参考公式及参考数据：①对于一组数据（u1，v1），（u2，v2），…，（u n，v n），其回归直线的斜率和截距的公式分别为, .②参考数据：表中u i=Inx i，= .另：In4.06≈1.40.计算时，所有的小数都精确到0.01.（1）根据图中所示的散点图判断y=ax+b和y=clnx+d哪个更适宜作为销售量y关于利润x的回归方程类型？（给出判断即可，不需要说明理由）；（2）根据（1）中的判断结果及参考数据，求出y关于x的回归方程；（3）根据回归方程分析：设该科普书一个季度的利润总额为：（单位：千元），当季销售量y为何值时，该书一个季度的利润总额预报值最大？（季利润总额=季销售量×每本书的利润）22.某险种的基本保费为（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：（I）记A为事件：“一续保人本年度的保费不高于基本保费”．求P（A）的估计值；（Ⅱ）记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”．求P（B）的估计值；（Ⅲ）求续保人本年度的平均保费估计值．23.为了研究55岁左右的中国人睡眠质量与心脑血管病是否有关联，某机构在适龄人群中随机抽取了100万个样本，调查了他们每周是否至少三个晚上出现了三种失眠症状，症状：入睡困难；症状：醒得太早；症状：不能深度入睡或做梦，得到的调查数据如下：数据1：出现症状人数为8.5万，出现症状人数为9.3万，出现症状人数为6.5万，其中含症状同时出现1.8万人，症状同时出现1万人，症状同时出现2万人，症状同时出现0.5万人；数据2：同时有失眠症状和患心脑血管病的人数为5万人，没有失眠症状且无心脑血管病的人数为73万人.（Ⅰ）依据上述数据试分析55岁左右的中国人患有失眠症的比例大约多少？（Ⅱ）根据以上数据完成如下列联表，并根据所填列联表判断能否有95%的把握说明失眠与心脑血管病存在“强关联”？参考数据如下：0.500.05参考公式：答案一、单选题1. B2. D3. B4. B5. D6. D7. D8. D9. B 10. C二、填空题11. 7 12. 13. 30 14. 15 15. 2 16. 10 17. 1.6三、解答题18. （1）解：由题意，知高一、高二、高三年级的人数之比为，由于采用分层抽样方法从中选取人，因此，高一年级应选取人，高二年级应选取人，高三年级应选取人.（2）解：由（1）知，被选取的名学生高一、高二、高三年级分别有人、人、人，所以，从这名学生任选名，且名学生分别来自三个年级的概率为.（3）解：由题意知，随机变量的所有可能取值为，且服从超几何分布，（）.所以，随机变量的分布列为所以，随机变量的数学期望为.19. 解：解：（Ⅰ）由题意可得：应分别从B,C题的答卷中抽出5份，2份．（Ⅱ）由题意可知，A题答案得优的概率为，显然被抽出的A题的答案中得优的份数x的可能取值为0,1,2,3，且．；；；随机变量x的分布列为：所以．20. （1）解：依题意：故则，故管理时间与土地使用面积线性相关．（2）解：依题意，完善表格如下：计算得的观测值为故有99.9%的把握认为村民的性别与参与管理的意愿具有相关性．（3）解：依题意，的可能取值为0，1，2，3，从该贫困县中随机抽取一名，则取到不愿意参与管理的男性村民的概率为，故故的分布列为则数学期望为（或由，得21. （1）解：y=cln x+d更适宜作为销售量y关于利润x的回归方程类型（2）解：令u=lnx，先建立y关于u的线性回归方程，由于,=6.63+10.20×1.75=24.48，所以x关于u的线性回归方程为=24.48-10.20u，即y关于x的回归方程为=24.48-10.20lnx.（3）解：由题意得z=xy=x（24.48-10.20lnx），z'=[x（24.48-10.20lnx）]'=14.28-10.20lnx，令z'=0 即14.28-10.20lnx=0，解得lnx=1.40，所以x≈4.06.当x∈（0，4.06）时，z'>0，所以z在（0，4.06）上单调递增，当x∈（4.06，+∞）时，z'<0，所以z在（4.06，+∞）上单调递减，所以当x=4.06时，即季销量y=10.20千本时，季利润总额预报值最大22. 解：（I）记A为事件：“一续保人本年度的保费不高于基本保费”．事件A的人数为：60+50＝110，该险种的200名续保，P（A）的估计值为：；（Ⅱ）记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”．事件B的人数为：30+30＝60，P（B）的估计值为：；（Ⅲ）续保人本年度的平均保费估计值为1.1925a．23. 解：（Ⅰ）设{出现症状的人}、{出现症状的人}、{出现症状的人}（表示有限集合元素个数）根据数据1可知，，，，所以得患失眠症总人数为20万人，比例大约为20%（Ⅱ）根据数据2可得：有95%的把握说明失眠与中风或心脏病存在“强关联”.第11 页共11 页。

2017年高考数学（考点解读+命题热点突破）专题17 统计与统计案例文编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2017年高考数学（考点解读+命题热点突破）专题17 统计与统计案例文）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2017年高考数学（考点解读+命题热点突破）专题17 统计与统计案例文的全部内容。

专题17 统计与统计案例文【命题热点突破一】抽样方法某工厂生产的甲、乙、丙、丁四种不同型号的产品分别有150件、120件、180件、150件．为了调查产品的情况，需从这600件产品中抽取一个容量为100的样本，若采用分层抽样法，设甲产品中应抽取的产品件数为x，某件产品A被抽到的概率为y,则x，y的值分别为（）A．25,错误! B．20，错误!C．25，错误! D．25，错误!【答案】D【特别提醒】三种抽样方法均是等概率抽样,当总体是由差异明显的几个部分组成时，往往选用分层抽样的方法．【变式探究】从编号分别为0，1，2，…，79的80件产品中，采用系统抽样的方法抽取容量为10的样本，若编号为58的产品在样本中,则该样本中产品的最大编号为________．【答案】74【解析】每8件产品抽取一件,编号为58的产品在样本中，则样本中产品的最大编号为58＋16＝74.【命题热点突破二】用样本估计总体【2016高考山东】某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5,30］，样本数据分组为［17.5，20), [20，22.5)，［22。

5,25)，［25，27.5）,[27.5，30).根据直方图，这200名学生中每周的自习时间不少于22。

2021高考数学一复习统计与统计案例专项练习（含答案）题型归纳每一门科学都有其建立、发展和客观条件，统计科学则是统计工作经验、社会经济理论、计量经济方法融合、提炼、发展而来的一种边缘性学科。

以下是____-____高考数学一复习统计与统计案例专项练习，请考生掌握。

一、选择题11.(文)(____重庆理，3)已知变量_与y正相关，且由观测数据算得样本平均数=3，=3.5，则由该观测数据算得线性回归方程可能为()A.=0.4_+2.3B.=2_-2.4C.=-2_+9.5D.=-0.3_+4.4[答案] A[解析] 因为变量_和y正相关，所以回归直线的斜率为正，排除C、D;又将点(3,3.5)代入选项A和B的方程中检验排除B，所以选A.(理)一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了8次试验，收集数据如下：零件数_(个) 10 20 30 40 50 60 70 80 加工时间y(min) 62 68 75 81 89 95 102 108 设回归方程为y=b_+a，则点(a，b)在直线_+45y-10=0的()A.左上方B.左下方C.右上方D.右下方[答案] C[解析] =45，=85，a+45b=85，a+45b-100，故点(a，b)在直线_+45y-10=0的右上方，故选C.12.(____沈阳市质检)某高校进行自主招生，先从报名者中筛选出400人参加笔试，再按笔试成绩择优选出100人参加面试.现随机调查了24名笔试者的成绩，如下表所示：分数段 [60,65) [65,70) [70,75) [75,80) [80,85) [85,90) 人数 2 3 4 9 51 据此估计允许参加面试的分数线大约是()A.75B.80C.85D.90[答案] B[解析] 由题可知，在24名笔试者中应选出6人参加面试.由表可得面试分数线大约为80.故选B.13.(____陕西文，5)对一批产品的长度(单位：毫米)进行抽样检测，下图为检测结果的频率分布直方图.根据标准，产品长度在区间[20,25)上为一等品，在区间[15,20)和[25,30)上为二等品，在区间[10,15)和[30,35]上为三等品.用频率估计概率，现从该批产品中随机抽取1件，则其为二等品的概率是()A.0.09B.0.20C.0.25D.0.45[答案] D[解析] 解法1：用样本估计总体.在区间[15,20)和[25,30)上的概率为0.045+[1-(0.02+0.04+0.06+0.03)5=0.45.解法2：由图可知，抽得一等品的概率P1=0.065=0.3;抽得三等品的概率为P3=(0.02+0.03)5=0.25.故抽得二等品的概率为1-(0.3+0.25)=0.45.14.(____江西理，6)某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系，随机抽查52名中学生，得到统计数据如表1至表4，则与性别有关联的可能性最大的变量是()A.成绩B.视力C.智商D.阅读量[答案] D[解析] A中，K2==;B中，K2==;C中，K2==;D中，K2==.因此阅读量与性别相关的可能性最大，所以选D.15.(文)某养兔场引进了一批新品种，严格按照科学配方进行喂养，四个月后管理员称其体重(单位：kg)，将有关数据进行整理后分为五组，并绘制频率分布直方图(如图所示).根据标准，体重超过6kg属于超重，低于5kg的不够分量.已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25、0.20、0.10、0.05，第二小组的频数为400，则该批兔子的总数和体重正常的频率分别为()A.1000,0.50B.800,0.50C.800,0.60D.1000,0.60[答案] D[解析] 第二组的频率为1-0.25-0.20-0.10-0.05=0.40，所以兔子总数为=1000只，体重正常的频率为0.40+0.20=0.60.故选D.(理)(____山东理，7)为了研究某药品的疗效，选取若干名志愿者进行临床试验.所有志愿者的舒张压数据(单位：kPa)的分组区间为[12,13)，[13,14)，[14,15)，[15,16)，[16,17]，将其按从左到右的顺序分别编号为第一组，第二组，，第五组.下图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为()A.6B.8C.12D.18[答案] C[解析] 第一、二两组的频率为0.24+0.16=0.4志愿者的总人数为=50(人).第三组的人数为：500.36=18(人)有疗效的人数为18-6=12(人)二、填空题16.(____辽宁文，16)为了考察某校各班参加课外书法小组的人数，从全校随机抽取5个班级，把每个班级参加该小组的人数作为样本数据，已知样本平均数为7，样本方差为4，且样本数据互不相同，则样本数据中的最大值为________.[答案] 10[解析] 设5个班级中参加的人数分别为_1，_2，_3，_4，_5，则=7，=4，即5个整数平方和为20，_1，_2，_3，_4，_5这5个数中最大数比7大，但不能超过10，因此最大为10，平方和20=0+1+1+9+9=(7-7)2+(8-7)2+(6-7)2+(10-7)2+(4-7)2.因此参加的人数为4,6,7,8,10，故最大值为10，最小值为4.三、解答题17.(文)(____重庆文，17)20名学生某次数学考试成绩(单位：分)的频率分布直方图如下：(1)求频率分布直方图中a的值;(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;(3)从成绩在[50,70)的学生中任选2人，求此2人的成绩都在[60,70)中的概率. [分析] 由频率之和为1，求a，然后求出落在[50,60)和[60,70)中的人数，最后用列举法求古典概型的概率.[解析] (1)组距为10，(2a+3a+6a+7a+2a)10=200a=1，a==0.005.(2)落在[50,60)中的频率为2a10=20a=0.1，落在[50,60)中的人数为2.落在[60,70)中的学生人数为3a1020=30.0051020=3.(3)设落在[50,60)中的2人成绩为A1，A2，落在[60,70)中的3人为B1，B2，B3.则从[50,70)中选2人共有10种选法，={(A1，A2)，(A1，B1)，(A1，B2)，(A1，B3)，(A2，B1)，(A2，B2)，(A2，B3)，(B1，B2)，(B1，B3)，(B2，B3)}其中2人都在[60,70)中的基本事件有3个：(B1，B2)，(B1，B3)，(B2，B3)，故所求概率p=.(理)(____辽宁理，18)一家面包房根据以往某种面包的销售记录，绘制了日销售量的频率分布直方图，如图所示.将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立.(1)求在未来连续3天里，有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率;(2)用_表示在未来3天里日销售量不低于100个的天数，求随机变量_的分布列，期望E(_)及方差D(_).[解析] (1)设A1表示事件日销售量不低于100个，A2表示事件日销售量低于50个，B表示事件在未来连续3天是有连续2天日销售量不低于100个且另一天销售量低于50个，因此P(A1)=(0.006+0.004+0.002)50=0.6P(A2)=0.00350=0.15，P(B)=0.60.60.152=0.108.(2)_可能取的值为0,1,2,3，相应的概率为P(_=0)=C(1-0.6)3=0.064，P(_=1)=C0.6(1-0.6)2=0.288.P(_=2)=C0.62(1-0.6)=0.432.P(_=3)=C0.63=0.216.分布列为_ 0 1 2 3 P 0.064 0.288 0.432 0.216 因为_～B(3,0.6)所以期望E(_)=30.6=1.8，方差D(_)=30.6(1-0.6)=0.72.18.(文)为加强中学生实践、创新能力和团队精神的培养，促进教育教学改革，郑州市教育局举办了全市中学生创新知识竞赛.某校举行选拔赛，共有200名学生参加，为了解成绩情况，从中选取50名学生的成绩(得分均为整数，满分为100分)进行统计.请你根据尚未完成的频率分布表，解答下列问题：分组频数频率一 60.5～70.5 a 0.26 二 70.5～80.5 15 c 三 80.5～90.5 18 0.36 四 90.5～100.5 b d 合计 50 e (1)若用系统抽样的方法抽取50个样本，现将所有学生随机地编号为000,001,002，，199，试写出第二组第一位学生的编号;(2)求出a、b、c、d、e的值(直接写出结果)，并作出频率分布直方图;(3)若成绩在85.5～95.5分的学生为二等奖，问参赛学生中获得二等奖的学生约为多少人.[解析] (1)004(2)a，b，c，d，e的值分别为13,4,0.30,0.08,1.频率分布直方图如下：(3)由样本中成绩在80.5～90.5的频数为18，成绩在90.5～100.5的频数为4，可估计成绩在85.5～95.5的人数为11人，故获得二等奖的学生约为11=44人. (理)(____山西省高考联合模拟)为了了解某年级1000名学生的百米成绩情况，随机抽取了若干学生的百米成绩，成绩全部介于13s与18s之间，将成绩按如下方式分成五组：第一组[13,14);第二组[14,15);第五组[17,18].按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前3个组的频率之比为3819，且第二组的频数为8.(1)将频率当作概率，求调查中随机抽取了多少个学生的百米成绩;(2)若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1秒的概率.[解析] (1)设图中从左到右前3个组的频率分别为3_,8_,19_依题意，得3_+8_+19_+0.321+0.081=1，_=0.02，设调查中随机抽取了n个学生的百米成绩，则80.02=，n=50，调查中随机抽取了50个学生的百米成绩.(2)百米成绩在第一组的学生数为30.02150=3，记他们的成绩为a、b、c百米成绩在第五组的学生数有0.08150=4，记他们的成绩为m、n、p、q，则从第一、五组中随机取出两个成绩，基本事件有{a，b}、{a，c}、{a，m}、{a，n}、{a，p}、{a，q}、{b，c}、{b，m}、{b，n}、{b，p}、{b，q}、{c，m}、{c，n}、{c，p}、{c，q}、{m，n}、{m，p}、{m，q}、{n，p}、{n，q}、{p，q}，共21个其中满足成绩的差的绝对值大于1s所包含的基本事件有{a，m}、{a，n}、{a，p}、{a，q}、{b，m}、{b，n}、{b，p}、{b，q}、{c，m}、{c，n}、{c，p}、{c，q}，共12个，所以P==.____-____高考数学一复习统计与统计案例专项练习及答案解析的全部内容就是这些，希望考生可以取得优异的成绩。

2021届高考数学-统计与统计案例提分练（详解）1．完成下列抽样调查，较为合理的抽样方法依次是（）①从30件产品中抽取3件进行检查；②某校高中三个年级共有2460人，其中高一830人、高二820人、高三810人，为了了解学生对数学的建议，拟抽取一个容量为300的样本；③某剧场有28排，每排有32个座位，在一次报告中恰好坐满了听众，报告结束后，为了了解听众意见，需要请28名听众进行座谈．A．①简单随机抽样，②系统抽样，③分层抽样B．①分层抽样，②系统抽样，③简单随机抽样C．①系统抽样，②简单随机抽样，③分层抽样D．①简单随机抽样，②分层抽样，③系统抽样【答案】D【解析】①中，总体数量不多，适合用简单随机抽样；②中，某校高中三个年纪共有2460人，其中高一830人、高二820人、高三810人，适合于分层抽样；③中，总体数量较多且编号有序，适合于系统抽样．故选D．2．调查机构对某高科技行业进行调查统计，得到该行业从业者学历分布饼状图、从事该行业岗位分布条形图，如图所示．给出下列三种说法：①该高科技行业从业人员学历为博士的占一半以上；②该高科技行业中从事科技岗位的人数超过总人数的30%；③该高科技行业中从事运营岗位的人员主要是本科生．其中正确的个数为（）A．0个B．1个C．2个D．3个【答案】C【解析】在①中，由该行业从业者学历分布饼状图得到：该高科技行业人员中学历为博士的占一半以上，故①正确；一、选择题在②中，由从事该行业岗位分布条形图得到：在高科技行业中从事科技岗位的人数超过总人数的30%， 故②正确；在③中，由该行业从业者学历分布饼状图、从事该行业岗位分布条形图，无法得到该高科技行业中从事运营岗位的人员主要是本科生，故③错误．故选C ．3．某市为最大限度的吸引“高精尖缺”人才，向全球“招贤纳士”，推进了人才引入落户政策，随着人口增多，对住房要求也随着而来，而选择购买商品房时，住户对商品房的户型结构越来越重视，因此某商品房调查机构随机抽取n 名市民，针对其居住的户型机构和满意度进行了调查，如图1调查的所有市民中四居室共200户，所占比例为13，二居室住户占16，如图2是有分层抽样的方法从所有调查的市民的满意度问卷中，抽取10%的调查结果绘制成的统计图，则下列说法正确的是（ ）A ．样本容量为70B ．样本中三居室住户共抽取了25户C ．根据样本可估计对四居室满意的住户有70户D ．样本中对三居室满意的有15户【答案】D【解析】如图1调查的所有市民中四居室共200户，所占比例为13，二居室住户占16， ∴20060013=，二居室有16001006⨯=户，三居室有300户， 由频率分布直方图和扇形统计图得：在A 中，样本容量为60010%60n =⨯=，故A 错误；在B 中，样本中三居室住户共抽取了30010%30⨯=户，故B 错误；在C 中，根据样本可估计对四居室满意的住户有20040%80⨯=户，故C 错误；在D 中，样本中对三居室满意的有30010%50%15⨯⨯=户，故D 正确，故选D ．4．如图是某市2017年3月1日至3月16日的空气质量指数趋势统计图，空气质量指数（AQI ）小于100表示空气质量油量，空气质量指数大于200表示空气重度污染，则关于该市这16日的空气质量，下列说法不正确的是（）A．出现过连续4天空气重度污染B．空气重度污染的频率为0.5C．相邻两天空气质量指数之差的最大值195D．空气质量指数的平均值小于200【答案】C∼日这4天连续重度污染，故A正确；【解析】依题意，根据图中信息，121516天中有8天重度污染，故B正确；-=≠，故C错误；相邻两天空气质量指数之差的最大的为7日和8日，最大值为2608317719516个数据中大于200和小于200的各有8个，大于200的8个数据接近200，而小于200的8个数据与200相差较大，故平均值小于200，故D正确，故选C．5．如图是某赛季甲，乙两名篮球运动员9场比赛所得分数的茎叶图，则下列说法错误的是（）A．甲所得分数的极差为22B．乙所得分数的中位数为18C．两人所得分数的众数相等D．甲所得分数的平均数低于乙所得分数的平均数【答案】D-=，A正确；【解析】甲所得分数的极差为331122乙所得分数的中位数为18，B正确；甲所得分数的众数为22，乙所得分数的众数为22，C正确，故选D．6．甲、乙两名运动员分别进行了5次射击训练，成绩如下：甲：7，7，8，8，10；乙：8，9，9，9，10；。

2021届高三（新高考）数学大题优练 成对数据的统计分析例1．这一年来人类与新型冠状病毒的“战争”让人们逐渐明白一个道理，人类社会组织模式的差异只是小事情，病毒在地球上存在了三四十亿年，而人类的文明史不过只有几千年而已，人类无法消灭病毒，只能与之共存或者病毒自然消亡，在病毒面前，个体自由要服从于集体或者群体生命的价值．在传染病学中，通常把从致病刺激物侵入机体内或者对机体发生作用起，到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期，因此我们应该注意做好良好的防护措施和隔离措施．某研究团队统计了某地区10000名患者的相关信息，得到如表表格：潜伏期（天）(]0,2(]2,4(]4,6(]6,8(]8,10 (]10,12 (]12,14人数6001900300025001600250150（1）新冠肺炎的潜伏期受诸多因素的影响，为研究潜伏期与年龄的关系，通过分层抽样从10000名患者中抽取200人进行研究，完成下面的2×2列联表，并判断能否在犯错误的概率不超过0.001的前提下认为潜伏期与患者年龄有关？潜伏期8≤天潜伏期8>天总计 60岁以上（含60岁）150 60岁以下 30 总计200（2）依据上述数据，将频率作为概率，且每名患者的潜伏期是否超过8天相互独立．为了深入研究，该团队在这一地区抽取了20名患者，其中潜伏期不超过8天的人数最有可能是多少？附：()()()()()22n ad bc K a b c d a c b d -=++++．()20P K k ≥0.150 0.100 0.050 0.025 0.010 0.005 0.001 0k2.0722.7063.8415.0246.6357.87910.828【答案】（1）表格见解析，能；（2）16名．【解析】（1）由表中数据可知，潜伏期大于8天的人数为16002501502004010000++⨯=人，补充完整的2×2列联表如下，潜伏期8≤天潜伏期8>天总计 60岁以上（含60岁）13020150优选例题所以()220013*********.66710.8281505016040K ⨯⨯-⨯=≈>⨯⨯⨯，故能在犯错误的概率不超过0.001的前提下认为潜伏期与患者年龄有关．（2）该地区10000名患者中潜伏期不超过8天的人数为6001900300025008000+++=名， 将频率视为概率，潜伏期不超过8天的概率为80004100005=，所以抽取的20名患者中潜伏期不超过8天的人数最有可能是420165⨯=名． 例2．某种机械设备随着使用年限的增加，它的使用功能逐渐减退，使用价值逐年减少，通常把它使用价值逐年减少的“量”换算成费用，称之为“失效费”．某种机械设备的使用年限x （单位：年）与失效费y （单位：万元）的统计数据如下表所示：（1） （2）求出y 关于x 的线性回归方程，并估算该种机械设备使用10年的失效费．参考公式：相关系数()()niix x y y r --=∑线性回归方程ˆˆˆy bx a =+中斜率和截距最小二乘估计计算公式()()()121ˆniii nii x x y y bx x ==--=-∑∑，ˆˆa y bx=-． 参考数据：()71()14.00i i i x x y y =--=∑，()7217.08i i y y =-=∑14.10≈．【答案】（1）见解析；（2）ˆ0.5 2.3yx =+，7.3万元． 【解析】（1）由题意，知123456747x ++++++==，2.903.30 3.604.40 4.805.20 5.904.307y ++++++==，()()()()()()()()72222222211424344454647428ii x x =-=-+-+-+-+-+-+-=∑，∴结合参考数据知：14.000.9914.10r ==≈≈．因为y 与x 的相关系数近似为0.99，所以y 与x 的线性相关程度相当大， 从而可以用线性回归模型拟合y 与x 的关系．（2）∵()()()7172114ˆ0.528iii ii x x y y bx x ==--===-∑∑，∴ˆˆ 4.30.54 2.3a y bx=-=-⨯=． ∴y 关于x 的线性回归方程为ˆ0.5 2.3yx =+， 将10x =代入线性回归方程，得ˆ0.510 2.37.3y=⨯+=． ∴估算该种机械设备使用10年的失效费为7.3万元．例3．近年来，明代著名医药学家李时珍故乡黄冈市蕲春县大力发展大健康产业，蕲艾产业化种植已经成为该县脱贫攻坚的主要产业之一，已知蕲艾的株高y (单位：cm)与一定范围内的温度x (单位：℃)有关，现收集了蕲艾的13组观测数据，得到如下的散点图：现根据散点图利用y a =+dy c x=+建立y 关于x的回归方程，令s =1t x=得到如下数据：且(,i is y 与,i i t y (i ＝1，2，3，…，13)的相关系数分别为1，2，且2．（1）用相关系数说明哪种模型建立y 与x 的回归方程更合适； （2）根据（1）的结果及表中数据，建立y 关于x 的回归方程； （3）已知蕲艾的利润z 与x 、y 的关系为1202z y x =-，当x 为何值时，z 的预报值最大． 参考数据和公式：021*********⨯=．．．，116721222476374⨯=．．．15.7365=，对于一组数据(),i i u v (i ＝1，2，3，…，n )，其回归直线方程v u αβ=+的斜率和截距的最小二乘法估计分别为1221ni ii nii u v nu vunuβ==-⋅=-∑∑，v u αβ=-，相关系数ni i u v nu vr -⋅=∑【答案】（1）用d y c x =+模型建立y 与x 的回归方程更合适；（2）10ˆ111.54y x=-；（3）当温度为20℃时这种草药的利润最大．【解析】（1）由题意知20.9953r =-，10.8858r ==≈，因为121r r <<，所有用dy c x=+模型建立y 与x 的回归方程更合适． （2）因为1311322113 2.1ˆ100.2113i ii ii t y t ydtt ==-⋅-===--∑∑，ˆˆ109.94100.16111.54c y dt =-=+⨯=， 所以ˆy关于x 的回归方程为10ˆ111.54y x=-． （3）由题意知110120012020(111.54)2230.8(ˆ)2230.8202210.8222ˆzy x x x x x =-=--=-+≤-=， 所以22.8ˆ10z ≤，当且仅当20x℃时等号成立，所以当温度为20℃时这种草药的利润最大．1．在新型冠状病毒疫情期间，某高中学校实施线上教学，为了解线上教学的效果，随机抽取了100名学生对线上教学效果进行评分(满分100分)，记低于80的评分为“效果一般”，不低于80分为“效果较好”． （1）请补充完整22⨯列联表；通过计算判断，有没有99%的把握认为线上教学效果评分为“效果较好”与性别有关？效果一般效果较好合计 男20女 1555合计（2）用（1）中列联表的数据估计全校线上教学的效果，用频率估计概率．从该校学生中任意抽取3人，记所抽取的3人中线上教学“效果较好”的人数为X ，求X 的分布列和数学期望． 附表及公式：()20P K k ≥0.15 0.10 0.05 0.025 0.010 0k2.0722.7063.8415.0246.635其中()()()()()22n ad bc k a b c d a c b d -=++++，n a b c d =+++．2．如图是M 市旅游局宣传栏中的一幅标题为“2012~2019年我市接待游客人次”的统计图．根据该统计图提供的信息解决下列问题．模拟优练（1）求M 市在所统计的这8年中接待游客人次的平均值和中位数；（2）在所统计的8年中任取两年，记其中接待游客人次不低于平均数的年份数为X ，求X 的分布列和数学期望()E X ；（3）由统计图可看出，从2016年开始，M 市接待游客的人次呈直线上升趋势，请你用线性回归分析的方法预测2021年M 市接待游客的人次．①参考公式：对于一组数据()11,x y ，()22,x y ，…，(),n n x y ，其回归直线ˆˆybx a =+的斜率和截距的最小二乘法估计分别为()()()1122211ˆn niii ii i nni ii i x x y y x y nxybx x xnx ====---==--∑∑∑∑，ˆˆa y bx=-． ②参考数据：3．首届中国国际进口博览会在国家会展中心（上海）举行，吸引了58个“一带一路”沿线国家的超过1000多家企业参展，成为共建“一带一路”的又一个重要支撑．某企业为了参加这次盛会，提升行业竞争力，加大了科技投入．该企业连续6年来的科技投入x （百万元）与收益y （百万元）的数据统计如下：根据散点图的特点，甲认为样本点分布在指数曲线2bx y c =⋅的周围，据此他对数据进行了一些初步处理．如下表：其中2log i i z y =，16i i z z ==∑．（1）（ⅰ）请根据表中数据，建立y 关于x 的回归方程（保留一位小数）；（ⅱ）根据所建立的回归方程，若该企业想在下一年收益达到2亿，则科技投入的费用至少要多少？（其中2log 5 2.3≈）（2）乙认为样本点分布在二次曲线2y mx n =+的周围，并计算得回归方程为20.9212.0y x =-，以及该回归模型的相关指数20.94R =，试比较甲乙两人所建立的模型，谁的拟合效果更好．附：对于一组数据()11,u v ，()22,u v ，()33,u v ，⋅⋅⋅，(),n n u v ，其回归直线v u αβ=+的斜率和截距的最小二乘估计分别为()()()121ˆniii nii v v u u u u β==--=-∑∑，ˆˆv u αβ=-．相关指数：()()22121ˆ1ˆni i i nii v v R v v---=--∑∑．4．重庆十一中某组同学为参加第20届中国青少年机器人竞赛重庆赛区选拔赛，需要从工厂订制零件，已知该厂有两条不同生产线A 和B ，同学们为保证质量，现从各自生产的产品中分别随机抽取20件，进行品质鉴定，鉴定成绩的茎叶图如下所示：该零件的质量评价标准规定：鉴定成绩达到[)90,100的零件，质量等级为优秀；鉴定成绩达到[)80,90的零件，质量等级为良好；鉴定成绩达到[)60,80的零件，质量等级为合格．将这组数据的频率视为整批产品的概率．（1）请完成下面质量等级与生产线产品列联表，并判断能不能在犯错误的概率不超过0.05的情况下，认为产品等级是否达到良好以上与生产产品的生产线有关；（2的分布列，并求X 的数学期望；（3）为了确定机器人身上的零件个数i x 与使用寿命()1,2,5i y i =的关系，同时又兼顾灵敏性，同学们通过实践研究把i x 和()1,2,5i y i =的数据作了初步处理，得到下面的散点图及一些统计量的值．上表中i i w x =，15i i w w ==∑．根据散点图直接判断（不必说明理由）y a bx =+与dy c x=+哪一个适宜作为y 关于x 的回归方程类型？ 并根据表中数据建立y 关于x 的回归方程．附：22()()()()()n ad bc K a b c d a c b d -++++=．对于一组数据11,u v ，22,u v ，…，,n n u v ，其回归直线v u =+的斜率和截距的最小二乘估计分别为()()()1122211ˆnnii i i i i nni ii i uu v v u v nuvu u unu β====---==--∑∑∑∑，ˆˆv u αβ=-．1．【答案】（1）列联表见解析，有99%的把握认为；（2）分布列见解析，95． 【解析】（1）由题意，补充后的列联表为：效果一般 效果较好 合计男 2520 45女 1540 55 合计4060100则()22100254015208.249 6.63540604 555K ⨯⨯-⨯=≈>⨯⨯⨯，因此有99%的把握认为线上教学效果评分为“效果较好”与性别有关． （2）随机变量X 的值可能为0,1,2,3， 由题可知，线上教学“效果较好”的频率为6031005=，则33,5X B ⎛⎫ ⎪⎝⎭， 可得()303280C 5125P X ⎛⎫=== ⎪⎝⎭；()21323361C 55125P X ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭； ()22323542C 55125P X ⎛⎫⎛⎫=== ⎪⎪⎝⎭⎝⎭；()5333273C 5125P X ⎛⎫=== ⎪⎝⎭． 则随机变量X 的分布列为X0 123P8125361255412527125所以()8365427901231251251251255E X =⨯+⨯+⨯+⨯=（或()39355E X =⨯=）． 2．【答案】（1）平均数为401.25(万人次)，中位数为290(万人次)；（2）分布列见解析，数学期望为34；（3）1365万人次． 【解析】（1）平均数为110150180250330510720960401.258+++++++=(万人次)，中位数为2503302902+=(万人次)． （2）不低于平均数的有3年，X 的可能取值为0，1，2，参考答案则()2528C 50C 14P X ===；()115328C C 151C 28P X ===；()2328C 32C 28P X ===． 所以X 的分布列为故()5012142828284E X =⨯+⨯+⨯==． （3）简化变量：1.5x '=，0y '=，411050i ii x y =''=∑，2114ii x ='=∑．414222141050ˆ210144 1.54i ii i i x y x y bx x ==''''-===-⨯''-∑∑，ˆˆ0210 1.5315a y bx ''=-=-⨯=-． ˆ210315yx =-''． 当2021x =时，5x '=，ˆ735y'=，所以ˆ630735y -=，所以ˆ1365y =． 即2021年接待的游客约为1365万人次．3．【答案】（1）（ⅰ）0.512x y +=；（ⅱ）13.2百万元；（2）甲建立的回归模型拟合效果更好． 【解析】（1）（ⅰ）2468101276x +++++==，令22log log z y bx c ==+，令2log a c =，则z bx a =+．根据最小二乘估计可知：()()()6162134.70.570iii ii x x zzb x x ==--==≈-∑∑， 从而 4.50.571a z bx =-=-⨯=，故回归方程为0.51z x =+，即0.512x y +=． （ⅱ）设0.512200x +≥，解得20.51log 200x +≥，即244log 513.2x ≥+≈， 故科技投入的费用至少要13.2百万元，下一年的收益才能达到2亿．（2）甲建立的回归模型的残差：则()621298.5iii y y =-=∑，从而2298.5110.020.980.9412730.4R =-≈-=>，即甲建立的回归模型拟合效果更好．4．【答案】（1）列联表见解析，不能在误差不超过0.05的情况下，认为产品等级是否达到良好以上与生产产品的机器有关；（2）分布列见解析，() 1.2E X =；（3）d y c x =+更适合，12ˆ 5.48yx=+． 【解析】（1）由已知可得，22⨯列联表为：2()40(121468)403.636 3.841()()()()2020182211n ad bc K a b c d a c b d -⨯⨯-⨯====<++++⨯⨯⨯，所以不能在误差不超过0.05的情况下，认为产品等级是否达到良好以上与生产产品的机器有关． （2）从茎叶图可以知道，样本中优秀的产品有2个来自A 工厂，3个来自B 工厂， 所以X 的可能取值为0，1，2．2225C (0)0.1C P X ===，112325C C (1)0.6C P X ===，2325C (2)0.3C P X ===， X 的分布列为：所以()0E X =（3）根据散点图的形状更接近函数d y c x =+的图象可以判断出d y c x =+更适合，令1w x=，先建立y 关于w 的线性回归方程．由5152221530.150.4611ˆ121.45850.465i iiiiw y wydw w==--⨯⨯===-⨯-∑∑，ˆˆ11120.46 5.48c y dw=-=-⨯=．所以y关于w的线性回归方程为ˆ 5.4812y w=+，因此y关于x的回归方程为12ˆ 5.48yx=+．。

高考数学第一轮复习提分专练习题：统计及统计案例查字典数学网高中频道收集和整理了2021年高考数学第一轮复习提分专练习题：统计及统计案例，以便高三学生更好的梳理知识，轻松备战。

一、选择题1.对某商店一个月内每天的顾客人数进行统计，得到样本的茎叶图(如图所示)，则该样本的中位数、众数、极差分别是()A.46,45,56B.46,45,53C.47,45,56D.45,47,53答案：A 命题立意：本题考查中位数、众数、极差等特点数与茎叶图，难度中等.解题思路：利用相关概念求解.由茎叶图可知，第15个数据是45，第1 6个数据是47，因此30天中的顾客人数的中位数是45和47的平均数，即为46.显现次数最多的是45，故众数是45;最大数据68与最小数据12的差是56，即极差是56，故选A.2.在100个零件中，有一级品20个，二级品30个，三级品50个，从中抽取20个作为样本：采纳简单随机抽样法，将零件编号为00,01,02，，9 9，从中抽出20个;采纳系统抽样法，将所有零件分成20组，每组5个，然后每组中随机抽取1个;采纳分层抽样法，随机从一级品中抽取4个，二级品中抽取6个，三级品中抽取10个，则()A.不论采取哪种抽样方法，这100个零件中每个被抽到的概率差不多上B.两种抽样方法，这100个零件中每个被抽到的概率差不多上，并非如此C.两种抽样方法，这100个零件中每个被抽到的概率差不多上，并非如此D.采纳不同的抽样方法，这100个零件中每个被抽到的概率各不相同答案：A 解题思路：由于简单随机抽样法、系统抽样法与分层抽样法均是等可能性抽样，因此不论采取哪种抽样方法，这100个零件中每个被抽到的概率差不多上，故选A.3.从某中学一、二两个班中各随机抽取10名学生，测量他们的身高(单位：cm)后获得身高数据的茎叶图如图甲，在这20人中，记身高在[150,160)，[160,170)，[170,180)，[180,190]的人数依次为A1，A2，A3，A4，图乙是统计样本中身高在一定范畴内的人数的程序框图，则下列说法正确的是()A.甲可知一、二两班中平均身高较高的是一班，图乙输出的S的值为1 8B.甲可知一、二两班中平均身高较高的是二班，图乙输出的S的值为1 6C.甲可知一、二两班中平均身高较高的是二班，图乙输出的S的值为1 8D.甲可知一、二两班中平均身高较高的是一班，图乙输出的S的值为1 6答案：C 命题立意：本题要紧考查统计与程序框图的相关知识，统计问题与程序框图的结合有可能成为高考命题的热点，此类题目考查的方式多样，难度适中.在该题中对程序框图的考查要紧表达在对其循环结构的考查.此类题目易显现的问题要紧是不能从整体上准确把握程序框图，无法确定赋值语句、输出语句中各个变量与实际问题的联系，从而不能确定程序框图所要解决的实际问题中的相关数据.因此解决此类问题第一要明确程序框图中的各类数据与实际问题中数据之间的对应关系，准确把握实际问题中数据的实际意义.解题思路：由茎叶图可知，一班学生身高的平均数为170.3，二班学生身高的平均数为170.8，故二班学生的平均身高较高.由题意可知，A1=2，A 2=7，A3=9，A4=2，由程序框图易知，最后输出的结果为S=7+9+2=18.4.下表是降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗y(吨标准煤)的几组对应数据，依照表中提供的数据，求出y关于x的线性回来方程=0.7x+0.35，那么表中m的值为()x 3 4 5 6 y 2.5 m 4 4.5 A.4 B.3.5C.3D.4.5答案：C 命题立意：本题考查统计的相关知识，难度中等.解题思路：依题意得=(3+4+5+6)=4.5，=(2.5+m+4+4.5)=，由于回来直线必通过样本中心点，因此有=0.74.5+0.35，解得m=3，故选C.5.某调查机构对本市小学生课业负担情形进行了调查，设平均每人每天做作业的时刻为x分钟.有1 000名小学生参加了此项调查，调查所得数据用程序框图处理，若输出的结果是680，则平均每天做作业的时刻在0～60分钟内的学生的频率是()A.680B.320C.0.68D.0.32答案：D 解题思路：程序框图统计的是作业时刻为60分钟以上的学生的数量，因此由输出结果为680知，有680名学生的作业时刻超过60分钟，因此作业时刻在0～60分钟内的学生总数有320人，故所求频率为0.32.6.两组各7名同学体重(单位：kg)数据的茎叶图.设，两组数据的平均数依次为1，2，标准差依次为s1和s2，那么()要练说，得练听。

押题05统计【押题方向】统计图表广泛应用于生产与生活之中,而近年高考试题强调问题的实际背景,这使得统计图表成为高考的一个热点,从近几年高考试题看,高考试题对统计图表的应用,不局限于课本涉及到的频率分部直方图与茎叶图,生产与生活中广泛使用的扇形图、条形图、折线图、雷达图等都曾在高考试题中出现过,这类试题可以是客观题,也可以是解答题,若以客观题形式出现,一般为基础题,求解的关键是能从图表中“读”出相关信息.【模拟专练】1．（2021·山东临沂市·高三一模）某学校组建了演讲，舞蹈､航模､合唱，机器人五个社团，全校3000名学生每人都参加且只参加其中一个社团，校团委从这3000名学生中随机选取部分学生进行调查，并将调查结果绘制了如下不完整的两个统计图：则选取的学生中参加机器人社团的学生数为（）A ．50B ．75C ．100D ．125【答案】B【详解】由题意，本次调查的人数为5010%=500÷人，其中合唱比赛所占的比例为2000.440%500==，所以机器人所占的比例为110%20%15%40%15%.----=，所以选取的学生中参加机器人社团的学生数为50015%75⨯=人.2．（2021·山东济宁市·高三一模）为了解某贫困地区实施精准扶贫后的成果，现随机抽取了该地区部分人员，调查了2020年其人均纯收入状况．经统计，这批人员的年人均纯收入数据（单位：百元）全部介于45至70之间．将数据分成5组，并得到如图所示的频率分布直方图．现采取分层抽样的方法，从[)55,60，[)60,65，[)65,70这三个区间中随机抽取6人，再从6人中随机抽取3人，则这三人中恰有2人年人均纯收入位于[)60,65的概率是（）A ．910B ．35C ．920D ．15【答案】D【详解】由图可知()0.070.060.020.0151a ++++⨯=，解得：0.04a =，[)55,60的频率为0.0650.3⨯=，[)60,65的频率为004502..⨯=，[)65,70的频率为0.0250.1⨯=，则对应的频率之比为3:2:1，则[)55,60组抽3人，[)60,65抽取2人，[)65,70抽取1人，则6人中随机抽取3人，则这三人中恰有2人年人均纯收入位于[)60,65的概率是21243615C C P C ==.3．（2020·邹城市第一中学高三其他模拟）2020年初，新型冠状病毒(COVID -19)引起的肺炎疫情爆发以来，各地医疗机构采取了各种针对性的治疗方法，取得了不错的成效，某地开始使用中西医结合方法后，每周治愈的患者人数如下表所示：周数(x )12345治愈人数(y )2173693142由表格可得y 关于x 的二次回归方程为2ˆ6yx a =+，则此回归模型第2周的残差(实际值与预报值之差)为（）A ．5B ．4C ．1D ．0【答案】C【详解】设2t x =，则()11491625115t =++++=，()12173693142585y =++++=586118a =-⨯=-，所以2ˆ68yx =-.令2x =，得2222176281ˆe y y =-=-⨯+=.故选：C4．（2020·山东淄博市·高三零模）某校学生的男女人数之比为2:3，按照男女比例通过分层随机抽样的方法抽到一个样本，样本中男生每天运动时间的平均值为100分钟、女生为80分钟．结合此数据，估计该校全体学生每天运动时间的平均值为（）A ．98分钟B ．90分钟C ．88分钟D ．85分钟【答案】C【详解】设样本中男生人数为2a ，女生人数为3a ，则样本容量为5a ，又男生每天运动时间的平均值为100分钟、女生为80分钟，所以该校全体学生每天运动时间的平均值为1002803885a aa⨯+⨯=,故选：C5．（2020·山东）下图为某地区2007年~2019年地方财政预算内收入、城乡居民储蓄年末余额折线图．根据该折线图，下列结论正确的是（）A ．财政预算内收入、城乡居民储蓄年末余额均呈增长趋势B ．财政预算内收入、城乡居民储蓄年末余额的逐年增长速度相同C ．财政预算内收入年平均增长量高于城乡居民储蓄年末余额年平均增长量D ．城乡居民储蓄年末余额与财政预算内收入的差额逐年增大【答案】D【详解】由图知，财政预算内收入2007、2008、2009年没有明显变化，故AB 错；由图可知，财政预算内收入年平均增长量低于城乡居民储蓄年末余额年平均增长量，故C 错；由图可知，城乡居民储蓄年末余额与财政预算内收入的差额逐年增大，即D 正确.故选：D ．【押题专练】1．某校举办抗击新冠疫情科普知识演讲活动，如图是七位评委为某选手打出的分数的茎叶图，去掉一个最高分和一个最低分后，剩下数据的中位数是（）A ．87B ．86C ．85D ．84【答案】D【详解】去掉最高分93和最低分79，剩余数据从小到大排序为84,84,84,86,87，则中位数为84.故选：D.2．学校为了调查学生在课外读物方面的支出情况，抽取了一个容量为n 的样本，其频率直方图如图所示，其中支出(单位：元)在[50，60]内的学生有30人，则n 的值为（）A ．100B ．1000C ．90D ．900【答案】A【详解】由频率直方图可知，三组的频率之和为(0.01＋0.024＋0.036)×10＝0.7，∴支出在[50，60]内的频率为1－0.7＝0.3，∴n ＝300.3＝100.故选：A 3．某地以“绿水青山就是金山银山”理念为引导，推进绿色发展，现要订购一批苗木，苗木长度与售价如下表：苗木长度x (厘米)384858687888售价y (元)16.818.820.822.82425.8由表可知，苗木长度x (厘米)与售价y (元)之间存在线性相关关系，回归方程为ˆˆ0.2yx a =+，则当苗木长度为150厘米时，售价大约为（）A ．33.3B ．35.5C ．38.9D ．41.5【答案】C【详解】因为3848586878886x +++++=63=，16.818.820.822.82425.86y +++++=21.5=，所以样本点中心为(63,21.5)，又回归直线ˆˆ0.2yx a =+经过(63,21.5)，所以ˆ21.50.263a =⨯+，所以ˆ8.9a =，所以回归方程为ˆ0.28.9yx =+，当150x =时，ˆ38.9y =厘米.则当苗木长度为150厘米时，售价大约为38.9厘米.故选：C4．某超市计划按月订购一种冷饮，根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关．如果最高气温不低于25℃，需求量为600瓶；如果最高气温位于区间[)20,25℃℃，需求量为300瓶；如果最高气温低于20℃，需求量为100瓶．为了确定6月份的订购计划，统计了前三年6月份各天的最高气温数据，得到下面的频数分布表：最高气温[)15,20[)20,25[)25,30[)30,35[)35,40天数45253818以最高气温位于各区间的频率估计最高气温位于该区间的概率．若6月份这种冷饮一天的需求量不超过x 瓶的概率估计值为0.1，则x =（）A ．100B ．300C ．400D ．600【答案】B【详解】这种冷饮一天的需求量不超过300瓶，当且仅当最高气温低于25℃，由表格数据知，最高气温低于25℃的频率为450.190+=，所以6月份这种冷饮一天的需求量不超过300瓶的概率估计值为0.1.故选:B ．5．劳动力调查是一项抽样调查.2021年的劳动力调查以第七次人口普查的最新数据为基础抽取相关住户进入样本，并且采用样本轮换模式．劳动力调查的轮换是按照“2102--”模式进行，即一个住户连续2个月接受调查，在接下来的10个月中不接受调查，然后再接受连续2个月的调查，经历四次调查之后退出样本．调查进行时保持每月进入样本接受第一次调查的新住户数量相同．若从第k 个月开始，每个月都有14的样本接受第一次调查，14的样本接受第二次调查，14的样本接受第三次调查，14的样本接受第四次调查，则k 的值为（）A ．12B ．13C ．14D ．15【答案】C【详解】假设每月新增一组人，将其编号为1,2,3,4,……，则每个月接受调查的情况为：1月：1；2月：1,2；3月：2,3；4月：3,4；5月：4,5；6月：5,6；7月：6,7；8月：7,8；9月：8,9；10月：9,10；11月：10,11；12月：11,12；13月：12,13,1；14月：14,13,2,1；15月：15,14,3,2；可知到第14个月开始，接受调查的有4组，并且分别是第一次调查、第二次调查、第三次调查和第四次调查.故选：C.6．一组数据30，29，28，27，26，24，23，22的中位数为（）A ．26B ．27C ．26和27D ．26.5【答案】D【详解】因为数据为30，29，28，27，26，24，23，22，所以中位数为272626.52+=．故选：D7．为了了解一片经济林的生长情况，随机抽取了其中60株树木的底部周长(单位：cm )，所得数据均在[80，130]上，其频率分布直方图如图所示，若在抽测的60株树木中，树木的底部周长小于100cm 的株数为（）A ．15B ．24C ．6D ．30【答案】B【详解】底部周长小于100cm 的树木的频率为()0.0250.015100.4+⨯=，故树木的底部周长小于100cm 的株数为0.46024⨯=，故选：B.8．某校抽取100名学生做体能测认，其中百米测试中，成绩全部介于13秒与18秒之间，将测试结果分成五组：第一组[)13,14，第二组[)14,15， ，第五组[]17,18．如图是按上述分组方法得到的频率分布直方图，若成绩低于a 即为优秀，如果优秀的人数为14人，则a 的估计值是（）A ．14B ．14.5C ．15D ．15.5【答案】B【详解】优秀人数所占的频率为140.14100=，测试结果位于[)13,14的频率为0.060.14<，测试结果位于[)13,15的频率为0.060.160.14+<，所以，()14,15a ∈，由题意可得()0.06140.160.14a +-⨯=，解得14.5a =.故选：B.9．空气质量指数AQI 是反映空气质量状况的指数，其对应关系如下表:AQI 指数值0~5051~100101~150151~200201~300300>空气质量优良轻度污染中度污染重度污染严重污染为监测某化工厂排放废气对周边空气质量指数的影响，某科学兴趣小组在校内测得10月1日—20日AQI 指数的数据并绘成折线图如下:下列叙述正确的是（）A ．这20天中AQI 指数值的中位数略大于150B ．这20天中的空气质量为优的天数占14C ．10月4日到10月11日，空气质量越来越好D ．总体来说，10月中旬的空气质量比上旬的空气质量好【答案】B【详解】由折线图知100以上有10个，100以下有10个，中位数是100两边两个数的均值，观察比100的数离100远点，因此两者均值大于100但小于150,A 错;空气质量为优的有5天，占14，B 正确;10月4日到10月11日，空气质量越来越差，C 错;10月上旬的空气质量AQI 指数值在100以下的多，中旬的空气质量AQI 指数值在100以上的多，上旬的空气质量比中旬的空气质量好，D 错.10．2020年全球经济都受到了新冠疫情影响，但我国在中国共产党的正确领导下防控及时､措施得当，很多企业的生产所受影响甚微.我国某电子公司于2020年6月底推出了一款领先于世界的5G 电子产品，现调查得到该5G 产品上市时间x 和市场占有率y (单位：%)的几组相关对应数据.如图所示的折线图中，横轴1代表2020年8月，2代表2020年9月……，5代表2020年12月，根据数据得出y 关于x 的线性回归方程为0.042y x a=+.若用此方程分析并预测该产品市场占有率的变化趋势，则该产品市场占有率最早何时能超过0.5%(精确到月)（）A ．2021年5月B ．2021年6月C ．2021年7月D ．2021年8月【答案】D【详解】根据表中数据，计算()11234535x =⨯++++=，()10.020.050.10.150.180.15y =⨯++++=代入回归方程得0.10.0423a =⨯+$，解得0.026a =-$.所以线性回归方程为： 0.0420.026y x =-，由0.0420.0260.5,x ->解得13x ≥，预计上市13月时，即最早在2021年8月，市场占有率能超过0.5%.故选:D11．某校甲､乙课外活动小组(两小组人数相等)20次活动成绩组成一个样本，得到如图所示的茎叶图，若甲､乙两组平均成绩分别用1x ，2x 表示，标准差分别用1s ，2s 表示，则（）A ．12x x >，12s s >B ．12x x >，12s s <C ．12x x <，12s s >D ．12x x <，12s s <【答案】C【详解】根据茎叶图可得，甲组数据集中在310—330附近，乙组数据主要集中在320—350附近，则可判断乙组的平均数更高，即12x x <，并且乙组数据呈“单峰”分布，数据更集中，故标准差更小，即12s s >.故选：C.12．甲、乙两名射击运动爱好者在相同条件下各射击10次，中靶环数情况如图所示．则甲、乙两人中靶环数的方差分别为（）A ．7，7B ．7，1.2C ．1.1，2.3D ．1.2，5.4【答案】D【详解】实线的数字为：2,4,6,8,7,7,8,9,9,10，虚线的数字为：9,5,7,8,7,6,8,6,7,7，所以()12+4+6+8+7+7+8+9+9+10=710x 乙，()19+5+78768677710x +++++++=甲,()()()()()2222221=9-7+5-7778777 1.210S ⎡⎤+-+-++-=⎣⎦ 甲()()()()()2222221=2-7+4-76787107 5.410S ⎡⎤+-+-++-=⎣⎦ 乙.故选：D13．某高中为了解学生课外知识的积累情况，随机抽取200名同学参加课外知识测试，测试共5道题，每答对一题得20分，答错得0分.已知每名同学至少能答对2道题，得分不少于60分记为及格，不少于80分记为优秀，测试成绩百分比分布图如图所示，则下列说法正确的是（）A ．该次课外知识测试及格率为90%B ．该次课外知识测试得满分的同学有30名C ．该次测试成绩的中位数大于测试成绩的平均数D ．若该校共有3000名学生，则课外知识测试成绩能得优秀的同学大约有1440名【答案】C【详解】由图知，及格率为18%92%-=，故A 错误.该测试满分同学的百分比为18%32%48%---12%=，即有12%20024⨯=名，B 错误.由图知，中位数为80分，平均数为408%6032%80⨯+⨯+48%10012%72.8⨯+⨯=分，故C 正确.由题意，3000名学生成绩能得优秀的同学有3000(48%12%)1800⨯+=，故D 错误.故选：C14．2020年广东12月份天气预报历史记录中1号至8号的数据如表所示，则（）日期最高气温/C︒最低气温/C︒12月1日231412月2日231312月3日201112月4日191012月5日21912月6日211512月7日231212月8日2311A ．这8天的最高气温的极差为5C ︒B ．这8天的最高气温的中位数为23C ︒C ．这8天的最低气温的极差为5C ︒D ．这8天的最低气温的中位数为11.5C︒【答案】D【详解】这8天的最高气温的极差为23194C -=︒，这8天的最高气温的中位数为212322C 2+=︒，这8天的最低气温的极差为1596C -=︒，这8天的最低气温的中位数为111211.5C 2+=︒，故选：D ．15．2020年5月我国抗击新冠肺炎疫情工作取得阶段性胜利，各地有序推进复工复产，下面是某地连续11天复工复产指数折线图，下列说法正确的是（）A．这11天复工指数和复产指数均逐日增加.B．这11天期间，复产指数的极差大于复工指数的极差C．第3天至第11天复工复产指数均超过80%D．第9天至第11天复工指数的增量大于复产指数的增量【答案】C【详解】第8天比第7天的复工指数和复产指数均低，A错；这11天期间，复产指数的极差小于复工指数的极差：两者最高差不多，但最低的复工指数比复产指数低得多，B错；第3天至第11天复工复产指数均超过80%，C正确；第9天至第11天复工指数的增量小于复产指数的增量，D错误．。

专题10.1 统计与统计案例一、选择题1.（2020·四川省内江市第六中学高三月考（理））国家统计局发布数据显示，2020年1月份全国CPI（居民消费价格指数）同比上涨5.4%，环比上涨1.4%.下图是2019年1月到2020年1月全国居民消费价格同比（与去年同期相比）和环比（与上月相比）涨跌幅，则下列判断错误的是（）++++++++++++=，（参考数据：1.7 1.5 2.3 2.5 2.7 2.7 2.8 2.8 3.0 3.8 4.5 4.5 5.440.2 +-+-++++++=）0.5 1.00.40.10.10.40.70.90.90.4 1.4 5.8A．各月同比全部上涨，平均涨幅超过3%B．各月环比有涨有跌，平均涨幅超过0.3%C．同比涨幅最大的月份，也是环比涨幅最大的月份D．环比跌幅最大的月份，也是同比涨幅最小的月份【答案】D【解析】由统计图可知，各月同比全部上涨，平均涨幅为()++++++++++++÷⨯≈，超过3%，故1.7 1.5 2.3 2.5 2.7 2.7 2.8 2.8 3.0 3.8 4.5 4.5 5.4131% 3.09%A正确；各月环比有涨有跌，平均涨幅为()+-++-+++++++÷⨯≈，超过0.3%，0.5 1.00.40.10.00.10.40.70.90.90.40.0 1.4131%0.446%故B正确；同比涨幅最大的是2020年1月，环比涨幅最大的也是2020年1月，故C正确；环比跌幅最大的是2019年3月，同比涨幅最小的是2019年2月，故D错误，故选：D.2．（2020·广西高三其他模拟（理））如图所示是某年第一季度五省GDP情况图，则下列说法中不正确的是（）A．该年第一季度GDP增速由高到低排位第3的是山东省B．该年第一季度浙江省的GDP总量最低C．该年第一季度GDP总量和增速由高到低排位均居同一位次的省份有2个D．与去年同期相比，该年第一季度的GDP总量实现了增长【答案】B【解析】由折线图可知A、D项均正确，该年第一季度GDP总量和增速由高到低排位均居同一位的省份有江苏均第一.河南均第四，共2个，故C项正确：今年浙江省的GDP增长率最低.故B项不正确.故选：B.3．（2020·云南高三期末（文））我国古代著名的数学著作中，《周髀算经》、《九章算术》、《孙子算经》、《五曹算经》、《夏侯阳算经》、《孙丘建算经》、《海岛算经》、《五经算术》、《缀术》和《缉古算经》，称为“算经十书”.某校数学兴趣小组为了解本校学生对《周髀算经》、《九章算术》、《孙子算经》阅读的情况，随机调查了100名学生，阅读情况统计如下表，则该100名学生中阅读过《九章算术》的人数为（）A．60B．70C．80D．90【答案】C【解析】根据统计表可知，只阅读过《周髀算经》没阅读过《九章算术》的人数为706010-=人，所以只阅读过《九章算术》没阅读过《周髀算经》的人数为907020-=人，所以阅读过《九章算术》的人数为602080+=人.故选：C4．（2020·河北沧州·高三期中）2020年10月1日是中秋节和国庆节双节同庆，很多人外出旅行或回家探亲，因此交通比较拥堵．某交通部门为了解从A城到B城实际通行所需时间，随机抽取了n台车辆进行统计，结果显示这些车辆的通行时间（单位：分钟）都在[30,55]内，按通行时间分为[30,35)，[35,40)，[40,45)，[45,50)，[50,55]五组，频率分布直方图如图所示，其中通行时间在[30,35)内的车辆有235台，则通行时间在[45,50)内的车辆台数是（）A．450B．325C．470D．500【答案】C【解析】因为[30,35)，[35,40)，[40,45)，[50,55]四组通行时间的频率分别是0.1，0.25，0.4，0.05，----=，所以通行时间在[45,50)内的频率是10.10.250.40.050.2⨯=．通过的车辆台数是2352470故选：C．5．某工厂为了对40个零件进行抽样调查，将其编号为00，01，…38，39．现要从中选出5个，利用下面的随机数表，从第一行第3列开始，由左至右依次读取，选出来的第5个零件编号是（）0647 4373 8636 9647 3661 4698 6371 6233 2616 8045 6011 14109577 7424 6762 4281 1457 2042 5332 3732 2707 3607 5124 5179A．36B．16C．11D．14【答案】C【解析】利用随机数表，从第一行第3列开始，由左至由一次读取，即47开始读取，在编号范围内的提取出来，可得36,33,26,16,11，则选出来的第5个零件编号是11.故选：C.6．（2020·四川高三月考（文））下图为某地区2007年~2019年地方财政预算内收入、城乡居民储蓄年末余额折线图．根据该折线图，下列结论正确的是（）A．财政预算内收入、城乡居民储蓄年末余额均呈增长趋势B．财政预算内收入、城乡居民储蓄年末余额的逐年增长速度相同C．财政预算内收入年平均增长量高于城乡居民储蓄年末余额年平均增长量D．城乡居民储蓄年末余额与财政预算内收入的差额逐年增大【答案】D【解析】由图知，财政预算内收入2007、2008、2009年没有明显变化，故AB 错；由图可知，财政预算内收入年平均增长量低于城乡居民储蓄年末余额年平均增长量，故C 错； 由图可知，城乡居民储蓄年末余额与财政预算内收入的差额逐年增大，即D 正确. 故选：D ．7．（2020·云南民族大学附属中学高三期中（文））S 大学艺术系表演专业的报考人数连创新高，2010年报名刚结束，某考生想知道这次报考该专业的人数．已知该专业考生的考号是按0001，0002，⋅⋅⋅的顺序从小到大依次排列的，他随机了解了50名考生的考号，经计算，这50个考号的和是25025，估计2010年报考S 大学艺术系表演专业的考生大约有（ ） A ．2000人 B ．1500人C ．1000人D ．500人【答案】C 【解析】由题意知，考生的考号是从0001，0002⋅⋅⋅从小到大排列的， 50个考生的考号和为25025，考号平均数：2502550050≈， 以此估计考号中位数为500，故大约有25001000⨯=人． 故选：C ．8．某实验室对小白鼠体内x ，y 两项指标进行研究，连续五次实验所测得的这两项指标数据如下表：已知y 与x 具有线性相关关系，利用上表中的五组数据求得回归直线方程为y bx a =+.若下一次实验中170x =，利用该回归直线方程预测得117y =，则b 的值为（ ）A ．0.45B ．0.54C ．0.5D ．0.48【答案】B 【解析】由已知表格中的数据，求得：1201101251301151205x ++++==，9283909689905y ++++==，则12090b a +=，①，又因为下一次实验中170x =，利用该回归直线方程预测得117y =，则170117b a+=，②，联立①②，解得：0.54b=.故选B9．为了解大学生对体育锻炼的兴趣，某高校从4万多名在校大学生中抽取了男､女生各200名进行了调查，得到如下统计图：对比两图中信息并进行分析，下列说法正确的是（）A．大量出汗并感到很疲乏的男生人数是女生人数的2倍B．男生中运动时间超过1小时的超过70%C．女生的平均运动强度高于男生的平均运动强度D．运动时间在0.5~1小时内的男生人数与运动时间在1~2小时内的女生人数相同【答案】D【解析】对于A，大量出汗并感到很疲乏的男生超过110人，而女生约50人，因此大量出汗并感到很疲乏的男生人数比女生人数的2倍还要多，因此A不正确；对于B，男生中运动时间在0~1小时内的超过70人，占所有男生的比例超过70100%35%200⨯=，因此男生中运动时间超过1小时的占比没达到70%，因此B不正确；对于C，由图易知男生的平均运动强度高于女生的平均运动强度，因此C不正确；对于D，运动时间在0.5~1小时内的男生人数有50人，运动时间在1~2小时内的女生人数也有50人，因此D正确.10.（2020·全国高三专题练习）某地两防指挥部在汛期对当地一条河流连续进行监测，下表是最近几日该河流某段的水位情况. 河流水位表而根据河流的堤防情况规定：水位超过一定高度将分别启动相应预警措施(见下表)，当水位达到保证水位时，防汛进入紧急状态，防汛部门要按照紧急防汛期的权限，采取各种必要措施，确保堤防等工程的安全，并根据“有限保证､无限负责”的精神，对于可能出现超过保证水位的工程抢护和人员安全做好积极准备. 水位预警分级表现已根据河流水位表得到水位y 的回归直线方程为ˆ0.21 3.228yx =+，据上表估计（ ） A ．第8日将要启动洪水橙色预警 B ．第10日将要启动洪水红色预警 C ．第11日将要启动洪水红色预警 D ．第12日将要启动洪水红色预警【答案】D 【解析】因为回归直线方程为ˆ0.21 3.228yx =+， 当8x =时，水位y 的估计值为()ˆ0.218 3.228 4.908 4.7,5.1y=⨯+=∈，所以第8日将要启动洪水黄色预警，故A 错误；当10x =时，水位y 的估计值为()ˆ0.2110 3.228 5.328 5.1,5.6y=⨯+=∈，所以第10日将要启动洪水橙色预警，故B 错误；当11x =时，水位y 的估计值为()ˆ0.2111 3.228 5.538 5.1,5.6y=⨯+=∈，所以第11日将要启动洪水橙色预警，故C 错误；当12x =时，水位y 的估计值为ˆ0.2112 3.228 5.748 5.6y =⨯+=>，所以第12日将要启动洪水红色预警，故选：D. 二、多选题11．（2020·江苏高三期中）（多选题）比较甲、乙两名学生的数学学科素养的各项能力指标值（满分为5分，分值高者为优），绘制了如图所示的六维能力雷达图，例如图中甲的数学抽象指标值为4，乙的数学抽象指标值为5，则下面叙述正确的是（ ）A ．甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值B ．甲的数学建模能力指标值优于乙的直观想象能力指标值C ．乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平D ．甲的数学运算能力指标值优于甲的直观想象能力指标值 【答案】AC 【解析】对于A 选项，甲的逻辑推理能力指标值为4，乙的逻辑推理能力指标值为3，所以甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值，故选项A 正确；对于B 选项，甲的数学建模能力指标值为3，乙的直观想象能力指标值为5，所以乙的数学建模能力指标值优于甲的直观想象能力指标值，故选项B 错误； 对于C 选项，甲的六维能力指标值的平均值为()12343453466⨯+++++=，乙的六维能力指标值的平均值为()123543543466⨯+++++=>，所以乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平，所以选项C 正确；对于D 选项，甲的数学运算能力指标值为4，甲的直观想象能力指标值为5，所以甲的数学运算能力指标值不优于甲的直观想象能力指标值，所以选项D 错误. 故选：AC.12．（多选题） 2.5PM 是评估空气质量的一个重要指标，我国 2.5PM 标准采用世卫组织设定的最宽限值，即 2.5PM 日均值在335/g m μ以下空气质量为一级，在33575/g m μ之间空气质量为二级，在375/g m μ以上空气质量为超标.如图为某地区2019年10月1日到10月12日的 2.5PM 日均值（单位：3/g m μ）的统计图，则下列叙述正确的是（ ）A ．该地区这12天中空气质量超标的日期为10月6日B ．该地区这12天 2.5PM 日均值的中位数为351/g m μC ．该地区这12天 2.5PM 日均值的平均数为353/g m μD ．该地区从10月6日到10月11日的 2.5PM 日均值持续减少 【答案】AC 【解析】对于A ，12天中，只有10月6日的 2.5PM 日均值大于375/g m μ，故10月6日空气质量超标，A 正确； 对于B ，12天的 2.5PM 日均值按照从小到大顺序排列，位于第6和第7位的日均值为350/g m μ和353/g m μ，故中位数为5153522+=3/g m μ，B 错误； 对于C ，平均数355455665688253464236385053/12g m μ+++++++++++==，C 正确； 对于D ，10月11日的 2.5PM 日均值大于10月10日的 2.5PM 日均值，D 错误. 故选：AC.13．（多选题）研究与试验发展（R&D ）经费支出指统计年度内全社会实际用于基础研究、应用研究和试验发展的经费支出．根据国家统计局发布的全国科技经费投入统计公报，得到2015—2019年研究与试验发展经费支出及其增长速度的统计图如图所示，则（ ）A ．2015—2019年研究与试验发展经费支出呈增长趋势B ．2015—2019年研究与试验发展经费支出的增长速度逐年增大C ．2015—2019年研究与试验发展经费支出的增长速度的极差为3.6%D ．2016—2019年研究与试验发展经费支出增长速度的增量最大的是2016年 【答案】AC 【解析】从统计图可以看出，2015—2019年研究与试验发展经费支出呈增长趋势，但增长速度先增后减再增，故A 对，B 错；增长速度的最大值为12.5%，最小值为8.9%，则极差为3.6%，故C 正确；由题中数据计算可知2016，2017年的研究与试验发展经费支出增长速度的增量均为1.7%，故D 错误． 故选：AC .14．（2020·湖南雅礼中学月考）已知由样本数据点集合(){},1,2,,ii x y i n =，求得的回归直线方程为1.50.5y x =+，且3x =，现发现两个数据点()1.2,2.2和()4.8,7.8误差较大，去除后重新求得的回归直线l 的斜率为1.2，则（ ） A ．变量x 与y 具有正相关关系 B ．去除后的回归方程为 1.2 1.4y x =+ C ．去除后y 的估计值增加速度变快 D ．去除后相应于样本点()2,3.75的残差为0.05【答案】AB 【解析】因为回归直线方程为 1.50.5y x =+，1.50>， 所以变量x 与y 具有正相关关系.故A 正确. 当3x =时，315055y ..=⨯+=，样本点为()3,5，去掉两个数据点()1.2,2.2和()4.8,7.8后，样本点还是()3,5， 又因为去除后重新求得的回归直线l 的斜率为1.2， 所以5312.a =⨯+， 解得 1.4a =，所以去除后的回归方程为 1.2 1.4y x =+，故B 正确.因为1.5 1.2>，所以去除后y 的估计值增加速度变慢，故C 错误. 因为 1.22 1.4 3.8y =⨯+=，所以 3.75 3.80.05y y -=-=-，故D 错误. 故选：AB 三、填空题15．（2020·江苏高考真题）已知一组数据4,2,3,5,6a a -的平均数为4，则a 的值是_____. 【答案】2 【解析】∵数据4,2,3,5,6a a -的平均数为4 ∴4235620a a ++-++=，即2a =. 故答案为：2.16．（2019·江苏高考真题）已知一组数据6，7，8，8，9，10，则该组数据的方差是____. 【答案】53. 【解析】由题意，该组数据的平均数为678891086+++++=，所以该组数据的方差是22222215[(68)(78)(88)(88)(98)(108)]63-+-+-+-+-+-=. 17. 为了解某班学生喜爱打篮球是否与性别有关，对该班50名学生进行了问卷调查，得到了如下的22⨯列联表：则在犯错误的概率不超过________的前提下认为喜爱打篮球与性别有关.附：()()()()()22n ad bcKa b c d a c b d-=++++.【答案】0.005【解析】根据所给的列联表，得到()2225020155108.3337.879302025K⨯⨯-⨯=≈>⨯⨯，至少有99.5%的把握说明喜爱打篮球与性别有关，即在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.故答案为：0.005.18．（2018·全国高二单元测试）某高校“统计初步”课程的教师随机调查了选该课的一些学生情况，具体数据如下表：为了判断主修统计专业是否与性别有关系，根据表中的数据，计算得到K2＝________(保留三位小数)，所以判定________(填“能”或“不能”)在犯错误的概率不超过0.05的前提下认为主修统计专业与性别有关系．【答案】4.844能【解析】根据提供的表格得2250(1320710)4.844 3.84123272030K⨯⨯-⨯=≈>⨯⨯⨯.∴所以可以在犯错误的概率不超过0.05的前提下认为主修统计专业与性别有关系．故答案为（1）4.844；（2）能.19. （2018·全国高二课时练习）统计推断，当________时，在犯错误的概率不超过0．05的前提下认为事件A与B有关；当________时，认为没有充分的证据显示事件A与B是有关的．【答案】k>3．841k≤2．706【解析】当k>3．841时，就有在犯错误的概率不超过0．05的前提下认为事件A与B有关，当k≤2．706时认为没有充分的证据显示事件A与B是有关的．20．（2020·北京丰台·高一期末）在一次数学测验中，某学习小组10位同学的得分情况如下表，则该小组成绩的众数是__________；平均数是__________．【答案】8585【解析】因为分数为85的人数最多，所以众数为85，又951+902+854+802+7518510⨯⨯⨯⨯⨯=，所以平均数为85，故答案为：85；85.21．（2020·广东高一期末）某研究机构对高三学生的记忆力x和判断力y进行统计分析，得表数据.请上表提供的数据，求出y 关于x 的线性回归方程_______________，据此可预测判断力为4的同学的记忆力为_______________.【答案】0.7 2.3y x =-； 9. 【解析】设y 关于x 的线性回归方程为ˆˆy bx a =+，直线过样本中心点(),x y由表格数据得68101294x +++==，235644y +++==，416283105126158i i i x y ==⨯+⨯+⨯+⨯=∑，4222221681012344ii x==+++=∑，故根据最小二乘原理知12221158494ˆ0.734449ni ii ni i x y nx ybx nx==--⨯⨯===-⨯-∑∑， ˆˆ40.79 2.3a y bx =-=-⨯=-，即线性回归方程为0.7 2.3y x =-；将4y =代入方程，得9x =，即可预测判断力为4的同学的记忆力为9. 故答案为：0.7 2.3y x =-；9. 四、解答题22.（2020·拉孜县中学高三月考（理））2018年播放的电影《我不是药神》引起了很大的轰动，治疗特种病的创新药研发成了当务之急.为此，某药企加大了研发投入，市场上治疗一类慢性病的特效药品A 的研发费用x （百万元）和销量y （万盒）的统计数据如下：（1）根据最小二乘法求出y 与x 的线性回归方程ˆˆˆy bx a =+；（2）利用（1）中的回归方程，预测销售10万盒特效药品A 需要多少研发费用？附：回归直线的斜率和截距的最小二乘法估计公式为：1221ˆni i i n i i x y nxy b x nx==-=-∑∑，ˆˆa y bx =-.【答案】（1）0.6204ˆ.1y x =+；（2）15.9（百万元）.【解析】（1）依题意得：1234535x ++++==，0.7 1.5 2.0 2.5 3.325y ++++==， 所以1510.72 1.53 2.04 2.55 3.336.2i i i x y ==⨯+⨯+⨯+⨯+⨯=，553230xy =⨯⨯=，122222251234555i i x ==++++=，2255345x =⨯=.所以515221536.2300.625ˆ5545i i i i i x y xy b x x ==∑--===∑--， 20.62ˆ30.14ˆay bx =-=-⨯=. 所以所求回归方程为：0.6204ˆ.1yx =+. （2）由（1）中的回归方程0.6204ˆ.1yx =+得： 100.620.14x =+，解得15.9x ≈（百万元）.故销售10万盒特效药品A 需要15.9（百万元）的研发费用.23．（2020·安徽省太和第一中学高三月考（文））为了加快恢复疫情过后的经济，各地旅游景点相继推出各种优惠政策，刺激旅游消费．8月份，某景区一纪念品超市随机调查了180名游客到该超市购买纪念品的情况，整理数据，得到下表：（Ⅰ）估计8月份游客到该超市购买纪念品不少于90元的概率；（Ⅱ）估计8月份游客到该超市购买纪念品金额的平均值（结果精确到0.1，同一组中的数据用该组区间的中点值作代表）；（Ⅲ）完成下面的22⨯列联表，并判断能否有99.5％的把握认为购买纪念品的金额与年龄有关．附：()()()()()22n ad bc K a b c d a c b d -=++++，n a b c d =+++．【答案】（Ⅰ）0.5；（Ⅱ）91.7；（Ⅲ）表格见解析，有. 【解析】（Ⅰ）估计8月份游客到该超市购买纪念品不少于90元的概率为3040200.5180++=．（Ⅱ）估计8月份游客到该超市购买纪念品金额的平均值为1520453075401053013540165201650091.7180180⨯+⨯+⨯+⨯+⨯+⨯=≈．（Ⅲ）填写22⨯列联表，如下：则()2218024408036288011.667.8796012010476247K ⨯⨯-⨯==≈>⨯⨯⨯，因此，有99.5％的把握认为购买纪念品的金额与年龄有关．24．为了更好了解某年入伍新兵的身高情况，解放军某部随机抽取100名新兵，分别对他们的身高进行了测量，并将测量数据分为以下五组：[160,165)，[165,170)，[170,175)，[175,180)，[180,185]进行整理，如下表所示：（1）在下面的图纸中，画出频率分布直方图；（2）若在第4，5两组中，用分层抽样的方法抽取6名新兵，再从这6名新兵中随机抽取2名新兵进行体能测试，求这2名新兵来自不同组的概率．【答案】（1）直方图见解析；（2）8 15.【解析】（1）频率分布直方图如下图所示：（2）因为第4，5组共有30名新兵，所以利用分层抽样从中抽取6名，每组应抽取的人数分别为：第4组：206430⨯=名，第5组：106230⨯=名， 设第4组抽取的4名新兵分别为1A ，2A ，3A，4A ，第5组抽取的2名新兵分别为1B ，2B ． 从这6名新兵中随机抽取2名新兵，有以下15种情况：12{,}A A ，13{,}A A ，14{,}A A ，11{,}A B ，12{,}A B ，23{,}A A ，24{,}A A ，21{,}A B ，22{,}A B ，34{,}A A ，31{,}A B ，32{,}A B ，41{,}A B ，42{,}A B ，12{,}B B ， 这2名新兵来自不同组的情况有以下8种：11{,}A B ，12{,}A B ，21{,}A B ，22{,}A B ，31{,}A B ，32{,}A B ，41{,}A B ，42{,}A B ，故所求的概率P =815． 25．产品质量是企业的生命线，企业非常重视产品生产线的质量，为提高产品质量，某企业引进了生产同一种产品的A ，B 两条生产线，为比较两条生产线生产的产品的质量，从A ，B 生产线生产的产品中各随机抽取了100件产品进行检测，将产品等级结果和频数制成了如下的统计图：（1）填写下面列联表，并根据列联表判断是否有95%的把握认为产品是否为一级品生产线有关．（2）以样本估计总体，若生产一件一级品可盈利100元，生产一件二级品可盈利50元，生产一件三级品亏损20元．①分别估计A ，B 生产线生产一件产品的平均利润； ②你认为哪条生产线的利润较为稳定？说明理由．附：()()()()()22n ad bc K a b c d a c b d -=++++，其中n a b c d =+++．【答案】（1）表格见解析，有；（2）①46元；50元；②A 生产线的利润更为稳定，理由见解析. 【解析】（1）根据频数分布直方图得出列联表，计算2K ，与临界值表相比较，即可得到结论.（2）①利用平均数的计算公式分别求出A ，B 两条生产线生产一件产品的平均利润；②计算方差，得出两条生产线利润的稳定性.解：（1）根据已知数据可得列联表如下：()2220020653580 5.64355145100100K ⨯⨯-⨯=≈>3.841⨯⨯⨯，参照临界值表可知，有95%的把握认为产品是否为一级品与生产线有关. （2）①A 生产线生产一件产品的平均利润为100206050202046100⨯+⨯-⨯=（元），B 生产线生产一件产品的平均利润为100355040202550100⨯+⨯-⨯=（元）. ②A 生产线生产的产品利润的方差()()()()222110046205046602046201464100D A ⎡⎤=⨯-⨯+-⨯+--⨯=⎣⎦，B 生产线生产的产品利润的方差()()()()222110050355050402050252100100D B ⎡⎤=⨯-⨯+-⨯+--⨯=⎣⎦，因为()()D A D B =，所以A 生产线的利润更为稳定.26．（2019·贵州贵阳·高三期末（文））某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究，他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数，得到如下资料： )Cy (颗)（1）从3月1日至3月5日中任选2天，记发芽的种子数分别为m ，n ，求事件25302530m n ⎧⎨⎩的概率；（2）甲，乙两位同学都发现种子的发芽数与昼夜温差近似成线性关系，给出的拟合直线分别为22y x =.与2.53y x =-，试利用“最小平方法(也称最小二乘法)的思想"，判断哪条直线拟合程度更好；（3）你能找到一条比甲乙两个同学更好的拟合直线吗？如果能请求出直线方程，如果不能请说明理由.(()()()1122211ˆ·n niii ii i nni ii i x x y y x y nx y bx x xnx ====---==--∑∑∑∑，ˆˆa y bx=-) 【答案】（1）310；（2）用直线 2.53y x =-的拟合效果好；（3）方程为ˆ 3.110.1yx =-. 【解析】（1）,m n 的取值情况有(23,25),(23,30),(23,26),(23,16),(25,30),(25,26),(25,16)，(30,26),(30,16),(26,16)基本事件总数为10.设“25302530m n ⎧⎨⎩”为事件A ，则事件A 包含的基本事件为(25,30),(25,26),(30,26)所以3()10P A =，故事件“25302530m n ⎧⎨⎩”的概率为310（2）将甲､乙所作拟合直线分别计算y 的值得到下表用22y x =.作为拟合直线时，所得到的y 值与y 的实际值的差的平方和为 222221(2223)(24.225)(28.630)(26.426)(19.816)18.2S =-+-+-+-+-=用 2.53y x =-作为拟合直线时，所得到的y 值与y 的实际值的差的平方和为222222(2223)(24.525)(29.530)(2726)(19.516)14.75S =-+-+-+-+-=由于12S S >，故用直线 2.53y x =-的拟合效果好（3）由列表得：11,24x y ==，15215615;1351i i i i i xx y ====∑∑ 设回归方程为ˆybx a =+ 则11222135151124ˆˆ3.1,24 3.11110.1615511i i i n i i n x y nxy b a y bx xnx ==--⨯⨯====-=-⨯=--⨯-∑∑ 故所求方程为ˆ 3.110.1yx =- 27．（2020·四川高二期中（理））成都是全国闻名的旅游城市，有许多很有特色的旅游景区.某景区为了提升服务品质，对过去100天每天的游客数进行了统计分析，发现这100天每天的游客数都没有超出八千人，统计结果见下面的频率分布直方图：（1）估计该景区每天游客数的中位数和平均数；（2）为了研究每天的游客数是否和当天的最高气温有关，从这一百天中随机抽取了5天，统计出这5天的游客数（千人）分别为0.8、3.7、5.1、5.6、6.8，已知这5天的最高气温（℃）依次为8、18、22、24、28. （ⅰ）根据以上数据，求游客数y 关于当天最高气温x 的线性回归方程（系数保留一位小数）；（ⅱ）根据（ⅰ）中的回归方程，估计该景区这100天中最高气温在20℃～26℃内的天数（保留整数）.参考公式：由最小二乘法所得回归直线的方程是ˆˆˆy bx a =+； 其中，()()()1122211ˆn ni i i ii i n n ii i i x x y y x y nx y b x x x nx ====---==--∑∑∑∑，ˆˆa y bx =-. 本题参考数据：()()5170i i i x x y y =--=∑，()521232i i x x =-=∑.【答案】（1）3750人，3820人；（2）（ⅰ）ˆ0.3 1.6y x =-；（ⅱ）26天.【解析】（1）左边三个矩形的面积之和为0.32，左边四个矩形的面积之和大于0.5，故中位数在第四个矩形中， 所以中位数为：0.1831 3.750.24+⨯=. 平均数为：0.50.07 1.50.09 2.50.16 3.50.24 4.50.18⨯+⨯+⨯+⨯+⨯5.50.146.50.077.50.05 3.82+⨯+⨯+⨯=，所以，该景区这一百天中每天游客数的中位数约为3750人，平均数约为3820人. （2）（ⅰ）20x =， 4.4y =，70ˆ0.3232b =≈，ˆˆ 4.40.320 1.6a y bx =-=-⨯=-， ˆ0.3 1.6yx ∴=-. （ⅱ）当最高气温在20℃~26℃内时，当20x 时，ˆ0.320 1.6=4.4y=⨯-； 当26x =时，ˆ0.326 1.6=6.2y=⨯-； 根据ˆ0.3 1.6yx =-得游客数在4.4~6.2内， 直方图中这个范围内方块的面积为：()()5 4.40.180.14 6.260.070.262-⨯++-⨯=， 天数为0.26210026⨯≈，所以，这100天中最高气温在20℃~26℃内的天数约为26天.。