材料力学第十三章习题

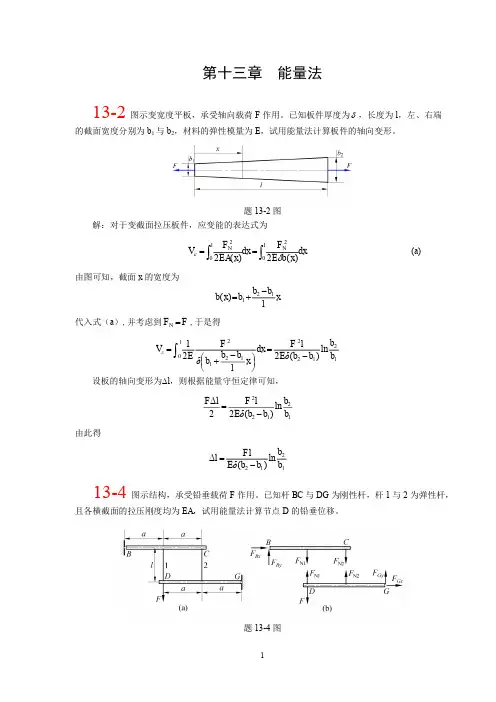
材料力学(金忠谋)第六版答案第14章第十三章 动载荷13－1 铸铁杆AB 长m l 8.1=，以等角速度绕垂直轴O －O 旋转如图示。

已知铸铁的比重3/74m kN =γ，许用拉应力[]MPa 40=σ，材料的弹性模量E ＝160 Gpa 。

试求此杆的极限转速，并计算此杆在转速m r n /100=时的绝对伸长。

解： （1） 极限转速m rn s s l g l g A A Ndl gA dr r qd r Nd x r gAdr ma r qd x r a jx dl n n 1092260137.114175.130799.010*******.92)2(][2][)2(21][)2(21)()()()()(235222222222====⨯⨯⨯⨯⨯=≤≤≤======⎰πωωγσωσωγσσωγωγω（2） 当n ＝1000m rcm m Eg l r EA r Nd l s n l 0252.01052.28.91016039.072.104107423)2(2)(2172.1046010002602492233220=⨯=⨯⨯⨯⨯⨯⨯⨯===∆=⨯==-⎰ωππω（2）吊索： MPa A P d d 55.2105276.14max=⨯==-σ13－3 轴上装一钢质圆盘，盘上有一圆孔。

若轴与盘以s140=ω的匀角速度旋转，论求轴内由这一圆孔引起的最大正应力。

解：23max max 22225.1212.021*********.01060041411060064003.03.047800640404.0mMN W M mN L P N Na gA ma P s m r a z d d d d n n d n =⨯⨯==⋅=⨯⋅===⨯⨯⨯⨯=⋅⋅⋅===⨯==πσπδγω13－4 飞轮轮缘的平均直径D ＝1.2m ，材料比重3/72m kN =γ，弹性模量GPa E 200=，轮缘与轮幅装配时的过盈量mmD2.0=∆，若不计轮相的影响，求飞轮允许的最大转速。

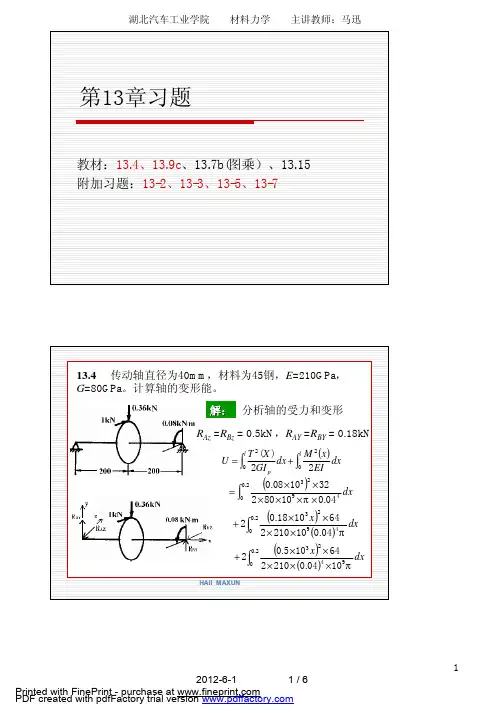
揭示材料力学的奥秘知到章节测试答案智慧树2023年最新山东农业工程学院第一章测试1.从材料力学的角度来讲，为了使构件能正常的工作，必须使构件具有足够的（）。

参考答案:其余选项都是2.材料力学研究的内力是构件各部分的相互作用力。

（）参考答案:错3.因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。

（）参考答案:错4.材料力学只限于研究弹性范围内的小变形情况。

（）参考答案:对5.角应变是变形后，构件中任意两根微线段夹角角度的变化量。

（）参考答案:错第二章测试1.在下列说法中，正确的是（）。

参考答案:内力随外力的增大而增大2.用截面法求内力时，是对（）建立平衡方程而求解的。

参考答案:左段或右段3.关于轴向拉压杆件轴力的说法中，错误的是（）。

参考答案:轴力是沿杆轴作用的外力4.计算M－M面上的轴力。

（）参考答案:-P5.梁在某一段内作用有向下的分布载荷时，在该段内它的弯矩图为( )参考答案:上凸曲线第三章测试1.拉杆伸长后，横向会缩短，这是因为杆有横向应力存在。

（）参考答案:错2.虎克定律适用于弹性变形范围内。

（）参考答案:错3.材料的延伸率与试件的尺寸有关。

（）参考答案:对4.应用拉压正应力公式的条件是（）。

参考答案:外力的合力沿杆轴线；5.一圆截面直杆，两端受的拉力相同，若将长度增大一倍其他条件不变，则下列结论错误的是( ）。

参考答案:伸长量不变第四章测试1.挤压发生在局部表面，是连接件在接触面上的相互压紧；而压缩是发生在杆件的内部。

（）参考答案:对2.剪断钢板时，所用外力使钢板产生的应力大于材料的屈服极限。

（）参考答案:错3.在平板与螺栓之间加一垫片，可以提高（）的强度。

参考答案:平板挤压4.在冲床上将钢板冲出直径为d的圆孔，冲力F与（）。

参考答案:与直径d成正比5.对于圆柱形连接件的挤压强度问题，应该直接用受挤压的半圆柱面来计算挤压应力。

（）参考答案:错第五章测试1.圆杆受扭时，杆内各点均处于纯剪切状态。

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。

试问在杆件的任一横截面m-m上存在何种内力分量，并确定其大小。

解：从横截面m-m将杆切开，横截面上存在沿轴线的内力偶矩分量M x，即扭矩，其大小等于M。

1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。

解：应力p与斜截面m-m的法线的夹角α=10°，故σ＝p cosα=120×cos10°=118.2MPaτ＝p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布，截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正应力均为零。

试问杆件横截面上存在何种内力分量，并确定其大小。

图中之C点为截面形心。

解：将横截面上的正应力向截面形心C简化，得一合力和一合力偶，其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。

试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。

解：第二章轴向拉压应力2-1试计算图示各杆的轴力，并指出其最大值。

解：(a) F N AB=F, F N BC=0, F N，max=F(b) F N AB=F, F N BC=－F, F N，max=F(c) F N AB=－2 kN, F N2BC=1 kN, F N CD=3 kN, F N，max=3 kN(d) F N AB=1 kN, F N BC=－1 kN, F N，max=1 kN2-2 图示阶梯形截面杆AC，承受轴向载荷F1=200 kN与F2=100 kN，AB段的直径d1=40 mm。

材料力学第十三章习题13-2图示压杆的截面为矩形，h=60mm，b=40mm，杆长l=2.0m，材料为Q235钢，E=2.1×105MPa。

两端约束示意图为：在正视图(a)的平面内相当于铰支；在俯视图(b)的平面内为弹性固定，采用μ=0.8。

试求此杆的临界力F cr。

13-4图示结构中，两根杆的横截面均为50×50mm2正方形，材料的弹性模量E=70×103MPa，试用欧拉公式确定结构失稳时的荷载F值。

13-6图示5根圆杆组成的正方形结构。

a=1m，各结点均为铰接，杆的直径均为d=35mm，截面类型为a类。

材料均为Q235钢，[σ]=170MPa，试求此时的容许荷载F。

又若力F的方向改为向外，容许荷载F又应为多少？13-9图示结构中，1、2两杆为材料相同的圆杆，1杆直径d1=16mm，2杆直径d2=32mm，已知材料的弹性模量E=200GPa，比例极限σp＝200MPa，屈服极限σs＝235MPa，结构的强度安全因素n=1.5，稳定安全因素n st=2.0。

试求该结构的容许荷载。

13-12一支柱系由4根75×75×6（见图）的角钢所组成。

截面类型为b类。

支柱的两端为铰支，柱长6ml ，a=210mm，压力为450kN。

若材料为Q235钢，容许应力[σ]=170MPa。

试校核支柱的稳定性。

13-14图示梁杆结构，材料均为Q235钢。

AB梁为16号工字钢，BC杆为d=的圆杆。

已知弹性模量E=200GPa，比例极限σp＝200MPa，屈服极限60mmσs＝235MPa，强度安全因数n=1.4，稳定安全因数n st=3，求容许荷载[]F。

材料力学习题09683(总54页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除第1章习题1-1 试求图1-18所示杆件指定截面上的内力。

图1-18 求杆件指定截面上的内力1-2 如图1-19所示的圆轴在皮带力作用下等速转动，两皮带轮直径均为d。

试说明圆轴将发生何种变形，并求B轮左侧截面和右侧截面上的内力分量。

图1-19 求皮带轮轴的内力1-3 已知镗刀杆刀头C上受切削力P x=750N，P y=,P z=5kN，刀尖C点位于x-y平面内(见图1-20)。

试求镗刀杆根部A面的内力(镗刀杆自重不计)。

图1-20 求镗刀杆根部的内力1-4 横截面为等边三角形的杆，已知该截面上的正应力σ0为均匀分布(见图1-21)。

试求截面上的内力分量及其作用点。

1-5 图1-22拉伸试样上A、B两点的距离l称为标距。

受拉力作用后，用变形仪量出两点距离的增量为Δl=5×10-2mm。

若原长为l=100mm，试求A、B 两点间的平均应变εm。

图1-21 三角形截面的杆图1-22拉伸试样1-6 图1-23所示三角形薄板受外力作用而变形，角点B垂直向上的位移为，但AB和BC仍保持为直线。

试求沿OB的平均应变，并求AB、BC两边在B点的角度改变。

图1-23 三角形薄板第2章习题2-1 试求图2-38所示各杆在指定的横截面上的轴力，并作轴力图。

图2-38 求杆指定截面上的轴力并绘轴力图2-2 正方形截面钢杆，杆长为2l，截面边长为a，在中段铣去长为l、宽为a/2的槽。

受力如图2-39所示。

设P =15kN,l =1m,a =20mm,E =200GPa。

求杆内最大正应力及总伸长。

图2-39 局部削弱杆件的应力及变形2-3 在图2-40所示结构中，若钢拉杆BC的横截面直径为10mm，试求拉杆内的应力。

设由BC联接的1和2两部分均为刚体。

图2-40 求拉杆BC的应力2-4 图2-41所示为一夹紧装置，已知螺栓为M20(其螺纹部分内径d= mm)，许用应力[σ]=50MPa，若工件所受夹紧力为25kN。

60º60º习题1图材料力学第13章作业1．正三角形截面压杆，其两端为球铰链约束，加载方向通过压杆轴线。

当载荷超过临界值，压杆发生屈曲时，横截面将绕哪一根轴转动？现有四种答案，请判断哪一种是正确的。

（A ） 绕y 轴；（B ） 绕通过形心C 的任意轴； （C ） 绕z 轴； （D ） 绕y 轴或z 轴。

2． 根据压杆稳定性设计准则，压杆的许可载荷[][]stcr Pn A σF =。

当横截面面积A 增加一倍时，试分析压杆的许可载荷将按下列四种规律中的哪一种变化？ （A ）增加1倍； （B ）增加2倍； （C ）增加l ／2倍；（D ）压杆的许可载荷随着A 的增加呈非线性变化。

3． 图示托架中杆AB 的直径d ＝40 mm 。

长度l ＝800 mm 。

两端可视为球铰链约束，材料为Q235钢。

试：1．求托架的临界载荷；2．若已知工作载荷 ，校核托架是否安全；3．若横梁为No.184． 图示结构中BC 为圆截面杆，其直径D =80mm ，AC 为边长A =70mm 的正方形截面杆，已知该结构的结束情况为A 端固定，B 、C 为球铰。

两杆材料相同为Q235钢，弹性模量E =210GPa ，σP =195MPa ，235=s σMPa 。

它们可以各自独立发生弯曲互不影响。

若该结构的稳定安全因数 2.5=st n ，试求所承受的最大安全压力。

5． 图示结构中AC 与CD 杆均用3号钢制成，C 、D 两处均为球铰。

已知d =20mm ，b =100mm ，h =180mm ；E =200GPa ，240=s σMPa ，b 400Mpa σ=；强度安全因数n =2.0，稳定安全因数n st ＝3.0。

试确定该结构的最大许可载荷。

6．上端铰支,下端固定,长l = 5.5m 的压杆,由两根10号槽钢焊接而成.槽钢截面对形心主惯轴Z 的惯性矩z I = 198.3 cm 4,对图11.2中的y 轴的惯性矩y I = 162.7cm 4,截面面积A = 12．74cm 2,已知杆材料的E = 200Gpa,MPa p 200=σ，许用应力[]MPa 170=σ，稳定安全系数n s t = 3.0.试求压杆的许用载荷。

第⼗三章钢筋混凝⼟设计原理课后习题答案第⼗三章1 什么是双向梁柱抗侧⼒体系？框架结构既要承受竖向重⼒荷载，⼜要承受⽔平风荷载，在地震区还要承受地震作⽤。

竖向荷载的⽅向是单⼀的，但⽔平荷载的⽅向却是随机的。

为了提⾼框架结构的侧向刚度，特别是要提⾼框架结构的抗扭刚度，以满⾜《规范》所规定的位移⾓限值、位移⽐限值和周期⽐限值。

框架结构师由梁板柱组成的空间结构，如果结构⼀个⽅向的抗侧⼒较弱时，会率先开裂和破坏，将导致结构丧失空间协调⼯作的能⼒，从⽽导致结构的严重破坏，甚⾄倒塌。

2柱⽹布置的基本要求是什么？（1），柱⽹布置应满⾜⽣产⼯艺的要求（2），柱⽹布置应满⾜建筑平⾯布置的要求（3），柱⽹布置要使结构受⼒合理（4），柱⽹布置应⽅便施⼯3承重框架有哪些布置⽅案？（1），横向框架承重⽅案（2），纵向框架承重⽅案（3），纵横向框架混合承重⽅案4如何确定框架结构的计算单元？其计算简图是什么？基本假定有哪些？为⽅便常忽略结构纵向和横向之间的空间联系，忽略各构件的抗扭作⽤，将横向框架和纵向框架分别按平⾯框架进⾏分析计算。

通常，横向框架的间距，荷载和间距都相同，因此取出有代表性的⼀品中间横向框架作为计算单元。

计算简图见书182页。

基本假定：1，没有⽔平位移。

2，某楼层的竖向荷载只对本层框架梁及与其相连的楼层产⽣内⼒。

5.竖向荷载如何简化到框架梁上⾯的？什么是等效荷载？如何等效？竖向荷载可以通过分层法简化到框架梁上假定（1）没有⽔平位移（2）某楼层的竖向荷载只对本层框架梁及与其相连的楼层柱产⽣内⼒。

分层法是利⽤叠加原理多层框架在多层荷载同时作⽤下的内⼒，可以看成是各层竖向荷载单独作⽤的内⼒的叠加。

等效荷载：等效荷载是指为了简化问题，⽤新的荷载代替原来复杂的荷载，但要保证两种荷载给构件带来的效应是相同的。

6.风荷载是如何简化到框架梁上的？风荷载对框架梁的作⽤⼀般都可以简化为作⽤于框架节点上的⽔平⼒采⽤反弯点法或者D值法将风荷载简化到框架梁上，⼆者的简化条件不同，D值法是反弯点法的改进，先求出个柱的杆端弯矩，然后根据节点平衡条件求得梁端弯矩，进⽽求出梁端剪⼒。

第 十三 章 能 量 法一、选择题1．一圆轴在图1所示两种受扭情况下，其（ A ）。

A 应变能相同，自由端扭转角不同； B 应变能不同，自由端扭转角相同； C 应变能和自由端扭转角均相同； D 应变能和自由端扭转角均不同。

（图1）2．图2所示悬臂梁，当单独作用力F 时，截面B 的转角为θ，若先加力偶M ，后加F ，则在加F 的过程中，力偶M （ C ）。

A 不做功；B 做正功；C 做负功，其值为θM ；D 做负功，其值为θM 21。

3．图2所示悬臂梁，加载次序有下述三种方式：第一种为F 、M 同时按比例施加；第二种为先加F ，后加M ；第三种为先加M ，后加F 。

在线弹性范围内，它们的变形能应为（ D ）。

A 第一种大； B 第二种大； C 第三种大； D 一样大。

4．图3所示等截面直杆，受一对大小相等，方向相反的力F 作用。

若已知杆的拉压刚度为EA ，材料的泊松比为μ，则由功的互等定理可知，该杆的轴向变形为EAFlμ，l 为杆件长度。

（提示：在杆的轴向施加另一组拉力F 。

） A 0； B EAFb ； CEAFbμ； D 无法确定。

（图2） （图3）二、计算题1．图示静定桁架，各杆的拉压刚度均为EA 相等。

试求节点C 的水平位移。

解：解法1-功能原理，因为要求的水平位移与P 力方向一致，所以可以用这种方法。

由静力学知识可简单地求出各杆的内力，如下表所示。

()()EAaP EAPa EA Pa P C 22222212222++=∆可得出：()EAPaC 122+=∆解法2-卡氏定理或莫尔积分，这两种方法一致了。

则C 点水平位移为：()EAPaC 122+=∆2．图示刚架，已知各段的拉压刚度均为EA ，抗弯刚度均为EI 。

试求A 截面的铅直位移。

解：采用图乘法，如果不计轴向拉压，在A 点施加单位力，则刚架内力图和单位力图如图所示。

h Fl Fl l h Fl l l Fl EI A 23313221+=⋅⋅+⋅⋅=∆EA Fhdx EA F dx EA N N dx EA N N h h BC BC lAB AB AN=--+=+=∆⎰⎰⎰202010)1)((0故A 点总的铅直位移为：EAFhEI h Fl Fl A ++=∆33233．试求图示悬臂梁B 截面的挠度和转角（梁的EI 为已知常数）。