导数测试卷(带答案)

1．设函数f(x)在0x 处可导，则xx f x x f x ∆-∆-→∆)()(lim000等于A ．)('0x fB ．)('0x f -C ．0'()f x -D ．0'()f x -- 2．若13)()2(lim000=∆-∆+→∆xx f x x f x ，则)('0x f 等于 A ．32 B ．23C ．3D ．23．若函数f(x)的导数为f ′(x)=-sinx ，则函数图像在点（4，f （4））处的切线的倾斜角为A ．90°B ．0°C ．锐角D ．钝角 4．对任意x ，有34)('x x f =，f(1)=-1，则此函数为A ．4)(x x f =B ．2)(4-=x x fC ．1)(4+=x x fD ．2)(4+=x x f 5．设f(x)在0x 处可导，下列式子中与)('0x f 相等的是 （1）x x x f x f x ∆∆--→∆2)2()(lim000； （2）x x x f x x f x ∆∆--∆+→∆)()(lim 000；（3）x x x f x x f x ∆∆+-∆+→∆)()2(lim000（4）x x x f x x f x ∆∆--∆+→∆)2()(lim 000.A ．（1）（2）B ．（1）（3）C ．（2）（3）D ．（1）（2）（3）（4） 6．若函数f(x)在点0x 处的导数存在，则它所对应的曲线在点))(,(00x f x 处的切线方程是___. 7．已知曲线xx y 1+=，则==1|'x y _____________.8．设3)('0-=x f ，则=---→hh x f h x f h )3()(lim000_____________.9．在抛物线2x y =上依次取两点，它们的横坐标分别为11=x ，32=x ，若抛物线上过点P 的切线与过这两点的割线平行，则P 点的坐标为_____________. 10．曲线3)(x x f =在点A 处的切线的斜率为3，求该曲线在A 点处的切线方程. 11．在抛物线2x y =上求一点P ，使过点P 的切线和直线3x-y+1=0的夹角为4π. 12．判断函数⎩⎨⎧<-≥=)0()0()(x x x x x f 在x=0处是否可导.13．求经过点（2，0）且与曲线xy 1=相切的直线方程. 同步练习X030131．函数y =f （x ）在x =x 0处可导是它在x =x 0处连续的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2．在曲线y =2x 2－1的图象上取一点（1，1）及邻近一点（1+Δx ，1+Δy ），则xy ∆∆ 等于A ．4Δx +2Δx 2B ．4+2ΔxC ．4Δx +Δx 2D ．4+Δx3．若曲线y =f （x ）在点（x 0，f （x 0））处的切线方程为2x +y －1=0，则A ．f ′（x 0）>0B ．f ′（x 0）<0C ．f ′（x 0）=0D ．f ′（x 0）不存在4．已知命题p ：函数y =f （x ）的导函数是常数函数；命题q ：函数y =f （x ）是一次函数，则命题p 是命题q 的 A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．设函数f （x ）在x 0处可导，则0lim→h hh x f h x )()(00--+等于A ．f ′（x 0）B ．0C ．2f ′（x 0）D ．－2f ′（x 0）6．设f （x ）=x （1+|x |），则f ′（0）等于A ．0B ．1C ．－1D ．不存在7．若曲线上每一点处的切线都平行于x 轴，则此曲线的函数必是___________． 8．曲线y =x 3在点P （2，8）处的切线方程是___________．9．曲线f （x ）=x 2+3x 在点A （2，10）处的切线斜率k =___________． 10．两曲线y =x 2+1与y =3－x 2在交点处的两切线的夹角为___________． 11．设f （x ）在点x 处可导，a 、b 为常数，则lim→∆x xx b x f x a x f ∆∆--∆+)()(=___________．12．已知函数f （x ）=⎩⎨⎧>+≤++0 012x b ax x x x ，试确定a 、b 的值，使f （x ）在x =0处可导． 13．设f （x ）=)()2)(1()()2)(1(n x x x n x x x +⋅⋅⋅++-⋅⋅⋅--，求f ′（1）．14．利用导数的定义求函数y =|x |（x ≠0）的导数．同步练习 X030211．物体运动方程为s =41t 4－3，则t =5时的瞬时速率为A ．5 m/sB ．25 m/sC ．125 m/sD ．625 m/s2．曲线y =x n （n ∈N ）在点P （2，)22n 处切线斜率为20，那么n 为A ．7B ．6C ．5D ．4 3．函数f （x ）=x x x 的导数是A ．81x（x >0） B ．－887x（x >0） C ．8781x（x >0） D ．881x（x >0）4．f （x ）与g （x ）是定义在R 上的两个可导函数，若f （x ），g （x ）满足f ′（x ）=g ′（x ），则f （x ）与g （x ）满足 A ．f （x ）=g （x ）B ．f （x ）－g （x ）为常数函数C ．f （x ）=g （x ）=0D ．f （x ）+g （x ）为常数函数5．两车在十字路口相遇后，又沿不同方向继续前进，已知A 车向北行驶，速率为30 km/h ，B 车向东行驶，速率为40 km/h ，那么A 、B 两车间直线距离的增加速率为 A ．50 km/hB ．60 km/hC ．80 km/hD ．65 km/h6．细杆AB 长为20 cm ，AM 段的质量与A 到M 的距离平方成正比，当AM =2 cm 时，AM 段质量为8 g ，那么，当AM =x 时，M 处的细杆线密度ρ（x ）为A ．2xB ．4xC ．3xD ．5x7．曲线y =x 4的斜率等于4的切线的方程是___________．8．设l 1为曲线y 1=sin x 在点（0，0）处的切线，l 2为曲线y 2=cos x 在点（2π，0）处的切线，则l 1与l 2的夹角为___________． 9．过曲线y =cos x 上的点（21,6π）且与过这点的切线垂直的直线方程为_____________．10．在曲线y =sin x （0<x <π）上取一点M ，使过M 点的切线与直线y =x 23平行，则M 点的坐标为___________．11．质点P 在半径为r 的圆周上逆时针做匀角速率运动，角速率为1 r a d/s ，设A 为起点，那么t 时刻点P 在x 轴上射影点M 的速率为___________．12．求证：双曲线xy =a 2上任一点处的切线与两坐标轴构成的三角形面积等于常数．13．路灯距地平面为8 m ，一个身高为1．6 m 的人以84 m/min 的速率在地面上行走，从路灯在地平面上射影点C ，沿某直线离开路灯，求人影长度的变化速率v ．14．已知直线x +2y －4=0与抛物线y 2=4x 相交于A 、B 两点，O 是坐标原点，试在抛物线的弧上求一点P ，使△PAB 面积最大．同步练习 X030311．若f （x ）=sin α－cos x ，则f ′（α）等于A ．sin αB ．cos αC ．sin α+cos αD ．2sin α2．f （x ）=ax 3+3x 2+2，若f ′（－1）=4，则a 的值等于A ．319B ．316 C ．313D ．3103．函数y =x sin x 的导数为A ．y ′=2x sin x +x cos xB ．y ′=xx 2sin +x cos xC ．y ′=xx sin +x cos x D ．y ′=xx sin －x cos x4．函数y =x 2cos x 的导数为A ．y ′=2x cos x －x 2sin xB ．y ′=2x cos x +x 2sin xC ．y ′=x 2cos x －2x sin xD ．y ′=x cos x －x 2sin x5.若y =(2x 2-3)(x 2-4),则y ’= .6. 若y =3cosx -4sinx ,则y ’= .7．与直线2x －6y +1=0垂直，且与曲线y =x 3+3x 2－1相切的直线方程是______． 8．质点运动方程是s =t 2（1+sin t ），则当t =2时，瞬时速度为___________． 9.求曲线y=x3+x2-1在点P （-1，-1）处的切线方程.10．用求导的方法求和：1+2x +3x 2+…+nx n －1（x ≠1）．11．水以20米3/分的速度流入一圆锥形容器，设容器深30米，上底直径12米，试求当水深10米时，水面上升的速度．同步练习 X030321．函数y =22xa x +（a >0）的导数为0，那么x 等于A ．aB ．±aC ．－aD ．a 22．函数y =xxsin 的导数为 A ．y ′=2sin cos xxx x + B ．y ′=2sin cos xxx x - C ．y ′=2cos sin xxx x -D ．y ′=2cos sin xxx x + 3.若21,2xy x +=-则y ’= . 4.若423335,x x y x -+-=则y ’= . 5.若1cos ,1cos xy x+=-则y ’= .6．已知f （x ）=354337xx x x ++，则f ′（x ）=___________．7．已知f （x ）=xx++-1111，则f ′（x ）=___________．8．已知f （x ）=xx2cos 12sin +，则f ′（x ）=___________．9．求过点（2，0）且与曲线y =x 1相切的直线的方程．10.质点的运动方程是23,s t t=+求质点在时刻t=4时的速度.同步练习 X030411．函数y =2)13(1-x 的导数是 A ．3)13(6-x B ．2)13(6-x C ．－3)13(6-x D ．－2)13(6-x2．已知y =21sin2x +sin x ，那么y ′是A ．仅有最小值的奇函数B ．既有最大值，又有最小值的偶函数C ．仅有最大值的偶函数D ．非奇非偶函数 3．函数y =sin 3（3x +4π）的导数为 A ．3sin 2（3x +4π）cos （3x +4π） B ．9sin 2（3x +4π）cos （3x +4π）C ．9sin 2（3x +4π）D ．－9sin 2（3x +4π）cos （3x +4π）4.若y=（sinx-cosx 3)，则y ’= .5. 若y=2cos 1x +，则y ’= .6. 若y=sin 3(4x+3)，则y ’= .7．函数y =（1+sin3x ）3是由___________两个函数复合而成． 8．曲线y =sin3x 在点P （3π，0）处切线的斜率为___________．9.求曲线2211(2,)(3)4y M x x =-在处的切线方程. 10. 求曲线sin 2(,0)y x M π=在处的切线方程.11．已知函数y =（x ）是可导的周期函数，试求证其导函数y =f ′（x ）也为周期函数．同步练习 X030421．函数y =cos （sin x ）的导数为A ．－［sin （sin x ）］cos xB ．－sin （sin x ）C ．［sin （sin x ）］cos xD ．sin （cos x ）2．函数y =cos2x +sin x 的导数为A ．－2sin2x +xx2cos B ．2sin2x +xx 2cosC ．－2sin2x +xx 2sin D ．2sin2x －xx 2cos3．过曲线y =11+x 上点P （1，21）且与过P 点的切线夹角最大的直线的方程为 A ．2y －8x +7=0 B ．2y +8x +7=0 C ．2y +8x －9=0D ．2y －8x +9=04．函数y =x sin （2x －2π）cos （2x +2π）的导数是______________． 5．函数y =)32cos(π-x 的导数为______________．6．函数y =cos 3x1的导数是___________．7.已知曲线y=2400x + +53(100-x) (0100≤≤x ) 在点M 处有水平切线,8．若可导函数f （x ）是奇函数，求证：其导函数f ′（x ）是偶函数．9．用求导方法证明：21C 2C n n ++…+n n n C =n ·2n －1． 同步练习 X030511．函数y =ln （3－2x －x 2）的导数为A ．32+x B ．2231x x -- C ．32222-++x x xD ．32222-+-x x x2．函数y =lncos2x 的导数为A ．－tan2xB ．－2tan2xC ．2tan xD ．2tan2x3．函数y =x ln 的导数为A ．2x x lnB ．xx ln 2C ．xx ln 1 D ．xx ln 214．在曲线y =59++x x 的切线中，经过原点的切线为________________． 5．函数y =log 3cos x 的导数为___________． 6.函数y =x 2lnx 的导数为 . 7. 函数y =ln （lnx ）的导数为 . 8. 函数y =lg (1+cosx )的导数为9. 求函数y =ln 22132x x+-的导数．10. 求函数y = 12．求函数y =ln （21x +－x ）的导数．同步练习 X030521．下列求导数运算正确的是A ．（x +x 1）′=1+21xB ．（log 2x ）′=2ln 1xC ．（3x ）′=3x log 3eD ．（x 2cos x ）′=－2x sin x 2．函数y =xxa 22-（a >0且a ≠1），那么y ′为A ．xxa 22-ln aB ．2（ln a ）xx a 22-C ．2（x －1）xxa 22-·ln aD ．（x －1）xxa 22-ln a3．函数y =sin32x 的导数为A ．2（cos32x ）·32x ·ln3B ．（ln3）·32x ·cos32xC ．cos32xD ．32x ·cos32x4．设y =xx ee 2)12(+，则y ′=___________． 5．函数y =x22的导数为y ′=___________．6．曲线y =e x －e ln x 在点（e ，1）处的切线方程为___________．7.求函数y=e 2x lnx 的导数. 8．求函数y =x x （x >0）的导数．9．设函数f （x ）满足：af （x ）+bf （x 1）=xc（其中a 、b 、c 均为常数，且|a |≠|b |），试求f ′（x ）同步练习 x030611．若f （x ）在［a ，b ］上连续，在（a ，b ）内可导，且x ∈（a ，b ）时，f ′（x ）>0，又f （a ）<0，则A ．f （x ）在［a ，b ］上单调递增，且f （b ）>0B ．f （x ）在［a ，b ］上单调递增，且f （b ）<0C ．f （x ）在［a ，b ］上单调递减，且f （b ）<0D ．f （x ）在［a ，b ］上单调递增，但f （b ）的符号无法判断 2．函数y =3x －x 3的单调增区间是A ．（0，+∞）B ．（－∞，－1）C ．（－1，1）D ．（1，+∞） 3．三次函数y =f （x ）=ax 3+x 在x ∈（－∞，+∞）内是增函数，则A ．a >0B ．a <0C ．a =1D ．a =314．f （x ）=x +x2（x >0）的单调减区间是A ．（2，+∞）B ．（0，2）C ．（2，+∞）D ．（0，2）5．函数y =sin x cos 2x 在（0，2）上的减区间为A ．（0，arctan 22） B ．（arctan2,22π） C ．（0，2π）D ．（arctan 2,21π）6．函数y =x ln x 在区间（0，1）上是A ．单调增函数B ．单调减函数C ．在（0，e 1）上是减函数，在（e 1，1）上是增函数D ．在（0，e 1）上是增函数，在（e1，1）上是减函数7．函数f （x ）=cos 2x 的单调减区间是___________． 8．函数y =2x +sin x 的增区间为___________．9．函数y =232+-x x x的增区间是___________． 10．函数y =xxln 的减区间是___________．11．已知0<x <2π，则tan x 与x +33x 的大小关系是tan x _____x +33x ．12．已知函数f （x ）=kx 3－3（k +1）x 2－k 2+1（k >0）．若f （x ）的单调递减区间是（0，4）. （1）求k 的值； （2）当k <x 时，求证：2x >3－x1．13．试证方程sin x =x 只有一个实根．14．三次函数f （x ）=x 3－3bx +3b 在［1，2］内恒为正值，求b 的取值范围．同步练习 X030711．下列说法正确的是A ．当f ′（x 0）=0时，则f （x 0）为f （x ）的极大值B ．当f ′（x 0）=0时，则f （x 0）为f （x ）的极小值C ．当f ′（x 0）=0时，则f （x 0）为f （x ）的极值D ．当f （x 0）为函数f （x ）的极值且f ′（x 0）存在时，则有f ′（x 0）=0 2．下列四个函数，在x =0处取得极值的函数是①y =x 3 ②y =x 2+1 ③y =|x | ④y =2x A ．①②B ．②③C ．③④D ．①③3．函数y =216xx的极大值为 A ．3 B ．4 C ．2 D ．54．函数y =x 3－3x 的极大值为m ，极小值为n ，则m +n 为A ．0B ．1C ．2D ．4 5．y =ln 2x +2ln x +2的极小值为A ．e －1B ．0C ．－1D ．16．y =2x 3－3x 2+a 的极大值为6，那么a 等于A ．6B ．0C ．5D ．17．函数f （x ）=x 3－3x 2+7的极大值为___________．8．曲线y =3x 5－5x 3共有___________个极值．9．函数y =－x 3+48x －3的极大值为___________；极小值为___________．10．函数f （x ）=x －3223x 的极大值是___________，极小值是___________．11．若函数y =x 3+ax 2+bx +27在x =－1时有极大值，在x =3时有极小值，则a =___________，b =___________．12．已知函数f （x ）=x 3+ax 2+bx +c ，当x =－1时，取得极大值7；当x =3时，取得极小值．求这个极小值及a 、b 、c 的值．13．函数f （x ）=x +xa+b 有极小值2，求a 、b 应满足的条件．14．设y =f （x ）为三次函数，且图象关于原点对称，当x =21时，f （x ）的极小值为－1，求函数的解析式．同步练习 X030811．下列结论正确的是A ．在区间[a ，b]上，函数的极大值就是最大值B ．在区间[a ，b]上，函数的极小值就是最小值C ．在区间[a ，b]上，函数的最大值、最小值在x=a 和x=b 时到达D ．在区间[a ，b]上连续的函数f(x)在[a ，b]上必有最大值和最小值 2．函数14)(2+-=x x x f 在[1，5]上的最大值和最小值是A ．f(1)，f(3)B ．f(3)，f(5)C ．f(1)，f(5)D ．f(5)，f(2) 3．函数f(x)=2x-cosx 在(-∞，+∞)上A ．是增函数B ．是减函数C ．有最大值D ．有最小值 4．函数a ax x x f --=3)(3在(0，1)内有最小值，则a 的取值范围是 A ．0<a<1 B ．a<1 C ．a>0 D ．21<a 5．若函数x x a x f 3sin 31sin )(+=在3π=x 处有最值，那么a 等于A ．2B ．1C ．332 D ．0 6．函数5224+-=x x y ，x ∈[-2，2]的最大值和最小值分别为 A ．13，-4 B ．13，4 C ．-13，-4 D ．-13，4 7．函数x xe y =的最小值为________________. 8．函数f(x)=sinx+cosx 在]2,2[ππ-∈x 时函数的最大值，最小值分别是___. 9．体积为V 的正三棱柱，底面边长为___________时，正三棱柱的表面积最小．10．函数21)(x x x f -+=的最大值为__________，最小值为____________。

导数应用测试题一、选择题：(本大题共12小题,每小题5分, 共60分) 1．设函数f(x)在0x 处可导，则xx f x x f x ∆-∆-→∆)()(lim000等于 （ ）A ．)('0x fB ．)('0x f -C ．)('0x f --D ．)(0x f -- 2．若13)()2(lim000=∆-∆+→∆xx f x x f x ，则)('0x f 等于 （ ） A ．32 B ．23C ．3D ．2 3．曲线x x y 33-=上切线平行于x轴的点的坐标是（ ）A ．（-1，2）B ．（1，-2）C ．（1，2）D ．（-1，2）或（1，-2） 4．若函数f(x)的导数为f ′(x)=-sinx ，则函数图像在点（4，f （4））处的切 线的倾斜角为（ ）A ．90°B ．0°C ．锐角D ．钝角5．函数5123223+--=x x x y 在[0，3]上的最大值、最小值分别是 （ ）A ．5，－15B ．5，－4C ．－4，－1D ．5，－166．一直线运动的物体，从时间t 到t+△t 时，物体的位移为△s ，那么ts t ∆∆→∆0lim 为（ ）A ．从时间t 到t+△t 时，物体的平均速度B ．时间t 时该物体的瞬时速度C ．当时间为△t 时该物体的速度D ．从时间t 到t+△t 时位移的平均变化率7．关于函数762)(23+-=x x x f ，下列说法不正确的是（ ）A ．在区间（∞-，0）内，)(x f 为增函数B ．在区间（0，2）内，)(x f 为减函数C ．在区间（2，∞+）内，)(x f 为增函数D ．在区间（∞-，0）),2(+∞⋃内，)(x f 为增函数8．对任意x ，有34)('x x f =，f(1)=-1，则此函数为 （ ） A ．4)(x x f = B ．2)(4-=x x f C ．1)(4+=x x f D ．2)(4+=x x f9．函数y=2x 3-3x 2-12x+5在[0,3]上的最大值与最小值分别是 （ ）A.5 , -15B.5 , 4C.-4 , -15D.5 , -1610．抛物线y=x 2到直线x-y-2=0的最短距离为 （ ）A ．2B 。

导数的计算练习题及答案1. 计算函数f(x) = 3x^2 - 4x + 2的导数f'(x)。

解答：根据函数f(x) = 3x^2 - 4x + 2，使用导数的定义来计算导数f'(x)。

f'(x) = lim(delta x -> 0) (f(x + delta x) - f(x)) / delta x代入函数f(x)的表达式：f'(x) = lim(delta x -> 0) [(3(x + delta x)^2 - 4(x + delta x) + 2) -(3x^2 - 4x + 2)] / delta x化简并展开：f'(x) = lim(delta x -> 0) [3(x^2 + 2x * delta x + (delta x)^2) - 4x - 4 * delta x + 2 - 3x^2 + 4x - 2] / delta xf'(x) = lim(delta x -> 0) [3x^2 + 6x * delta x + 3(delta x)^2 - 4x - 4* delta x + 2 - 3x^2 + 4x - 2] / delta xf'(x) = lim(delta x -> 0) [6x * delta x + 3(delta x)^2 - 4 * delta x] / delta xf'(x) = lim(delta x -> 0) [6x + 3 * delta x - 4]由于求导数时delta x趋近于0，所以delta x也可以看作一个无穷小量，其平方项可以忽略不计，即delta x^2 = 0。

化简结果：f'(x) = 6x - 4所以函数f(x) = 3x^2 - 4x + 2的导数f'(x)为6x - 4。

2. 计算函数g(x) = 2sin(x) + 3cos(x)的导数g'(x)。

【巩固练习】一、选择题1．设函数310()(12)f x x =-，则'(1)f =（ ）A ．0B ．―1C ．―60D ．602．（2014 江西校级一模）若2()2ln f x x x =-，则'()0f x >的解集为（ ）A.(0,1)B.()(),10,1-∞-C. ()()1,01,-+∞D.()1,+∞3．（2014春 永寿县校级期中）下列式子不正确的是（ ）A.()'23cos 6sin x x x x +=-B. ()'1ln 22ln 2x x x x -=- C. ()'2sin 22cos 2x x = D.'2sin cos sin x x x x x x -⎛⎫= ⎪⎝⎭ 4．函数4538y x x =+-的导数是（ ） A ．3543x + B ．0 C ．3425(43)(38)x x x ++- D ．3425(43)(38)x x x +-+- 5．（2015 安徽四模）已知函数()f x 的导函数为'()f x ，且满足关系式2'()3(2)ln f x x xf x =++，则'(2)f 的值等于（ ）A. 2B.-2C.94 D.94- 6．设曲线1(1)1x y x x +=≠-在点（3，2）处的切线与直线ax+y+1=0垂直，则a=（ ） A ．2 B ．12 C ．―12D ．―2 7．23log cos (cos 0)y x x =≠的导数是（ ）A ．32log tan e x -⋅B ．32log cot e x ⋅C ．32log cos e x -⋅D ．22log cos e x 二、填空题8．曲线y=sin x 在点,12π⎛⎫ ⎪⎝⎭处的切线方程为________。

9．设y=(2x+a)2，且2'|20x y ==，则a=________。

10．31sin x x '⎛⎫-= ⎪⎝⎭____________，()2sin 25x x '+=⎡⎤⎣⎦____________。

导数专题测试卷一、填空题：请把答案填在题中横线上（每小题5分，共70分）．1．32()32f x ax x =++,若(1)4f '-=,则a 的值等于____________2．如果()f x 为偶函数，且导数()f x 存在，则()0f '的值为____________ 3．0()0f x '=是函数()f x 在点0x 处取极值的____________条件4．已知32()26(f x x x m m =-+为常数）在[2,2]-上有最大值3，那么此函数在[2,2]-上的最小值为____________5．曲线x y ln =在点(,1)M e 处的切线的斜率是_________，切线的方程为______________．6．函数5523--+=x x x y 的单调递增区间是_____________________．7．若函数343y x bx =-+有三个单调区间，则b 的取值范围是 ． 8已知函数3221()3f x x a x ax b =+++，当1x =-时函数()f x 的极值为712-，则(2)f = ．9．)(x f ,)(x g 分别是定义在R 上的奇函数和偶函数，当0<x 时,0)(')()()('>+x g x f x g x f ，且0)3(=-g ，则不等式0)()(<x g x f 的解集是____ 10．以函数12y x =为导数的函数()f x 图象过点（9，1），则函数()f x ＝_________．11．在曲线106323-++=x x x y 的切线中斜率最小的切线方程是____________. 12．如圆的半径以2 cm/s 的等速度增加，则圆半径R =10 cm 时，圆面积增加的速度是__________．13．已知x R ∈，奇函数32()f x x ax bx c =--+在[1,)+∞上单调，则字母,,a b c 应满足的条件是__________．14．已知函数()log a f x x =和()2log (22),(0,1,)a g x x t a a t R =+->≠∈的图象在2x =处的切线互相平行，则t =__________．二、解答题（6小题，共90分）解答应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）已知抛物线42-=x y 与直线2+=x y（Ⅰ）求两曲线的交点；（Ⅱ）求抛物线在交点处的切线方程．16．（本小题满分14分）已知函数3f x x x=-()3f x的单调区间；（Ⅰ）求()f x在区间[-3,2]上的最值．（Ⅱ）求()17．（本小题满分15分）设5221)(23+--=x x x x f ，当[2,2]x ∈-时，0)(<-m x f 恒成立，求实数m 的取值范围．18．（本小题满分15分）已知*,N n m ∈且n m <<1，试用导数证明不等式：m n n m )1()1(+>+．19．（本小题满分16分）已知某质点的运动方程为32()s t t bt ct d =+++，下图的曲线是其运动轨迹的一部分． （Ⅰ）试求b 、c 之值；（Ⅱ）若当1[,4]2t ∈时，2()3s t d <恒成立，求d 的取值范围．20．（本小题满分16分）设函数23)(3++-=x x x f 分别在1x 、2x 处取得极小值、极大值．xoy 平面上点A 、B 的坐标分别为))(,(11x f x 、))(,(22x f x ,该平面上动点P 满足4=∙PB PA ,点Q 是点P 关于直线)4(2-=x y 的对称点．求：（Ⅰ）点A 、B 的坐标； （Ⅱ）动点Q 的轨迹方程．参考答案一、1．310 2．0 3．必要不充分；4．37-；5．1e0x e y -=； 6．5(,),(1,)3-∞-+∞；7. (0,)+∞；8．539．(－∞，－3)∪(0，3)10．322173x -； 11．0113=--y x ；12． 40π cm 2/s ；13．0,3a c b ==≤； 14．6．15．解：（1）由⎩⎨⎧-=+=422x y x y ，求得交点A （－2,0），B （3,5） （2）因为x y 2/=，则6|,4|3/2/=-===x x y y所以抛物线在A 、B 两点处的切线方程分别为)2(4+-=x y 与)3(65-=-x y 即084=++y x 与0136=--y x16．解：(I) 32()3,'()333(1)(1).f x x x f x x x x =-∴=-=+-令 '()0,f x =得1, 1.x x =-= 若 (,1)(1,)x ∈-∞-+∞则'()0f x >， 故()f x 在(,1)-∞-上是增函数，()f x 在(1,)+∞上是增函数 若 (1,1),x ∈-则'()0f x <，故()f x 在(1,1)-上是减函数(II) (3)18,(1)2,(1)2,(2)2f f f f -=--==-=3 ()18.x f x ∴=--当时，在区间[-3,2]取到最小值为 1 2 () 2.x f x ∴=-当或时，在区间[-3,2]取到最大值为17．解：23)(2/--=x x x f ，由0)(/>x f 得0232>--x x ，即32-<x 或1>x ；由0)(/<x f 得0232<--x x 即132<<-x ，所以函数单调增区间是)32,(--∞，),1(+∞；函数的单调减区间是)1,32(-。

导数单元测试题班级姓名一、选择题1．已知函数y＝f(x)＝x2＋1，则在x＝2，Δx＝0.1时，Δy的值为( ) A．0.40 B．0.41 C．0.43 D．0.442．函数f(x)＝2x2－1在区间(1,1＋Δx)上的平均变化率ΔyΔx等于( )A．4 B．4＋2Δx C．4＋2(Δx)2D．4x3．设f′(x0)＝0，则曲线y＝f(x)在点(x0，f(x0))处的切线( ) A．不存在B．与x轴平行或重合C．与x轴垂直D．与x轴相交但不垂直4．曲线y＝－1x在点(1，－1)处的切线方程为( )A．y＝x－2 B．y＝x C．y＝x＋2 D．y＝－x－25．下列点中，在曲线y＝x2上，且在该点处的切线倾斜角为π4的是( )A．(0,0) B．(2,4) C．(14，116) D．(12，14)6．已知函数f(x)＝1x，则f′(－3)＝( )A．4 B.19C．－14D．－197．函数f(x)＝(x－3)e x的单调递增区间是( )A．(－∞，2) B．(0,3) C．(1,4) D．(2，＋∞) 8．“函数y＝f(x)在一点的导数值为0”是“函数y＝f(x)在这点取极值”的( ) A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件9．函数f(x)的定义域为开区间(a，b)，导函数f′(x)在(a，b)内的图象如图所示，则函数f(x)在开区间(a，b)内的极小值点有( )A．1个B．2个C．3个D．4个10．函数f(x)＝－x2＋4x＋7，在x∈[3,5]上的最大值和最小值分别是( )A．f(2)，f(3) B．f(3)，f(5) C．f(2)，f(5) D．f(5)，f(3)11．函数f(x)＝x3－3x2－9x＋k在区间[－4,4]上的最大值为10，则其最小值为( )A．－10 B．－71 C．－15 D．－2212．一点沿直线运动，如果由始点起经过t秒运动的距离为s＝14t4－53t3＋2t2，那么速度为零的时刻是( )A．1秒末 B．0秒 C．4秒末 D．0,1,4秒末二、填空题13．设函数y＝f(x)＝ax2＋2x，若f′(1)＝4，则a＝________.14．已知函数y＝ax2＋b在点(1,3)处的切线斜率为2，则ba＝________.15．函数y＝x e x的最小值为________．16．有一长为16 m的篱笆，要围成一个矩形场地，则矩形场地的最大面积是________m2.三、解答题17．求下列函数的导数：(1)y＝3x2＋x cos x； (2)y＝x1＋x； (3)y＝lg x－e x.18．已知抛物线y＝x2＋4与直线y＝x＋10，求：(1)它们的交点； (2)抛物线在交点处的切线方程．19．已知函数f(x)＝13x3－4x＋4.(1)求函数的极值；(2)求函数在区间[－3,4]上的最大值和最小值．导数单元测试题答案班级 姓名一、选择题1．已知函数y ＝f (x )＝x 2＋1，则在x ＝2，Δx ＝0.1时，Δy 的值为( ) A ．0.40 B ．0.41 C ．0.43 D ．0.44解析：选B.Δy ＝f (2.1)－f (2)＝2.12－22＝0.41.2．函数f (x )＝2x 2－1在区间(1,1＋Δx )上的平均变化率Δy Δx等于( )A ．4B ．4＋2ΔxC ．4＋2(Δx )2D ．4x解析：选B.因为Δy ＝[2(1＋Δx )2－1]－(2×12－1)＝4Δx ＋2(Δx )2，所以Δy Δx＝4＋2Δx ，故选B.3．设f ′(x 0)＝0，则曲线y ＝f (x )在点(x 0，f (x 0))处的切线( ) A ．不存在 B ．与x 轴平行或重合 C ．与x 轴垂直 D ．与x 轴相交但不垂直解析：选B.函数在某点处的导数为零，说明相应曲线在该点处的切线的斜率为零．4．曲线y ＝－1x在点(1，－1)处的切线方程为( )A ．y ＝x －2B ．y ＝xC ．y ＝x ＋2D ．y ＝－x －2解析：选A.f ′(1)＝li m Δx →0 －11＋Δx ＋11Δx ＝li mΔx →0 11＋Δx ＝1，则在(1，－1)处的切线方程为y ＋1＝x －1，即y ＝x －2.5．下列点中，在曲线y ＝x 2上，且在该点处的切线倾斜角为π4的是( )A ．(0,0)B ．(2,4)C ．(14，116)D ．(12，14)故选D.6．已知函数f (x )＝1x，则f ′(－3)＝( )A ．4 B.19C ．－14D ．－19解析：选D.∵f ′(x )＝－1x 2，∴f ′(－3)＝－19.7．函数f (x )＝(x －3)e x的单调递增区间是( )A ．(－∞，2)B ．(0,3)C ．(1,4)D ．(2，＋∞)解析：选D.f ′(x )＝(x －3)′e x ＋(x －3)(e x )′＝(x －2)e x， 令f ′(x )>0，解得x >2，故选D.8．“函数y ＝f (x )在一点的导数值为0”是“函数y ＝f (x )在这点取极值”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件解析：选B.对于f (x )＝x 3，f ′(x )＝3x 2，f ′(0)＝0，不能推出f (x )在x ＝0处取极值，反之成立．故选B.9．函数f (x )的定义域为开区间(a ，b )，导函数f ′(x )在(a ，b )内的图象如图所示，则函数f (x )在开区间(a ，b )内的极小值点有()A ．1个B ．2个C ．3个D ．4个解析：选A.函数f (x )的定义域为开区间(a ，b )，导函数f ′(x )在(a ，b )内的图象如题图所示，函数f (x )在开区间(a ，b )内有极小值点即函数由减函数变为增函数的点，其导数值为由负到正的点，只有1个．10．函数f (x )＝－x 2＋4x ＋7，在x ∈[3,5]上的最大值和最小值分别是( )A ．f (2)，f (3)B ．f (3)，f (5)C ．f (2)，f (5)D ．f (5)，f (3) 解析：选B.∵f ′(x )＝－2x ＋4， ∴当x ∈[3,5]时，f ′(x )<0， 故f (x )在[3,5]上单调递减，故f (x )的最大值和最小值分别是f (3)，f (5)．11．函数f (x )＝x 3－3x 2－9x ＋k 在区间[－4,4]上的最大值为10，则其最小值为( )A ．－10B ．－71C ．－15D ．－22解析：选B.f ′(x )＝3x 2－6x －9＝3(x －3)(x ＋1)． 由f ′(x )＝0得x ＝3，－1.又f (－4)＝k －76，f (3)＝k －27， f (－1)＝k ＋5，f (4)＝k －20. 由f (x )max ＝k ＋5＝10，得k ＝5， ∴f (x )min ＝k －76＝－71.12．一点沿直线运动，如果由始点起经过t 秒运动的距离为s ＝14t 4－53t 3＋2t 2，那么速度为零的时刻是( ) A ．1秒末 B ．0秒 C ．4秒末 D ．0,1,4秒末解析：选D.∵s ′＝t 3－5t 2＋4t ，令s ′＝0，得t 1＝0，t 2＝1，t 3＝4，此时的函数值最大，故选D. 二、填空题13．设函数y ＝f (x )＝ax 2＋2x ，若f ′(1)＝4，则a ＝________. 答案：1 14．已知函数y ＝ax 2＋b 在点(1,3)处的切线斜率为2，则b a＝________.答案：215．函数y ＝x e x的最小值为________．解析：令y ′＝(x ＋1)e x＝0，得x ＝－1. 当x <－1时，y ′<0；当x >－1时，y ′>0.∴y min ＝f (－1)＝－1e.答案：－1e16．有一长为16 m 的篱笆，要围成一个矩形场地，则矩形场地的最大面积是________m 2. 解析：设矩形的长为x m ，则宽为16－2x 2＝(8－x ) m(0<x <8)，∴S (x )＝x (8－x )＝－x 2＋8x∴S ′(x )＝－2x ＋8，令S ′(x )＝0， 则x ＝4，又在(0,8)上只有一个极值点， 且x ∈(0,4)时，S (x )单调递增， x ∈(4,8)时，S (x )单调递减， 故S (x )max ＝S (4)＝16. 答案：16 三、解答题17．求下列函数的导数： (1)y ＝3x 2＋x cos x ；(2)y ＝x1＋x；(3)y ＝lg x －e x.解：(1)y ′＝6x ＋cos x －x sin x .(2)y ′＝1＋x －x ＋x 2＝1＋x2.(3)y ′＝(lg x )′－(e x)′＝1x ln10－e x. 18．已知抛物线y ＝x 2＋4与直线y ＝x ＋10，求： (1)它们的交点；(2)抛物线在交点处的切线方程．解：(1)由⎩⎪⎨⎪⎧y ＝x 2＋4，y ＝x ＋10，得x 2＋4＝10＋x ，即x 2－x －6＝0，∴x ＝－2或x ＝3.代入直线的方程得y ＝8或13. ∴抛物线与直线的交点坐标为(－2,8)或(3,13)．(2)∵y ＝x 2＋4，∴y ′＝lim Δx →0 x ＋Δx 2＋4－x 2＋Δx＝lim Δx →0 Δx 2＋2x ·ΔxΔx＝lim Δx →0 (Δx ＋2x )＝2x . ∴y ′|x ＝－2＝－4，y ′|x ＝3＝6，即在点(－2,8)处的切线斜率为－4，在点(3,13)处的切线斜率为6. ∴在点(－2,8)处的切线方程为4x ＋y ＝0； 在点(3,13)处的切线方程为6x －y －5＝0.19．已知函数f (x )＝13x 3－4x ＋4.(1)求函数的极值；(2)求函数在区间[－3,4]上的最大值和最小值．解：(1)f ′(x )＝x 2－4，解方程x 2－4＝0， 得x 1＝－2，x 2＝2.当从上表可看出，当x ＝－2时，函数有极大值，且极大值为3；而当x ＝2时，函数有极小值，且极小值为－43.(2)f (－3)＝13×(－3)3－4×(－3)＋4＝7，f (4)＝13×43－4×4＋4＝283，与极值比较，得函数在区间[－3,4]上的最大值是283，最小值是－43.。

一、选择题(每题只有一个选项是正确的，每题5分，共60分，在每题给出的四个选项中，只有一项为哪一项符合题目要求的。

)1．某函数的导数为y′＝12(x－1)，那么这个函数可能是 ()A．y＝ln1－x B．y＝ln11－xC．y＝ln(1－x) D．y＝ln11－x2．(2021•江西)设函数f(x)＝g(x)＋x2，曲线y＝g(x)在点(1，g(1))处的切线方程为y＝2x＋1，那么曲线y＝f(x)在点(1，f(1))处切线的斜率为 ()A．4 B．－14 C．2 D．－123．(2021•辽宁)曲线y＝xx－2在点(1，－1)处的切线方程为 ()A．y＝x－2 B．y＝－3x＋2C．y＝2x－3 D．y＝－2x＋14．曲线y＝ex在点(2，e2)处的切线与坐标轴所围成三角形的面积为 ()A.94e2 B．2e2 C．e2 D.e225．函数y＝f(x)，y＝g(x)的导函数的图象如图，那么y＝f(x)，y＝g(x)的图象可能是()6．设y＝8x2－lnx，那么此函数在区间(0，14)和(12，1)内分别 ()A．单调递增，单调递减B．单调递增，单调递增C．单调递减，单调递增D．单调递减，单调递减7．以下关于函数f(x)＝(2x－x2)ex的判断正确的选项是 ()①f(x)＞0的解集是{x|0＜x＜2}；②f(－2)是极小值，f(2)是极大值；③f(x)没有最小值，也没有最大值．A．①③ B．①②③C．② D．①②8．f(x)＝－x3－x，x∈[m，n]，且f(m)•f(n)＜0，那么方程f(x)＝0在区间[m，n]上() A．至少有三个实根 B．至少有两个实根C．有且只有一个实根 D．无实根9．函数f(x)＝x3＋ax2＋(a＋6)x＋1有极大值和极小值，那么实数a的取值范围是() A．－1＜a＜2 B．－3＜a＜6 C．a＜－3或a＞6 D．a＜－1或a＞210．要做一个圆锥形漏斗，其母线长为20cm，要使其体积最大，其高应为 ()A.2033cm B．100cm C．20cm D.203cm11．(2021•河南省实验中学)假设函数f(x)＝(2－m)xx2＋m的图象如下图，那么m的范围为 ()A．(－∞，－1) B．(－1,2) C．(1,2) D．(0,2)12．定义在R上的函数f(x)满足f(4)＝1.f′(x)为f(x)的导函数，函数y＝f′(x)的图象如下图．假设两正数a，b满足f(2a＋b)＜1，那么b＋2a＋2的取值范围是 ()A．(13，12) B．(－∞，12)∪(3，＋∞)C．(12，3) D．(－∞，－3) 二、填空题(本大题共4小题，每题5分，共20分，请将答案填在题中的横线上。

完整版)导数大题练习带答案1.已知 $f(x)=x\ln x-ax$，$g(x)=-x^2-2$，要求实数 $a$ 的取值范围。

Ⅰ）对于所有 $x\in(0,+\infty)$，都有 $f(x)\geq g(x)$，即$x\ln x-ax\geq -x^2-2$，整理得 $a\leq \ln x +\frac{x}{2}$，对于 $x\in(0,+\infty)$，$a$ 的取值范围为 $(-\infty。

+\infty)$。

Ⅱ）当 $a=-1$ 时，$f(x)=x\ln x+x$，求 $f(x)$ 在 $[m。

m+3]$ 上的最值。

$f'(x)=\ln x+2$，令 $f'(x)=0$，解得 $x=e^{-2}$，在 $[m。

m+3]$ 上，$f(x)$ 单调递增，所以最小值为$f(m)=me^{m}$。

Ⅲ）证明：对于所有 $x\in(0,+\infty)$，都有 $\lnx+1>\frac{1}{x}$。

证明：$f(x)=\ln x+1-\frac{1}{x}$，$f'(x)=\frac{1}{x}-\frac{1}{x^2}=\frac{1}{x^2}(x-1)>0$，所以$f(x)$ 在 $(0,+\infty)$ 上单调递增，即对于所有$x\in(0,+\infty)$，都有 $\ln x+1>\frac{1}{x}$。

2.已知函数 $f(x)=\frac{2}{x}+a\ln x-2(a>0)$。

Ⅰ）若曲线 $y=f(x)$ 在点 $P(1,f(1))$ 处的切线与直线$y=x+2$ 垂直，求函数 $y=f(x)$ 的单调区间。

$f'(x)=-\frac{2}{x^2}+a$，在点 $P(1,f(1))$ 处的切线斜率为 $f'(1)=a-2$，由于切线垂直于直线 $y=x+2$，所以 $a-2=-\frac{1}{1}=-1$，解得 $a=1$。

C.2
D. 3
2
13.对于三次函数 f (x) ax3 bx2 cx d （ a 0 ），定义：设 f (x) 是函数 y f (x) 的
导数，若方程 f (x) 0 有实数解 x0，则称点（x0，（f x0））为函数 y f (x) 的“拐点”．有
同学发现:“任何一个三次函数都有‘拐点’；任何一个三次函数都有对称中心；且‘拐点’
)
99
A. a b c
B. c > b > a
C. c > a > b
D. a > c > b
10. f (x)是函数f (x)的导函数, 将y f (x)和y f (x) 的图象画在同一直角坐标系中，不
可能正确的是
()
11.已知函数 y xf (x) 的图象如图 3 所示（其中 f (x) 是函数 f (x) 的导函数）．下面四个图 象中， y f (x) 的图象大致是（ ）
常数 为方程 f (x) = x 的实数根。 (1) 求证：当 x > 时，总有 x > f (x) 成立； (2) 对任意 x1、x2 若满足| x1－ | < 1,| x2－ | < 1,求证：| f (x1)－f (x2)| < 2.
25.（本小题满分 12 分）
已知函数 f (x) ax3 bx2 ，当 x 1 时，有极大值 3 ；
f
( ) ， f 3
(x ) 为 f(x)的导函数，令 a＝
12，b＝log32，则下列关系
正确的是( )
A．f(a)>f(b) B．f(a)<f(b)
C．f(a)＝f(b)
D．f(|a|)<f(b)
16.设在函数 y x sin x cos x 的图象上的点 x0, y0 处的切线斜率为 k，若 k g x0 ，则

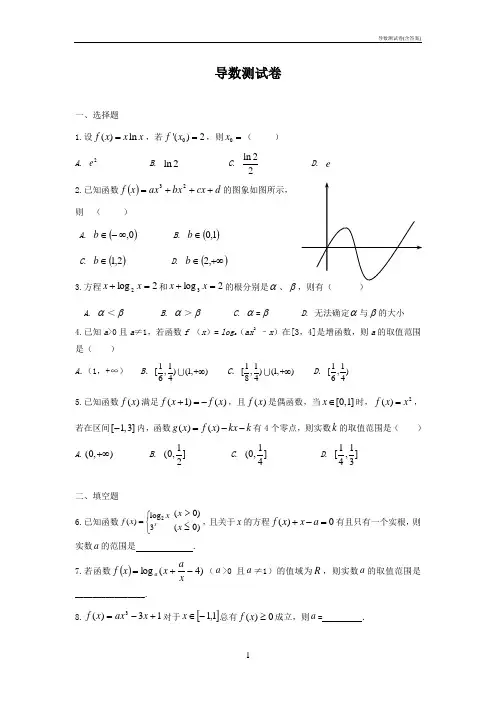
导数测试卷一、选择题1.设()ln f x x x =，若0'()2f x =，则0x =（ ）A . 2eB . ln 2C .ln 22D . e2.已知函数()d cx bx ax x f +++=23的图象如图所示，则 （ ）A . ()0,∞-∈bB . ()1,0∈bC . ()2,1∈bD . ()+∞∈,2b3.方程2log 2=+x x 和2log 3=+x x 的根分别是α、β A . α＜β B . α＞β C . α=β D . 无法确定α与β的大小4.已知a >0且a ≠1，若函数f （x ）= log a （ax 2–x ）在[3，4]是增函数，则a 的取值范围是（ ）A ．（1，+∞）B ．11[,)(1,)64+∞C ．11[,)(1,)84+∞D ．11[,)64 5.已知函数()f x 满足(1)()f x f x +=-，且()f x 是偶函数，当[0,1]x ∈时，2()f x x =，若在区间[1,3]-内，函数()()g x f x kx k =--有4个零点，则实数k 的取值范围是（ ）A .(0,)+∞B . 1(0,]2C . 1(0,]4D . 11[,]43二、填空题6.已知函数⎩⎨⎧=xx x f 3log )(2)0()0(≤>x x ，且关于x 的方程0)(=-+a x x f 有且只有一个实根，则实数a 的范围是 ． 7.若函数())4(log -+=xax x f a （a >0且a ≠1）的值域为R ，则实数a 的取值范围是________________.8.13)(3+-=x ax x f 对于[]1,1-∈x 总有0)(≥x f 成立，则a = ．9.已知函数3()(1).1axf x a a -=≠- （1）若a ＞0,则()f x 的定义域是 ；（2）若()f x 在区间(]0,1上是减函数，则实数a 的取值范围是 .10.已知函数()f x 的定义域为[]15,-，部分对应值如下表, ()f x 的导函数()y f x '=的图象如图所示. 下列关于()f x 的命题：①函数()f x 的极大值点为0，4； ②函数()f x 在[]02,上是减函数；③如果当[]1x ,t ∈-时，()f x 的最大值是2，那么t 的最大值为4； ④当12a <<时，函数()y f x a =-有4个零点； ⑤函数()y f x a =-的零点个数可能为0、1、2、3、4个． 其中正确命题的序号是 ．三、解答题11.已知函数)(21)1ln()(2R m x x m x f ∈-+=，满足.1)0(='f （1）求函数)(x f 的单调区间； （2）若关于x 的方程c x x x f ++-=243)(在[0，2]恰有两个不同的实根，求实数c 的取值范围。

导数及其应用一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符号题目要求的。

)1．(2011·烟台调研)三次函数f(x)＝mx 3－x 在(－∞，＋∞)上是减函数，则m 的取值范围是( )A ．m<0B ．m<1C ．m≤0D ．m≤1[答案] A[解析] f′(x)＝3mx 2－1，由条件知f′(x)≤0在(－∞，＋∞)上恒成立，∴⎩⎪⎨⎪⎧m<0Δ＝12m≤0，∴m<0，故选A.2．(文)(2011·山东淄博一中期末)曲线y ＝13x 3＋x 在点⎝ ⎛⎭⎪⎫1，43处的切线与坐标轴围成的三角形面积为( )A ．1 B.19 C.13 D.23[答案] B[解析] ∵y′＝x 2＋1，∴曲线y ＝13x 3＋x 在点(1，43)处的切线斜率k ＝y′|x ＝1＝1＋1＝2，∴k ＝2，切线方程为y －43＝2(x －1)，即6x －3y －2＝0，令x ＝0得y ＝－23，令y ＝0得x ＝13，∴S ＝12×13×23＝19.(理)(2011·辽宁沈阳二中检测)由曲线xy ＝1，直线y ＝x ，y ＝3所围成的平面图形的面积为( )A.329B ．2－ln3C ．4＋ln3D ．4－ln3[答案] D[解析] 如图，平面图形的面积为⎠⎛13⎝ ⎛⎭⎪⎫y －1y dy ＝[12y 2－lny]|31＝4－ln3.[点评] 本题考查定积分求曲边形的面积，关键是根据定积分的几何意义把求解的面积归结为函数在区间上的定积分，再根据微积分基本定理求解．在把曲边形面积转化为定积分时，可以以x 为积分变量、也可以以y 为积分变量，如果是以x 为积分变量，则被积函数是以x 为自变量的函数，如果是以y 为积分变量，则被积函数是以y 为自变量的函数．本题如果是以x 为积分变量，则曲边形ABC 的面积是不如以y 为积分变量简明．3．(文)(2011·陕西咸阳模拟)已知函数f(x)＝ax 2－1的图像在点A(1，f(1))处的切线l 与直线8x －y ＋2＝0平行，若数列⎩⎨⎧⎭⎬⎫1f n 的前n 项和为S n ，则S 2010的值为( ) A.20102011 B.10052011 C.40204021D.20104021[答案] D[解析] ∵f′(x)＝2ax ，∴f(x)在点A 处的切线斜率为f′(1)＝2a ，由条件知2a ＝8，∴a ＝4，∴f(x)＝4x 2－1，∴1f n ＝14n 2－1＝12n －1·12n ＋1＝12⎝ ⎛⎭⎪⎫12n －1－12n ＋1∴数列⎩⎨⎧⎭⎬⎫1f n 的前n 项和S n ＝1f 1＋1f 2＋…＋1f n ＝12⎝ ⎛⎭⎪⎫1－13＋12⎝ ⎛⎭⎪⎫13－15＋…＋12⎝ ⎛⎭⎪⎫12n －1－12n ＋1 ＝12⎝ ⎛⎭⎪⎫1－12n ＋1＝n 2n ＋1，∴S 2010＝20104021. (理)(2011·辽宁丹东四校联考)设函数f(x)＝ax 2＋b(a≠0)，若⎠⎛03f(x)dx ＝3f(x 0)，则x 0＝( )A ．±1 B. 2 C ．± 3 D ．2[答案] C[解析] ⎠⎛03f(x)dx ＝⎠⎛03(ax 2＋b)dx＝⎪⎪⎪⎝ ⎛⎭⎪⎫13ax 3＋bx 30＝9a ＋3b. 由⎠⎛03f(x)dx ＝3f(x 0)得，9a ＋3b ＝3ax 20＋3b ， ∴x 20＝3，∴x 0＝± 3.4．(文)(2011·山西太原调研)曲线y ＝x 3－3x 2＋1在点(－1，－3)处的切线与坐标轴所围成的封闭图形的面积为( )A ．2B ．3C ．4D ．5[答案] A[解析] y′|x ＝－1＝(3x 2－6x)|x ＝－1＝9，∴切线方程为y ＋3＝9(x ＋1)，即9x －y ＋6＝0，令x ＝0得y ＝6，令y ＝0得x ＝－23，∴所求面积S ＝12×6×23＝2，故选A.(理)(2011·宁夏银川一中检测)求曲线y ＝x 2与y ＝x 所围成图形的面积，其中正确的是( )A ．S ＝⎠⎛01(x 2－x)dxB ．S ＝⎠⎛01(x －x 2)dxC ．S ＝⎠⎛01(y 2－y)dy D ．S ＝⎠⎛01(y －y)dy[答案] B[分析] 根据定积分的几何意义，确定积分上、下限和被积函数．[解析] 两函数图象的交点坐标是(0,0)，(1,1)，故积分上限是1，下限是0，由于在[0,1]上，x≥x 2，故函数y ＝x 2与y ＝x 所围成图形的面积S ＝⎠⎛01(x －x 2)dx.5．(2011·福州市期末、河北冀州期末)已知实数a 、b 、c 、d 成等比数列，且函数y ＝ln(x ＋2)－x 当x ＝b 时取到极大值c ，则ad 等于( )A ．－1B ．0C ．1D ．2[答案] A[分析] 利用导数可求b 、c ，由a 、b 、c 、d 成等比数列可得ad ＝bc.[解析] y′＝1x ＋2－1，令y′＝0得x ＝－1，当－2<x<－1时，y′>0，当x>－1时，y′<0，∴b ＝－1，c ＝ln(－1＋2)－(－1)＝1，∴ad ＝bc ＝－1，故选A.6．(2011·黄冈市期末)设a ∈R ，函数f(x)＝e x＋a·e －x的导函数是f′(x)，且f′(x)是奇函数，若曲线y ＝f(x)的一条切线的斜率是32，则切点的横坐标为( )A ．－ln22B ．－ln2C ．ln2 D.ln22[答案] C[解析] ∵f′(x)＝e x－ae －x为奇函数，∴a ＝1，设切点为P(x 0，y 0)，则f′(x 0)＝ex 0－e －x 0＝32，∴ex 0＝2，∴x 0＝ln2.7．(2011·日照调研)下列图象中，有一个是函数f(x)＝13x 3＋ax 2＋(a 2－1)x ＋1(a ∈R ，a≠0)的导数f′(x)的图象，则f(－1)的值为( )A.13 B ．－13C.73 D ．－13或53[答案] B[解析] f′(x)＝x 2＋2ax ＋a 2－1，其图象为开口向上的抛物线，故不是第一个图；第二个图中，a ＝0，f ′(x)＝x 2－1，但已知a≠0，故f′(x)的图象为第三个图，∴f′(0)＝0，∴a ＝±1，又其对称轴在y 轴右边，∴a ＝－1，∴f(x)＝13x 3－x 2＋1，∴f(－1)＝－13，故选B.8．(2011·潍坊一中期末)设f′(x)是函数f(x)的导函数，将y ＝f(x)和y ＝f′(x)的图象画在同一个直角坐标系中，不可能正确的是( )[答案] D[解析] A 中，当f(x)为二次函数时，f′(x)为一次函数，由单调性和导数值的符号关系知A 可以是正确的，同理B 、C 都可以是正确的，但D 中f(x)的单调性为增、减、增，故f′(x)的值应为正负正，因此D 一定是错误的．9．(2011·北京学普教育中心)若函数f(x)＝2x 2－lnx 在其定义域内的一个子区间(k －1，k ＋1)内不是．．单调函数，则实数k 的取值范围是( ) A ．[1，＋∞) B ．[1，32)C ．[1,2)D ．[32，2)[答案] B[解析] 因为f(x)定义域为(0，＋∞)，f′(x)＝4x －1x ，由f′(x)＝0，得x ＝12.据题意，⎩⎪⎨⎪⎧k －1<12<k ＋1k －1≥0，解得1≤k<32，选B.10．(2011·江西吉安质检)已知曲线方程f(x)＝sin 2x ＋2ax(a ∈R)，若对任意实数m ，直线l ：x ＋y ＋m ＝0都不是曲线y ＝f(x)的切线，则a 的取值范围是( )A ．(－∞，－1)∪(－1,0)B ．(－∞，－1)∪(0，＋∞)C ．(－1,0)∪(0，＋∞)D ．a ∈R 且a≠0，a≠－1[答案] B[解析] 若存在实数m ，使直线l 是曲线y ＝f(x)的切线，∵f′(x)＝2sinxcosx ＋2a ＝sin2x ＋2a ，∴方程sin2x ＋2a ＝－1有解，∴－1≤a≤0，故所求a 的取值范围是(－∞，－1)∪(0，＋∞)，选B.11．(2011·彭州中学月考)若关于x 的不等式x 3－3x 2－9x ＋2≥m 对任意x ∈[－2,2]恒成立，则m 的取值范围是( )A ．(－∞，7]B ．(－∞，－20]C ．(－∞，0]D ．[－12,7][答案] B[解析] 令f(x)＝x 3－3x 2－9x ＋2，则f ′(x)＝3x 2－6x －9，令f ′(x)＝0得x ＝－1或x ＝3(舍去)．∵f(－1)＝7，f(－2)＝0，f(2)＝－20. ∴f(x)的最小值为f(2)＝－20， 故m≤－20，综上可知应选B.12．(2011·蚌埠二中质检)定义在R 上的函数f(x)满足f(4)＝1，f′(x)为f(x)的导函数，已知函数y ＝f′(x)的图象如图所示．若两正数a ，b 满足f(2a ＋b)<1，则b ＋2a ＋2的取值范围是( )A.⎝ ⎛⎭⎪⎫13，12B.⎝⎛⎭⎪⎫－∞，12∪(3，＋∞) C.⎝ ⎛⎭⎪⎫12，3 D ．(－∞，－3)[答案] C[解析] 由y ＝f′(x)的图象知，x>0时，f′(x)>0，x<0时，f′(x)<0，∴y ＝f(x)在(－∞，0)上单调递减，在(0，＋∞)上单调递增，∵两正数a ，b 满足f(2a ＋b)<1且f(4)＝1，∴2a ＋b<4，如图，b ＋2a ＋2表示点A(－2，－2)与线段BC 上的点连线的斜率，其中B(2,0)，C(0,4)，∵k AB ＝12，k AC ＝3，a>0，b>0，∴12<b ＋2a ＋2<3.第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题，每小题4分，共16分，把正确答案填在题中横线上) 13．(2011·四川广元诊断)曲线y ＝xe x＋2x ＋1在点(0,1)处的切线方程为________． [答案] y ＝3x ＋1[解析] y′＝e x＋xe x＋2，y′|x ＝0＝3，∴切线方程为y －1＝3(x －0)，即y ＝3x ＋1. 14．(文)(2011·广东省高州长坡中学期末)函数f(x)＝1＋log 2x ，f(x)的反函数为g(x)，则g′(2)＝________.[答案] 2ln2[解析] 由y ＝1＋log 2x 得x ＝2y －1，∴f(x)的反函数为g(x)＝2x －1，∴g′(x)＝2x －1ln2，∴g′(2)＝2ln2.(理)(2011·辽宁沈阳二中检测)如图，函数y ＝f(x)的图象在点P 处的切线方程是y ＝－x ＋8，则f(5)＋f′(5)＝________.[答案] 2[解析] f(5)＋f′(5)＝(－5＋8)＋(－1)＝2.15．(文)函数y ＝13x 3－ax 2＋x －2a 在R 上不是单调函数，，则a 的取值范围是________．[答案] (－∞，－1)∪(1，＋∞)[解析] y′＝x 2－2ax ＋1，若函数在R 上单调，应有y′≥0恒成立，∴4a 2－4≤0，∴a 2≤1，∴－1≤a≤1，因此所求a 的取值范围是(－∞，－1)∪(1，＋∞)．(理)(2011·安徽巢湖质检)定积分⎠⎛12|3－2x|dx ＝________[答案] 12[解析] ⎠⎛12|3－2x|dx ＝2⎠⎛21.5(2x －3)dx ＝2(x 2－3x)|21.5＝2×14＝12.16．(2011·湖南长沙一中期末)对于三次函数f(x)＝ax 3＋bx 2＋cx ＋d(a≠0)，定义：设f″(x)是函数y ＝f(x)的导数y ＝f′(x)的导数，若方程f″(x)＝0有实数解x 0，则称点(x 0，f(x 0))为函数y ＝f(x)的“拐点”．有同学发现“任何一个三次函数都有‘拐点’；任何一个三次函数都有对称中心；且‘拐点’就是对称中心．”请你将这一发现为条件，求(1)函数f(x)＝x 3－3x 2＋3x 对称中心为________．(2)若函数g(x)＝13x 3－12x 2＋3x －512＋1x －12，则g ⎝ ⎛⎭⎪⎫12011＋g ⎝ ⎛⎭⎪⎫22011＋g ⎝ ⎛⎭⎪⎫32011＋g ⎝ ⎛⎭⎪⎫42011＋…＋g ⎝⎛⎭⎪⎫20102011＝________.[答案] (1)(1,1) (2)2010[解析] (1)f′(x)＝3x 2－6x ＋3，f″(x)＝6x －6，令6x －6＝0得x ＝1，f(1)＝1，∴f(x)的对称中心为(1,1)．(2)令h(x)＝13x 3－12x 2＋3x －512，k(x)＝1x －12，h′(x)＝x 2－x ＋3，h″(x)＝2x －1，由2x －1＝0得x ＝12，h ⎝ ⎛⎭⎪⎫12＝13×⎝ ⎛⎭⎪⎫123－12×⎝ ⎛⎭⎪⎫122＋3×12－512＝1，∴h(x)的对称中心为⎝ ⎛⎭⎪⎫12，1，∴h(x)＋h(1－x)＝2，x ＝12011，22011，…，20102011.又k(x)的对称中心为⎝ ⎛⎭⎪⎫12，0， ∴k(x)＋k(1－x)＝0，x ＝12011，22011，…，20102011.∴g ⎝ ⎛⎭⎪⎫12011＋g ⎝ ⎛⎭⎪⎫22011＋…＋g ⎝ ⎛⎭⎪⎫20102011＝h ⎝ ⎛⎭⎪⎫12011＋h ⎝ ⎛⎭⎪⎫22011＋…＋h ⎝ ⎛⎭⎪⎫20102011＋k ⎝ ⎛⎭⎪⎫12011＋k ⎝⎛⎭⎪⎫22011＋…＋k ⎝ ⎛⎭⎪⎫20102011＝2010. 三、解答题(本大题共6个小题，共74分，解答应写出文字说明，证明过程或演算步骤) 17．(本小题满分12分)(文)(2011·山西太原调研)已知函数f(x)＝13x 3－ax 2＋(a 2－1)x＋b(a ，b ∈R)，其图象在点(1，f(1))处的切线方程为x ＋y －3＝0.(1)求a ，b 的值；(2)求函数f(x)的单调区间，并求出f(x)在区间[－2,4]上的最大值． [解析] (1)f′(x)＝x 2－2ax ＋a 2－1， ∵(1，f(1))在x ＋y －3＝0上，∴f(1)＝2， ∵(1,2)在y ＝f(x)上，∴2＝13－a ＋a 2－1＋b ，又f′(1)＝－1，∴a 2－2a ＋1＝0， 解得a ＝1，b ＝83.(2)∵f(x)＝13x 3－x 2＋83，∴f′(x)＝x 2－2x ，由f′(x)＝0可知x ＝0和x ＝2是f(x)的极值点，所以有，＋∞)，单调递减区间是(0,2)∵f(0)＝83，f(2)＝43，f(－2)＝－4，f(4)＝8，∴在区间[－2,4]上的最大值为8.(理)(2011·淄博期末)定义在R 上的函数f(x)＝ax 3＋bx 2＋cx ＋3同时满足以下条件：①f(x)在(0,1)上是减函数，在(1，＋∞)上是增函数；②f′(x)是偶函数；③f(x)在x ＝0处的切线与直线y ＝x ＋2垂直．(1)求函数y ＝f(x)的解析式；(2)设g(x)＝lnx －mx ，若存在实数x ∈[1，e]，使g(x)<f′(x)，求实数m 的取值范围．[解析] (1)f′(x)＝3ax 2＋2bx ＋c ，∵f(x)在(0,1)上是减函数，在(1，＋∞)上是增函数，∴f′(1)＝3a ＋2b ＋c ＝0① 由f′(x)是偶函数得：b ＝0②又f(x)在x ＝0处的切线与直线y ＝x ＋2垂直，f′(0)＝c ＝－1③ 由①②③得：a ＝13，b ＝0，c ＝－1，即f(x)＝13x 3－x ＋3.(2)由已知得：存在实数x ∈[1，e]，使lnx －m x <x 2－1即存在x ∈[1，e]，使m>xlnx －x 3＋x设M(x)＝xlnx －x 3＋x x ∈[1，e]，则M′(x)＝lnx －3x 2＋2设H(x)＝lnx －3x 2＋2，则H′(x)＝1x －6x ＝1－6x2x∵x ∈[1，e]，∴H′(x)<0，即H(x)在[1，e]上递减 于是，H(x)≤H(1)，即H(x)≤－1<0，即M′(x)<0 ∴M(x)在[1，e]上递减，∴M(x)≥M(e)＝2e －e 3于是有m>2e －e 3为所求．18．(本小题满分12分)(2011·四川资阳模拟)函数f(x)＝ax 3－6ax 2＋3bx ＋b ，其图象在x ＝2处的切线方程为3x ＋y －11＝0.(1)求函数f(x)的解析式；(2)若函数y ＝f(x)的图象与y ＝13f′(x)＋5x ＋m 的图象有三个不同的交点，求实数m的取值范围；(3)是否存在点P ，使得过点P 的直线若能与曲线y ＝f(x)围成两个封闭图形，则这两个封闭图形的面积相等？若存在，求出P 点的坐标；若不存在，说明理由．[解析] (1)由题意得f′(x)＝3ax 2－12ax ＋3b ， ∵f′(2)＝－3且f(2)＝5，∴⎩⎪⎨⎪⎧12a －24a ＋3b ＝－3，8a －24a ＋6b ＋b ＝5，即⎩⎪⎨⎪⎧4a －b ＝1，－16a ＋7b ＝5，解得a ＝1，b ＝3，∴f(x)＝x 3－6x2＋9x ＋3.(2)由f(x)＝x 3－6x 2＋9x ＋3可得，f′(x)＝3x 2－12x ＋9，13f′(x)＋5x ＋m ＝13(3x 2－12x＋9)＋5x ＋m ＝x 2＋x ＋3＋m ，则由题意可得x 3－6x 2＋9x ＋3＝x 2＋x ＋3＋m 有三个不相等的实根， 即g(x)＝x 3－7x 2＋8x －m 的图象与x 轴有三个不同的交点，g′(x)＝3x 2－14x ＋8＝(3x －2)(x －4)，则g(x)，g′(x)的变化情况如下表.则函数f(x)的极大值为g ⎝ ⎭⎪⎫3＝27－m ，极小值为g(4)＝－16－m.y ＝f(x)的图象与y ＝13f′(x)＋5x ＋m 的图象有三个不同交点，则有⎩⎪⎨⎪⎧g ⎝ ⎛⎭⎪⎫23＝6827－m>0，g 4＝－16－m<0，解得－16<m<6827.(3)存在点P 满足条件．∵f(x)＝x 3－6x 2＋9x ＋3，∴f′(x)＝3x 2－12x ＋9＝3(x －1)(x －3)，由f′(x)＝0，得x 1＝1，x 2＝3.当x<1时，f′(x)>0；当1<x<3时，f′(x)<0；当x>3时，f′(x)>0.可知极值点为A(1,7)，B(3,3)，线段AB 中点P(2,5)在曲线y ＝f(x)上，且该曲线关于点P(2,5)成中心对称．证明如下：∵f(x)＝x 3－6x 2＋9x ＋3，∴f(4－x)＝(4－x)3－6(4－x)2＋9(4－x)＋3 ＝－x 3＋6x 2－9x ＋7，∴f(x)＋f(4－x)＝10，上式表明，若点A(x ，y)为曲线y ＝f(x)上任一点，其关于P(2,5)的对称点A(4－x,10－y)也在曲线y ＝f(x)上，曲线y ＝f(x)关于点P(2,5)对称．故存在点P(2,5)，使得过该点的直线若能与曲线y ＝f(x)围成两个封闭图形，则这两个封闭图形的面积相等．19．(本小题满分12分)(2011·烟台调研)已知函数f(x)＝ax 3＋bx 2的图象经过点M(1,4)，曲线在点M 处的切线恰好与直线x ＋9y ＝0垂直，(1)求实数a 、b 的值；(2)若函数f(x)在区间[m ，m ＋1]上单调递增，求m 的取值范围． [解析] (1)∵f(x)＝ax 3＋bx 2的图象经过点M(1,4)， ∴a ＋b ＝4.①f′(x)＝3ax 2＋2bx ，则f′(1)＝3a ＋2b ， 由条件f′(1)·(－19)＝－1，即3a ＋2b ＝9，②由①②式解得a ＝1，b ＝3.(2)f(x)＝x 3＋3x 2，f′(x)＝3x 2＋6x ， 令f′(x)＝3x 2＋6x≥0得x≥0或x≤－2，∴f(x)的单调递增区间为(－∞，－2]和[0，＋∞)由条件知m≥0或m ＋1≤－2， ∴m≥0或m≤－3.20．(本小题满分12分)(2011·厦门期末)已知函数f(x)＝1＋alnxx ，(a ∈R)．(1)若函数f(x)在x ＝1处取得极值，求实数a 的值；(2)在(1)条件下，若直线y ＝kx 与函数y ＝f(x)的图象相切，求实数k 的值． [解析] (1)∵f(x)＝1＋alnxx，∴f′(x)＝ax ·x－1＋alnx x 2＝a －1－alnxx 2， ∵函数f(x)在x ＝1处取得极值，∴f′(1)＝a －1＝0， ∴a ＝1经检验，a ＝1时，函数f(x)在x ＝1处取得极值．(2)由(1)可知，a ＝1，∴f(x)＝1＋lnx x ，∴f′(x)＝－lnxx ，设切点A ⎝ ⎛⎭⎪⎫x 0，1＋lnx 0x 0，∴k ＝f′(x 0)＝－lnx 0x 20 又k ＝k OA ＝1＋lnx 0x 20，∴1＋lnx 0x 20＝－lnx 0x 20， ∴lnx 0＝－12，∴x 0＝e －12，∴k ＝e2.21．(本小题满分12分)(2011·华安、连城、永安、漳平、龙海、泉港六校联考)已知函数f(x)＝x 3＋ax 2＋b 的图象在点P(1,0)处的切线与直线3x ＋y ＝0平行．(1)求常数a ，b 的值；(2)求函数f(x)在区间[0，m]上的最小值和最大值(m>0)． [解析] (1)f′(x)＝3x 2＋2ax f′(1)＝3＋2a ＝－3，∴a ＝－3 f(1)＝a ＋b ＋1＝0，∴b ＝2.(2)f(x)＝x 3－3x 2＋2，f′(x)＝3x 2－6x令f′(x)＝0得，x 1＝0，x 2＝2，当x<0或x>2时，f′(x)>0，当0<x<2时，f′(x)<0， ∴f(x)增区间为(－∞，0)和(2，＋∞)，减区间为(0,2)， f(0)＝2，令f(x)＝x 3－3x 2＋2＝2得x ＝0或x ＝3. ∴f(0)＝f(3)＝2， ①当0≤m≤2时f(x)min ＝f(m)＝m 3－3m 2＋2 f(x)max ＝f(0)＝2 ②当2<m≤3时 f(x)min ＝f(2)＝－2 f(x)max ＝f(0)＝2 ③当m>3时 f(x)min ＝f(2)＝－2 f(x)max ＝f(m)＝m 3－3m 2＋2.22．(本小题满分12分)(文)已知函数f(x)＝x 3－3ax 2－3a 2＋a(a>0)． (1)求函数f(x)的单调区间；(2)若曲线y ＝f(x)上有两点A(m ，f(m))、B(n ，f(n))处的切线都与y 轴垂直，且函数y ＝f(x)在区间[m ，n]上存在零点，求实数a 的取值范围．[解析] (1)f′(x)＝3x 2－6ax ＝3x(x －2a)．令f′(x)＝0，得x 1＝0，x 2＝2a 列表如下：由上表可知，函数的单调递增区间为(－∞，(0,2a)．(2)由(1)可知，m ＝0，n ＝2a 且在x ＝0，x ＝2a 处分别取得极值． f(0)＝－3a 2＋a ，f(2a)＝－4a 3－3a 2＋a. 由已知得函数y ＝f(x)在区间[0,2a]上存在零点， ∴f(0)×f(2a)≤0即(－3a 2＋a)(－4a 3－3a 2＋a)≤0 ∴a 2(3a －1)(4a －1)(a ＋1)≤0 ∵a>0∴(3a －1)(4a －1)≤0，解得14≤a≤13故实数a 的取值范围是[14，13]．(理)(2011·北京学普教育中心联考版)已知函数f(x)＝x 2＋ax －lnx ，a ∈R ； (1)若函数f(x)在[1,2]上是减函数，求实数a 的取值范围；(2)令g(x)＝f(x)－x 2，是否存在实数a ，当x ∈(0，e](e 是自然对数的底数)时，函数g(x)的最小值是3，若存在，求出a 的值；若不存在，说明理由．[解析] f′(x)＝2x ＋a －1x ＝2x 2＋ax －1x ≤0在[1,2]上恒成立令h(x)＝2x 2＋ax －1，x ∈[1,2]，∴h(x)≤0在[1,2]上恒成立∴⎩⎪⎨⎪⎧h 1＝1＋a≤0h 2＝7＋2a≤0得⎩⎪⎨⎪⎧a≤－1a≤－72，∴a≤－72.(2)假设存在实数a ，使g(x)＝f(x)－x 2，x ∈(0，e]有最小值3 g(x)＝ax －lnx ，x ∈(0，e]，g′(x)＝a －1x ＝ax －1x①当a≤0时，g′(x)<0，g(x)在(0，e]上单调递减 ∴g(x)min ＝g(e)＝ae －1＝3，∴a ＝4e(舍去)②当0<1a <e 即a>1e 时，在(0，1a )上，g′(x)<0；在(1a，e]上，g′(x)>0∴g(x)在(0，1a ]上单调递减，在(1a，e]上单调递增∴g(x)min ＝g ⎝ ⎛⎭⎪⎫1a ＝1＋lna ＝3，∴a ＝e 2满足条件③当1a ≥e 即0<a≤1e 时，g′(x)<0，g(x)在(0，e]上单调递减g(x)min ＝g(e)＝ae －1＝3 ∴a ＝4e >1e(舍去)综上所述，存在a ＝e 2使得当x ∈(0，e]时，g(x)有最小值3.。

【巩固练习】一、选择题1．设函数310()(12)f x x =-，则'(1)f =（ ）A ．0B ．―1C ．―60D ．602．（2014 江西校级一模）若2()2ln f x x x =-，则'()0f x >的解集为（ ）A.(0,1)B.()(),10,1-∞-C. ()()1,01,-+∞D.()1,+∞3．（2014春 永寿县校级期中）下列式子不正确的是（ ）A.()'23cos 6sin x x x x +=-B. ()'1ln 22ln 2x x x x -=- C. ()'2sin 22cos 2x x = D.'2sin cos sin x x x x x x -⎛⎫= ⎪⎝⎭ 4．函数4538y x x =+-的导数是（ ） A ．3543x + B ．0 C ．3425(43)(38)x x x ++- D ．3425(43)(38)x x x +-+- 5．（2015 安徽四模）已知函数()f x 的导函数为'()f x ，且满足关系式2'()3(2)ln f x x xf x =++，则'(2)f 的值等于（ ）A. 2B.-2C.94 D.94- 6．设曲线1(1)1x y x x +=≠-在点（3，2）处的切线与直线ax+y+1=0垂直，则a=（ ） A ．2 B ．12 C ．―12D ．―2 7．23log cos (cos 0)y x x =≠的导数是（ ）A ．32log tan e x -⋅B ．32log cot e x ⋅C ．32log cos e x -⋅D ．22log cos e x 二、填空题8．曲线y=sin x 在点,12π⎛⎫ ⎪⎝⎭处的切线方程为________。

9．设y=(2x+a)2，且2'|20x y ==，则a=________。

10．31sin x x '⎛⎫-= ⎪⎝⎭____________，()2sin 25x x '+=⎡⎤⎣⎦____________。

导数的测试题及答案一、选择题（每题5分，共20分）1. 函数f(x)=x^2的导数是：A. 2xB. x^2C. 2D. x答案：A2. 函数g(x)=sin(x)的导数是：A. cos(x)B. sin(x)C. xD. 1答案：A3. 函数h(x)=e^x的导数是：A. e^xB. e^(-x)C. xD. 1答案：A4. 函数k(x)=ln(x)的导数是：A. xB. 1/xC. ln(x)D. e^x答案：B二、填空题（每题5分，共20分）1. 函数f(x)=3x^2+2x-5的导数是______。

答案：6x+22. 函数g(x)=x^3-4x^2+7的导数是______。

答案：3x^2-8x3. 函数h(x)=1/x的导数是______。

答案：-1/x^24. 函数k(x)=sqrt(x)的导数是______。

答案：1/(2*sqrt(x))三、计算题（每题10分，共40分）1. 求函数f(x)=x^4-2x^3+3x^2-4x+5的导数。

答案：4x^3-6x^2+6x-42. 求函数g(x)=x^5+3x^4-2x^3+x^2-5的导数。

答案：5x^4+12x^3-6x^2+2x3. 求函数h(x)=e^(2x)-3e^x+2的导数。

答案：2e^(2x)-3e^x4. 求函数k(x)=ln(x^2)-2ln(x)+3的导数。

答案：2/x-2/x结束语：以上是导数的测试题及答案，希望同学们通过这些题目能够更好地理解和掌握导数的概念和计算方法。

《函数与导数》测试题一、选择题1.函数的单调递增区间是（ )A. B.（0,3） C.（1,4) D 。

解析 ，令，解得,故选D2。

已知直线y=x+1与曲线相切，则α的值为 （ ）A.1 B. 2 C 。

-1 D 。

-2 解:设切点，则,又。

故答案 选B 3。

已知函数在R 上满足，则曲线在点处的切线方程是（ )A. B 。

C. D 。

解析 由得几何,即，∴∴，∴切线方程，即选A4。

存在过点的直线与曲线和都相切，则等于（） A ．或 B ．或 C ．或 D ．或解析 设过的直线与相切于点，所以切线方程为即，又在切线上，则或，x e x x f )3()(-=)2,(-∞),2(+∞()()(3)(3)(2)x x x f x x e x e x e '''=-+-=-()0f x '>2x >y ln()x a =+00(,)P x y 0000ln 1,()y x a y x =+=+0'01|1x x y x a===+00010,12x a y x a ∴+=∴==-∴=()f x 2()2(2)88f x f x x x =--+-()y f x =(1,(1))f 21y x =-y x =32y x =-23y x =-+2()2(2)88f x f x x x =--+-2(2)2()(2)8(2)8f x f x x x -=--+--22()(2)44f x f x x x --=+-2()f x x =/()2f x x =12(1)y x -=-210x y --=(1,0)3y x =21594y ax x =+-a 1-25-641-21474-25-6474-7(1,0)3y x =300(,)x x 320003()y x x x x -=-230032y x x x =-(1,0)00x =032x =-当时，由与相切可得， 当时，由与相切可得,所以选. 5。

数学导数竞赛试题及答案试题一：求函数 \( f(x) = 3x^2 - 2x + 1 \) 的导数。

答案一：函数 \( f(x) = 3x^2 - 2x + 1 \) 的导数是 \( f'(x) = 6x - 2 \)。

试题二：若函数 \( g(x) = x^3 + 2x^2 - 5x + 7 \)，求 \( g'(2) \)。

答案二：首先求导得到 \( g'(x) = 3x^2 + 4x - 5 \)，然后代入 \( x = 2 \) 得到 \( g'(2) = 3(2)^2 + 4(2) - 5 = 12 + 8 - 5 = 15 \)。

试题三：求函数 \( h(t) = \ln(t) + t^2 \) 的导数。

答案三：函数 \( h(t) = \ln(t) + t^2 \) 的导数是 \( h'(t) = \frac{1}{t} + 2t \)。

试题四：若 \( k(\theta) = \theta^3 \sin(\theta) \)，求 \( k'(\pi/4) \)。

答案四：首先求导得到 \( k'(\theta) = 3\theta^2 \sin(\theta) +\theta^3 \cos(\theta) \)，然后代入 \( \theta = \pi/4 \) 得到\( k'(\pi/4) = 3(\pi/4)^2 \sin(\pi/4) + (\pi/4)^3 \cos(\pi/4) \)。

试题五：求函数 \( m(z) = z^4 - 4z^3 + 6z^2 \) 的导数。

答案五：函数 \( m(z) = z^4 - 4z^3 + 6z^2 \) 的导数是 \( m'(z) = 4z^3 - 12z^2 + 12z \)。

结束语：以上是数学导数竞赛的五道试题及其答案，希望对参赛者有所帮助。

导数是微积分中的一个重要概念，掌握其求解方法对于理解函数的局部变化和全局行为至关重要。