天津中考数学压轴题全搞定汇编

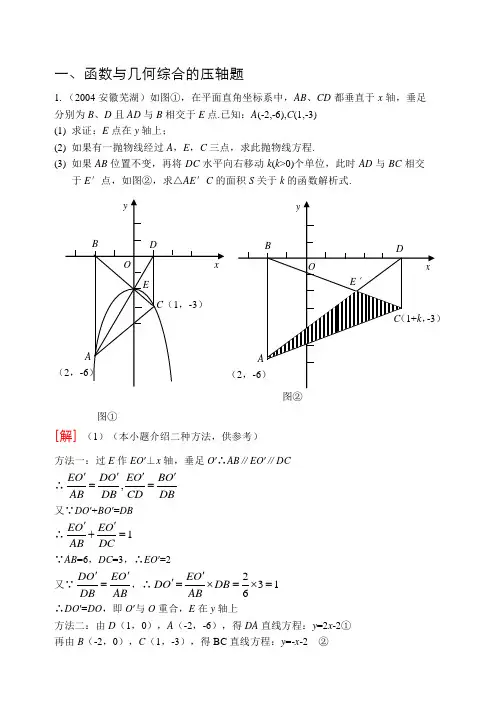
一、函数与几何综合的压轴题1.（2004安徽芜湖）如图①，在平面直角坐标系中，AB 、CD 都垂直于x 轴，垂足分别为B 、D 且AD 与B 相交于E 点.已知：A (-2,-6),C (1,-3) (1) 求证：E 点在y 轴上；(2) 如果有一抛物线经过A ，E ，C 三点，求此抛物线方程.(3) 如果AB 位置不变，再将DC 水平向右移动k (k >0)个单位，此时AD 与BC 相交于E ′点，如图②，求△AE ′C 的面积S 关于k 的函数解析式.[解] （1）（本小题介绍二种方法，供参考）方法一：过E 作EO ′⊥x 轴，垂足O ′∴AB ∥EO ′∥DC ∴,EO DO EO BO AB DB CD DB ''''==又∵DO ′+BO ′=DB ∴1EO EO AB DC''+= ∵AB =6，DC =3，∴EO ′=2又∵DO EO DB AB ''=，∴2316EO DO DB AB ''=⨯=⨯=∴DO ′=DO ，即O ′与O 重合，E 在y 轴上方法二：由D （1，0），A （-2，-6），得DA 直线方程：y =2x -2① 再由B （-2，0），C （1，-3），得BC 直线方程：y =-x -2 ②图①图②联立①②得02x y =⎧⎨=-⎩∴E 点坐标（0，-2），即E 点在y 轴上（2）设抛物线的方程y =ax 2+bx +c (a ≠0)过A （-2，-6），C （1，-3）E （0，-2）三点，得方程组42632a b c a b c c -+=-⎧⎪++=-⎨⎪=-⎩解得a =-1,b =0,c =-2 ∴抛物线方程y =-x 2-2（3）（本小题给出三种方法，供参考）由（1）当DC 水平向右平移k 后，过AD 与BC 的交点E ′作E ′F ⊥x 轴垂足为F 。

同（1）可得：1E F E FAB DC''+= 得：E ′F =2 方法一：又∵E ′F ∥AB E F DF AB DB '⇒=，∴13DF DB = S △AE ′C = S △ADC - S △E ′DC =11122223DC DB DC DF DC DB ∙-∙=∙=13DC DB ∙=DB=3+k S=3+k 为所求函数解析式方法二：∵ BA ∥DC ，∴S △BCA =S △BDA ∴S △AE ′C = S △BDE ′()1132322BD E F k k '=∙=+⨯=+ ∴S =3+k 为所求函数解析式.证法三：S △DE ′C ∶S △AE ′C =DE ′∶AE ′=DC ∶AB =1∶2同理：S △DE ′C ∶S △DE ′B =1∶2,又∵S △DE ′C ∶S △ABE ′=DC 2∶AB 2=1∶4 ∴()2213992AE C ABCD S S AB CD BD k '∆==⨯+∙=+梯形 ∴S =3+k 为所求函数解析式.2. （2004广东茂名）已知：如图，在直线坐标系中，以点M （1，0）为圆心、直径AC 为22的圆与y 轴交于A 、D 两点.（1）求点A 的坐标；（2）设过点A 的直线y ＝x ＋b 与x 轴交于点B.探究：直线AB 是否⊙M 的切线？并对你的结论加以证明；（3）连接BC ，记△ABC 的外接圆面积为S 1、⊙M 面积为S 2，若421hS S =，抛物线 y ＝ax 2＋bx ＋c 经过B 、M 两点，且它的顶点到x 轴的距离为h .求这条抛物线的解析式.[解]（1）解：由已知AM ＝2，OM ＝1，在Rt △AOM 中，AO ＝122=-OM AM ，∴点A 的坐标为A （0，1）（2）证：∵直线y ＝x ＋b 过点A （0，1）∴1＝0＋b 即b ＝1 ∴y ＝x ＋1 令y ＝0则x ＝－1 ∴B （—1，0），AB ＝2112222=+=+AO BO 在△ABM 中，AB ＝2，AM ＝2，BM ＝2222224)2()2(BM AM AB ==+=+∴△ABM 是直角三角形，∠BAM ＝90° ∴直线AB 是⊙M 的切线（3）解法一：由⑵得∠BAC ＝90°，AB ＝2，AC ＝22， ∴BC ＝10)22()2(2222=+=+AC AB∵∠BAC ＝90° ∴△ABC 的外接圆的直径为BC ，∴πππ25)210()2(221=∙=∙=BC S而πππ2)222()2(222=∙=∙=AC S421h S S = ，5,4225=∴=h h 即 ππ 设经过点B （—1，0）、M （1，0y ＝a （＋1）（x －1），（a≠0）即y ＝ax 2－a ，∴－a ＝±5，∴a ＝±5 ∴抛物线的解析式为y ＝5x 2－5或y ＝－5x 2＋5 解法二：（接上） 求得∴h ＝5由已知所求抛物线经过点B （—1，0）、M （1、0），则抛物线的对称轴是y 轴，由题意得抛物线的顶点坐标为（0，±5）∴抛物线的解析式为y ＝a （x －0）2±5又B （－1,0）、M （1,0）在抛物线上，∴a±5＝0， a ＝±5∴抛物线的解析式为 y ＝5x 2－5或y ＝－5x 2＋5 解法三：（接上）求得∴h ＝5因为抛物线的方程为y ＝ax 2＋bx ＋c （a≠0）由已知得⎪⎩⎪⎨⎧-===⎪⎩⎪⎨⎧==⎪⎪⎪⎩⎪⎪⎪⎨⎧±=-=+-=++5055c 0b 5544002c b a a ab ac c b a c b a 或 ＝－ 解得∴抛物线的解析式为 y ＝5x 2－5或y ＝－5x 2＋5.3.(2004湖北荆门)如图，在直角坐标系中，以点P （1，－1）为圆心，2为半径作圆，交x 轴于A 、B 两点，抛物线)0(2>++=a c bx ax y 过点A 、B ，且顶点C 在⊙P 上. (1)求⊙P 上劣弧⌒AB 的长； (2)求抛物线的解析式；(3)在抛物线上是否存在一点D ，使线段OC 与PD若不存在，请说明理由.[解] （1）如图，连结PB ，过P 作PM ⊥x 轴，垂足为在Rt △PMB 中，PB=2,PM=1, ∴∠MPB＝60°，∴∠APB ＝120° ⌒AB 的长＝342180120ππ=⋅⋅︒︒ （2）在Rt △PMB 中，PB=2,PM=1,则MB ＝MA ＝3. 又OM=1，∴A （1－3，0），B （1＋3，0）， 由抛物线及圆的对称性得知点C 在直线PM 上， 则C(1，－3).点A 、B 、C 在抛物线上，则⎪⎪⎩⎪⎪⎨⎧++=-+-+-=++++=c b a c b a c b a 3)31()31(0)31()31(022 解之得⎪⎩⎪⎨⎧-=-==221c b a ∴抛物线解析式为222--=x x y（3）假设存在点D ，使OC 与PD 互相平分，则四边形OPCD 为平行四边形，且PC ∥OD.又PC ∥y 轴，∴点D 在y 轴上，∴OD ＝2，即D （0，－2）.又点D （0，－2）在抛物线222--=x x y 上，故存在点D （0，－2）， 使线段OC 与PD 互相平分.4.（2004湖北襄樊）如图，在平面直角坐标系内，Rt △ABC 的直角顶点C （0在y 轴的正半轴上，A 、B 是x 轴上是两点，且OA ∶OB ＝3∶1，以OA 、OB 为直径的圆分别交AC 于点E ，交BC 于点F .直线EF 交OC 于点Q . （1）求过A 、B 、C 三点的抛物线的解析式；（2）请猜想：直线EF 与两圆有怎样的位置关系？并证明你的猜想.（3）在△AOC 中，设点M 是AC 边上的一个动点，过M 作MN ∥AB 交OC 于点N .试问：在x 轴上是否存在点P ，使得△PMN 是一个以MN 为一直角边的等腰直角三角形？若存在，求出P[解] (1)在Rt △ABC 中，OC ⊥AB ，∴△AOC ≌△COB .∴OC 2＝OA ·OB . ∵OA ∶OB ＝3∶1,C ∴23.OB OB = ∴OB ＝1.∴OA ＝3.∴A (-3,0),B (1,0).设抛物线的解析式为2.y ax bx c =++则930,0,a b c a b c c ⎧-+=⎪++=⎨⎪=⎩解之，得a b c ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩∴经过A 、B 、C三点的抛物线的解析式为23y x =-- (2)EF 与⊙O 1、⊙O 2都相切.证明：连结O 1E 、OE 、OF .∵∠ECF ＝∠AEO ＝∠BFO ＝90°, ∴四边形EOFC 为矩形. ∴QE ＝QO . ∴∠1＝∠2.∵∠3＝∠4,∠2+∠4＝90°， ∴EF 与⊙O 1相切. 同理：EF 理⊙O 2相切.(3)作MP ⊥OA 于P ，设MN ＝a ,由题意可得MP ＝MN ＝a . ∵MN ∥OA ,∴△CMN ∽△CAO .∴.MN CNAO CO =∴3a =解之，得a =此时，四边形OPMN 是正方形.∴3.2MN OP ==∴3(,0).2P -考虑到四边形PMNO 此时为正方形，∴点P 在原点时仍可满足△PNN 是以MN 为一直角边的等腰直角三角形.故x 轴上存在点P 使得△PMN 是一个以MN为一直角边的等腰直角三角形且3(,0)2P -或(0,0).P 5.（2004湖北宜昌）如图，已知点A(0，1)、C(4，3)、E(415，823)，P 是以AC 为对角线的矩形ABCD 内部(不在各边上)的—个动点，点D 在y 轴，抛物线y ＝ax 2+b x +1以P 为顶点．(1)说明点A 、C 、E 在一条条直线上；(2)能否判断抛物线y ＝ax 2+b x +1的开口方向?请说明理由；(3)设抛物线y ＝ax 2+b x +1与x 轴有交点F 、G(F 在G 的左侧)，△GAO 与△FAO 的面积差为3，且这条抛物线与线段AE 有两个不同的交点．这时能确定a 、b 的值吗?若能，请求出a 、b 的值；若不能，请确定a 、b 的取值范围． (本题图形仅供分析参考用)[解] （1）由题意，A(0，1)、C(4，3)确定的解析式为：y=21x 将点E 的坐标E(415，823)代入y=21x +1中，左边=823，右边=21×415+1=823， ∵左边=右边，∴点E 在直线y=21x +1上，即点A 、C 、E 在一条直线上.（2）解法一：由于动点P 在矩形ABCD 内部，∴点P 的纵坐标大于点A 的纵坐标，而点A 与点P 都在抛物线上，且P 为顶点，∴这条抛物线有最高点，抛物线的开口向下解法二：∵抛物线y=ax 2+b x +c 的顶点P 的纵坐标为ab a 442—，且P 在矩形ABCD 内部，∴1＜a b a 442—＜3，由1＜1—a b 42得—ab 42＞0，∴a ＜0，∴抛物线的开口向下.（3）连接GA 、FA ，∵S △GAO —S △FAO =3 ∴21GO ·AO —21FO ·AO=3 ∵OA=1，∴GO —FO=6. 设F （x 1,0）、G （x 2,0），则x 1、x 2为方程ax 2+b x +c=0的两个根，且x 1＜x 2，又∵a ＜0，∴x 1·x 2=a1＜0，∴x 1＜0＜x 2， ∴GO= x 2，FO= —x 1，∴x 2—（—x 1）=6， 即x 2+x 1=6，∵x 2+x 1= —a b ∴—ab=6， ∴b= —6a ,∴抛物线解析式为：y=ax 2—6ax +1, 其顶点P 的坐标为由方程组 y=ax 2—6ax +1 y=21x +1 得：ax 2—（6a +21）x =0 （3，1—9a ）, ∵顶点P 在矩形ABCD 内部， ∴1＜1—9a ＜3, ∴—92＜a ＜0.∴x =0或x =a a 216=6+a21. 当x =0时，即抛物线与线段AE 交于点A ，而这条抛物线与线段AE 有两个不同的交 点，则有：0＜6+a 21≤415，解得：—92≤a ＜—121 综合得：—92＜a ＜—121 ∵b= —6a ，∴21＜b ＜346.（2004湖南长沙）已知两点O(0，0)、B(0，2)，⊙A 过点B 且与x 轴分别相交于点O 、C ，⊙A 被y 轴分成段两圆弧，其弧长之比为3∶1，直线l 与⊙A 切于点O ，抛物线的顶点在直线l 上运动. （1）求⊙A 的半径；（2）若抛物线经过O 、C 两点，求抛物线的解析式；（3）过l 上一点P 的直线与⊙A 交于C 、E 两点，且PC ＝CE ，求点E 的坐标； （4）若抛物线与x 轴分别相交于C 、F 两点，其顶点P 的横坐标为m ，求△PEC 的面积关于m 的函数解析式.[解] (1)由弧长之比为3∶1，可得∠BAO ＝90º再由AB ＝AO ＝r ，且OB ＝2，得r ＝ 2 (2)⊙A 的切线l 过原点，可设l 为y ＝kx任取l 上一点(b ，kb )，由l 与y 轴夹角为45º可得： b ＝－kb 或b ＝kb ，得k ＝－1或k ＝1， ∴直线l 的解析式为y ＝－x 或y ＝x又由r ，易得C(2，0)或C(－2，0)由此可设抛物线解析式为y ＝ax (x －2)或y ＝ax (x ＋2) 再把顶点坐标代入l 的解析式中得a ＝1 ∴抛物线为y ＝x 2－2x 或y ＝x 2＋2x……6分(3)当l 的解析式为y ＝－x 时，由P 在l 上，可设P(m ，－m)(m ＞0) 过P 作PP′⊥x 轴于P′，∴OP′＝|m|，PP′＝|－m|，∴OP ＝2m 2，又由切割线定理可得：OP 2＝PC·PE,且PC ＝CE ，得PC ＝PE ＝m ＝PP′7分∴C 与P′为同一点，即PE ⊥x 轴于C ，∴m ＝－2，E(－2，2)…8分 同理，当l 的解析式为y ＝x 时，m ＝－2，E(－2，2)(4)若C(2，0)，此时l 为y ＝－x ，∵P 与点O 、点C 不重合，∴m≠0且m≠2， 当m ＜0时，FC ＝2(2－m)，高为|y p |即为－m ， ∴S ＝22(2)()22m m m m --=-同理当0＜m ＜2时，S ＝－m 2＋2m ；当m ＞2时，S ＝m 2－2m ；∴S ＝222(02)2(02)m m m m m m m ⎧-<>⎨-+<<⎩或 又若C(－2，0)， 此时l 为y ＝x ，同理可得；S ＝222(20)2(20)m m m m m m m ⎧+<->⎨---<<⎩或7.（2006江苏连云港）如图，直线4+=kx y 与函数)0,0(>>=m x xmy 的图像交于A 、B 两点，且与x 、y 轴分别交于C 、D 两点．（1）若COD ∆的面积是AOB ∆的面积的2倍，求k 与m 之间的函数关系式； （2）在（1）的条件下，是否存在k 和m ，使得以AB 为直径的圆经过点)0,2(P ．若存在，求出k 和m 的值；若不存在，请说明理由．[解]（1）设),(11y x A ，),(22y x B (其中2121,y y x x ><)，由AOB COD S S ∆∆=2，得)(2BOD AOD COD S S S ∆∆∆-= ∴21·OC ·2=OD (21·OD ·-1y 21·OD ·2y )，(21y OC =又4=OC ，∴8)(221=-y y ，即84)(21221=-+y y y y ， 由xmy =可得y m x =，代入4+=kx y 可得042=--km y y ①∴421=+y y ，km y y -=⋅21，∴8416=+km ，即mk 2-=． 又方程①的判别式08416>=+=∆km ，∴所求的函数关系式为mk 2-=)0(>m ． （2）假设存在k ,m ，使得以AB 为直径的圆经过点)0,2(P则BP AP ⊥，过A 、B 分别作x 轴的垂线，垂足分别为M ∵MAP ∠与BPN ∠都与APM ∠互余，∴MAP ∠ BPN ∠=． ∴Rt MAP ∆∽Rt NPB ∆，∴NBMPPN AM =． ∴212122y x x y -=-，∴0)2)(2(2121=+--y y x x ， ∴0)2)(2(2121=+--y y y m y m ， 即0)(4)(222121212=+++-y y y y y y m m ②由（1）知421=+y y ，221=⋅y y ，代入②得01282=+-m m ，∴2=m 或6，又m k 2-=，∴⎩⎨⎧-==12k m 或⎪⎩⎪⎨⎧-==316k m ， ∴存在k ,m ，使得以AB 为直径的圆经过点)0,2(P ，且⎩⎨⎧-==12k m 或⎪⎩⎪⎨⎧-==316k m ． 8.（2004江苏镇江）已知抛物线2(5)5(0)y mx m x m =--->与x 轴交于两点1(,0)A x 、2(,0)B x 12()x x <，与y 轴交于点C ，且AB =6.（1）求抛物线和直线BC 的解析式.（2）在给定的直角坐标系中，画抛物线和直线BC .（3）若P 过A 、B 、C 三点，求P 的半径.（4）抛物线上是否存在点M ，过点M 作MN x ⊥轴于点N ，使MBN ∆被直线BC分成面积比为13:的两部分？若存在，请求出点M 的坐标；若不存在，请说明理由.[解]（1）由题意得：12122155,, 6.m x x x x x x m m--+=⋅=-= 221212520()436,36,m x x x x m m -⎛⎫+-=+= ⎪⎝⎭解得1251,.7m m ==-经检验m =1，∴抛物线的解析式为：24y x =+或：由2(5)50m x m x ---=得，1x =或5x m-=0,m >516, 1.m m-∴-=∴= 抛物线的解析式为24 5.y x x =+-由2450x x +-=得125, 1.x x =-=∴A （－5，0），B （1，0），C （0，－5）. 设直线BC 的解析式为,y kx b =+ 则5,5,0. 5.b b k b k =-=-⎧⎧∴⎨⎨+==⎩⎩ ∴直线BC 的解析式为5 5.y x =- (2)图象略.（3）法一：在Rt AOC D 中，5,45.OA OC OAC ==∴∠=︒90BPC ∴∠=︒.又BC == ∴P的半径PB == 法二：由题意，圆心P 在AB 的中垂线上，即在抛物线245y x x =+-的对称轴直线2x =-上，设P （－2，－h ）（h ＞0），连结PB 、PC ，则222222(12),(5)2PB h PC h =++=-+，由22PB PC =，即2222(12)(5)2h h ++=-+，解得h =2.(2,2),P P ∴--∴的半径PB ==.法三：延长CP 交P 于点F .为P 的直径，90.CAF COB ∴∠=∠=︒ 又,.ABC AFC ACF OCB ∠=∠∴D ~D,.CF AC AC BCCF BC OC OC⋅∴=∴=又AC ==5,CO BC ===∞5CF ∴==（4）设MN 交直线BC 于点E ，点M 的坐标为2(,45),t t t +-则点E 的坐标为(,55).t t -若13,MEB ENB S S =D D ::则13.ME EN =::2434,45(55).3EN MN t t t ∴=∴+-=-::解得11t =（不合题意舍去），25,3t =540,.39M ⎛⎫∴ ⎪⎝⎭若31,MEB ENB S S =D D ::则31.ME EN =::214,454(55).EN MN t t t ∴=∴+-=-::解得31t =（不合题意舍去），415,t =()15,280.M ∴∴存在点M ，点M 的坐标为540,39⎛⎫⎪⎝⎭或（15，280）.9. 如图，⊙M 与x 轴交于A 、B 两点，其坐标分别为)03(，-A 、)01(，B ，直径CD ⊥x 轴于N ，直线CE 切⊙M 于点C ，直线FG 切⊙M 于点F ，交CE 于G ，已知点G 的横坐标为3.(1) 若抛物线m x x y +--=22经过A 、B 、D 三点，求m 的值及点D 的坐标. (2) 求直线DF 的解析式.(3) 是否存在过点G 的直线，使它与（1）中抛物线的两个交点的横坐标之和等于4？若存在，请求出满足条件的直线的解析式；若不存在，请说明理由.[解] (1) ∵抛物线过A 、B 两点，∴11)3(-=⨯-m，m =3.∴抛物线为322+--=x x y .又抛物线过点D ，由圆的对称性知点D 为抛物线的顶点. ∴D 点坐标为)41(，-.(2) 由题意知：AB =4.∵CD ⊥x 轴，∴NA =NB =2. ∴ON =1. 由相交弦定理得：NA ·NB =ND ·NC ， ∴NC ×4=2×2. ∴NC =1. ∴C 点坐标为)11(--，.设直线DF 交CE 于P ，连结CF ，则∠CFP =90°. ∴∠2+∠3=∠1+∠4=90°. ∵GC 、GF 是切线， ∴GC =GF . ∴∠3=∠4. ∴∠1=∠2. ∴GF =GP . ∴GC =GP . 可得CP =8.∴P 点坐标为)17(-，设直线DF 的解析式为b kx y +=则⎩⎨⎧-=+=+-174b k b k 解得⎪⎪⎩⎪⎪⎨⎧=-=82785b k∴直线DF 的解析式为：82785+-=x y(3) 假设存在过点G 的直线为11b x k y +=，（第9题图）则1311-=+b k ，∴1311--=k b .由方程组⎩⎨⎧+--=--=3213211x x y k x k y 得034)2(112=--++k x k x 由题意得421=--k ，∴61-=k . 当61-=k 时，040<-=∆， ∴方程无实数根，方程组无实数解. ∴满足条件的直线不存在.10.（2004山西）已知二次函数212y x bx c =++的图象经过点A （－3，6），并与x 轴交于点B （－1，0）和点C ，顶点为P.（1）求这个二次函数的解析式，并在下面的坐标系中画出该二次函数的图象； （2）设D 为线段OC 上的一点，满足∠DPC ＝∠BAC ，求点D 的坐标； （3）在x 轴上是否存在一点M ，使以M 为圆心的圆与AC 、PC 所在的直线及y 轴都相切？如果存在，请求出点M 的坐标；若不存在，请说明理由.[解] （1）解：∵二次函数212y x bx c =++的图象过点A （－3，6），B （－1，0）得9362102b c b c ⎧-+=⎪⎪⎨⎪-+=⎪⎩ 解得132b c =-⎧⎪⎨=-⎪⎩∴这个二次函数的解析式为：21322y x x =-- 由解析式可求P （1，－2），C （3，0） 画出二次函数的图像（2）解法一：易证：∠ACB ＝∠PCD ＝45°又已知：∠DPC ＝∠BAC ∴△DPC ∽△BAC ∴DC PCBC AC=易求4AC PC BC === ∴43DC = ∴45333OD =-= ∴5,03D ⎛⎫⎪⎝⎭解法二：过A 作AE ⊥x 轴，垂足为E.设抛物线的对称轴交x 轴于F. 亦可证△AEB ∽△PFD 、 ∴PE EBPF FD=. 易求：AE ＝6，EB ＝2，PF ＝2∴23FD =∴25133OD =+= ∴5,03D ⎛⎫ ⎪⎝⎭（3）存在.（1°）过M 作MH ⊥AC ，MG ⊥PC 垂足分别为H 、G ，设AC 交y 轴于S ，CP 的延长线交y 轴于T∵△SCT 是等腰直角三角形，M 是△SCT 的内切圆圆心， ∴MG ＝MH ＝OM又∵MC =且OM ＋MC ＝OC3,3OM OM +==得∴()3,0M（2°）在x 轴的负半轴上，存在一点M ′ 同理OM′＋OC ＝M′C，OM OC ''+=得3OM '= ∴M′()3,0- 即在x 轴上存在满足条件的两个点.11.（2004浙江绍兴）在平面直角坐标系中，A （－1，0），B （3，0）.（1）若抛物线过A ，B 两点，且与y 轴交于点（0，－3），求此抛物线的顶点坐标；（2）如图，小敏发现所有过A ，B 两点的抛物线如果与y 轴负半轴交于点C ，M 为抛物线的顶点，那么△ACM 与△ACB 的面积比不变，请你求出这个比值； （3）若对称轴是AB 的中垂线l 的抛物线与x 轴交于点E ，F ，与y 轴交于点C ，过C 作CP ∥x 轴交l 于点P ，M 为此抛物线的顶点.若四边形PEMF 是有一个内角为60°的菱形，求次抛物线的解析式.[解] （1）322--=x x y ，顶点坐标为（1，－4）.（2）由题意，设y ＝a （x ＋1）（x －3）， 即y ＝ax 2－2ax －3a ，∴ A （－1，0），B （3，0），C （0，－3a ）， M （1，－4a ），∴ S △ACB ＝21×4×a 3-＝6a ，而a ＞0， ∴ S △ACB ＝6A 、 作MD ⊥x 轴于D ，又S △ACM ＝S △ACO ＋S OCMD －S △AMD ＝21·1·3a ＋21（3a ＋4a ）－21·2·4a ＝a ， ∴ S △ACM ：S △ACB ＝1：6.（3）①当抛物线开口向上时，设y ＝a （x －1）2＋k ，即y ＝ax 2－2ax ＋a ＋k ， 有菱形可知k a +＝k ，a ＋k ＞0，k ＜0， ∴ k ＝2a-， ∴ y ＝ax 2－2ax ＋2a， ∴ 2=EF . 记l 与x 轴交点为D ，若∠PEM ＝60°，则∠FEM ＝30°，MD ＝DE·tan30°＝66， ∴ k ＝－66，a ＝36， ∴ 抛物线的解析式为666326312+-=x x y .若∠PEM ＝120°，则∠FEM ＝60°，MD ＝DE·tan60°＝26， ∴ k ＝－26，a ＝6， ∴ 抛物线的解析式为266262+-=x x y . ②当抛物线开口向下时，同理可得666326312-+-=x x y ，266262-+-=x x y . 12.（2005北京）已知：在平面直角坐标系xOy 中，一次函数y k x k=-4的图象与x 轴交于点A ，抛物线y a xb x c =++2经过O 、A 两点。

解答压轴题2022年天津数学中考真题汇编1.已知点A(1,0)是抛物线y=ax2+bx+m（a，b，m为常数，a≠0，m<0）与x轴的一个交点．(1) 当a=1，m=−3时，求该抛物线的顶点坐标；(2) 若抛物线与x轴的另一个交点为M(m,0)，与y轴的交点为C，过点C作直线l平行于x轴，E是直线l上的动点，F是y轴上的动点，EF=2√2．①当点E落在抛物线上（不与点C重合），且AE=EF时，求点F的坐标；②取EF的中点N，当m为何值时，MN的最小值是√222.已知抛物线y=x2−bx+c（b，c为常数，b>0）经过点A(−1,0)，点M(m,0)是x轴正半轴上的动点．(1) 当b=2时，求抛物线的顶点坐标；(2) 点D(b,y D)在抛物线上，当AM=AD，m=5时，求b的值；(3) 点Q(b+12,y Q)在抛物线上，当√2AM+2QM的最小值为33√24时，求b的值．3.在平面直角坐标系中，O(0,0)，A(1,0)．已知抛物线y=x2+mx−2m（m是常数），顶点为P．(1) 当抛物线经过点A时，求顶点P的坐标；(2) 若点P在x轴下方，当∠AOP=45∘时，求抛物线的解析式；(3) 无论m取何值，该抛物线都经过定点H．当∠AHP=45∘时，求抛物线的解析式．4.已知抛物线y=x2+bx−3（b是常数）经过点A(−1,0)．(1) 求该抛物线的解析式和顶点坐标；(2) P(m,t)为抛物线上的一个动点，P关于原点的对称点为Pʹ．①当点Pʹ落在该抛物线上时，求m的值；②当点Pʹ落在第二象限内，PʹA2取得最小值时，求m的值．5.已知抛物线C：y=x2−2x+1的顶点P，与y轴的交点为Q，点F(1,12)．(1) 求点P，Q的坐标；(2) 将抛物线C向上平移得到抛物线Cʹ，点Q平移后的对应点为Qʹ，且FQʹ=OQʹ．①求抛物线Cʹ的解析式；②若点P关于直线QʹF的对称点为K，射线FK与抛物线Cʹ相交于点A，求点A的坐标．答案1. 【答案】(1) 当 a =1，m =−3 时，抛物线的解析式为 y =x 2+bx −3， ∵ 抛物线经过点 A (1,0)， ∴0=1+b −3，解得 b =2， ∴ 抛物线的解析式为 y =x 2+2x −3， ∵y =x 2+2x −3=(x +1)2−4， ∴ 抛物线的顶点坐标为 (−1,−4)．(2) ① ∵ 抛物线 y =ax 2+bx +m 经过点 A (1,0) 和 M (m,0)，m <0， ∴0=a +b +m ，0=am 2+bm +m ，即 am +b +1=0， ∴a =1，b =−m −1，∴ 抛物线的解析式为 y =x 2−(m +1)x +m ， 根据题意，得点 C (0,m )，点 E (m +1,m )， 过点 A 作 AH ⊥l 于点 H ， 由点 A (1,0)，得点 H (1,m )，在 Rt △EAH 中，EH =1−(m +1)=−m ，HA =0−m =−m ， ∴AE =√EH 2+HA 2=−√2m ， ∵AE =EF =2√2，∴−√2m =2√2，解得 m =−2，此时，点 E (−1,−2)，点 C (0,−2)，有 EC =1， ∵ 点 F 在 y 轴上，∴ 在 Rt △EFC 中，CF =√EF 2−EC 2=√7， ∴ 点 F 的坐标为 (0,−2−√7) 或 (0,−2+√7)． ②由 N 是 EF 的中点，得 CN =12EF =√2，根据题意，点 N 在以点 C 为圆心、 √2 为半径的圆上， 由点 M (m,0)，点 C (0,m )，得 MO =−m ，CO =−m ， ∴ 在 Rt △MCO 中，MC =√MO 2+CO 2=−√2m ，当 MC ≥√2，即 m ≤−1 时，满足条件的点 N 落在线段 MC 上， MN 的最小值为 MC −NC =−√2m −√2=√22，解得 m =−32；当 MC <√2，即 −1<m <0 时，满足条件的点 N 落在线段 CM 的延长线上， MN 的最小值为 NC −MC =√2−(−√2m)=√22，解得 m =−12，∴ 当 m 的值为 −32或 −12时，MN 的最小值是 √22．2. 【答案】(1) ∵ 抛物线 y =x 2−bx +c 经过点 A (−1,0)，∴ 1+b +c =0， 即 c =−b −1．当 b =2 时，y =x 2−2x −3=(x −1)2−4， ∴ 抛物线的顶点坐标为 (1,−4)．(2) 由（1）知，抛物线的解析式为 y =x 2−bx −b −1． ∵ 点 D (b,y D ) 在抛物线 y =x 2−bx −b −1 上， ∴ y D =b 2−b ⋅b −b −1=−b −1． 由 b >0，得 b >b2>0，−b −1<0，∴ 点 D (b,−b −1) 在第四象限，且在抛物线对称轴 x =b2 的右侧． 如图，过点 D 作 DE ⊥x 轴，垂足为 E ，则点 E (b,0)． ∴ AE =b +1，DE =b +1．得 AE =DE ． ∴ 在 Rt △ADE 中，∠ADE =∠DAE =45∘． ∴ AD =√2AE ．由已知 AM =AD ，m =5， ∴ 5−(−1)=√2(b +1)． ∴ b =3√2−1．(3) ∵ 点 Q (b +12,y Q ) 在抛物线 y =x 2−bx −b −1 上，∴ y Q =(b +12)2−b (b +12)−b −1=−b 2−34．可知点 Q (b +12,−b2−34) 在第四象限，且在直线 x =b 的右侧，考虑到 √2AM +2QM =2(√22AM +QM)，可取点 N (0,1)，如图，过点 Q 作直线 AN 的垂线，垂足为 G ，QG 与 x 轴相交于点 M ， 有 ∠GAM =45∘，得√22AM =GM ，则此时点 M 满足题意．过点 Q 作 QH ⊥x 轴于点 H ，则点 H (b +12,0)， 在 Rt △MQH 中，可知 ∠QMH =∠MQH =45∘． ∴ QH =MH ，QM =√2MH ．∵ 点 M (m,0)，∴ 0−(−b2−34)=(b +12)−m ，解得 m =b2−14．∵ √2AM +2QM =33√24， ∴ √2[(b2−14)−(−1)]+2√2[(b +12)−(b2−14)]=33√24．∴ b =4．3. 【答案】(1) ∵ 抛物线 y =x 2+mx −2m 经过 A (1,0)， ∴0=1+m −2m ，解得 m =1． ∴ 抛物线的解析式为 y =x 2+x −2． ∵y =x 2+x −2=(x +12)2−94，∴ 顶点 P 的坐标为 (−12,94)． (2) 由题意可知，抛物线 y =x 2+mx −2m 的顶点 P 的坐标为 (−m 2,−m 2+8m4)．由点 A (1,0) 在 x 轴正半轴上，点 P 在 x 轴下方，∠AOP =45∘，知点 P 在第四象限． 如图 1，过点 P 作 PQ ⊥x 轴于点 Q ， 则 ∠POQ =∠OPQ =45∘． 可知 PQ =OQ ，即m 2+8m4=−m2，解得 m 1=0，m 2=−10．当 m =0 时，点 P 不在第四象限，舍去． ∴m =−10．∴ 抛物线解析式为 y =x 2−10x +20．(3) 由 y =x 2+mx −2m =(x −2)m +x 2 可知，当 x =2 时，无论 m 取何值，y 都等于 4，得点 H 的坐标为 (2,4)．如图 2，过点 A 作 AD ⊥AH ，交射线 HP 于点 D ，分别过点 D ，H 作 x 轴的垂线，垂足分别为 E ，G ，则 ∠DEA =∠AGH =90∘． ∵∠DAH =90∘，∠AHD =45∘， ∴∠ADH =45∘． ∴AH =AD ．∵∠DAE +∠HAG =∠AHG +∠HAG =90∘， ∴∠DAE =∠AHG ． 在 △ADE 和 △HAG 中， {∠DEA =∠AGH =90∘,∠DAE =∠AHG,AD =HA,∴△ADE ≌△HAG ．∴DE =AG =1，AE =HG =4．可得点 D 的坐标为 (−3,1) 或 (5,−1)．①当点 D 的坐标为 (−3,1) 时，可得直线 DH 的解析式为 y =35x +145．∵P (−m2,−m 2+8m4) 在直线 y =35x +145上，∴−m 2+8m4=35×(−m 2)+145，解得 m 3=−4，m 4=−145． 当 m =−4 时，点 P 与点 H 重合，不符合题意， ∴m =−145．②当点 D 的坐标为 (5,−1) 时，可得直线 DH 的解析式为 y =−53x +223．∵P (−m 2,−m 2+8m4) 在直线 y =−53x +223上，∴−m 2+8m4=−53×(−m2)+223，解得 m 5=−4（舍），m 6=−223． ∴m =−223．综上，m =−145 或 m =−223． 故抛物线解析式为 y =x 2−145x +285或 y =x 2−223x +443．4. 【答案】(1) ∵ 抛物线 y =x 2+bx −3 经过点 A (−1,0)， ∴ 0=1−b −3，解得 b =−2． ∴ 抛物线的解析式为 y =x 2−2x −3． ∵ y =x 2−2x −3=(x −1)2−4，∴ 顶点坐标为 (1,−4)．(2) ①由点 P (m,t ) 在抛物线 y =x 2−2x −3 上，有 t =m 2−2m −3． 又点 Pʹ 和 P 关于原点对称，有 Pʹ(−m,−t )． ∵ 点 Pʹ 落在抛物线 y =x 2−2x −3 上，∴ −t =(−m )2−2(−m )−3，即 t =−m 2−2m ＋3． ∴ m 2−2m −3=−m 2−2m +3． 解得 m 1=√3，m 2=−√3．②由题意知，Pʹ(−m,−t ) 在第二象限， ∴ −m <0，−t >0，即 m >0，t <0．又抛物线 y =x 2−2x −3 的顶点坐标是 (1,−4)，得 −4≤t <0． 过点 Pʹ 作 PʹH ⊥x 轴，H 为垂足，又 H (−m,0)． 又 A (−1,0)，t =m 2−2m −3，则 PʹH 2=t 2，AH 2=(−m +1)2=m 2−2m +1=t +4． 当点 A 和 H 不重合时，在 Rt △PʹAH 中，PʹA 2=PʹH 2+AH 2； 当点 A 和 H 重合时，AH =0，PʹA 2=PʹH 2，符合上式． ∴ PʹA 2=PʹH 2+AH 2，即 PʹA 2=t 2+t +4(−4≤t <0)． 记 yʹ=t 2+t +4，则 yʹ=(t +12)2+154．∴ 当 t =−12 时，yʹ 取得最小值．把 t =−12代入 t =m 2−2m −3，得 −12=m 2−2m −3．解得 m 1=2−√142，m 2=2+√142．由 m >0，可知 m =2−√142不符合题意．∴ m =2+√142．5. 【答案】(1) ∵ y =x 2−2x +1=(x −1)2， ∴ 顶点 P 的坐标为（1,0）． ∵ 当 x =0 时，y =1， ∴ 点 Q 的坐标为（0,1）．(2) ①根据题意，设抛物线 Cʹ 的解析式为 y =x 2−2x +m ， 则点 Qʹ 的坐标为 (0,m )，其中 m >1．得 OQʹ=m ． ∵ 点 F (1,12)，过点 F 作 FH ⊥OQʹ，垂足为 H ， 则 FH =1，QʹH =m −12．在 Rt △FQʹH 中，根据勾股定理， 得 FQʹ2=QʹH 2+FH 2．∴ FQʹ2=(m −12)2+12=m 2−m +54．∵ FQʹ=OQʹ，∴ m 2−m +54=m 2，解得 m =54． ∴ 抛物线 Cʹ 的解析式为 y =x 2−2x +54．②由①有，Qʹ(0,54)，F (1,12)，P (1,0)， ∴ 直线 FQʹ 的解析式为 y =−34x +54①，∵FQʹ⊥PK ，P (1,0)，∴ 直线 PK 的解析式为 y =43x −43 ②联立①②得出，直线 FQʹ 与 PK 的交点 M 坐标为 (3125,825)，∵ 点 P ，K 关于直线 FQʹ 对称， ∴K (3725,1625)． ∵F (1,12)，∴ 直线 FK 的解析式为 y =724x +524③，∵ 射线 FK 与抛物线 C ′：y =x 2−2x +54④相交于点 A ， ∴ 联立③④得，{x ＝53,y ＝2536或 {x ＝58,y ＝2564（舍）， ∴A (53,2536)．。

2024学年天津市和平区二十一中中考数学押题卷考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

一、选择题（共10小题，每小题3分，共30分）1．下列图形中，是正方体表面展开图的是（）A．B．C． D．2．改革开放40年以来，城乡居民生活水平持续快速提升，居民教育、文化和娱乐消费支出持续增长，已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出，如图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图．说明：在统计学中，同比是指本期统计数据与上一年同期统计数据相比较，例如2018年第二季度与2017年第二季度相比较；环比是指本期统计数据与上期统计数据相比较，例如2018年第二季度与2018年第一季度相比较．根据上述信息，下列结论中错误的是（）A．2017年第二季度环比有所提高B．2017年第三季度环比有所提高C．2018年第一季度同比有所提高D．2018年第四季度同比有所提高3．小明家1至6月份的用水量统计如图所示，关于这组数据，下列说法错误的是（）．A ．众数是6吨B ．平均数是5吨C ．中位数是5吨D ．方差是4．一艘在南北航线上的测量船，于A 点处测得海岛B 在点A 的南偏东30°方向，继续向南航行30海里到达C 点时，测得海岛B 在C 点的北偏东15°方向，那么海岛B 离此航线的最近距离是（ ）（结果保留小数点后两位）（参考数据：≈1.732，≈1.414）A ．4.64海里B ．5.49海里C ．6.12海里D ．6.21海里 5．函数y=ax 2+1与ay x=（a≠0）在同一平面直角坐标系中的图象可能是（ ） A ． B ． C ． D ．6．四张分别画有平行四边形、菱形、等边三角形、圆的卡片，它们的背面都相同。

九年级数学冲刺讲义二次函数12题1. 已知关于x的函数同时满足下列三个条件：①函数的图象不经过第二象限；②当x＜2时，对应的函数值y＜0；③当x＜2时，函数值y随x的增大而增大．你认为符合要求的函数的解析式可以是：（写出一个即可，答案不唯一）．2．已知抛物线y=ax2+bx+c（b＞a＞0）与x轴最多有一个交点，现有以下四个结论：①该抛物线的对称轴在y轴左侧；②关于x的方程ax2+bx+c+2=0无实数根；③a﹣b+c≥0；④的最小值为3．其中，正确结论的个数为（）A．1个B．2个C．3个D．4个3．已知抛物线y=﹣x2+x+6与x轴交于点A，点B，与y轴交于点C．若D为AB的中点，则CD的长为（）A．B．C．D．4．已知二次函数y=（x﹣h）2+1（h为常数），在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为5，则h的值为（）A．1或﹣5 B．﹣1或5 C．1或﹣3 D．1或35．已知二次函数y=ax2+bx+c（a≠0）的图象如图，且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根，有下列结论：①b2﹣4ac＞0；②abc＜0；③m＞2．其中，正确结论的个数是（）A．0 B．1 C．2 D．36．若关于x的一元二次方程（x﹣2）（x﹣3）=m有实数根x1、x2，且x1≠x2，有下列结论：①x1=2，x2=3；②m＞﹣；③二次函数y=（x﹣x1）（x﹣x2）+m的图象与x轴交点的坐标为（2，0）和（3，0）．其中，正确结论的个数是（）A．0 B．1 C．2 D．37．已知二次函数y=ax 2+bx+c （a≠0）的图象如图所示，有下列结论：①b 2﹣4ac ＞0；②abc ＞0；③8a+c ＞0；④9a+3b+c ＜0其中，正确结论的个数是（ ）A ．1B ．2C ．3D ．48．已知二次函数y=ax 2+bx+c （a≠0）的图象如图所示，有下列5个结论：①abc ＞0；②b ＜a+c ；③4a+2b+c ＞0；④2c ＜3b ；⑤a+b ＞m （am+b ）（m≠1的实数）．其中正确的结论有（ ）A ．2个B ．3个C ．4个D ．5个9. 已知抛物线y=x 2-(2m-1)x+2m 不经过第三象限，且当x>2时，函数值y 随x 的增大而增大，则实数m 的取值范围是（ ）A.0≤m≤1.5B.m≥1.5C.0≤m≤1D.0<m≤1.5网格题18题1. 如图，在下列网格中，每个小正方形的边长都是1，点A 、B 、Q 、P 均为格点。

天津市武清区重点名校2024届中考数学最后冲刺浓缩精华卷注意事项：1．答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）1．图1～图4是四个基本作图的痕迹，关于四条弧①、②、③、④有四种说法：弧①是以O为圆心，任意长为半径所画的弧；弧②是以P为圆心，任意长为半径所画的弧；弧③是以A为圆心，任意长为半径所画的弧；弧④是以P为圆心，任意长为半径所画的弧；其中正确说法的个数为（）A．4 B．3 C．2 D．12．“保护水资源，节约用水”应成为每个公民的自觉行为．下表是某个小区随机抽查到的10户家庭的月用水情况，则下列关于这10户家庭的月用水量说法错误的是（）月用水量（吨） 4 5 6 9户数（户） 3 4 2 1A．中位数是5吨B．众数是5吨C．极差是3吨D．平均数是5.3吨3．如图，平面直角坐标系xOy中，矩形OABC的边OA、OC分别落在x、y轴上，点B坐标为（6，4），反比例函数6的图象与AB边交于点D，与BC边交于点E，连结DE，将△BDE沿DE翻折至△B'DE处，点B'恰好落在正yx比例函数y=kx图象上，则k的值是（）A ．25-B ．121-C ．15-D ．124-4．估计3﹣2的值应该在（ ） A ．﹣1﹣0之间B ．0﹣1之间C ．1﹣2之间D ．2﹣3之间5．每个人都应怀有对水的敬畏之心，从点滴做起，节水、爱水，保护我们生活的美好世界．某地近年来持续干旱，为倡导节约用水，该地采用了“阶梯水价”计费方法，具体方法：每户每月用水量不超过4吨的每吨2元；超过4吨而不超过6吨的，超出4吨的部分每吨4元；超过6吨的，超出6吨的部分每吨6元．该地一家庭记录了去年12个月的月用水量如下表，下列关于用水量的统计量不会发生改变的是（ ） 用水量x （吨） 3 4 5 6 7 频数1254﹣xxA ．平均数、中位数B ．众数、中位数C ．平均数、方差D ．众数、方差6．二次函数2y ax bx c =++（a ≠0）的图象如图所示，则下列命题中正确的是（ ）A ．a ＞b ＞cB ．一次函数y =ax +c 的图象不经第四象限C ．m （am +b ）+b ＜a （m 是任意实数）D ．3b +2c ＞07．如图，在平面直角坐标系中，直线y=k 1x+2（k 1≠0）与x 轴交于点A ，与y 轴交于点B ，与反比例函数y=2k x在第二象限内的图象交于点C ，连接OC ，若S △OBC =1，tan ∠BOC=13，则k 2的值是（ ）A ．3B ．﹣12C ．﹣3D ．﹣68．如图，等腰三角形ABC 的底边BC 长为4，面积是16，腰AC 的垂直平分线EF 分别交AC ，AB 边于E ，F 点.若点D 为BC 边的中点，点M 为线段EF 上一动点，则CDM 周长的最小值为( )A ．6B ．8C ．10D ．129．下列图形是中心对称图形的是（ ）A ．B ．C ．D ．10．某春季田径运动会上，参加男子跳高的15名运动员的成绩如下表所示： 成绩()m 1.50 1.60 1.65 1.70 1.75 1.80 人数124 332这些运动员跳高成绩的中位数是（ ） A ．1.65mB ．1.675mC ．1.70mD ．1.75m二、填空题（共7小题，每小题3分，满分21分） 11．抛物线y=2x 2+4x ﹣2的顶点坐标是_______________．12．有一组数据：3，a ，4，6，7，它们的平均数是5，则a ＝_____，这组数据的方差是_____． 13．一个正四边形的内切圆半径与外接圆半径之比为：_________________14．如图，在平面直角坐标系中，点O 为坐标原点，点P 在第一象限，⊙P 与x 轴交于O ，A 两点，点A 的坐标为（6，0），⊙P 的半径为13，则点P 的坐标为_______.15．分解因式：22a 4a 2-+=_____．16．从“线段，等边三角形，圆，矩形，正六边形”这五个图形中任取一个，取到既是轴对称图形又是中心对称图形的概率是_____．17．不等式组13210x x -≤⎧⎨-<⎩的解集为_____．三、解答题（共7小题，满分69分）18．（10分）小明参加某个智力竞答节目，答对最后两道单选题就顺利通关．第一道单选题有3个选项，第二道单选题有4个选项，这两道题小明都不会，不过小明还有一个“求助”没有用（使用“求助”可以让主持人去掉其中一题的一个错误选项）．如果小明第一题不使用“求助”，那么小明答对第一道题的概率是 ．如果小明将“求助”留在第二题使用，请用树状图或者列表来分析小明顺利通关的概率．从概率的角度分析，你建议小明在第几题使用“求助”．（直接写出答案）19．（5分）如图二次函数的图象与x 轴交于点()30A -,和()10B ,两点，与y 轴交于点()0,3C ，点C 、D 是二次函数图象上的一对对称点，一次函数的图象经过B 、D求二次函数的解析式；写出使一次函数值大于二次函数值的x的取值范围；若直线BD 与y 轴的交点为E 点，连结AD 、AE ，求ADE ∆的面积；20．（8分）如图，在平面直角坐标系中，等边三角形ABC 的顶点B 与原点O 重合，点C 在x 轴上，点C 坐标为（6，0），等边三角形ABC 的三边上有三个动点D 、E 、F （不考虑与A 、B 、C 重合），点D 从A 向B 运动，点E 从B 向C 运动，点F 从C 向A 运动，三点同时运动，到终点结束，且速度均为1cm/s ，设运动的时间为ts ，解答下列问题： （1）求证：如图①，不论t 如何变化，△DEF 始终为等边三角形．（2）如图②过点E 作EQ ∥AB ，交AC 于点Q ，设△AEQ 的面积为S ，求S 与t 的函数关系式及t 为何值时△AEQ 的面积最大？求出这个最大值．（3）在（2）的条件下，当△AEQ 的面积最大时，平面内是否存在一点P ，使A 、D 、Q 、P 构成的四边形是菱形，若存在请直接写出P 坐标，若不存在请说明理由？21．（10分）如图，AB为⊙O的直径，D为⊙O上一点，以AD为斜边作△ADC，使∠C=90°，∠CAD=∠DAB求证：DC是⊙O的切线；若AB=9，AD=6，求DC的长．，，，，五类校本课22．（10分）某中学为了了解在校学生对校本课程的喜爱情况，随机调查了部分学生对A B C D E程的喜爱情况，要求每位学生只能选择一类最喜欢的校本课程，根据调查结果绘制了如下的两个不完整统计图.请根据图中所提供的信息，完成下列问题：(1)本次被调查的学生的人数为；(2)补全条形统计图(3)扇形统计图中，C类所在扇形的圆心角的度数为；，两类校本课程的学生约共有多少名.(4)若该中学有2000名学生，请估计该校最喜爱C D23．（12分）已知：如图，平行四边形ABCD，对角线AC与BD相交于点E，点G为AD的中点，连接CG，CG的延长线交BA的延长线于点F，连接FD．求证：AB=AF；若AG=AB，∠BCD=120°，判断四边形ACDF的形状，并证明你的结论．24．（14分）如图，已知AC和BD相交于点O，且AB∥DC，OA=OB．求证：OC=OD．参考答案一、选择题（每小题只有一个正确答案，每小题3分，满分30分）1、C【解题分析】根据基本作图的方法即可得到结论．【题目详解】解：（1）弧①是以O为圆心，任意长为半径所画的弧，正确；（2）弧②是以P为圆心，大于点P到直线的距离为半径所画的弧，错误；（3）弧③是以A为圆心，大于12AB的长为半径所画的弧，错误；（4）弧④是以P为圆心，任意长为半径所画的弧，正确．故选C．【题目点拨】此题主要考查了基本作图，解决问题的关键是掌握基本作图的方法．2、C【解题分析】根据中位数、众数、极差和平均数的概念，对选项一一分析，即可选择正确答案．【题目详解】解：A、中位数＝（5+5）÷2＝5（吨），正确，故选项错误；B、数据5吨出现4次，次数最多，所以5吨是众数，正确，故选项错误；C、极差为9﹣4=5（吨），错误，故选项正确；D、平均数=（4×3+5×4+6×2+9×1）÷10=5.3，正确，故选项错误．故选：C．【题目点拨】此题主要考查了平均数、中位数、众数和极差的概念．要掌握这些基本概念才能熟练解题．3、B【解题分析】根据矩形的性质得到，CB∥x轴，AB∥y轴，于是得到D、E坐标，根据勾股定理得到ED，连接BB′，交ED于F，过B′作B′G⊥BC于G，根据轴对称的性质得到BF=B′F，BB′⊥ED求得BB′，设EG=x，根据勾股定理即可得到结论．【题目详解】解：∵矩形OABC，∴CB∥x轴，AB∥y轴．∵点B坐标为（6，1），∴D的横坐标为6，E的纵坐标为1．∵D，E在反比例函数6yx=的图象上，∴D（6，1），E（32，1），∴BE=6﹣32=92，BD=1﹣1=3，∴ED22BE BD+3132．连接BB′，交ED于F，过B′作B′G⊥BC于G．∵B，B′关于ED对称，∴BF=B′F，BB′⊥ED，∴BF •ED =BE •BD BF =3×92， ∴BF， ∴BB设EG =x ，则BG =92﹣x ． ∵BB ′2﹣BG 2=B ′G 2=EB ′2﹣GE 2， ∴222299()()22x x --=-，∴x =4526， ∴EG =4526，∴CG =4213，∴B ′G =5413，∴B ′（4213，﹣213），∴k =121-．故选B ． 【题目点拨】本题考查了翻折变换（折叠问题），矩形的性质，勾股定理，熟练掌握折叠的性质是解题的关键． 4、A 【解题分析】【题目详解】解：∵12，∴1-2﹣2＜2-2，∴-1﹣2＜0即3-2在-1和0之间． 故选A ． 【题目点拨】此题主要考查了估算无理数大小，正确得出3的取值范围是解题关键． 5、B 【解题分析】由频数分布表可知后两组的频数和为4，即可得知频数之和，结合前两组的频数知第6、7个数据的平均数，可得答案． 【题目详解】∵6吨和7吨的频数之和为4-x+x=4， ∴频数之和为1+2+5+4=12，则这组数据的中位数为第6、7个数据的平均数，即=5，∴对于不同的正整数x ，中位数不会发生改变， ∵后两组频数和等于4，小于5，∴对于不同的正整数x ，众数不会发生改变，众数依然是5吨. 故选B ． 【题目点拨】本题主要考查频数分布表及统计量的选择，由表中数据得出数据的总数是根本，熟练掌握平均数、中位数、众数的定义和计算方法是解题的关键． 6、D 【解题分析】解：A ．由二次函数的图象开口向上可得a ＞0，由抛物线与y 轴交于x 轴下方可得c ＜0，由x =﹣1，得出2ba=﹣1，故b ＞0，b =2a ，则b ＞a ＞c ，故此选项错误；B ．∵a ＞0，c ＜0，∴一次函数y =ax +c 的图象经一、三、四象限，故此选项错误；C ．当x =﹣1时，y 最小，即a ﹣b ﹣c 最小，故a ﹣b ﹣c ＜am 2+bm +c ，即m （am +b ）+b ＞a ，故此选项错误；D ．由图象可知x =1，a +b +c ＞0①，∵对称轴x =﹣1，当x =1，y ＞0，∴当x =﹣3时，y ＞0，即9a ﹣3b +c ＞0② ①+②得10a ﹣2b +2c ＞0，∵b =2a ，∴得出3b +2c ＞0，故选项正确； 故选D ．点睛：此题主要考查了图象与二次函数系数之间的关系，二次函数与方程之间的转换，会利用特殊值代入法求得特殊的式子，如：y =a +b +c ，然后根据图象判断其值． 7、C【解题分析】如图，作CH ⊥y 轴于H ．通过解直角三角形求出点C 坐标即可解决问题. 【题目详解】解：如图，作CH ⊥y 轴于H ．由题意B （0，2）， ∵112OB CH ⋅⋅=， ∴CH=1， ∵tan ∠BOC=1,3CH OH = ∴OH=3， ∴C （﹣1，3），把点C （﹣1，3）代入2k y x=，得到k 2=﹣3， 故选C ． 【题目点拨】本题考查反比例函数于一次函数的交点问题，锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型． 8、C 【解题分析】连接AD ，由于△ABC 是等腰三角形，点D 是BC 边的中点，故AD ⊥BC ，再根据三角形的面积公式求出AD 的长，再再根据EF 是线段AC 的垂直平分线可知，点C 关于直线EF 的对称点为点A ，故AD 的长为CM+MD 的最小值，由此即可得出结论． 【题目详解】 连接AD ，∵△ABC是等腰三角形，点D是BC边的中点，∴AD⊥BC，∴S△ABC=12BC•AD=12×4×AD=16，解得AD=8，∵EF是线段AC的垂直平分线，∴点C关于直线EF的对称点为点A，∴AD的长为CM+MD的最小值，∴△CDM的周长最短=（CM+MD）+CD=AD+12BC=8+12×4=8+2=1．故选C．【题目点拨】本题考查的是轴对称-最短路线问题，熟知等腰三角形三线合一的性质是解答此题的关键．9、B【解题分析】根据中心对称图形的概念，轴对称图形与中心对称图形是图形沿对称中心旋转180度后与原图重合,即可解题.A、不是中心对称图形，故本选项错误；B、是中心对称图形，故本选项正确；C、不是中心对称图形，故本选项错误；D、不是中心对称图形，故本选项错误．故选B.考点：中心对称图形.【题目详解】请在此输入详解！10、C【解题分析】根据中位数的定义解答即可．【题目详解】解：在这15个数中，处于中间位置的第8个数是1.1，所以中位数是1.1．所以这些运动员跳高成绩的中位数是1.1．故选：C．【题目点拨】本题考查了中位数的意义．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数．二、填空题（共7小题，每小题3分，满分21分）11、（﹣1，﹣1）【解题分析】利用顶点的公式首先求得横坐标，然后把横坐标的值代入解析式即可求得纵坐标．【题目详解】 x=-422⨯=-1， 把x=-1代入得：y=2-1-2=-1．则顶点的坐标是（-1，-1）．故答案是：（-1，-1）．【题目点拨】本题考查了二次函数的顶点坐标的求解方法，可以利用配方法求解，也可以利用公式法求解．12、5 1． 【解题分析】∵一组数据：3，a ，4，6，7，它们的平均数是5，∴346755a ++++=⨯，解得，5a =，∴2222221[(35)(55)(45)(65)(75)]5s =-+-+-+-+-＝1. 故答案为5，1.13、【解题分析】如图，正方形ABCD 为⊙O 的内接四边形，作OH ⊥AB 于H ，利用正方形的性质得到OH 为正方形ABCD 的内切圆的半径，∠OAB ＝45°，然后利用等腰直角三角形的性质得OA ＝OH 即可解答.【题目详解】解：如图，正方形ABCD 为⊙O 的内接四边形，作OH ⊥AB 于H ，则OH 为正方形ABCD 的内切圆的半径，∵∠OAB ＝45°，∴OA ＝OH ， ∴ 即一个正四边形的内切圆半径与外接圆半径之比为, 故答案为：．【题目点拨】本题考查了正多边形与圆的关系：把一个圆分成n （n 是大于2的自然数）等份，依次连接各分点所得的多边形是这个圆的内接正多边形，这个圆叫做这个正多边形的外接圆．理解正多边形的有关概念．14、（3，2）．【解题分析】过点P 作PD ⊥x 轴于点D ，连接OP ，先由垂径定理求出OD 的长，再根据勾股定理求出PD 的长，故可得出答案．【题目详解】过点P 作PD ⊥x 轴于点D ，连接OP ，∵A （6，0），PD ⊥OA ，∴OD=12OA=3， 在Rt △OPD 中 ∵13 OD=3，∴PD=2∴P(3，2) .故答案为（3，2）．【题目点拨】本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．15、()22a 1-【解题分析】分析：要将一个多项式分解因式的一般步骤是首先看各项有没有公因式，若有公因式，则把它提取出来，之后再观察是否是完全平方公式或平方差公式，若是就考虑用公式法继续分解因式．因此，先提取公因式2后继续应用完全平方公式分解即可：()()2222a 4a 22a 2a 12a 1-+=-+=-． 16、45. 【解题分析】试题分析：在线段、等边三角形、圆、矩形、正六边形这五个图形中，既是中心对称图形又是轴对称图形的有线段、圆、矩形、正六边形，共4个，所以取到的图形既是中心对称图形又是轴对称图形的概率为45. 【题目点拨】本题考查概率公式，掌握图形特点是解题关键，难度不大.17、﹣2≤x ＜12【解题分析】根据解不等式的步骤从而得到答案.【题目详解】1-x 32x-10≤⎧⎨⎩①＜②， 解不等式①可得：x ≥－2，解不等式②可得：x ＜12， 故答案为－2≤x ＜12. 【题目点拨】本题主要考查了解不等式，解本题的要点在于分别求解①，②不等式，从而得到答案.三、解答题（共7小题，满分69分）18、（1）13；（2）19；（3）第一题. 【解题分析】（1）由第一道单选题有3个选项，直接利用概率公式求解即可求得答案；（2）画出树状图，再由树状图求得所有等可能的结果与小明顺利通关的情况，继而利用概率公式即可求得答案； （3）由如果在第一题使用“求助”小明顺利通关的概率为：18；如果在第二题使用“求助”小明顺利通关的概率为：19；即可求得答案．【题目详解】（1）如果小明第一题不使用“求助”，那么小明答对第一道题的概率=13；故答案为13； （2）画树状图为：共有9种等可能的结果数，其中两个都正确的结果数为1，所以小明顺利通关的概率为19； （3）建议小明在第一题使用“求助”．理由如下：小明将“求助”留在第一题，画树状图为：小明将“求助”留在第一题使用，小明顺利通关的概率=18， 因为18＞19， 所以建议小明在第一题使用“求助”．【题目点拨】本题考查的是概率，熟练掌握树状图法和概率公式是解题的关键.19、（1）()()31y x x =-+-；（2）2x <-或1x >；（3）1.【解题分析】（1）直接将已知点代入函数解析式求出即可；（2）利用函数图象结合交点坐标得出使一次函数值大于二次函数值的x 的取值范围；（3）分别得出EO ，AB 的长，进而得出面积．【题目详解】（1）∵二次函数与x 轴的交点为()30A -,和()10B , ∴设二次函数的解析式为：()()31y a x x =+-∵()0,3C 在抛物线上，∴3=a(0+3)(0-1)，解得a=-1，所以解析式为：()()31y x x =-+-；（2）()()31y x x =-+-=−x 2−2x ＋3，∴二次函数的对称轴为直线1x =-；∵点C 、D 是二次函数图象上的一对对称点；()0,3C∴()2,3D -；∴使一次函数大于二次函数的x 的取值范围为2x <-或1x >；（3）设直线BD ：y ＝mx ＋n ，代入B （1，0），D （−2，3）得023m n m n ⎧⎨-⎩＋＝＋＝， 解得：11m n -⎧⎨⎩＝＝， 故直线BD 的解析式为：y ＝−x ＋1，把x ＝0代入()()31y x x =-+-得，y=3，所以E （0，1），∴OE ＝1，又∵AB ＝1，∴S △ADE ＝12×1×3−12×1×1＝1． 【题目点拨】此题主要考查了待定系数法求一次函数和二次函数解析式，利用数形结合得出是解题关键．20、（1）证明见解析；（2）当t=3时，△AEQ 93cm 2；（3）（3，0）或（6，30，3 【解题分析】（1）由三角形ABC 为等边三角形，以及AD=BE=CF ，进而得出三角形ADF 与三角形CFE 与三角形BED 全等，利用全等三角形对应边相等得到BF=DF=DE ，即可得证；（2）先表示出三角形AEC 面积，根据EQ 与AB 平行，得到三角形CEQ 与三角形ABC 相似，利用相似三角形面积比等于相似比的平方表示出三角形CEQ 面积，进而表示出AEQ面积，利用二次函数的性质求出面积最大值，并求出此时Q 的坐标即可；（3）当△AEQ 的面积最大时，D 、E 、F 都是中点，分两种情形讨论即 可解决问题；【题目详解】（1）如图①中，∵C （6，0），∴BC=6在等边三角形ABC 中，AB=BC=AC=6，∠A=∠B=∠C=60°，由题意知，当0＜t ＜6时，AD=BE=CF=t ，∴BD=CE=AF=6﹣t ，∴△ADF ≌△CFE ≌△BED （SAS ），∴EF=DF=DE ，∴△DEF 是等边三角形，∴不论t 如何变化，△DEF 始终为等边三角形；（2）如图②中，作AH ⊥BC 于H ，则AH=AB•sin60°=33，∴S △AEC =12×3（6﹣t ）=33(6)2t -， ∵EQ ∥AB ，∴△CEQ ∽△ABC ，∴CEQ ABC S S =（CE CB ）2=2(6)36t -，即S △CEQ =2(6)36t -S △ABC =2(6)36t -×323(6)t -，∴S△AEQ=S△AEC﹣S△CEQ=33(6)2t-﹣23(6)4t-=﹣34（t﹣3）2+934，∵a=﹣34＜0，∴抛物线开口向下，有最大值，∴当t=3时，△AEQ的面积最大为934cm2，（3）如图③中，由（2）知，E点为BC的中点，线段EQ为△ABC的中位线，当AD为菱形的边时，可得P1（3，0），P3（6，3，当AD为对角线时，P2（0，3），综上所述，满足条件的点P坐标为（3，0）或（6，30，3．【题目点拨】本题考查四边形综合题、等边三角形的性质和判定、菱形的判定和性质、二次函数的性质等知识，解题的关键是学会构建二次函数解决最值问题，学会用分类讨论的思想思考问题，属于中考压轴题．21、（1）见解析；（2）25【解题分析】分析：（1）如下图，连接OD，由OA=OD可得∠DAO=∠ADO，结合∠CAD=∠DAB，可得∠CAD=∠ADO，从而可得OD∥AC，由此可得∠C+∠CDO=180°，结合∠C=90°可得∠CDO=90°即可证得CD是⊙O的切线；（2）如下图，连接BD，由AB是⊙O的直径可得∠ADB=90°=∠C，结合∠CAD=∠DAB可得△ACD∽△ADB，由此可得AD ABCD BD=，在Rt△ABD中由AD=6，AB=9易得BD=35，由此即可解得CD的长了.详解：（1）如下图，连接OD．∵OA=OD，∴∠DAB=∠ODA，∵∠CAD=∠DAB，∴∠ODA=∠CAD∴AC∥OD∴∠C+∠ODC=180°∵∠C=90°∴∠ODC=90°∴OD⊥CD，∴CD是⊙O的切线．（2）如下图，连接BD，∵AB是⊙O的直径，∴∠ADB=90°，∵AB=9，AD=6，∴BD=2296-=45=35，∵∠CAD=∠BAD，∠C=∠ADB=90°，∴△ACD∽△ADB，∴AD AB CD BD=，∴6935 CD=，∴CD=185=259．点睛：这是一道考查“圆和直线的位置关系与相似三角形的判定和性质”的几何综合题，作出如图所示的辅助线，熟悉“圆的切线的判定方法”和“相似三角形的判定和性质”是正确解答本题的关键.22、(1)300；(2)见解析；(3)108°；(4)约有840名.【解题分析】（1）根据A种类人数及其占总人数百分比可得答案；（2）用总人数乘以B的百分比得出其人数，即可补全条形图；（3）用360°乘以C类人数占总人数的比例可得；（4）总人数乘以C、D两类人数占样本的比例可得答案．【题目详解】解：（1）本次被调查的学生的人数为69÷23%=300（人），故答案为：300；（2）喜欢B类校本课程的人数为300×20%=60（人），补全条形图如下：（3）扇形统计图中，C类所在扇形的圆心角的度数为360°×90300=108°，故答案为：108°；（4）∵2000×90+36300=840，∴估计该校喜爱C，D两类校本课程的学生共有840名．【题目点拨】本题考查条形统计图、扇形统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解题关键．条形统计图能清楚地表示出每个项目的数据．23、（1）证明见解析；（2）结论：四边形ACDF是矩形．理由见解析.【解题分析】（1）只要证明AB=CD，AF=CD即可解决问题；（2）结论：四边形ACDF是矩形．根据对角线相等的平行四边形是矩形判断即可；【题目详解】（1）证明：∵四边形ABCD是平行四边形，∴BE∥CD，AB=CD，∴∠AFC=∠DCG，∵GA=GD，∠AGF=∠CGD，∴△AGF≌△DGC，∴AF=CD，∴AB=CF．（2）解：结论：四边形ACDF是矩形．理由：∵AF=CD，AF∥CD，∴四边形ACDF是平行四边形，∵四边形ABCD是平行四边形，∴∠BAD=∠BCD=120°，∴∠FAG=60°，∵AB=AG=AF，∴△AFG是等边三角形，∴AG=GF，∵△AGF≌△DGC，∴FG=CG，∵AG=GD，∴AD=CF，∴四边形ACDF是矩形．【题目点拨】本题考查平行四边形的判定和性质、矩形的判定、全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题.24、证明见解析.【解题分析】试题分析：首先根据等边对等角可得∠A=∠B，再由DC∥AB，可得∠D=∠A，∠C=∠B，进而得到∠C=∠D，根据等角对等边可得CO=DO．试题解析：证明：∵AB∥CD∴∠A＝∠D ∠B＝∠C∵OA=OB∴∠A＝∠B∴∠C＝∠D∴OC＝OD考点：等腰三角形的性质与判定，平行线的性质。

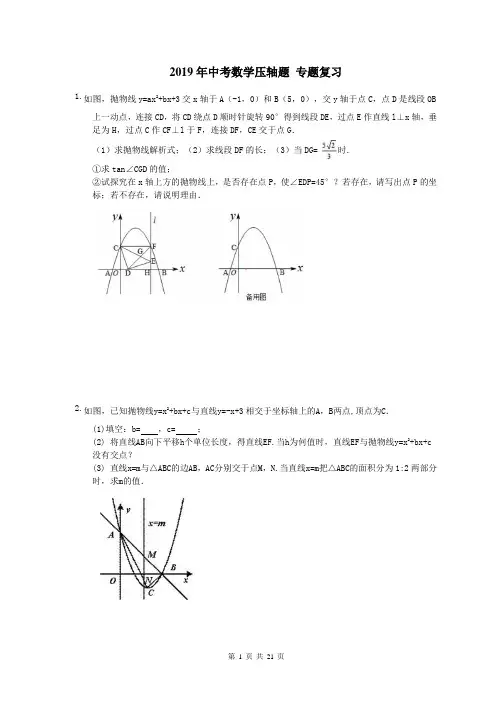
2019年中考数学压轴题专题复习1.如图，抛物线y=ax2+bx+3交x轴于A（-1，0）和B（5，0），交y轴于点C，点D是线段OB上一动点，连接CD，将CD绕点D顺时针旋转90°得到线段DE，过点E作直线l⊥x轴，垂足为H，过点C作CF⊥l于F，连接DF，CE交于点G．（1）求抛物线解析式；（2）求线段DF的长；（3）当DG=时.①求tan∠CGD的值；②试探究在x轴上方的抛物线上，是否存在点P，使∠EDP=45°？若存在，请写出点P的坐标；若不存在，请说明理由．2.如图，已知抛物线y=x2+bx+c与直线y=-x+3相交于坐标轴上的A，B两点,顶点为C．(1)填空：b= ，c= ；(2) 将直线AB向下平移h个单位长度，得直线EF.当h为何值时，直线EF与抛物线y=x2+bx+c没有交点？(3) 直线x=m与△ABC的边AB，AC分别交于点M，N.当直线x=m把△ABC的面积分为1:2两部分时，求m的值．3.已知二次函数y=x2-2mx+4m-8．（1）当x≤2时,函数值y随x的增大而减小，求m的取值范围；（2）以抛物线y=x2-2mx+4m-8的顶点A为一个顶点作该抛物线的内接正△AMN(M,N两点在抛物线上).请问：△AMN的面积是与m无关的定值吗？若是，请求出这个定值；若不是，请说明理由；（3）若抛物线y=x2-2mx+4m-8与x轴交点的横坐标均为整数,求整数m的值．4.如图，在平面直角坐标系中，二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点，与y轴交于点C，连接BC，点D为抛物线的顶点，点P是第四象限的抛物线上的一个动点（不与点D重合）．（1）求∠OBC的度数；（2）连接CD、BD、DP，延长DP交x轴正半轴于点E，且S△OCE=S四边形OCDB，求此时P点的坐标；（3）过点P作PF⊥x轴交BC于点F，求线段PF长度的最大值．5.已知O点为坐标原点，抛物线y=ax2+bx+c(a≠0)与y轴交于点C，且O，C两点间的距离为3.1(1)求点C的坐标；(2)抛物线y1=ax2+bx+c(a≠0)与x轴交于点A(x1,0),B(x2,0),x1∙x2<0,|x1|+|x2|=4.点A，C在直线y2=-3x+t上.①求该抛物线的顶点坐标；②将抛物线y1=ax2+bx+c(a≠0)向左平移n(n>0)个单位，记平移后y随x的增大而增大的部分为P，直线y2=-3x+t向下平移n个单位，当平移后的直线与P有公共点，求2n2-5n的最小值.6.如图所示，已知抛物线y=x2﹣1与x轴交于A、B两点，与y轴交于点C．（1）求A、B、C三点的坐标；（2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积；（3）在x轴上方的抛物线上是否存在一点M，过M作MG⊥x轴于点G，使以A、M、G三点为顶点的三角形与△PCA相似？若存在，请求出M点的坐标；否则，请说明理由．7.如图1，已知抛物线y=﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C点，点P是抛物线上在第一象限内的一个动点，且点P的横坐标为t．（1）求抛物线的表达式；（2）设抛物线的对称轴为l，l与x轴的交点为D．在直线l上是否存在点M，使得四边形CDPM 是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．（3）如图2，连接BC，PB，PC，设△PBC的面积为S．①求S关于t的函数表达式；②求P点到直线BC的距离的最大值，并求出此时点P的坐标．8.如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A（1,3）,B（4,0）两点．（1）求出抛物线的解析式；（2）在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；（3）点P是线段AB上一动点，（点P不与点A、B重合），过点P作PM∥OA，交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，若△BCN、△PMN的面积S△B C N、S△P M N满足S△B C N=2S△P M N，求出MN:NC的值，并求出此时点M的坐标．9.如图1，平面之间坐标系中，等腰直角三角形的直角边BC在x轴正半轴上滑动，点C的坐标为（t，0），直角边AC=4，经过O，C两点做抛物线y1=ax（x﹣t）（a为常数，a＞0），该抛物线与斜边AB交于点E，直线OA：y2=kx（k为常数，k＞0）（1）填空：用含t的代数式表示点A的坐标及k的值：A ，k ；（2）随着三角板的滑动，当a=时：①请你验证：抛物线y1=ax（x﹣t）的顶点在函数y=-0.25x2的图象上；②当三角板滑至点E为AB的中点时，求t的值；（3）直线OA与抛物线的另一个交点为点D，当t≤x≤t+4，|y2﹣y1|的值随x的增大而减小，当x≥t+4时，|y2﹣y1|的值随x的增大而增大，求a与t的关系式及t的取值范围．10.如图，已知抛物线y=（x+2）（x﹣4）（k为常数，且k＞0）与x轴从左至右依次交于A，B两点，与y轴交于点C，经过点B的直线y=﹣x+b与抛物线的另一交点为D．（1）若点D的横坐标为﹣5，求抛物线的函数表达式；（2）若在第一象限内的抛物线上有点P，使得以A，B，P为顶点的三角形与△ABC相似，求k的值；（3）在（1）的条件下，设F为线段BD上一点（不含端点），连接AF，一动点M从点A出发，沿线段AF以每秒1个单位的速度运动到F，再沿线段FD以每秒2个单位的速度运动到D后停止，当点F的坐标是多少时，点M在整个运动过程中用时最少？11.如图1，二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点，与y轴交于点C．若tan∠ABC=3，一元二次方程ax2+bx+c=0的两根为﹣8、2．（1）求二次函数的解析式；（2）直线l绕点A以AB为起始位置顺时针旋转到AC位置停止，l与线段BC交于点D，P 是AD的中点．①求点P的运动路程；②如图2，过点D作DE垂直x轴于点E，作DF⊥AC所在直线于点F，连结PE、PF，在l运动过程中，∠EPF的大小是否改变？请说明理由；（3）在（2）的条件下，连结EF，求△PEF周长的最小值．12.在等腰△ABC中，AB=AC=10，BC=12，D为底边BC的中点，以D为顶点的角∠PDQ=∠B．（1）如图1，若射线DQ经过点A，DP交AC边于点E，直接写出与△CDE相似的三角形；（2）如图2，若射线DQ交AB于点F，DP交AC边于点E，设AF=x，AE为y，试写出y与x的函数关系式；（不要求写出自变量的取值范围）（3）在（2）的条件下，连接EF，则△DEF与△CDE相似吗？试说明理由．13.如图，在平面直角坐标系中，直线交x轴于点P，交y轴于点A，抛物线的图象过点E(-1，0)，并与直线相交于A、B两点.（1）求抛物线的解析式（关系式）；（2）过点A作AC⊥AB交x轴于点C，求点C的坐标；（3）除点C外，在坐标轴上是否存在点M，使得△MAB是直角三角形？若存在，请求出点M的坐标，若不存在，请说明理由.14.如图，已知在平面直角坐标系中，点A（4，0）是抛物线y=ax2+2x﹣c上的一点，将此抛物线向下平移6个单位后经过点B（0，2），平移后所得的新抛物线的顶点记为C，新抛物线的对称轴与线段AB的交点记为P．（1）求平移后所得到的新抛物线的表达式，并写出点C的坐标；（2）求∠CAB的正切值；（3）如果点Q是新抛物线对称轴上的一点，且△BCQ与△ACP相似，求点Q的坐标．15.如图，抛物线y=ax2+bx+c经过A（1，0）、B（4，0）、C（0，3）三点．（1）求抛物线的解析式；（2）如图①，在抛物线的对称轴上是否存在点P，使得四边形PAOC的周长最小？若存在，求出四边形PAOC周长的最小值；若不存在，请说明理由．（3）如图②，点Q是线段OB上一动点，连接BC，在线段BC上是否存在这样的点M，使△CQM 为等腰三角形且△BQM为直角三角形？若存在，求点M的坐标；若不存在，请说明理由．答案1.2.3.解：4.解：（1）∵y=x2﹣2x﹣3=（x﹣3）（x+2），∴由题意得，A（﹣1，0），B（3，0），C（0，﹣3），D（1，﹣4）．在Rt△OBC中，∵OC=OB=3，∴△OBC为等腰直角三角形，∴∠OBC=45°．（2）如图1，过点D作DH⊥x轴于H，此时S四边形OCDB=S梯形OCDH+S△HBD，∵OH=1，OC=3，HD=4，HB=2，∴S梯形OCDH=0.5•（OC+HD）•OH=7.5，S△HBD=0.5•HD•HB=4，∴S四边形OCDB=7.5．∴S△OCE=S四边形OCDB=7.5=，∴OE=5，∴E（5，0）．设l DE：y=kx+b，∵D（1，﹣4），E（5，0），∴，解得，∴l DE：y=x﹣5．∵DE交抛物线于P，设P（x，y），∴x2﹣2x﹣3=x﹣5，解得 x=2 或x=1（D点，舍去），∴x P=2，代入l DE：y=x﹣5，∴P（2，﹣3）．（3）如图2，设l BC：y=kx+b，∵B（3，0），C（0，﹣3），∴，解得，∴l BC：y=x﹣3．∵F在BC上，∴y F=x F﹣3，∵P在抛物线上，∴y P=x P2﹣2x P﹣3，∴线段PF长度=y F﹣y P=x F﹣3﹣（x P2﹣2x P﹣3），∵x P=x F，∴线段PF长度=﹣x P2+3x P=﹣（x P﹣1.5）2+2.25，（1＜x P≤3），∴当x P=1.5时，线段PF长度最大为2.25．5.解：（1）令x=0，则y=c，故C（0，c），∵OC的距离为3，∴|c|=3，即c=±3，∴C（0，3）或（0，-3）；（2）∵x1x2＜0，∴x1，x2异号，①若C（0，3），即c=3，把C（0，3）代入y2=-3x+t，则0+t=3，即t=3，∴y2=-3x+3，把A（x1，0）代入y2=-3x+3，则-3x1+3=0，即x1=1，∴A（1，0），∵x1，x2异号，x1=1＞0，∴x2＜0，∵|x1|+|x2|=4，∴1-x2=4，解得：x2=-3，则B（-3，0），代入y1=aa-b-3＝09a+3b-3＝0，解得：a＝1b＝-2，∴y1=x2-2x-3=（x-1）2-4，则当x≥1时，y随x增大而增大，综上所述，若c=3，当y随x增大而增大时，x≤-1；若c=-3，当y随x增大而增大时，x≥1；（3）①若c=3，则y1=-x2-2x+3=-（x+1）2+4，y2=-3x+3，y1向左平移n个单位后，则解析式为：y3=-（x+1+n）2+4，则当x≤-1-n时，y随x增大而增大，y2向下平移n个单位后，则解析式为：y4=-3x+3-n，要使平移后直线与P有公共点，则当x=-1-n，y3≥y4，即-（-1-n+1+n）2+4ax2+bx+3得，a+b+3＝09a-3b+3＝0，解得：a＝-1b＝-2，∴y1=-x2-2x+3=-（x+1）2+4，则当x≤-1时，y随x增大而增大．②若C（0，-3），即c=-3，把C（0，-3）代入y2=-3x+t，则0+t=-3，即t=-3，∴y2=-3x-3，把A（x1，0），代入y2=-3x-3，则-3x1-3=0，即x1=-1，∴A（-1，0），∵x1，x2异号，x1=-1＜0，∴x2＞0 ∵|x1|+|x2|=4，∴1+x2=4，解得：x2=3，则B（3，0），代入y1=ax2+bx+3得，-1-n）+3-n，得：n≤-1，∵n＞0，∴n≤-1不符合条件，应舍去；②若c=-3，则y1=x2-2x-3=（x-1）2-4，y2=-3x-3，y1向左平移n个单位后，则解析式为：y3=（x-1+n）2-4，则当x≥1-n时，y随x增大而增大，y2向下平移n个单位后，则解析式为：y4=-3x-3-n，要使平移后直线与P有公共点，则当x=1-n，y3≤y4，即（1-n-1+n）2-4≤-3（1-n）-3-n，解得：n≥1，综上所述：n≥1，2n2-5n=2（n-54）2-25/8，∴当n=54时，2n2-5n的最小值为：-25/8．6.7.解：8.【解答】解：（1）∵A （1，3），B （4，0）在抛物线y=mx 2+nx 的图象上，∴，解得，∴抛物线解析式为y=﹣x2+4x；（2）存在三个点满足题意，理由如下：当点D在x轴上时，如图1，过点A作AD⊥x轴于点D，∵A（1，3），∴D坐标为（1，0）；当点D在y轴上时，设D（0，d），则AD2=1+（3﹣d）2，BD2=42+d2，且AB2=（4﹣1）2+（3）2=36，∵△ABD是以AB为斜边的直角三角形，∴AD2+BD2=AB2，即1+（3﹣d）2+42+d2=36，解得d=，∴D点坐标为（0，）或（0，）；综上可知存在满足条件的D点，其坐标为（1，0）或（0，）或（0，）；（3）如图2，过P作PF⊥CM于点F，∵PM∥OA，∴Rt△ADO∽Rt△MFP，∴==3，∴MF=3PF，在Rt△ABD中，BD=3，AD=3，∴tan∠ABD=，∴∠ABD=60°，设BC=a，则CN=a，在Rt△PFN中，∠PNF=∠BNC=30°，∴tan∠PNF==，∴FN=PF，∴MN=MF+FN=4PF，∵S△B C N=2S△P M N，∴a2=2××4PF2，∴a=2PF，∴NC=a=2PF，∴==，∴MN=NC=×a=a，∴MC=MN+NC=（+）a，∴M点坐标为（4﹣a，（+）a），又M点在抛物线上，代入可得﹣（4﹣a）2+4（4﹣a）=（+）a，解得a=3﹣或a=0（舍去），OC=4﹣a=+1，MC=2+，∴点M的坐标为（+1，2+）．9.10.11.12.【解答】解：（1）与△CDE相似的三角形为△ABD，△ACD，△ADE；理由如下：∵AB=AC，D为底边BC的中点，∴∠B=∠C，AD⊥BC，∴∠ADB=∠ADC=90°，∴△ABD∽△ACD，∵∠PDQ=∠B，∴∠PDQ=∠C，又∵∠DAE=∠CAD，∴△ADE∽△ACD；∵∠CDE+∠PDQ=90°，∴∠C+∠PDQ=90°，∴∠CED=90°=∠ADC，又∵∠C=∠C，∴△CDE∽△CAD，∴△△ABD∽△ACD∽△ADE∽△CDE；（2）∵∠FDC=∠B+∠BDF，∠FDC=∠FDE+∠EDC，∴∠EDC=∠BDF，∴△BDF∽△CDE，∴，∵D为BC的中点，∴BD=CD=6，∴∴y=；（3）△DEF与△CDE相似．理由如下：如图所示：由（2）可知：△BDF∽△CDE，则，∵BD=CD，∴，又∵∠EDF=∠C，∴△DEF∽△CED．13.14.15.解：第21 页共21 页。

2023天津中考数学压轴题
一辆汽车以每小时60公里的速度行驶，行驶了4小时后，剩余的路程还有多少公里？
一个长方形花坛的长是8米，宽是5米，如果每平方米能种3株花，那么这个花坛最多能种多少株花？
一桶水有30升，小明用每分钟2升的速度倒水，需要多少分钟才能倒完？
一个正方形的边长是6厘米，求其面积和周长。

一条绳子长12米，小明每天用1.5米的速度剪断，需要多少天才能剪断整条绳子？
一个三角形的底边长是10厘米，高是8厘米，求其面积。

一辆自行车以每小时15公里的速度行驶，行驶了3小时后，剩余的路程还有多少公里？一个长方形的长是18米，宽是5米，求其面积和周长。

一桶油有40升，小明用每分钟3升的速度倒油，需要多少分钟才能倒完？
一个正方形的边长是9厘米，求其面积和周长。

天津师范大学附属实验中学中考数学期末几何综合压轴题模拟汇编一、中考几何压轴题1．问题发现：（1）如图1，在Rt △ABC 中，∠BAC=30°，∠ABC ＝90°，将线段AC 绕点A 逆时针旋转，旋转角α=2∠BAC ， ∠BCD 的度数是 ；线段BD ，AC 之间的数量关系是 ． 类比探究：（2）在Rt △ABC 中，∠BAC=45°，∠ABC ＝90°，将线段AC 绕点A 逆时针旋转，旋转角α=2∠BAC ，请问（1）中的结论还成立吗？；拓展延伸：（3）如图3，在Rt △ABC 中，AB ＝2，AC ＝4，∠BDC ＝90°，若点P 满足PB ＝PC ，∠BPC ＝90°，请直接写出线段AP 的长度．2．类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整．原题：如图1，在平行四边形ABCD 中，点E 是BC 的中点，点F 是线段AE 上一点，BF 的延长线交射线CD 于点G ．若3AF EF ，求CD CG的值．（1）尝试探究在图1中，过点E 作//EH AB 交BG 于点H ，则AB 和EH 的数量关系是_________，CG 和EH 的数量关系是_________，CD CG 的值是_________． （2）类比延伸如图2，在原题的条件下，若()0AF m m EF =>，则CD CG 的值是_________（用含有m 的代数式表示），试写出解答过程．（3）拓展迁移如图3，梯形ABCD 中，//DC AB ，点E 是BC 的延长线上的一点，AE 和BD 相交于点F ．若AB a CD =，BC b BE=，()0,0a b >>，则AF EF 的值是________（用含a 、b 的代数式表示）． 3．已知：如图1所示将一块等腰三角板BMN 放置与正方形ABCD 的B 重合，连接AN 、CM ，E 是AN 的中点，连接BE ．（观察猜想）（1）CM 与BE 的数量关系是________；CM 与BE 的位置关系是________；（探究证明）（2）如图2所示，把三角板BMN 绕点B 逆时针旋转(090)αα<<，其他条件不变，线段CM 与BE 的关系是否仍然成立，并说明理由；（拓展延伸）（3）若旋转角45α=，且2NBE ABE ∠=∠，求BC BN的值． 4．（1）问题探究：如图1，在正方形ABCD 中，点E 、F 、G 分别是BC 、AB 、CD 上的点，且FG AE ⊥，求证：FG AE =；（2）类比应用：如图2，在矩形ABCD 中，AB nBC =，FG AE ⊥，将矩形ABCD 沿FG 折叠使点A 落在E 点处，得到矩形FEPG ．①若点E 为BC 的中点，试探究FG 与AF 的数量关系；②拓展延伸：连CP ，当32n =时，210GF =，34tan CGP ∠=，求CP 的长． 5．综合与实践背景阅读：“旋转”即物体绕一个点或一个轴做圆周运动．在中国古典专著《百喻经·口诵乘船法而不解用喻》中记载：“船盘回旋转，不能前进．”而图形旋转即：在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转，这个定点叫做旋转中心，转动的角叫做旋转角．综合实践课上，“睿智”小组专门探究了正方形的旋转，情况如下：在正方形ABCD 中，点O 是线段BC 上的一个动点，将正方形ABCD 绕点O 顺时针旋转得到正方形A B C D ''''（点A '，B '，C '，D 分别是点A ，B ，C ，D 的对应点）．设旋转角为α（0180α<<︒）．操作猜想：（1）如图1，若点O 是BC 中点，在正方形ABCD 绕点旋转过程中，连接AA '，BB '，DD '，则线段AA '与DD '的数量关系是_______；线段AA '与BB '的数量关系是________． 探究验证：（2）如图2，在（1）的条件下，在正方形ABCD 绕点O 旋转过程中，顺次连接点B ，B '，C ，C '，B ．判断四边形''BB CC 的形状，并说明理由．拓展延伸：（3）如图3，若2BO CO =，在正方形ABCD 绕点O 顺时针旋转的过程中，设直线BB '交线段AA '于点P ．连接OP ，并过点O 作OQ BB '⊥于点Q ．请你补全图形，并直接写出OP OQ的值． 6．如图，已知ABC 和ADE 均为等腰三角形，AC BC =，DE AE =，将这两个三角形放置在一起．（1）问题发现：如图①，当60ACB AED ∠=∠=︒时，点B 、D 、E 在同一直线上，连接CE ，则线段BD 、CE 之间的数量关系是_________，CEB ∠=_________︒；（2）拓展探究：如图②，当ACB AED α∠=∠=时，点B 、D 、E 不在同一直线上，连接CE ，求出线段BD 、CE 之间的数量关系及BD 、CE 所在直线相交所成的锐角的大小（都用含α的式子表示），并说明理由：（3）解决问题：如图③，90ACB AED ∠=∠=︒，10AC =2AE =CE 、BD ，在AED 绕点A 旋转的过程中，当CE 所在的直线垂直于AD 时，请你直接写出BD 的长．7．（阅读理解）定义：如果四边形的某条对角线平分一组对角，那么把这条对角线叫“协和线”，该四边形叫做“协和四边形”．（深入探究）（1）如图1，在四边形ABCD 中，AB BC =，AD CD =，请说明：四边形ABCD 是“协和四边形”．（尝试应用）（2）如图2，四边形ABCD 是“协和四边形”，BD 为“协和线”，AB AD ⊥，60ADC ∠=︒，若点E 、F 分别为边AD 、DC 的中点，连接BE ，BF ，EF ．求：①DEF 与BEF 的面积的比；②EBF ∠的正弦值．（拓展应用）（3）如图3，在菱形ABCD 中，8AB =，120BAD ∠=︒，点E 、F 分别在边AD 和BC 上，点G 、K 分别在边AB 和CD 上，点N 为BE 与GF 的交点，点M 在EF 上，连接MN ，若四边形BGEF ，DHMK 都是“协和四边形”，“协和线”分别是GF 、HK ，求MN 的最小值．8．在ABC ∆中，BD AC ⊥于点D ，点Р为射线BD 上任一点（点B 除外）连接AP ，将线段PA 绕点Р顺时针方向旋转α︒，ABC α=∠，得到PE ，连接CE ．（1）（观察发现）如图1，当BA BC =，且60ABC ∠=︒时，BP 与CE 的数量关系是___________，BC 与CE 的位置关系是___________．（2）（猜想证明）如图2，当BA BC =，且90ABC ∠=︒时，（1）中的结论是否成立？若成立，请予以证明；若不成立，请说明理由．（请选择图2，图3中的一种情况予以证明或说理）（3）（拓展探究）在（2）的条件下，若8AB =，52AP =，请直接写出CE 的长． 9．如图1，在Rt ABC 中，90ACB ∠=︒，点P 在斜边AB 上，点D ､E ､F 分别是线段PA ､PB ､PC 的中点，易知DEF 是直角三角形．现把DEF 以点P 为中心，顺时针旋转α，其中0360α︒<<︒．连接AD ､BE ､CF ．（1）操作发现如图2，若点P 是AB 的中点，连接PF ，可以发现=AD CF ______CF BE=______； （2）类比探究如图3，Rt ABC 中，CP AB ⊥于点P ，请判断AD CF 与CF BE 的大小，结合图2说明理由； （3）拓展提高在（2）的条件下，如果30CAB ∠=︒，且4AB =，在DEF 旋转的过程中，当以点C ､D ､F ､P 四点为顶点的四边形与以点B ､E ､F ､P 四点为顶点的四边形都是平行四边形时，直接写出线段AD ､CF ､BE 的长．10．已知：60AOC BOC ∠=∠=︒，过平面内一点P 分别向OA 、OB 、OC 画垂线，垂足分别为D 、E 、F ．（问题引入）如图①，当点P 在射线OC 上时，求证：OD OE =．（类比探究）（1）如图②，当点P 在AOC ∠内部，点E 在射线OB 上时，求证：OD OE OF +=．∠内部，点E在射线OB的反向延长线上时，在图③中画出示意图，并（2）当点P在AOC直接写出线段OD、OE、OF之间的数量关系．（知识拓展）如图④，AB、CD、EF是O的三条弦，都经过圆内一点P，且++的数量关系，并证明你的结论．∠=∠=︒．判断PA PD PE60FPD BPD++与PB PC PF11．如图l，在正方形ABCD ABCD中，8AB=AB=8，点E E在AC AC上，且22AE=，⊥于点E，交AB于点F，连接CF，DE．AE=过E点作EF AC22（问题发现）（1）线段DE与CF的数量关系是________，直线DE与CF所夹锐角的度数是___________；（拓展探究）（2）当AEF∆绕点A顺时针旋转时，上述结论是否成立？若成立，请写出结论并结合图2给出证明；若不成立，请说明理由；（解决问题）（3）在（2）的条件下，当点E 到直线AD 的距离为2时，请直接写出CF 的长． 12．问题提出（1）如图（1），在等边三角形ABC 中，点M 是BC 上的任意一点（不含端点B 、C ），连接AM ，以AM 为边作等边三角形AMN ，连接CN ，则∠ACN ＝ °．类比探究（2）如图（2），在等边三角形ABC 中，点M 是BC 延长线上的任意一点（不含端点C ），其他条件不变，（1）中的结论还成立吗？请说明理由．拓展延伸（3）如图（3），在等腰三角形ABC 中，BA ＝BC ，点M 是BC 上的任意一点（不含端点B 、C ），连接AM ，以AM 为边作等腰三角形AMN ，使AM ＝MN ，连接CN ．添加一个条件，使得∠ABC ＝∠ACN 仍成立，写出你所添加的条件，并说明理由．13．我们定义：连结凸四边形一组对边中点的线段叫做四边形的“准中位线”．（1）概念理解：如图1，四边形ABCD 中，F 为CD 的中点，90ADB ∠=︒，E 是AB 边上一点，满足DE AE =，试判断EF 是否为四边形ABCD 的准中位线，并说明理由．（2）问题探究：如图2，ABC ∆中，90ACB ∠=︒，6AC =，8BC =，动点E 以每秒1个单位的速度，从点A 出发向点C 运动，动点F 以每秒6个单位的速度，从点C 出发沿射线CB 运动，当点E 运动至点C 时，两点同时停止运动．D 为线段AB 上任意一点，连接并延长CD ，射线CD 与点,,,A B E F 构成的四边形的两边分别相交于点,M N ，设运动时间为t ．问t 为何值时，MN 为点,,,A B E F 构成的四边形的准中位线．（3）应用拓展：如图3，EF 为四边形ABCD 的准中位线，AB CD =，延长FE 分别与BA ，CD 的延长线交于点,M N ，请找出图中与M ∠相等的角并证明．14．如图（1），已知点G 在正方形ABCD 的对角线AC 上，,GE BC ⊥垂足为点,E GF CD ⊥，垂足为点F ．（1）证明与推断：①求证：四边形CEGF 是正方形；②推断：AG BE 的值为_ _； （2）探究与证明：将正方形CEGF 绕点C 顺时针方向旋转a 角)045(a ︒<<︒，如图（2）所示，试探究线段AG 与BE 之间的数量关系，并说明理由；（3）拓展与运用：若24AB EC ==，正方形CEGF 在绕点C 旋转过程中，当A E G 、、三点在一条直线上时，则BE = ．15．（1）观察发现：如图1，在ABC ∆中，AC BC =，90ACB ∠=︒，点D 是ACB ∠的平分线CM 上一点，将线段CD 绕点C 逆时针旋转90°到CE ，连结BE 、BD ，DE 交BC 于F ．填空：①线段BD 与BE 的数量关系是_________；②线段BC 与DE 的位置关系是_________．（2）拓展探究：如图2，在ABC ∆中，AC BC =，ACB α∠=，点D 是边AB 的中点，将CD 绕点C 逆时针旋转α到CE ，连结BE 、DE ，DE 交BC 于F ．（1）中的结论是否仍然成立？请说明理由．（3）拓展应用：如图3，在ABC ∆中，AB AC =，60BAC ∠=︒，2BC =，ACB ∠的平分线交AB 于D ，点E 是射线CD 上的一点，将CE 绕点C 顺时针旋转60°到CF ，连结AE 、AF 、EF ，EF 与AC 相交于G ，若以A 、F 、G 为顶点的三角形与ADE ∆全等，直接写出EF 的长．16．如图1所示，边长为4的正方形ABCD 与边长为()14a a <<的正方形CFEG 的顶点C 重合，点E 在对角线AC 上．（问题发现）如图1所示，AE 与BF 的数量关系为________；（类比探究）如图2所示，将正方形CFEG 绕点C 旋转，旋转角为()030αα<<︒，请问此时上述结论是否还成立？如成立写出推理过程，如不成立，说明理由；（拓展延伸）若点F 为BC 的中点，且在正方形CFEG 的旋转过程中，有点A 、F 、G 在一条直线上，直接写出此时线段AG 的长度为________17．如图1，在Rt △ABC 中，∠A ＝90°，AB ＝AC ，点D ，E 分别在边AB ，AC 上，AD ＝AE ，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点．（1）观察猜想：图1中，线段PM 与PN 的数量关系是 ，位置关系是 ；（2）探究证明：把△ADE 绕点A 逆时针方向旋转到图2的位置，连接MN ，BD ，CE ，判断△PMN 的形状，并说明理由；（3）拓展延伸：把△ADE 绕点A 在平面内自由旋转，若AD ＝4，AB ＝10，请直接写出△PMN 面积的最大值．18．问题情境：两张直角三角形纸片中，90BAC DAE ∠=∠=︒．连接BD ，CE ，过点A 作BD 的垂线，分别交线段BD ，CE 于点M ，N （ABC ∆与ADE ∆在直线MN 异侧）．特例分析：（1）如图1，当AB AC AD AE ===时，求证：2BD AN =； 拓展探究： （2）当12AB AD AC AE ==，探究下列问题： ①如图2，当AB AD =时，直接写出线段BD 与AN 之间的数量关系： ； ②如图3，当AB AD ≠时，猜想BD 与AN 之间的数量关系，并说明理由； 推广应用： （3）若图3中，AB ADk AC AE==，设ABD ∆的面积为S ，则ACE ∆的面积为 ．（用含k ，s 的式子表示）19．[探索发现]（1）如图①，△ABC 与△ADE 为等腰三角形，且两顶角∠ABC ＝∠ADE ，连接BD 与CE ，则△ABD 与△ACE 的关系是 ；[操作探究]（2）在△ABC 中，AB ＝AC ＝3，∠BAC ＝100°，D 是BC 的中点，在线段AD 上任取一点P ，连接PB ，将线段PB 绕点P 按逆时针方向旋转80°，点B 的对应点是点E ，连接BE ，得到△BPE ，随着点P 在线段AD 上位置的变化，点E 的位置也在变化，点E 可能在直线AD 的左侧，也可能在直线AD 上，还可能在直线AD 的右侧．请你探究，当点E 在直线AD 上时，如图②所示，连接CE ，判断直线CE 与直线AB 的位置关系，并说明理由． [拓展应用]（3）在（2）的应用下，请在图③中画出△BPE ，使得点E 在直线AD 的右侧，连接CE ，试求出点P 在线段AD 上运动时，AE 的最小值．20．如图，在ABC 中，AB AC =，90BAC ∠=︒，5AB =，D 为底边BC 上一动点，连接AD ，以AD 为斜边向左上方作等腰直角ADE ，连接BE ．观察猜想：（1）当点E 落在线段AB 上时，直接写出EB ，ED 的数量关系：EB _______ED ． 类比探究：（2）如图2，当点D 在线段BC 上运动时，请问（1）中结论是否仍然成立？若成立，请证明；若不成立，请说明理由；拓展延伸：（3）在点D 运动过程中，当7BE =时，请直接写出线段CD 的长．【参考答案】***试卷处理标记，请不要删除一、中考几何压轴题1．（1）120°，BD=AC ；（2）不成立，理由详见解析；（3）或． 【分析】（1）过点D 作DE ⊥BC ，通过线段之间的转换得到AC 与DE 之间的关系，在直角三角形BDE 中通过BD 与DE 的关系，得到BD 解析：（1）120°，7AC ；（2）不成立，理由详见解析；（32或32 【分析】（1）过点D 作DE ⊥BC ，通过线段之间的转换得到AC 与DE 之间的关系，在直角三角形BDE 中通过BD 与DE 的关系，得到BD,AC 之间的关系. （2）类比（1）的解法，找线段之间的关系. (3)分情况进行讨论，画出符合题意得图形进行求解. 【详解】解：（1）如图3，过点D 作DE ⊥BC ，垂足为E ，设BC=m ．在Rt △ABC 中，∠BAC=30°，由BC=AB·tan30°，BC=AC·sin30°，得AC=2m ，3， ∵AC=AD ，∠CAD=2×30°=60°，∴△ACD 为等边三角形，∴∠ACD=60°，CD=AC=2m ， ∴∠BCD=60°×2=120°，在Rt △DEC 中，∠DCE=180°-120°=60°，DC=2m ，∴CE=CD·cos60°=m ，DE=CE·tan60°3，∴在Rt △BED 中，()()2232m m +7m ，∴BD AC 7m7，故7AC ．故答案为：120°；7AC ． （2）不成立，理由如下：设BC=n ，在Rt △ABC 中，∠BAC=45°，∠ABC=90°，∴BC=AB=m ，22， ∵AC=AD ，∠CAD=90°，∴△CAD 为等腰直角三角形，∴∠ACD=45°，2， ∴∠BCD=2×45°=90°，在Rt △BCD 中，()222n n +5n ，∴BD AC 52n n1010．答案为：90°；10．故结论不成立． （3）AP 2或32∵PB=PC ，∴点P 在线段BC 的垂直平分线上，∵∠BAC=∠BCP=90°，故A 、B 、C 、P 四点共圆，以线段BC 的中点为圆心构造⊙O ，如图4，图5，分类讨论如下： ①当点P 在直线BC 上方时，如图4，作PM ⊥AC ，垂足为M ，设PM=x ．∵PB=PC ，∠BPC=90°，∴△PBC 为等腰直角三角形，∴∠PBC=45°，∵∠PAC=∠PBC=45°，∴△AMP 为等腰直角三角形，∴AM=PM=x ，22x ， 在Rt △ABC 中，AB=2，AC=4，∴222+452∴PC=BC·sin45°10 在Rt △PMC 中，∵∠PMC=90°，PM=x ，10，CM=4-x ，∴()222410x x +-=，解得：11x =，23x =（舍），∴2x 2②当点P 在直线BC 的下方时，如图5，作PN ⊥AB 的延长线，垂足为N ，设PN=y ． 同上可得10△PAN 为等腰三角形，∴AN=PN=y ，∴BN=y-2， 在Rt △PNB 中，∵∠PNB=90°，PN=y ，BN=y-2，10，∴()222210y y +-=，解得：13y =，21y =-（舍），∴2=32AP 2或32 【点睛】本题考查的是等边三角形的判定和性质、勾股定理、以及旋转变换的性质，掌握类比思想解题是解决本题的关键．2．（1）；；；（2）；（3）． 【分析】（1）本问体现“特殊”的情形，是一个确定的数值．如答图1，过E 点作平行线，构造相似三角形，利用相似三角形和中位线的性质，分别将各相关线段均统一用EH 来表示，最解析：（1）3AB EH =；2CG EH =；32；（2）2m；（3）ab ．【分析】（1）本问体现“特殊”的情形，3AFEF=是一个确定的数值．如答图1，过E 点作平行线，构造相似三角形，利用相似三角形和中位线的性质，分别将各相关线段均统一用EH 来表示，最后求得比值； （2）本问体现“一般”的情形，AFm EF=不再是一个确定的数值，但（1）问中的解题方法依然适用，如答图2所示．（3）本问体现“类比”与“转化”的情形，将（1）（2）问中的解题方法推广转化到梯形中，如答图3所示． 【详解】解：（1）依题意，过点E 作//EH AB 交BG 于点H ，如图1所示．则有ABF EHF ，∴3AB AFEH EF==， ∴3AB EH =． ∵ABCD ，//EH AB ，∴//EH CD ， 又∵E 为BC 中点， ∴EH 为BCG 的中位线， ∴2CG EH =．3322CD AB EH CG CG EH ===． 故答案为：3AB EH =；2CG EH =；32． （2）如图2所示，作//EH AB 交BG 于点H ，则EFH AFB △△．∴AB AFm EH EF==， ∴AB mEH =． ∵AB CD =， ∴CD mEH =． ∵////EH AB CD ， ∴BEH BCG △△．∴2CG BCEH BE==， ∴2CG EH =． ∴22CD mEH mCG EH ==． 故答案为：2m． （3）如图3所示，过点E 作//EH AB 交BD 的延长线于点H ，则有////EH AB CD ． ∵//EH CD ， ∴BCD BEH △△， ∴=CD BCb EH BE=， ∴CD bEH =． 又ABa CD=， ∴AB aCD abEH ==． ∵//EH AB ， ∴ABFEHF ，∴==AF AB abEHab EF EH EH=． 故答案为：ab ．【点睛】本题的设计独特：由平行四边形中的一个特殊的例子出发（第1问），推广到平行四边形中的一般情形（第2问），最后再通过类比、转化到梯形中去（第3问）．各种图形虽然形式不一，但运用的解题思想与解题方法却是一以贯之：即通过构造相似三角形，得到线段之间的比例关系，这个比例关系均统一用同一条线段来表达，这样就可以方便地求出线段的比值．本题体现了初中数学的类比、转化、从特殊到一般等思想方法，有利于学生触类旁通、举一反三．3．（1）；；（2）成立，理由见解析；（3） 【分析】（1）【观察猜想】根据正方形ABCD ，得到AB=CB ，由等腰三角形BMN ，得到BM=BN ，可证明Rt △BAN ≌Rt △BCM （HL)，又根据E 是A解析：（1）2CM BE =；CM BE ⊥；（2）成立，理由见解析；（3）62-【分析】（1）【观察猜想】根据正方形ABCD ，得到AB=CB ，由等腰三角形BMN ，得到BM=BN ，可证明Rt△BAN≌Rt△BCM（HL)，又根据E是AN的中点，即可证明CM=2BE，根据等边对等角得到∠ABE=∠BCM，∠ABE+∠BMC=90∘即可证明CM⊥BE．（2）【探究证明】延长BE至F使EF= BE，连接AF，先证明△AEF≌△NEB，再证明△FAB≌MBC，得到CM=BF=2BE，∠BCM=∠ABF，得到∠ABF+∠FBC=90°，进而求得∠BCM+∠EBC=90°，即可证明EB⊥CM；（3）[拓展延伸] 由a=45°得到∠ABE= 15°，由前面可得∠BMC= 30°，过C作CG⊥MB于G，设CG为m，则BC=2m，MG=3m，所以MB= BN=3m-m，最后求得BCBN的值．【详解】解:【观察猜想】(1)CM =2BE ；CM⊥BE；如图1所示图1∵正方形ABCD，∴AB=CB，∵等腰三角形BMN，∴BM=BN，∴Rt△BAN≌Rt△BCM（HL)，∴∠BAN=∠BCM，又∵E是AN的中点，∴BE=AE=NE=12AN，∴CM=2BE，∵BE=AE，∴∠BAN=∠ABE，∴∠ABE=∠BCM，∴∠ABE+∠BMC=∠BCM+∠BMC=90∘∴∠BPM=90∘∴CM⊥BE．【探究证明】(2)CM = 2BE，CM ⊥ BE仍然成立．如图2所示，延长BE至F使EF= BE，连接AF，∵AE= EN，∠AEF=∠NEB，EF= BE，∴△AEF≌△NEB∴AF= BN，∠F=∠EBN，∴AF//BN，AF= BM，∴∠FAB+∠ABN = 180°，∵∠MBN= ∠ABC= 90°，∴∠NBC+∠ABN= 90°，∴∠NBA+∠FAD= 90°，∴∠CBN= ∠FAD∴∠FAB=∠MBC，∵AB=BC，∴△FAB≌MBC，∴CM=BF=2BE，∠BCM=∠ABF，∵∠ABF+∠FBC=90°∴∠BCM+∠EBC=90°，∴EB⊥CM；[拓展延伸] (3)由a=45°得∠MBA=∠ABN= 45°，∵∠NBE= 2∠ABE，∴∠ABE= 15°，由前面可得∠MCB=∠ABE= 15°，∠MBC= 135°，∴∠BMC= 180°-15°-135°=30°，如图3所示，过C作CG⊥MB于G，图3设CG为m则BC=2m ，MG=3m ，所以MB= BN=3m-m ， ∴26223BC m BM m m-==-． 【点睛】本题考查了正方形的性质，全等三角形的性质和判定，等腰直角三角形的性质，直角三角形的性质，解题的关键是灵活运用以上性质解决问题．4．（1）见解析；（2）①；② 【分析】（1）过点作于，证，即可证得；（2）①设，则，利用勾股定理求得，再利用勾股定理表示出，再证明，可得，由此可得，进而可求得答案； ②过点P 作于点，先由①得，再证解析：（1）见解析；（2）①2414AF n FG+=；②955CP = 【分析】（1）过点G 作GH AB ⊥于H ，证ABE GHF ≅，即可证得FG AE =； （2）①设AF EF x ==，则FB AB AF nBC x =-=-，利用勾股定理求得2418n x BC AF n+=⋅=，再利用勾股定理表示出2221()4AE n BC =+，再证明ABEGHF ，可得AE AB ABn FG GH BC===，由此可得222n FG AE =，进而可求得答案； ②过点P 作PM BC ⊥于点M ，先由①得33102AE FG ==，再证明∠BFE ＝∠CGP ，可得34BE tan BFE BF ∠==，进而利用勾股定理可求得3BE =，4BF =，9AB =，最后根据BEF MPE △△，可得EF BF BEPE ME MP==，计算即可． 【详解】（1）证明：如图，过点G 作GH AB ⊥于H ，则∠AHG ＝∠FHG ＝90°，∵在正方形ABCD 中，∴∠HAD ＝∠D ＝∠B ＝90°，AD ＝AB ，∴四边形AHGD 为矩形， ∴AD ＝HG ， ∴AB ＝HG ， ∵FG AE ⊥， ∴∠FQA ＝90°， ∴∠AFQ ＋∠BAE ＝90°， ∵∠FHG ＝90°， ∴∠AFQ ＋∠FGH ＝90°， ∴∠BAE ＝∠FGH ， ∴在ABE △与GHF △中BAE HGF AB HGB FHG ∠=∠⎧⎪=⎨⎪∠=∠⎩ ∴ABE GHF ≅（ASA ），∴FG AE =；()2①∵点E 为BC 的中点，∴12BE CE BC ==， ∵折叠，∴设AF EF x ==， ∴FB AB AF nBC x =-=-， 在Rt BFE 中，BF 2＋BE 2＝EF 2， ∴()2221()2nBC x BC x -+=，解得：2418n x BC AF n +=⋅=，又∵222AE AB BE =+， ∴2221()4AE n BC =+，如图，过点G 作GH AB ⊥于H ，则∠AHG ＝∠FHG ＝90°，∵在矩形ABCD 中，∴∠HAD ＝∠BCD ＝∠B ＝90°，∴四边形AHGD 为矩形，∴BC ＝HG ，∵∠FHG ＝90°，∴∠AFQ ＋∠FGH ＝90°，∵FG AE ⊥，∴∠FQA ＝90°，∴∠AFQ ＋∠BAE ＝90°，∴∠BAE ＝∠FGH ，又∵∠FHG ＝∠D ＝90°，∴ABE GHF ， AE AB AB n FG GH BC ∴===， AE nFG ∴=，222n FG AE ∴=，22221()4n FG n BC +∴=， 2222414n FG BC n +∴=⋅， 又∵2418n AF BC n+=⋅， 22222(41)64n AF BC n +∴=⋅， ∴2224116AF n FG +=， ∴2414AF n FG +=； ②如图，过点P 作PM BC ⊥于点M ，∵210GF =32n =， ∴由①得33102AE FG ==∵∠EPG ＝∠GCE ＝90°，∠EOC ＝∠GOP ，∴∠CGP ＝∠OEC ，∵∠FEP ＝∠B ＝90°，∴∠OEC ＋∠BEF ＝90°，∠BFE ＋∠BEF ＝90°，∴∠BFE ＝∠OEC ，∴∠BFE ＝∠CGP ，又∵34tan CGP ∠=， ∴34BE tan BFE BF ∠==， ∴设3BE x =，4BF x =，则5EF AF x ==，9AB x =，()()(22293x x ∴+=， 解得：1x =，3BE ∴=，4BF =，9AB =，263BC AB ∴==， 3CE ∴=，6PE AD ==，90FEP FAD ∠=∠=︒，BEFMPE ∴， EF BF BE PE ME MP∴==， 5436ME MP∴==， 245ME ∴=，185MP =， 249355CM ∴=-=，CP ∴==【点睛】本题考查了正方形和矩形的性质，全等三角形和相似三角形的判定及性质，折叠的性质，勾股定理，题目综合性较强，有一定的难度，熟练掌握并灵活运用相关知识是解决本题的关键．5．（1）；；（2）矩形，见解析；（3）见解析，．【分析】（1）如图，连接OA 、OA′、OD 、OD′，根据旋转的性质可得OA=OA′、OD =OD′，∠AOA′=∠DOD′=，根据勾股定理可得OA=O解析：（1）AA DD ''=；AA ''=；（2）矩形，见解析；（3）见解析，OP OQ【分析】（1）如图，连接OA 、OA ′、OD 、OD ′，根据旋转的性质可得OA =OA ′、OD =OD ′，∠AOA ′=∠DOD ′=α，根据勾股定理可得OA =OD ，利用SAS 可证明△AOA ′≌△DO D′，根据全等三角形的性质可得AA ′=DD ′，根据旋转的性质可得∠BOB ′=α，根据OB OB OA OA'='△OAA ′∽△OBB ′，根据相似三角形的性质即可得答案；（2）根据旋转的性质可得BC B C ''=，OB OB '=，OC OC '=，根据点O 是BC 中点即可得出OB OC OB OC ''===，根据对角线相等且互相平分的四边形是矩形即可证明四边形''BB CC 是矩形； （3）根据题意，补全图形，连接OA 、OA ′，作AM ⊥BP 于M ，A ′N ⊥BP 于N ，根据勾股定理可得OA OA ''==，根据平角的定义及直角三角形两锐角互余的性质可得''ABM A B N ∠=∠，利用AAS 可证明△ABM ≌△A ′B ′N ，可得AM =A ′N ，利用AAS 可证明△APM ≌△A ′PN ，可得AP A P '=，根据等腰三角形“三线合一”的性质可得∠A ′OP =12∠AOA ′=12α，∠QOB ′=1122BOB α'∠=，根据角的和差关系可得∠POQ =∠A ′OB ′，即可证明△OQP ∽△OB ′A ′，根据相似三角形的性质即可得答案．【详解】（1）如图，连接OA 、OA ′、OD 、OD ′，∵将正方形ABCD 绕点O 顺时针旋转得到正方形A B C D ''''，旋转角为α，∴OA =OA ′、OD =OD ′，∠AOA ′=∠DOD ′=α，∴△AOA ′≌△DO D′，∴AA ′=DD ′，∵点O 是BC 中点，∴OB =1122BC AB =， ∴OA，∵将正方形ABCD 绕点O 顺时针旋转得到正方形A B C D ''''，旋转角为α，∴∠BOB ′=∠AOA ′=α， ∵OB OBOA OA'==' ∴△OAA ′∽△OBB ′， ∴''AA OA BB OB= ∴AA ''，故答案为：AA DD ''=；AA ''=（2）四边形''BB CC 是矩形；理由如下：∵正方形ABCD 绕点O 顺时针旋转得到正方形A B C D ''''，∴BC B C ''=，OB OB '=，OC OC '=，∵点O 是BC 中点，∴OB OC OB OC ''===四边形''BB CC 是平行四边形，∵BC B C ''=，∴四边形''BB CC 是矩形．（3）如图，补全图形如下：连接OA 、OA ′，作AM ⊥BP 于M ，A ′N ⊥BP 于N ， ∵2BO CO =，∴AB =BC =32OB ， ∴OA ′=OA 2213AB OB +'13， ∵∠OB ′A ′=90°， ∴'''90A B N OB B ∠+∠=︒，∵'OB OB =，∴''OB B OBB ∠=∠，∵'90ABM OBB ∠+∠=︒，∴ABM A B N ''∠=∠，∵''AB A B =，''AMB A NB ∠=∠，∴△ABM ≌△A ′B ′N ，∴AM =A ′N （AAS ），∵''AMB A NB ∠=∠，'APM A PN ∠=∠，∴△APM ≌△A ′PN ，∴AP=A′P ，∵OA =OA ′，∴∠A ′OP =12∠AOA ′=12α， ∵OB =OB ′，OQ ⊥BB ′，∴∠QOB ′='1122BOB α∠=， ∴∠QOB ′+∠B ′OP =∠A ′OP +∠B ′OP ，即∠POQ =∠A ′OB ′，∵∠OQP =∠OB ′A ′=90°，∴△OQP ∽△OB ′A ′，∴''132OP OA OQ OB ==．【点睛】本题考查旋转的性质、矩形的判定、全等三角形的判定与性质及相似三角形的判定与性质，熟练掌握全等三角形及相似三角形的判定定理并正确作出辅助线构造全等三角形及相似三角形是解题关键．6．（1），60；（2），；（3）或【分析】（1）证明，得出，，即可得出结论；（2）证明，即可得出结论；（3）先判断出，再求出，①当点在点上方时，先判断出四边形是矩形，求出，再根据勾股定理求出，解析：（1）BD CE =，60；（2）2sin 2BD EC α=⋅⋅，902α︒-；（3）242【分析】（1）证明ACE ABD ∆≅∆，得出CE BD =，AEC ADB ∠=∠，即可得出结论；（2）证明ACE ABD ∆∆∽，即可得出结论；（3）先判断出2BD CE =，再求出25AB =①当点E 在点D 上方时，先判断出四边形APDE 是矩形，求出2AP DP AE ==32BP =22BD =②当点E 在点D 下方时，同①的方法得，2AP DP AE ==32BP =42BD BP DP =+=，即可得出结论．【详解】解：（1）如图①中，在ABC ∆为等腰三角形，AC BC =，60ACB ∠=︒，ABC ∆∴是等边三角形，AC AB ∴=，60CAB ∠=︒，同理：AE AD =，60AED ADE EAD ∠=∠=∠=︒，EAD CAB ∴∠=∠，EAC DAB ∠=∠∴，()ACE ABD SAS ∴∆≅∆，CE BD ∴=，AEC ADB ∠=∠，点B 、D 、E 在同一直线上，180120ADB ADE ∴∠=︒-∠=︒，AEC 120∴∠=︒，60CEB AEC AEB ∴∠=∠-∠=︒，故答案为：BD CE =，60．（2）如图②中，2sin 2BD CE α=⋅，BD 、CE 所在直线相交所成的锐角的大小为902α︒-． 理由：延长BD 交CE 的延长线于T ，设AE 交BT 于点O ．在等腰三角形ABC 中，AC BC =，ACB α∠=，2sin 2AB AC α∴=⋅，同理，2sin 2AD AE α=⋅，∴AE AC AD AB =，DAE CAB ∠=∠，EAC DAB ∠=∠∴，ACE ABD ∴∆∆∽，∴2sin 2BD AB EC AC α==，ECA DBA ∴∠=∠，2sin 2BD EC α=⋅⋅， COT AOB ∠=∠， 902CTO CAB α∴∠=∠=︒-． BD ∴、CE 所在直线相交所成的锐角的大小为902α︒-．（3）由（2）知，ACE ABD ∆∆∽，2BD CE ∴=， 在Rt ABC △中，10AC =，225AB AC ∴==，①当点E 在点D 上方时，如图③，过点A 作AP BD ⊥交BD 的延长线于P ，当CE AD ⊥时，可证135AEC ADB ∠=∠=︒，45ADE ∠=︒，90EDB ∴∠=︒，90PDE AED APD ∴∠=∠=∠=︒，∴四边形APDE 是矩形，AE DE =，∴矩形APDE 是正方形，2AP DP AE ∴===，在Rt APB 中，根据勾股定理得，2222(25)(2)32BP AB AP =-=-=，22BD BP PD ∴=-=．②当点E 在点D 下方时，如图④同①的方法得，2AP DP AE ===，32BP =，42BD BP DP ∴=+=，综上所述，BD 的长为222【点睛】此题是几何变换综合题，主要考查了旋转的性质，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理，等边三角形的性质，判断出△ACE ∽△ABD 是解本题的关键．7．（1）证明见解析；（2）①；②；（3）．【分析】（1）如图（见解析），先根据三角形全等的判定定理与性质可得，再根据“协和四边形”的定义即可得证；（2）①先根据“协和四边形”的定义、三角形全等的解析：（1）证明见解析；（2）①3:5；②5314；（3）23． 【分析】（1）如图（见解析），先根据三角形全等的判定定理与性质可得,ABD CBD ADB CDB ∠=∠∠=∠，再根据“协和四边形”的定义即可得证； （2）①先根据“协和四边形”的定义、三角形全等的判定定理可得ABD CBD ≅，从而可得AD CD =，再根据等边三角形的判定与性质可得,1,2B E D EF F DE D OE EF F ⊥===，然后设2EF DE DF a ===，解直角三角形可得83,33BD a OD a ==，从而可得533OB a =，最后利用三角形的面积公式即可得； ②如图（见解析），设2EF DE DF a ===，先利用勾股定理可得2213BF BE a ==，再利用三角形的面积公式可得577EH a =，然后根据正弦三角函数的定义即可得； （3）如图（见解析），先解直角三角形可得43BP =，再根据菱形的性质、平行线的性质可得EBF BEP ∠=∠，从而可得NEM BEP ∠=∠，然后根据垂线段最短可得当MN EF ⊥时，MN 取得最小值，最后根据相似三角形的判定与性质即可得．【详解】证明：（1）如图，连接BD ，在ABD △和CBD 中，AB BC AD CD BD BD =⎧⎪=⎨⎪=⎩， ()ABD CBD SSS ∴≅，,ABD CBD ADB CDB ∴∠=∠∠=∠，BD ∴平分ABC ∠和ADC ∠，∴四边形ABCD 是“协和四边形”；（2）①如图，设BD 与EF 相交于点O ，BD 为“协和线”，BD ∴平分ABC ∠和ADC ∠，,ABD CBD ADB CDB ∴∠=∠∠=∠，在ABD △和CBD 中，ABD CBD BD BD ADB CDB ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()ABD CBD ASA ∴≅，AD CD ∴=，∵点E 、F 分别为边AD 、DC 的中点， 1122DE AD DC DF ∴===， 60ADC ∠=︒，DEF ∴是等边三角形，EF DE DF ==， 1,2BD EF OE EF ∴⊥=（等腰三角形的三线合一）， 设2EF DE DF a ===，则4,AD a OE a ==， ∵在Rt ABD △中，1302ADB ADC ∠=∠=︒，3cos 3AD BD a ADB ∴==∠， 在Rt DOE 中，223OD DE OE a -， 53OB BD OD ∴=-=， 132152DEF BEF EF OD SOD S OB EF OB ⋅∴===⋅， 即DEF 与BEF 的面积的比为3:5；②如图，过点E 作EH BF ⊥于点H ，由（2）①知，BD 垂直平分EF ，BE BF ∴=，设2EF DE DF a ===，则4,AD a OE a ==， 同（2）①可得：533OB a =， 222213BF BE OE OB a ∴==+=， 1122BEF S EF OB BF EH =⋅=⋅， 153122122323a a aEH ∴⨯⋅=⨯， 解得577EH a =， 则在Rt BEH 中，57537sin 142213EH EBF BE a a ∠===； （3）如图，过点B 作BP AD ⊥，交DA 延长线于点P ，120BAD ∠=︒，18060BAP BAD ∴∠=︒-∠=︒，在Rt ABP 中，3sin 843BP AB BAP =⋅∠== 四边形ABCD 是菱形，//DP BC ∴，EBF BEP ∴∠=∠，同（2）①可证：GF 垂直平分BE ，1,2BF EF BN EN BE ∴===， EBF NEM ∴∠=∠，NEM BEP ∴∠=∠，由垂线段最短可知，当MN EF ⊥时，MN 取得最小值， 在NEM 和BEP △中，90NEM BEP NME P ∠=∠⎧⎨∠=∠=︒⎩， NEM BEP ∴~，12MN EN BP BE ∴==12=， 解得MN =即MN 的最小值为【点睛】本题考查了三角形全等的判定定理与性质、解直角三角形、菱形的性质、相似三角形的判定与性质等知识点，较难的是题（3），利用垂线段最短得出当MN EF ⊥时，MN 取得最小值是解题关键．8．（1），；（2）成立，不成立，与的关系为，见解析；（3）2或14【分析】（1）连接AE ，证明△ABC 、△APE 为等边三角形， 再证明，根据全等三角形的性质可得BP=CE ，，再求得，即可得，所有．解析：（1）BP CE =，BC CE ⊥；（2）BC CE ⊥成立，BP CE =不成立，BP 与CE 的关系为CE =，见解析；（3）2或14【分析】（1）连接AE ，证明△ABC 、△APE 为等边三角形， 再证明ABP ACE ∆∆≌，根据全等三角形的性质可得BP=CE ，ABP ACE ∠=∠，再求得30ABP ACE ∠=∠=︒，即可得90ACE ACB ∠+∠=︒，所有BC CE ⊥．（2）BC CE ⊥成立，BP CE =不成立，BP 与CE 的关系为CE =．选图2证明：连接AE ，易证BAP CAE ∆∆∽，根据相似三角形的性质可得CE CA BP BA ==ACE ABP ∠=∠，根据等腰直角三角形的性质可得45ABD CBD ACB ACE ∠==︒∠∠==∠，由此可得90BCE BCA ACE ∠=∠+∠=︒，结论可证；选图3证明，类比图2的证明方法即可； （3）分图2和图3两种情况求CE 的长即可．【详解】（1）如图，连接AE ，∵BA BC =，且60ABC ∠=︒，∴△ABC 为等边三角形，∴60ABC BAC ACB ∠=∠=∠=︒，AB =AC ，∵PE PA =，且60APE α∠==︒，∴△APE 为等边三角形，∴60PAE ∠=︒，AP =AE ，∴BAC PAC PAE PAC ∠-∠=∠-∠，∴BAP CAE ∠=∠；在△BAP 和△CAE 中，AB AC BAP CAE AP AE =⎧⎪∠=∠⎨⎪=⎩， ∴ABP ACE ∆∆≌，∴BP=CE ，ABP ACE ∠=∠，∵BD AC ⊥，BA BC =， 60ABC ∠=︒，∴∠ABP =30°，∴30ABP ACE ∠=∠=︒，∴90ACE ACB ∠+∠=︒，∴BC CE ⊥．故答案为：BP CE =，BC CE ⊥．（2）BC CE ⊥成立，BP CE =不成立，BP 与CE 的关系为2CE BP =．理由如下：选图2证明：连接AE ，由题意可知：ABC ∆、APE ∆均为等腰直角三角形，∴45BAC PAE ∠=∠=︒，2AC AE AB AP= ∴BAP PAD CAE PAD ∠+∠=∠+∠，即BAP CAE ∠=∠；又∵AC AE AB AP =， ∴BAP CAE ∆∆∽，∴2CE CA BP BA==，ACE ABP ∠=∠， ∵AB BC =，BD AC ⊥，∴45ABD CBD ACB ACE ∠==︒∠∠==∠，∴454590BCE BCA ACE ∠=∠+∠=︒+︒=︒，∴BC CE ⊥，∴BC CE ⊥，2CE BP =．选图3证明：理由如下：连接AE ，由题意可知：ABC ∆、APE ∆均为等腰直角三角形，∴45BAC PAE ∠=∠=︒，2AC AE AB AP==， ∴BAC PAD PAE PAD ∠+∠=∠+∠，即BAP CAE ∠=∠，又∵AC AE AB AP=， ∴BAP CAE ∆∆∽，∴2CE CA BP BA==，ACE ABP ∠=∠， ∵AB BC =，BD AC ⊥，∴45ABD CBD ACB ACE ∠==︒∠∠==∠，∴454590BCE BCA ACE ∠=∠+∠=︒+︒=︒，∴BC CE ⊥，∴BC CE ⊥，2CE BP =；（3）2CE =或14．如图，。

2019年中考数学压轴题专题复习1.如图，二次函数y=ax2+bx+c的图象交x轴于A、B两点，交y轴于点C，且B（1，0），C（0，3），将△BOC绕点O按逆时针方向旋转90°，C点恰好与A重合．（1）求该二次函数的解析式；（2）若点P为线段AB上的任一动点，过点P作PE∥AC，交BC于点E，连结CP，求△PCE 面积S的最大值；（3）设抛物线的顶点为M，Q为它的图象上的任一动点，若△OMQ为以OM为底的等腰三角形，求Q点的坐标．2.如图,在平面直角坐标系中,直线y=-2x＋10与x轴,y轴相交于A,B两点,点C的坐标为（8,4）,连接AC,BC．（1）求过O,A,C三点的抛物线的解析式,并判断△ABC的形状；（2）动点P从O点出发,沿OB以每秒两个单位长度的速度向点B运动,同时动点Q从点B 出发,沿BC以每秒一个单位长度的速度向点C运动,规定其中一个动点到达端点时另一个动点也随之停止运动,设运动时间为t秒,当t为何值时，PA＝QA？；（3）在抛物线的对称轴上，是否存在点M，使A，B，M为顶点的三角形是等腰三角形？若存在，直接写出M点的坐标；若不存在，请说明理由．3.如图,已知抛物线经过点A（﹣2,0），点B（﹣3,3）及原点O,顶点为C．（1）求抛物线的解析式；（2）P是抛物线的第一象限内的动点，过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形与△BOC相似？若存在,求出点P的坐标；若不存在,请说明理由；（3）是否存在动点D在抛物线上,动点E在抛物线的对称轴上,且以AO为边,以A、O、D、E 为顶点的四边形是平行四边形,若存在，请直接写出点D的坐标；若不存在,请说明理由．4.如图1,在Rt△ABC中,∠C=90°，BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动，速度为每秒k厘米,行完AC全程用时8秒；点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒(0<x<8),△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米．（1）求y1与x的函数关系，并在图2中画出y1的图象；（2）如图2,y2的图象是抛物线的一部分,其顶点坐标是（4,12）,求点P的速度及AC的长；（3）在图2中,点G是x轴正半轴上一点(0<OG<6)过G作EF垂直于x轴,分别交y1、y2于点E、F．①说出线段EF的长在图1中所表示的实际意义；②当0＜x＜６时，求线段EF长的最大值．5.如图1，已知抛物线y=﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C点，点P是抛物线上在第一象限内的一个动点，且点P的横坐标为t．（1）求抛物线的表达式；（2）设抛物线的对称轴为l，l与x轴的交点为D．在直线l上是否存在点M，使得四边形CDPM是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．（3）如图2，连接BC，PB，PC，设△PBC的面积为S．①求S关于t的函数表达式；②求P点到直线BC的距离的最大值，并求出此时点P的坐标．6.（1）问题：如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°.求证：AD•BC=AP•BP．（2）探究：如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．（3）应用：请利用（1）（2）获得的经验解决问题：如图3，在△ABD中，AB=12，AD=BD=10．点P以每秒1个单位长度的速度，由点A出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当以D为圆心，以DC为半径的圆与AB相切，求t的值．7.如图1，一副直角三角板满足AB=BC，AC=DE，∠ABC=∠DEF=90°∠EDF=30°，【操作1】将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上，再将三角板DEF绕点E旋转，并使边DE与边AB交于点P，边EF与边BC于点Q．在旋转过程中，如图2，当时，EP与EQ满足怎样的数量关系？并给出证明．【操作2】在旋转过程中，如图3，当时EP与EQ满足怎样的数量关系？，并说明理由．【总结操作】根据你以上的探究结果，试写出当时，EP与EQ满足的数量关系是什么？其中m的取值范围是什么？（直接写出结论，不必证明）．8.如图，抛物线y=-x2+2x+3与x轴相交于A、B两点，与y轴交于点C，顶点为D，抛物线的对称轴DF与BC相交于点E，与x轴相交于点F．(1)求线段DE的长；(2)设过E的直线与抛物线相交于点M(x1，y1)，N(x2，y2)，试判断当|x1-x2|的值最小时，直线MN与x轴的位置关系，并说明理由；(3)设P为x轴上的一点，∠DAO+∠DPO=∠α，当tan∠α=4时，求点P的坐标．9.已知抛物线y=ax2+bx+c与x轴交于A(-1，0),B(5，0),与y轴交于C(0，3).直线y=x+1与抛物线交于A、E两点，与抛物线对称轴交于点D.(1)求抛物线解析式及E点坐标；(2)在对称轴上是否存在一点M，使ACM为等腰三角形？若存在，请直接写出M点坐标；若不存在，请说明理由.(3)若一点P在直线y=x+1上从A点出发向AE方向运动，速度为单位/秒，过P点作PQ//y轴，交抛物线于Q点.设时间为t秒(0≤t≤6)，PQ的长度为L，找出L与t的函数关系式，并求出PQ最大值.10.如图，已知抛物线y=ax2+2x+6（a≠0）交x轴与A，B两点（点A在点B左侧），将直尺WXYZ与x轴负方向成45°放置，边WZ经过抛物线上的点C（4，m），与抛物线的另一交点为点D，直尺被x轴截得的线段EF=2，且△CE F的面积为6．（1）求该抛物线的解析式；（2）探究：在直线AC上方的抛物线上是否存在一点P，使得△ACP的面积最大？若存在，请求出面积的最大值及此时点P的坐标；若不存在，请说明理由．（3）将直尺以每秒2个单位的速度沿x轴向左平移，设平移的时间为t秒，平移后的直尺为W′X′Y′Z′，其中边X′Y′所在的直线与x轴交于点M，与抛物线的其中一个交点为点N，请直接写出当t为何值时，可使得以C、D、M、N为顶点的四边形是平行四边形．11.如图1，对称轴为直线x=的抛物线经过B（2，0）、C（0，4）两点，抛物线与x轴的另一交点为A（1）求抛物线的解析式；（2）若点P为第一象限内抛物线上的一点，设四边形COBP的面积为S，求S的最大值；（3）如图2，若M是线段BC上一动点，在x轴是否存在这样的点Q，使△MQC为等腰三角形且△MQB为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．12.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)．（1）求抛物线的解析式及A、B两点的坐标；（2）在(1)中抛物线的对称轴l上是否存在一点P，使AP+CP的值最小？若存在,求AP+CP的最小值，若不存在，请说明理由；（3）以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式．13.已知函数y=ax2+x+1的图象与x轴只有一个公共点．（1）求这个函数关系式；（2）如图所示，设二次函数y=ax2+x+1图象的顶点为B，与y轴的交点为A，P为图象上的一点，若以线段PB为直径的圆与直线AB相切于点B，求P点的坐标；（3）在(2)中，若圆与x轴另一交点关于直线PB的对称点为M，试探索点M是否在抛物线y=ax2+x+1上，若在抛物线上，求出M点的坐标；若不在，请说明理由．14.如图1，点C、B分别为抛物线C：y1=x2+1，抛物线C2：y2=a2x2+b2x+c2的顶点．分别过点B、C1作x轴的平行线，交抛物线C1、C2于点A、D，且AB=BD．（1）求点A的坐标：（2）如图2，若将抛物线C1：“y1=x2+1”改为抛物线“y1=2x2+b1x+c1”．其他条件不变，求CD的长和a2的值；（3）如图2，若将抛物线C1：“y1=x2+1”改为抛物线“y1=4x2+b1x+c1”，其他条件不变，求b1+b2的值______（直接写结果）．15.如图，已知在ΔABC中,∠C=90°,AC=8cm,BC=6cm,D是斜边AB的中点.点P从点B出发沿BC方向匀速运动，速度为1 cm/s；同时,点Q从点A出发,沿AC方向匀速运动,速度为2 cm/s.当点Q 停止运动时，点P也停止运动.连接PQ、PD、QD.设运动时间为t（s）（0<t<4）．（1）当t为何值时,ΔPQC是等腰直角三角形？（2）设ΔPQD的面积为y（cm2）,求y与t之间的函数关系式；是否存在某一时刻t，使ΔPQD 的面积是RtΔABC的面积的四分之一？若存在，求出t的值；若不存在，请说明理由；（3）是否存在某一时刻t，使QD⊥PD？若存在，求出t的值；若不存在，请说明理由．答案1.解：2.解：（1）在y ＝－2x ＋10中，当x ＝0时，y ＝10，y ＝0时，x ＝5，∴A （5，0），B （0，10），∵抛物线经过O （0，0），故设过O ，A ，C 三点的抛物线的解析式为y ＝ax 2＋bx （a ≠ 0），则⎩⎨⎧=+=+4b 8a 640b 5a 25，解得：∴过O ，A ，C 三点的抛物线的解析式为y ＝61x 2－65x ，∵BA2＝102＋52＝125，BC2＝82＋62＝100，AC2＝32＋42＝25，∴AC2＋BC2＝BA2，即△ABC为直角三角形，且∠ACB＝90°；（2）作CE⊥y轴于E点，QD⊥y轴于D点，QF⊥x轴于点F，△BEC中，BE︰EC︰BC＝6︰8︰10＝3︰4︰5，∵CE⊥y轴，QD⊥y轴，∴QD∥ CE ，∴△BDQ ∽△BEC，∴BD︰DQ︰BQ＝BE︰EC︰BC＝3︰4︰5，∵BQ＝t，∴BD＝t，DQ＝t，∴QA2＝QF2＋FA2＝（10－t）2＋（5－t）2＝t2－20t＋125PA2＝（2t）2＋52＝4t2＋25，若PA＝QA，则PA2＝QA2，∴4t2＋25＝t2－20t＋125，∴3t2＋20t－100＝0，解之得：t1＝，t2＝－10，∵0≤t≤5，∴t＝∴当t＝秒时，PA＝QA；（3）存在满足条件的点M．M1（，），M2（，－），M3（，），M4（，）．3.（3）存在，D点坐标为（1，3）或（﹣3，3）．当以A、O、D、E为顶点的平行四边形时，且AO为边，则有DE=AO=2，且DE∥AO，∴D点只能在x轴上方，过点E作DE∥x轴，交抛物线与点D，如图2，设D点横坐标为x，∵E点在抛物线对称轴上，∴E点横坐标为﹣1，∴DE=|x+1|=2，解得x=1或x=﹣3，∴D点坐标为（1，3）或（﹣3，3）．4.解：（1）∵，CD＝3，CQ＝x，∴．图象如图所示．（2）方法一：，CP＝8k－xk，CQ＝x，∴．∵抛物线顶点坐标是（4，12），∴．解得．则点P的速度每秒厘米，AC＝12厘米．方法二：观察图象知，当x=4时，△PCQ面积为12．此时PC＝AC－AP＝8k－4k＝4k，CQ＝4．∴由，得．解得．则点P的速度每秒厘米，AC＝12厘米．方法三：设y2的图象所在抛物线的解析式是．∵图象过（0，0），（4，12），（8，0），∴解得∴．①∵，CP＝8k－xk，CQ＝x，∴．②比较①②得.则点P的速度每秒厘米，AC＝12厘米．（3）①观察图象，知线段的长EF＝y2－y1，表示△PCQ与△DCQ的面积差（或△PDQ面积）．②由⑵得.（方法二，）∵EF＝y2－y1，∴EF＝，∵二次项系数小于０，∴在范围，当时，最大．5.解：6.【解答】（1）证明：如图1，∵∠DPC=∠A=∠B=90°，∴∠ADP+∠APD=90°，∠BPC+∠APD=90°，∴∠APD=∠BPC，∴△ADP∽△BPC，∴，∴AD•BC=AP•BP；（2）结论AD•BC=AP•BP仍成立；理由：证明：如图2，∵∠BPD=∠DPC+∠BPC，又∵∠BPD=∠A+∠APD，∴∠DPC+∠BPC=∠A+∠APD，∵∠DPC=∠A=θ，∴∠BPC=∠APD，又∵∠A=∠B=θ，∴△ADP∽△BPC，∴，∴AD•BC=AP•BP；（3）解：如下图，过点D作DE⊥AB于点E，∵AD=BD=10，AB=12，∴AE=BE=6∴DE==8，∵以D为圆心，以DC为半径的圆与AB相切，∴DC=DE=8，∴BC=10﹣8=2，∵AD=BD，∴∠A=∠B，又∵∠DPC=∠A，∴∠DPC=∠A=∠B，由（1）（2）的经验得AD•BC=AP•BP，又∵AP=t，BP=12﹣t，∴t（12﹣t）=10×2，∴t=2或t=10，∴t的值为2秒或10秒．7.【解答】（操作1）EP=EQ，证明：连接BE，根据E是AC的中点和等腰直角三角形的性质，得：BE=CE，∠PBE=∠C=45°，∵∠BEC=∠FED=90°∴∠BEP=∠CEQ，在△BEP和△CEQ中，∴△BEP≌△CEQ（ASA），∴EP=EQ；如图2，EP：EQ=EM：EN=AE：CE=1：2，理由是：作EM⊥AB，EN⊥BC于M，N，∴∠EMP=∠ENC，∵∠MEP+∠PEN=∠PEN+∠NEF=90°，∴∠MEP=∠NEF，∴△MEP∽△NEQ，∴EP：EQ=EM：EN=AE：CE=1：2；如图3，过E点作EM⊥AB于点M，作EN⊥BC于点N，∵在四边形PEQB中，∠B=∠PEQ=90°，∴∠EPB+∠EQB=180°，又∵∠EPB+∠MPE=180°，∴∠MPE=∠EQN，∴Rt△MEP∽Rt△NEQ，∴=，Rt△AME∽Rt△ENC，∴=m=，∴=1：m=，EP与EQ满足的数量关系式1：m，即EQ=mEP，∴0＜m≤2+，（因为当m＞2+时，EF和BC变成不相交）．8.9.解：(1)y=-0.6x2+2.4x+3,E(10/3,13/3)；(2)M(2，-1),(2，1),(2，3+),(2，3-)；(3)L=-0.6t2+1.4t+2(0≤t≤10/3)；L=0.6t2-1.4t-4(10/3<t≤5).当t=5时，L最大=4.10.解：11.【解答】解：（1）由对称性得：A（﹣1，0），设抛物线的解析式为：y=a（x+1）（x﹣2），把C（0，4）代入：4=﹣2a，a=﹣2，∴y=﹣2（x+1）（x﹣2），∴抛物线的解析式为：y=﹣2x2+2x+4；（2）如图1，设点P（m，﹣2m2+2m+4），过P作PD⊥x轴，垂足为D，∴S=S梯形+S△PDB=m（﹣2m2+2m+4+4）+（﹣2m2+2m+4）（2﹣m），S=﹣2m2+4m+4=﹣2（m﹣1）2+6，∵﹣2＜0，∴S有最大值，则S大=6；（3）如图2，存在这样的点Q，使△MQC为等腰三角形且△MQB为直角三角形，理由是：设直线BC的解析式为：y=kx+b，把B（2，0）、C（0，4）代入得：，解得：，∴直线BC的解析式为：y=﹣2x+4，设M（a，﹣2a+4），过A作AE⊥BC，垂足为E，则AE的解析式为：y=x+，则直线BC与直线AE的交点E（1.4，1.2），设Q（﹣x，0）（x＞0），∵AE∥QM，∴△ABE∽△QBM，∴①，由勾股定理得：x2+42=2×[a2+（﹣2a+4﹣4）2]②，由①②得：a1=4（舍），a2=，当a=时，x=，∴Q（﹣，0）．12.13.解：（1）当a = 0时，y = x+1，图象与x轴只有一个公共点,当a≠0时,△=1- 4a=0,a = ，此时，图象与x轴只有一个公共点．∴函数的解析式为：y=x+1 或`y=x2+x+1（2）设P为二次函数图象上的一点，过点P作PC⊥x轴于点C．∵是二次函数，由（1）知该函数关系式为：y=x2+x+1，则顶点为B（-2，0），图象与y轴的交点坐标为A（0，1）∵以PB为直径的圆与直线AB相切于点B ∴PB⊥AB 则∠PBC=∠BAO∴Rt△PCB∽Rt△BOA ∴，故PC=2BC，设P点的坐标为(x，y)，∵∠ABO是锐角，∠PBA是直角，∴∠PBO是钝角，∴x<-2∴BC=-2-x，PC=-4-2x，即y=-4-2x， P点的坐标为(x，-4-2x)∵点P在二次函数y=x2+x+1的图象上，∴-4-2x=x2+x+1解之得：x1=-2，x2=-10∵x<-2 ∴x=-10，∴P点的坐标为：(-10，16)（3）点M不在抛物线上由（2）知：C为圆与x 轴的另一交点，连接CM，CM与直线PB的交点为Q，过点M作x轴的垂线，垂足为D，取CD的中点E，连接QE，则CM⊥PB，且CQ=MQ∴QE∥MD，QE=MD，QE⊥CE∵CM⊥PB，QE⊥CE PC⊥x 轴∴∠QCE=∠EQB=∠CPB∴tan∠QCE= tan∠EQB= tan∠CPB =CE=2QE=2×2BE=4BE，又CB=8，故BE=，QE=∴Q点的坐标为(-，)可求得M点的坐标为(，)∵=≠∴C点关于直线PB的对称点M不在抛物线上。