小学数学知识点精讲精练之：火车行程问题

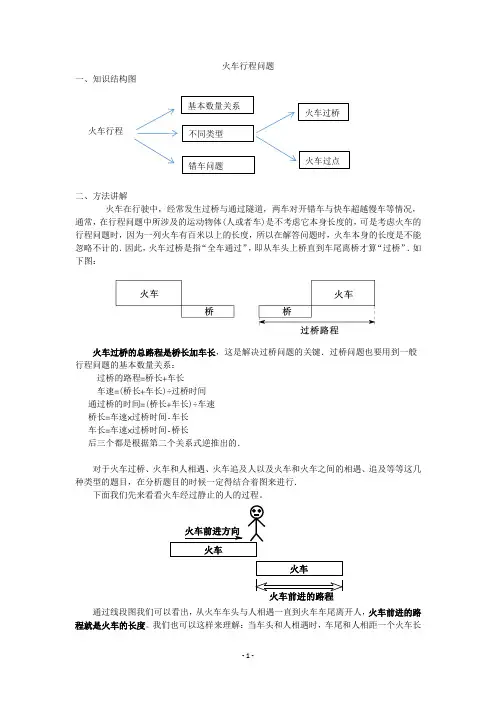
火车行程问题一、知识结构图火车行程二、方法讲解火车在行驶中，经常发生过桥与通过隧道，两车对开错车与快车超越慢车等情况，通常，在行程问题中所涉及的运动物体(人或者车)是不考虑它本身长度的，可是考虑火车的行程问题时，因为一列火车有百米以上的长度，所以在解答问题时，火车本身的长度是不能忽略不计的．因此，火车过桥是指“全车通过”，即从车头上桥直到车尾离桥才算“过桥”．如下图：火车过桥的总路程是桥长加车长，这是解决过桥问题的关键．过桥问题也要用到一般行程问题的基本数量关系：过桥的路程=桥长+车长车速=(桥长+车长)÷过桥时间通过桥的时间=(桥长+车长)÷车速桥长=车速×过桥时间-车长车长=车速×过桥时间-桥长后三个都是根据第二个关系式逆推出的．对于火车过桥、火车和人相遇、火车追及人以及火车和火车之间的相遇、追及等等这几种类型的题目，在分析题目的时候一定得结合着图来进行．下面我们先来看看火车经过静止的人的过程。

通过线段图我们可以看出，从火车车头与人相遇一直到火车车尾离开人，火车前进的路程就是火车的长度。

我们也可以这样来理解：当车头和人相遇时，车尾和人相距一个火车长火车前进的路程火车度，所以整个过程就是车尾和人的相遇问题。

以上是人不动情况下的火车行程问题，下面我们来介绍一下行人和火车的相遇和追及问题，如下图所示：车头遇到行人火车我们可以将火车看成一个点：开始的时候行人和车尾的距离为一个车长，结束的时候行人和车尾相遇了。

也就是说，从火车与行人的相遇到错开，这个过程可以看成是行人与车尾相遇了。

也就是说，从火车与行人的相遇到错开，这个过程可以看成是行人与车尾的相遇问题，火车和行人经过的路程和等于火车的长度。

类似的，对于火车追行人的过程，从追上到离开，火车和行人的路程差等于火车的长度。

我们仍可以将火车看成一个点：开始的时候行人在车尾前面，距离为一个车场，结束的时候车尾恰好追上了行人。

火车行程问题两列火车错车用的时间是：(A的车身长+B的车身长)÷(A车的速度+B车的速度)两列火车超车用的时间是：(A的车身长+B的车身长)÷(A车的速度-B车的速度)(注：A车追B车)火车过桥问题，可用下面的关系式求火车通过的时间：(列车长度+桥的长度)÷列车速度火车通过两座桥，或通过一座桥，隧道，车头走过的长度是：桥长+火车长或隧道长+火车长其中火车长一样，比较长和隧道长，再比较所用的时间的差，就又求出火车的速度以及车身长。

人坐在列车上往窗外看另一列车，相当人在一定时间内走过一座桥。

例1：一列慢车，车身长120米，车速是每秒15米，一列快车车身长160米，车速是每秒20米，两车在双轨轨道上相向而行，从车头相遇到车尾相离要用多少秒钟？解答：(120+160)÷(15+20)=280÷35=8(秒)答：两车从车头相遇到车尾相离用8秒钟。

例2：一列火车长150米，每秒行20米，全车通过一座450米长的大桥，需多长时间？解：(150+450)÷20=30(秒)答：需要30秒。

例3：一列客车通过860米长的大桥，需要45秒钟，用同样速度穿过620米长的隧道需要35秒钟，求这列客车行驶的速度及车身的长度各多少米。

解：这列客车每秒行驶：(860－620)÷(45－35)=240÷10=24(米)这列客车的车身长：24×45－860=1080-860=220(米)答：这列客车每秒行驶24米，车身长220米。

例4：某小学三、四年级学生共528人，排成四路纵队去看电影，队伍进行的速度是每分25米，前后两人都相距1米，现在队伍要走过一座桥，整个队伍从上桥到离桥共需16分，这座桥走多少米？解：队伍长：1×(528÷4-1)=131(米)队伍行进的路程：25×16=400(米)桥长：400－131=269(米)答：这座桥长269米。

小学数学：火车行程问题火车问题是行程问题中又一种较典型的专题。

由于火车有一定的长度，因此在研究有关火车相遇与追及，以及火车过桥、穿越隧道等问题时，列车运动的总路程与其它类型的行程问题就有区别，这也是解决火车行程问题的关键。

因此，对于这一类型的题目，要弄清和理解火车、桥、隧道等长度，在物体运动垃程中的作用，这样才能正确运用路程，速度和时间这三者之间的关系予以解答。

解答火车问题的一般数量关系式是：相遇交错（迎面错车）而垃过的时间=火车长度的和÷速度和追及相离（超错而过）的时间=火车长度的和÷速度差在解答过程中．题目具体条件或要求的不同，解答的方法也有区别。

例1 ：南京长江大桥长6700 米，一列长100 米的客车，以每分钟400 米的速度通过大桥，求这列客车通过大桥需要多少分钟?【思路导航】从客车头到达大桥至车尾离开大桥，客车通过大桥所行驶的总路程是桥长和车长相加的和。

已知桥长与车长及客车行驶的速度，就容易求出这列客车经过大桥所需的时间了。

【示范解答】（6700+100）÷ 400=17（分钟）答：客车通过大桥需要17 分钟。

例2 ：一列火车长240 米，以每秒25 米的速度行驶着。

到达一座大桥时，从上桥到离桥共用30 秒，那么这座桥全长多少米?【思路导航】火车过桥的路程是车长+桥长，已知火车过桥的速度及时间，可求火车过桥的总路程，从中减去车身长就是桥长。

【示范解答】25×30－240=510（米）答：这座桥全长510 米。

例3 ：某列火车通过360 米的第一个山洞用了24 秒。

接着通过第二个长216 米的山洞用了16 秒。

那么这列火车的速度和长度分别是多少?【思路导航】求这列火车的长度必须要知道列车通过山洞的速度及路程。

因此解答此题的关键是求出列车的速度。

已知条件告诉我们这列火车通过两个长度不同的山洞用了二个不同的时间，所以可以通过两个山洞的长度差与所用的时间差来求出这列火车的速度，有了车速及时间，求车身长就容易了。

第31讲行程问题（四）一、专题简析：通过前面对行程应用题的学习，同学们可以发现，行程问题大致分为以下三种情况：（1）相向而行：相遇时间=距离÷速度和（2）相背而行：相背距离=速度×时间（3）同向而行：追及时间=追及距离÷速度差如果上述的几种情况交织在一起，组成的应用题将会丰富多彩、千变万化。

解答这些问题时，我们还是要理清题中已知条件与所求问题之间的关系，同时采用“转化”、“假设”等方法，把复杂的数量关系转化为简单的数量关系，把一复杂的问题转化为几个简单的问题逐一进行解决。

二、精讲精练例1甲、乙两地相距420千米，一辆汽车从甲地开到乙地共用了8小时，途中，有一段路在整修路面，汽车行驶这段路时每小时只能行20千米，其余时间每小时行60千米。

整修路面的一段路长多少千米？1、一辆汽车从甲城到乙城共行驶395千米，用了5小时。

途中一部分公路是高速公路，另一部分是普通公路。

已知汽车在高速公路上每小时行105千米，在普通公路上每小时行55千米。

汽车在高速公路上行驶了多少千米？2、小明家离体育馆2300米，有一天，他以每分钟100米的速度去体育馆看球赛。

出发几分钟后发现，如果以这样的速度走下去一定迟到，他马上改用每分钟180米的速度跑步前进，途中共用15分钟，准时到达了体育馆。

问：小明是在离体育馆多远的地方开始跑步的？例2 客、货两车同时从甲、乙两站相对开出，客车每小时行54千米，货车每小时行48千米。

两车相遇后又以原速前进，到达对方站后立即返回，两车再次相遇时客车比货车多行21.6千米。

甲、乙两站间的路程是多少千米？1、乙、慢两车同时从甲、乙两地相对开出并往返行驶。

快车每小时行80千米，慢车每小时行45千米。

两车第二次相遇时，快车比慢车多行了210千米。

求甲、乙两地间的路程。

2、甲、乙两地相距216千米，客货两车同时从甲、乙两地相向而行。

已知客车每小时行58千米，货车每小时行50千米，到达对方出发点后立即返回。

第31讲行程问题（四）一、专题简析：通过前面对行程应用题的学习，同学们可以发现，行程问题大致分为以下三种情况：（1）相向而行：相遇时间=距离÷速度和（2）相背而行：相背距离=速度×时间（3）同向而行：追及时间=追及距离÷速度差如果上述的几种情况交织在一起，组成的应用题将会丰富多彩、千变万化。

解答这些问题时，我们还是要理清题中已知条件与所求问题之间的关系，同时采用“转化”、“假设”等方法，把复杂的数量关系转化为简单的数量关系，把一复杂的问题转化为几个简单的问题逐一进行解决。

二、精讲精练例1甲、乙两地相距420千米，一辆汽车从甲地开到乙地共用了8小时，途中，有一段路在整修路面，汽车行驶这段路时每小时只能行20千米，其余时间每小时行60千米。

整修路面的一段路长多少千米？1、一辆汽车从甲城到乙城共行驶395千米，用了5小时。

途中一部分公路是高速公路，另一部分是普通公路。

已知汽车在高速公路上每小时行105千米，在普通公路上每小时行55千米。

汽车在高速公路上行驶了多少千米？2、小明家离体育馆2300米，有一天，他以每分钟100米的速度去体育馆看球赛。

出发几分钟后发现，如果以这样的速度走下去一定迟到，他马上改用每分钟180米的速度跑步前进，途中共用15分钟，准时到达了体育馆。

问：小明是在离体育馆多远的地方开始跑步的？例2客、货两车同时从甲、乙两站相对开出，客车每小时行54千米，货车每小时行48千米。

两车相遇后又以原速前进，到达对方站后立即返回，两车再次相遇时客车比货车多行21.6千米。

甲、乙两站间的路程是多少千米？1、乙、慢两车同时从甲、乙两地相对开出并往返行驶。

快车每小时行80千米，慢车每小时行45千米。

两车第二次相遇时，快车比慢车多行了210千米。

求甲、乙两地间的路程。

2、甲、乙两地相距216千米，客货两车同时从甲、乙两地相向而行。

已知客车每小时行58千米，货车每小时行50千米，到达对方出发点后立即返回。

小学数学火车行程问题知识点
两列火车错车用的时间是：
（A的车身长+B的车身长）÷（A车的速度+B车的速度）
两列火车超车用的时间是：
（A的车身长+B的车身长）÷（A车的速度-B车的速度）（注：A车追B车）
火车过桥问题，可用下面的关系式求火车通过的时间：
（列车长度+桥的长度）÷列车速度
火车通过两座桥，或通过一座桥，隧道，车头走过的长度是：桥长+火车长或隧道长+火车长
其中火车长一样，比较长和隧道长，再比较所用的时间的差，就又求出火车的速度以及车身长。

人坐在列车上往窗外看另一列车，相当人在一定时间内走过一座桥。

1、例1：一列慢车，车身长120米，车速是每秒15米，一列快车车身长160米，车速是每秒20米，两车在双轨轨道上相向而行，从车头相遇到车尾相离要用多少秒钟？
解答：（120+160）÷（15+20）=280÷35=8（秒）
答：两车从车头相遇到车尾相离用8秒钟。

2、例2：一列客车每分钟行1000米，一列货车每分钟750米，货车比客车的车身长135米。

两车在平行的轨道上同向行驶，当客车从后面超过货车，两车交叉的时间为1分30秒。

求货车与客车的车身长各是多少米？
解：（1000－750）×1.5=250×1.5=375（米）
这“375米”就正好是客车与货车的长度之和，题目已经告诉我们货车比客车的车身长135米，这两车的长度，列式如下：（375+135）÷2 （375－135）÷2
=510÷2 =240÷2
=255（米）=120（米）
答：货车长255米，客车长120米。

第九章行程问题•火车过桥典型题训练1（难度等级★★）例一座大桥长2400米，一列火车以900米/分钟的速度通过大桥，从车头开上桥到车尾离开桥共需3分钟。

这列火车长多少米？解从火车车头开上桥到车尾离开桥，火车行驶的路程正好等于火车自身车长与桥长之和，而路程可根据“路程＝速度×时间”求解。

火车行驶的路程：900×3＝2700（米）火车车长：2700－2400＝300（米）答：这列火车长300米。

提示：过桥问题的主要关系式有：桥长＋车长＝路程，速度×过桥时间＝路程。

这里的路程指从火车车头上桥开始到火车车尾离开桥为止，即火车行驶的路程。

1．一列货车全长240米，每秒行驶15米，列车连续通过一条隧道和一座桥，共用40秒，桥长150米。

这条隧道全长多少米？2．一列火车全长280米，从路边站立的一个人旁边完全经过用了10秒，以同样的速度完全通过一座长3080米的大桥（从车头上桥到车尾离桥），需要几分钟？3．一列货车全长800米，完全通过一座长1700米的大桥用了5分钟。

过桥后，这列货车以同样的速度从路边站立的一个人旁边经过，完全经过这个人需要多少分钟？典型题训练2（难度等级★★★）例某列火车完全通过（从车头进隧道到车尾离开隧道）360米的第一条隧道用了24秒，接着完全通过第二条长216米的隧道用了16秒，这列火车的长度是多少米？解火车通过第二个隧道比第一个隧道少用了8秒，是因为隧道短了360－216＝144（米），即这8秒钟走了144米。

这样可以求出火车的速度，进而求出火车24秒行驶的距离，这段距离包含了火车的长度和第一个隧道的长度，这样就求出了火车的长度。

火车的速度：（360－216）÷（24－16）＝18（米/秒）火车在24秒行驶的距离：24×18＝432（米）火车的长度：432－360＝72（米）答：这列火车长72米。

1．一列客车完全通过一条528米长的隧道用了29秒，接着完全通过396米长的隧道用了23秒。

火车过桥常见题型及解题方法（一）、行程问题基本公式：路程=速度⨯时间总路程=平均速度⨯总时间；（二）、相遇、追及问题：速度和⨯相遇时间=相遇路程速度差⨯追及时间=追及路程；（三）、火车过桥问题1、火车过桥（隧道）：一个有长度、有速度，一个有长度、但没速度，解法：火车车长＋桥(隧道)长度(总路程) ＝火车速度×通过的时间；2、火车＋树(电线杆)：一个有长度、有速度，一个没长度、没速度，解法：火车车长(总路程)＝火车速度×通过时间；2、火车＋人：一个有长度、有速度，一个没长度、但有速度，（1）、火车＋迎面行走的人：相当于相遇问题，解法：火车车长(总路程) ＝(火车速度＋人的速度)×迎面错过的时间；（2）火车＋同向行走的人：相当于追及问题，解法：火车车长(总路程) ＝(火车速度—人的速度) ×追及的时间；（3）火车＋坐在火车上的人：火车与人的相遇和追及问题解法：火车车长(总路程) ＝(火车速度±人的速度) ×迎面错过的时间（追及的时间）；4、火车＋火车：一个有长度、有速度，一个也有长度、有速度，（1）错车问题：相当于相遇问题，解法：快车车长＋慢车车长(总路程) ＝ (快车速度＋慢车速度) ×错车时间；（2）超车问题：相当于追及问题，解法：快车车长＋慢车车长(总路程) ＝ (快车速度—慢车速度) ×错车时间；模块一、火车过桥（隧道、树）问题【巩固】一列火车长360米，每秒钟行驶16米，全车通过一条隧道需要90秒钟，求这条隧道长多少米？【巩固】一列火车经过南京长江大桥，大桥长6700米，这列火车长100米，火车每分钟行400米，这列客车经过长江大桥需要多少分钟？【巩固】一列火车长160米，全车通过一座桥需要30秒钟，这列火车每秒行20米，求这座桥的长度．【例1】(2009年第七届“希望杯”六年级一试)四、五、六3个年级各有100名学生去春游，都分成2列(竖排)并列行进．四、五、六年级的学生相邻两行之间的距离分别是1米、2米、3米，年级之间相距5米．他们每分钟都行走90米，整个队伍通过某座桥用4分钟，那么这座桥长米．【巩固】一列火车长450米，铁路沿线的绿化带每两棵树之间相隔3米，这列火车从车头到第1棵树到车尾离开第101棵树用了0.5分钟．这列火车每分钟行多少米？【例2】小红站在铁路旁，一列火车从她身边开过用了 21秒．这列火车长 630米，以同样的速度通过一座大桥，用了1.5 分钟．这座大桥长多少米？【巩固】（2008年第八届“春蕾杯”小学数学邀请赛）小胖用两个秒表测一列火车的车速。

火车的行程问题在考虑人、汽车、飞机等的行程问题时，这些运动的人和物体自身长度不影响行程，在行程问题中把它们看作一个点在运动。

而火车的车身较长，在有些行程问题中，路程与车身长有关，因此就必须加以考虑。

特例：1、火车迎面过人的时间内，人车共行路程是车身长。

2、火车过隧道(或桥)的时间内，火车行的路程等于车长与隧道(或桥)长之和。

(1)迎面错车两车错车时间内，共行路程是两车车身长的和，错车“车速”是两车车速的和，即：(2)同向超车两列火车同向超车的时间内，快车多行的路程是两车车身长之和，超车“车速”是两车车速的差，即：小张和小王各以一定速度在周长为500米的环形跑道上跑步，小王速度是180米/分。

(1)小张和小王从同一地点同时出发，反向跑步，75秒后两人第一次相遇，小张的速度是多少？(2)小张和小王从同一地点同时出发，沿同一方向跑步，小张跑多少圈后才能第一次追上小王？A、B是圆的直径的两端，小强在A点、小明在B点，同时出发反向而行，他们在离A点80米的C处第一次相遇；在离B点60米的D处第二次相遇，求圆的周长？绕湖一周是24千米，小张和小王从湖边某一地点同时出发反向而行。

小王以4千米/小时的速度每走1小时后休息5分钟，小张以6千米/小时的速度每走50分钟后休息10分钟。

问：两人出发后多少时间第一次相遇？绕人民大会堂一周是600米，小张骑车速度是200米/分，小王步行速度是50米/分，他们从同一地点同时出发，同方向绕人民大会堂环行。

问：出发后多少时间小张追上小王？A、B是圆的直径的两端，甲从A、乙从B同时同向出发，甲走一周要15分钟，乙走一周要20分钟，问出发后多少时间甲追上乙？一个圆周长70厘米，甲、乙两只爬虫从同一点同时出发，同向爬行，甲以4厘米/秒的速度不停地爬行，乙爬行15厘米后，立即反向爬行，并且速度增加1倍，在离出发点30厘米处与甲相遇，问爬虫乙原来的速度是多少？小张步行从甲村到乙村去，小李骑自行车从乙村往甲村去，他们同时出发，1小时后在途中相遇，他们分别继续前进。

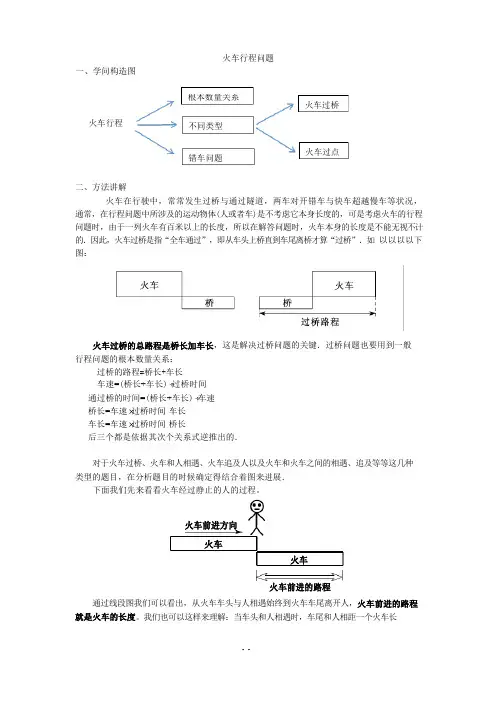
火车过桥 火车过点火车前进方向火车火车行程问题一、学问构造图火车行程二、方法讲解火车在行驶中，常常发生过桥与通过隧道，两车对开错车与快车超越慢车等状况， 通常，在行程问题中所涉及的运动物体(人或者车)是不考虑它本身长度的，可是考虑火车的行程问题时，由于一列火车有百米以上的长度，所以在解答问题时，火车本身的长度是不能无视不计的．因此，火车过桥是指“全车通过”，即从车头上桥直到车尾离桥才算“过桥”．如 以以以以下图：火车过桥的总路程是桥长加车长，这是解决过桥问题的关键．过桥问题也要用到一般行程问题的根本数量关系：过桥的路程=桥长+车长车速=(桥长+车长)÷过桥时间通过桥的时间=(桥长+车长)÷车速桥长=车速×过桥时间-车长车长=车速×过桥时间-桥长后三个都是依据其次个关系式逆推出的．对于火车过桥、火车和人相遇、火车追及人以及火车和火车之间的相遇、追及等等这几种类型的题目，在分析题目的时候确定得结合着图来进展．下面我们先来看看火车经过静止的人的过程。

火车前进的路程通过线段图我们可以看出，从火车车头与人相遇始终到火车车尾离开人，火车前进的路程就是火车的长度。

我们也可以这样来理解：当车头和人相遇时，车尾和人相距一个火车长火车根本数量关系不同类型错车问题度，所以整个过程就是车尾和人的相遇问题。

以上是人不动状况下的火车行程问题，下面我们来介绍一下行人和火车的相遇和追及问题，如以以以以下图所示：火车前进方向车尾离开行人车头遇到行人 火车行人的路程火车前进的路程火车的长度我们可以将火车看成一个点：开头的时候行人和车尾的距离为一个车长，完毕的时候行人和车尾相遇了。

也就是说，从火车与行人的相遇到错开，这个过程可以看成是行人与车尾相遇了。

也就是说，从火车与行人的相遇到错开，这个过程可以看成是行人与车尾的相遇问题，火车和行人经过的路程和等于火车的长度。

类似的，对于火车追行人的过程，从追上到离开，火车和行人的路程差等于火车的长 度。

第36讲火车行程问题一、专题简析：有关火车过桥、火车过隧道、两列火车车头相遇到车尾相离等问题，也是一种行程问题。

在考虑速度、时间和路程三种数量关系时，必须考虑到火车本身的长度。

如果有些问题不容易一下子看出运动过程中的数量关系，可以利用作图或演示的方法来帮助解题。

解答火车行程问题可记住以下几点：1、火车过桥（或隧道）所用的时间=[桥（隧道长）＋火车车长]÷火车的速度；2、两列火车相向而行，从相遇到相离所用的时间=两火车车身长度和÷两车速度和；3、两车同向而行，快车从追上到超过慢车所用的时间=两车车身长度和÷两车速度差。

二、精讲精练例1甲火车长210米，每秒行18米；乙火车长140米，每秒行13米。

乙火车在前，两火车在双轨车道上行驶。

甲火车从后面追上到完全超过乙火车要用多少秒？练习一1、一列快车长150米，每秒行22米；一列慢车长100米，每秒行14米。

快车从后面追上慢车到超过慢车，共需几秒钟？2、小明以每秒2米的速度沿铁路旁的人行道跑步，身后开来一列长188米的火车，火车每秒行18米。

问：火车追上小明到完全超过小明共用了多少秒钟？例2 一列火车长180米，每秒钟行25米。

全车通过一条120米的山洞，需要多长时间？练习二1、一列火车长360米，每秒行18米。

全车通过一座长90米的大桥，需要多长时间？2、一座大桥长2100米。

一列火车以每分钟800米的速度通过这座大桥，从车头上桥到车尾离开共用3.1分钟。

这列火车长多少米？例3 有两列火车，一车长130米，每秒行23米；另一列火车长250米，每秒行15米。

现在两车相向而行，从相遇到离开需要几秒钟？练习三1、有两列火车，一列长260米，每秒行18米；另一列长220米，每秒行30米。

现两列车相向而行，从相遇到相离需要几秒钟？2、一列火车长500米，要穿过一个长150米的山洞，如果火车每秒钟行26米，那么，从车头进洞到车长全部离开山洞一共要用几秒钟？例4 一列火车通过2400米的大桥需要3分钟，用同样的速度从路边的一根电线杆旁边通过，只用了1分钟。

第27讲火车行程问题教学目标清楚理解火车行程问题中的等量关系；能够透过分析实际问题，提炼出等量关系；培养分析问题，解决实际问题，综合归纳整理的能力，以及理论联系实际的能力；知识梳理一、基本公式路程=时间×速度时间=路程÷速度速度=路程÷时间二、火车行程问题有关火车过桥（隧道）、两列火车车头相遇到车尾相离等问题，是一种行程问题。

在考虑速度、时间和路程三种数量关系时，必须考虑到火车本身的长度。

如果遇到复杂的情况，可利用作图或演示的方法来帮助解题。

解答火车行程问题可记住以下几点：1、火车过桥（或隧道）所用的时间=[桥长（隧道长）＋火车车长]÷火车的速度；2、两列火车相向而行，从相遇到相离所用的时间=两火车车身长度和÷两车速度和；3、两车同向而行，快车从追上到超过慢车所用的时间=两车车身长度和÷两车速度差。

典例分析考点一：求时间例1、一列火车长150米，每秒钟行19米。

全车通过长800米的大桥，需要多少时间？【解析】列车过桥，就是从车头上桥到车尾离桥止。

车尾经过的距离=车长+桥长，车尾行驶这段路程所用的时间用车长与桥长和除以车速。

火车长桥长火车所走的路程解：（800+150）÷19=50（秒）答：全车通过长800米的大桥，需要50秒。

例2、一列火车长119米，它以每秒15米的速度行驶，小华以每秒2米的速度从对面走来，经过几秒钟后火车从小华身边通过？【解析】本题是求火车车头与小华相遇时到车尾与小华相遇时经过的时间。

依题意，必须要知道火车车头与小华相遇时，车尾与小华的距离、火车与小华的速度和。

解：（1）火车与小华的速度和：15+2=17（米/秒）（2）相距距离就是一个火车车长：119米（3）经过时间：119÷17=7（秒）答：经过7秒钟后火车从小华身边通过。

考点二：求隧道长例1、一列火车长200米，以每秒8米的速度通过一条隧道，从车头进洞到车尾离洞，一共用了40秒。

行程问题---火车问题（巨人大班课讲义）一、火车过桥例1 （1）一列火车长180米，每秒行20米，这列火车通过320米大桥，需要多少时间？（2）一列火车以每秒20米的速度，通过一座长200米的大桥，共用21秒，这列火车长多少米？练1 一列火车长700米，以每分钟500米的速度通过一座长1300米的大桥，从车头上桥到车尾离桥需要多少分钟？例2（1）一列长为264米的火车经过一根电线杆用了22秒（电线杆宽度忽略不计）之后，又用了44秒经过一个隧道，那么隧道长度为多少米？（2）一列火车经过一座350米的桥用了30秒，又经过一座560米的桥用了44秒，这列火车多长？练2 一列火车用12秒经过一座300米长的大桥，又用了20秒经过一座长540米的隧道，求火车的速度和车长。

二、火车与人例3 （1）费叔叔沿着一条与铁路平行的公路散步，每分钟60米迎面开来一列长300米的火车，从车头与费叔叔相遇到火车尾离开，共用了20秒，求火车的速度。

（2）小月沿着一条与铁路平行的公路散步，她散步的速度是每秒2米，这时从小月身后开来一列火车，从车头追上小月到车尾离开小月共用了18秒，已知火车速度是每秒17米，求火车车长。

练3 一个人以每分钟60米的速度沿铁路步行，一列长144米的客车从对面开来，从他身边通过用8秒钟，客车的速度是每秒多少米？例4许三多所在的钢七连队伍长450米，以每秒1.5米的速度行进，许三多以每秒3米的速度从队尾跑到队头需要多长时间？然后从队头返回队尾，又需要多少时间？练4 某学校组织学生春游，队伍长540米，并以每秒2米的速度前进，一名学生以每秒4米的速度从队尾跑到队头，再回到队尾，共用多少分钟？三、两火车相遇追及例5（1）一列火车长180米，每秒行20米；另一列火车长200米，每秒行18米，两车相向而行，他们从车头相遇到车尾相离要经过多少时间？（2）甲火车长370米，每秒行15米，乙火车长350米，每秒行21米，两车同向而行，乙车从追上甲车到完全超过甲车需要多长时间？练5已知快车长182米，每秒行20米，慢车长218米，每秒行18米。

【小学五年级奥数讲义】火车行程问题
一、专题简析：
有关火车过桥、火车过隧道、两列火车车头相遇到车尾相离等问题，也是一种行程问题。

在考虑速度、时间和路程三种数量关系时，必须考虑到火车本身的长度。

如果有些问题不容易一下子看出运动过程中的数量关系，可以利用作图或演示的方法来帮助解题。

解答火车行程问题可记住以下几点：
1、火车过桥（或隧道）所用的时间=[桥（隧道长）＋火车车长]÷火车的速度；
2、两列火车相向而行，从相遇到相离所用的时间=两火车车身长度和÷两车速度和；
3、两车同向而行，快车从追上到超过慢车所用的时间=两车车身长度和÷两车速度差。

二、精讲精练
例1甲火车长210米，每秒行18米；乙火车长140米，每秒行13米。

乙火车在前，两火车在双轨车道上行驶。

甲火车从后面追上到完全超过乙火车要用多少秒？
1。

五年级数学培优：火车行程问题【专题导引】有关火车过桥、火车过遂道、两列火车车头相遇到车尾相离等问题，也是一种行程问题.在考虑速度、时间和路程三种数量关系时，必须考虑到火车本身的长度.如果有些问题不容易一下子看出运动过程中的数量关系，可以利用作图或演示的方法来帮助解题.解答火车行程问题可记住以下几点：1、火车过桥（或隧道）所用的时间[桥（隧道长）+火车身长]÷火车的速度.2、两列火车相向而行，从相遇到相离所用的时间=两火车车身长度和÷两车速度和.3、两车同向而行，快车从追上到超过慢车所用的时间=两车车身长度和÷两车速度差.【预备思考题1】一列火车车长180米，每秒行20米，这列火车通过320米长的大桥，需要多少时间？【预备思考题2】一列火车通过一座长456米的桥需要80秒，用同样的速度通过一条399米的隧道要77秒.求这列火车的速度.【典型例题】【例1】甲火车长210米，每秒行18米，乙火车长140米，每秒行13米.乙火车在前，两火车在双轨车道上行驶.求甲火车从后面追上到完全超过乙火车要用多少秒？【试一试】1、一列快车长150米，每秒行22米，一列慢车长100米，每秒行14米.快车从后面追上慢车到超过慢车，共需多少秒钟？2、小明以每秒2米的速度沿铁路旁的人行道跑步，身后开来一列长188米的火车，火车每秒行18米，问：火车追上小明到完全超过小明共用了多少秒钟？【例2】一列火车长180米，每秒钟行25米.全车通过一条120米的山洞，需要多少时间？【试一试】1、一列火车长360米，每秒行18米.全车通过一座长90米的大桥，从车头上桥到车尾离开共用3.1分钟，这列火车长多少米？2、一座大桥长2100米.一列火车以每分钟800米的速度通过这座大桥，从车上桥到车尾离开共用3、1分钟，这列火车长多少米？【例3】有两列火车，一车长130米，每秒行23米，另一车长250米，每秒行15米，现在两车相向而行，问从相遇到离开需要几秒钟？【试一试】1、有两列火车，一车长360米，每秒行18米，另一车长216米，每秒行30米，现在两车相向而行，问从相遇到离开一共需要几秒钟？2、有两列火车，一列长220米，每秒行22米，另一列长200米迎面开来，两车从相遇到离开共用了10秒钟，求另一列火车的速度？【例4】一列火车通过2400米的大桥需要3分钟，用同样的速度从路边的一根电线杆旁边通过，只用了1分钟.求这列火车的速度.【试一试】1、一列火车从小明身旁通过用了15秒，用同样的速度通过一座长100米的桥用了20秒.这列火车的速度是多少？2、一列火车长900米，从路边的一棵大树旁通过用了1.5分钟，以同样的速度通过一座大桥用了3.5分钟.求这座大桥的长度.【﹡例5】甲列车每秒行20米，乙列车每秒行14米，若两列车齐头并进，则甲车行40秒超过乙车，若两列车齐尾并进，则甲车行30秒超过乙，求甲列车和乙列车各长多少米？【﹡试一试】1、一列快车长200米，每22米，一列慢车长160米，每秒行17米，两列车齐头并进，快车超过慢车要多少秒？若齐尾并进，快车超过慢车要多少秒？2、快车每秒行18米，慢车每秒行10米.两列火车同时同方向齐头并进，行10秒钟后快车超过慢车；如果两列火车齐尾并进，则7秒钟后快车超过慢车.求两列火车的车长.课外作业家长签名：1、一列火车车长400米，以每分800米的速度通过一条长2800米长的隧道，需要多少时间？2、一列火车经过一根有信号灯的电线杆用了9秒，通过一座468米长的铁桥用了35秒，这列车长多少米？3、A火车长180米，每秒行18米，B火车每秒行15米，两火车同方向行驶，A 火车从追上B火车到超过它共用了100秒钟，求B火车长多少米？4、五年级384个同学排成两路纵队郊游，每两个同学相隔0.5米，队伍以每分钟61米的速度通过一座长207米的大桥，一共需要多少时间？5、有两列火车，一车长320米，每秒行18米，另一列火车以每秒22米的速度迎面开来，两车从相遇到离开共用了15秒，求另一列火车的车长.6、一列火车通过200米的大桥需要80秒，同样的速度通过144米长的隧道需要72秒.求火车的速度和车长.7、王叔叔沿铁路边散步，他每分钟走50米，迎面驶来一列长280米的列车，他与列车车头相遇到车尾相离共用了半分钟，求这列火车的速度.。

第36 讲火车行程问题一、专题简析：有关火车过桥、火车过隧道、两列火车车头相遇到车尾相离等问题，也是一种行程问题。

在考虑速度、时间和路程三种数量关系时，必须考虑到火车本身的长度。

如果有些问题不容易一下子看出运动过程中的数量关系，可以利用作图或演示的方法来帮助解题。

解答火车行程问题可记住以下几点：1、火车过桥（或隧道）所用的时间=[ 桥（隧道长）＋火车车长] ÷火车的速度；2、两列火车相向而行，从相遇到相离所用的时间=两火车车身长度和÷两车速度和；3、两车同向而行，快车从追上到超过慢车所用的时间=两车车身长度和÷两车速度差。

二、精讲精练例 1 甲火车长210 米，每秒行18 米；乙火车长140 米，每秒行13 米。

乙火车在前，两火车在双轨车道上行驶。

甲火车从后面追上到完全超过乙火车要用多少秒？练习一1、一列快车长150 米，每秒行22 米；一列慢车长100 米，每秒行14 米。

快车从后面追上慢车到超过慢车，共需几秒钟？2、小明以每秒 2 米的速度沿铁路旁的人行道跑步，身后开来一列长188米的火车，火车每秒行18 米。

问：火车追上小明到完全超过小明共用了多少秒钟？例 2 一列火车长180 米，每秒钟行25 米。

全车通过一条120 米的山洞，需要多长时间？练习二1、一列火车长360 米，每秒行18 米。

全车通过一座长90 米的大桥，需要多长时间？2、一座大桥长2100 米。

一列火车以每分钟800 米的速度通过这座大桥，从车头上桥到车尾离开共用 3.1 分钟。

这列火车长多少米？例 3 有两列火车，一车长130 米，每秒行23 米；另一列火车长250 米，每秒行15 米。

现在两车相向而行，从相遇到离开需要几秒钟？练习三1、有两列火车，一列长260米，每秒行18米；另一列长220米，每秒行30 米现两列车相向而行，从相遇到相离需要几秒钟？2、一列火车长500 米，要穿过一个长150 米的山洞，如果火车每秒钟行26 米，那么，从车头进洞到车长全部离开山洞一共要用几秒钟？例 4 一列火车通过2400 米的大桥需要 3 分钟，用同样的速度从路边的一根电线杆旁边通过，只用了 1 分钟。

小学数学知识点精讲精练之：火车行程问题火车行程问题清楚理解火车行程问题中的等量关系；能够透过分析实际问题，提炼出等量关系；培养分析问题，解决实际问题，综合归纳整理的能力，以及理论联系实际的能力；一、基本公式路程=时间×速度时间=路程÷速度速度=路程÷时间二、火车行程问题有关火车过桥（隧道）、两列火车车头相遇到车尾相离等问题，是一种行程问题。

在考虑速度、时间和路程三种数量关系时，必须考虑到火车本身的长度。

如果遇到复杂的情况，可利用作图或演示的方法来帮助解题。

解答火车行程问题可记住以下几点：1、火车过桥（或隧道）所用的时间=[桥长（隧道长）＋火车车长]÷火车的速度；2、两列火车相向而行，从相遇到相离所用的时间=两火车车身长度和÷两车速度和；3、两车同向而行，快车从追上到超过慢车所用的时间=两车车身长度和÷两车速度差。

考点一：求时间例1、一列火车长150米，每秒钟行19米。

全车通过长800米的大桥，需要多少时间？教学目标知识梳理典例分析【解析】列车过桥，就是从车头上桥到车尾离桥止。

车尾经过的距离=车长+桥长，车尾行驶这段路程所用的时间用车长与桥长和除以车速。

火车长桥长火车所走的路程解：（800+150）÷19=50（秒）答：全车通过长800米的大桥，需要50秒。

例2、一列火车长119米，它以每秒15米的速度行驶，小华以每秒2米的速度从对面走来，经过几秒钟后火车从小华身边通过？【解析】本题是求火车车头与小华相遇时到车尾与小华相遇时经过的时间。

依题意，必须要知道火车车头与小华相遇时，车尾与小华的距离、火车与小华的速度和。

解：（1）火车与小华的速度和：15+2=17（米/秒）（2）相距距离就是一个火车车长：119米（3）经过时间：119÷17=7（秒）答：经过7秒钟后火车从小华身边通过。

考点二：求隧道长例1、一列火车长200米，以每秒8米的速度通过一条隧道，从车头进洞到车尾离洞，一共用了40秒。