4工程流体力学 第四章流体动力学基础
- 格式:ppt
- 大小:2.87 MB
- 文档页数:4


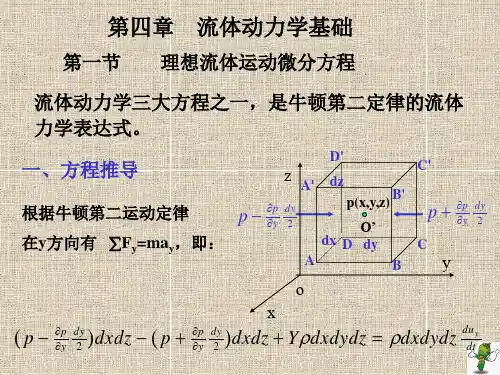




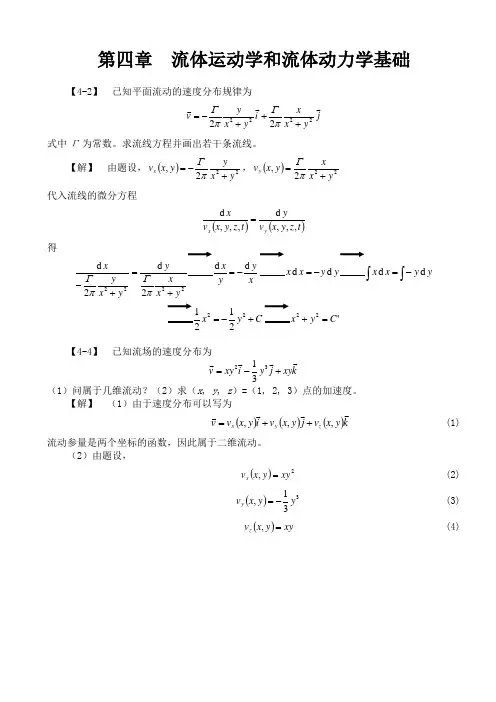
第四章 流体运动学和流体动力学基础【4-2】 已知平面流动的速度分布规律为j yx xi y x y v 222222+++-=πΓπΓ 式中Γ为常数。
求流线方程并画出若干条流线。
【解】 由题设,()222,y x y y x v x +-=πΓ,()222,y x xy x v y+=πΓ 代入流线的微分方程()()t z y x v yt z y x v x y x ,,,d ,,,d =得222222d y x x y x yx+=+-πΓπΓxy y d -=yy x x d d -=⎰⎰-=y y x x d dC y x +-=22212'22C y x =+【4-4】 已知流场的速度分布为k xy j y i xy v +-=3231(1)问属于几维流动?(2)求(x , y , z )=(1, 2, 3)点的加速度。
【解】 (1)由于速度分布可以写为()()()k y x v j y x v i y x v v z y x,,,++= (1) 流动参量是两个坐标的函数,因此属于二维流动。
(2)由题设,()2,xy y x v x = (2)()331,y y x v y -= (3)()xy y x v z =, (4)()()()()4322223222310231031d d xy xy y y xy xy zxyxy y y xy x xy xy t z vv y v v x v v t v t v a x z x y x x x x x =+⋅-+=∂∂+∂∂-∂∂+∂∂=∂∂+∂∂+∂∂+∂∂==(5)()52333332331031003131313131d d y y y y z xy y y y y x xy y t zv v yv v xv v tv tv a y zy yy xy y y =+-⋅-+=⎪⎭⎫ ⎝⎛-∂∂+⎪⎭⎫ ⎝⎛-∂∂-⎪⎭⎫ ⎝⎛-∂∂+⎪⎭⎫ ⎝⎛-∂∂=∂∂+∂∂+∂∂+∂∂== (6)()()()()3323232031031d d xy x y y xy xy zxy xy y y xy x xy xy t z vv y v v x v v t v t v a z z z y z x z z z =+⋅-⋅+=∂∂+∂∂-∂∂+∂∂=∂∂+∂∂+∂∂+∂∂==(7)将x =1,y=2,z =3代入式(5)(6)(7),得31621313144=⨯⨯==xy a x3322313155=⨯==y a y 31621323233=⨯⨯==xy a z【4-15】 图4-28所示为一文丘里管和压强计,试推导体积流量和压强计读数之间的关系式。


闻建龙主编的《工程流体力学》习题参考答案第一章绪论1-1 物质是按什么原则分为固体和液体两大类的?解:从物质受力和运动的特性将物质分成两大类:不能抵抗切向力,在切向力作用下可以无限的变形(流动),这类物质称为流体。
如空气、水等。
而在同等条件下,固体则产生有限的变形。
因此,可以说:流体不管是液体还是气体,在无论多么小的剪应力(切向)作用下都能发生连续不断的变形。
与此相反,固体的变形与作用的应力成比例,经一段时间变形后将达到平衡,而不会无限增加。
1-2 何谓连续介质假设?引入连续介质模型的目的是什么?在解决流动问题时,应用连续介质模型的条件是什么?解:1753年,欧拉首次采用连续介质作为流体宏观流动模型,即不考虑流体分子的存在,把真实的流体看成是由无限多流体质点组成的稠密而无间隙的连续介质,甚至在流体与固体边壁距离接近零的极限情况也认为如此,这个假设叫流体连续介质假设或稠密性假设。
流体连续性假设是流体力学中第一个根本性假设,将真实流体看成为连续介质,意味着流体的一切宏观物理量,如密度、压力、速度等,都可看成时间和空间位置的连续函数,使我们有可能用数学分析来讨论和解决流体力学问题。
在一些特定情况下,连续介质假设是不成立的,例如:航天器在高空稀薄气体中飞行,超声速气流中激波前后,血液在微血管(1μm )内的流动。
1-3 底面积为25.1m 的薄板在液面上水平移动(图1-3),其移动速度为s m 16,液层厚度为mm 4,当液体分别为C 020的水和C 020时密度为3856m kg的原油时,移动平板所需的力各为多大?题1-3图解:20℃ 水:s Pa ⋅⨯=-3101μ20℃,3/856m kg =ρ, 原油:s Pa ⋅⨯='-3102.7μ水: 233/410416101m N u =⨯⨯=⋅=--δμτ 油: 233/8.2810416102.7m N u =⨯⨯=⋅'=--δμτ 1-4 在相距mm 40=δ的两平行平板间充满动力粘度s Pa ⋅=7.0μ液体(图1-4),液体中有一边长为mm a 60=的正方形薄板以s m u 15=的速度水平移动,由于粘性带动液体运动,假设沿垂直方向速度大小的分布规律是直线。
流体力学概念总结第一章绪论工程流体力学的研究对象:工程流体力学以流体(包括液体和气体)为研究对象,研究流体宏观的平衡和运动的规律,流体与固体壁面之间的相互作用规律,以及这些规律在工程实际中的应用。
第二章流体的主要物理性质流体的概念:凡是没有固定的形状,易于流动的物质就叫流体流体质点:包含有大量流体分子,并能保持其宏观力学性能的微小单元体。
连续介质的概念:在流体力学中,把流体质点作为最小的研究对象,从而把流体看成是1)由无数连续分布、彼此无间隙地2)占有整个流体空间的流体质点所组成的介质密度:单位体积的流体所具有的质量称为密度,以ρ表示重度:单位体积的流体所受的重力称为重度,以γ表示比体积:密度的倒数称为比体积,以υ表示。
它表示单位质量流体所占有的体积流体的相对密度:是指流体的重度与标准大气压下4℃纯水的重度的比值,用d表示。
流体的热膨胀性:在一定压强下,流体体积随温度升高而增大的性质称为流体的热膨胀性。
流体的压缩性:在一定温度下,流体体积随压强升高而减少的性质称为流体的压缩性可压缩流体:ρ随T和p变化量很大,不可视为常量不可压缩流体:ρ随T和p变化量很小,可视为常量。
流体的粘性:流体流动时,在流体内部产生阻碍运动的摩擦力的性质叫流体的粘性。
牛顿内摩擦定律:牛顿经实验研究发现,流体运动产生的内摩擦力与沿接触面法线方向的速度变化(即速度梯度)成正比,与接触面的面积成正比,与流体的物理性质有关,而与接触面上的压强无关。
这个关系式称为牛顿内摩擦非牛顿流体:通常把满足牛顿内摩擦定律的流体称为牛顿流体,此时不随d/dn而变化,否则称为非牛顿流体。
动力粘度μ:动力粘度表示单位速度梯度下流体内摩擦应力的大小,它直接反映了流体粘性的大小运动粘度ν:在流体力学中,动力粘度与流体密度的比值称为运动粘度,以ν表示。
实际流体:具有粘性的流体叫实际流体(也叫粘性流体),理想流体:就是假想的没有粘性(μ=0)的流体第三章流体静力学流体的平衡:(或者说静止)是指流体宏观质点之间没有相对运动,达到了相对的平衡。
第4章 理想流体动力学自测题一、思考题4.1何谓系统和控制体?它们有何区别与联系?试写出系统—控制体的输运公式并说明其物理意义。
4.2说明连续性方程的物理意义。
4.3说明欧拉运动微分方程的物理意义。
4.4试写出理想流体的伯努利方程,并且说明此方程的物理意义以及它的适用条件。
4.5何谓缓变流和急变流?在缓变流截面上,压强分布有何规律?4.6为什么要引入动能修正系数这个概念?其物理意义是什么?4.7说明动量方程和动量矩方程的适用条件。
二、选择题4.1连续性方程表示流体运动遵循 守恒定律。
(C )(A )能量 (B )动量 (C )质量 (D )流量4.2水在一条管道中流动,如果两过流断面的管径比2/21=d d ,则速度比=21/υυ 。
(C )(A )2 (B )1/2 (C )4 (D )1/44.3在 流动中,伯努利方程不成立。
(D )(A )恒定 (B )理想流体 (C )不可压缩 (D )可压缩4.4文丘里管用于测量 。
(D )(A )点流速 (B )压强 (C )密度 (D )流量4.5毕托管用于测量 。
(A )(A )点流速 (B )压强 (C )密度 (D )流量4.6应用总流的伯努利方程时,两断面间 。
(D )(A )必须是缓变流 (B )必须是急变流(C )不能出现急变流 (D )可以出现急变流4.7伯努利方程中gV g p z 22αρ++表示 。
(A ) (A )单位重量流体具有的机械能 (B )单位质量流体具有的机械能(C )单位体积流体具有的机械能 (D )通过过流断面流体的总机械能4.8水平放置的渐扩管,如忽略水头损失,断面形心的压强,有以下关系 。
(C )(A )21p p > (B )21p p = (C )21p p < (D )不定4.9应用总流的动量方程求流体对物体合力时,进、出口的压强应使用 。
(B )(A )绝对压强 (B )相对压强(C )大气压强 (D )真空值三、计算题4.1如图所示,设一虹吸管a=2m,h=6m,d=15cm 。
t u zy x z y x X z d d d d d d d d ρρ=+d d d 1u u u p p p⎡⎤⎡⎤∂∂∂元流伯努利方程的物理意义和几何意义测压管测压管测压管测压管O A OA●均匀流与非均匀流、非均匀渐变流与急变流⏹均匀流与非均匀流——依流线形状及过水断面上的流速是否沿流程而变化进行分类。
①均匀流:迁移加速度为零。
所有流线是平行的直线。
②非均匀流:迁移加速度不为零。
流线不平行或虽然平行但不是直线。
渐变流与急变流——非均匀流流场中流线彼此呈近似平行直线的流动,称为渐变流。
流场中,流线彼此不平行,流线间夹角比较大或流线曲率比较大的流动为急变流。
g u3ρ总流能量方程的应用条件●应用条件(1)均质不可压缩流体的恒定流;(2)作用在流体上的质量力中只有重力;(3)均匀流或渐变流断面(4)在所取的两过水断面之间,流量保持不变。
●应用要点(1)过水断面取均匀流或渐变流断面(2)位置高度(3)计算点选取,明渠取水面点,管流取中心点(4)压强取绝对压强和相对压强均可,但两断面要统一z1221A A v v =211112=++g v g p z αρ⇒p p =-ρ(211z z =∆p文丘里流量计测流量23332111+++=+v p z vαα()应用要点β1.恒定流,不可压缩流体;2.过水断面为均匀流或渐变流,但两断面之间可为急变流;3. 是作用在控制体上的所有外力之和;力和流速都是矢量4.=1.0;∑F应用要点⎪⎭⎪⎬⎫=-+=-+=-+∑∑∑z z z z y y y y x x x x F v Q v Q v Q F v Q v Q v Q F v Q v Q v Q )()()(111333222111333222111333222βββρβββρβββρ5.有分流或汇流时,动量的变化量=变化后的动量-变化前的动量;6.计算压力时,只能采用相对压强;7.选择合适的计算用控制体,与连续性方程、能量方程联立求解弯管和分岔管内等水流对管壁的作用力坐标系列三大方程如图所示,将一平板放置在自由射流之中,并且垂直于射流的轴线,该平板截去射流流量的一部分Q1,射流的其余部分偏转一角度θ,已知:流速v=30m/s,流量Q=36L/s,流量Q1=12L/s,试求:(1)不计摩擦力射流对平板的作用力;(2)射流的偏转角θ值。