高中数学 多项式函数的导数素材
- 格式:doc
- 大小:98.50 KB
- 文档页数:2
为函数
_____ _ 的图象的顶点在第四象限,则其导
o
y
x
-33
)
(x
f
y'
=
()y f x ='()f x 为( )
(安微省合肥市2010年高三第二次教学质量检测文科)函数()y f x =的图像如下右)
(x f y '=
(2010年浙江省宁波市高三“十校”联考文科)如右图所示是某
一容器的三视图,现向容器中匀速注水,容器中水面的高度h 随时间t 变化的可能图象是( )
象大致形状是( )
2009湖南卷文)若函数()y f x =的导函数在区间[,]a b 上是增函数,则函数
()x 在区间[,]a b 上的图象可能是
y
y
y
14.(2008年福建卷12)已知函数y=f(x),y=g(x)的导函数的图象如下图,那么y=f(x),
y=g(x)的图象可能是( )
15.(2008珠海一模文、理)设是函数的导函数,将和的图)('x f )(x f )(x f y =)('x f y =像画在同一个直角坐标系中,不可能正确的是( )
A .
B .
C .
D .16.(湖南省株洲市2008届高三第二次质检)已知函数
)(x f y =的导函数)(x f y '=的图像如下,则(
)
函数)(x f 有1个极大值点,1个极小值点
y。


高二数学常用导数公式大全在学习数学的时候公式是一定要牢牢记住的,下面为大家带来了高二数学常用导数公式大全,一起来回顾一下吧! 导数(Derivative)是微积分中的重要基础概念。
当函数y=f(x)的自变量X在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df/dx(x0)。
1.y=c(c为常数) y'=02.y=x^n y'=nx^(n-1)3.y=a^x y'=a^xlnay=e^x y'=e^x4.y=logax y'=logae/xy=lnx y'=1/x5.y=sinx y'=cosx6.y=cosx y'=-sinx7.y=tanx y'=1/cos^2x8.y=cotx y'=-1/sin^2x9.y=arcsinx y'=1/√1-x^210.y=arccosx y'=-1/√1-x^211.y=arctanx y'=1/1+x^212.y=arccotx y'=-1/1+x^2在推导的过程中有这几个常见的公式需要用到:1.y=f[g(x)],y'=f'[g(x)]?g'(x)『f'[g(x)]中g(x)看作整个变量,而g'(x)中把x看作变量』2.y=u/v,y'=u'v-uv'/v^23.y=f(x)的反函数是x=g(y),则有y'=1/x'证:1.显而易见,y=c是一条平行于x轴的直线,所以处处的切线都是平行于x的,故斜率为0。
用导数的定义做也是一样的:y=c,⊿y=c-c=0,lim⊿x→0⊿y/⊿x=0。
2.这个的推导暂且不证,因为如果根据导数的定义来推导的话就不能推广到n为任意实数的一般情况。


高考数学中的多项式函数的性质结论总结多项式函数在高考数学中扮演着十分重要的角色,因为多项式函数具有很多独特的性质和性质结论,掌握这些性质和性质结论能够帮助我们更好地解决数学问题,尤其是高考中考题的解答。
本文将为大家总结多项式函数的性质和性质结论,以期为大家的高考备考提供一定的参考。
1. 多项式函数的定义和性质多项式函数是指形如$f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0$ 的函数,其中$a_n,a_{n-1},...,a_0$都是实数且$n$为非负整数。
多项式函数有以下性质:(1)多项式函数是连续的。
(2)多项式函数的导函数也是多项式函数。
(3)多项式函数在实数集上有定义域和值域,这两者都是无限的。
2. 多项式函数的零点和系数特征(1)零点定理:如果$f(x)$是一个$n$次多项式函数,那么$f(x)$的零点个数是不超过$n$的。
(2)系数定理1:如果$f(x)$是一个$n$次多项式函数,那么$\sum\limits_{i=0}^{n}a_i$等于$f(x)$在$x=1$处的值。
(3)系数定理2:如果$f(x)$是一个$n$次多项式函数,那么$a_i$($0\le i\le n$)等于$f(x)$在$x=0$处的$i$次导数的系数。
3. 多项式函数的极限和导数多项式函数的极限和导数有以下结论:(1)多项式函数在$x\rightarrow \pm \infty$时的极限等于$x$的最高项次数的项的系数的符号所决定。
(2)多项式函数的导数是一个比原函数次数低1的多项式函数。
(3)多项式函数的$k$阶导数的最高项系数是$k$次系数乘以$k$的阶乘。
4. 多项式函数的求根和因式分解多项式函数的求根和因式分解有以下结论:(1)求根定理:$f(x)$为$n$次多项式函数,则$f(x)=a_n(x-x_1)(x-x_2)...(x-x_n)$,其中$x_1,x_2,...,x_n$是多项式函数的零点。

1常见函数的导数公式在微积分中,函数的导数是衡量函数变化率的工具。
它表示了函数曲线上其中一点的切线斜率,也可以用来求解最值、确定函数的凹凸性和拐点等。
常见函数的导数公式是微积分中的基础知识,本文将介绍常见函数的导数公式,包括多项式函数、三角函数、指数函数、对数函数和分段函数的导数公式。
多项式函数是由常数和幂函数通过加法和乘法得到的函数。
对于多项式函数 f(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0,其中a_n、a_{n-1}、..、a_0 是常数,n 是正整数,它的导数 f'(x) 的公式如下:f'(x) = na_nx^{n-1} + (n-1)a_{n-1}x^{n-2} + ... + 2a_2x + a_1三角函数是三角比的函数,包括正弦函数、余弦函数和正切函数等。
它们的导数公式如下:(1) 正弦函数的导数:f'(x) = cos(x)(2) 余弦函数的导数:f'(x) = -sin(x)(3) 正切函数的导数:f'(x) = sec^2(x)(4) 反正弦函数的导数:f'(x) = 1 / sqrt(1 - x^2)(5) 反余弦函数的导数:f'(x) = -1 / sqrt(1 - x^2)(6)反正切函数的导数:f'(x)=1/(1+x^2)指数函数和对数函数是常见的指数和对数运算的函数,它们的导数公式如下:(1) 指数函数的导数:f'(x) = a^x * ln(a),其中 a > 0 且a ≠ 1(2) 对数函数的导数:f'(x) = 1 / (x * ln(a)),其中 a > 0 且 a ≠ 1分段函数是由不同部分的函数组成的函数,它们的导数公式需要分段讨论。
以下是一些常见的分段函数的导数公式:(1)取整函数的导数。
取整函数是指将实数转化为最接近的整数的函数,其导数为:f'(x)=0,若x不是整数f'(x)=不存在,若x是整数(2)绝对值函数的导数。


高考数学总复习教程第2讲 导数、多项式函数的导数一、本讲进度2.1导数的背景 2.2导数的概念 2.3多项式函数的导数,课本P30~39 二、学习指导本讲通过运动物体在某一时刻的瞬时速度(0lim →∆t ts ∆∆)、曲线在某一点处的切线的斜率(0lim→∆x xy∆∆)、生产的边际成本(0lim →∆q q c ∆∆)三个实例( 也导数的三个重要应用,特别地,曲线在某一点处切线的斜率即是导数的几何意义).抽象出它们共同的、实质性的东西:函数的变化量△y 与自变量的变化△x 的比值当△x →0时的极限,并定义为函数f (x)在这一点处的导数.(课本P33页)并进而定义了导函数(简称导数)(课本P34页).导数应用很广泛,经常需要求导,如果都用定义求一遍,不胜其烦,人们就用定义推导出一些常见函数的导函数,并作为公式加以应用.课本内只介绍了两个求导公式:C /=0,及/)(n x =1-n nx (n 为正整数)课P36已予推导;两个法则:[f (x )±g (x ) ]/=/f (x )±g /(x ). [Cf(x )]/=C /f (x) .请同学们根据定义自行证明一下上述两个法则后再往下看:[f (x )±g (x ) ]/= 0lim>∆x xx g x f x x g x x f ∆±-∆+±∆+)]()([)]()([= 0lim >∆x x x g x x g x f x x f ∆-∆+±-∆+)]()([)]()([=0lim >∆x x x f x x f ∆-∆+)()(±0lim >∆x xx g x x g ∆-∆+)()(=)(/x f ±)(/x g/)]([x Cf =0lim >∆x x x Cf x x Cf ∆-∆+)()(=0lim >∆x (C ·x x f x x f ∆-∆+)()()=C 0lim >∆x xx f x x f ∆-∆+)()(=)(/x Cf .有了这些工具,我们就能求出一切多项式函数的导数了. 另外,∵xy ∆∆=x x f x x f ∆-∆+)()(00≈)(0/x f , ∴△y ≈)(0/x f ·△x .当△x 很小时,可把它作为一个简单易记的近似计算公式。

导数在多项式函数中的应用根据我校的生源特点和大部分学生参加成人高考的数学教学要求,导数在多项式函数中的应用成为一个数学教学重点。
本人结合中专数学教学实践,就导数在多项式函数中的应用作个初步总结。
有关导数在多项式函数中的应用主要类型有:求函数的切线,判断函数的单调性,求函数的极值和最值,这些类型成为近几年成人高考必考题,是成人高考数学教学的重点之一。
1用导数求函数的切线根据导数的几何意义,函数y=f(x)在点x0处的导数的几何意义,就是曲线y=f(x)在点P(x0,f(x0))处的切线的斜率。
也就是说,曲线y=f(x)在点P(x0,f(x0))处的切线的斜率是f′(x0) ,相应的切线方程为y-y0= f′(x0)(x-x0)。
例1、求曲线y=x3-3x2-1在点(1,-3)处的切线方程。
分析:根据导数的几何意义求解。
解:∵y′= 3x2-6x,∴y′|x=1= -3,即所求切线的斜率为-3.故所求切线的方程为y+3 = -3(x-1),即为:y = -3x2用导数判断多项式函数的单调性利用导数判断多项式函数的单调性的步骤是:(1)求导数f′(x);(2)求驻点(使f′(x)=0的点x);(3)多项式函数f(x)的定义域R由驻点分成一些区间;(4)在各区间内由f′(x)的正负,确定函数的单调性。
若在多项式函数中含字母系数,往往要分类讨论。
例2.求函数y=x3-3x2-1的单调区间。
分析:求出导数y′,令y′=0,解出x的取值范围即可。
解:y′= 3x2-6x=3x(x-2), 令y′=0得x1=0,x2=2。
由x1=0,x2=2把R分成三个区间(-∞,0);(0,2);(2,+∞)列表如表13用导数求多项式函数的极值求多项式函数极值的步骤是:(1)求导数f′(x);(2)求驻点;(3)多项式函数f(x)的定义域R由驻点分成一些区间;(4)在各区间内由f′(x)的正负,确定函数的极值;(判断在每个驻点(如x1)的左右侧,导函数f′(x)的符号如何变化,如果f′(x)的符号由正变负,则f(x1)是极大值;如果f′(x)的符号由负变正,则f(x1)是极小值。


100个复杂函数求导1.函数 f(x) = x^3 的导数是 f'(x) = 3x^2。
2.函数 f(x) = sin(x) 的导数是 f'(x) = cos(x)。
3.函数 f(x) = e^x 的导数是 f'(x) = e^x。
4.函数 f(x) = log(x) 的导数是 f'(x) = 1/x。
5.函数 f(x) = x^2 + sin(x) 的导数是 f'(x) = 2x +cos(x)。
6.函数 f(x) = x^3 + e^x 的导数是 f'(x) = 3x^2 + e^x。
7.函数 f(x) = sin(x^2) 的导数是 f'(x) = 2x*cos(x^2)。
8.函数 f(x) = x^2log(x) 的导数是 f'(x) = 2x log(x) +x^2/x = 2x*log(x) + x。
9.函数 f(x) = x^3 - sin(x) 的导数是 f'(x) = 3x^2 -cos(x)。
10.函数 f(x) = x^4 + e^2 的导数是 f'(x) = 4x^3 + 0 =4x^3。
11.函数 f(x) = x^5 - 2x^4 + 3x^3 的导数是 f'(x) =15x^4 - 24x^3 + 9x^2。
12.函数 f(x) = log(x^2) 的导数是 f'(x) = 2x/x^2 =2/x。
13.函数 f(x) = x^2log(x) - sin(x) 的导数是 f'(x) =2x log(x) + x^2/x - cos(x) = 2x*log(x) + x -cos(x)。
14.函数 f(x) = x^4 + e^(-x) 的导数是 f'(x) = 4x^3 -e^(-x)。
15.函数 f(x) = x^3sin(x) 的导数是 f'(x) = 3x^2cos(x)+ x^3*cos(x)。
勒让德多项式的导数勒让德多项式是一种多项式,它由十六世纪法国数学家艾萨克勒让德发现。
它以一种分段函数的形式表示出来,在符号表示方面它是一种简单的表达方法,其中的每个分段函数是一个指数函数。
关于它的发现,有许多传说,但没有实际的史料证明其发现者。
勒让德多项式表示式可以分解成一组段函数,即每个分段函数都是一个指数函数,最常用的分段函数为简单指数函数,它的表达式为axn 。
其中a>0,n为整数,其可以表示的函数的形状和范围取决于n的值。
当a>0,n>0时,形状总是上凸的;当a<0,n>0时,形状总是下凸的;当a>0,n<0时,形状总是下凸的;当a<0,n<0时,形状总是上凸的。
求勒让德多项式的导数,就是求取每个指数函数的导数,并将其组合在一起。
指数函数的导数可以表示为anxn-1。
当a>0,n>0时,它的导数总是正的;当a<0,n>0时,它的导数总是负的;当a>0,n<0时,它的导数总是负的;当a<0,n<0时,它的导数总是正的。
因此,对于一个勒让德多项式:f(x)=a1xn1 +a2xn2 +,+ akxnk,其导数可表示为:f(x)=a1n1xn1 -1 +a2n2xn2 -1 +,+aknkxnk -1 。
勒让德多项式的导数也有许多用途,如研究不同指数函数的极限,求解微分方程等。
例如,研究不同指数函数的极限时,可以先求出多项式的导数,然后再求出极限值。
此外,在求解微分方程时,勒让德多项式的导数也是很有用的,可以将原来非常复杂的方程分解成一系列简单的指数函数,从而减少解方程的难度。
勒让德多项式的介绍及其导数的求取,对于我们研究高等数学的不同方面意义重大,它也帮助我们深入了解指数函数,掌握求解微分方程的技巧,为我们学习高等数学提供了更多帮助。
14个求导公式范文一、一次函数求导公式:1. y = kx + b,其中k为常数,b为常数,求导得到dy/dx = k。
以y = 2x + 3为例,求导得到dy/dx = 2二、幂函数求导公式:2. y = x^n,其中n为常数,求导得到dy/dx = nx^(n-1)。
以y = x^3为例,求导得到dy/dx = 3x^2三、指数函数求导公式:3. y = a^x,其中a为常数且a>0且a≠1,求导得到dy/dx = a^x * ln(a)。
以y = 2^x为例,求导得到dy/dx = 2^x * ln(2)。
四、对数函数求导公式:4. y = logₐ(x),其中a为常数且a>0且a≠1,求导得到dy/dx = 1 / (x * ln(a))。
以y = log₂(x)为例,求导得到dy/dx = 1 / (x * ln(2))。
五、三角函数求导公式:5. y = sin(x),求导得到dy/dx = cos(x)。
6. y = cos(x),求导得到dy/dx = -sin(x)。
7. y = tan(x),求导得到dy/dx = sec^2(x)。
8. y = cot(x),求导得到dy/dx = -csc^2(x)。
9. y = sec(x),求导得到dy/dx = sec(x) * tan(x)。
10. y = csc(x),求导得到dy/dx = -csc(x) * cot(x)。
六、反三角函数求导公式:11. y = arcsin(x),求导得到dy/dx = 1 / sqrt(1 - x^2)。
12. y = arccos(x),求导得到dy/dx = -1 / sqrt(1 - x^2)。
13. y = arctan(x),求导得到dy/dx = 1 / (1 + x^2)。
14. y = arccot(x),求导得到dy/dx = -1 / (1 + x^2)。
以上是14个常见的求导公式,可以用于求解各种函数的导数。
用导数研究报告三次多项式曲线引言在数学中,多项式函数是一类重要的函数。
其中,三次多项式函数的特点是在自变量的三次方次项与一次方次项之间存在关系。
因此,研究三次多项式函数的性质对于数学理论的发展具有重要意义。
导数的定义导数是用来描述函数变化率的工具。
对于函数$f(x)$,它的导数$f'(x)$可以通过以下公式计算:$$f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$$三次多项式函数的导数对于三次多项式函数$P(x)$,它的一般形式可以表示为:$$P(x) = ax^3 + bx^2 + cx + d$$其中$a$,$b$,$c$和$d$为常数。
为了研究三次多项式函数的性质,我们需要计算它的导数。
根据导数的定义,可以得到三次多项式函数$P(x)$的导数$P'(x)$:$$P'(x) = 3ax^2 + 2bx + c$$三次多项式曲线的特点通过对三次多项式函数的导数$P'(x)$进行分析,我们可以得到三次多项式曲线的一些特点:1. 曲线的斜率:导数$P'(x)$描述了曲线在不同点上的斜率。
当导数为正时,曲线上升;当导数为负时,曲线下降;当导数为零时,曲线达到极值点。
2. 曲线的拐点:拐点是指曲线从凸向上凹或从凹向上凸变化的点。
在三次多项式曲线上,拐点的位置可以通过导数$P'(x)$的二阶导数来确定。
3. 曲线的极值点:极值点是曲线上最高或最低的点。
在三次多项式曲线上,极值点可以通过导数$P'(x)$的一阶导数为零的点来确定。
结论通过导数的研究,我们可以了解到三次多项式曲线的斜率、拐点和极值点的位置,进而对曲线的形状和性质进行分析。
这为进一步研究和应用三次多项式函数提供了重要的理论基础。
需要注意的是,在实际应用中,有时会出现多个极值点或拐点的情况。
此外,导数可以应用于许多其他数学领域,如最优化问题和微分方程的求解等。
导数的一些有用公式一阶导数的有用公式1. 除一元外多元数的求导法则:如果f是关于x的m次多项式,那么f'(x)是关于x的m-1次多项式。
2. 单调函数和极大值定理:如果f '(x)是一元函数f单调递增(减)或者在区间上恒等于0,那么f(x)在该区间上非极大值;3. 先导数定理:如果u=f(x)和v=g(y)是定义在同一个区间上的连续函数,那么有 u+v,u-v,uv,u/v等,他们的导数分别是f'(x)+g'(y),f'(x)-g'(y),f(x)g'(y)+f'(x)g(y), (f(x)g'(y)-f'(x)g(y))/g(y)^2;4. 抛物线:如果f(x)=ax^2+bx+c, 那么f'(x)=2ax+b;5. 二次函数的极值:如果f(x)=ax^2+bx+c, 那么其导数f'(x)=2ax+b=0,可以得到极值点为-b/2a;6. 指数函数:如果f(x)=a^x, 那么f'(x)=ln(a)*a^x, 其中a>0;7. 对数函数:如果f(x)=lnx,那么f'(x)=1/x;8. 三角函数:(1)cos x的导数为-sin x,(2)sin x的导数为cos x,(3)tan x的导数为sec^2x;9. 反三角函数:(1)arcsin x的导数为1/sqrt(1-x^2),(2)arccos x的导数为-1/sqrt(1-x^2),(3)arctan x的导数为1/(1+x^2),(4)arccot x的导数为-1/(1+x^2);10. 高次幂函数:如果f(x)=x^n(n>1), 那么其导数为f'(x)=nx^(n-1);11. e为底的指数函数:如果f(x)=e^x, 那么其导数为f'(x)=e^x.。
多项式函数的导数
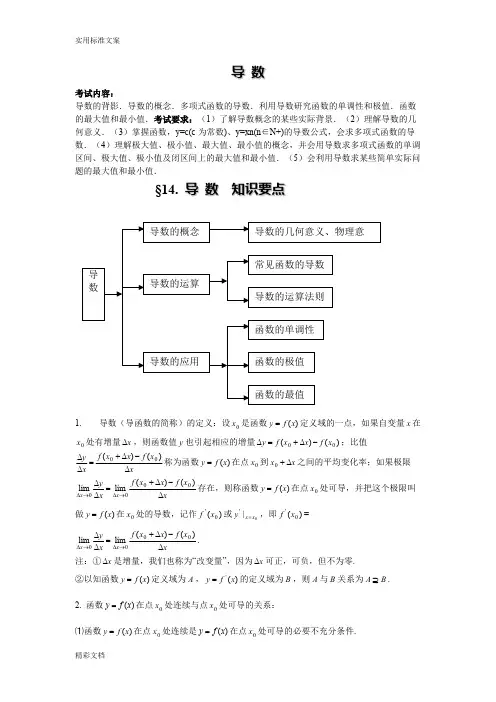
教学目的:会用导数的运算法则求简单多项式函数的导数
教学重点:导数运算法则的应用
教学难点:多项式函数的求导
一、复习引入
1、已知函数2)(x x f =,由定义求)4()(/
/f x f ,并求
2、根据导数的定义求下列函数的导数: (1)常数函数C y = (2)函数)(*N n x y n ∈=
二、新课讲授
1、两个常用函数的导数:
2、导数的运算法则:
如果函数)()(x g x f 、有导数,那么
也就是说,两个函数的和或差的导数,等于这两个函数的导数的和或差;常数与函数的积的导数,等于常数乘函数的导数.
例1:求下列函数的导数:
(1)37x y = (2)43x y -= (3)3
534x x y +=
(4))2)(1(2-+=x x y (5)b a b ax x f 、()()(2+=为常数
)
例2:已知曲线331x y =上一点)3
82(,P ,求: (1)过点P 的切线的斜率; (2)过点P 的切线方程.
三、课堂小结:多项式函数求导法则的应用
四、课堂练习:1、求下列函数的导数:
(1)28x y = (2)12-=x y (3)x x y +=2
2 (4)x x y 433-= (5))23)(12(+-=x x y (6))4(32-=x x y
2、已知曲线24x x y -=上有两点A (4,0),B (2,4),求:
(1)割线AB 的斜率AB k ;(2)过点A 处的切线的斜率AT k ;(3)点A 处的切线的方程.
3、求曲线2432+-=x x y 在点M (2,6)处的切线方程.
五、课堂作业
1、求下列函数的导数:
(1)1452+-=x x y (2)7352++-=x x y (3)101372-+=x x y
(4)333x x y -+= (5)453223-+-=x x x y (6))3)(2()(x x x f -+=
(7)1040233)(34-+-=x x x x f (8)x x x f +-=2)2()(
(9))3)(12()(23x x x x f +-= (10)x x y 4)12(32-+=
2、求曲线32x x y -=在1-=x 处的切线的斜率。
3、求抛物线241x y =
在2=x 处及2-=x 处的切线的方程。
4、求曲线1323+-=x x y 在点P (2,-3)处的切线的方程。