当前位置：文档之家 › Lecture 4 第二章 2.1 热平衡PN结(2013)

Lecture 4 第二章 2.1 热平衡PN结(2013)

  • 格式：ppt
  • 大小：710.50 KB
  • 文档页数：1

下载文档原格式

  / 1

合集下载

PN结

PN结

硅平面工艺的主体
国家级精品课程——半导体器件物理与实验
第二章 PN结
引
4-1 氧化工艺：
言
1957年，人们发现硅表面的二氧化硅层具有阻止杂质向硅内 扩散的作用。这一发现直接导致了氧化工艺的出现。 二氧化硅薄膜的作用： （1）对杂质扩散的掩蔽作用； （2）作为MOS器件的绝缘栅材料； （3）器件表面钝化作用；
二、电场和电势分布：
1. 内建电势差（势垒）：
EC
漂移
扩散
EFp
ห้องสมุดไป่ตู้
Ei
EV
扩散
q 0 E C
EV
q 0 k T ln
EFn Ei
Na Nd ni2
( 2 1 1) ( 2 1 2)
两种证明方法：
（1）费米能级法：
漂移
Na Nd 0 VT ln ni2
q 0 ( Ei E Fp ) ( E Fn Ei ) , ( 2 1 3) Ei E Fp k T ln E Fn Ei k T ln p0 N k T ln a , ( 2 1 4) ni ni n0 N k T ln d , ( 2 1 5) ni ni
国家级精品课程——半导体器件物理与实验
第二章 PN结
2.1 热平衡（无偏压） PN结
二、电场和电势分布：
1. 内建电势差（势垒）：
（2）静电势法： 取费米势为电势能的零点。
P型电 中性区 -xp 边界区
qNd


-qNa
xn
N型电 中性区
x
p0 ni exp / VT (1 10 10 )
在《半导体器件指南》一书中，定义了67种主要的半导体器 件及其相关的110多个变种。然而，所有这些器件都只由以 下的少数几种器件单元组成。

第2章_PN结

第2章_PN结

kT dn 由爱因斯坦关系 可得 Edx q n
kT 上式在整个势垒区积分 Edx xp q
xn
E
dV dx
n xn kT kT nn 0 V xn V x p ln ln q np0 n xp q
V xn V x p VD N D nn 0 N A p p0
第2章 PN 结
1
第2章 PN 结

PN 结是构成各种半导体器件的基本单元。 PN结中的载流子既有漂移运动，又有扩散运动； 既有产生，又有复合，这些性质集中反映在半导体 的导电特性中。
P区 NA
N区 ND
2
第2章 PN 结
1、PN 结的形成
在同一块N型（或P型）半导体单晶上，用特定 的工艺方法把P型（或N型）杂质掺入其中，使这块 单晶相连的二个不同区域分别具有N型区和P型区的 导电类型，在二者交界面以及交界面两侧的过渡区 即称为PN结。
40
（4）玻尔兹曼边界条件
即在势垒区两端，载流子分布满足玻尔兹曼分布。
（5）忽略半导体表面对电流的影响。
（6）只考虑一维情况。
41
理想PN结的伏安特性
正向偏压V＞0时，P区边界-xp处的非平衡少子浓度
qV qVD qV n p x p n p 0 exp nn 0 exp kT kT P区边界 x x p 处的过剩载流子浓度
（1）小注入条件
满足下列条件的PN结）
即注入的非平衡少子浓度比平衡多子浓度小得多；
（2）耗尽层近似
即外加电压都降落在耗尽层（势垒区）上，耗尽层 以外的半导体是电中性的，因此注入的少子在 P区 和N区只作扩散运动；

第二章-PN-结二极管演示教学

第二章-PN-结二极管演示教学
步骤： 求解“非少子”的扩散
方程 →求“非少子”浓度的
边界值 →求“非少子”浓度梯
度 →分别求电子、空穴的
扩散电流密度 →求PN结电流
2.1 直流特性
2.1 直流特性
PN结N区边界处少子扩散电流密度：
由：jp
qp0
Dp Lp
jp
q
pn0
exp
qV kT
1
Dp Lp
PN结P区边界处少子扩散电流密度：
（3）小电流下，正向电流比理论值大；要考虑势垒复合电流的 影响。
（4）大电流下，正向电流比理论值小，势垒区以外存在大注入 自建电场。 IF与 eqVF2KT成 正 比 。
（5）反向电流比理论值大；要考虑表面漏电流及势垒产生电流 JG的影响。
（6）当T升高时，JF增大，JR增大。
2.1 直流特性
2.1.6 大注入 1.大注入定义：正偏工作，注入载流子密度等于或
2.1.3 反向PN结 （1）反向PN结的少子抽取
反向电压使 势垒区宽度变宽 势垒高度变高
外加电场与内建电场方向相同
增强空间电荷区中的电场
破坏扩散漂移运动平衡
漂移运动强于扩散运动 抽取少子
Ln
Lp
2.1 直流特性
P区 jp
(2)反向PN结中载流子的运动
Ln
N区
jn Lp
2.1 直流特性
2.1.4 V-I 特性方程 一、理想PN结模型
空间电荷区中的电场减弱 破坏扩散与漂移运动间的 平衡
扩散运动强于漂移运动 注入少子 注入的少子边扩散边复合
2.1 直流特性
P区
（2）正向PN结中载流子的运动
电流在 N 型区中主要由电子携带
jn

第二章PN结资料

第二章PN结资料

2.4 空间电荷区的复合电流和产生电流
• 低偏压：空间电荷区的复合电流占优势 • 偏压升高： 扩散电流占优势 • 更高偏压： 串联电阻的影响
I （A）
103
串联电阻
实验数据 104
105
106
107
斜率 q KT
108
109
斜率 q
2 KT
1 0 10 0.1 0.2 0.3 0.4 0.5 0.6 0.7
• 由于这个原因，也把空间电 荷区称为势垒区。
3.耗尽层 -突变结
• 突变结势垒中的电场、电势分布 • 耗尽层近似：在空间电荷区中，与电离杂质浓度相比，自由载流子浓度
可以忽略，这称为耗尽近似。 • 杂质完全电离：
• 在N侧和P侧泊松方程可以分别简化为：
d dx22 qN D0xxn d dx22 qN A0xxn
0
•
边界条件： pnxpn0 pn0expV V T1
xW n xxn
pnxpn0AexpL xpBexpL xp
A pn0 exp k q 0 V T 1 exp L xn p pn0 exp V V T 1 exp L xn p B0
p n x p n 0 p n 0 e x p V V T 1 e x p x n L p x x x n
I0expV V T1
Shockley方程
•
正向偏压：
I
I0
exp
V VT
• 反向偏压： I I 0 • I0称为饱和电流
• 正向偏压情况下的PN结
载流子浓度
P型
np pn0
N型 pn pn0
空间电荷层
xp 0 xn
x
（a）少数载流子分布

2.1 热平衡PN结

2.1 热平衡PN结

2、热平衡PN结能带图和空间电荷分布
画热平衡PN结能带图。能带图的依据是： 1.费米能级恒定。于是N侧中性区费米能级EFn相对P 侧中性区费米能级向下移动EFn-EFp。 2. N侧各个能级（EC、EV及真空能级E0等）与EFn平 行地向下移动EFn-EFp。 3.在空间电荷区，真空能级连续。除费米能级外， 各个能级与真空能级平行。
0
W 2
x
边界条件为：
W W ε ( ) = ε ( ) = 0 2 2
半导体器件物理 Dr. B. Li &J. Han
积分并应用边界条件后得电场分布为：
2 x 2 aqW ε (x ) = 1 = ε max 8kε 0 W
2
2x 2 1 W
半导体器件物理 Dr. B. Li &J. Han
将 Ei (x ) 代入载流子浓度表达式中，得：
Ei (xn ) qψ (x ) E F n(x ) = ni exp KT
Ei ( x n ) E F = ni exp KT qψ ( x ) exp KT
W 2 W 2
2 ε (x ) dx = ε max W 3
ε max
半导体器件物理 Dr. B. Li &J. Han
2 1 aq = kε (12ψ 0 )3 8 0
1 3
7、平衡PN结的载流子浓度
平衡载流子浓度可表示为：
Ei E F n = ni exp KT
ε (x )
P
N
xp
x
0
ψ (x )
xn
x
电势分布
ψ0
qψ ( x )
电子的电位能分布
半导体器件物理 Dr. B. Li &J. Han

PN结 2013-11-8

PN结 2013-11-8
2.1.3平衡PN结的载流子浓度分布
2.1.0 PN结初识 本征半导体 晶体结构 载流子浓度
Si Si
n 0 =p0 =n i =C T e
1/2
3/2 Eg / T
n0 p0 n
2 i
Si
Si
跟费米能 级的关系 能带图
E E ( F i) n0 ni e T E F =E i Ei E F p n e( T ) 0 i
多子：电子 少子：空穴
P 型半导体
－ － － － － － － － － － － －
－ － － － － －
多子：空穴
－ － － － － －
少子：电子
PN 结
离子束刻蚀和离子注入
N区
PN结二极管制造过程
PN结结构
P区
Si 衬底
PN结二极管制造过程
PN结结构
P型硅 (P掺杂)
N区 P区
采用离子注入的方法实现
p 2 p p E p p0 Dp 2 p E p p Gp t x x x p
2. 单边稳态注入： p x p 0 e

x Lp
L ， p D p p
3. 平衡状态下载流子浓度和费米能级的关系
E Ei n0 ni exp( F ） k0T E EF p0 ni exp( i ) k0T np=n i2
2.1.1 平衡PN结能带图
◎ 空间电荷区的形成
N型区与P型区的能带如何变化 ？ N型区与P型区交界面处载流子如何运动 ？
• 空间电荷
• 空间电荷区 • 内建电场
◎PN 结的形成—费米能级
P型 N型
2.1.1 平衡PN结能带图

半导体物理 第二章 PN结 图文

半导体物理 第二章 PN结 图文

国家级精品课程——半导体器件物理与实验
第二章 PN结
引言
4-4 外延工艺：
外延是一种薄膜生长工艺，外延生长是在单晶衬底上沿晶体 原来晶向向外延伸生长一层薄膜单晶层。
外延工艺可以在一种单晶材料上生长另一种单晶材料薄膜。
外延工艺可以方便地形成不同导电类型，不同杂质浓度，杂 质分布陡峭的外延层。
外延技术：汽相外延(PVD，CVD）、液相外延（LPE）、分 子束外延（MBE）、热壁外延（HWE）、原子层外延技术。
硅平面工艺的主体
国家级精品课程——半导体器件物理与实验
第二章 PN结
引言
4-1 氧化工艺：
1957年，人们发现硅表面的二氧化硅层具有阻止杂质向硅内 扩散的作用。这一发现直接导致了氧化工艺的出现。 二氧化硅薄膜的作用： （1）对杂质扩散的掩蔽作用； （2）作为MOS器件的绝缘栅材料； （3）器件表面钝化作用； （4）集成电路中的隔离介质和绝缘介质； （5）集成电路中电容器元件的绝缘介质。 硅表面二氧化硅薄膜的生长方法： 热氧化和化学气相沉积方法。
N(x) （a）
Na
Nd xj
（b） -a(x - xj)
引言
扩 SiO2 散 结 N-Si
杂质扩散
P
N-Si
N-Si
由扩散法形成的P-N结，杂质浓度从P区到N区是
逐渐变化的，通常称之为缓变结，如图所示。设 P-N结位置在x=xj处，则结中的杂质分布可表示为： x
Na Nd (x xj), Na Nd (x xj)
Al
液体
Al
P
N-Si
N-Si
N-Si
把一小粒铝放在一块N型单晶硅片上， 加热到一定温度，形成铝硅的熔融体， 然后降低温度，熔融体开始凝固，在N 型硅片上形成含有高浓度铝的P型硅薄 层，它和N型硅衬底的交界面即为P-N 结（称之为铝硅合金结）。

半导体器件物理第二章

半导体器件物理第二章

n p = n p 0 eV VT
类似地，可有
（4）
p n = p n 0 eV VT
（5）
（4）式和（5）式分别为书中（2-29）和（2-30）式它们确定了空间电 荷层边缘的少数载流子浓度。
2.2 加偏压的 P-N 结
空间电荷效应和扩散近似 • 电中性区有很高的过量载流子而无显著的空间电荷效应
pn nn
np0 np
x′
x′
In
Ip
In
In
Ip − xp
0
− xp
xn
x
− xp
0
xn
x
x′
xn
x
（a）少数载流子分布
（b）少数载流子电流
（c）电子电流和空穴电流
图2-9 反向偏压情况下的的P-N结
2.4空间电荷区的复合电流和产生电流 2.4空间电荷区的复合电流和产生电流
概念： 概念： • 正偏复合电流：正偏压使得空间电荷层边缘处的载流子浓 正偏复合电流： 度增加，以致 pn > ni2 。这些过量载流子穿越空间电荷层， 度增加， 这些过量载流子穿越空间电荷层， 使得载流子浓度可能超过平衡值， 使得载流子浓度可能超过平衡值，预料在空间电荷层中会 有载流子复合发生， 有载流子复合发生，相应的电流称为空间电荷区复合电流 • 反偏产生电流：在 P − N 结反向偏压的情况下，空间电荷 反偏产生电流： 结反向偏压的情况下， 于是会有载流子的产生 载流子的产生， 区中 np < ni2 。于是会有载流子的产生，相应的电流即为空 间电荷区产生电流 产生电流。 间电荷区产生电流。
x = xn
（3）
dψ x (3)式可改写为 E = Em (1 − ) 因为E = − , dx xn

5 第二章 2.1 平衡PN结

5 第二章 2.1 平衡PN结

Physics of Semiconductor Devices
五 平衡PN结的载流子分布
在空间电荷区靠近P区边界Xp处，电子浓度等于P区的平衡少子浓度np0，
空穴浓度等于P区平衡多子浓度pp0 ；在靠近N区边界Xn处，空穴浓度等于
N区的平衡少子浓度pN0 ，电子浓度等于N区的平衡多子浓度nN0 。在空间 电荷区，空穴浓度从Xp处的pp0减小到Xn的pN0 ，电子浓度从Xn处的nN0减
s Emax n N D qxp N A
小到Xp处的np0 。
Physics of Semiconductor Devices
在PN结形成过程中，电子从N区向P区扩散，从而在结面的N区侧留下不能 移动的电离施主；空穴自P区向N区扩散，留下了不能移动的电离受主（负 电中心）。在空间电荷区内可移动载流子的分布是按指数规律变化的，变 化显著，绝大部分区域的载流子浓度远远小于中性区域，即在空间电荷区 的载流子基本已被耗尽，因此，空间电荷区又称为耗尽区或耗尽层。
小结
1、制造工艺不同，杂质分布不同。 2、通常将PN结的杂质分布 分为突变结和缓变结。合
金法和表面浓度高的浅扩散结可认为是突变结，而表
面浓度低的深扩散结，可认为是线性缓变结。
Physics of Semiconductor Devices
工艺过程
Physics of Semiconductor Devices
E0 M
qN D X 0 2
Physics of Semiconductor Devices
Physics of Semiconductor Devices
D dA Q

s1 s 2 s3
1 x q( xn x) N D s 1 x q( x x p ) N A s ( xn x 0) (0 x x p )

第二章pn结

第二章pn结
精品文档
n区空间电荷区边界处(x=xn )空穴扩散电流
Jdp (xn ) qDp
d pn (x)
dx
q Dp Lp
pn0 (eqV /kT
1)
p区空间电荷区边界处(x=-xp )电子扩散电流
Jdn (xp )
qDn
d np (x)
dx
q
Dn Ln
np0 (eqV /kT
1)
假定空穴电流和电子电流在空间电荷区为常数
• 扩散
精品文档
离子注入与扩散(kuòsàn)技术
精品文档
化学(huàxué)气相淀积技术（CVD） 键合技术（SDB）
精品文档
2.pn结掺杂(chān zá)分布 均匀分布：p-n结界面二侧p型和n型区杂质浓度分布均
匀，称为突变结。 缓变分布：杂质浓度从界面向两侧逐渐提高，称为缓
变结
精品文档
W
2
q
0
耗尽区总电势差
1/ 2
耗尽区等效杂质浓度
2 0
q
VD V N0
1/ 2
突变pn结的空间电荷区中最大电场强度一般化表述
耗尽区总电势差
VD
V
，等效杂质浓度N0
ND NA ND NA
反偏时V 为负值，接触电势差与外加电压绝对值相加；
正偏时V 为正值，接触电精势品文档差与外加电压绝对值相减。
3. 常用(chánɡ yònɡ)概念
精品文档
4.pn结空间电荷区的形成(xíngchéng)
产生自建电场 形成接触(jiēchù)电势差 能带结构变化
精品文档
5.两个近似条件 耗尽近似 中性近似
结论： 空间电荷区内(qū nèi)只有电离的施主和受主，没有自由载

lecture4.2温度传感器(PN结温度传感器)

lecture4.2温度传感器(PN结温度传感器)
3kT ln I 总 3I 9 * qR6
式中R*相当于原理电路的电阻R0。 T12的作用是在刚接通电源 时，提供一个小电源是传感器开始工作。T6能使T7和T8集电极 电压平衡，同时在工作电压接反时又能起到保护器件的作用。
2，AD590的结构及性能 AD590是美国哈里斯公司生产的 采用激光修正的精密集成温度 传感器。 AD590有3种封装形式： T0-52封装、陶瓷封装（测量范 围均为-50~+150℃）T0-92 封装（测温范围0~+70℃ ） AD590M的测量范围是-55~ +150 ℃，最大非线性误差为 ±0.3 ℃，响应时间仅20μs, 线性误差低至±0.05 ℃，功 耗约2mW。
37页图1-50
AD590系列产品主要技术指标
型号 主要技术指标
最大非线性误差/ ℃ 额定温度系数/μA/K 额定输出电流/μA AD590I AD590J AD590K AD590L AD590M ±0.3 ±1.5 ±0.8 1.0 298.2（+25.2 ℃） ±0.4 ±0.3
长期温度漂移/ ℃/月
温度控制器
40页图1-55b


AD590，RD、R+R1+R2上部和R3+R2下部组成测温电桥。 调节R2，设定一温度T0的参考电压。 温度变化时，通过T1和T2的导通截至，来实现温度控制。
2，摄氏温度计
41页图1-56 当t为0℃，V+与地间电位为 2.73V，调节39kΩ和5kΩ电 位器使V0为0V，即2.7kΩ电 阻上压降2.73V，当温度为 t℃时，V0为 V0=V+-2.73V=10(mV/ ℃)•t(℃)
晶体管温度传感器
1. 基本原理 由晶体管原理可知，NPN晶体管的基极-发射极电压Vbe 与温度T的关系为： kT Vbe Vg 0 ln( AT / I c ) q 式中Vg0=Eg0/q（Eg0为硅单晶的禁带宽度），A为发射 结面积，η是与材料和工艺有关的常数。 当Ic一定且T不太高时，Vbe基本与温度成线性关系，当温 度较高时候，产生一定非线性偏移。

第二章2.1 PN 结的平衡状态

第二章2.1 PN 结的平衡状态

εs 1 Emax Vbi = −∫ E(x)dx = ( xn + xp ) Emax = −xp 2qN0 2
xn
2
或
Emax
2qN0 = Vbi εs
1 2
（2-10） ）
个方程， 以上建立了 3 个方程，即( 2-6 ) 、( 2-7 ) 和 ( 2-10 ) ，
xn = xp =
2.1.4 线性缓变结
在线性缓变结中， 在线性缓变结中，杂质分布为 ND - NA = ax ， 耗尽近似下的泊松方程为 耗尽近似下的泊松方程为 ND − NA
dE q q = ( ND − NA ) = ax dx εs εs
边界条件为
xd − 2
0
xd 2
x
xd xd E (− ) = E ( ) = 0 2 2
C=−
E(x) = q
q
εs
NDxn
(0 ≤ x ≤ xn )
（2-5a） ）
εs
( x − xn ) ND
同理， 耗尽区中求解泊松方程， 同理，在 P 区耗尽区中求解泊松方程，得
E(x) = −
q
εs
( x+ x ) N
p
A
(−xp ≤ x ≤ 0)
（2-5b） ）
P
NE Emax−源自p0xnx
1 2
1 3
Emax
2 1 aq = (12Vbi ) 3 8 εs
结的各公式， 以上关于平衡 PN 结的各公式，都可推广到有外加电压时 如果设外加电压全部降落在耗尽区上， 的情形 。 如果设外加电压全部降落在耗尽区上， 则 只需将各 公式中的 Vbi 用 (Vbi – V) 代替即可。注意外加电压的参考极性 代替即可。 与 Vbi 相反。 相反。 例如，已知平衡时势垒区中的载流子浓度及其乘积为 例如，

第2章 PN结

第2章 PN结

－ － － － － －
+ + +
P
IS
内电场 外电场
N
–
内电场被加 强，少子的漂 移加强，由于 少子数量很少， 形成很小的反 向电流。
+
PN 结加反向电压时，PN结变宽，反向电流较小， 反向电阻较大，PN结处于截止状态。 温度越高少子的数目越多，反向电流将随温度增加。
3.了解PN结的电流方程
PN结所加端电压 u 与流过它的电流 i 的关系为：
PN结的形成：
浓度差 多子扩散空间电荷区(杂质离子) 内 电
场
促使少子漂移 阻 止 多 子 扩 散
PN结的实质：PN结=空间电荷区=耗尽层
2.2
PN结的单向导电性
P接正、N接负
1. PN结加正向电压（正向偏置）
PN 结变窄
－－－ － － － + + + + + + － － － － － －I + + + + + + －－－ － － － + + + + + +
IS IS
约为
约为
(109 ~ 1016 ) (106 ~ 108 )
A A
I S 随温度的升高而增大，还与PN结面积
成正比的增大。
I I S (e
V 为正值，且
V VT
1)
V 100 mV
）时
V VT （或
V VT
I ISe
V 为负值，且
V VT
时
பைடு நூலகம்
I I S
4.PN结的伏安特性

第二章 PN结

第二章 PN结

PN结的反向抽取作用
势垒区电场增强漂移 > 扩散N区一侧 xn 处的空 穴被强场扫向 P 区，而P 区 一侧 x p 处的电子则被扫 向N区。
np0
qVD nn 0 exp kT
－xp处少子（电 子）浓度：
n x p nn 0e n p 0e
s
n
其中NB是轻掺杂的基体浓度(意 指p+-n结的ND)．电场在x＝W处 降为零，因此
0
NA N D
xn W
x
E
W
Em
E ( x) qNB
qNBW
0
m
x
s
s
(W x) Em (1
x ) W
Vbi （ d）

Vbi
0
W
x
如图(c)所示
（a）在热平衡时，单边突变结 （N A N D） （b）空间电荷分布 （c）电场分布 （d)随距离改变的电势分布，其中Vbi 为内建电势
nx ni e
px ni e
平衡PN结势垒区两侧电子浓度之间的关系
热平衡时，中性区的多数载流子浓度大致与杂质浓度相
等，用nn0和np0分别表示在n和p侧的平衡电子浓度．则：
kT N A N D kT nn 0 p p 0 kT n n 0 VD ln ln ln 2 2 q ni q ni q n p 0
np0 pp0 ni2
所以 n p 0
qVD 同理 nn 0 exp kT
qVD pn 0 p p 0 exp kT
可见，耗尽区边界上，电子和空穴浓度与热平衡时的 V D 有关，即与结上的电势有关。

半导体器件物理PPT课件

半导体器件物理PPT课件

3)加反偏压时 耗尽层宽度为 W W
W
P
N
VR +
能量 （E ）
IR
（c ）
qy 0 VR
qVR
✓N区接正电位，在远离PN结空间电荷区的中性区，EFn 及诸能级相对P区 EFp下移 qVR 。
✓在空间电荷区由于载流子耗尽，通过空间电荷区时 EFn 和 EFp不变。
✓势垒高度增加至 q(y 0 VR ) ，增高的势垒阻挡载流子通过PN结扩散，通
1)热平衡时
耗尽层宽度为 W
P
2)加正向偏压时
能量 （E ）
N
W
（a ）
耗尽层宽度为 W W
PN结
W
P
NV+来自能量（E ）E Fn
E Fp
（b ）
qy 0 EC EF
qy0 V
qV EFn
2.2加偏压的PN结
加正向偏压时
W
P
N
能量
（E ）
E Fn
E Fp
qy0 V
qV EFn
V
+
（b ）
3)正确画出热平衡PN 结的能带图（图2-3a、b）。
4)利用中性区电中性条件导出空间电荷区内建电势差公式：
y0
y n
y
p
VT
ln
Nd Na ni2
（2-1-7）
5)解Poisson方程求解单边突变结SCR内建电场、内建电势、内建电势差和耗
尽层宽度。
PN结
PN结
2.2加偏压的PN结
1.加偏压的PN结的能带图
(e)曝光后去掉扩散窗口 （f)腐蚀SiO2后的晶片 胶膜的晶片
PN结
引言
采用硅平面工艺制备PN结的主要工艺过程

2.1 热平衡PN结

2.1 热平衡PN结

LD ≈ 3 ×10 6 cm
半导体器件物理 Dr. B. Li &J. Han
因此，边界层的厚度小于耗尽区的宽度。边界层完 全可以忽略。 PN结可划分为 中性区 耗尽区
P
N
半导体器件物理 Dr. B. Li &J. Han
3、热平衡PN结内建电势差 内建电势差：由于内建电场，空间电荷区两侧存
在电势差，这个电势差叫做内建电势差（用ψ 0 表 示）。 以导出空间电荷区内建电势差公式。
Nd Na ψ 0 = ψ n ψ p = VT ln 2 ni
利用中性区电中性条件和费米能级恒定两种方法可
（2-7）
半导体器件物理 Dr. B. Li &J. Han
方法一：（中性区电中性条件）
由一维泊松方程和取费米势为零基准时，电子空 穴密度公式：
半导体器件物理 Dr. B. Li &J. Han
将 Ei (x ) 代入载流子浓度表达式中，得：
Ei (xn ) qψ (x ) E F n(x ) = ni exp KT
Ei ( x n ) E F = ni exp KT qψ ( x ) exp KT
半导体器件物理 Dr. B. Li &J. Han
1、空间电荷区的形成
平衡多子： P区： p po = N a >> ni N区： nno = N d >> ni
ni2 ni2 = = << ni p po N a ni2 ni2 = = << ni nno N d
P区 N区
Na-，pp0 Nd+，nn0
区产生的电场称为内建电场，方向为由N 区指向P 区。电场的 存在会引起漂移电流，方向为由N 区指向P 区。 扩散电流： P 区 漂移电流： P 区 N 区 N 区

第2章_PN结

第2章_PN结
PN结
P
N
3
PN 结类型
按材料分为同质结，和异质结 按导电类型分为同型结和异型结
按杂质的分布分为突变结和线性缓变结
4
2 、 PN结的形成过程
工艺方法

合金法


扩散法
生长法


离子注入法
光刻工艺(硅平面工艺）
5
合金法制造PN结过程
熔融
Al N-Si P-Si
突变结 P区与N区的交界面处的杂质浓度分布是突变的， 此法称为合金结，又称突变结。
PN结的内建电势(接触电势) 0 由内建电场所导致的N区和P区的电位差。
15
平衡PN结能带图
P

2.1.1 平衡PN结能带图
空间电荷区
N
xp
内建电场
0
xn
: 接触电势差 （内建电势）
电位 电子的电势能
0
q 0

空间电荷区又称 势垒区 耗尽层
qVD EFN
EC Ei EF EV Ei EV
正向注入--少子注入
非平衡载流子的电注入： 由于外加正向偏压的作用 使非平衡载流子进入半导 体的过程。
正向注入的过程（扩散近似）

N区注入P区电子→势垒边界 xp积累→P区的非平衡少子→ 浓度梯度→P区扩散→边扩散 边复合→形成空穴扩散电流。 P区注入N区空穴→势垒边界 xn积累→N区的非平衡少子→ 浓度梯度→N区扩散→边扩散 边复合→形成电子扩散电流。
N
P
ND -NA
xj
x
10
2.1 热平衡PN 结
2.1.1 PN结空间电荷区 2.1.2 电场分布于电势分布
11
2.1.1 PN结空间电荷区
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

突变结近似
线性缓变结近似
杂质扩散PN结的杂质分布示意图
2013,02-06
2、离子注入法
在掩模板窗口附近的横向分布为余误差分布，纵向近似 为高斯分布。
2013,02-06
3、形成机理
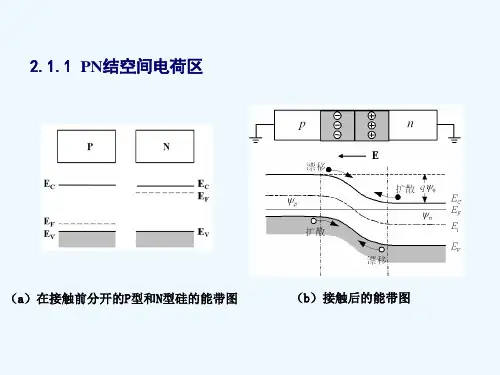
当这两部分半导体靠得很近，甚至相互接触时，由于交界面存 在着电子和空穴的浓度差，N区中的电子要向P区扩散， P区中 的空穴要向N 区扩散。这样，对于P区，空穴离开后，留下了不 可动的带负电的电离受主，这些电离受主在PN结的P区侧形成 了一个负电荷区；同样的，在N区由出现了由电离施主构成的正 电荷区，这个交界区域就是PN结。通常把PN结附近的这些电离 施主和电离受主所带的电荷称为空间电荷，它们所在的区域称 为空间电荷区。
N
P
由于电荷密度是均匀的，所以平行结面方向上电场强度不变。 在交界面上具有最大的电场强度。
2013,02-06
从xn至x求积分，可推导出电势： 取x xn处, 0作为边界条件
qNd xn2 (1 x )2
2
xn
空间电荷区的内建电势差为：
0 (xn ) (xp )
d
dx
qNd
k 0
一、PN结的形成机理与自建电势
1. 扩散法
在N型或P型单晶硅片上，通过氧化、光刻、扩散等工艺制得的PN结，其 杂质分布由扩散过程及杂质补偿决定。在这种PN结中，杂质浓度从P区到 N区是逐渐变化的，通常称为缓变结。
2013,02-06
表面浓度很低，结深很深的扩散结，看作线性缓变结； 表面浓度很高，结深很浅的扩散结，看作单边突变结。
2013,02-06
对于N侧、P侧的泊松方程可简化为：
d 2
dx2
qNd
,
d 2
dx2
qNa
,
0 x xn - xp x 0
对于整个半导体来说，空间电荷区的电中性要求PN结两边的
电荷相等，即：
Na xp Nd xn
整个空间电荷区的宽度为：
W xp xn
2013,02-06
若令Na>>Nd，则xn>> xp ，W≈xn。这在物理上意味着在重掺杂 一边的空间电荷区的厚度是可以忽略的。结果是，在轻掺杂的 一边可以单独解泊松方程求得结的特性。
(x) qa x2 c 2
分布曲线
εM
x xm c qaxm2
2
8
x=0
d 2
dx 2
q ax
？ M
qaxm2
8
最大电场强度
缓变结的电场强度为抛物线分布，突变结的电场强度为线性
分布，所以缓变结的最大电场强度比突变结要低，这对提高
PN结的反向击穿电压具有指导意义。
2013,02-06
平 衡 PN 结 具 有 统 一 费米能级，恰好体现 了每一种载流子的扩 散运动和漂移运动电 流相互抵消，从而没 有净电流通过PN结
平衡PN结的能带图
2013,02-06
能带的相对位移是PN结空间电荷区存在自建电场的结果，由于 自建电场的方向是由N区指向P区的，表明P区的电势比N区的 电势低。而能带图是按电子能量的高低画的，所以P区电子的 势能比N区的势能高，也就是电子的电势能-qψ(x)由N区向P区 不断升高。
2013,02-06
平衡PN结的载流子分布特性曲线
2013,02-06
四、缓变结空间电荷区的电场
对于线性缓变结，耗尽层内空间电荷分布可表示为：
Nd Na ax 式中，a为杂质浓度的斜率（参见P64图2-2b）
泊松方程改写为：
d 2
dx2
q ax
d 2
dx2
q
(Na
Nd
)
Nd Na ax
2013,02-06
qψD
电势变化量
EFn EFp q D
接触电势差
ψD
2013,02-06
qψD
平衡PN结空间电荷区内能带发生弯曲，它反映了 空间电荷区内电子势能的变化。电子从势能低的N 区向势能高的P区运动，必须克服这个势能“高 坡” ；同理，空穴必须克服这个势能“势垒”才 能从P区到达N区，这个势能“高坡”通常称为PN 结的“势垒”，所以空间电荷区也叫势垒区。
则可以得到耗尽层的宽度和自建电势为：
W
12
qa
0
1/ 3
0
2VT
ln
aW 2ni
2013,02-06
（1）电场
线性缓变结的电场强度也是在P区和N区的交界面处最大，而边界 处为零。与单边突变结不同的是，其正、负电荷区的宽度相等
即：xn = xp =1/2 xm
2013,02-06
试分析线性缓变结空间电荷区的电场、宽度和电势
2013,02-06
N半导体的费米能级EFn位于本征费米能级Ei之上，P型半导体的费 米能级EFp位于本征费米能级Ei之下。当N型和P型半导体结合成 PN结时，若没有外加电压，则有统一的费米能级EF ，即费米能级 处处相等。也就是说，N区的能带相对于P区下移（或者说P区的
能带相对N区上移），从而使得两个区的费米能级拉平。
由（于2：）电势
(x) (x)dx
(x) qa x2 c 2
0
2VT
ln
aW 2ni
(x) (x)dx qa x3 qaxM2 x c
6
8
边界条件
x 0,(x) 0 c 0
空间电荷区电势差
ቤተ መጻሕፍቲ ባይዱ
0
( xm
2
) (
xm 2
)
qaxm3
12
xm
12
qa
0
1/ 3
2013,02-06
2013,02-06
P
N
空穴扩散 空穴漂移
电子扩散
电子漂移 自建电场
出现空间电荷区后，在空间电荷区中 形成一个电场，电场的方向由带正电 的N区指向带负电的P区，这个电场 称为自建电场。
由于电场的存在使得电子和空 穴产生漂移运动，与它们的扩 散运动正好相反，当电场强到 使载流子的漂移运动和扩散运 动相抵消时（大小相等、方向 相反），此时的PN结达到了平 衡态，这就是平衡PN结。
可得边界层的宽度约为一特征长度的3倍，此特征长度称为非本
征德拜(Debye)长度：
LD
q
VT
Nd Na
1/ 2
通常情况下，它远小于耗尽区的宽度，因此边界层可以忽略不计
因此：
可简单的将PN结化分为中性区和耗尽区（空间电荷区）
2013,02-06
一维情况下，电荷分布与静电势之间的关系可用柏松方程表示：
Na )]
0
2013,02-06
中性区的电势求解
假设Na＝0，p<<n，再令Na＝p =0，则远离结的N型中性区中
的电势为:
n
VT
ln
ND ni
n nie /VT n ＝ ND
对于P型中性区的电势为：
p
VT
ln
Na ni
p nie /VT
则在N型一边与P型中性区之间的电位差为：
0
n
p
VT
(x xn )
由于xp很小，由电势连续性： (xp ) (0)
则有： 0 (xn ) (0)
即：
0
qNd xn2
2
2013,02-06
根据上式，可得耗尽层的宽度为：
0
qNd xn2
2
1/ 2
W
xn
2 0
qNd
2013,02-06
三 平衡PN结的载流子分布
在空间电荷区靠近P区边界Xp处，电子浓度等于P区的平衡少子浓 度np0，空穴浓度等于P区平衡多子浓度pp0 ；在靠近N区边界Xn处， 空穴浓度等于N区的平衡少子浓度pn0 ，电子浓度等于N区的平衡 多子浓度nn0 。在空间电荷区，空穴浓度从Xp处的pp0减小到Xn的 pn0 ，电子浓度从Xn处的nn0减小到Xp处的np0 。
d 2
dx2
q
[(n
p)
(Nd
Na )]
n nie /VT ; p nie /VT
费米势取为零基准
上式可用于分析PN结中的各个区域：离开结的中性区；有固定电荷但无自
由载流子的耗尽区；在中性区和耗尽区之间的边界层。
中性区：空间电荷的总密度为零，则有：
d 2
dx2 0
q [(n
p) (Nd
自建势场由N区指向P区， 表明P区的电势（电位） 比N区的电势低
2013,02-06
因浓度差
PN结的形成机理
多子的扩散运动
由杂质离子形成空间电荷区
空间电荷区形成内电场
内电场促使少子漂移
内电场阻止多子扩散
形成PN结
2013,02-06
二 空间电荷区的电场与宽度
对于突变结的边界层，难以得到解析解，利用数值法进行求解。
2013,02-06
第二章 PN结 Lecture 4：§2.1
热平衡PN结
一般将锗和硅称为第一代半导体材料。将砷化镓、磷化铟等称为第二代半导 体材料，而将宽禁带的碳化硅、氮化镓和金刚石等称为第三代半导体材料
1. PN结的形成机理与接触电势 2. 空间电荷区的电场与宽度 3. 平衡PN结的载流子分布
2013,02-06
d 2
dx2
qNd
,
0 x xn
d
dx
qNd
(x xn )
从xn至x作一次积分
2013,02-06
1 dEi d
q dx dx
在x
xn处,
d
dx
0用做边界条件。
m (1
x xn
)
d
dx
qNd