流函数与势函数

流函数和势函数公式流函数与势函数是描述流体运动的两个重要概念，在流体力学中被广泛应用。

本文将介绍流函数和势函数的基本概念、性质以及求解方法。

1.流函数的概念和性质流函数是描述在二维定常流动中，各个流线上速度矢量的旋转情况的函数。

对于二维流动，假设流体流动的速度场为V(x,y)，则流函数Ψ(x,y)定义为：V=∇Ψ=(∂Ψ/∂x,∂Ψ/∂y)其中，∇Ψ是流函数Ψ的梯度向量。

流函数的性质如下：1)斜率定理：沿着流线的方向，流函数的局部斜率等于流体的速度分量。

2)流线定理：流线上的流函数值保持不变，即Ψ为常数。

3)流函数的连续性：在空间中的流函数是连续的，除非在相应的流体内有边界。

4)流函数的耗散性：流函数对时间是线性的，即流函数在时间方向上是耗散的。

2.势函数的概念和性质势函数是描述流体在无旋力场中流动时所具备的性质的函数。

无旋力场是指速度场的旋度等于零。

对于二维流动，假设流体流动的速度场为V(x,y)，则势函数φ(x,y)定义为：V=∇φ=(∂φ/∂x,∂φ/∂y)其中，∇φ是势函数φ的梯度向量。

势函数的性质如下：1)势函数的梯度向量是速度向量。

2)势流是不可压缩的，即∇·V=0。

3)势函数满足拉普拉斯方程，即∇²φ=0。

4)由于速度场的旋度等于零，势函数是无旋的。

3.流函数和势函数的关系在二维流动中，流函数和势函数之间存在一种特殊的关系，称为流函数-势函数耦合关系。

根据流函数和势函数的定义，可以得到流函数和势函数的关系：Ψ = ∫(∂φ/∂y)dx + f(y)φ = ∫(∂Ψ/∂x)dy + g(x)其中，f(y)和g(x)是任意常数函数。

根据流函数-势函数耦合关系可以求解流体的速度场，并且满足连续性方程和运动方程。

4.求解流函数和势函数的方法求解流函数和势函数的方法有多种，常用的方法有分离变量法、解析法和数值法。

4.1分离变量法分离变量法是将流函数和势函数分解为各自的变量函数，并通过解偏微分方程的边值问题来确定这些变量函数。

一、流函数流函数概念的提出是仅对不可压缩流体的平面流动而言的。

所谓平面流动是指流场中各点的流速都平行于某一固定平面，并且各物理量在此平面的垂直方向上没有变化。

由不可压缩流体的平面流动的连续方程得平面流动的流线微分方程为式(1)是式(2)成为某一函数的全微分的必要且充分的条件，即于是很显然，在流线上dψ=0或ψ=C。

每条流线对应一个常数值，所以称函数ψ为流函数。

对于不可压缩流体的平面流动，用极坐标表示的连续方程、流函数的微分和速度分量分别为：流函数具有明确的物理意义：平面流动中两条流线间单位厚度通过的体积流量等于两条流线上的流函数常数之差。

在流函数ψ的定义中，为保证流函数变化值dψ与流量增量值dq v 同号，规定绕B点逆时针方向穿过曲线AB的流量为正，反之为负，这是指通过z方向为单位高度的柱面的体积流量。

里的流量qv通过A点的流线的流函数值ψ1，通过B点的流线的流函数值ψ2，则通过AB柱面的体积流量为在引出流函数这个概念时，既没有涉及流体是粘性的还是非粘性的，也没有涉及流体是有旋的还是无旋的。

所以，无论是理想流体还是粘性流体，无论是有旋流动还是无旋流动，只要是不可压缩流体的平面流动，就存在流函数，对于xoy平面内的无旋流动，有 z=0，即：也可得即不可压缩流体的平面无旋流动的流函数满足拉普拉斯方程，也是调和函数。

对于极坐标系，该满足拉普拉斯方程为二、速度势函数对于无粘性（理想）流体的无旋流动而言，由斯托克斯定理可知，沿流场中任意封闭周线的速度线积分，即速度环量均为零。

对于无旋流动，该封闭周线所包围的速度环量为零，有对于理想流体无旋流动，从参考点A到另一点B的速度线积分与点A 至点B的路径无关，上式中ds表示连接点A与点B的任意微元曲线。

也就是说，速度线积分仅仅取决于B点相对于A点的位置，具有单值势函数的特征。

由无旋流动的充要条件可知即：上式是成为某一函数的全微分的必要且充分条件。

函数成为速度势函数，简称速度势。

流函数和势函数公式(一)资深创作者列举流函数和势函数公式的相关公式，并进行例解释。

流函数公式二维空间中的流函数公式在二维空间中，流函数用于描述流体的运动状态。

对于二维流动，在直角坐标系下，流函数的公式可以表示为：ψ = ∫(Vx dy - Vy dx)其中，Vx和Vy分别表示流体在x和y方向的速度分量。

ψ表示流函数。

举例：假设在二维平面内，某个点(x, y)的速度分量分别为Vx = x*y和Vy = x^2。

那么该点处的流函数可以计算如下：ψ = ∫(x*y dy - x^2 dx)三维空间中的流函数公式在三维空间中，流函数的公式稍有不同。

在直角坐标系下，流函数可以表示为：ψ = ∫(Vx dy dz - Vy dx dz + Vz dx dy)其中，Vx、Vy和Vz分别表示流体在x、y和z方向的速度分量。

ψ表示流函数。

Vx = x^2，Vy = y^2和Vz = z^2。

那么该点处的流函数可以计算如下：ψ = ∫(x^2 dy dz - y^2 dx dz + z^2 dx dy)势函数公式二维空间中的势函数公式在二维空间中，势函数用于描述流体的势能分布。

对于二维流动，在直角坐标系下，势函数的公式可以表示为：φ = ∫(Vx dx + Vy dy)其中，Vx和Vy分别表示流体在x和y方向的速度分量。

φ表示势函数。

举例：假设在二维平面内，某个点(x, y)的速度分量分别为Vx = 2x和Vy = 3y。

那么该点处的势函数可以计算如下：φ = ∫(2x dx + 3y dy)三维空间中的势函数公式在三维空间中，势函数的公式稍有不同。

在直角坐标系下，势函数可以表示为：φ = ∫(Vx dx + Vy dy + Vz dz)其中，Vx、Vy和Vz分别表示流体在x、y和z方向的速度分量。

φ表示势函数。

Vx = x^2，Vy = y^2和Vz = z^2。

那么该点处的势函数可以计算如下：φ = ∫(x^2 dx + y^2 dy + z^2 dz)总结：•流函数公式和势函数公式分别用于描述流体的运动状态和势能分布。

一、流函数流函数概念的提出是仅对不可压缩流体的平面流动而言的。

所谓平面流动是指流场中各点的流速都平行于某一固定平面，并且各物理量在此平面的垂直方向上没有变化。

由不可压缩流体的平面流动的连续方程得平面流动的流线微分方程为式(1)是式(2)成为某一函数的全微分的必要且充分的条件，即于是很显然，在流线上dψ=0或ψ=C。

每条流线对应一个常数值，所以称函数ψ为流函数。

对于不可压缩流体的平面流动，用极坐标表示的连续方程、流函数的微分和速度分量分别为：流函数具有明确的物理意义：平面流动中两条流线间单位厚度通过的体积流量等于两条流线上的流函数常数之差。

在流函数ψ的定义中，为保证流函数变化值dψ与流量增量值dq v 同号，规定绕B点逆时针方向穿过曲线AB的流量为正，反之为负，这是指通过z方向为单位高度的柱面的体积流量。

里的流量qv通过A点的流线的流函数值ψ1，通过B点的流线的流函数值ψ2，则通过AB柱面的体积流量为在引出流函数这个概念时，既没有涉及流体是粘性的还是非粘性的，也没有涉及流体是有旋的还是无旋的。

所以，无论是理想流体还是粘性流体，无论是有旋流动还是无旋流动，只要是不可压缩流体的平面流动，就存在流函数，对于xoy平面内的无旋流动，有 z=0，即：也可得即不可压缩流体的平面无旋流动的流函数满足拉普拉斯方程，也是调和函数。

对于极坐标系，该满足拉普拉斯方程为二、速度势函数对于无粘性（理想）流体的无旋流动而言，由斯托克斯定理可知，沿流场中任意封闭周线的速度线积分，即速度环量均为零。

对于无旋流动，该封闭周线所包围的速度环量为零，有对于理想流体无旋流动，从参考点A到另一点B的速度线积分与点A 至点B的路径无关，上式中ds表示连接点A与点B的任意微元曲线。

也就是说，速度线积分仅仅取决于B点相对于A点的位置，具有单值势函数的特征。

由无旋流动的充要条件可知即：上式是成为某一函数的全微分的必要且充分条件。

函数成为速度势函数，简称速度势。

一、流函数流函数概念的提出是仅对不可压缩流体的平面流动而言的。

所谓平面流动是指流场中各点的流速都平行于某一固定平面，并且各物理量在此平面的垂直方向上没有变化。

由不可压缩流体的平面流动的连续方程得du dv--- =—―dx dy平面流动的流线微分方程为吗一血" ⑵式(1)是式(2)成为某一函数的全微分的必要且充分的条件，即于是很显然，在流线上(1屮二0或屮二C。

每条流线对应一个常数值, 所以称函数屮为流函数。

对于不可压缩流体的平面流动，用极坐标表示的连续方程、流函数的微分和速度分量分别为:(1)dr dddy/流函数具有明确的物固愿契：平面流动中两条流线间单位厚度通过的体积流量等于两条流线上的流函数常数之差。

在流函数屮的定义中，为保证流函数变化值（1屮与流量增量值dq、同号，规定绕B点逆时针方向穿过曲线AB的流量为正，反之为负，这里的流量4,.是指通过z方向为单位高度的柱面的体积流量。

通过A点的流线的流函数值屮1 ,通过B点的流线的流函数值屮2 ，则通过AB柱面的体积流量为¥ r w 辛q v = \V -dZ = J \u cos(n7 x) +v cos(再y)](SA A["字 + v(-务问二j (T -vdx)AB\(1屮=屮2_屮\A在引出流函数这个概念时，既没有涉及流体是粘性的还是非粘性的，也 没有涉及流体是有旋的还是无旋的。

所以，无论是理想流体还是粘性流 体，无论是有旋流动还是无旋流动，只要是不可压缩流体的平面流动, 就存在流函数，dv du .----- —=0对于xoy 平面内的无旋流动，有CO Z =0,即：去Oy口2 才屮 d 2i// 门VV=—r + —r=0也可得dx创即不可压缩流体的平面无旋流动的流函数满足拉普拉斯方程，也是调和 函数。

对于极坐标系，该满足拉普拉斯方程为d 2u/ 1 du/ 1 d 2u/ c+ -- +——^=0 dr 2 r dr r 2 d02二、速度势函数屮】对于无粘性（理想）流体的无旋流动而言，由斯托克斯定理可知， 沿流场中任意封闭周线的速度线积分，即速度环量均为零。

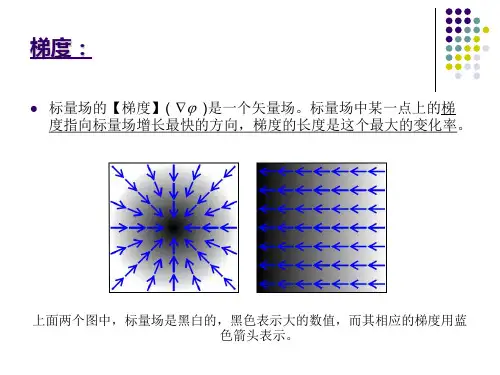
流函数和势函数公式流体力学中的流函数可以用来描述流体的速度场。

速度场表示流体在空间中各点的速度分布情况。

对于无旋的流动，可以引入流函数，流函数可以唯一地确定流线。

流线是流体在给定时刻通过各点的轨迹线。

在无旋的流动中，速度场可以通过流函数的梯度得到。

流函数可以按照如下公式定义：ψ=ψ(x,y,z)其中，ψ是流函数，表示速度场在其中一截面上的流函数值，(x,y,z)是该截面上的坐标。

流函数满足拉普拉斯方程：∇²ψ=0其中，∇²是拉普拉斯算子，表示流函数对坐标的二阶混合偏导数的和，等于零表示流函数满足拉普拉斯方程。

流函数的物理意义是流线沿着这个函数的等值线的方向运动。

通过给定流函数值，可以确定流线的轨迹。

势函数是流体力学中另一个重要的数学工具。

势函数用来描述无旋的流动场中的速度场。

对于无旋的流动，速度场可以通过势函数的梯度得到。

势函数可以按照如下公式定义：φ=φ(x,y,z)其中，φ是势函数，表示速度场在其中一截面上的势函数值，(x,y,z)是该截面上的坐标。

势函数满足亥姆霍兹方程：∇²φ=0势函数的物理意义是速度场是势函数的梯度。

通过给定势函数值，可以确定速度场的分布情况。

流函数和势函数是流体力学中流动的描述工具。

通过流函数和势函数，可以方便地描述流体的流动和速度场。

流函数适用于无旋流动，通过流函数的梯度可以得到速度场。

势函数适用于无旋流动，通过势函数的梯度可以得到速度场。

流函数和势函数是相互对偶的工具，二者之间有一个互逆的关系。

在实际应用中，流函数和势函数在求解流体问题中起着重要的作用。

通过流函数和势函数，可以方便地计算速度场和流线，从而解决各种涉及流体流动的问题。

总结起来，流函数和势函数是流体力学中用来描述流动的两个重要的数学工具。

流函数用来描述无旋流动的速度场，势函数用来描述无旋流动场中的速度场。

二者分别满足拉普拉斯方程和亥姆霍兹方程。

流函数和势函数在解决流体流动问题中具有重要的作用。