下载文档原格式
⼤学物理学第3版（课后答案）_习题五习题五5-1 振动和波动有什么区别和联系?平⾯简谐波动⽅程和简谐振动⽅程有什么不同?⼜有什么联系?振动曲线和波形曲线有什么不同?解: (1)振动是指⼀个孤⽴的系统(也可是介质中的⼀个质元)在某固定平衡位置附近所做的往复运动，系统离开平衡位置的位移是时间的周期性函数，即可表⽰为；波动是振动在连续介质中的传播过程，此时介质中所有质元都在各⾃的平衡位置附近作振动，因此介质中任⼀质元离开平衡位置的位移既是坐标位置，⼜是时间的函数，即． (2)在谐振动⽅程中只有⼀个独⽴的变量时间，它描述的是介质中⼀个质元偏离平衡位置的位移随时间变化的规律；平⾯谐波⽅程中有两个独⽴变量，即坐标位置和时间，它描述的是介质中所有质元偏离平衡位置的位移随坐标和时间变化的规律．当谐波⽅程中的坐标位置给定后，即可得到该点的振动⽅程，⽽波源持续不断地振动⼜是产⽣波动的必要条件之⼀．(3)振动曲线描述的是⼀个质点的位移随时间变化的规律，因此，其纵轴为，横轴为；波动曲线描述的是介质中所有质元的位移随位置，随时间变化的规律，其纵轴为，横轴为．每⼀幅图只能给出某⼀时刻质元的位移随坐标位置变化的规律，即只能给出某⼀时刻的波形图，不同时刻的波动曲线就是不同时刻的波形图．5-2 波动⽅程=cos ［()+］中的表⽰什么?如果改写为=cos ()，⼜是什么意思?如果和均增加，但相应的［()+］的值不变，由此能从波动⽅程说明什么?解: 波动⽅程中的表⽰了介质中坐标位置为的质元的振动落后于原点的时间；则表⽰处质元⽐原点落后的振动位相；设时刻的波动⽅程为则时刻的波动⽅程为其表⽰在时刻，位置处的振动状态，经过后传播到处．所以在中，当，均增加时，的值不会变化，⽽这正好说明了经过时间，波形即向前传播了的距离，说明描述的是⼀列⾏进中的波，故谓之⾏波⽅程．5-3 波在介质中传播时，为什么介质元的动能和势能具有相同的位相，⽽弹簧振⼦的动能和势能却没有这样的特点?解: 我们在讨论波动能量时，实际上讨论的是介质中某个⼩体积元内所有质元的能量．波动动能当然是指质元振动动能，其与振动速度平⽅成正⽐，波动势能则是指介质的形变势能．形变势能由介质的相对形变量(即应变量)决定．如果取波动⽅程为，)(t f y =x t ),(t x f y =)(t f y =t ),(t x f y =x t )(cos u xt A y -=ω)(t f y =y t ),(t x f y =y x x y A ωu x t -0?u xy A 0?ωω+-u x t u x ωt x ωu x t -0?u x /x u x ωx t )cos(0φωω+-=u x()(cos[0φωω+?+-?+=?+u x x t t A y t t t x t ?t u x ?+)(u x t ωω-t x )(u x t ωω-t ?t u x ?=?)cos(0φωω+-=u xt A y dV ),(t x f y =则相对形变量(即应变量)为.波动势能则是与的平⽅成正⽐．由波动曲线图(题5-3图)可知，在波峰，波⾕处，波动动能有极⼩(此处振动速度为零)，⽽在该处的应变也为极⼩(该处)，所以在波峰，波⾕处波动势能也为极⼩；在平衡位置处波动动能为极⼤(该处振动速度的极⼤)，⽽在该处的应变也是最⼤(该处是曲线的拐点)，当然波动势能也为最⼤．这就说明了在介质中波动动能与波动势能是同步变化的，即具有相同的量值．题5-3图对于⼀个孤⽴的谐振动系统，是⼀个孤⽴的保守系统，机械能守恒，即振⼦的动能与势能之和保持为⼀个常数，⽽动能与势能在不断地转换，所以动能和势能不可能同步变化． 5-4 波动⽅程中，坐标轴原点是否⼀定要选在波源处? =0时刻是否⼀定是波源开始振动的时刻? 波动⽅程写成=cos ()时，波源⼀定在坐标原点处吗?在什么前提下波动⽅程才能写成这种形式?解: 由于坐标原点和开始计时时刻的选全完取是⼀种主观⾏为，所以在波动⽅程中，坐标原点不⼀定要选在波源处，同样，的时刻也不⼀定是波源开始振动的时刻；当波动⽅程写成时，坐标原点也不⼀定是选在波源所在处的．因为在此处对于波源的含义已做了拓展，即在写波动⽅程时，我们可以把介质中某⼀已知点的振动视为波源，只要把振动⽅程为已知的点选为坐标原点，即可得题⽰的波动⽅程．5-5 在驻波的两相邻波节间的同⼀半波长上，描述各质点振动的什么物理量不同，什么物理量相同?解: 取驻波⽅程为，则可知，在相邻两波节中的同⼀半波长上，描述各质点的振幅是不相同的，各质点的振幅是随位置按余弦规律变化的，即振幅变化规律可表⽰为．⽽在这同⼀半波长上，各质点的振动位相则是相同的，即以相邻两波节的介质为⼀段，同⼀段介质内各质点都有相同的振动位相，⽽相邻两段介质内的质点振动位相则相反．5-6 波源向着观察者运动和观察者向波源运动都会产⽣频率增⾼的多普勒效应，这两种情况有何区别?解: 波源向着观察者运动时，波⾯将被挤压，波在介质中的波长，将被压缩变短，(如题5-6图所⽰)，因⽽观察者在单位时间内接收到的完整数⽬()会增多，所以接收频率增⾼；⽽观察者向着波源运动时，波⾯形状不变，但观察者测到的波速增⼤，即，因⽽单位时间内通过观察者完整波的数⽬也会增多，即接收频率也将增⾼．简单地说，前者是通过压缩波⾯(缩短波长)使频率增⾼，后者则是观察者的运动使得单位时间内通过的波⾯数增加⽽升⾼频率．x y ??/x y ??/0/=??xy t y A ωu xt -0=t )(cos u xt A y -=ωvtcos 2cos 2=xA λπ2cos2λ'/u B v u u +='λu '题5-6 图多普勒效应5-7 ⼀平⾯简谐波沿轴负向传播，波长=1.0 m ，原点处质点的振动频率为=2. 0 Hz ，振幅＝0.1m ，且在=0时恰好通过平衡位置向轴负向运动，求此平⾯波的波动⽅程．解: 由题知时原点处质点的振动状态为，故知原点的振动初相为,取波动⽅程为则有5-8 已知波源在原点的⼀列平⾯简谐波，波动⽅程为=cos()，其中，，为正值恒量．求：(1)波的振幅、波速、频率、周期与波长；(2)写出传播⽅向上距离波源为处⼀点的振动⽅程； (3)任⼀时刻，在波的传播⽅向上相距为的两点的位相差．解: (1)已知平⾯简谐波的波动⽅程()将上式与波动⽅程的标准形式⽐较，可知：波振幅为，频率，x λνA t y 0=t 0,000<=v y 2π])(2cos[0φλπ++=xT t A y ]2)12(2cos[1.0ππ++=x t y )224cos(1.0πππ++=x t m y A Cx Bt -A B C l d )cos(Cx Bt A y -=0≥x )22cos(λππυxt A y -=A πυ2B =波长，波速，波动周期． (2)将代⼊波动⽅程即可得到该点的振动⽅程将，及代⼊上式，即得．5-9 沿绳⼦传播的平⾯简谐波的波动⽅程为=0.05cos(10)，式中,以⽶计，以秒计．求：(1)波的波速、频率和波长；(2)绳⼦上各质点振动时的最⼤速度和最⼤加速度； (3)求=0.2m 处质点在=1s 时的位相，它是原点在哪⼀时刻的位相?这⼀位相所代表的运动状态在=1.25s 时刻到达哪⼀点?解: (1)将题给⽅程与标准式相⽐，得振幅，频率，波长，波速．(2)绳上各点的最⼤振速，最⼤加速度分别为(3)m 处的振动⽐原点落后的时间为故,时的位相就是原点()，在时的位相，即π．设这⼀位相所代表的运动状态在s 时刻到达点，则5-10 如题5-10图是沿轴传播的平⾯余弦波在时刻的波形曲线．(1)若波沿轴正向传播，该时刻，，，各点的振动位相是多少?(2)若波沿轴负向传播，上述各点的振动位相⼜是多少?解: (1)波沿轴正向传播，则在时刻，有题5-10图C πλ2=C Bu ==λυB T πυ21==l x =)cos(Cl Bt A y -=t )(212x x -=λπφd x x =-12C πλ2=Cd =?φy x t ππ4-x y t x t t )22cos(x t A y λππυ-=05.0=A m 5=υ1-s 5.0=λm 5.2==λυu 1s m -?ππω5.005.010max =?==A v 1s m -?222max 505.0)10(ππω=?==A a 2s m -?2.0=x 08.05.22.0==u x s 2.0=x m 1=t s 0=x对于点：∵，∴对于点：∵，∴对于点：∵，∴对于点：∵，∴ (取负值：表⽰点位相，应落后于点的位相) (2)波沿轴负向传播，则在时刻，有对于点：∵，∴对于点：∵，∴对于点：∵，∴对于点：∵，∴(此处取正值表⽰点位相超前于点的位相)5-11 ⼀列平⾯余弦波沿轴正向传播，波速为5m ·s -1，波长为2m ，原点处质点的振动曲线如题5-11图所⽰． (1)写出波动⽅程；(2)作出=0时的波形图及距离波源0.5m 处质点的振动曲线．解: (1)由题5-11(a)图知，m ，且时，，∴，⼜，则题5-11图(a)取，则波动⽅程为(2) 时的波形如题5-11(b)图题5-11图(b) 题5-11图(c) 将m 代⼊波动⽅程，得该点处的振动⽅程为O 0,0<=O O v y 2πφ=O A 0,=+=A A v A y 0=A φB 0,0>=B B v y 2πφ-=B C 0,0<=C Cv y 23πφ-=C C B A 、、O x t O 0,0>'='O O v y 2πφ-='O A 0,='+='A A v A y 0='A φB 0,0<'='B B v y 2πφ= B C 0,0>'='C C v y 23πφ='C C B A 、、O x t 1.0=A 0=t 0,000>=v y 230πφ=5.225===υuHz ππυω52==])(cos[0φω+-=u xt A y )]235(5cos[1.0ππ+-=x t y m 0=t 5.0=x如题5-11(c)图所⽰． 5-12 如题5-12图所⽰，已知=0时和=0.5s 时的波形曲线分别为图中曲线(a)和(b) ，波沿轴正向传播，试根据图中绘出的条件求： (1)波动⽅程； (2)点的振动⽅程．解: (1)由题5-12图可知，，，⼜，时，，∴，⽽，，∴故波动⽅程为(2)将代⼊上式，即得点振动⽅程为题5-12图5-13 ⼀列机械波沿轴正向传播，=0时的波形如题5-13图所⽰，已知波速为10 m ·s -1，波长为2m ，求： (1)波动⽅程；(2) 点的振动⽅程及振动曲线； (3) 点的坐标；(4) 点回到平衡位置所需的最短时间．解: 由题5-13图可知，时，，∴，由题知，，则∴(1)波动⽅程为)5cos(1.0)235.05.055cos(1.0πππππ+=+?-=t t y m t t x P 1.0=A m 4=λm 0=t 0,000<=v y 20πφ=25.01==??=t x u 1s m -?5.042===λυu Hz ππυω==2]2)2(cos[1.0ππ+-=x t y m 1=P x m P tt y ππππcos 1.0)]2cos[(1.0=+-=m x t P P P 1.0=A m 0=t 0,200<=v A y 30πφ=2=λm 10=u 1s m -?5210===λυuHz ππυω102==]3)10(10cos[.01ππ+-=x t y m题5-13图(2)由图知，时，，∴(点的位相应落后于点，故取负值)∴点振动⽅程为(3)∵∴解得(4)根据(2)的结果可作出旋转⽮量图如题5-13图(a)，则由点回到平衡位置应经历的位相⾓题5-13图(a)∴所属最短时间为5-14 如题5-14图所⽰，有⼀平⾯简谐波在空间传播，已知P 点的振动⽅程为=cos( )． (1)分别就图中给出的两种坐标写出其波动⽅程；(2)写出距点距离为的点的振动⽅程．解: (1)如题5-14图(a)，则波动⽅程为如图(b)，则波动⽅程为题5-14图(2) 如题5-14图(a)，则点的振动⽅程为如题5-14图(b)，则点的振动⽅程为0=t 0,2<-=P P v A y 34πφ-=P P 0P )3410cos(1.0ππ-=t y p πππ34.135==x mP πππφ6523=+=121106/5===ππωφt s P y A0?ω+t P b Q ])(cos[0φω+-+=u xu l t Ay ])(cos[0φω++=u xt A y Q ])(cos[0φω+-=u bt A A Q Q5-15 已知平⾯简谐波的波动⽅程为(SI)．(1)写出=4.2 s 时各波峰位置的坐标式，并求此时离原点最近⼀个波峰的位置，该波峰何时通过原点?(2)画出=4.2 s 时的波形曲线．解:(1)波峰位置坐标应满⾜解得 (…) 所以离原点最近的波峰位置为．∵故知,∴，这就是说该波峰在前通过原点，那么从计时时刻算起，则应是，即该波峰是在时通过原点的．题5-15图(2)∵，∴，⼜处，时，⼜，当时，，则应有5-16 题5-16图中(a)表⽰=0时刻的波形图，(b)表⽰原点(=0)处质元的振动曲线，试求此波的波动⽅程，并画出=2m 处质元的振动曲线．解: 由题5-16(b)图所⽰振动曲线可知,，且时，，故知,再结合题5-16(a)图所⽰波动曲线可知，该列波沿轴负向传播，且，若取题5-16图则波动⽅程为])(cos[0φω++=u bt A A Q )24(cos x t A y +=πt t ππk x t 2)24(=+)4.8(-=k x m ,2,1,0±±=k 4.0-m u xt t t ωωππ+=+242=u 1s m -?2.024.0=-='?t s 2.0s 42.02.4=-s 4s 2,4==u πω1s m -?12===ωπλuuT m 0=x 2.4=t s ππφ8.1642.40=?=A A y 8.02.44cos 0-=?=πA y -=πφ17=xπππ1728.16=+x 1.0=x m 2.4=t s t x x 2=T s 2.0=A m 0=t 0,000>=v y 20πφ-=x 4=λm ])(2cos[0φλπ++=xT t Ay5-17 ⼀平⾯余弦波，沿直径为14cm 的圆柱形管传播，波的强度为18.0×10-3J ·m -2·s -1，频率为300 Hz ，波速为300m ·s -1，求： (1)波的平均能量密度和最⼤能量密度? (2)两个相邻同相⾯之间有多少波的能量? 解: (1)∵∴(2)5-18 如题5-18图所⽰，和为两相⼲波源，振幅均为，相距，较位相超前，求：(1) 外侧各点的合振幅和强度； (2) 外侧各点的合振幅和强度解：（1）在外侧，距离为的点，传到该点引起的位相差为5-19 如题5-19图所⽰，设点发出的平⾯横波沿⽅向传播，它在点的振动⽅程为;点发出的平⾯横波沿⽅向传播，它在点的振动⽅程为，本题中以m 计，以s 计．设＝0.4m ，＝0.5 m ，波速=0.2m ·s -1，求：(1)两波传到P 点时的位相差；(2)当这两列波的振动⽅向相同时，处合振动的振幅；*(3)当这两列波的振动⽅向互相垂直时，处合振动的振幅．解: (1)]2)42(2cos[2.0ππ-+=x t y u w I =53106300100.18--?=?==u I w 3m J -?4max 102.12-?==w w 3m J -?νπλπωud w d w V W 224141===7251024.9300300)14.0(41106--?==πJ 1S 2S 1A 4λ1S 2S 2π1S 2S 1S 1S 1r 1S 2S P πλλππφ=+--=)4(2211r r 0,0211===-=A I A A A 2S 2S 1r 1S 2S 0)4(2222=-+-=r r λλππφ2121114,2A A I A A A A ===+=B BP B t y π2cos 10231-?=C CP C )2cos(10232ππ+?=-t y y t BP CP u P P )(2)(12BP CP ---=?λ(BP CP u --=ωπ0)4.05.0(2.02=--=ππ题5-19图(2)点是相长⼲涉，且振动⽅向相同，所以(3)若两振动⽅向垂直，⼜两分振动位相差为，这时合振动轨迹是通过Ⅱ，Ⅳ象限的直线，所以合振幅为5-20 ⼀平⾯简谐波沿轴正向传播，如题5-20图所⽰．已知振幅为，频率为波速为．(1)若=0时，原点处质元正好由平衡位置向位移正⽅向运动，写出此波的波动⽅程；(2)若从分界⾯反射的波的振幅与⼊射波振幅相等，试写出反射波的波动⽅程，并求轴上因⼊射波与反射波⼲涉⽽静⽌的各点的位置．解: (1)∵时，，∴故波动⽅程为m题5-20图(2)⼊射波传到反射⾯时的振动位相为(即将代⼊)，再考虑到波由波疏⼊射⽽在波密界⾯上反射，存在半波损失，所以反射波在界⾯处的位相为若仍以点为原点，则反射波在点处的位相为，因只考虑以内的位相⾓，∴反射波在点的位相为，故反射波的波动⽅程为此时驻波⽅程为故波节位置为P 321104-?=+=A A A P m 033122211083.210222--?=?==+=A A A A mx A νu t O x 0=t 0,000>=v y 20πφ-=]2)(2cos[ππ--=u x t v Ax 2432πλλπ-?-πππλλπ-=+-?-2432O O ππλλπ25432-=-?-π2O 2π-]2)(2cos[ππυ-+=u x t A y 反]2)(2cos[ππυ--=u x t A y ]2)(2cos[ππυ-++u x t A )22cos(2cos 2ππυπυ-=t u x A 2)12(22πλππυ+==k x ux故(…)根据题意，只能取，即5-20 ⼀驻波⽅程为=0.02cos20cos750(SI)，求：(1)形成此驻波的两列⾏波的振幅和波速； (2)相邻两波节间距离．解: (1)取驻波⽅程为故知，则，∴(2)∵所以相邻两波节间距离5-22 在弦上传播的横波，它的波动⽅程为=0.1cos(13+0.0079) (SI)试写出⼀个波动⽅程，使它表⽰的波能与这列已知的横波叠加形成驻波，并在=0处为波节．解: 为使合成驻波在处形成波节，则要反射波在处与⼊射波有的位相差，故反射波的波动⽅程为5-23 两列波在⼀根很长的细绳上传播，它们的波动⽅程分别为=0.06cos()(SI), =0.06cos()(SI)．(1)试证明绳⼦将作驻波式振动，并求波节、波腹的位置； (2)波腹处的振幅多⼤?=1.2m 处振幅多⼤? 解: (1)它们的合成波为出现了变量的分离，符合驻波⽅程特征，故绳⼦在作驻波振动．令，则，k=0,±1，±2…此即波腹的位置；令,则，…，此即波节的位置． (2)波腹处振幅最⼤，即为m ；处的振幅由下式决定，即5-24 汽车驶过车站时，车站上的观测者测得汽笛声频率由1200Hz 变到了1000 Hz ，设空⽓中声速为330m ·s -1，求汽车的速率．解: 设汽车的速度为，汽车在驶近车站时，车站收到的频率为4)12(λ+=k x ,2,1,0±±=k k 1,0λλ43,41=x y x t t u xA y πυπυ2cos 2cos2=01.0202.0==A m 7502=πυπυ2750=202=u πυ5.37202/7502202=?==πππυu 1s m -?314.01.020/2====πυπυυλu m 157.02==λx m 1y t x x 0=x 0=x π)0079.013cos(1.02π--=x t y 1y t x ππ4-2y t x ππ4+x )4cos(06.0)4cos(06.0t x x y ππππ++-=t x ππ4cos cos 12.0=ππk x =k x =2)12(ππ+=k x 21)12(+=k x ,2,1,0±±=k 12.02.1=x m 097.0)2.1cos(12.0=?=π驻A ms v汽车驶离车站时，车站收到的频率为联⽴以上两式，得5-25 两列⽕车分别以72km ·h -1和54 km ·h -1的速度相向⽽⾏，第⼀列⽕车发出⼀个600 Hz的汽笛声，若声速为340 m ·s -1，求第⼆列⽕车上的观测者听见该声⾳的频率在相遇前和相遇后分别是多少?解: 设鸣笛⽕车的车速为，接收鸣笛的⽕车车速为，则两者相遇前收到的频率为两车相遇之后收到的频率为1υυs v u u -=2υυs v u u +=3010012001000120030021211=+-?=+-=υυυυυu1s m -?201=v 1s m -?152=v 1s m -?6656002034015 3400121=?-+=-+=υυv u v u Hz 54160020340153400121=?+-=+-=υυv u v u Hz。
大学物理振动与波练习题与答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第二章 振动与波习题答案12、一放置在水平桌面上的弹簧振子，振幅2100.2-⨯=A 米，周期50.0=T 秒，当0=t 时 (1) 物体在正方向的端点；(2) 物体在负方向的端点；(3) 物体在平衡位置，向负方向运动； (4) 物体在平衡位置，向正方向运动。
求以上各种情况的谐振动方程。
【解】：π=π=ω45.02 )m ()t 4cos(02.0x ϕ+π=， )s /m ()2t 4cos(08.0v π+ϕ+ππ=(1) 01)cos(=ϕ=ϕ，， )m ()t 4cos(02.0x π=(2) π=ϕ-=ϕ，1)cos(， )m ()t 4cos(02.0x π+π=(3) 21)2cos(π=ϕ-=π+ϕ， ， )m ()2t 4cos(02.0x π+π= (4) 21)2cos(π-=ϕ=π+ϕ， ， )m ()2t 4cos(02.0x π-π=13、已知一个谐振动的振幅02.0=A 米，园频率πω4=弧度／秒，初相2/π=ϕ。
(1) 写出谐振动方程；(2) 以位移为纵坐标，时间为横坐标，画出谐振动曲线。
【解】：)m ()2t 4cos(02.0x π+π= ， )(212T 秒=ωπ=15、图中两条曲线表示两个谐振动(1) 它们哪些物理量相同，哪些物理量不同? (2) 写出它们的振动方程。
【解】：振幅相同，频率和初相不同。
虚线： )2t 21cos(03.0x 1π-π= 米实线： t cos 03.0x 2π= 米16、一个质点同时参与两个同方向、同频率的谐振动，它们的振动方程为t 3cos 4x 1= 厘米)32t 3cos(2x 2π+= 厘米试用旋转矢量法求出合振动方程。
【解】：)cm ()6t 3cos(32x π+=17、设某一时刻的横波波形曲线如图所示，波动以1米／秒的速度沿水平箭头方向传播。
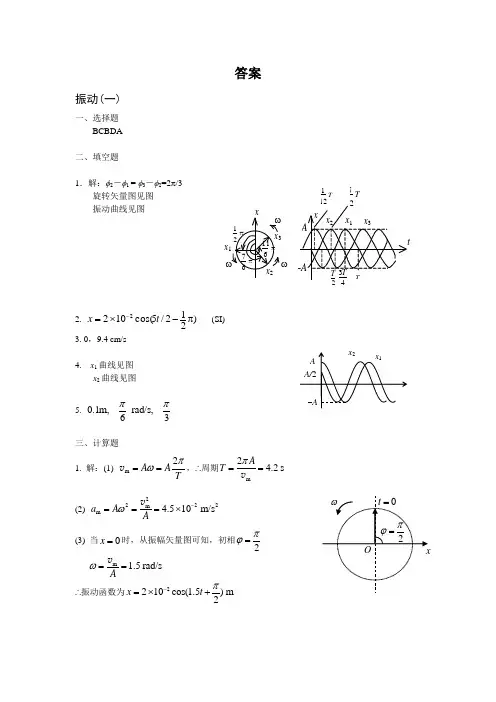
答案振动(一)一、选择题BCBDA二、填空题1．解：φ2－φ1 = φ3－φ2=2π/3旋转矢量图见图 振动曲线见图2. )212/5cos(1022π-⨯=-t x (SI)3. 0，9.4 cm/s4. x 1曲线见图x 2曲线见图5. 0.1m ,rad/s,63ππ三、计算题1. 解：(1) m 2A ATπω==v ，∴周期m2 4.2s A T π==v(2) 2222m m 4.510m/s a A Aω-===⨯v(3) 当0x =时，从振幅矢量图可知，初相2πϕ=m 1.5r a d /sAω==v ∴振动函数为2210cos(1.5)m 2x t π-=⨯+TT1T 5ω x12T 1212. 解：弹簧劲度系数 260 2.010N /m 0.3F k x===⨯ 静止时弹簧伸长量为 0249.80.196m 2.010m g x k⨯===⨯(1) 设向下为正方向，则 0ϕ= （若设向上为正方向，则 ϕπ=）；0.1mA =7.07r a d /sω== 振动函数为 0.1cos(7.07)m x t =(2) 物体在平衡位置上方5cm （即0.05m ），此时弹簧的净伸长为 00.050.1960.050.146m l x =-=-=弹簧对物体的拉力 2000.14629.2N F kl ==⨯=(3) 5cm 是振幅之半，物体从平衡位置到振幅之半所需最短时间是112T ，2T πω=∴10.074s 126t T πω===3．解：(1) 容器中每滴入一油滴的前后，水平方向动量值不变，而且在容器回到O 点滴入下一油滴前， 水平方向动量的大小与刚滴入上一油滴后的瞬间后的相同。
依此，设容器第一次过O 点油滴滴入前的速度为v ，刚滴入第个油滴后的速度为v ′,则有 v v '+=)(nm M M ① 3分系统机械能守恒 2202121v M kl = ② 2分22)(2121v '+=nm M kx③ 2分由①、②、③、解出0)/(l nm M M x +=2分(2) 时间间隔( t n +1-t n )应等于第n 滴油滴入容器后振动系统周期T n 的一半．k nm M T t t t n n n n /)(211+==-=∆+π 3分4．解：由旋转矢量图和 |v A | = |v B | 可知 T /2 = 4秒， ∴ T = 8 s ， ν = (1/8) s -1， ω = 2πν = (π /4) s -1 3分 (1) 以AB 的中点为坐标原点，x 轴指向右方．t = 0时， 5-=x cm φcos A =t = 2 s时， 5=x cm φφωsin )2cos(A A -=+= 由上二式解得 tg φ = 1因为在A 点质点的速度大于零，所以φ = -3π/4或5π/4（如图） 2分 25c o s/==φx A cm 1分∴ 振动方程 )434c o s (10252π-π⨯=-t x (SI) 1分 (2)速率 )434s i n (41025d d 2π-π⨯π-==-t t x v (SI) 2分 当t = 0 时，质点在A 点221093.3)43sin(10425d d --⨯=π-⨯π-==tx v m/s 1分5*．解：令θ 为杆和竖直线之间的夹角．运动方程为：θθθθc o s s i n s i n 21/d d 222kL MgL t J --= 3分θ 很小时，sin θ ≈θ ，cos θ ≈1所以：0/d d )21(222=++tJ kL MgL θθ 2分上式中231ML J =是杆绕其一端的转动惯量，所以0/d d 31)21(22=++tML Lk Mg θθ可知杆作角谐振动，并得到 )2/()2(3ML kL Mg +=ω2分)2(322/2kL Mg ML T +π=π=ω 1分振动(二)一、选择题ADDBB二、填空题 1．T /8，3T /8 2．222/2T mA π3．动能曲线见图 势能曲线见图 机械能曲线见图4．0.02 5．0三、计算题1.解：设小球的质量为m ，则弹簧的劲度系数 0/l mg k =．选平衡位置为原点，向下为正方向．小球在x 处时，根据牛顿第二定律得T220d /d )(t x m x l k mg =+- 将 0/l mg k = 代入整理后得0//d d 022=+l gx t x∴ 此振动为简谐振动，其角频率为． 3分 π===1.958.28/0l g ω 2分设振动表达式为 )c o s (φω+=t A x由题意： t = 0时，x 0 = A=2102-⨯m ，v 0 = 0，解得 φ = 0 1分∴ )1.9c o s (1022t x π⨯=- 2分2．解一：(1) 取平衡位置为原点，向下为x 正方向．设物体在平衡位置时弹簧的伸长量为∆l ，则有l k mg ∆=, 加拉力F 后弹簧又伸长x 0，则0)(0=+-+∆x l k mg F解得F = kx 02分 由题意，t = 0时v0 = 0；x = x 0 则 02020)/(x x A =+=ωv 2分又由题给物体振动周期4832=T s, 可得角频率 Tπ=2ω, 2ωm k =∴ 444.0)/4(22=π==A T m kA F N 1分 (2) 平衡位置以下1 cm 处： )()/2(2222x A T -π=v 2分 221007.121-⨯==vm E K J 2分2222)/4(2121x T m kxE p π=== 4.44³10-4J 1分解二：(1) 从静止释放，显然拉长量等于振幅A （5 cm ），kA F = 2分2224νωπ==m m k ，ν = 1.5 Hz 2分 ∴ F = 0.444 N 1分(2) 总能量 221011.12121-⨯===FA kAE J 2分当x = 1 cm 时，x = A /5，E p 占总能量的1/25，E K 占24/25． 2分∴ 21007.1)25/24(-⨯==E E K J ， 41044.425/-⨯==E E p J 1分3．解：(1) 选地心为x 坐标原点，向上为x 轴正方向．质量为m 的物体在地球内部距地心为x 处受到的地心引力为232/)3/4(/x m x G x G M m F ρπ-=-=3/4x Gm ρπ-= 3分由牛顿第二定律得 xm x Gm =π-3/4ρ， 03/4=π+x G xρ 1分 令 3/420ρωG π=， 则 020=+x x ω． 显然物体作简谐振动． 2分(2) 2/10)/3(4/32/2ρρωG G T π=ππ=π=已知 G = 6.67³10-11 N ²m 2²kg -2，ρ = 5.5³103 kg/m 3代入上式 T = 5.07³103 s 2分 物体从地面落到地心的时间 t = T /4 = 1.27³103 s 2分4．解：选平板位于正最大位移处时开始计时，平板的振动方程为 t A x π=4c o s (SI)t A xπ4c o s π162-= (SI) 1分 (1) 对物体有 x m N mg =- ① 1分 t A mg xm mg N ππ+=-=4cos 162 (SI) ②物对板的压力为 t A mg N F ππ--=-=4cos 162 (SI)t ππ--=4c o s 28.16.192 ③ 2分 (2) 物体脱离平板时必须N = 0，由②式得 1分 04c o s 162=ππ+t A mg (SI) Aq t 2164cos π-=π 1分若能脱离必须 14cos ≤πt (SI) 即221021.6)16/(-⨯=π≥g A m 2分5．解：依合振动的振幅及初相公式可得 φ∆++=c o s 2212221A A A A A 22210)4143cos(65265-⨯π-π⨯⨯⨯++=m21081.7-⨯= m 2分)4/c o s (6)4/3c o s (5)4/s i n (6)4/3s i n (5a r c t g π+ππ+π=φ = 84.8°=1.48 rad 2分则所求的合成振动方程为 )48.110cos(1081.72+⨯=-t x (SI) 1分波动（一）一、选择题CBDCD 二、填空题1．φλ+π-/2Lλk L ± ( k = 1，2，3，…) λ)12(21+±k L ( k = 0, 1，2，…)2．1cos x y A t u ωϕ⎡+⎤⎛⎫=++ ⎪⎢⎥⎝⎭⎣⎦3. ]4/)/(cos[11π+-=u L t A y ω；uL L )(21+ω4. ]2)2(2cos[π-+-π=ux t uA y λ]2)2(2c o s [π+-π=t uA y P λ5．0.2cos m 22p y t ππ⎛⎫=-⎪⎝⎭三、计算题1. 解：反射波在x 点引起的振动相位为 π+π--+π-=+21)55(4x t t φωπ-π+π+=10214x t 3分反射波表达式为)10214cos(01.0π-π+π+=x t y (SI) 2分或 )214c o s (01.0π+π+=x t y (SI)2．解： λxu t A y -π=2c o s = -0.01 m 1分1.0,2d d ===t x ty v 0)2s i n (2=-ππ-=λλxut uA 2分22d d ty a =)2c o s ()2(2λλxut uA -ππ-= = 6.17³103m/s 22分3．解：用旋转矢量解此题，如图可得A为代表P 点振动的旋转矢量. 210)cos sin 3(21-⨯-=t t y P ωω210)]cos()21cos(3(21-⨯π++π-=t t ωω)3/4c o s (1012π+⨯=-t ω (SI)． 3分波的表达式为：]2/234c o s [1012λλω-π-π+⨯=-x t y )312c o s (1012π+π-⨯=-λωxt (SI) 2分4．解：从y －x 波形图中可知 40m,A λ==由振幅矢量图可知 ,2P Q πϕϕπ=-=)由20m/s u =可得 2s,rad/s T uλωπ==∴=0.2cos()m20.2cos()mP Q y t y t ππππ∴=-=+5．解：(1) 由y －x 曲线可知160m λ=。
第一章 运动的描述1、解：设质点在x 处的速度为v ，62d d d d d d 2x txx t a +=⋅==v v ()x x xd 62d 02⎰⎰+=v v v()2 213xx +=v2、解：=a d v /d t 4=t ， d v 4=t d t⎰⎰=vv 0d 4d tt tv 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰=x 2=t 3 /3+x 0 (SI)3、解： ct b t S +==d /d vc t a t ==d /d v()R ct b a n /2+=根据题意：a t =a n即()R ct b c /2+=解得cb c R t -=4、解：根据已知条件确定常量k()222/rad 4//s Rt t k ===v ω24t =ω, 24Rt R ==ωvs t 1=时，v = 4Rt 2 = 8 m/s 2s /168/m Rt dt d a t ===v22s /32/m R a n ==v()8.352/122=+=nt a a a m/s 25、解：(1) 球相对地面的初速度=+='v v v 030 m/s抛出后上升高度9.4522='=gh v m/s 离地面高度H = (45.9+10) m =55.9 m(2) 球回到电梯上时电梯上升高度＝球上升高度2021)(gt t t -+=v v v 08.420==gt v s 6、解： 设人到船之间绳的长度为l ，此时绳与水面成θ角，由图可知222s h l +=将上式对时间t 求导，得ts s t l ld d 2d d 2= 根据速度的定义，并注意到l ,s 是随t 减少的，∴tsv v t l v d d ,d d 0-==-=船绳即 θcos d d d d 00v v s lt l s l t s v ==-=-=船 或 sv s h s lv v 02/1220)(+==船 将船v 再对t 求导，即得船的加速度320222022002)(d d d d d d sv h s v s l s v s lv s v v s t sl t l st v a =+-=+-=-==船船 7、解：(1)大船看小艇，则有1221v v v-=，依题意作速度矢量图如图(a)由图可知1222121h km 50-⋅=+=v v v方向北偏西︒===87.3643arctan arctan21v v θ (2)小船看大船，则有2112v v v-=，依题意作出速度矢量图如图(b)，同上法，得5012=v 1h km -⋅，方向南偏东o 87.36第二章 运动定律与力学中的守恒定律1、解：(1)位矢j t b i t a rωωsin cos += (SI)可写为t a x ωcos =，t b y ωsin =t a t x x ωωsin d d -==v ，t b ty ωωυcos d dy == 在A 点(a ，0) ，1cos =t ω，0sin =t ω E KA =2222212121ωmb m m y x =+v v 在B 点(0，b ) ，0cos =t ω，1sin =t ωE KB =2222212121ωma m m y x =+v v (2) j ma i ma F y x +==j t mb i t ma ωωωωsin cos 22--由A →B ⎰⎰-==020d cos d a a x x x t a m x F W ωω=⎰=-022221d a ma x x m ωω ⎰⎰-==b b y y t b m y F W 020dy sin d ωω=⎰-=-b mb y y m 022221d ωω2、解：A 、B 两球发生弹性正碰撞，由水平方向动量守恒与机械能守恒，得B B A A A A m m m v v v +=0①2220212121B B A A A A m m m v v v +=② 联立解出0A B A B AA m m m m v v +-=，02A BA AB m m m v v += 由于二球同时落地，∴0>A v ，B A m m >；且B B A A L L v v //=∴52==B A B A L L v v ，522=-A B Am m m 解出5/=B A m m3、解：(1) 释放后，弹簧恢复到原长时A 将要离开墙壁，设此时B 的速度为v B 0，由机械能守恒，有2/3212020B m kx v = 得mk x B 300=v A 离开墙壁后，系统在光滑水平面上运动，系统动量守恒，机械能守恒，当弹簧伸长量为x 时有022211B m m m v v v =+①202222221121212121B m m kx m v v v =++②当v 1 =v 2时，由式①解出v 1 =v 2mkx B 3434/300==v (2) 弹簧有最大伸长量时，A 、B 的相对速度为零v 1 =v 2 =3v B 0/4，再由式②解出0max 21x x =4、解：二滑块在弹力作用下将沿水平导杆作振动. 因导杆光滑，不产生摩擦阻力, 故整个系统的机械能守恒，而且沿水平方向的动量守恒(等于零)．当二滑块运动到正好使弹簧垂直于二导杆时，二滑块所受的弹力的水平分力同时为零，这时二滑块的速度将分别达到其最大速度v 1和v 2且此时弹簧为原长，弹簧势能为零。
版权归原著所有 本答案仅供参考习题33-1．如图，一质点在几个力作用下沿半径为20R m =的圆周运动，其中有一恒力0.6F i =N ，求质点从A 开始沿逆时针方向经3/4圆周到达B 的过程中，力F 所做的功。
解：本题为恒力做功，考虑到B 的坐标为（R -，R ）， ∴2020B A r r r i j ∆=-=-+，再利用：A F r =⋅∆， 有：0.6(2020)12A i i j =⋅-+=-（焦耳）3-2．质量为m =0.5kg 的质点，在x O y 坐标平面内运动，其运动方程为x =5t 2,y =0.5(SI),从t =2s 到t =4s 这段时间内，外力对质点的功为多少？ 解：由功的定义：A F r =⋅∆，题意：250.5r t i j =+24(4)(2)60r r r i →∆=-=，220.5105d rF m i i d t==⋅=∴560300A i i J =⋅=。
3-3．劲度系数为k 的轻巧弹簧竖直放置，下端悬一小球，球的质量为m ，开始时弹簧为原长而小球恰好与地接触。
今将弹簧上端缓慢提起，直到小球能脱离地面为止，求此过程中外力的功。
解：由于小球缓慢被提起，所以每时刻可看成外力与弹性力相等，则：F k x =，选向上为正向。
当小球刚脱离地面时：max mg k x =，有：max mgx k=， 由做功的定义可知：max222122mg x k m g A k xd x k x k===⎰。
3-4．如图，一质量为m 的质点，在半径为R 的半球形容器中，由静止开始自边缘上的A 点滑下，到达最低点B 时，它对容器的正压力数值为N ，求质点自A 滑到B 的过程中，摩擦力对其做的功。
分析：f A 直接求解显然有困难，所以使用动能定理，那就要知道它的末速度的情况。
解：求在B 点的速度：2v N G m R -=，可得：R G N mv )(21212-= 由动能定理： 2102f mgR A mv +=-∴11()(3)22f A N G R mgR N mg R =--=-3-5．一弹簧并不遵守胡克定律，其弹力与形变的关系为2(52.838.4)F x x i =--，其中F 和x 单位分别为N 和m 。
习题33-1．原长为m 5.0的弹簧，上端固定，下端挂一质量为kg 1.0的物体，当物体静止时，弹簧长为m 6.0．现将物体上推，使弹簧缩回到原长，然后放手，以放手时开始计时，取竖直向下为正向，写出振动式。
（g 取9.8）解：振动方程：cos()x A t ωϕ=+，在本题中，kx mg =，所以9.8k =； ∴ω===。
取竖直向下为x 正向，弹簧伸长为0.1m 时为物体的平衡位置，所以如果使弹簧的初状态为原长，那么：A =0.1m ，当t =0时，x =-A ，那么就可以知道物体的初相位为π。
所以：0.1cos x π=+）即：)x =-。
3-2．有一单摆，摆长m 0.1=l ，小球质量g 10=m ，0=t 时，小球正好经过rad 06.0-=θ处，并以角速度0.2rad/s θ= 向平衡位置运动。
设小球的运动可看作简谐振动，试求：（1）角频率、频率、周期；（2）用余弦函数形式写出小球的振动式。
（g 取9.8）解：振动方程：cos()x A t ωϕ=+ 我们只要按照题意找到对应的各项就行了。
（1）角频率： 3.13/rad s ω===，频率：0.5Hz ν=== ，周期：22T s ===； （2）振动方程可表示为：cos 3.13A t θϕ=+（），∴ 3.13sin 3.13A t θϕ=-+ （） 根据初始条件，0t =时：cos A θϕ=，0(12sin 0(343.13Aθϕ>=-< ，象限），象限）可解得：2008.810227133 2.32A m ϕ-=⨯==-=-，， 所以得到振动方程：28.810cos 3.13 2.32t m θ-=⨯-（） 。
3-3．一质点沿x 轴作简谐振动，振幅为cm 12，周期为s 2。
当0=t 时，位移为cm 6，且向x 轴正方向运动。
求：（1）振动表达式；（2）s 5.0=t 时，质点的位置、速度和加速度；（3）如果在某时刻质点位于cm 6-=x ，且向x 轴负方向运动，求从该位置回到平衡位置所需要的时间。
大学物理学——振动和波振 动班级 学号 姓名 成绩内容提要1、简谐振动的三个判据（1）；（2）；（3）2、描述简谐振动的特征量： A 、T 、γ；T1=γ，πγπω22==T3、简谐振动的描述：（1）公式法 ；（2）图像法；（3）旋转矢量法4、简谐振动的速度和加速度：)2cos()sin(v00πϕωϕωω++=+-==t v t A dt dx m ； a=）（）（πϕωϕωω±+=+=0m 0222t a t cos -dtxd A 5、振动的相位随时间变化的关系：6、简谐振动实例弹簧振子：，单摆小角度振动：，复摆：0mgh dt d 22=+θθJ ,T=2mghJπ 7、简谐振动的能量：222m 21k 21A A Eω==系统的动能为：）（ϕωω+==t sin m 21mv 212222A E K ；系统的势能为：）ϕω+==t (cos k 21kx 21222A E P8、两个简谐振动的合成（1）两个同方向同频率的简谐振动的合成合振动方程为：）（ϕω+=t cos x A其中，其中；。
＊(2) 两个同方向不同频率简谐振动的合成拍：当频率较大而频率之差很小的两个同方向简谐运动合成时，其合振动的振幅表现为时而加强时而减弱的现象，拍频：12-γγγ=＊（3）两个相互垂直简谐振动的合成合振动方程：）（1221221222212-sin )(cos xy 2y x ϕϕϕϕ=--+A A A A ，为椭圆方程。
练习一一、 填空题1．一劲度系数为k 的轻弹簧，下端挂一质量为m 的物体，系统的振动周期为T 1。
若将此弹簧截去一半的长度，下端挂一质量为m/2的物体，则系统的周期T 2等于 。
2．一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为：A ＝ ；=ω ;=ϕ 。
3．如图，一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上，做成一复摆。
已知细棒绕过其一端的轴的转动惯量J ＝3/2ml ，此摆作微小振动的周期为 。
