下载文档原格式
＊收稿日期：２００６－０３－１５＊＊作者简介：张磊（１９８２－），男，北京市人，北京化工大学硕士研究生。
对于高架吊车这样一个非线性被控对象的控制，传统的控制方法很难满足其控制性能，而模糊控制不依赖于被控对象的数学模型，且控制系统的鲁棒性能好，尤其适应于那些模型不确定、非线性、时变、时滞的被控对象。
但是，模糊控制器在实际设计中，对于实际经验的依赖性很大，在实际设计时，如何选取控制量和控制规则，需要编制大量的程序进行仿真分析，或是控制器设计完后通过实验分析，从而确定其控制方案。
显然这两种方法都需要经过反复实验才能确定，因而费时、费力。
针对上述问题，可以通过计算机仿真进行模糊控制器的设计，分析，调试。
并可以利用Ｍａｔｌａｂ平台中的Ｓ函数进行实物的动画模拟仿真。
１数学模型的建立带有悬挂物的移动吊车如图１所示。
质量为Ｍ的小车在水平力Ｆ的作用下沿水平方向前进，在Ｍ的重心上挂有一个质量为ｍ的重物，小车水平运动时，ｍ在惯性的作用下，左右摇摆，产生与垂直方向为!的夹角，车在水平方向上的位移为ｘ，速度为ｖ，悬挂物体的速度由水平和切向速度合成，其速度为"。
设广义坐标为ｘ和!，则整个系统的动能为：Ｔ＝１２Ｍｘ"２＋１２ｍ"２＝１２（Ｍ＋ｍ）ｘ"２＋１２ｍ（ｌ!"）２＋ｍｌｘ"!"ｃｏｓ!系统的势能为：Ｖ＝－ｍｇｌｃｏｓ!则有：Ｌ＝Ｔ－Ｖ＝１２（Ｍ＋ｍ）ｘ"２＋１２ｍ（ｌ!"）２＋ｍｌｘ"!"ｃｏｓ!＋ｍｇｌｃｏｓ!根据系统的拉格朗日方程，最终导出的被控对象的非线性数学模型为：（Ｍ＋ｍ）ｘ#＋ｍｌ!#ｃｏｓ!－ｍｌ!"２ｓｉｎ!＝Ｆ（ｔ）ｌ!#＋ｘ#ｃｏｓ!＋ｇｓｉｎ!＝!"$０（１）基于Ｍａｔｌａｂ环境下高架吊车的控制及动画模拟仿真＊张磊＊＊陈娟（北京化工大学信息科学与技术学院，北京１０００２９）摘要：针对高架吊车的两自由度控制，给出了模糊控制方案。
桥式起重机起升系统非线性建模及仿真吴世安 计三有武汉理工大学交通与物流工程学院 武汉 430063摘 要：桥式起重机系统较为复杂，具有时变、非线性的特点，现有设计手册利用动载系数放大设计无法准确量化动载大小。
为进一步研究起重机动力学特性，文中根据多体动力学理论建立刚柔耦合模型，根据桥式起重机起升及下降过程，考虑钢丝绳松弛长度、钢丝绳刚度变化等因素，结合弹性地基力学模型，基于时变刚度与时变激励建立起升系统非线性动力学模型。
利用Runge-Kutta积分法仿真得到起升及下降阶段钢丝绳拉力、过载系数、主梁振动、钢丝绳刚度变化数据。
结果表明，钢丝绳松弛长度对拉力最大值有较大影响。
关键词：桥式起重机；动力学模型；时变刚度；刚柔耦合；仿真中图分类号：TH215 文献标识码：A 文章编号：1001-0785（2023）07-0045-06Abstract: The bridge crane system is complex, time-varying and nonlinear, and the existing design manual can not accurately quantify the dynamic load by using the dynamic load coefficient to enlarge the design. In order to further study the dynamic characteristics of cranes, a rigid-flexible coupling model was established according to the multi-body dynamics theory. According to the hoisting and descending process of bridge crane, a nonlinear dynamic model of hoisting system was built based on the time-varying stiffness and time-varying excitation, considering the factors such as the relaxation length and stiffness change of steel wire rope and the mechanical model of elastic foundation. Runge-Kutta integration method was used for simulation, and the variation data of wire rope tension, overload coefficient, main girder vibration and wire rope stiffness during hoisting and descending stages were obtained. The results show that the relaxation length of wire rope has great influence on the maximum tension.Keywords:bridge crane; dynamic model; time-varying stiffness; rigid-flexible coupling; simulation0 引言起重机械是使用吊钩或其他取物装置吊挂重物，在空间进行升降、运移等循环作业的机械，通过垂直机构与水平机构的相关运动来完成转运过程[1]。
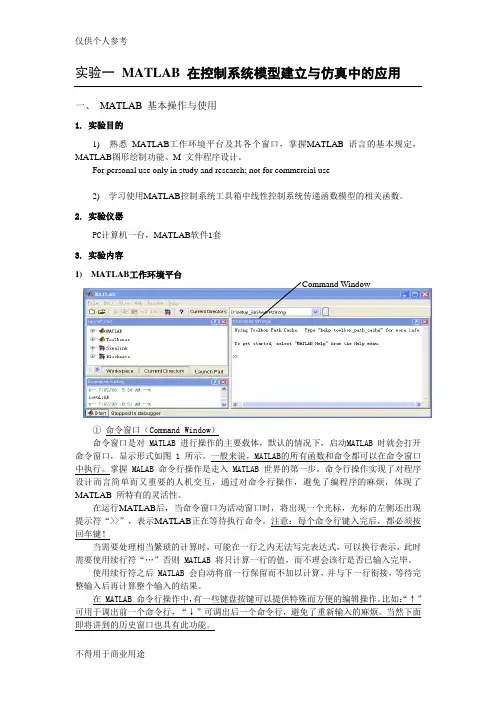
实验一MATLAB 在控制系统模型建立与仿真中的应用一、MATLAB 基本操作与使用1. 实验目的1) 熟悉MATLAB工作环境平台及其各个窗口，掌握MATLAB 语言的基本规定，MATLAB图形绘制功能、M 文件程序设计。
For personal use only in study and research; not for commercial use2) 学习使用MATLAB控制系统工具箱中线性控制系统传递函数模型的相关函数。
2. 实验仪器PC计算机一台，MATLAB软件1套3. 实验内容1) MATLAB工作环境平台Command Window图1 在英文Windows 平台上的MATLAB6.5 MATLAB工作平台①命令窗口（Command Window）命令窗口是对 MATLAB 进行操作的主要载体，默认的情况下，启动MATLAB 时就会打开命令窗口，显示形式如图 1 所示。
一般来说，MATLAB的所有函数和命令都可以在命令窗口中执行。
掌握 MALAB 命令行操作是走入 MATLAB 世界的第一步。
命令行操作实现了对程序设计而言简单而又重要的人机交互，通过对命令行操作，避免了编程序的麻烦，体现了MATLAB所特有的灵活性。
在运行MATLAB后，当命令窗口为活动窗口时，将出现一个光标，光标的左侧还出现提示符“>>”，表示MATLAB正在等待执行命令。
注意：每个命令行键入完后，都必须按回车键！当需要处理相当繁琐的计算时，可能在一行之内无法写完表达式，可以换行表示，此时需要使用续行符“…”否则 MATLAB 将只计算一行的值，而不理会该行是否已输入完毕。
使用续行符之后 MATLAB 会自动将前一行保留而不加以计算，并与下一行衔接，等待完整输入后再计算整个输入的结果。
在 MATLAB 命令行操作中，有一些键盘按键可以提供特殊而方便的编辑操作。
比如：“↑”可用于调出前一个命令行，“↓”可调出后一个命令行，避免了重新输入的麻烦。
桥式起重机吊重Fuzzy-LQR防摆控制器的设计李军;李学鋆【摘要】桥式起重机大小车联合运动可以提高作业效率,在其吊重防摆控制中加入大车运动更具工程意义.针对桥式起重机防摆定位控制具有非线性、强耦合、不确定等特点,设计Fuzzy-LQR控制吊重摆动.根据Lagrange方程建立三维动力学模型并在大小车运动方向对其进行解耦;通过信息融合技术将模糊控制器的多输入进行降维处理,解决模糊规则爆炸问题,结合LQR控制原理搭建Simulink仿真模型.选用CXTD16t-19.5m双梁桥式起重机进行仿真模拟,结果表明:运用Fuzzy-LQR分别控制解耦后的大小车运动或者大小车联合运动都能达到防摆定位的目的.【期刊名称】《机械设计与制造》【年(卷),期】2018(000)008【总页数】4页(P233-236)【关键词】桥式起重机;防摆控制;Fuzzy-LQR控制;LQR;模糊控制【作者】李军;李学鋆【作者单位】重庆交通大学机电与车辆工程学院,重庆 400074;重庆交通大学机电与车辆工程学院,重庆 400074【正文语种】中文【中图分类】TH161 引言起重机使用柔性绳索起吊重物使得结构轻便，提高了作业效率，但存在很大的安全隐患和控制问题。
为了推进起重机吊具的自动化控制和智能化控制，对起重机吊具的防摆定位控制进行研究具有十分重要的意义[1]。
针对起重机吊重防摆定位出现了PID控制、最优控制、滑模控制、模糊控制、神经网络控制、反步控制和无源控制等控制方法。
由于起重机吊重的非线性特性，单一的起重机吊重防摆定位控制方式存在各种不足，因此利用多种控制方法相结合，实现优势互补，可以弥补不足，提高控制精度和控制反应速度。
文献[2]建立了桥式起重机三维二自由度动力学模型、传递函数及建立仿真模型并通过解耦的处理方式利用小车控制吊重摆角，这种方式不仅可以快速控制摆角而且可以保证起重机定位。
最后实验仿真验证该方法可行，但存在抖振和严重超调。
基于Matlab的汽车运动控制系统设计
Matlab是一款强大的工具，它可以用于汽车动力学控制系统
的建模、仿真和优化。
下面是基于Matlab的汽车运动控制系
统的设计流程：
1. 汽车运动学建模，包括车辆加速度、速度、位置等基本变量的建模，并建立数学模型。
2. 汽车动力学建模，包括发动机、传动系统、制动系统等的建模，推导出相关的动力学方程。
3. 设计控制器，选择合适的控制算法，并根据模型参数进行控制器设计。
4. 建立仿真模型，将汽车运动学、动力学模型以及控制器整合在一起，建立仿真模型，并进行仿真。
5. 分析仿真结果，通过仿真结果分析系统的性能，包括控制效果、鲁棒性等。
6. 修改设计，对仿真结果进行修改，优化设计，重新进行仿真。
7. 实现控制器，将控制器转换为代码并实现到实际控制系统中。
8. 验证系统性能，进行实车测试，验证系统性能及仿真结果的准确性。
总体而言，基于Matlab的汽车运动控制系统设计可以提高设计效率，减少设计成本，确保系统性能及仿真结果的准确性。
使用Matlab进行车辆控制和自动驾驶系统设计随着科技的发展和人们对便捷出行的需求不断增加，车辆控制和自动驾驶系统成为了一个备受关注和研究的领域。
Matlab作为一款强大的数学建模和仿真软件，可以为车辆控制和自动驾驶系统的设计提供极大的帮助。
本文将就如何使用Matlab进行车辆控制和自动驾驶系统设计进行探讨。
首先，车辆控制是车辆驶向目标位置或按照预定运动轨迹运动的过程。
在车辆控制中，总体来说有两种主要方式：基于物理模型的控制和基于试验数据的控制。
基于物理模型的控制是通过对车辆的物理特性进行建模，并结合相应的控制算法来实现车辆的控制。
而基于试验数据的控制，则是通过对车辆运动数据进行统计与分析，建立数据模型，进而进行车辆的控制。
在Matlab中，可以使用Simulink工具箱提供的车辆动力学模型进行车辆控制。
车辆动力学模型是一种实现车辆运动轨迹控制的常用方法。
通过将车辆的运动特性转化为数学模型，在Matlab中进行仿真，可以更加直观地预测车辆的运动行为，并进行相应的控制设计。
例如，可以通过建立车辆的悬挂系统、转向系统、制动系统等子系统模型，对车辆在不同工况下的运动特性进行建模和仿真分析。
同时，Matlab还提供了用于控制设计的工具箱，如Control System Toolbox、Robust Control Toolbox等，这些工具箱包含了丰富的控制算法和方法，能够帮助用户进行车辆控制的设计和优化。
用户可以根据车辆系统的特点和需求，选择适合的控制算法，并进行参数调整和模拟验证。
而对于自动驾驶系统设计来说，Matlab同样发挥着重要的作用。
自动驾驶系统设计是指实现车辆自主感知、决策和执行的过程。
在Matlab中，可以使用Computer Vision Toolbox进行图像处理和视觉感知，通过对车辆周围环境的实时识别和分析，实现自主导航和避障功能。
同时，Matlab还可以结合Deep LearningToolbox进行深度学习算法的应用，利用神经网络模型对复杂交通场景进行理解和预测。
桥式吊车小车运动控制系统建模及MATLAB仿真（附程序）桥式吊车运动控制系统的建模及MATLAB仿真(附程序)1简介桥式起重机是横架于车间、仓库及露天堆场的上方，用来吊运各种物体的机械设备，通常称为“天车”或“吊车”。
它是机械工业、冶金工业和化学工业中应用最广泛的一种起重机械。
实际生产中的桥式吊车（天车）类似，是一个MIMO复杂控制系统。
桥式吊车系统由三部分组成：桥架驱动系统，车体驱动系统和重物装吊系统。
其工作流程为：先将重物起吊至预先设定好的高度，然后吊车运动将重物运到想要放置的位置上方，最后把重物下放到想要放置的位置上。
2确定要研究的系统为桥式吊车运动控制系统桥式吊车系统工作示意图见下图1：pMmxzFθmg图1桥式吊车工作示意图对于如上桥式吊车控制系统，首先做如下假设：1)吊车的行走运动仅限于吊车一个自由度，即假设桥架不运动，只有吊车在桥架上行走。
2)吊车行走时吊装重物的绳索长度不变。
图中，x坐标为水平方向，z坐标为垂直方向。
重物的摆动是由吊车与重物的运动产生的，可以根据动力学有关规律建立吊车及重物的运动方程式。
1)在水平方向，吊车和重物整体受力为F(t)，由牛顿第二定律得（1）2)在垂直于绳索方向，重物受力为，由牛顿第二定律得（2）由吊车在行走时吊装重物的绳索长度不变的假设可得出下面两个关系式：（3）（4）式中，为绳索长度。
由（3）可得（5）（5）代入（1）得：（6）同样由式（4）可得：（7）将（5）（7）代入（2）得（8）又尽量小，所以有如下近似式：，，将（6），（8）线性化可得：（9）（10）由（9）和（10）计算得（11）和（12）3）吊车驱动装置的方程式。
吊车由电动机驱动，简化的认为电动机是一个时间常数为的一阶惯性环节，即它产生的驱动力F(t)与其控制电压v(t)之间满足方程式：（13）其中K为放大系数。
3选择系统的输入、输出变量和状态变量选择5个状态变量分别为：，，，，；输入变量为：；两个输出变量为：，。
线性系统理论上机实验报告
题目：桥式吊车小车运动控制系统的建模及MATLAB 仿真
班级：控制[专研]-12；
学号：2012309030122号；
姓名：邵晓琳
完成时间：2012-12-22
桥式吊车小车运动控制系统的建模及MATLAB仿真
[摘要]桥式起重机是横架于车间、仓库及露天堆场的上方，用来吊运各种物体的机械设备，通常称为“天车”或“行车”“吊车”。
它是机械工业、冶金工业和化学工业中应用最广泛的一种起重机械。
实际生产中的桥式吊车（天车）类似，与倒立摆类似是自动控制最为经典的实验模型，是一个MIMO复杂控制系统，可以作为控制理论算法研究的理想实验平台。
桥式吊车系统由三部分组成：桥架驱动系统，小车驱动系统和重物撞吊系统。
其工作流程为：先将重物起吊至预先设定好的高度，然后小车运动将重物运到想要放置的位置上方，最后把重物下放到想要放置的位置上。
目录
1确定要研究的系统为桥式吊车运动控制系统 (3)
2 选择系统的输入、输出变量和状态变量 (7)
3建立状态空间描述 (7)
4 分析系统的稳定性 (8)
5 判断系统的能控性 (10)
6 采用状态反馈进行系统综合 (11)
7 实验结论 (15)
1确定要研究的系统为桥式吊车运动控制系统
桥式吊车系统工作示意图见下图1：
图1 桥式吊车工作示意图
对于如上桥式吊车控制系统，首先做如下假设：
①吊车的行走运动仅限于小车一个自由度，即假设桥架不运动，只有小车在桥架上行走。
②小车行走时吊装重物的绳索长度不变。
图中，x 坐标为水平方向，z 坐标为垂直方向。
重物的摆动是由小车与重物的运动产生的，可以根据动力学有关规律建立小车及重物的运动方程式。
（1）在水平方向，小车和重物整体受力为F(t)，由牛顿第二定律得
()()()
M m MX t mX t F t ''''+=
（1-1）
（2）在垂直于绳索方向，重物受力为sin ()mg t θ，由牛顿第二定律得
()cos ()()sin ()sin ()
m m mX t t mZ t t mg t θθθ''''+=
（1-2）
由小车在行走时吊装重物的绳索长度不变的假设可得出下面两个关系式：
()sin ()()
m M X t l t X t θ+=
（1-3）
()cos ()
m Z t l t θ=
（1-4）
式中，l 为绳索长度。
由（1-3）可得
2()()cos ()()sin ()()
m M X t X t l t t l t t θθθθ'''''''=-+
（1-5）
（1-5）代入（1-1）得：
2()()cos ()()sin ()()()M
M m X t ml t t ml t t F t θθθθ'''''+-+=
（1-6）
同样由式（1-4）可得：
2()cos ()()sin ()()
m Z t l t t l t t θθθθ'''''=--
（1-7）
将（1-5）（1-7）代入（1-2）得
()cos ()()sin ()
M X t t l t g t θθθ''''-=
（1-8）
又θ(t)尽量小，所以有如下近似式：
sin ()()t t θθ≈，cos ()1t θ≈，2
sin ()()0t t θθ'≈
将（1-6），（1-8）线性化可得：
()()()()
M M m X t ml t F t θ''''+-=
（1-9）
()()()
M X t l t g t θθ''''-=
（1-10）
由（1-9）和（1-10）计算得
1
()()()M mg X t t F t M M
θ''=-
+
㈠
和
()1
()()()M m g t t F t Ml Ml
θθ+''=-
+
㈡
（4）小车驱动装置的方程式。
小车由电动机驱动，简化的认为电动机是一个时间常数为d T 的一阶惯性环节，即它产生的驱动力F(t)与其控制电压v(t)之间满足方程式：
T F ()()()
d t F t Kv t '+=
㈢
其中K 为放大系数。
2 选择系统的输入、输出变量和状态变量
选择5个状态变量分别为：
1M X X =，2M X X '=，3X θ=，4X θ'=，5X F =；
输入变量为： u=v ；
两个输出变量为： 1M y X =，2y θ=。
3 建立状态空间描述
根据㈠㈡㈢式可得出描述小车运动系统的状态空间表达式为：
010
000100
0000
010
0()10000100
d d mg
M M x x u M m g Ml Ml K T T •
⎡⎤
⎢⎥⎡⎤⎢⎥-⎢⎥
⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥+⎢⎥⎢⎥
-
⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦-⎢⎥⎣
⎦
x y ⎥
⎦
⎤⎢⎣⎡=0010000001 选取适当参数:对一个实际的桥式吊车小车运动系统，假定具有如下各具体参数：M=1000kg,m=4000kg,l=10m,K=100N/V 。
将它们代入上面的状态空间表达式得：
3401
000039.20
10000010000 4.901000
1100x x u -•
-⎡⎤⎡⎤
⎢⎥⎢⎥-⎢⎥⎢⎥
⎢⎥⎢⎥=+⎢⎥⎢⎥-⎢⎥⎢⎥
⎢⎥⎢⎥-⎣⎦⎣⎦
x y ⎥⎦
⎤⎢⎣⎡=0010000001
4 分析系统的稳定性
用特征值法。
在MATLAB 中输入以下程序： eig(A) ans =
0 + 2.2136i
0 - 2.2136i
-1
系统的5个开环特征值不全位于S左平面上，有4个位于虚轴上，所以系统为临界不稳定。
构造系统仿真模型如下
系统输出仿真波形如下图所示：
5 判断系统的能控性
使用MATLAB判断系统的能控性，输入以下程序：
A=[0 1 0 0 0;0 0 -39.2 0 0.001;0 0 0 1 0;0 0 -4.9 0 0.0001;0 0 0 0 -1];
B=[0;0;0;0;100];
C=[1 0 0 0 0;0 0 1 0 0];
rct=rank(ctrb(A,B))
rct =
5
根据判别系统能控性的定理，该系统的能控性矩阵满秩，所以该系统是能控的。
6 采用状态反馈进行系统综合
因为系统是能控的，所以，可以通过状态反馈来任意配置极点。
例如将极点配置在：s1=-0.16-j0.16 s2=-0.16+j0.16 s3,s4,s5=-1。
在MATLAB中输入：
P=[-0.16+0.16i,-0.16-0.16i,-1,-1,-1];
K=acker(A,B,P)
求出状态反馈矩阵K：
K =
0.52245 4.8327 -1420.7 -137.21 0.0232
在MATLAB中输入
A-B*K
ans =
0 1 0 0 0
0 0 -39.2 0 0.001
0 0 0 1 0
0 0 -4.9 0 0.0001
-52.245 -483.27 1.4207e+005 13721 -3.32
因此综合后系统的状态空间描述为：
340100000039.2010000010000 4.9010052.245483.2714207013721 3.32100x x u -•
-⎡⎤⎡⎤
⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦
x y ⎥
⎦⎤⎢⎣⎡=0010000001
采用MATLAB/Simulink构造系统状态反馈控制系统的仿真模型，如下图所示。
运行仿真程序，得到仿真曲线如下图：
将极点配置在：s1=-0.2 s2=-0.2 s3,s4,s5=-1。
计算出K=[0.40816
5.3061 -1438.1 -119.06 0.024]此时输出y的仿真曲线如下：
将极点配置在：s1=-0.16+0.16i s2=-0.16-0.16i s3=-1 s4=-2 s5=-3。
计算出K=[3.1347 25.339 -2145.4 553.73 0.0532]此时输出y的仿真曲线如下：
7 实验结论
通过比较3组不同的极点配置下状态反馈系统的输出响应曲线和原系统的输出响应曲线可以看出，不同的极点配置对系统性能有一定的影响，但只要极点都配置在S左平面，就可以保证系统具有一定的动态和稳态性能。
