当前位置：文档之家 › 信号与系统习题答案第三章

信号与系统习题答案第三章

  • 格式：doc
  • 大小：2.18 MB
  • 文档页数：37

下载文档原格式

  / 37

合集下载

【信号与系统(郑君里)课后答案】第三章习题解答

【信号与系统(郑君里)课后答案】第三章习题解答

3-1 解题过程：（1）三角形式的傅立叶级数（Fourier Series ，以下简称 FS ）f ( t ) = a ++∞cos ( n ω t) + b sin ( n ω t ) a 0 ∑ n 1n 1 n =1式中ω1 =2π，n 为正整数，T 1 为信号周期T 11 t +T（a ）直流分量a 0 = 0 ∫ 1 f ( t ) dtT1 t2 t +T（b ）余弦分量的幅度a n = 0∫ 1f ( t ) cos ( n ω1t ) dtT1 t 02 t +T（c ）正弦分量的幅度b n = 0 ∫ 1f ( t ) sin ( n ω1t ) dtT 1 t（2）指数形式的傅立叶级数+∞f ( t ) = ∑ F ( n ω1 )e jn ω1tn =其中复数频谱F n= F ( n ω1 ) = 1 ∫t 0 +T 1f ( t ) e − jn ω1t dt T 1 t 0F n =1( a n − jb n ) F − n = 1 ( a n + jb n ) 2 2由图 3-1 可知， f ( t ) 为奇函数，因而a 0 = a n = 04 Tb n = T ∫02= 2Eπ n4TE−2EEf (t ) sin ( n ω t ) dt =sin ( n ω t ) dt = cos ( n ω t = 1 − cos ( n π2T 1 ∫0 2 1 n t 1 n ) 1n = 2, 4,n = 1, 3,所以，三角形式的 FS 为2 E1 12π f ( t ) =sin ( ω1t ) +sin ( 3ω1t ) +sin ( 5ω1t ) +ω1 =π 3 5T指数形式的 FS 的系数为1n = 0, ±2, ±4,F n = − jb n jE=2 n = 0,−± 1, ±3,n π1所以，指数形式的 FS 为f ( t ) = − jE π ej ω1t+ πjE e − j ω1t − 3jE π e j 3ω1t + 3jEπ e − j 3ω1t +3-15 分析：半波余弦脉冲的表达式 f ( t ) =πτ E cos t u t+ τ 2求 f ( t ) 的傅立叶变换有如下两种方法。

信号与系统 梁风梅主编 电子工业出版社 ppt第三章答案

信号与系统 梁风梅主编 电子工业出版社 ppt第三章答案

习题三3.1考虑一个连续时间LTI 系统，满足初始松弛条件，其输入)(t x 与输出)(t y 的关系由下列微分方程描述：d ()4()()d y t y t x t t+= (1)若输入(13)()()j t x t e u t -+=，求输出)(t y 。

(2)若输入()e cos(3)()t x t t u t -=，求输出)(t y 。

解：此系统的特征方程为40s += 所以4()t h y t Ae -= (1)(13)()()j tx t eu t -+=设(13)()e j t p y t Y -+= 则(13)(13)(13)(13j)e 4e e ,0j tj t j t Y Y t -+-+-+-++=>解得11336jY j -==+ 所以4(13)1()()()e e ()6t j t h p j y t y t y t A u t --+-⎛⎫=+=+ ⎪⎝⎭又因为初始松弛，所以106jA -+= 即16j A -=所以4(13)11()()()()()66t j th p j j y t y t y t e e u t --+--=+=+ (2)()cos(3)()t x t e t u t -=是(1)中(13)()()j tx t eu t -+=的实部，用2()x t 表示cos(3)()t e t u t -，用1()x t 表示(13)()j t e u t -+观察得{}21()Re ()x t x t =所以{}421111()Re ()cos(3)sin(3)()666t t t y t y t e e t e t u t ---⎛⎫==-++ ⎪⎝⎭3.2若离散时间LTI 系统的输入[]x n 与输出][n y 的关系由下述差分方程给出：][]1[25.0][n x n y n y =--求系统的单位冲激响应][n h 。

解：[]0.25[1][]h n h n n δ=-+因为该系统是因果的，所以0n <时，[]0h n =2231[0]0.25[1][0]01111[1]0.25[0][1]1044111[2]0.25[1][2]0444111[3]0.25[2][3]0444 (111)[]0.25[1][]0444n nh h h h h h h h h n h n n δδδδδ-=-+=+==+=⨯+==+=⨯+==+=⨯+==-+=⨯+=综上，1[][]4n h n u n = 3.3系统S 为两个系统1S 与2S 的级联：S1：因果LTI 系统，[]0.5[1][]w n w n x n =-+； S2: 因果LTI 系统，[][1][]y n ay n bw n =-+][n x 与][n y 的关系由下列差分方程给出：[]0.125[2]0.75[1][]y n y n y n x n +---=(1) 确定a 与b 。

信号与系统王明泉第三章习题解答

信号与系统王明泉第三章习题解答
（3）周期信号的傅里叶变换；
（4）频域分析法分析系统；
（5）系统的无失真传输；
（6）理想低通滤波器；
（7）系统的物理可实现性；
3.3本章的内容摘要
3.3.1信号的正交分解
两个矢量 和 正交的条件是这两个矢量的点乘为零，即：
如果 和 为相互正交的单位矢量，则 和 就构成了一个二维矢量集，而且是二维空间的完备正交矢量集。也就是说，再也找不到另一个矢量 能满足 。在二维矢量空间中的任一矢量 可以精确地用两个正交矢量 和 的线性组合来表示，有
条件1：在一周期内，如果有间断点存在，则间断点的数目应是有限个。
条件2：在一周期内，极大值和极小值的数目应是有限个。
条件3:在一周期内，信号绝对可积，即
（5）周期信号频谱的特点
第一：离散性，此频谱由不连续的谱线组成，每一条谱线代表一个正弦分量，所以此谱称为不连续谱或离散谱。
第二：谐波性，此频谱的每一条谱线只能出现在基波频率 的整数倍频率上。
(a)周期、连续频谱； (b)周期、离散频谱；
(c)连续、非周期频谱； (d)离散、非周期频谱。
答案：(d)
题7、 的傅里叶变换为
答案：
分析：该题为典型信号的调制形式
题8、 的傅里叶变换为
答案：
分析：根据时移和频移性质即可获得
题9、已知信号 如图所示，且其傅里叶变换为
试确定：
(1)
(2)
(3)
解：
(1)将 向左平移一个单位得到
对于奇谐函数，满足 ，当 为偶数时， ， ；当 为奇数时， ， ，即半波像对称函数的傅里叶级数展开式中只含奇次谐波而不含偶次谐波项。
（4）周期信号傅里叶级数的近似与傅里叶级数的收敛性
一般来说，任意周期函数表示为傅里叶级数时需要无限多项才能完全逼近原函数。但在实际应用中，经常采用有限项级数来代替无限项级数。无穷项与有限项误差平方的平均值定义为均方误差，即 。式中， ， 。研究表明， 越大， 越小，当 时， 。

第三章作业答案_1-7

第三章作业答案_1-7

a2 N =
1 1 T 1 T − j (4 N π / T ) t 2 x t e dt = x(t )e− j (4 Nπ / T )t dt + ∫T x(t )e− j (4 Nπ / T )t dt ( ) ∫ ∫ T T T 0 T 2 =
T 1 T T ( ∫ 2 x(t )e − j (4 Nπ / T )t dt + ∫T − x(t − )e− j (4 Nπ / T )t dt ) T 0 2 2 T 1 T ( ∫ 2 x(t )e − j (4 Nπ / T ) t dt + ∫ 2 − x(t )e− j (4 Nπ / T )t dt ) = 0 0 T 0
+∞
e − j 2ω （答案） 2 + jω
+∞ +∞ −∞
X ( jϖ ) = ∫ x(t )e − jωt dt = ∫ e −2 ( t − 2) u (t − 2)e − jωt dt = ∫ e −2 ( t − 2) e − jωt dt
−∞ 2
= ∫ e −( 2+ jω )t + 4 dt =
jkπt
，由已知条件 k ≤ 4 时，H(jw)不为零，而 k ≥ 5 ，H(jw)=0
jkπt
故响应为： y k (t ) = H ( jkπ ) a k e 当 k > 5 时，激励 x k (t ) = a k e 此有 y (t ) =
= (1 −
k 5
)a k e jkπt ， k ≤ 4
(2) 由于系统的单位冲激响应 h(t)已知，可以据此而求出其频谱。因为 h(t)是方波脉冲，直 接由典型信号的频谱得：
FT h(t ) ←→ H ( jω ) =

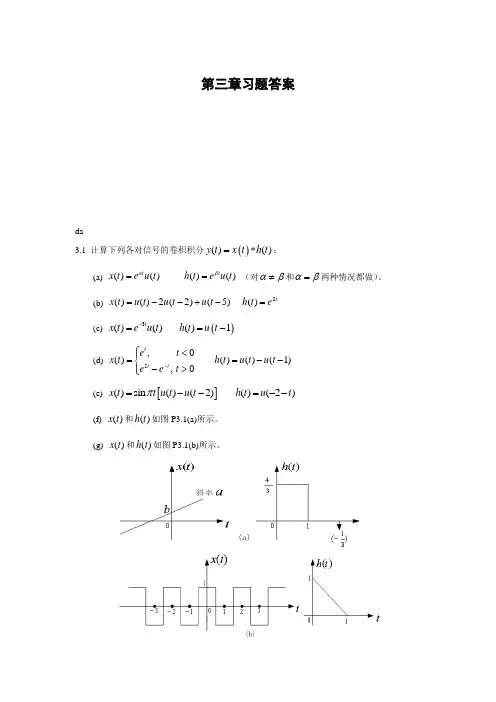
信号与线性系统题解第三章

信号与线性系统题解第三章

第三章习题答案da3.1 计算下列各对信号的卷积积分()()()y t x t h t =*：(a) ()()()()t tx t e u t h t e u t αβ==（对αβ≠和αβ=两种情况都做）。

(b) 2()()2(2)(5)()tx t u t u t u t h t e =--+-=(c) ()3()()()1tx t eu t h t u t -==-(d) 5,0()()()(1),0tt t e t x t h t u t u t e e t -⎧<⎪==--⎨->⎪⎩(e) []()sin ()(2)()(2)x t t u t u t h t u t π=--=--(f) ()x t 和()h t 如图P3.1(a)所示。

(g) ()x t 和()h t 如图P3.1(b)所示。

图P3.1 解：(a) ()()0()()()(0)t ttty t x t h t eed eed t βτατβαβτττ------=*==>⎰⎰当αβ≠时，()1()()ttey t e u t αβββα----=-当αβ=时，()()t y t te u t α-=(b) 由图PS3.1(a)知， 当1t ≤时，252()2()22(2)2(5)021()22t t t t t y t ed ed e e e ττττ----⎡⎤=-=-+⎣⎦⎰⎰ 当13t ≤≤时，252()2()22(2)2(5)121()22t t t t t y t ed ed e e e ττττ-----⎡⎤=-=-+⎣⎦⎰⎰ 当36t ≤≤时，52()2(5)211()2t t t y t ed e e ττ---⎡⎤=-=-⎣⎦⎰ 当6t >时，()0y t =(c) 由图PS3.1(b)知，当1t ≤时，()0y t = 当1t >时，133(1)01()13t t y t ed e ττ----⎡⎤==-⎣⎦⎰3(1)1()1(1)3t y t e u t --⎡⎤∴=--⎣⎦(d) 由图PS3.1(d)知： 当0t ≤时，11()tt t t y t e d e eττ--==-⎰当01t <≤时，055(1)1014()(2)255t ttt t y t e d e e d e eeτττττ-----=+-=+--⎰⎰当1t >时，555(1)(1)111()(2)2255t tt tt t y t e ed eeeeτττ------=-=-+-⎰(e) 如下图所示：(f) 令()11()(2)3h t h t t δ⎡⎤=+--⎢⎥⎣⎦，则11()()()(2)3y t x t h t x t =*-- 由图PS3.1(h)知，11424()()()()(21)333t t y t x t h t a b d a t b ττ-=*=+=-+⎰2411()(21)(2)()3333a y t tb a t b a t b x t ∴=-+---=+= (g) ()x t 是周期信号，由此可推知()()()y t x t h t =*也是周期的，且周期也为2。

[信号与系统作业解答]第三章

[信号与系统作业解答]第三章

解：
f (t)cos( 0t)
F1( )
1 2
[F(
0) F(
0 )]
f (t)e j 0t F2( ) F(
0)
f (t)cos( 1t)
F3( )
1 2
[F(
1) F(
1)]
3-39 确定下列信号的最低抽样率与奈奎斯特间隔。
（1） Sa(100t )
（3）Sa(100t) Sa(50t)
解：（1）因为Sa(100t) 50G200( ) ，最高频率为 m 100 rad / s ，所以最低抽样
cos( 0t) u(t)
1 2
[(
0) (
0)] *
()
1 j
1 2
(
( 2
0)
1 j(
0)
0) (
0)
(
j
2
2
0
0)
1 j(
0)
3-34 若 f (t) 的频谱 F( ) 如图所示，利用卷积定理粗略画出 f (t)cos( 0t) ， f (t)ej 0t ，
f (t)cos( 1t) 的频谱（注明频谱的边界频率）。
f *(t)]
所以
F [fi(t)]
1 2j F
[f (t)
f *(t)]
1 [F( ) F *( 2j
)]
3-22 利用时域与频域的对称性，求下列傅里叶变换的时间函数。
1） F( ) (
0)
2） F( ) u(
0) u(
0)
3） F( )
0 (| | 0) 0 (others)
解：
1）已知变换对： (t) 1 ，根据对称性有1 2 ( ) ，再根据频移性质有，

信号与系统课后答案第三章作业答案

信号与系统课后答案第三章作业答案

初始为 0， C2 -4
y f (t) -4e3tu(t) 4e2tu(t)
全响应= yx (t)+y f (t) 4e2tu(t)-2e3tu(t)
3-2 描述某 LTI 系统的微分方程为
d2 y(t) dt 2

3dy(t) dt来自2y(t)

df (t) dt

6
1
1
(2e1 e1 et ) u(t)
e1(2 et ) u(t)
（2）
f
(t)

a[u(t
s) 2

u(t
2)]
h(t) b[u(t 2) u(t 3)]
f
(t)

h(t)

ab[(t

1 2
)
u(t
1 2
)

(t

1 2
)
u(t
1) 2

tu(t)

1 4
(et

e3t
)u(t)

1 2
t
e3tu(t)

[
1 4
et

(
1 2
t

1 4
)e3t
]u
(t)
3-19 一 个 LTI 系 统 ， 初 始 状 态 不 祥 。 当 激 励 为 f (t) 时 其 全 响 应 为
(2e3t sin 2t)u(t) ；当激励为 2 f (t) 时其全响应为 (e3t 2sin 2t)u(t) 。求
（1） 初始状态不变，当激励为 f (t 1) 时的全响应，并求出零输入相应、
零状态响应； （2） 初始状态是原来的两倍、激励为 2 f (t) 时系统的全响应。

信号与系统第三章习题答案

信号与系统第三章习题答案

d (t - 1) « e- jw
\ e-2( t -1)d (t - 1) « e- jw
(8) U (t ) - U (t - 3) Q 根据傅里叶变换的线性性质可得： 1 U (t ) « p d (w ) + jw 1 U (t - 3) « e - j 3w (p d (w ) + ) jw \ U (t ) - U (t - 3) « ( 1- e - j 3w )(p d (w ) + 1 ) jw
U (t - 1) « e - jw (pd (w ) +
t 1 U ( - 1) « 2e - j 2w (pd (2w ) + ) 2 j 2w Q d (aw ) = 1 d (w ) a
\ 2e- j 2wpd (2w ) = 2pd (2w )w =0 = pd (w ) \ 2e - j 2w (pd (2w ) +
e - jtd (t - 2 ) « e - j 2(w +1)
(6) e -2( t -1)d (t - 1) Q 根据傅里叶变换的性质 f (t ± t0 ) « e ± jwt0 F ( jw ) 可得： e -2( t -1)d (t - 1) = d (t - 1) d (t ) « 1 (t = 1)
d F ( jw ) - 2 F ( jw ) dw
y ''(t ) + 4 y '(t ) + 3 y (t ) = f (t ) y ''(t ) + 5 y '(t ) + 6 y (t ) = f '(t ) + f (t )
（1） 求系统的频率响应 H（jw）和冲激响应 h（t） ； （2） 若激励 f (t ) = e-2tU (t ) ，求系统的零状态响应 y f (t ) 。 解： 方程 1：

信号与系统王明泉科学出版社第三章习题解答

信号与系统王明泉科学出版社第三章习题解答
证明:有题知, （式中 ）
左右对t求导，得:
显然， 的指数傅里叶级数为 （式中 ）
3.9求题图3.9所示各信号的傅里叶变换。
题图3.9
解：根据定义
3.10计算下列每个信号的傅里叶变换。
（1） ；（2） ；
（3） ；（4）
（5） ；（6）
解: (1)
(2)
(3)由于
根据卷积乘积性质，得
(4)由于
所以
（5） ,设
第3章傅里叶变换与连续系统的频域分析
3.6本章习题全解
3.1证明函数集 在区间 内是正交函数集。
证明:对任意的自然数n,m (n m),有
=0
证毕
3.2一个由正弦信号合成的信号由下面的等式给出：
（1）画出这个信号的频谱图，表明每个频率成分的复数值。对于每个频率的复振幅，将其实部和虚部分开或者将其幅度和相位分开来画。
图3-19-3
3.21用傅里叶变换法求题图3.21所示周期信号 的傅里叶级数。
题图3.21
解:对x(t)一个周期信号x0(t)的傅里叶变换为
X0(j )=
=
傅里叶级数
3.22求题图3.22所示周期性冲激信号的频谱函数。
题图321-1
3.23已知 的幅频与相频特性如题图3.23所示，求其傅里叶逆变换 。
（a）（b）
题图3.12
解：令傅里叶变换对 ，
（1）根据已知图形可知：
，
已知有
所以
根据傅里叶变换的微积分性质
所以
即
（2） ，
根据（1）的结论得
根据傅里叶变换的微积分性质
所以
即
3.13利用傅里叶变换的对称性求下列信号的频谱函数。
(1) ；(2) ；

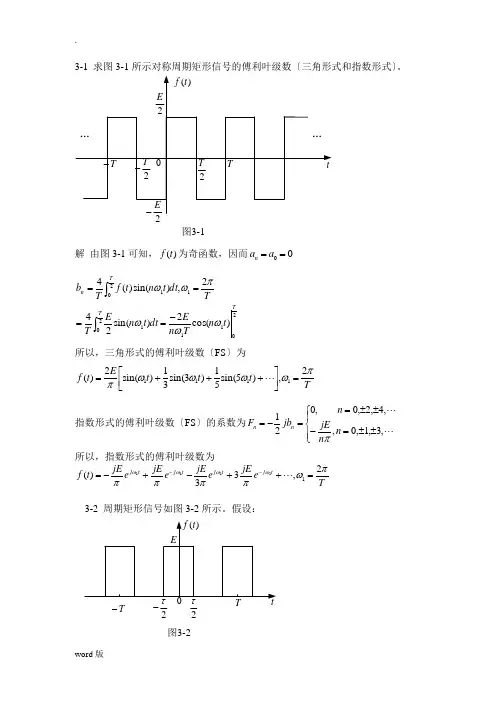
信号与系统课后习题与解答第三章

信号与系统课后习题与解答第三章

3-1 求图3-1所示对称周期矩形信号的傅利叶级数〔三角形式和指数形式〕。

图3-1解 由图3-1可知，)(t f 为奇函数，因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以，三角形式的傅利叶级数〔FS 〕为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数〔FS 〕的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以，指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。

假设：图3-22T-2-重复频率kHz f 5= 脉宽s μτ20=幅度V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。

解 对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数〔FS 〕的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n那么的指数形式的傅利叶级数〔FS 〕为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入，可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 假设周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1= ，V E 1=； )(2t f 的参数为s μτ5.1=，s T μ3= ，V E 3=，分别求：〔1〕)(1t f 的谱线间隔和带宽〔第一零点位置〕，频率单位以kHz 表示； 〔2〕)(2t f 的谱线间隔和带宽； 〔3〕)(1t f 与)(2t f 的基波幅度之比； 〔4〕)(1t f 基波与)(2t f 三次谐波幅度之比。

北邮信号与系统课后答案第3章部分1

北邮信号与系统课后答案第3章部分1

为功率信号
（d） P lim 1 T0 u t 2 dt lim 1 T0 1dt 1
T0
2T0 T0
T0 2T0 0
2
为功率信号。
【知识点】能量信号、功率信号 3-3 对信号 f (t) 在数值和时间两方面进行运算变成 af (bt)
（1）如果在全部时间
t
内， f (t) 是具有能量为 W 的能量信号，
f1 t 1
f2 t 1
0
1
2
3t
0
1
2
3t
锯齿形脉冲
正弦脉冲
题 3-6 图
解：
3
0 f1 t f2 t d t
31 t sin
tdt
- t cos
t - 3 sin
3
t
03 3
3
2 30
3
3
sin
2
tdt
31 1 - cos 2 t d t 3
03
02
3
2
C12 2
t2
fe t
- sin t
3
3
3 t - 2 sin t sin tdt
sin 2
1t
4
3 cos 2 1 t 4
15 cos 4 1 t 4
...
2
A 1 T A
sin 2
1t
2
2A 3 cos 2 1t
2A 15 cos 4 1t 2 ...
AA
2A
2A
cos 2
1t
3 cos 2 1t
15 cos 4 1t
...
9
随着T ， C12 ，当T
时使得 C12 0 。

信号与系统课程习题与解答

信号与系统课程习题与解答

《信号与系统》课程习题与解答第三章习题(教材上册第三章p160-p172)3-1～3-3,3-5,3-9,3-12,3-13,3-15～3-17,3-19,3-22,3-24,3-25,3-29,3-32第三章习题解答3-2 周期矩形信号如题图3-2所示。

若：求直流分量大小以及基波、二次和三次谐波的有效值。

解：直流分量⎰⎰--=⨯==2222301105)(1ττv Edt dt t f T a TTf(t)为偶函数，∴0=n b)(2cos )(222T n Sa T E tdt n t f T a n πττωττ⎰-==)(21T n Sa T E a F n n πςτ== 基波 =1a )1.0s i n (20)(2πππττ=T Sa T E有效值 39.11.0sin 22021≈=ππa二次谐波有效值 32.122≈a三次谐波有效值 21.123≈a3-3 若周期矩形信号)(1t f 和 )(2t f 波形如题图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1=，E=1V ；)(2t f 的参数为s μτ5.1=，s T μ3=，E=3V ，分别求：（1）)(1t f 的谱线间隔和带宽（第一零点位置），频率单位以kHz 表示； （2）)(2t f 的谱线间隔和带宽； （3） )(1t f 和 )(2t f 的基波幅度之比； （4） )(1t f 基波与)(2t f 三次谐波幅度之比。

解：（1）)(1t f s μτ5.0= s T μ1= E=1V 谱线间隔：khZ T 10001==∆带宽：KHzB f 20001==τ(2) )(2t f s μτ5.1= s T μ3= E=3V间隔：khZ T 310001==∆谱线带宽：KHzB f 320001==τ(3) )(1t f 基波幅度：ππτ2)2cos(4201==⎰dt t T E T a )(2t f 基波幅度：ππτ6)2cos(4201==⎰dt t T E T a幅度比：1：3（4） )(2t f 三次谐波幅度：ππτ2)23cos(4203-=⨯=⎰dt t T E T a 幅度比：1：13-5 求题图3-5所示半波余弦信号的傅立叶级数。

信号与系统第3章习题和重点

信号与系统第3章习题和重点

ZB
3-26
已知 f (t) = f1(t) + f2(t)的频谱密度函数 F(ω) = 4Sa(ω) − j
4
ω
，
为偶函数， 为奇函数， 且 f1(t)为偶函数， f2(t)为奇函数，试求 f1(t)和 f2(t) 。 解：由题意知
f1(t) ↔4Sa(ω) = AτSa( 2 ∴f1(t) = 2g2(t)
F = n 1 T 1 T
∫ ∫
3T 4 T 4
f (t)e− jnω0tdt
L − 2 L 2 2 2 −2T −T 0 T 2T t
() 1
− jnω0 T 2 ) = 1 (1−e− jnπ )
−
=
T 1 δ (t) −δ (t − )e− jnω0tdt = (1−e T 2 T − 4
0
T
ZB
3-4 已知周期信号 f (t)的前四分之一周期的波形如图所 且其余每一段四分之一周期的波形要与之相同， 示，且其余每一段四分之一周期的波形要与之相同，试 整个周期的波形。 就下列情况分别画出 f (t)整个周期的波形。 为偶函数， 解：(1) f (t)为偶函数，且只含偶次谐波
f (t)
∞
F(ω) =
∫ = e e ∫
=
−∞ 0 2t − jωt
e2tε(−t)e− jωtdt dt
−∞ (2− jω)t 0 e
2 − jω −∞
ZB
1 = 2 − jω 《信号与系统》SIGNALS AND SYSTEMS
3-19 设 f (t) ↔F(ω) ，试证： 试证： （1） ∫ ∞ f (t)dt = F(0) ） −
解： (2) 为非周期信号 T →∞

[信号与系统作业解答]第三章

[信号与系统作业解答]第三章

3-4 求下图所示周期三角信号的傅里叶级数（三角形式）。
解：从图中可知，周期信号的在[ T / 2,T / 2] 的表达式为
f (t)
2E T
t,
0
t
T /2
2E T
t
T /2 t 0
周期为T ，基频 0
2 T。
1）三角形式的傅里叶级数
f (t) a0
[an cos(n 0t) bn sin(n 0t)]
解：
f (t)cos( 0t)
F1( )
1 2
[F(
0) F(
0 )]
f (t)e j 0t F2( ) F(
0)
f (t)cos( 1t)
F3( )
1 2
[F(
1) F(
1)]
3-39 确定下列信号的最低抽样率与奈奎斯特间隔。
（1） Sa(100t )
（3）Sa(100t) Sa(50t)
解：（1）因为Sa(100t) 50G200( ) ，最高频率为 m 100 rad / s ，所以最低抽样
所以
F [fo(t)] 1 [F( ) 2
1 2F
[f (t)
F *( )]
f *( t)] j Im[F( )]
（2）因为 fr (t)
1 2
[f
(t)
f *(t)] ，
所以
F [fr (t)]
1 2F
[f (t)
f *(t)]
1 [F( ) F *( 2
)]
同样的， fi (t)
1 [f (t) 2j
1因为20010050sa最高频率为100所以最低抽样频率为2002又因为另一个分量1005025sa最高频率为100所以最低抽样频率为200341系统如图所示求最大抽样间隔max100020003000300030001000200010001000300010003000波形如下图所示可知的最高频率为3000要进行无失真的恢复则最低抽样频率为min6000对应的最大抽样间隔为maxmin波形如下图所示其中

信号与系统第三章习题部分参考答案

信号与系统第三章习题部分参考答案

↔ 2π e−a⎜−ω⎜
（4）单边指数信号 ∵ e−atu(t) ↔ 1 a + jw
∴ 1 ↔ 2π e−a(−w)u(−w) a + jt
即 1 ↔ 2π eawu(−w) a + jt
3.20 求下列各傅里叶变换的原函数
（1） F (ω) = δ (ω − ω0 ) （2） F (ω) = u(ω + ω0 ) − u(ω − ω0 )；
2π
（2）[1 + mf (t)]cos(w0t) = cos(w0t) + mf (t) cos(w0 (t)
↔
π [δ
(w
+
w0
)
+
δ
(w
−
w0
)]
+
m 2
{F[
j(w
+
w0
)
+
F[
j(w
−
w0
)]}
（3） f (6 − 3t) = f [−3(t − 2)] ↔ 1 F (− 1 jw)e− j2w
−τ τ
w
方法二 利用时域微分性质
对 f(t)求一阶导数得到
f
′(t)
=
1 τ
G2τ
(t)
−
δ
(t
+
τ
)
−
δ
(t
−
δ
)
F1 (w) = 2sa(wτ ) − 2 cos(wτ )
F1 (0) = 0
F (w) =
F1 (w) jw
+
πF1
(0)δ
(w)
=
j
2 [cos(wτ ) − sa(wτ )] w

信号与系统答案西北工业大学段哲民信号与系统1_3章答案

信号与系统答案西北工业大学段哲民信号与系统1_3章答案

第一章 习 题1-1 画出下列各信号的波形：(1) f 1(t)=(2-e -t )U(t); (2) f 2(t)=e -t cos10πt×[U(t -1)-U(t-2)]。

答案（1）)(1t f 的波形如图1.1（a ）所示.(2) 因t π10cos 的周期s T 2.0102==ππ,故)(2t f 的波形如图题1.1(b)所示.1-2 已知各信号的波形如图题1-2所示，试写出它们各自的函数式。

答案)1()]1()([)(1-+--=t u t u t u t t f)]1()()[1()(2----=t u t u t t f)]3()2()[2()(3----=t u t u t t f1-3 写出图题1-3所示各信号的函数表达式。

答案2002121)2(21121)2(21)(1≤≤≤≤-⎪⎩⎪⎨⎧+-=+-+=+=t t t t t t t f)2()1()()(2--+=t u t u t u t f)]2()2([2sin )(3--+-=t u t u t t f π)3(2)2(4)1(3)1(2)2()(4-+---++-+=t u t u t u t u t u t f1-4 画出下列各信号的波形：(1) f 1(t)=U(t 2-1); (2) f 2(t)=(t-1)U(t 2-1);(3) f 3(t)=U(t 2-5t+6); (4)f 4(t)=U(sinπt)。

答案(1) )1()1()(1--+-=t u t u t f ,其波形如图题1.4(a)所示.(2))1()1()1()1()]1()1()[1()(2---+--=--+--=t u t t u t t u t u t t f 其波形如图题1.4(b)所示.(3))3()2()(3-++-=t u t u t f ,其波形如图1.4(c)所示.(4) )(sin )(4t u t f π=的波形如图题1.4(d)所示.1-5 判断下列各信号是否为周期信号，若是周期信号，求其周期T 。

郑君里信号与系统习题答案

郑君里信号与系统习题答案

郑君⾥信号与系统习题答案第三章傅⾥叶变换⼀.周期信号的傅⾥叶级数⼆.傅⾥叶变换例题例题1：傅⾥叶级数——频谱图 ?例题2：傅⾥叶变换的性质 ?例题3：傅⾥叶变换的定义 ?例题4：傅⾥叶变换的性质 ?例题5：傅⾥叶变换的性质 ?例题6：傅⾥叶变换的性质例题7：傅⾥叶变换的性质、频响特性 ?例题8：傅⾥叶变换的性质 ?例题9：抽样定理–例题10：周期信号的傅⾥叶变换例3-1 周期信号 1. 画出单边幅度谱和相位谱；()?--??? ??++=328cos 265sin cos 3ππt t t t f 形式频谱：离散性、谐波性、收敛性周期矩形脉冲信号的频谱特点定义及傅⾥叶变换存在的条件典型⾮周期信号的频谱冲激函数和阶跃信号的傅⾥叶变换性质→应⽤：调制和解调→频分复⽤周期信号的傅⾥叶变换：由⼀些冲激函数组成抽样信号的傅⾥叶变换→抽样定理→应⽤：时分复⽤2. 画出双边幅度谱和相位谱。

双边幅度谱和相位谱例3-2 分析：f (t )不满⾜绝对可积条件，故⽆法⽤定义求其傅⾥叶变换，只能利⽤已知典型信号的傅⾥叶变换和性质求解。

下⾯⽤三种⽅法求解此题。

⽅法⼀：利⽤傅⾥叶变换的微分性质⽅法⼆：利⽤傅⾥叶变换的积分性质⽅法三：线性性质⽅法⼀：利⽤傅⾥叶变换的微分性质要注意直流，设f A(t )为交流分量，f D(t )为直流分量，则其中()?+-+? -++=ππππ328cos 2265cos cos 3t t t t f ?++??? ??-+=38cos 2315cos cos 3ππt t t()。

的傅⾥叶变换求信号 )(ωF t f ()()()t f t f t f D A +=()()()ωωωD A F F F +=()()()[]2321=∞+∞-=f f t f D ()()ωπδω3=D F ()()t f t f A'='()??? ??-='211t G t f A ()ωωωωj Ae F j -??=∴2Sa⽅法⼆：利⽤傅⾥叶变换的积分性质⽅法三：利⽤线性性质进⾏分解此信号也可以利⽤线性性质进⾏分解，例如例3-3已知信号f (t )波形如下，其频谱密度为F (j ω)，不必求出F (j ω)的表达式，试计算下列值：()ωωωωj e F j A -??=∴2Sa ()()()()ωπδωωωωωω32Sa +??? ??=+=∴-j e F F F j D为)()(21t f t f ()ωωωj e F -??? ??=2Sa 2()()()ωωωπωωωπωωωj e e j F j j --??? ??+=??? ???+=∴2Sa 2Sa 11 ()[]()()ωωωπδωωωj e F F F j -??? ??+=+=∴2Sa 311()[])1(2)1()()1()(-+--++-=t u t u t u t t u t f ()ωωπδj 1-()2121ωωωωωj e e j j j j ---+-()ωωωπδj e j -+22()()()ωπδωωω312+-=∴-j e F j ()()01=ωωF ()()?∞∞-ωωd 2F -t tj d ω(()?∞-====∴5.1d 00t t f F F ωω令t =0，则则例3-4按反褶－尺度－时移次序求解已知⽅法⼆：按反褶－时移－尺度次序求解已知⽅法三利⽤傅⾥叶变换的性质其它⽅法⾃⼰练习。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三章习题基础题3.1 证明cos t , cos(2)t , …, cos()nt (n 为正整数)，在区间(0,2)π的正交集。

它是否是完备集?解：(积分???)此含数集在(0,2)π为正交集。

又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰，对于所有的m 和n 。

由完备正交函数定义所以此函数集不完备。

3.2 上题的含数集在(0,)π是否为正交集？解：由此可知此含数集在区间(0,)π内是正交的。

3.3实周期信号()f t 在区间(,)22T T-内的能量定义为222()TT E f t dt -=⎰。

如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-内相互正交，证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的，求和信号的总能量。

解：(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰（少乘以2）由1()f t 与2()f t 在区间内正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。

和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰（少乘以2吧？）由1()f t 与2()f t 在区间(,)22T T-内不正交可得2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。

3.4 求下列周期信号的基波角频率Ω和周期T 。

（1）100j te（2） ]2/)3(cos[-t π（3）)4sin()2cos(t t + （4）cos(2)cos(3)cos(5)t t t πππ++（5）)4/sin()2/cos(t t ππ+ （6） )5/cos()3/cos()2/cos(t t t πππ++解：(1)角频率为Ω＝100rad s ，周期22100T s ππ==Ω (2)角频率为2rad s πΩ=，周期42T s π==(3)角频率为2rad s πΩ=，周期2T s ππ==Ω（先求T ，后求omg 吧？） (4)角频率为rad s πΩ=，周期22T s π==Ω(5)角频率为4rad s πΩ=，周期28T s π==Ω(6)角频率为30radsπΩ=，周期260T sπ==Ω3.5 用直接计算傅里叶系数的方法，求图示周期函数的傅里叶系数（三角形式或指数形式）。

解：(1)周期T=4,2TπΩ=2π=，则有1, 4k-1 t 4k+1f(t)=0, 4k+1 t 4k+3⎧⎨⎩（k是整数；怎么求的边界条件？）由此可得222()cos()()TTna f t n t d tT-=Ω⎰221()cos()22n tf t dtπ-=⎰111cos()22ntdtπ-=⎰2sin(),0,1,2,2nnnππ==22221()sin()()()sin()22TTnn tb f t n t d t f t dtπ--=Ω=⎰⎰111sin()0,1,2,22n tdtnπ-==⎰（X？）(2)周期T=2，2Tπππ==，则有sin(),221()0,2122t k t kf tk t kπ≤≤+⎧=⎨+<<+⎩由此可得：1121022111()()()sin()221,0,1,2,2(1)Tjn t jn t jn tTnnjn tF f t e d t f t e dt t e dtTennππ-Ω-Ω-Ω---Ω===+==±±-⎰⎰⎰（积分？3.6如图所示是4个周期相同的信号(1)用直接求傅里叶系数的方法求图（a ）所示信号的傅里叶级数（三角形式）； (2)将图（a ）的函数1()f t 左（或右）移，就得图（b ）的函数2()f t ，利用(1)的结果求2()f t 的傅里叶级数；(3)利用以上结果求图（c ）的函数3()f t 的傅里叶级数； (4)利用以上结果求图（d ）的信号4()f t 的傅里叶级数；解：(1)由1()f t 的波形可知12,2()0,2T t kT t kT T f t T kT t kT T ⎧≤≤+⎪⎪=⎨⎪+<<+⎪⎩ 令2T πΩ=，则有220212112121211222cos()sin()sin(),1,2,1cos()1cos()()cos()sin()4()()()()()2211cos()1cos()sin()4()T TT n n n n n n b n t dt t n t dt n T T T n n n f t n t n t n n T Tf t f t f t f t n n t n t n n πππππππππ-∞∞==∞∞===Ω=Ω=-=-=+Ω-Ω=+=--=+Ω-Ω⎰⎰∑∑∑∑2210222cos()()cos()T TT n a n t f t dt n t dtT T -=Ω=Ω⎰⎰2cos()1,1,2,()n n n ππ-==22102222sin()()sin()cos(),1,2,T T T n b n t f t dt t n t dtT T T n n n ππ-=Ω=Ω=-=⎰⎰则1()f t 的傅里叶级数为12111cos()1cos()()cos()sin()4()n n n n f t n t n t n n ππππ∞∞==-=+Ω-Ω∑∑(2)由2()f t 和1()f t 的波形图可知21()()2T f t f t =+或21()()2Tf t f t =- 则2()f t 的傅里叶数为21()()2Tf t f t =+2111cos()1cos()cos ()sin ()4()22n n n T n T n t n t n n ππππ∞∞==-⎡⎤⎡⎤=+Ω+-Ω+⎢⎥⎢⎥⎣⎦⎣⎦∑∑ 2111cos()1cos()cos()sin()4()n n n n n t n n t n n n ππππππ∞∞==-=+Ω+-Ω+∑∑ 2111cos()1cos()cos()cos()cos()sin()4()n n n n n n t n n t n n ππππππ∞∞==-=+Ω-Ω∑∑21111cos()1cos()sin()4()n n n n t n t n n πππ∞∞==-=+-Ω--Ω∑∑(3)由3()f t 的波形可知32()()f t f t =-则3()f t 的傅里叶级数为32()()f t f t =-21111cos()1cos()sin()4()n n n n t n t n n πππ∞∞==-=+-Ω--Ω∑∑ 21111cos()1cos()sin()4()n n n n t n t n n πππ∞∞==-=+Ω+Ω∑∑(4)有4()f t 的波形可知423()()()f t f t f t =+则4()f t 的傅里叶级数为[]4232121cos()1()()()cos()2()n n f t f t f t n t n ππ∞=-=+=+Ω∑3.7试画出图示信号的奇分量和偶分量解：（1）由1()f t 的波形求得1()f t -的波形 则奇分量的波形为()od f t =11()()2f t f t --偶分量的波形为()ed f t =11()()2f t f t +-（2）由2()f t 的波形求得2()f t -的波形 则奇分量的波形为()od f t =11()()2f t f t --偶分量的波形为()ed f t =11()()2f t f t +-3.8利用奇偶性判断图示各周期信号的傅里叶级数中所含有的频率分量。

解：（1） 由1()f t 的波形可知1()f t =1()f t -=1()2tf t -±则有 24()cos()t n a f t n t dt t =Ω⎰ ,0,1,2,n =…0n b =0242460a a a b b b ========……则1()f t 的傅里叶级数中含有的频率分量为奇次余弦波。

（2） 由2()f t 的波形可知 22()()f t f t =-- 则有 0n a =24()sin(),0,1,2,t n b f t n t dt n t =Ω=⎰…则2()f t 的傅里叶级数中含有的频率分量为正弦波。

（3） 由3()f t 的波形可知33()()f t f t =-则有 0n b =24()cos(),0,1,2,t n a f t n t dt n t =Ω=⎰…即3()f t 的傅里叶级数中含有的频率分量为奇次余弦波。

（4） 由4()f t 的波形可知，4()f t 为奇谐函数，即44()()2tf t f t =-±则有 0242460a a a b b b ========……即4()f t 的傅里叶级数中只含有奇次谐波，包括正弦波和余弦波。

3.9 如图的周期性方波电压作用于RL 电路，试求电流()i t 的前五次谐波。

解：由()s u t 的波形图可知周期22,1T Tππ=Ω==，则有 1,2222()30,2222{s k t k u t k t k ππππππππ-≤≤+=+≤≤+由此可得傅立叶级数的系数 222()cos()Tn s Ta u t n t dt T -=Ω⎰1()cos()su t nt dt πππ-=⎰221cos()nt dt πππ-=⎰ 221021,2,sin()2{n dt n n n πππππ-=====⎰时， a 0时，a n因()s u t 为偶数，则0,1,2,n b n ==则电路激励()s u t 的前五次谐波为5011222()cos(5)cos cos(3)cos(5)2235s n nau t a t t t t πππ==+=+-+∑ 由电路得系统微分方程为'()()()s i t i t u t +=欲求电流()i t 的前五次谐波，即求此微分方程激励的前五次谐波的特解。