北京市朝阳区2010年中考一模数学试题(扫描版,含答案)
- 格式:doc
- 大小:734.50 KB
- 文档页数:12
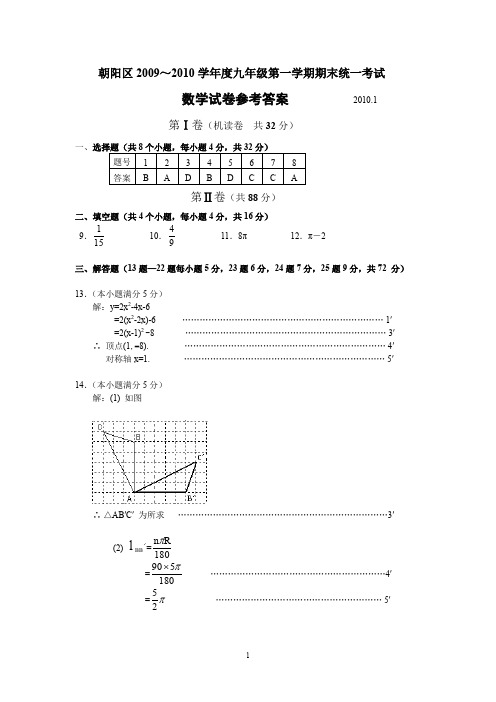
朝阳区2009~2010学年度九年级第一学期期末统一考试数学试卷参考答案 2010.1第Ⅰ卷(机读卷 共32分)一、第Ⅱ卷(共88分)二、填空题(共4个小题,每小题4分,共16分)9.151 10.94 11.8π 12.π-2三、解答题(13题—22题每小题5分,23题6分,24题7分,25题9分,共72 分)13.(本小题满分5分)解:y=2x 2-4x-6=2(x 2-2x)-6 …………………………………………………………… 1′ =2(x-1)2 -8 …………………………………………………………… 3′ ∴ 顶点(1,-8). …………………………………………………………… 4′ 对称轴x=1. …………………………………………………………… 5′14.(本小题满分5分)解:(1) 如图∴ △AB′C′ 为所求 ………………………………………………………………3′(2) l BB =180R n π=180590π⨯ ……………………………………………………4′ =π25 ………………………………………………… 5′15.(本小题满分5分)解:∵ CD ⊥AD ,EB ⊥AD ,∴ EB ∥CD.∴ △ABE ∽△ADC . …………………………………………………2′ ∴ AD AB CD EB =. …………………………………………………3′ ∵ EB=2,AB=3,AD=21,∴ 213CD 2=. ∴ CD=14.答:此树高为14米. ………………………………………………………5′16.(本小题满分5分)解:列表或树形图图略. ………………………………………………………3′ P=41 ………………………………………………………5′17.(本小题满分5分)解:(1) 由图可知,抛物线①经过点(2,0),且顶点是(1,-1) .可设抛物线①的解析式为 y =a (x-1)2-1,∴ a (2-1)2-1=0解得 a =1. …………………………………………………2′ ∴ 抛物线①的解析式为 y = (x-1)2-1.………………………………………3′ ∵ 抛物线②是由抛物线①平移后得到的,且顶点为坐标原点,∴ 抛物线②的解析式为 y = x 2. ………………………………………4′(2) ∵ 抛物线①的对称轴x=1,∴ 当x=1时,y=1.∴ 点A 的坐标为A(1,1). …………………………………………………5′18.(本小题满分5分)解:作直径CD ,连接BD , ………………………………1′∴ ∠CBD=90°. …………………………………… 2′∵ ∠A=30°,∴ ∠D=30°. ……………………………………… 3′∴ BC=21CD . ……………………………………… 4′ ∵ CD=4,∴ BC=2. …………………………………………… 5′19.(本小题满分5分)解:连接OB ,∵ △ABC 内接于⊙O ,AD=5,∴ OB=OA=5. ………………………………………………… 1′∵ ∠ADB =90°,BC=8,∴ BD=BC 21= 4.……………………………………………………………3′∴ OD=22BD OB -=3. …………………………………4′∴ AD=AO+OD=8.∴ S △ABC =AD BC ⨯21 =32. ……………………………… 5′20.(本小题满分5分)解:做CD ⊥AB 于点D , …………………………1′由题意可知,∠CAB=30°,∠CBD=60°,∴ ∠ACB=∠BCD=30°.∴ AB=CB=8. ………………………………2′在Rt △CDB 中,∵∠CDB=90°,∠CBD=60°,∴ ∠BCD=30°,BD = 4. ……………………………………………3′由勾股定理得,CD=34 ……………………………………………4′≈6.928>5.∴船继续向东航行无触礁危险. ………………………………………5′21.(本小题满分5分)解:设△BOA 的内切圆⊙M 与OA 、OB 、AB 分别切于点D 、E 、F ,且半径为x .…… 1′∵ ∠AOB= 90°,OA=3,OB=4,∴ AB=5. …………………………… 2′∴ OD=OE=MD=ME=x ,BE=BF=4-x , AD=AF=3-x .…………………………… 3′∴ (4-x)+(3-x)=5 .解得 x=1. ……………………………………4′∴ d+AB=2+5=7. ……………………………………5′22.(本小题满分5分)证明:(1)连接OE ,∵ EF=AF , ∴ ∠A=∠AEF .∵ OE=OB ,∴ ∠OEB=∠OBE .…………………………………… 1′∵ ∠C=90°,∴ ∠A+∠ABC=90°.∴ ∠AEF+∠OEB=90°.∴ ∠FEO=90°. ………………………………………2′∵ OE 是⊙O 半径,∴ EF 是⊙O 的切线. ………………………………3′解:(2) ∵∠C=90°,BC=12,AC=9,∴ AB=15.∵ BD 是直径,∴∠DEB=90°.∴ ∠DEB=∠C .∵ ∠B=∠B ,∴ △DEB ∽△ACB . …………………………………………………………… 4′ ∴ ACDE AB BD =. ∴ 9159DE =,527=DE . ……………………………………………………… 5′23.(本小题满分6分)解:(1) 当-3<x <1时,y 的值大于0; ………………………………………… 2′(2) 当x <-1时,y 随x 的增大而增大; …………………………………… 4′(3) 由图可知,二次函数y=ax 2+bx+c (a≠0)的图象与x 轴交于点(-3,0),与y 轴交于点(0,1.5),对称轴为x=1.由抛物线的对称性可知抛物线y=ax 2+bx+c (a≠0)与x 轴的另一个交点为(1,0) .∴ 可列方程组为⎩⎨⎧=++=+-.05.1,05.139b a b a 解得 ,121⎪⎩⎪⎨⎧-=-=.b a ∴ 解析式为.23212+--=x x y ……………………………………………… 5′ ∵ ax 2+bx+c =k , ∴ ax 2+bx+c -k =0.∵ 方程ax 2+bx+c =k 有两个不相等的实数根, ∴ )(42k c a b -->0. 即 (-1)2 -4×0)23)(21(>--k . 解得 k <2. ………………………………………………………………… 6′24.(本小题满分7分)解:(1)已知抛物线y 1=-x 2+bx+c 经过点A(1,0), B(0,-2),∴ 01b c,200 c.=-++⎧⎨-=++⎩ 解得 b 3,c 2.=⎧⎨=-⎩ ∴ 所求抛物线的解析式为y 1=-x 2 +3x-2 .…………………………… 2′(2)解法1: ∵ A(1,0),B(0,-2), ∴ OA=1,OB=2.由旋转性质可得O′A=O A=1,O′B′=OB=2.∴ B′ 点的坐标为 (3,-1) .∵ 抛物线y 1的顶点D (32,14),且抛物线y 2 是由y 1沿对称轴平移后得到的,∴ 可设y 2 的解析式为y 2= - (x -32)2 +k . ∵ y 2经过点B′,∴ - (3 -32)2 +k= -1.解得k=54. ∴ y 2= - (x -32)2 +54. …………………………………………………………… 4′ 解法2:同解法1 得B′ 点的坐标为 (3,-1) .∵ 当x=3时,由y 1=-x 2 +3x-2得y=-2,可知抛物线y 1过点 (3,-2) .∴ 将抛物线y 1沿y 轴向上平移1个单位后过点B′.∴ 平移后的抛物线y 2的解析式为:y 2=-x 2 +3x-1 . …………………………… 4′(3)∵ y 1=-x 2+3x-2 = -(x-32)2 +14,y 2=-x 2 +3x-1= -(x-32)2 +54, ∴ 顶点D (32,14),D 1(32,54). ∴ DD 1=1. 又B 1(0,-2),B 1(0,-1),∴ BB 1=1.设M 点坐标为(m ,n) ,∵ BB 1=DD 1,由11MBB MDD S 2S ∆∆=,可知当m≤0时,符合条件的M 点不存在; …………………………………… 5′ 而当0<m<32时,有m=2(32-m),解得m=1; 当m>32时,有m=2(m -32),解得m=3. 当m=1时,n=1; 当m=3时,n=-1.∴ M 1(1,1),M 2 (3,-1).…………………………………………………………… 7′25.(本小题满分9分)(1)答:OD=OE .证明:连结OC (如图).∵ AB 为⊙O 直径,∴ ∠ACB =90°.∵ AC=BC ,∴△ACB 是等腰直角三角形.∵ AO =BO ,∴ CO ⊥AB ,∠ACO =21∠ACB =45°. ∴ ∠ACO =∠B =45°.又 ∠DOC +∠COE =∠BOE +∠EOC =90°,∴ ∠DOC =∠BOE .∵ OC=OB ,∴ △OCD ≌△OBE .∴ OD =OE . ………………………………2′(2)共有四种情况,① 当点C 与点E 重合,即CE =0时,OE =OB ;② 当点E 为CB 中点,即CE =1时,OE =BE ;③ 当点E 在线段CB 上,且CE =2时,OB =EB ;④当E在CB的延长线上,且CE=2时,OB=EB.……………………6′(3)答:MD∶ME=1∶3 .证明:分别过点M作MF⊥AC、MH⊥BC,垂足分别是F、H.(如图)∵∠A=∠B=45°, ∴ Rt△AFM∽Rt△BHM.∴FM AM1 HM BM3==.∵∠C=90°,∴∠FMH=90°.∴∠FMD+∠DMH=∠EMH+∠HMD=90°.∴∠FMD=∠EMH.∴ Rt△FMD∽Rt△HME.∴MD MF1ME HM3==.……………………………………………………………9′(说明:以上答案仅供参考,若有不同解法,只要过程和解法都正确,可相应给分)。

崇文区2009-2010学年度第二学期初三统一练习(一)2010.5英语试卷第一部分听力理解(共24分)一、听对话,选择与对话内容相符的图片。
每段对话读两遍。
(共4分,每小题1分)1. A. B. C.2. A. B. C.3. A. B. C.4. A. B. C.二、听对话或独白,根据对话或独白的内容,选择正确答案。
每段对话或独白读两遍。
(共12分,每小题1分)请听一段对话,回答第5至6小题。
5. What is Bob reading?A. A letterB. A bookC. A newspaper6. Where will Bob study in the future?A. In EnglandB. In ChinaC. In America请听一段对话,回答第7至8小题。
7. Where does the man want to go?A. To a cinema.B. To a theatreC. To a library8. How long will it take the man to get there by bus?A. 20 minutes.B. 30 minutes.C. 60 minutes.请听一段对话,回答第9至10小题。
9. What is Mr. White doing at the moment?A. He is sleeping.B. He is having lunch.C.He is having a meeting.10. What will the man tell Mr White to do?A.To visit a friend.B.To call back.C. To go home.请听一段对话,回答第11至13小题。
11. What does the man want to buy?A. A pair of glasses.B. A pair of trousers.C. A pair of shoes.12. What’s the size?A. Size 6.B. Size 7.C. Size 8.13. How much will the man pay?A. 50 dollars.B. 25 dollars.C.15 dollars.请听一段独白,回答第14至16小题。

2010年北京市朝阳区初三数学二模试题及答案2010年朝阳区初三二模数学试题2010.6第Ⅰ卷(选择题32分)一、选择题(共8个小题,每小题4分,共32分) 1.6的倒数是A .-6B .±61C .61- D .61 2.全球可被人类利用的淡水总量仅占地球上总水量的0.00003,因此珍惜水、保护水,是我们每一位公民义不容辞的责任.其中数字0.00003用科学记数法表示为A .4103-⨯ B .5103-⨯ C .4103.0-⨯D .5103.0-⨯3.已知()2b 3a 2=++-,则ab 等于A .-6B .6C .-1D .14.某校抽取九年级的7名男生进行了1次体能测试,其成绩分别为75,90,85, 75,85,95,75,(单位:分)这次测试成绩的众数和中位数分别是 A .85,75 B .75,80 C .75,85 D .75,755.若一个多边形的内角和是外角和的2倍,则这个多边形的边数是A .8B .6C .5D .46.已知一个圆锥的底面半径是5cm ,侧面积是65πcm 2,则圆锥的母线长是 A . 6.5 B . 13 C .15D .267.如图,△ABC 被一个矩形所截,矩形的一条边与AB 、AC 分别交于点D 、E ,另一条边与BC 在同一条直线上.如果点D 恰为AB 的三等分点,那么图中阴影部分面积是△ABC 面积的A .31 B .91 C . 94 D .95 8.已知二次函数y 1=x 2-x-2和一次函数y 2=x+1的两个交件的点P 共有______个.三、解答题(共13个小题,共72 分) 13.(本小题5分)计算: ︒+-+-60sin 223282314.(本小题5分)已知a 2+2a=4,求121111122+-+÷--+a aa a a 的值.15.(本小题5分)已知:如图,AC 与BD 相交于点O ,且OB=OC ,OA=OD . 求证:∠ABC =∠DCB .15题图16.(本小题5分)如图,是四张不透明且质地相同的数字卡片.将卡片洗匀后,背面朝上放置在桌面上.(1)求随机抽取一张卡片,恰好得到数字3的概率;(2)为能赢得一张上海世博会的门票,李明与王刚请张红做裁判,张红用以上四张卡片设计了一个方案(见右侧信息图),但李明却认为这个方案设计的不公平.请你用列表法或树形图法求出概率说明李明的说法是否正确.方案随机抽取一17.(本小题5分)如图,反比例函数xk y =(x >0)的图象过点A .(1)求反比例函数的解析式; (2)若点B 在xk y =(x >0)的图象上, 求直线AB 的解析式.18.列方程(组)解应用题(本小题5分)“五一”期间某校学生到相距学校10千米的“老年公寓”开展“献爱心”活动,部分同学骑自行车从学校出发,20分钟后另部分同学乘汽车从学校出发,结果乘汽车的同学比骑自行车的同学提前10分钟到达“老年公寓”.已知汽车速度是自行车速度的4倍,求两种车的速度各是多少?19.(本小题5分)在下面所给的图形中,若连接BC,则四边形ABCD 是矩形,四边形CBEF是平行四边形.(1)请你在图1中画出两条线段,将整个图形分为两部分,使这两部分面积相等(不写画法);(2)请你在图2中画出一条线段,将整个图形分为两部分,使这两部分面积相等.简要说明你的画法.20.(本小题5分)已知:如图, AB 是⊙O 的直径, AB=AC ,BC 交⊙O 于点D ,延长CA 交⊙O 于点F ,连接DF ,DE ⊥CF 于点E . (1)求证:DE 是⊙O 的切线;(2)若AB=10,4cos 5C ∠=,求EF 的长.21.(本小题5分)阅读下列材料,然后解答后面的问题:利用完全平方公式(a ±b)2=a 2±2ab+b 2,通过配方可对a 2+b 2进行适当的变形,如a 2+b 2= (a+b)2-2ab 或a 2+b 2= (a -b)2+2ab .从而使某些问题得到解决.例:已知a+b=5,ab=3,求a 2+b 2的值.解:a 2+b 2= (a+b)2-2ab = 52-2×3=19.问题:(1)已知6a1a =+,则22a 1a+=________;(2)已知a–b =2,ab=3,求a4+b4的值.22.(本小题5分)已知抛物线222m-=与直线xxy+mx=交点的横坐标均y2为整数,且2<m,求满足要求的m的整数值.23.(本小题7分)如图,平行四边形ABCD中,AD=8,CD=4,∠D=60°,点P与点Q是平行四边形ABCD边上的动点,点P以每秒1个单位长度的速度,从点C运动到点D,点Q以每秒2个单位长度的速度从点A→点B→点C运动.当其中一个点到达终点时,另一个点随之停止运动.点P与点Q同时出发,设运动时间为t,△CPQ的面积为S.(1)求S关于t的函数关系式;(2)求出S的最大值;(3)t为何值时,将△CPQ以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.24.(本小题7分)如图1,四边形ABCD,将顶点为A的角绕着顶点A 顺时针旋转,若角的一条边与DC的延长线交于点F,角的另一条边与CB的延长线交于点E,连接EF.(1)若四边形ABCD为正方形,当∠EAF=45°时,有EF=DF -BE.请你思考如何证明这个结论(只思考,不必写出证明过程);(2)如图2,如果在四边形ABCD中,AB=AD,1∠BAD时,EF与DF、BE ∠ABC=∠ADC=90°,当∠EAF=2之间有怎样的数量关系?请写出它们之间的关系式(只需写出结论);(3)如图3,如果四边形ABCD中,AB=AD,∠ABC与∠ADC1∠BAD时,EF与DF、BE之间有怎样的互补,当∠EAF=2数量关系?请写出它们之间的关系式并给予证明.(4)在(3)中,若BC=4,DC=7,CF=2,求△CEF的周长(直接写出结果即可).图 1 图 2 图325.(本小题8分)如图,边长为2的正方形ABCO中,点F为x轴上一点,CF=1,过点B作BF的垂线,交y轴于点E.(1)求过点E、B、F的抛物线的解析式;(2)将∠EBF绕点B顺时针旋转,角的一边交y轴正半轴于点M,另一边交x轴于点N,设BM与(1)中抛物线的另一个交点为点G,且点G的横坐标为6,EM与NO5有怎样的数量关系?请说明你的结论.(3)点P在(1)中的抛物线上,且PE与y轴所成锐角的正切值为3,求点P的坐标.22010年朝阳区中考二模数学试题答案一、选择题(共8个小题,每小题4分,共32分)二、填空题(共4个小题,每小题4分,共16分) 9. -210. 3511. n2112.4三、解答题(共13个小题,共72 分) 13. (本小题5分)解:原式=2323242⨯+-+-……………………………………………4分 =0 ……………………………………………………………………5分 14. (本小题5分)解:原式=1a )1a ()1a )(1a (11a 12+-⋅-+-+ ………………………………………2分2)1a (1a 1a 1+--+=……………………………………………………3分2)1a (2+= ……………………………………………………………4分当422=+a a 时,原式2)1a (2+=52=.………………………………5分15. (本小题5分)证明: ∵. OB=OC ,∴∠ACB=∠DBC. …………………………………………………… 1分∵OA =OD , ∴AC=BD . ………………………………………………………… 2分又∵BC =CB ,∴△AB C ≌△DCB .………………………………………………………… 4分∴∠ABC=∠DCB . ……………………………………………………… 5分16.(本小题5分)(1) P (3)=21 …………………………………………………………………… 1分(2)表格或树形图略 ………………………………………………………… 2分因为)(83p ,奇= )(85p ,偶= (4)分所以抽取的数字之和为偶数的概率大于数字之和为奇数的概率.所以这个方案设计的不公平,李明的说法是正确的.………………………… 5分17.(本小题5分)解:(1)∵ 反比例函数xk y =(x >0)的图象过点A , ∴k=6. ……………………………………………………………………… 1分∴ 反比例函数的解析式为x6y =. ………………………………………… 2分 (2)∵ 点B 在x 6y =的图象上,且其横坐标为6,∴ 点B 的坐标为(6,1). ………………………………………………… 3分设直线AB 的解析式为)0k (b kx y ≠+=, 把点A 和点B 的坐标分别代入)0k (b kx y ≠+=,⎩⎨⎧+=+=.b k 61,b k 23 解得,.4b 21k ⎪⎩⎪⎨⎧=-= …………………………………………… 4分 ∴直线AB的解析式为4x 21y +-= ……………………………………… 5分18. (本小题5分)解:设自行车的速度为x 千米/时,则汽车的速度为4x 千米/时,…………… 1分由题意,得 2141010=-x x . 解得x=15. (3)分经检验:x=15是原方程的解. ……………………………………………… 4分则604=x .答:自行车的速度为15千米/时,则汽车的速度为60千米/时.……………… 5分19. (本小题5分) 解:(1)如图1或图2 ………………………………………………………… 2分(2)如图3 ……………………………………………………………………… 4分过矩形ABCD的中心O1和平行四边形CBEF的中心O2画线段MN,交AD于M,交EF于N,则线段MN为所求. (5)分20. (本小题5分)证明:(1)连接OD,………………………… 1分∵OB=OD,∴∠B=∠1.∵AB=AC, ∴∠B=∠C.∴∠1=∠C.∴OD∥AC.………………………… 2分∵DE⊥CF于点E,∴∠CED=90°.∴∠ODE=∠CED=90°.∴ DE是⊙O的切线.………………………… 3分解:(2) 连接AD,∵AB是⊙O的直径,∴∠ADB=90°.∵cosC=cosB=54.∵AB=10,∴BD=AB ·cosB=8. …………………………………………… 4分∵∠F=∠B =∠C .∴DF=DC=8.且cosF=cosC=54.在Rt △DEF 中,EF=DF ·cosF=532. …………………………………………………………… 5分 21.(本小题5分) 解:(1)34. ………………………………………………………………… 2分(2)∵abb a b a 2)(222-+=-,∴abb a b a2)(222+-=+=4+6=10. ………………………………………………………… 4分∴22222442)(b a b a b a-+=+=100-18=82.……………………………………………………… 5分 22.(本小题5分) 解:∵抛物线22m mx 2x y +-=与直线x y 2=相交,∴x2m mx 2x 22=+-.…………………………………………………………1分 ∴0m x )1m (2x22=++-.∴[]m 4)1m (222≥-+-.解得21m -≥.…………………………………………………………………… 2分∵2m <, ∴2m 21<≤-. …………………………………………………… 3分∵ m 为整数,∴ m=0,1. ∵抛物线22m mx 2x y +-=与直线x 2y =交点的横坐标均为整数, 即方程x2m mx 2x22=+-的根为整数.当m=0时,x 2-2x=0,解得 x=0或x=2,两根均为整数,∴m=0符合题意. ……………………… 4分 当m=1时,01x 4x2=+-,∵ △=(-4)2-4=12,∴ x 2-4x+1=0没有整数根,∴m=1不符合题意,舍去. ∴ 满足条件的m 的整数值为0.………………………………………………… 5分23. (本小题7分)解:(1)①当 0 < t ≤ 2时,如图1,过点B 作BE⊥DC,交DC 的延长线于点E , ∵∠BCE=∠D=60°,∴BE=43. ∵ CP=t , ∴t 32t 3421BE CP 21S CPQ =⨯=⋅=∆. …………………………………… 2分 ② 当 2 < t ≤ 4时,如图2,CP=t ,BQ=2t-4,CQ=8-(2t-4)=12-2t . 过点P 作PF ⊥BC ,交BC 的延长线于点F . ∵∠PCF=∠D=60°,∴PF=t 23.∴ t 33t 23t 23)t 212(21PF CQ 21S 2CPQ+-=⨯-=⋅=∆.……………………4分(2)当 0 < t ≤ 2时,t=2时,S 有最大值43.当 2< t ≤ 4时, 329)3t (23t 33t 23S22CPQ+--=+-=∆,t=3时,S有最大值39.2综上所述,S的最大值为9.………………………………………………… 5分32(3)当0 < t ≤ 2时, △CPQ不是等腰三角形,∴不存在符合条件的菱形.…………………………………………………… 6分当 2 < t ≤ 4时,令CQ=CP,即t=12-2t,解得t=4.∴当t=4时,△CPQ是等腰三角形.即当t=4时,以△CPQ一边所在直线为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.………………………………………………………………………… 7分24. (本小题7分)解:(2)EF=DF-BE.……………………………………………………………… 1分(3)EF=DF-BE.…………………………………………………………………… 2分证明:在DF上截取DM=BE,连接AM.如图,∵∠D+∠ABC=∠ABE+∠ABC=180°,∴∠D=∠ABE.∵AD=AB,∴△ADM≌△ABE.∴AM=AE.……………………………3分∴∠DAM=∠BAE.1∠BAD,∵∠EAF=∠BAE+∠BAF=21∠BAD.∴∠DAM+∠BAF=21∠BAD.∴∠MAF=2∴∠EAF=∠MAF.………………………………………………………… 4分∵AF是△EAF与△MAF的公共边,∴△EAF≌△MAF.∴EF=MF.∵MF=DF-DM=DF-BE,∴EF=DF-BE.…………………………………………………………… 5分 (4) △CEF 的周长为15. (7)分25. (本小题8分)解:(1)由题意,可得点B (2,2). ∵ CF=1, ∴ F ( 3,0 ) .在正方形ABCD 中,∠ABC=∠OAB=∠BCF =90°,AB=AC , ∵ BE ⊥BF ,∴∠EBF =90°.∴∠EBF=∠ABC .即∴∠ABE+∠EBC=∠EBC+∠CBF. ∴∠ABE=∠CBF . ∴△ABE ≌△CBF . ∴ AE=CF . ∴E(0,1) . ………………………………………………………………………… 1分设过点E 、B 、F 的抛物线的解析式为y=ax 2+bx+1,∴ ⎩⎨⎧=++=++01b 3a 9,21b 2a 4 ∴⎪⎪⎩⎪⎪⎨⎧=-=613b ,65a∴抛物线的解析式为y=65-x2+613x+1. …………………………………… 2分(2)∵ 点G(56,y )在抛物线y=65-x 2 +613x +1上,y=65-×(56)2+613×56+1=512.∴ G (56,512). 设过点B 、G 的直线解析式为y=kx+b, ∴⎪⎩⎪⎨⎧=+=+512b k 56,2b k 2 ∴⎪⎩⎪⎨⎧=-=3b ,21k∴ 过点B 、G 的直线解析式为y=21-x+3. ∴ 直线y=21-x+3与y 轴交于点M(0,3) . ………………………………… 3分∴ EM=2.可证∴△ABM ≌△CBN .∴CN=AM .∴N (1,0) . ∴ON=1.∴EM=2ON .…………………………………………………………………… 4分(3)∵ 点P 在抛物线y=65-x 2 +613x +1上, 可设点P 坐标为(m ,65-m 2+613m +1). 如图2①过点P 1作P 1H 1⊥y 轴于点H 1,连接P 1E .∴ tan∠H 1EP 1=23,∴23E H H P 111=. 即2311m 613m 65m 2=-++-.…… 5分解得m 1=59,m 2=0(不合题意,舍去). ②过点P 2作P 2H 2⊥y 轴于点H 2,连接P 2E .∴ tan ∠H 2EP 2=23,∴23E H H P 222=. 图即23)1m 613m 65(1m2=++--. …………………………………………6分解得m 3=517,m 4=0(不合题意,舍去). 当m 1=59时,65-m 2 +613m +1=511; 当m 3=517时,65-m 2 +613m +1=519-. 综上所述,点P 1(59,511),P 2(517,519-)为所求.…………………… 8分说明:各解答题不同的正确解法参照以上标准给分.。

2010年北京各区一模数学试题复数、算法、集合、简易逻辑、推理与证明、平面几何平面几何1. (崇文·理·题3)已知PA 是O 的切线,切点为A ,2PA =,AC 是O 的直径,PC 交O 于点B ,30PAB ∠=,则O 的半径为 ( )PAA .1B .2CD .【解析】 C ;30,2tan30PAPCAPAB CA ∠=∠===2. (东城·理·题3)如图,已知AB 是⊙O 的一条弦,点P 为AB 上一点,PC OP ⊥,PC 交⊙O 于C ,若4AP =,2PB =,则PC 的长是( )A .3B .C .2D OPCB A【解析】 B ;延长CP 交于圆上一点,得到一条圆的弦,易知P点为该弦的中点,有28PC PA PB=⋅=.3.(丰台·理·题9)在平行四边形ABCD中,点E是边AB的中点,DE与AC交于点F,若AEF∆的面积是12cm,则CDF∆的面积是2cm.【解析】4;HGFEDCBA取CD的中点G,连结BG交AC于H,则∵BE DG∥且1122BE AB CD DG===,∴四边形BEDG为平行四边形∴AF FH HC==∴44DFC AEFS S==△△4.(海淀·理·题10)如图,AB为O的直径,且8AB=,P为OA的中点,过P作O的弦CD,且:3:4CP PD=,则弦CD的长度为.【解析】7;由8AB =得2,6AP PB ==.由已知和相交弦定理得:3:4CP PD AP PB CP PD ⋅=⋅⎧⎨=⎩,解得34CP PD =⎧⎨=⎩. 于是347CD CP PD =+=+=.【解析】【解析】94,5;22(26)164PC PA PB PC=⋅=⨯+=⇒=;连结OC,知OC PC⊥,于是5PO=,2239235CO OE OP PE=⋅⇒==+.BCO EPDA5.(宣武·理·题11)若,,A B C是O⊙上三点,PC切O⊙于点C,110,40ABC BCP∠=︒∠=︒,则AOB∠的大小为.【解析】60︒;如图,弦切角40PCB CAB∠=∠=︒,于是18030ACB CAB ABC∠=︒-∠-∠=︒,从而260AOB ACB∠=∠=︒.PO CBA6.(朝阳·理·题12)如图,圆O是ABC∆的外接圆,过点C的切线交AB的延长线于点D,3CD AB BC===,则BD的长为;AC的长为.ODCB【解析】 374,.()24CD DB DA DB AB BD BD =⋅=⋅+⇒=.又由DCB CAB ∠=∠知BCD ACD ∆≅∆.于是BC BD CDAC CD AD ==. 即33727BD AC AC CD ==⇒=.7. (西城·理·题12) 如图,PC 切O 于点C ,割线PAB 经过圆心O ,弦CD AB ⊥于点E .已知O 的半径为3,2PA =,则PC = .OE = .AD E OCB【解析】 94,5;22(26)164PC PA PB PC =⋅=⨯+=⇒=;连结OC ,知OC PC ⊥,于是5PO =,2239235CO OE OP PE =⋅⇒==+.BCOE PD A坐标系与参数方程1. (海淀·理·题4)在平面直角坐标系xOy 中,点P的直角坐标为(1,.若以原点O 为极点,x 轴正半轴为极轴建立极坐标系,则点P 的极坐标可以是( )A .π1,3⎛⎫- ⎪⎝⎭B .4π2,3⎛⎫ ⎪⎝⎭C .π2,3⎛⎫- ⎪⎝⎭ D .4π2,3⎛⎫- ⎪⎝⎭ 【解析】C ;易知2ρ==,()π2π3k k θ=-∈Z .2. (朝阳·理·题9)已知圆的极坐标方程为2cos ρθ=,则圆心的直角坐标是 ;半径长为 . 【解析】 ()1,0,1;由22cos ρρθ=,有222xy x+=,即圆的直角坐标方程为()2211x y -+=.于是圆心坐标为()1,0,半径为1.3. (崇文·理·题11)将参数方程12cos ,2sin ,x y θθ=+⎧⎨=⎩(θ为参数)化成普通方程为 . 【解析】 ()2214x y -+=;由12cos ,2sin x y θθ-==知()2214x y -+=.4. (石景山·理·题11)如图,已知PE 是圆O 的切线.直线PB 交圆O 于A 、B 两点,4PA =,12AB =,43AE =.则PE 的长为_____,ABE ∠的大小为________.POEBA【解析】 8,30︒;24(412)64PE PA PB =⋅=⨯+=,则8PE =;由222PEPA AE =+,可知90PAE ∠=︒,即90BAE ∠=︒,由3tan AE ABE AB∠==,得30ABE ∠=︒.5. (西城·理·题11)将极坐标方程2cos ρθ=化成直角坐标方程为 .【解析】2220x y x +-=;2222cos 2x y xρρθ=⇒+=.6. (东城·理·题12)圆的极坐标方程为sin 2cos ρθθ=+,将其化成直角坐标方程为 ,圆心的直角坐标为 .【解析】 2215(1)()24x y -+-=,11,2⎛⎫⎪⎝⎭; 222sin 2cos 2x y y xρρθρθ=+⇒+=+.7. (东城·理·题12)圆的极坐标方程为sin 2cos ρθθ=+,将其化成直角坐标方程为 ,圆心的直角坐标为 .【解析】 2215(1)()24x y -+-=,11,2⎛⎫⎪⎝⎭; 222sin 2cos 2x y y xρρθρθ=+⇒+=+.8. (宣武·理·题12)若直线:0l x =与曲线:x a C y φφ⎧=⎪⎨=⎪⎩(φ为参数,0a >)有两个公共点,A B ,且||2AB =,则实数a 的值为 ;在此条件下,以直角坐标系的原点为极点,x 轴正方向为极轴建立坐标系,则曲线C 的极坐标方程为 .【解析】22,4cos 20ρρθ-+=;曲线C :22()2x a y -+=,点C 到l2a=,因此||22AB a =⇒=;222(2cos )(2sin )ρθθ-+=,即24cos 20ρρθ-+=.9. (丰台·理·题12)在平面直角坐标系xOy 中,直线l 的参数方程为11x y t =⎧⎨=+⎩(参数t ∈R ),圆C 的参数方程为cos 1sin x y θθ=+⎧⎨=⎩(参数[)0,2πθ∈),则圆心到直线l的距离是.直线方程为1y x =+,圆的方程为()2211x y -+=.于是圆心()1,0到直线10x y -+=.复数1. (海淀·理·题1)在复平面内,复数1ii z =-(i 是虚数单位)对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【解析】C ;()()1i1i i 1i iz -==--=--,该复数对应的点位于第三象限.2. (丰台·理·题1)如果1i1i a z a -=+为纯虚数,则实数a 等于( ) A .0 B .1- C .1 D .1-或1 【解析】 D ;设i z x =,0x ≠则1ii 1i a x a -=+()1i 0ax a x ⇔+-+=100ax a x +=⎧⇔⎨+=⎩11a x =⎧⇔⎨=-⎩或11a x =-⎧⎨=⎩.3. (石景山·理·题1)复数21i+等于( ) A .2i - B .2i C .1i -D .1i +【解析】C ;22(1i)2(1i)1i 1i (1i)(1i)2--===-++-.4. (东城·理·题1)i 是虚数单位,若12ii(,)1i a b a b +=+∈+R ,则a b +的值是( )A .12-B .2- C .2D .12【解析】C ;12i (12i)(1i)3i1i (1i)(1i)2++-+==++-,于是31222a b +=+=. 5. (朝阳·理·题1)复数112ii ++等于 ( ) A .12i + B .12i - C .12- D .12 【解析】D ;计算容易有1i 11i 22+=+.6. (海淀·文·题1)在复平面内,复数()i 1i -(i 是虚数单位)对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 【解析】 A ;()i 1i 1i-=+,对应的点为()1,1位于第一象限.7. (丰台·文·题1)复数1i1i z -=+化简的结果等于( ) A .i - B .i C .2i - D .2i 【解析】 A ;1i1i z -=+()()()21i 2i i 1i 1i 2--===-+-.8. (石景山·文·题1)复数21i+等于( ) A .2i - B .2i C .1i -D .1i +【解析】C ;22(1i)2(1i)1i 1i (1i)(1i)2--===-++-.9. (东城·文·题1)计算复数1i1i-+的结果为( ) A .i - B .i C .1- D .1 【解析】 A ;21i (1i)i 1i 2--==-+. 10. (朝阳·文·题1)复数22(1)i i+等于 ( ) A .2 B .-2 C .2i - D .2i 【解析】 C ;()221221i ii i +==--. 11. (宣武·理·题3)若复数z 满足2i 1iz=+,则z 对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限【解析】B ;2i(1i)22iz =+=-+.12. (宣武·文·题4)设i 是虚数单位,则复数(1i)2i z =+⋅所对应的点落在( )A .第一象限B .第二象限C .第三象限D .第四象限【解析】B ;22iz =-+.13. (西城·文·题9)i 是虚数单位,1i 1i+=+ . 【解析】 11i22+;11i 1i i i 1i 22-++=+=+.14. (西城·理·题9)若(2i)i i a b -=+,其中,a b ∈R ,i 为虚数单位,则a b += . 【解析】 3;2i i a b +=+1,2a b ⇒==. 15. (崇文·理·题9)如果复数()()2i 1i m m ++(其中i 是虚数单位)是实数,则实数m =___________. 【解析】 1-;()()()()223i 1i 1mm m m i m ++=-++.于是有3101mm +=⇒=-.16. (崇文·文·题10)如果复数()()2i 1i m m ++(其中i 是虚数单位)是实数,则实数m =___________. 【解析】 -1;()()()()223i 1i 1m m mm m i++=-++.于是有3101mm +=⇒=-.算法1. (丰台·文·题3)在右面的程序框图中,若5x =,则输出i 的值是( )x > 109i = i + 1NY 输出i结束x = 3x -2i = 0输入x开始A .2B .3C .4D .5【解析】C ;51337109325→→→→,对应的4i =.2.(石景山·理·题4)一个几何体的三视图如图所示,那么此几何体的侧面积(单位:2cm)为()A.80B.60C.40D.20【解析】A;几何体如图,是正四棱锥,底边长8,侧面底边上的高为5,因此侧面积为1854802⨯⨯⨯=.3.(西城·理·题5)阅读右面的程序框图,运行相应的程序,输出的结果为()A.1321B.2113C.813D.138【解析】D;===<;1,2,320===<;,x y zx y z1,1,220.===>,故输出1388,13,2120x y z4.(东城·理·题5)如图是一个算法的程序框图,若该程序输出的结果为4,则判断框中应填入的条件是()5A.4?T> T>B.4?T<C.3?D.3?T<【解析】B;循环一次得:12,1,2i T S ===;两次得:1123,2,263i T S ===+=;三次得:2134,3,3124i T S ===+=;四次得:3145,4,4205i T S ===+=,此时需要跳出循环,故填4?T <.5. (东城·文·题5)按如图所示的程序框图运算,若输入6x =,则输出k 的值是( )A .3B .4C .5D .6【解析】B ;6x =,0k =,13x =,1k =,27x =,2k =,55x =,3k =,111x =,4k =,111100x =>,跳出循环,输出4k =.6. (石景山·文·题6)已知程序框图如图所示,则该程序框图的 功能是( )A .求数列1n ⎧⎫⎨⎬⎩⎭的前10项和()n *∈N B .求数列12n ⎧⎫⎨⎬⎩⎭的前10项和()n *∈N C .求数列1n ⎧⎫⎨⎬⎩⎭的前11项和()n *∈N D .求数列12n ⎧⎫⎨⎬的前11项和()n *∈N 【解析】注意n 和k 的步长分别是2和1.7. (西城·文·题6)阅读右面的程序框图,运行相应的程序,输出的结果为( )A .1321B .2113C .813 D .138【解析】D ;1,1,220x y z ===<;1,2,320x y z ===<;,8,13,2120x y z ===>,故输出138.8. (海淀·理科·题7) 已知某程序框图如图所示,则执行该程序后输出的结果是( )第 7 题A .1-B .1C .2D .12【解析】A;∵()i==,∴对应的120100mod3a=-.9.(朝阳·文·题11)如图,下程序框图的程序执行后输出的结果是.【解析】55;将经过i次运行后的,n S值列表如下.于是55S=.10.(宣武·文·题12)执行如图程序框图,输出S的值等于.12题图【解析】20;运算顺序如下1,1,23,4,36,10,410,20,54A S i A S i A S i A S i===→===→===→===>,输出S,故20S=.11.(崇文·理·题12)(崇文·文·题12)某程序框图如图所示,该程序运行后输出,M N 的值分别为 .【解析】13,21;依据程序框图画出运行n 次后,,M N i 的值.n1 2 3 i2 3 4 M2 5 13 N3 8 21 4次运行后43i =>,于是有13,21M N ==. 12. (丰台·理·题13)在右边的程序框图中,若输出i 的值是4,则输入x 的取值范围是 .【解析】(]2,4;∵328228->⇔>,x xx x->⇔>,322810x x->⇔>x x->⇔>,324232104∴要使得刚好进行4次运算后输出的82x>,则有24x<≤.13.(朝阳·理·题13)右边程序框图的程序执行后输出的结果是.【解析】625;将经过i 次运行后的,n S 值列表如下.i1 2 3 4 5 ... m ...25 n3 5 7 9 11 21m + 51 S 14 9 16 25 2m 625 于是625S =.14. (海淀·文·题13) 已知程序框图如图所示,则执行该程序后输出的结果是_______________.结束输出 a i = i +1否是a = 1-1ai ≥ 20a = 2 , j = 1开始【解析】12;a = -1 , j = 3a = 12, j = 2a = 2 , j = 1∵()202mod 3i ==,∴对应的12a =.集合简易逻辑推理与证明1. (崇文·文·题1)已知全集U =R ,集合{}|12A x x =->,{}2|680B x x x =-+<,则集合()UA B = ( )A .{}|14x x -≤≤B .{}|23x x <≤C . {}|23x x <≤D .{}|14x x -<< 【解析】 D ;容易解得{3A x x x =>或者}0x <,{}26B x x =<<. 于是()UA B ={}23x x <≤.2. (西城·理·题1)设集合{|1}P x x =>,2{|0}Q x x x =->,则下列结论正确的是( )A .P Q =B .P Q R =C .P Q D .Q P 【解析】 C ;(1,)P =+∞,(,0)(1,)Q =-∞+∞.3. (宣武·理·题1)设集合20.3{|0},2P x x m =-=≤,则下列关系中正确的是( ) A .m P ⊂ B .m P ∉ C .{}m P ∈ D .{}m P【解析】D ;{|0P x x =≤≤,0.3022m <=<<,故m P ∈,因此{}m P4. (崇文·理·题1)已知全集U =R ,集合{}|12A x x =->,{}2|680B x x x =-+<,则集合()UA B =( )A .{}|14x x -≤≤B .{}|14x x -<<C .{}|23x x <≤D .{}|23x x <≤ 【解析】D ;容易解得{3A x x x =>或者}0x <,{}26B x x =<<. 于是()UA B ={}23x x <≤.5. (西城·文·题1)设集合{|1}P x x =>,{|(1)0}Q x x x =->,下列结论正确的是( )A .P Q =B .P Q R =C .P QD .Q P【解析】C ;(1,)P =+∞,(,0)(1,)Q =-∞+∞.6. (宣武·文·题1)设集合{|4},sin 40A x x m ==︒≤,则下列关系中正确的是( ) A .m A ⊂ B .m A ⊄ C .{}m A ∈ D .{}m A ∉【解析】D ;正确的表示法,m A ∈,{}m A,{}m A ∉.7. (东城·理·题2)设全集{33,}I x x x =-<<∈Z ,{1,2}A =,{2,1,2}B =--,则()IA B 等于( )A .{1}B .{1,2}C .{2}D .{0,1,2}【解析】D ;{2,1,0,1,2}I =--,{0,1}IB =,故(){0,1,2}I AB =.8. (石景山·文·题2)已知命题 :p x ∀∈R ,2x ≥,那么命题p ⌝为( )A .,2x x ∀∈R ≤B .,2x x ∃∈<RC .,2x x ∀∈-R ≤D .,2x x ∃∈<-R【解析】B ;全称命题的否定是存在性命题,将∀改为∃,然后否定结论.9. (东城·文·题2)设集合{1,2,4,6}A =,{2,3,5}B =,则韦恩图中阴影部分表示的集合( )A .{2}B .{3,5}C .{1,4,6}D .{3,5,7,8}【解析】B ;阴影部分表示{3,5}UAB =.10. (丰台·理·题2) 设集合[)1{|(),0,}2xM y y x ==∈+∞,(]2{|log ,0,1}N y y x x ==∈,则集合M N 是( )A .[)(,0)1,-∞+∞B .[)0,+∞C .(],1-∞D .(,0)(0,1)-∞ 【解析】 C ;(]0,1M =,(],0N =-∞,因此(],1MN =-∞.11. (石景山·理·题2)已知命题 :p x ∀∈R ,2x ≥,那么命题p ⌝为( )A .,2x x ∀∈R ≤B .,2x x ∃∈<RC .,2x x ∀∈-R ≤D .,2x x ∃∈<-R【解析】 B ;全称命题的否定是存在性命题,将∀改为∃,然后否定结论.12. (朝阳·文·题2)命题:0p x ∀>,都有sin 1x -≥,则 ( )A .:0p x ⌝∃>,使得sin 1x <-B .:0p x ⌝∀> ,使得sin 1x <-C .:0p x ⌝∃>,使得sin 1x >-D .:0p x ⌝∀>,使得sin 1x -≥【解析】 A ;由命题的否定容易做出判断.13. (海淀·文·题7)给出下列四个命题:①若集合A 、B 满足A B A =,则A B ⊆;②给定命题,p q ,若“p q ∨”为真,则“p q ∧”为真; ③设,,a b m ∈R ,若a b <,则22am bm <;④若直线1:10l ax y ++=与直线2:10l x y -+=垂直,则1a =. 其中正确命题的个数是( )A .1B .2C .3D .4【解析】 B ;命题①和④正确.14. (丰台·文·题7)若集合{}0,1,2P =,10(,),,20x y Q x y x y P x y ⎧⎫-+>⎧⎪⎪=∈⎨⎨⎬--<⎩⎪⎪⎩⎭,则Q 中元素的个数是( )A .3B .5C .7D .9【解析】 B ;(){},|12,,Q x y x y x y P =-<-<∈, 由{}0,1,2P =得x y -的取值只可能是0和1. ∴()()()()(){}0,0,1,1,2,2,1,0,2,1Q =,含有5个元素.15. (崇文·文·题8)如果对于任意实数x ,[]x 表示不超过x 的最大整数. 例如[]3.273=,[]0.60=.那么“[][]x y =”是“1x y -<”的 ( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【解析】 A ;由[][][][]1,1x x x y y y <+<+≤≤.于是有[][]()[][]1111x y x y x y -=+<-<+-=-则1x y -<.不妨设33,24x y ==,于是3331424x y -=-=<.但是[][]1,0.x y ==16. (东城·文·题9)已知命题3:(1,),log 0p x x ∀∈+∞>,则p 为 . 【解析】 030(1,),log 0x x ∃∈+∞≤;全称命题的否定为存在命题.17. (宣武·文·题10)命题“任意常数列都是等比数列”的否定形式是 .【解析】 存在一个常数列不是等比数列;全称命题的否定是存在性命题.18. (海淀·理·题11)给定下列四个命题:① “π6x =”是“1sin 2x =”的充分不必要条件; ② 若“p q ∨”为真,则“p q ∧”为真;③ 若a b <,则22am bm <;④ 若集合A B A =,则A B ⊆. 其中为真命题的是 (填上所有正确命题的序号). 【解析】 ①,④;19. (海淀·理·题14)在平面直角坐标系中,点集(){}22,|1A x y x y =+≤, {(,)|4,0,340}B x y x y x y =-≤≥≥,则 ⑴点集(){}1111(,)3,1,,P x y x x y y x y A ==+=+∈所表示的区域的面积为_____;⑵点集{}12121122(,),,(,),(,)Q x y x x x y y y x y A x y B ==+=+∈∈所表示的区域的面积为 . 【解析】 π;18π+.;⑴如左图所示,点集P 是以()3,1为圆心1为半径的圆,其表示区域的面积为π; ⑵如右图所示,点集Q 是由三段圆弧以及连结它们的三条切线段围成的区域,其面积为()1π433451π18π2OPQ OABP PCDQ OFEQ S S S S ++++=⨯⨯+++⨯+=+△.20. (海淀·文·题14) 在平面直角坐标系中,点集(){}22,|1A x y x y =+≤, (){},|11,11B x y x y =--≤≤≤≤,则⑴点集(){}1111(,)3,1,,P x y x x y y x y A ==+=+∈所表示的区域的面积为_____;⑵点集{}12121122(,),,(,),(,)Q x y x x x y y y x y A x y B ==+=+∈∈所表示的区域的面积为.【解析】π,12π+;⑴如左图所示,点集P是以()3,1为圆心1为半径的圆,其表示区域的面积为π;⑵如右图所示,点集Q是由四段圆弧以及连结它们的四条切线段围成的区域,其面积为+.12π。

2010年朝阳区中考二模数学试题2010.6第Ⅰ卷(选择题32分)一、选择题(共8个小题,每小题4分,共32分) 1.6的倒数是A .-6B .±61 C .61- D .61 2.全球可被人类利用的淡水总量仅占地球上总水量的0.00003,因此珍惜水、保护水,是我们每一位公民义不容辞的责任.其中数字0.00003用科学记数法表示为A .4103-⨯B .5103-⨯C .4103.0-⨯ D .5103.0-⨯ 3.已知()02b 3a 2=++-,则ab 等于A .-6B .6C .-1D .14.某校抽取九年级的7名男生进行了1次体能测试,其成绩分别为75,90,85, 75,85,95,75,(单位:分)这次测试成绩的众数和中位数分别是A .85,75B .75,80C .75,85D .75,75 5.若一个多边形的内角和是外角和的2倍,则这个多边形的边数是A .8B .6C .5D .46.已知一个圆锥的底面半径是5cm ,侧面积是65πcm 2,则圆锥的母线长是A . 6.5B . 13C .15D .26 7.如图,△ABC 被一个矩形所截,矩形的一条边与AB 、AC 分别交于点D 、E ,另一条边与BC 在同一条直线上.如果点D 恰为AB 的三等分点,那么图中阴影部分面积是△ABC 面积的A .31 B .91 C . 94D .958.已知二次函数y 1=x 2-x-2和一次函数y 2=x+1的两个交点分别为A(-1,0),B(3,4), 当y 1>y 1时,自变量x 的取值范围是A . x <-1或x >3B .-1<x <3C .x <-1D .x >3第Ⅱ卷 (填空题和解答题,共88分)二、填空题(共4个小题,每小题4分,共16分)9.若分式2x 4x 2--的值为0,则x 的值为 .10.某中学团委为玉树地震灾区组织捐款活动,九(1)班生活委员对本班30名同学的捐款情况进行了统计,并绘制了条形图(如图),那么九(1)班同学本次平均每人捐款____元. 11.我们知道,投掷一枚均匀的硬币,正面朝上的概率是21;投掷两枚均匀的硬币,同时出现两个正面朝上的概率是41;投掷三枚均匀的硬币,同时出现三个正面朝上的概率是81;那么投掷n枚均匀硬币,出现n 个正面朝上的概率是_______.12.在菱形ABCD 中,对角线AC ,BD 相交于点O ,且AC=12,BD=16,E 为AD 的中点,点P 在BD 上移动,若△POE 为等腰三角形,则所有符合条件的点P 共有______个.三、解答题(共13个小题,共72 分) 13.(本小题5分)计算:︒+-+-60sin 223282314.(本小题5分)已知a 2+2a=4,求121111122+-+÷--+a a a a a 的值.15.(本小题5分)已知:如图,AC 与BD 相交于点O ,且OB=OC ,OA=OD . 求证:∠ABC =∠DCB .16.(本小题5分)如图,是四张不透明且质地相同的数字卡片.将卡片洗匀后,背面朝上放置在桌面上. (1)求随机抽取一张卡片,恰好得到数字3的概率; (2)为能赢得一张上海世博会的门票,李明与王刚请张红做裁判,张红用以上四张卡片设计了一个方案(见右侧信息图),但李明却认为这个方案设计的不公平.请你用列表法或树形图法求出概率说明李明的说法是否正确.17.(本小题5分)如图,反比例函数xky =(x >0)的图象过点A . (1)求反比例函数的解析式; (2)若点B 在xky =(x >0)的图象上, 求直线AB 的解析式.18.列方程(组)解应用题(本小题5分)“五一”期间某校学生到相距学校10千米的“老年公寓”开展“献爱心”活动,部分同学骑自行车从学校出发,20分钟后另部分同学乘汽车从学校出发,结果乘汽车的同学比骑自行车的同学提前10分钟到达“老年公寓”.已知汽车速度是自行车速度的4倍,求两种车的速度各是多少?19.(本小题5分)在下面所给的图形中,若连接BC ,则四边形ABCD 是矩形,四边形CBEF 是平行四边形. (1)请你在图1中画出两条线段,将整个图形分为两部分,使这两部分面积相等(不写画法); (2)请你在图2中画出一条线段,将整个图形分为两部分,使这两部分面积相等.简要说明你的画法.20.(本小题5分)已知:如图, AB 是⊙O 的直径, AB=AC ,BC 交⊙O 于点D ,延长CA 交⊙O 于点F ,连接DF ,DE ⊥CF 于点E . (1)求证:DE 是⊙O 的切线; (2)若AB=10,4cos 5C ∠=,求EF 的长.21.(本小题5分)阅读下列材料,然后解答后面的问题:利用完全平方公式(a±b)2 =a 2±2ab+b 2,通过配方可对a 2+b 2进行适当的变形,如a 2+b 2= (a+b)2 -2ab 或a 2+b 2 = (a -b)2 +2ab .从而使某些问题得到解决.例:已知a+b=5,ab=3,求a 2+b 2的值. 解:a 2+b 2= (a+b)2 -2ab = 52 -2×3=19. 问题:(1)已知6a1a =+,则22a 1a +=________;(2)已知a –b =2,ab=3,求a 4+b 4的值.22.(本小题5分)已知抛物线222m mx x y +-=与直线x y 2=交点的横坐标均为整数,且2<m ,求满足要求的m 的整数值.23.(本小题7分)如图,平行四边形ABCD 中,AD=8,CD=4,∠D=60°,点P 与点Q 是平行四边形ABCD 边上的动点,点P 以每秒1个单位长度的速度,从点C 运动到点D ,点Q 以每秒2个单位长度的速度从点A→点B→点C 运动. 当其中一个点到达终点时,另一个点随之停止运动.点P 与点Q 同时出发,设运动时间为t ,△CPQ 的面积为S .(1)求S 关于t 的函数关系式; (2)求出S 的最大值;(3)t 为何值时,将△CPQ 以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.24.(本小题7分)如图1,四边形ABCD ,将顶点为A 的角绕着顶点A 顺时针旋转,若角的一条边与DC 的延长线交于点F ,角的另一条边与CB 的延长线交于点E ,连接EF .(1)若四边形ABCD 为正方形,当∠EAF=45°时,有EF=DF -BE .请你思考如何证明这个结论(只思考,不必写出证明过程);(2)如图2,如果在四边形ABCD 中,AB=AD ,∠ABC=∠ADC=90°,当∠EAF=21∠BAD 时,EF 与DF 、BE 之间有怎样的数量关系?请写出它们之间的关系式(只需写出结论); (3)如图3,如果四边形ABCD 中,AB=AD ,∠ABC 与∠ADC 互补,当∠EAF=21∠BAD 时,EF 与DF 、BE 之间有怎样的数量关系?请写出它们之间的关系式并给予证明.(4)在(3)中,若BC=4,DC=7,CF=2,求△CEF 的周长(直接写出结果即可).图1 图2 图325.(本小题8分)如图,边长为2的正方形ABCO 中,点F 为x 轴上一点,CF=1,过点B 作BF 的垂线,交y 轴于点E .(1)求过点E 、B 、F 的抛物线的解析式;(2)将∠EBF 绕点B 顺时针旋转,角的一边交y 轴正半轴于点M ,另一边交x 轴于点N ,设BM 与(1)中抛物线的另一个交点为点G ,且点G 的横坐标为56,EM 与NO 有怎样的数量关系?请说明你的结论.(3)点P 在(1)中的抛物线上,且PE 与y 轴所成锐角的正切值为23,求点P 的坐标.。

北京市朝阳区九年级综合练习(一)数学试卷学校__________ 班级__________ 姓名__________ 考号__________考生须知1.本试卷共8页,共三道大题,28道小题,满分100分.考试时间120分钟.2.在试卷和答题卡上认真填写学校名称,班级、姓名和考号.3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.4.在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答.5.考试结束,请将本试卷、答题卡和草稿纸一并交回.一、选择题(共16分,每题2分)第1-8题均有四个选项,其中符合题意的选项只有一个.1. 如图是某几何体的三视图,该几何体是()A. 三棱柱B. 长方体C. 圆锥D. 圆柱【答案】A【解析】【分析】由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.【详解】解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是三角形可判断出这个几何体应该是三棱柱.故选:A.【点睛】此题考查了由三视图判断几何体,解题的关键是熟记一些简单的几何体的三视图.2. 2022年3月5日,国务院总理李克强代表国务院,向十三届全国人大五次会议作政府工作报告.报告中指出过去一年是党和国家历史上具有里程碑意义的一年,“十四五”实现良好开局,我国发展又取得新的重大成就.2021年国内生产总值达114万亿元,增长8.1%.将1140000用科学记数法表示应为()A.70.11410´ B.51.1410´ C.61.1410´ D.411.410´【答案】C 【解析】【分析】先确定a =1.14,再确定n =6,用科学记数法形式表示出来即可.【详解】解:∵1140000=61.1410´,故选C .【点睛】本题考查了大数的科学记数法,熟练掌握如何确定a 值,n 值是解题的关键.3. 实数a ,b 在数轴上对应的点的位置如图所示,下列结论中正确的是( )A. 0a b +> B. 0ab > C. 0a b -> D.||||a b >【答案】D 【解析】【分析】根据数轴上的位置确定a ,b 的正负和绝对值大小,再根据实数运算法则判断即可.【详解】解:根据实数a ,b 在数轴上对应点的位置可知,a <0,b >0,|a |>3>|b |,所以,a +b <0,ab <0,a −b <0, |a |>|b |,故选:D .【点睛】本题考查了实数在数轴上表示和实数的运算法则,解题关键是树立数形结合思想,熟练运用实数运用法则判断式子符号.4. 将一副三角尺(厚度不计)如图摆放,使有刻度的两条边互相平行,则图中1Ð的大小为( )A. 100°B. 105°C. 115°D. 120°【答案】B 【解析】【分析】先根据平行线的性质求出∠BCE的度数,然后根据平角的定义求解即可.【详解】解:如图所示,由题意得,∠ABC=30°,∠DCE=45°,AB∥CE∴∠BCE=∠ABC=30°,∴∠1=180°-∠BCE-∠DCE=105°,故选:B.【点睛】本题主要考查了三角板中角度的计算,平行线的性质,熟知平行线的性质是解题的关键.5. 下列多边形中,内角和与外角和相等的是()A. B. C. D.【答案】B【解析】【分析】根据多边形的内角和公式和多边形的外角和等于360°求解即可;【详解】解:多边形的外角和等于360°不变;A、三角形的内角和为:180°,不符合题意;B、四边形的内角和为:360°,符合题意;C、五边形的内角和为:540°,不符合题意;D、六边形的内角和为:720°,不符合题意;故选:B.【点睛】本题考查了多边形的内角和、多边形的外角和;熟练掌握多边形的内角和公式是解题的关键.6. 不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为( )A. 23 B. 12C. 13D. 14【答案】D 【解析】【分析】用列表法或树状图法可以列举出所有等可能出现的结果,然后看符合条件的占总数的几分之几即可.【详解】解:两次摸球的所有的可能性树状图如下:第一次 第二次开始 ììíïïîíìïíïîî红球红球绿球红球绿球绿球∴P 两次都是红球14=.故选D .【点睛】考查用树状图或列表法,求等可能事件发生的概率,关键是列举出所有等可能出现的结果数,然后用分数表示,同时注意“放回”与“不放回”的区别.7. 下图是国家统计局公布的2021月度涨跌幅度,月度同比和月度环比的平均数分别为,环同x x ,方差分别为22,环同s s ,则()A. 22,>>环环同同x x s s B. 22,><环环同同x x s s C. 22,<>环环同同x x s s D.22,<<环环同同x x s s 【答案】A【解析】【分析】先确定数组中的数据,分别计算平均数和方差,比较判断即可.【详解】解:∵环比的数据为:1,0.6,-0.5,-0.3,-0.2,-0.4,0.3,0.1,0,0.7,0.4,-0.3,∴10.60.50.3(0.3)=0.112+--++-»K 环,22222(10.1)(0.60.1)(0.50.1)(0.30.1)=0.212S -+-+--++--»K 环∵同比的数据为:-0.3,-0.2,0.4,0.9,1.3,1.1,1.0,0.8,0.7,1.5,2.3,1.5,∴(0.3)+(0.2)0.4+0.9+ 1.5=0.912x --++»K 同,22222(0.30.9)(0.20.9)(0.40.9)(1.50.9)=0.512S--+--+-++-»K 同∴22,>>环环同同x x s s ,故选A .【点睛】本题考查了折线统计图,平均数,方差的计算,熟练掌握计算公式是解题的关键.8. 点()()1122,,,A x y B x y 在反比例函数1y x =的图象上,下列推断正确的是( )A. 若12x x <,则12y y< B. 若12x x <,则12y y>C. 若120x x +=,则120y y += D. 存在12x x =,使得12y y ¹【答案】C 【解析】【分析】反比例函数1y x =的图象在一三象限,且在每个象限内,y 随x 到增大而减小.据此可判断.【详解】解:反比例函数1y x =的图象在一三象限,且在每个象限内,y 随x 到增大而减小,那么:A 、若12x x <,且(x 1,y 1)、(x 2,y 2)在同一个象限,则12y y >,故选项错误,不符合题意;B 、若12x x <,且(x 1,y 1)、(x 2,y 2)分别在三、一象限内,则12y y <,故选项错误,不符合题意;C 、若120x x +=,则12121212110x x y y x x x x ++=+==g ,故选项正确,符合题意;D 、若12x x =,则1211y y =,即y 1=y 2,另外,还可根据函数的定义:对于自变量x 的值,y都有唯一确定的值和它相对应,所以当12x x =时,12y y ¹不可能.故选项错误,不符合题意.故选:C .【点睛】此题考查了比较反比例函数值的大小,,解题的关键是数形结合,掌握函数的定义和反比例函数图象的性质.二、填空题(共16分,每题2分)9. 使分式11x -有意义的x 的取值范围是_________.【答案】x ≠1【解析】【详解】根据题意得:x -1≠0,即x ≠1. 故答案为:x ≠1.10. 分解因式:22242a ab b -+=_________.【答案】()22a b -【解析】【分析】首先提取公因式2,再根据完全平行方公式即可分解因式.【详解】解:22242a ab b -+()2222a ab b =-+()22a b =-,故答案为:()22a b -.【点睛】本题考查了利用提公因式法和完全平方公式分解因式,熟练掌握和运用分解因式的方法是解决本题的关键.11. 写出一个比4大且比5小的无理数:__.【答案】17(答案不唯一)【解析】【分析】由于4=5=,所以可写出一个二次根式,此根式的被开方数大于16且小于25即可.【详解】解:比4大且比5.(答案不唯一).【点睛】本题考查了对估算无理数的大小的应用,注意:无理数是指无限不循环小数,此题是一道开放型的题目,答案不唯一.12. 如图,,AC BC 是O e 的弦,,PA PB 是O e 的切线,若60C Ð=°,则P Ð=_________°.【答案】60【解析】【分析】因为,PA PB 是O e 的切线,由切线的性质得出P A ⊥OA ,PB ⊥OB ,得出∠P AO =∠PBO =90°,由圆周角定理可得∠AOB =2∠C =120º.,再由四边形内角和等于360°,即可得出结果.【详解】解:如图,连接OA ,OB ,∵,PA PB 是O e 的切线,∴P A ⊥OA ,PB ⊥OB ∴∠P AO =∠PBO =90°∵60C Ð=°,∴∠AOB =2∠C =120º,∵四边形内角和等于360º.∴在四边形AOBP 中,∠P =360º-90º-90º-120º=60º.故答案为:60.【点睛】此题考查了切线的性质、圆周角定理以及四边形内角和定理;解题的关键是利用切线的性质和圆周角定理结合四边形内角和等于360º求角.13. 如图,在ABC V 中,AB AC =,点D 在AC 上(不与点A ,C 重合),只需添加一个条件即可证明ABC V 和BDC V 相似,这个条件可以是____________(写出一个即可).【答案】∠A =∠CBD 或∠ABC =∠BDC 或=BC DCAC BC 或BC 2=AC ·DC (答案不唯一)【解析】【分析】相似三角形的判定定理:①两边对应成比例且夹角相等的两个三角形相似;②两角对应相等的两个三角形相似.据此解答即可.【详解】解:∵∠C =∠C∴添加∠A =∠CBD 或∠ABC =∠BDC 或=BC DCACBC 或BC 2=AC ·DC .故答案为:∠A =∠CBD 或∠ABC =∠BDC 或=BC DCAC BC 或BC 2=AC ·DC (答案不唯一).【点睛】此题考查了补充条件使两个三角形相似.解题的关键是熟知相似三角形的判定定理,特别注意用对应边成比例和一个角相等判定三角形相似的时候,其中相等的角一定要是这两条边的夹角.14. 如图,2022年北京冬奥会上,一些可看作正六边形的“小雪花”对称地排列在主火炬周围,中间空出了13个“小雪花”的位置来突出主火炬,在其中91个“小雪花”上面写有此次参会的国家或地区的名称,此外还有几个“小雪花”上面只有中国结图案,这些只有中国结图案的“小雪花”共有_________个.【答案】5【解析】【分析】根据图形先计算图中共有的小雪花的数量,再减去上面写有此次参会的国家或地区名称的小雪花,即可得答案.【详解】解:仔细观察图像可知,图中共有小雪花3×2+4×2+4×2+9×2+10×2+9×2+6×2+3×2=96(个)其中有在其中91个“小雪花”上面写有此次参会的国家或地区的名称,“∴小雪花”上面只有中国结图案有 96-91=5(个)故答案为:5.【点睛】本题考查了图形的规律,以及有理数的加减运算,解题的关键是仔细看图.15. 若关于x 的一元二次方程22(1)0-+-=a x a x a 有一个根是1x =,则=a ___________.【答案】-1【解析】【分析】根据一元二次方程和一元二次方程根的定义,可得2a a a-+-=,且10a-¹,即可求解.10【详解】解:根据题意得:2-+-=,10a a a解得:1a=-,a=或1∵10a¹,a-¹,即1∴1a=-.故答案为:-1.【点睛】本题主要考查了一元二次方程和一元二次方程根的定义,熟练掌握含有一个未知数,且未知数的最高次数为2的整式方程是一元二次方程是解题的关键.16. 尊老敬老是中华民族的传统美德,某校文艺社团的同学准备在“五一”假期去一所敬老院进行慰问演出,他们一共准备了6个节目,全体演员中有8人需参加两个或两个以上的节目演出,情况如下表:从演员换装的角度考虑,每位演员不能连续参加两个节目的演出,从节目安排的角度考虑,首尾两个节目分别是A,F,中间节目的顺序可以调换,请写出一种符合条件的节目先后顺序___________(只需按演出顺序填写中间4个节目的字母即可).【答案】EBDC##ECDB【解析】【分析】根据题意,可先确定第二个节目为节目E,继而确定第三个节目和第五个节目的可能性,最后确定了第四个节目,即可得到答案.【详解】由题意得,首尾两个节目分别是A,F,节目A参演演员有1、3、5、6、8,节目F参演演员有5、7,由于从演员换装的角度考虑,每位演员不能连续参加两个节目的演出故可先确定第二个节目为不含演员1、3、5、6、8的节目,即节目E ;第三个节目为不含2、7的节目,即节目B 或C第五个节目为不含5、7的节目,即节目B 或C所以,可确定第四个节目为节目D综上,演出顺序为节目AEBDCF 或AECDBF故答案为:EBDC 或ECDB (写一种即可).【点睛】本题考查了统计表、利用信息做出决策或方案,能够正确理解题意是解题的关键.三、解答题(共68分,第17-21题,每题5分,第22-24题,每题6分,第25题5分,第26题6分,第27,28题,每题7分)17. 计算:02cos30|3|(p +---°-.【答案】-1【解析】【分析】根据实数的计算,把各个部分的值求出来进行计算即可.【详解】解:原式=212´+-1--=-1.【点睛】本题考查了实数的混准确记忆特殊角的锐角三角函数值、绝对值化简、零指数幂、二次根式的化简是解题的关键.18. 解不等式组:()3242113x x x x ì--³-ïí+-<ïî【答案】4x <【解析】【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【详解】解不等式()324x x --³-,得:5x £,解不等式2113x x +-<,得:4x <,则不等式组的解集为4x <.【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.19. 已知230x x +-=,求代数式(23)(23)(3)+---x x x x 的值.【答案】0【解析】【分析】根据整式的乘法对代数式进行化简,整体代入即可得到答案.【详解】解:(23)(23)(3)+---x x x x =222(2)3(3)x x x ---=22493x x x --+=2339x x +- =23(3)x x +-∵230x x +-=∴原式=0即代数式(23)(23)(+---x x x x 的值为0.【点睛】本题考查整式的化简求值,根据整式的运算法则和乘法公式进行准确计算是解题的关键.20. 已知关于x 的一元二次方程210x ax a -+-=.(1)求证:该方程总有两个实数根;(2)若该方程的两个实数根都是整数,且其中一个根是另一个根的2倍,求a 的值.【答案】(1)见解析 (2)a 的值为3【解析】【分析】(1)根据一元二次方程20(0)ax bx c a ++=¹,根的判别式为△=24b ac =-△,进行化简即可证明;(2)根据根与系数的关系,以及根的倍数关系,列方程,解方程可得答案.【小问1详解】证明:()()()22241442a a a a a =---=-+=-n , ∵()220a -³,∴该方程总有两个实数根.【小问2详解】解:设该方程的一个根为x 1,则另外一个根为2 x 1,则1121221x x a x a +=ìí=-î①②,由①得13a x =,代入②可得:22990a a -+=,解之得13a =,232a =,又因为该方程的两个实数根都是整数,所以3a =.【点睛】本题考查一元二次方程根的判别式,根与系数的关系,根据题意,灵活运用所学知识是解题的关键.21. 中国古代数学家李子金在《几何易简集》中记载了圆内接正三角形的一种作法:“以半径为度,任用圆界一点为心,作两圆相交,又移一心,以交线为界,再作一交圆,其三线相交处为一角,其两线相交处为两角,直线界之亦得所求”.由记载可得作法如下:①作M e ,在M e 上取一点N ,以点N 为圆心,MN 为半径作N e ,两圆相交于A ,B 两点,连接AB ;②以点B 为圆心,AB 为半径作B e ,与M e 相交于点C ,与N e 相交于点D ;③连接AC ,AD ,BC ,BD .ABC V ,ABD △都是圆内接正三角形.(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)完成下面的证明,证明:连接AM,AN,MN,BM.∵==MA MN NA,∴AMNV为①_________.∴60Ð=°.AMN同理可得,60BMNÐ=°.∴120Ð=°.AMB∴60Ð=°(②____________)(填推理的依据).ACB∵BA BC=,∴ABCV是等边三角形.同理可得,ABD△是等边三角形.【答案】(1)见解析 (2)①等边三角形,②同弧上的圆周角等于圆心角的一半【解析】【分析】(1)按照作图的基本步骤规范画图即可.(2)根据圆的性质,等边三角形的判定解答.【小问1详解】根据作步骤,画图如下:【小问2详解】证明:如图,连接AM,AN,MN,BM.∵==MA MN NA,∴AMNV为等边三角形.∴60Ð=°.AMN同理可得,60BMNÐ=°.∴120Ð=°.AMB∴60Ð=°(同弧上的圆周角等于圆心角的一半)(填推理的依据).ACB∵BA BC=,∴ABCV是等边三角形.同理可得,ABD△是等边三角形.【点睛】本题考查了圆的基本作图,等边三角形的判定,圆周角定理,熟练掌握等边三角形的判定,灵活运用圆周角定理是解题的关键.22. 如图,在矩形ABCD中,AC,BD相交于点O,//BE AC.AE BD,//(1)求证:四边形AEBO 是菱形;(2)若2AB OB ==,求四边形AEBO 的面积.【答案】(1)见解析 (2)23【解析】【分析】(1)根据矩形的性质得出OA =OB ,进而利用菱形的判定解答即可;(2)根据菱形的性质及面积公式,解直角三角形即可求得.【小问1详解】证明://AE BD Q ,//BE AC \四边形AEBO 是平行四边形又Q 四边形ABCD 是矩形=BD AC \,1=2AO AC ,1=2BO BD =AO BO \ \四边形AEBO 是菱形【小问2详解】解:如图:连接EO ,交AB 于点FQ 四边形ABCD 是矩形=BD AC \,1=2AO AC ,1=2BO BD =AO BO \ 又2AB OB ==Q 2AB OB OA \===ABO \△是等边三角形,=60BAO аQ 四边形AEBO 是菱形AB EO \^,=EF OF=2=2sin 60222EO OF OA \×°=´´= \四边形AEBO 的面积为:11=22EO AB ×´【点睛】本题考查了矩形的性质,菱形的判定与性质,等边三角形的判定与性质,解直角三角形,作出辅助线是解决本题的关键.23. 如图,AB 为O e 的直径,C 为O e 上一点,AD 和过点C 的切线互相垂直,垂足为D .(1)求证:AC 平分DAB Ð;(2)若4cos 5CAD Ð=,5AB =,求CD 的长.【答案】(1)证明见详解(2)125【解析】【分析】(1)连接OC ,可证明//OC AD ,推导出OCA CAD Ð=Ð,又因为OA OC =,可得OCA OAC Ð=Ð,即可证明CAD OAC Ð=Ð,即AC 平分DAB Ð;(2)连接BC ,由AB 为O e 的直径可证明90ACB Ð=°,由(1)可知CAD OAC Ð=Ð,利用三角函数分别解Rt ABC V 、Rt ADC V ,解得AC 、AD 长度,再由勾股定理计算CD 的长即可.【小问1详解】证明:如图1,连接OC ,∵CD 为O e 切线,∴OC CD ^,∵AD CD ^,∴//OC AD ,∴OCA CAD Ð=Ð,又∵OA OC =,∴OCA OAC Ð=Ð,∴CAD OAC Ð=Ð,即AC 平分DAB Ð;【小问2详解】解:如图2,连接BC ,∵AB 为O e 的直径,∴90ACB Ð=°,∵CAD OAC Ð=Ð,∴cos cos AC OAC CAD AB==∠∠,即455AC =,解得4AC =,∵cos 45CAD AD AC Ð==,∴44164555AD AC ==´=,∴125CD ===.【点睛】本题主要考查了切线的性质、圆周角定理、三角函数解直角三角形以及勾股定理等知识,正确作出辅助线是解题关键.24. 某公园在人工湖里建造一道喷泉拱门,工人在垂直于湖面的立柱上安装喷头,从喷头喷出的水柱的形状可以看作是抛物线的一部分.安装后,通过测量获得如下数据,喷头高出湖面3米,在距立柱水平距离为d 米的地点,水柱距离湖面高度为h 米.(1)在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;(2)结合表中所给数据或所画图象,直接写出水柱最高点距离湖面的高度;(3)求h关于d的函数表达式;(4)公园希望游船能从喷泉拱门下穿过,已知游船的宽度约为2米,游船的平顶棚到湖面的高度约为1米,从安全的角度考虑,要求游船到立柱的水平距离不小于1米,顶棚到水柱的竖直距离也不小于1米,工人想只通过调整喷头距离湖面的高度(不考虑其他因素)就能满足上述要求,请通过计算说明应如何调整.【答案】(1)图见解析;(2)4米 (3)h=-d2+2d+3(4)水枪高度调节到5米以上【解析】【分析】(1)建立坐标系,描点,用平滑的曲线连线即可;(2)结合图象,得出最高点坐标为(1,4),进而得出结论;(3)利用顶点式h=a(d-1)2+4和点(3,0)即可求出h关于d的函数表达式;(4)设平移后的解析式为h1=-d2+3+m,根据题意求解即可.【小问1详解】解:如图所示【小问2详解】解:由图象得,最高点坐标为(1,4),∴水柱最高点距离湖面的高度为4米;【小问3详解】解:由题意,得设顶点式为h=a (d -1)2+4,又图象过点(3,0),∴a (3-1)2+4=0,解得a =-1,∴函数解析式h=-(d -1)2+4=-d 2+2d+3;【小问4详解】解:设水枪高度向上调整m 米时,游船恰好能从喷泉拱门下穿过,则平移后的解析式为h 1=-d 2+2d+3+m ,当横坐标为1+2=3时,纵坐标的值大于等于1+1=2,∴-32+6+3+m ≥2,解得m ≥2,∴水枪高度至少向上调整2米,∴水枪高度调节到5米以上.【点睛】本题考查二次函数喷泉的应用,二次函数解析式,二次函数图象的平移,解题的关键在于熟练掌握二次函数的图象建立二次函数模型.25. 某校初三年级有两个校区,其中甲校区有200名学生,乙校区有300名学生,两个校区所有学生都参加了一次环保知识竞赛,为了解两个校区学生的答题情况,进行了抽样调查,从甲、乙两个校区各随机抽取20名学生,对他们本次环保知识竞赛的成绩(百分制)进行了整理、描述和分析.下面给出了部分信息.a .甲校区成绩的频数分布直方图如下(数据分成4组:6070x £<,7080x £<,8090x £<,90100x ££);b .甲校区成绩在7080x £<这一组的是:74 74 75 77 77 77 77 78 79 79c .甲、乙两校区成绩的平均数、中位数如下:(1)写出表中m 的值;(2)两个校区分别对本次抽取的学生的成绩进行等级赋分,超过本校区的平均分就可以赋予等级A ,判断在本次抽取的学生中哪个校区赋予等级A 的学生更多,并说明理由;(3)估计该校初三年级所有学生本次环保知识竞赛的平直接写出结果).【答案】(1)78.5(2)乙校区赋予等级A 的学生更多,理由见解析(3)78【解析】【分析】(1)根据中位数的定义,将甲校区同学的成绩按从小到大顺序排序,找到第10、第11位的成绩,取平均值即可;(2)根据两个校区成绩的中位数和平均数,求出成绩超过平均数的人数,进行比较即可;(3)利用抽样调查学生的平均数估计总体学生的平均数即可求出答案.【小问1详解】解:甲校区成绩的中位数787978.52m +==.【小问2详解】解:乙校区赋予等级A 的学生更多,理由如下:甲校区成绩的平均数是79.5,第12位的成绩是79,8090x £<之间有7人,90100x ££之间有1人,可知成绩超过平均数的学生有8人,即赋予等级A 的学生有8人;乙校区成绩的平均数是77,中位数是81.5,可知成绩超过平均数的学生至少有10人,即赋予等级A 的学生至少有10人;所以乙校区赋予等级A 的学生更多.【小问3详解】解:估计甲校区200名学生成绩的平均数为79.5,乙校区300名学生成绩的平均数为77,因此估计该校初三年级所有学生本次环保知识竞赛的平均分为79.52007730078200300´+´=+,故答案为:78.【点睛】本题考查抽样调查的相关知识,熟练掌握平均数、中位数的定义以及利用样本估计总体的思想是解决问题的关键.26. 在平面直角坐标系xOy 中,点()()()123(2,0),1,,1,,2,--y y y 在抛物线2y x bx c =++上.(1)若12y y =,求3y 的值;(2)若213y y y <<,求3y 值的取值范围.【答案】(1)0 (2)340y -<<【解析】【分析】(1)将()11,y -和()21,y 分别代入函数解析式,根据12y y =,可解出b 的值,再将(2,0)-代入函数解析式,可解出c 的值;(2)若213y y y <<,由于函数图像开口向上,函数值越小离对称轴越近,函数值越大离对称轴越远,结合二次函数对称性可判断出对称轴2b 的取值范围,把点(2,0)-带入2y x bx c =++中求出24c b =-,进而可求出3y 值的取值范围.【小问1详解】解:将()11,y -和()21,y 分别代入解析式2y x bx c =++,得21(1)1y b c b c =--+=-+,2211y b c b c =++=++,12y y =Q ,11b c b c \-+=++,解得0b =,把点(2,0)-带入2y x c =+中,得20(2)c =-+,解得4c =-,\函数解析式为24y x =-当2x =,23240y =-=;【小问2详解】解:,2y x bx c =++Q 中,a 10=>,\函数图像开口向上,又213y y y <<Q 1102-+=Q ,12122-+=,1022b \-<<,解得10b -<<,把点(2,0)-带入2y x bx c =++中,得420b c -+=,24c b \=-,将()32,y 代入解析式2y x bx c =++,得342y b c =++,24c b =-Q ,34444y b b \=+-=,10b -Q <<,440b \-<<,即340y -<<.【点睛】本题主要考查了待定系数法求二次函数解析式和二次函数图像的性质,牢固掌握以上知识点并学会数形结合是做出本题的关键.27. 在ABC V 中,D 是BC 的中点,且90¹°∠BAD ,将线段AB 沿AD 所在直线翻折,得到线段AB ¢,作CE AB ∥交直线AB ¢于点E .(1)如图,若AB AC >,①依题意补全图形;②用等式表示线段,,AB AE CE 之间的数量关系,并证明;(2)若AB AC <,上述结论是否仍然成立?若成立,简述理由:若不成立,直接用等式表示线段,,AB AE CE 之间新的数量关系(不需证明).【答案】(1)①见解析;②AB AE CE =+ ,理由见解析(2)不成立,AB AE CE =-或CE AB AE=+【解析】【分析】(1)①根据题意作图即可;②连接,由折叠的性质可证,推出,再由平行线的性质及等腰直角三角形的性质得出,即可推出答案;(2)分两种情况,连接,由折叠的性质可证,推出,再由平行线的性质及等腰直角三角形的性质得出,即可推出答案.【小问1详解】①补全图形如图所示:②AB AE CE =+ ,理由如下:如图,连接B D B C ¢¢, ,Q 将线段AB 沿AD 所在直线翻折,得到线段AB ¢,,AB AB B AD BAD ¢¢\=Ð=Ð ,又AD AD =Q ,(SAS)B AD BAD ¢\D @D ,,AB D ABD B D BD ¢¢\Ð=Ð=,CE AB ∥Q ,BCE ABD \Ð=Ð,AB D BCE ¢\Ð=Ð,Q D 是BC 的中点,BD CD \= ,B D CD ¢\=,DB C DCB ¢¢\Ð=Ð,即AB D EB C BCE ECB ¢¢¢Ð+Ð=Ð+Ð,EB C ECB ¢¢\Ð=Ð,B E CE ¢\= ,AB AE B E AE CE ¢¢\=+=+ ,AB AB AE CE ¢\==+;【小问2详解】不成立,①AB AE CE =-,理由如下:如图,连接B D B C ¢¢,,Q 将线段AB 沿AD 所在直线翻折,得到线段AB ¢,,AB AB B AD BAD ¢¢\=Ð=Ð ,又AD AD =Q ,(SAS)B AD BAD ¢\D @D ,,AB D ABD B D BD ¢¢\Ð=Ð=,Q D 是BC 的中点,BD CD \= ,B D CD ¢\=,DB C DCB ¢¢\Ð=Ð,CE AB ∥Q ,180DCE ABD \Ð+Ð=°,即180ABD DCB ECB ¢¢Ð+Ð+Ð=°,180AB D DB C EB C ¢¢¢Ð+Ð+Ð=°Q ,180AB D DB C EB C ABD DCB ECB ¢¢¢¢¢\Ð+Ð+Ð=°=Ð+Ð+Ð,DCB DB C ¢¢Ð=ÐQ ,ECB EB C ¢¢\Ð=Ð,B E CE ¢\= ,AB AE B E AE CE ¢¢\=-=- ,AB AB AE CE ¢\==-.②CE AB AE =+,理由如下如图,连接B C¢,由题意得,,,AB AB BD B D B AB D ¢¢¢==Ð=Ð,Q D 是BC 的中点,BD CD \=,B D CD ¢\=,DB C DCB ¢¢\Ð=Ð,CE AB ∥Q ,B ECB \Ð=Ð,AB D ECB ¢\Ð=Ð,EB C ECB ¢¢\Ð=Ð,∴EC EB AE AB ¢==+.【点睛】本题考查了折叠的性质,平行线的性质,等腰三角形的性质,全等三角形的判定和性质,熟练掌握并灵活运用上述知识点是解题的关键.28. 在平面直角坐标系xOy 中,对于直线:º+l y kx b ,给出如下定义:若直线l 与某个圆相交,则两个交点之间的距离称为直线l 关于该圆的“圆截距”.(1)如图1,O e 的半径为1,当1,1k b ==时,直接写出直线l 关于O e 的“圆截距”;(2)点M 的坐标为(1,0),①如图2,若M e 的半径为1,当1b =时,直线l 关于M e 的“圆截距”小于45,求k的取值范围;②如图3,若M e 的半径为2,当k 的取值在实数范围内变化时,直线l 关于M e 的“圆截距”的最小值为2,直接写出b 的值.【答案】(1)2(2)①2k <-或102k -<£ ②b =【解析】【分析】(1)直线与圆的交点分别为()0,1A 和()1,0B -,则1OA OB ==,根据勾股定理计算即可.(2) ①根据圆的垂径定理,确定弦长为时,弦的位置,注意分类,确定直线的解析式,根据直线的增减性,确定k 的范围.②根据题意作出图形,然后利用等边三角形的性质及解三角形求解即可.【小问1详解】解:如图1,∵1,1k b ==,∴直线l 的解析式为1y x =+,∴直线与y 轴的交点为()0,1A ,与x 轴的交点为()1,0B -,∵O e 的半径为1,∴圆O 与y 轴的正半轴交点为()0,1A ,与x 轴的负半轴交点为()1,0B -,∴直线l 关于该圆的“圆截距”为AB ,∵1OA OB ==,∴AB =2211+=.【小问2详解】①如图2,设直线与y 轴正半轴交点为A ,且()0,1A ∵点M 的坐标为(1,0),M e 的半径为1,∴圆与x 轴正半轴交点为B (2,0),当1b =时,直线l 的解析式为1y kx =+,当直线经过点B 时,210k +=,解得k =12-;过点M 作MF AB ^,垂足为F ,∵1OA =,2OB =,∴AB ==,∴sin ABO Ð=5OA AB ==,∵1MB =,sin ABO Ð=5MF MB=,∴5MF =,5BF ==,设直线AB 与圆M 的另一个交点为C ,则2BC BF ==5,∵关于的“圆截距”小于45,∴k 的取值范围是102k -<£;设直线AM 与圆的一个交点为N ,∵点()0,1A ,点M 的坐标为(1,0),∴OA OM =,∴45AMO Ð=°,∴45BMN Ð=°,根据圆的对称性,直线AB 和直线AD 关于直线AN 对称,此时ED CB =,∴45DMN Ð=°,∴90DMB Ð=°,∴D 的坐标为()1,1-,∴11k +=-,解得2k =-,直线AD 的解析式为21y x =-+,∵关于的“圆截距”小于45,∴k的取值范围是2k<-;综上所述,k的取值范围是2k<-或12k-<£.②当k的取值在实数范围内变化时,直线l关于Me的“圆截距”的最小值为2,设直线与y轴交点为点()0,Q m,则过Q点的“圆截距”的最小值为2,如图所示:2RT=,MQ RT^,由题意得,RMT△为等边∴60MRQÐ=°,∴2sin60QM=´°=,∴OQ==,∴由对称性得b=.【点睛】本题考查了了垂径定理,一次函数的解析式和性质,特殊角的三角函数值,勾股定理,熟练掌握圆的性质,灵活运用特殊角的三角函数值是解题的关键.。
2010年北京市高级中等学校招生考试数 学 试 卷学校 姓名 准考证号考生须知 1.本试卷共6页,共五道大题,25道小题,满分120分。
考试时间120分钟。
2.在试卷和答题卡上准确填写学校名称、姓名和准考证号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
5.考试结束,将本试卷、答题卡和草稿纸一并交回。
一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个‧‧是符合题意的.1.2-的倒数是 A .12- B .12C .2-D .22.2010年6月3日,人类首次模拟火星载人航天飞行试验“火星 — 500”正式启动,包括中国志愿者王跃在内的6名志愿者踏上了为期12 480小时的“火星之旅”. 将12 480用科学记数法表示应为 A .312.4810⨯ B .50.124810⨯ C .41.24810⨯ D .31.24810⨯ 3.如图,在△ABC 中,点D E 、分别在边上,DE ∥BC ,若:3:4AD AB =,6AE =,则AC 等于AB AC 、A. 3B. 4C. 6D. 8 4.若菱形两条对角线的长分别为6和8,则这个菱形的周长为A .20B .16C .12D .105.从 1,2,3,4,5,6,7,8,9,10这十个数中随机取出一个数,取出的数是3的倍数的概率是A .15B .310C .13 D .126.将二次函数223y x x =-+化为2()y x h k =-+的形式,结果为A .2(1)4y x =++B .2(1)4y x =-+C .2(1)2y x =++D .2(1)2y x =-+ 7.10名同学分成甲、乙两队进行篮球比赛,他们的身高(单位:cm )如下表所示:队员1 队员2 队员3 队员4 队员5 甲队 177 176 175 172 175 乙队170175173174183设两队队员身高的平均数依次为x 甲,x乙,身高的方差依次为2S 甲,2S 乙,则下列关系中完全正确的是 A .x x =甲乙,22S S>乙甲B .x x =甲乙,22S S<乙甲 C.x x >甲乙,22S S >乙甲D .x x <甲乙,22S S<乙甲8.美术课上,老师要求同学们将右图所示的白纸只沿虚线裁开,用裁开的纸片和白纸上的阴影部分围成一个立体模型,然后放在桌面上,下面四个示意图中,只有一个‧‧‧‧符合上述要求,那么这个示意图是A BC D 二、填空题(本题共16分,每小题4分)9.若二次根式21x -有意义,则x 的取值范围是 . 10.分解因式:34m m -= .11.如图,AB 为⊙O 的直径,弦CD AB ⊥,垂足为点E ,连结OC ,若5OC =,8CD =,则AE = .12.右图为手的示意图,在各个手指间标记字母 A ,B ,C ,D.请你按图中箭头所指方向(即 A →B →C →D →C→B →A →B →C → … 的方式)从 A 开始数连续的正整数 1,2,3,4,…,当数到 12 时,对应的字母是 ;当字母C 第201次出现时,恰好数到的数是 ;当字母C 第21n +次出现时(n 为正整数),恰好数到的数是 (用含n 的代数式表示).三、解答题(本题共30分,每小题5分) 13.计算:101201043tan 603-⎛⎫-+--︒ ⎪⎝⎭.14.解分式方程 312422x x x -=--.15.已知:如图,点A B C D 、、、在同一条直线上,EA AD ⊥,FD AD ⊥,AE DF =,AB DC =. 求证:ACE DBF ∠=∠.16.已知关于 x 的一元二次方程 2410x x m -+-= 有两个相等的实数根,求m 的值及方程的根.17.列方程或方程组解应用题:2009年北京市生产运营用水和居民家庭用水的总和为5.8亿立方米,其中居民家庭用水比生产运营用水的3倍还多0.6亿立方米,问生产运营用水和居民家庭用水各多少亿立方米.18.如图,直线23y x =+与x 轴交于点A ,与y 轴交于点B .(1) 求A ,B 两点的坐标;(2) 过B 点作直线BP 与x 轴交于点P ,且使2OP OA =,求△ABP 的面积.四、解答题(本题共20分,每小题5分)19.已知:如图,在梯形ABCD 中,AD ∥BC ,2AB DC AD ===,4BC =.求B ∠的度数及AC 的长.20.已知:如图,在△ABC 中,D 是AB 边上一点,⊙O 过D B C 、、三点,290DOC ACD ∠=∠=︒.(1)求证:直线AC 是⊙O 的切线;(2)如果75ACB ∠=︒,⊙O 的半径为2,求BD 的长.21.根据北京市统计局公布的2006—2009年空气质量的相关数据,绘制统计图如下: 2006—2009年北京全年市区空气质量达到二级和好于二级的天数统计图由统计图中的信息可知,北京全年市区空气质量达到二级和好于二级的天数与上一年相比,增加最多的是 年,增加了 天;(2) 表1是根据《中国环境发展报告(2010)》公布的数据绘制的2009年十个城市空气质量达到二级和好于二级的天数占全年天数百分比的统计表,请将表1中的空缺部分补充完整(精确到1%);表1 2009年十个城市空气质量达到二级和好于二级的天数占全年天数百分比统计表城 市北京上海天津昆明 杭州广州南京成都沈阳西宁百分比91% 84% 100% 89% 95% 86% 86% 90% 77%(3) 根据表1中的数据将十个城市划分为三个组,百分比不低于95%的为A 组,不低于85%且低于95%的为B 组,低于85%的为C 组.按此标准,C 组城市 数量在这十个城市中所占的百分比为 %;请你补全右边的 扇形统计图.22.阅读下列材料:小贝遇到一个有趣的问题:在矩形ABCD 中,8AD =cm ,6AB =cm . 现有一动点P 按下列方式在矩形内运动:它从A 点出发,沿着与AB 边夹角为45︒的方向作直线运动,每次碰到矩形的一边,就会改变运动方向,沿着与这条边夹角为45︒的方向作直线运动,并且它一直按照这种 方式不停地运动,即当P 点碰到BC 边,沿与BC 边夹角为45︒的方向作直线运动,当P 点碰到CD 边,再沿着与CD 边夹角为45︒的方向作直线运动,…,如图1所示.问P 点第一次与D 点重合前‧‧‧与边相碰几次,P 点第一次与D 点重‧合时‧‧所经过的路径的总长是多少.小贝的思考是这样开始的 : 如图2,将矩形ABCD 沿直线CD 折叠,得到矩形11A B CD .由轴对称的知识,发现232P P P E =,11P A PE =. 请你参考小贝的思路解决下列问题:(1)P 点第一次与D 点重合前‧‧‧与边相碰 次;P 点从A 点出发到第一次与D 点重合时‧‧‧所经过的路径的总长是 cm ; (2) 进一步探究:改变矩形ABCD 中AD 、AB 的长,且满足AD AB >.动点P 从A 点出发,按照阅读材料中动点的运动方式,并满足前后连续两次与边相碰的位置在矩形ABCD 相邻的两边上. 若P 点第一次与B 点重合前‧‧‧与边相碰7次,则:A B A D 的值为 .2009年十个城市空气质量达到 二级和好于二级的天数占全年天数百分比分组统计图图1图2五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23.已知反比例函数ky x=的图象经过点(31)A -,. (1) 试确定此反比例函数的解析式;(2) 点O 是坐标原点,将线段OA 绕O 点顺时针旋转30°得到线段OB ,判断点B 是否在此反比例函数的图象上,并说明理由;(3) 已知点(36)P m m +, 也在此反比例函数的图象上(其中 0m <),过P 点作x 轴的垂线,交x 轴于点M . 若线段PM 上存在一点Q ,使得△OQM 的面积是12,设Q 点的纵坐标为n ,求2239n n -+的值.24.在平面直角坐标系xOy 中,抛物线22153244m my x x m m -=-++-+与x 轴的交点分别为原点O 和点A ,点(2,)B n 在这条抛物线上.(1) 求B 点的坐标;(2) 点P 在线段 OA 上,从O 点出发向A 点运动,过P 点作x 轴的垂线,与直线 OB 交于点E ,延长PE 到点D ,使得ED PE =,以PD 为斜边,在PD 右侧作等腰直角三角形PCD (当P 点运动时,C 点、D 点也随之运动).① 当等腰直角三角形 PCD 的顶点 C 落在此抛物线上时,求OP 的长;② 若P 点从O 点出发向A 点作匀速运动,速度为每秒1个单位,同时线段OA 上另一个点Q 从A 点出发向O 点作匀速运动,速度为每秒2个单位(当Q 点到达O 点时停止运动,P 点也同时停止运动).过Q 点作x 轴的垂线,与直线AB 交于点F ,延长QF 到点M ,使得FM QF =,以QM 为斜边,在QM 的左侧作等腰直角三角形QMN (当Q 点运动时,M 点、N 点也随之运动).若P 点运动到 t 秒时,两个等腰直角三角形分别有一条边恰好落在同一条直线上,求此刻t 的值.25.问题:已知△ABC 中,2B A C A C B ∠=∠,点D 是△ABC 内的一点,且AD CD =,BD BA =.探究DBC∠与ABC ∠度数的比值. 请你完成下列探究过程:先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.(1) 当90BAC ∠=︒时,依问题中的条件补全右图.观察图形,AB 与AC 的数量关系为 ;当推出15DAC ∠=︒时,可进一步可推出DBC ∠的度数为 ;可得到DBC ∠与ABC ∠度数的比值为 .(2) 当90BAC ∠≠︒时,请你画出图形,研究DBC ∠与ABC ∠度数的比值是否与(1)中的结论相同,写出你的猜想并加以证明.2010年北京市高级中等学校招生考试数学试卷答案一、选择题 1.A , 2.C , 3.D , 4.A , 5.B , 6.D , 7.B , 8.B , 二、填空题 9. x ≥21, 10. m (m +2)(m -2), 11. 2, 12. B 、603、6n +3; 三、解答题13. 解:原式=3-1+43-3=2+33。
北京市2010年高级中等学校招生考试一、选择题(本大题共8小题,共32.0分。
在每小题列出的选项中,选出符合题目的一项)1.−2的倒数是( )A. −B.C. −2D. 22.2010年6月3日,人类首次模拟火星载人航天飞行试验“火星—500”正式启动,包括中国志愿者王跃在内的6名志愿者踏上了为期12480小时的“火星之旅”.将12480用科学记数法表示应为( )A. 12.48×103B. 0.1248×105C. 1.248×104D. 1.248×1033.如图,在△ABC中,点D,E分别在AB,AC边上,DE//BC,若AD∶AB=3∶4,AE=6,则AC等于( )A. 3B. 4C. 6D. 84.若菱形两条对角线的长分别为6和8,则这个菱形的周长为( )A. 20B. 16C. 12D. 105.从1,2,3,4,5,6,7,8,9,10这十个数中随机取出一个数,取出的数是3的倍数的概率是( )A. B. C. D.6.将二次函数y=x 2−2x+3化为y=(x−ℎ)2+k的形式,结果为( )A. y=(x+1)2+4B. y=(x−1)2+4C. y=(x+1)2+2D. y=(x−1)2+27.10名同学分成甲、乙两队进行篮球比赛,他们的身高(单位:cm)如下表所示:队员1队员2队员3队员4队员5甲队177176175172175乙队170175173174183设两队队员身高的平均数依次为 甲, 乙,身高的方差依次为,,则下列关系中完全正确的是( )A. 甲= 乙,>B. 甲= 乙,<C. 甲> 乙,>D. 甲< 乙,<8.美术课上,老师要求同学们将下图所示的白纸只沿虚线裁开,用裁开的纸片和白纸上的阴影部分围成一个立体模型,然后放在桌面上,下面四个示意图中,只有一个符合上述要求,那么这个示意图是( )A. B.C. D.二、填空题(本大题共5小题,共21.0分)9.若二次根式有意义,则x的取值范围是________.10.分解因式:m 3−4m=________.11.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,若OC=5,CD=8,则AE= ________.12.下图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→⋯的方式)从A开始数连续的正整数1,2,3,4,…,当数到12时,对应的字母是________;当字母C第201次出现时,恰好数到的数是________;当字母C第2n+1次出现时(n为正整数),恰好数到的数是_________(用含n的代数式表示).13.阅读下列材料:小贝遇到一个有趣的问题:在矩形ABCD中,AD=8cm,AB=6cm.现有一动点P按下列方式在矩形内运动:它从A点出发,沿着与AB边夹角为45°的方向作直线运动,每次碰到矩形的一边,就会改变运动方向,沿着与这条边夹角为45°的方向作直线运动,并且它一直按照这种方式不停地运动,即当P点碰到BC边,沿着与BC边夹角为45°的方向作直线运动,当P点碰到CD边,再沿着与CD边夹角为45°的方向作直线运动……如图1所示.问P点第一次与D点重合前与边相碰几次,P点第一次与D点重合时所经过的路径的总长是多少.小贝的思考是这样开始的:如图2,将矩形ABCD沿直线CD折叠,得到矩形A 1B 1CD.由轴对称的知识,发现P 2P 3=P 2E,P 1A=P 1E.请你参考小贝的思路解决下列问题:(1)P点第一次与D点重合前与边相碰________次;P点从A点出发到第一次与D点重合时所经过的路径的总长是________cm;(2)进一步探究:改变矩形ABCD中AD,AB的长,且满足AD>AB.动点P从A点出发,按照阅读材料中动点的运动方式,并满足前后连续两次与边相碰的位置在矩形ABCD相邻的两边上.若P点第一次与B点重合前与边相碰7次,则AB∶AD的值为________.三、计算题(本大题共2小题,共10.0分)14.计算:.15.解分式方程四、解答题(本大题共10小题,共57.0分。
2010年北京数学一模解密预测试卷(四)题号—---------------- -三总分1617 18 19 20 21 22 23得分1.-3的相反数为2. “十一五”期间,我国教育事业发展成就显著,全国共有初中在校生6214.94 万 人,此人数用科学记数法表示为 3 .如图所示,数轴的一部分被墨水污染,被污染的部分内含有的整数4. 分解因式:3m 3-m =5. 在函数y—-—中,自变量X 的取值范围是6. 如图,D E 为AB AC 的中点,将△ ABC 沿线段DE 折叠,使点A 落在点 处,若/ B=500,则/ BDF=7•—人乘雪橇沿如图所示的斜坡笔直滑下,滑下的距离关系为s =10t 2t 2,若滑到坡底的时间为 4秒,则此人下降的高度为米。
&如图,AB 是O O 的直径,BC 是弦,ODL BC 于 E,交B C 于D 请写出两个不同类型 的正确结论:(1)9. 如图,如果以正方形 ABCD 勺对角线AC 为边作第二个正方形 ACEF 再 以对角线AE 为边作第三个正方形 AEGH 如此下去,…,已知正方形 ABCD 的面积S 1为1 ,按上述方法所作的正方形的面积依次为 S 2, S 3,…,S n(n 为正整数),那么第n 个正方形的面积 S n = 选择题(每小题3分,共18分)-1 .32.6(第 3 题)万人(保留3个有效数字)。
s (米)与时间tO第9题£ K£J£ 」£O t Ot Ot OtA. B. C. D.15.如图,一张矩形纸片沿 AB 对折,以AB 中点O 为顶点将平角五等分,并沿五等分的折线折叠,再沿10. 下列各式运算正确的是(.325A . X X XBC.X 3 亠 X 2 = X11•下列四幅图形中,表示两棵小树在同一时刻阳光下的影子的图形可能是A. B. C. D.12•如图,冰淇淋蛋筒下部呈圆锥形, 则蛋筒圆锥部分包装纸的面积 是( ) A. 20 cm 2 B . 40 cm 2 C. 20 二 cm 2D. 40 二 cm 213 .如图,是有几个相同的小正方体搭成的几何体的三种视图, 搭成这个几何体的小正方体的个数是( )A . 3 B. 4 (接缝忽略不计)土 T左视图 俯视图 (第 13 题)C. 5 D. 614 .如图所示:边长分别为 1和2的两个正方形,其一边在同一水平线上,小正方形沿该水平线自左向右 匀速穿过大正方形,设穿过的时间为 t ,大正方形内除去小正方形部分的面积为 S (阴影部分),那么S与t 的大致图象应为()5 cm则主视图CD剪开,使展开后为正五角星(正五边形对角线所构成的图形)17. (本题7分)如图,方格纸中的每个小方格都是边长为,则/ OCD等于(A. 108。