浙江省慈溪市横河初级中学九年级数学上册 1.2反比例函数的图像和性质教案(1) 浙教版

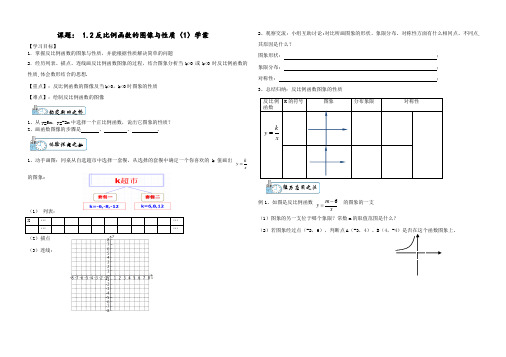
课题： 1.2反比例函数的图像与性质（1）学案【学习目标】1．掌握反比例函数的图象与性质，并能根据性质解决简单的问题2．经历列表、描点、连线画反比例函数图象的过程，结合图象分析当k>0或k<0时反比例函数的性质,体会数形结合的思想.【重点】：反比例函数的图像及当k>0，k<0时图象的性质 【难点】：绘制反比例函数的图像1、从y=5x ，y=-2x 中选择一个正比例函数，说出它图象的性质？2、画函数图像的步骤是 、 、 .1、动手画图：同桌从自选超市中选择一套餐，从选择的套餐中确定一个你喜欢的k 值画出 xk y =的图象;（1） 列表： X … ………（2）描点 （3）连线：2、观察交流：小组互助讨论:对比所画图象的形状、象限分布、对称性方面有什么相同点、不同点,其原因是什么？图象形状： ； 象限分布： ； 对称性： ； 3、总结归纳：反比例函数图象的性质例1、如图是反比例函数xm y 6-=的图象的一支 （1）图象的另一支位于哪个象限？常数m 的取值范围是什么？（2）若图象经过点（-2，6），判断点A （-3，4）、B （4，-4）是否在这个函数图象上。

反比例函数 K 的符号 图象分布象限 对称性xk y =构筑新旧之桥体验探究之趣经历应用之法例2：若图1是正比例函数y＝kx的图像，则反比例函数xky=的图像最有可能是（）1、已知反比例函数xy5=则其图象可能是（）A B C D2、试写出一个双曲线分布在第二、四象限的反比例函数。

3、反比例函数xky=的图象经过点（－1，2），那么这个反比例函数的解析式为，图象在第象限。

通过本节课的学习有哪些收获？1.知识收获？2.思想方法收获？小组实力大比拼抢答赛。

必做题：习题1.2第3题选做题：习题1.2 第4题勇攀能力之巅小试宝剑之锋共享收获之乐夯实新知之基。

一、核裂变1．裂变重核被中子轰击后分裂成两块质量差不多的新原子核，称为裂变．2．铀核裂变用中子轰击铀核，铀核发生裂变，铀核裂变的产物是多样的，其中最典型的反应是生成钡和氪，同时放出三个中子．核反应方程式为：235 92U＋10n→144 56Ba＋8936Kr＋310n.3．链式反应当一个中子引发一个铀核裂变后，反应释放出的中子又轰击其他原子核产生裂变，释放出的中子又轰击其他铀原子核……这样的反应一代接一代进行下去的过程，叫做裂变的链式反应．4．临界体积和临界质量通常把裂变物质能够发生链式反应的最小体积叫做它的临界体积，相应的质量叫做临界质量．5．发生链式反应的条件裂变物质的体积必须大于或等于临界体积，或裂变物质的质量必须大于或等于临界质量．如图所示为我国于1964年10月16日发射的第一颗原子弹爆炸成功的图片．同时，我国政府郑重承诺：中国在任何时候、任何情况下，都不首先使用核武器，不对无核国家或地区使用或威胁使用核武器．我国研制成功原子弹，极大地增强了我国的国防力量．你知道这其中蕴涵的物理知识吗？提示：原子弹是利用重核的裂变反应制成的，在极短时间内能够释放大量核能，发生猛烈爆炸．二、核电站原子核的链式反应可以在人工的控制下进行，从而实现了核能的可控释放，实现可控的条件是控制引起链式反应的中子的数目，方法是在核反应堆中的铀棒之间插入一些镉棒，镉具有极强的吸收中子的能力，当将镉棒插得深一些时，就能多吸收一些中子，使链式反应的速度慢下来，这种镉棒又叫控制棒．核能作为一种新型能源，在人类的发展过程中所起的作用越来越重要．核反应堆中发生着怎样的核反应？提示：核反应堆中发生的是可控链式反应．考点一重核的裂变及链式反应1．铀核的裂变(1)核子受激发：当中子进入铀235后，便形成了处于激发状态的复核，复核中由于核子的激烈运动，使核变成不规则的形状．(2)核子分裂：核子间的距离增大，因而核力迅速减弱，使得原子核由于质子间的斥力作用而分裂成几块，同时放出2～3个中子，这些中子又引起其他铀核裂变，这样，裂变就会不断地进行下去，释放出越来越多的核能．(3)核能的释放：由于重核的核子的平均质量大于中等质量原子核的核子的平均质量，因此，铀核裂变为中等质量的原子核时，会发生质量亏损，释放核能．(4)铀的存在形式在天然铀中，主要有两种同位素，99.3%的是238 92U,0.70%的是235 92U，虽然中子都能引起这两种铀核发生裂变，但它们和中子作用的情况明显不同．①235 92U俘获各种能量的中子都会发生裂变，且俘获低能量的中子发生裂变的概率大．②238 92U只有在俘获的中子的能量大于1 MeV时才能发生核反应，且裂变的几率较小．对于低于1 MeV 的中子只与铀核发生弹性碰撞，不能引起核反应．2．链式反应的条件铀块的体积大于或等于临界体积、质量大于或等于临界质量，只要满足其中之一即可．【例1】(多选)关于铀核裂变，下述说法正确的是( )A．铀核裂变的产物是多种多样的，但只能裂变成两种不同的核B．铀核裂变时还能同时释放2～3个中子C．为了使裂变的链式反应容易进行，最好用纯铀235D．铀块的体积对发生链式反应无影响1．什么是核裂变？2．什么是链式反应？3．链式反应发生的条件是什么？【答案】BC【解析】铀核受到中子的轰击，会发生裂变，裂变的产物是多种多样的，具有极大的偶然性，但裂变成两种不同的核的情况较多，也有的分裂成多种不同的核，并放出2～3个中子，铀235受中子的轰击时，裂变的概率大，而铀238只有俘获能量较高的中子时才能引起裂变，且裂变的概率小，而要发生链式反应，需使铀块体积大于或等于临界体积，故选项B、C正确．总结提能本题考查了重核裂变的知识．重核裂变是重核受中子轰击后分裂成中等质量核的反应，其释放能量的原因是重核的比结合能比中等质量核小．关于重核的裂变，以下说法正确的是( D )A．核裂变释放的能量等于它俘获中子时得到的能量B．中子进入铀块中时，一定发生链式反应C．重核裂变释放出大量能量，产生明显的质量亏损，所以核子数量减小D．由于重核的核子平均质量大于中等质量核的核子平均质量，所以重核裂变为中等质量的核时，要发生质量亏损，放出核能解析：根据重核发生裂变的条件和裂变放能的原理分析可知，裂变时因铀核俘获中子发生核反应，是核能转化为其他形式能的过程，而并非中子的能量，故A错误．链式反应是有条件的，即铀块的体积必须大于或等于其临界体积．如果体积小，中子进入铀块时，裂变中产生的中子散失到外界，没有足够的中子，则链式反应就不会发生，故B错误．在裂变反应中核子数是不会减少的，如235 92U＋10n―→9038Sr＋136 54Xe＋1010 n.其中各粒子质量分别为m U＝235.043 9 u，m n＝1.008 67 u，m Sr＝89.907 7 u，m Xe＝135.907 2 u，质量亏损为Δm＝(m U＋m n)－(m Sr＋m Xe＋10m n)≈0.151 0 u可见铀裂变的质量亏损是远小于一个核子的质量的，核子数是不会减少的，因此C错误．重核裂变为中等质量的原子核时，由于平均质量减小，发生质量亏损，从而释放出核能，故D正确．故选D.考点二核电站1．核心：核电站的核心是核反应堆，其简化示意图如下：各部分的作用如下：(1)铀棒：由天然铀或浓缩铀(铀235的含量占2%～4%)制成，它是核反应堆的燃料．(2)石墨(或重水)：石墨(或重水)作为减速剂，附着在铀棒周围，使反应生成的快速中子变为慢中子，便于铀235吸收，发生裂变．(3)镉棒：主要作用是吸收中子，控制反应速度，所以叫做控制棒．(4)混凝土防护层：屏蔽射线防止放射性污染．2．核电站发电的优点(1)消耗的核燃料少：一座百万千瓦级的核电站，一年只消耗浓缩铀30 t左右，而同样功率的火电站每年要消耗250万吨．(2)污染小：核电对环境的污染比火电小．【例2】铀核裂变的许多可能的核反应中的一个是U＋10n→141 56Ba＋9236Kr＋310n.23592(1)试计算一个铀235原子核裂变后释放的能量(235 92U、141 56Ba、9236Kr、10n的质量分别为235.043 9 u、140.913 9 u、91.897 3 u、1.008 7 u)；(2)1 kg铀235原子核发生上述裂变时能放出多少核能？它相当于燃烧多少煤释放的能量？(煤的热值为2.94×107 J/kg)【答案】(1)200.6 MeV (2)5.14×1026 MeV 2 800 t【解析】(1)铀核裂变的质量亏损为Δm＝(235.043 9＋1.008 7－140.913 9－91.897 3－3×1.008 7)u＝0.215 3 u.一个铀235原子核裂变后释放的能量为ΔE＝Δmc2＝0.215 3×931.5 MeV≈200.6 MeV.(2)1 kg铀235中含有原子核的个数为N＝103235×6.02×1023≈2.56×1024，1 kg铀235原子核发生裂变时释放的总能量E＝N·ΔE＝2.56×1024×200.6 MeV≈5.14×1026 MeV.设q为煤的热值，m为煤的质量，有E＝qm，所以m＝Eq＝5.14×1026×1.6×106×10－192.94×107kg≈2 800 t.总结提能解答此类题的关键在于如何把已知与所求联系起来，特别是要能考虑到利用相对原子质量和阿伏加德罗常数去计算1 kg铀所含的原子核的个数，只要能想到这儿，一切问题就都迎刃而解了．23592U受中子轰击时会发生裂变，产生139 56Ba和9436Kr，同时放出200 MeV的能量．现要建设发电能力是50万千瓦的核电站，用铀235作为原子锅炉的燃料．假设核裂变释放的能量全部被用来发电，那么一天需要纯铀235的质量为多少？若改用火力发电，需要燃烧值为2.94×107 J/kg的煤多少吨？阿伏加德罗常数为6.02×1023 mol－1.答案：0.527 kg 1.47×103 t解析：根据发电功率计算出每天应发电能的总量E ＝24 h×3.6×103×P ＝4.32×1013 J.要得到这么多能量需要裂变的铀原子数目n ＝4.32×10132×108×1.6×10－19＝1.35×1024(个)．则对应的质量m ＝nN ·μ＝1.35×10246.02×1023×235×10－3 kg ＝0.527 kg. 需要的煤的质量为m ′＝E2.94×107 J/kg ＝4.32×10132.94×107 kg ＝1.47×106 kg ＝1.47×103 t.重难疑点辨析 了解原子弹的原理原子弹是利用快中子导致链式反应而发生原子爆炸的武器．在裂变材料的体积大于临界体积时，可以使增殖系数K >1，这时中子数可逐代倍增，最后引起原子爆炸．对纯235 92U ，其K ＝2.若N 0＝1，则到第90代时，中子数已增到N ＝280个，其已大到相当于1 kg 铀的原子数，因此1 kg 纯235 92U 只要经过80代裂变就可以全部发生裂变．若将1 kg 铀做成球状，其直径不过5 cm ，而快中子的速度约为2×107 m·s －1，所以裂变进行得极其迅猛，其爆炸可在百分之一秒内完成．原子弹的结构形式有许多种，一般是将两块和多块小于临界体积的235 92U(或233 92U 、239 94Pu 等)放在一个密封的弹壳内，平时这几块相隔一定的距离，所以不会爆炸．使用时可通过引爆装置使它们骤然合为一体，由于其体积超过临界体积，爆炸立刻发生．【典例】 1964年10月16日，我国在新疆罗布泊沙漠成功地进行了第一颗原子弹试验，结束了中国无核时代．(1)原子弹爆炸实际上是利用铀核裂变时释放出很大能量，由于裂变物质的体积超过临界体积而爆炸．①完成下面核裂变反应方程式：U＋10n→()Xe＋9438Sr＋210n＋200 MeV.23592②铀原子核裂变自动持续下去的反应过程叫什么？(2)为了防止铀核裂变产物放出的各种射线危害人体和污染环境，需采取哪些措施？(写两种)【解析】(1)①根据核反应过程质量数、电荷数守恒可知，235 92U裂变为140 54Xe.②裂变自动持续下去的反应叫链式反应．(2)核反应堆外面需要修建很厚的水泥防护层，用来屏蔽射线；放射性核废料要装入特制的容器，埋入地层深处进行处理．【答案】(1)①140 54Xe ②链式反应(2)见解析原子弹与核电站都是核能利用的成果，都是利用了重核裂变，但原子弹爆炸时的反应速度是不可控的．1．镉棒在核反应堆中的作用是( D )A．使快中子变慢中子B．使慢中子变快中子C．使反应速度加快D．控制反应速度，调节反应速度的快慢解析：在核反应堆中石墨起变快中子为慢中子的作用，镉棒起吸收中子，控制反应速度，调节功率大小的作用．2.235 92U吸收一个慢中子后，分裂成136 54Xe和9038Sr，还放出( C )A．1个α粒子B．3个中子C．10个中子D．10个质子解析：设放出的粒子的质量数为x，电荷数为y，核反应过程满足质量数守恒和电荷数守恒．由题意可得⎩⎪⎨⎪⎧ 235＋1＝136＋90＋x 92＝54＋38＋y 解得⎩⎪⎨⎪⎧x ＝10，y ＝0. 由此判断该核反应放出的一定是中子，且个数是10.3．原子核反应有广泛的应用，如用于核电站等，在下列核反应中，属于核裂变反应的是( D )A.10 5B ＋10n→73Li ＋42HeB.238 92U→234 90Th ＋42HeC.14 7N ＋42He→17 8O ＋11H D.235 92U ＋10n→141 56Ba ＋9236Kr ＋310n解析：由链式反应特点知：反应过程中由一个中子引发裂变，放出2～3个中子促成链式反应，故D 正确．4．(多选)如图是慢中子反应堆的示意图，对核反应堆的下列说法正确的是( BC )A ．铀235容易吸收快中子发生裂变反应B ．快中子跟减速剂的原子核碰撞后能量减少，变成慢中子，慢中子容易被铀235俘获而引起裂变反应C ．控制棒由镉做成，当反应过于激烈时，使控制棒插入深一些，让它多吸收一些中子，链式反应的速度就会慢一些D ．若要使裂变反应更激烈一些，应使控制棒插入深一些，使大量快中子碰撞控制棒后变成慢中子，链式反应的速度就会快一些解析：根据铀235的特点，它更容易吸收慢中子而发生裂变，A 错误；在反应堆中减速剂的作用就是减少快中子能量从而更易让铀235吸收裂变，B 正确；链式反应的剧烈程度取决于裂变释放出的中子总数，镉控制棒可以吸收中子，因而可以控制核反应的快慢，即插入得深，吸收得多，反应将变慢，反之将加快，C 正确，D 错误．答案：1.10×103 kg解析：反应堆每年提供的核能E 总＝PT η，其中T 表示1年的时间．以M 表示每年消耗的235 92U 的质量，得M m U ＝E 总ΔE ，解得M ＝m U PT ηΔE，代入数据得M ＝1.10×103 kg.。

17.1.2反比例函数的图象和性质（教学设计）【教学目标】知识技能目标：会用描点法画出反比例函数的图像．能结合函数图象进行探索、理解并掌握反比例函数的性质。

过程方法目标：经历画图、观察、猜想、思考等数学活动，向学生渗透数形结合的思想方法，运用类比的方法让学生初步认识具体的反比例函数图象的特征．情感态度目标：让学生体会事物是有规律地变化着的观点．【教学重点】反比例函数的图象的形状特征。

【教学难点】难点：探索并掌握反比例函数的主要性质。

．【教学方法与教学手段】类比法、动手操作、组内交流、合作、讨论。

【教学过程】一、回顾旧知，引入新课1、问题：长方形的一边长为4，面积y和另一边长x之间有什么关系？2、此函数的图象是什么样子的？如何画出它的图象呢？3、正比例函数的性质填写下表：4、正比例函数的图像和性质是怎么得到的？是如何研究的？（经过哪几个步骤）二、递进设疑，导入新课问题：如果长方形的面积为4，一边长x和另一边长y之间又有什么关系呢？1、反比例函数的表达式 ___________________________2、解析式中自变量x的取值能为0吗？为什么______________________、3、画函数图象的方法是什么？4、函数做图的步骤是___________、_______________、____________。

【设计意图】利用学生已有的知识，激发学生的求知欲三、探索活动1，画出反比例函数xy 6=与x y 6-=的图像教学活动1：（1）引导学生运用画正比例函数图象的方法，分小组讨论尝试，采用列表、描点、连线的方法画出函数xy 6=与x y 6-=的图象。

（利用类比的方法，消除学生对函数的惧怕心理）（2） 老师边巡视，边指导，和学生一起找出错误的地方，分析原因。

（3） 老师在黑板上演示画反比例函数图象的步骤，展示正确的函数图象。

2，组内交流讨论画反比例函数图象容易出错的地方有哪些？（生评说总结，师补充）（1） 列表时x 不能为0，但有的学生会取0，取点不恰当，导致函数图象的不完整，不对称，为了便于计算和描点，应左右均匀，对称取值，且常取一些整数值。

《反比例函数的图像与性质》教学设计教学目标： 1. 知识与技能：会画反比例函数图象，理解反比例函数的图象和性质。

2. 过程与方法：感悟“数形结合”、“变化与对应”和“转化”的数学思想，并能应用数形结合和转化思想，根据反比例函数的图象探究其性质。

3.情感态度与价值观：在探索和交流的活动中，培养学生的观察、分析、探究、归纳及概括能力。

重点：经历画函数图像的过程，理解反比例函数的图象和性质。

难点：数形结合，灵活利用图像解决反比例函数问题。

教学过程：第一环节：创设情境，引入新知问题1 我们已经学习了正比例函数的哪些内容？是如何研究的？ 以正比例函数y=4x 为例。

师生活动：教师提问，学生思考、回答，教师根据学生回答的情况加以补充，并将答案填写在黑板的表格中，强调是从形状、位置、变化趋势三个方面去研究。

【设计意图】通过复习正比例函数的图象和性质，以及研究函数的一般方法，为学习反比例函数的图象和性质做好铺垫。

第二环节：观察探究，形成新知问题2 反比例函数的图象是什么样的？以画出反比例函数xy 4的图象为例，教师引导学生经历列表、描点、连线的过程。

（1）列表（如表1）：列表时，关注学生是否注意到自变量的取值应使函数有意义（即），同时，所取的点既要使自变量的取值有一定的代表性，又不至于使自变量或对应的函数值太大或是太小，以便于描点和全面反映图象的特征； （2）描点：一般情况下，所选的点越多图象越精确；（3）连线：引导学生用平滑的曲线，按照自变量从小到大的顺序连接各点，注意图象末端的延伸和延伸的趋势，得到反比例函数的图象。

师生活动：教师引导学生列表、描点、作图；展示学生作品；教师板书示范，并通过课件演示反比例函数图象的生成过程，给出双曲线的名称，并渗透它的形态特征.【设计意图】图象是直观地描述和研究函数的重要工具，通过经历用描点法画出反比例函数图象的基本步骤，可以使学生对反比例函数先有一个初步的感性认识。

在线分享文档：麦群超反比例函数的图象和性质【知识与技能】1. 会用描点法画反比例函数的图象；2. 理解反比例函数的性质.【过程与方法】 经历实验操作、探索思考、观察分析的过程中，培养学生探究、归纳及概括的能力.【情感态度】在通过画图探究反比例函数图象及其性质过程中，发展学生的合作交流意识，增强求知欲望.【教学重点】画反比例函数图象，理解反比例函数的简单性质【教学难点】 理解反比例函数性质，能用性质解决简单的问题.一、情境导入，初步认识问题 我们知道，一次函数y = 6x 的图象是一条直线，那么反比例函数y =6x 的图象是什么形状呢？你能用“描点”的方法画出函数的图象？【教学说明】教师提出问题，学生思考、交流，尝试着解决问题，教师巡视，关注学生的画图，及时纠正个别同学在画图中的不足和失误之处，帮助学生尽可能得到其合适的图象.二、思考探究，获取新知问题1 在同一坐标系中画出反比例函数y =6x 和y =12x的图象； 【教学说明】将全班同学分成两大组，分别完成问题y =6x 、y =12x的画图，在学生探索画反比例函数的图象过程中，教师应给予恰当点拨：如学生列表时，由于自变量x ≠0，故在x ＜0和x ＞0时，应各取三个以上的数据，以便使描点画图更精确些；在连线上，x ＜0和x ＞0 的两个分支应根据变化趋势用平滑曲线连接，但它们是不能相交的；列表中数据，描点时点的位置等不能出错，以保证图象更能反映出反比例函数的性质.在线分享文档让每个人平等地提升自我：麦群超 问题2 反比例函数y =-6x 和y =-12x的图象有什么共同特点？它们之间有什么关系？反比例函数y = 6x 和y =-6x的图象呢？同学间相互交流. 【教学说明】让两组同学分别交流，找出图象的特征，教师可分别参与讨论，帮助学生获取正确认知. 【归纳结论】由图象可发现：（1)它们都是由两条曲线组成，并且随|x|的不断增大（或减 小），曲线越来越接近x 轴（或y 轴），但这两条曲线永不相交；（2) y = 6x 和y =-6x 及y =12x 和y =-12x 的图象分别关于x 轴对称，也关于y 轴对称. 思考 观察函数y = 6x 和y =-6x 以及y =12x 和y =-12x 的图象. (1)你能发现它们的共同特征以及不同点吗？(2)每个函数的图象分别位于哪几个象限？ (3)在每个象限内y 随x 的变化如何变化？ 【归纳结论】反比例函数y =k x 的图象及其性质： (1)反比例函数y=k x (k 为常数，且k 0)的图象是双曲线； (2)当k ＞0时，双曲线的两个分支分别位于第一、三象限，在每个象限内，y 随x 值的增大而减小；(3)当k ＜0时，双曲线的两个分支分别位于第二、四象限，在每个象限内y 随x 值的增大而增大.三、典例精析，掌握新知例 如图，一次函数y = kx 十b 的图象与反比例函数y =m x 的图象相交于A 、B 两点.(1)根据图象，分别写出A 、B 的坐标；(2)求出两函数的解析式；(3)根据图象回答：当x 为何值时，一次函数的函数值大于反比例函数的函数值. 【分析】（1)观察图象，可直接写出A 、B 两点的坐标；（2)利用A 、B 两点的坐标，用待定系数法建立方程组求解，可确定两函数的解析式；（3 )通过两函数的交点A 、B 的坐标得出答案.解：（1)观察图象可知A ( -6，-2)，B （4，3)在线分享文档地提升自我By ：麦群超(2)由点B 在反比例函数y =m x 的图象上，所以把B (4，3)代入y =m x 得3 =4m ，故m =12，所以y=12x.由点A 、B 在一次函数y =kx 十b 的图象上，所以把A 、B 两点坐标代入y = kx 十b 得14326+2,1k b k k b b ⎧+==⎧⎪⎨⎨-=-⎩⎪=⎩解得 . 所以一次函数解析式为y = 12x+1.(3)由图象可知，当一6＜x ＜0或x ＞4时，一次函数的函数值大于反比例函数的函数值.【教学说明】本例有一定难度，教师可将题目展开，分步讲解，辅导学生克服对大题的恐惧.本题考查了从图象获取信息，应用待定系数法确定反比例函数与一次函数的关系式，以及利用图象比较函数值的大小等知识点. 四、运用新知，深化理解 1 .若反比例函数 y =21m x -的图象的一个分支在第三象限，则m 的取值范围是 . 2.如图是某一函数的一部分，则这个函数的表达式可能是（ ）A.y=5xB.y=-x+3C.y=-6xD.y=4x 【教学说明】学生独立完成，然后相互交流，谈谈自己的看法，教师应参与学生的讨论， 加深学生对反比例函数的图象及其性质的认识和理解，从而更好地掌握本节知识.在完成上述题目后，教师引导学生完成创优作业中本课时的“名师导学”部分. 【答案】1.m ＞122. C 五、师生互动，课堂小结 本节课学习了哪些知识？在知识应用过程中需要注意什么？你有哪些收获？1.布置作业：从教材“习题”中选取.在线分享文档让每个人平等2.完成创优作业中本课时的“课时作业”部分.“反比例函数的图象和性质”是反比例函数的教学重点，学生需要在理解的基础上熟练运用.在学习反比例函数图象和性质时k ＞0时，双曲线的两个分支在一、三象限；k ＜0时，双曲线的两个分支在二、四象限），学生可由画法观察图象得知.而增减性由解析式y =k x (k 0)可得到，学生也容易理解.但从图象观察增减性较难，借助计算机的动态演示就容易多了，所以本课教学最好用多媒体，因为运用多媒体比较函数图象，可以使学生更直观、更清楚地看清函数的变化，从而使学生加深对函数性质的理解.通过本课的教学，教师可深刻地体会到运用信息技术可加强数学课堂教学中的灵活性、直观性. 虽然制作起来比较麻烦，但能使课堂教学达到预想不到的效果，使课堂教学效率也明显提高.。

1.2反比例函数的图像和性质（一）一、教材背景分析到九年级上册一开始就学习“反比例函数”．这样编排的好处是因为反比例函数根据《数学课程课标》与原教材相比本章内容要求有所提高，主要表现在：其一性质的探索过程——根据图象和解析式探索并理解其性质；其二在实际问题中的应用．这是符合新课改的理念，总的来说是探讨知识发生的过程，培养学生自己探索问题，同时联系实际，提高学生分析解决问题的能力．与原浙教版相比，降低的地方是删去了反比例函数图象的性质：图象的两个分支都无限接近但永远达不到x轴和y轴．因为从教学实践看，学生对此不易理解，这条性质实际应用意义也不大．假如学生程度较好，老师在这方面也可以适当拓展．从编排顺序来看，原来浙教版中，本章内容放在初二下的“函数及其图象”一章中，编排顺序是平面直角坐标系—函数—正比例函数—反比例函数．本套教科书采用分步到位、穿插编排的方式．在八年级上册安排了“图形与坐标”、“一次函数”，反比例函数图像对思维要求比较高，图象分两支，且又是曲线，学生理解相对困难，略放后面与学生接受能力、认知水平相当，为学生探索理解反比例函数创造条件。

二、学习类型与任务分析①学习结果类型分析（一）学习结果：会画反比例函数的图像，通过反比例函数图象的分析，探索并掌握反比例函数图象的性质。

（1）反比例函数解析式和图像是数学事实；（2）反比例函数是数学概念；（3）用“描点法”画函数图像的一般步骤是数学原理；（4）用“描点法”画反比例函数图像是数学技能；（5）从函数解析式到函数图像的画法的数形结合的思想数学思想方法；（6）根据函数图像性质求自变量与函数的取值范围是数学问题解决。

②学习形式类型分析画反比例函数图像解析式(k 为常数，k ≠0)xk y 反比例函数的图像性质（二）学习形式：由于反比例函数的图像是根据反比例函数解析式用描点法得到的这是在原有知识的基础上学习一个水平更高的概念，常常采用发现学习的模式。

反比例函数的图像与性质教案教案标题：反比例函数的图像与性质教学目标：1. 理解反比例函数的定义及其特点；2. 掌握绘制反比例函数图像的方法；3. 理解反比例函数图像的性质。

教学准备：1. 教师：准备反比例函数的定义、性质和图像的讲解材料；2. 学生：准备笔、纸和计算器。

教学过程：导入（5分钟）：1. 引入反比例函数的概念，与学生一起回顾比例函数的定义及其性质；2. 提问：你们对反比例函数有什么了解？它与比例函数有何不同？讲解（15分钟）：1. 讲解反比例函数的定义：y = k/x，其中k为常数且不等于0；2. 解释反比例函数的性质：当x增大时，y减小；当x减小时，y增大；3. 通过实例演示如何计算反比例函数的值，并讨论k的正负对函数图像的影响；4. 讲解反比例函数图像的特点：曲线经过第一象限的原点，且与坐标轴无交点。

练习（15分钟）：1. 学生在纸上绘制反比例函数y = 3/x的图像，并标出至少5个点；2. 学生计算并填写表格：x取1、2、3、4、5时，对应的y值；3. 学生观察表格数据，并总结反比例函数图像的特点。

拓展（10分钟）：1. 引导学生思考：如果反比例函数的定义中的k为负数，图像会有什么变化？2. 学生尝试绘制反比例函数y = -2/x的图像，并与之前的图像进行比较；3. 学生讨论负数k对反比例函数图像的影响，并总结出结论。

归纳（5分钟）：1. 教师与学生一起总结反比例函数的图像与性质；2. 学生回答以下问题：反比例函数图像经过哪个象限的原点？与坐标轴是否有交点？作业：1. 学生完成课堂练习的剩余部分，并绘制反比例函数y = -4/x的图像；2. 学生回答书面问题：反比例函数图像的性质与比例函数图像的性质有何不同？评估：1. 教师检查学生在课堂练习中的图像绘制情况；2. 教师评估学生对反比例函数图像与性质的理解程度。

教学延伸：1. 学生可以进一步探索反比例函数的应用，如在实际问题中的应用；2. 学生可以尝试绘制更多不同参数的反比例函数图像，比较它们之间的差异。