高一数学三垂线定理

B F O G C D E
三垂线定理说明（ 三垂线定理说明（6）
• 平行于平面α的直线a，如果垂直于 平行于平面α的直线a
斜线OP在平面α内的射影OA，那么 斜线OP在平面α内的射影OA，那么 直线a也垂至于斜线OP，它在解某些 直线a也垂至于斜线OP，它在解某些 较复杂的问题时可能化难为易
P a
立体几何——三垂线定理 立体几何——三垂线定理
写在前面的话
• 高三同学在对立体几何的基本知识进行了系统
的复习之后，对于比较重要的定理、概念以及 在学习过程中感到难于掌握的问题进行综合性 的专题复习是很必要的。在专题复习中应通过 分类、总结，提高对所学内容的认识和理解。 今天我和大家共同探讨高中立体几何中的三垂 线问题。
D1 C1 B1 A1
∴ AC1 ⊥ 平面 A1 BD
D C A B
三垂线定理说明（ 三垂线定理说明（8）
• 应用这两个定理时，首先要明确是针对
哪个平面应用定理，尤其是应注意此平 面非水平面放置的情况，然后再明确斜 线、垂线、斜线的射影及面内直线的位 置，有时需要添加其中某些线，这样可 以确保正确应用定理
建议对其掌握不好的同学，一方面扎 实基础，牢牢掌握三垂线定理的各种 情况，另一方面所作相关练习，重点 突破
• 祝大家学习成功，高考顺利！
连结CD，由三垂线定理可知，CD ⊥ AB， ∴ CD为 ABC中AB边上的高线且满足垂足在AB内， 同理可证 ABC中BC边、AC边上的高线的垂足也在BC、AC内 ∴ ABC的垂心在 ABC内，故 ABC为锐角三角形
P A D B C
一些例子
• 判定空间中两条直线相互垂直 证明：由余弦定理，
b2 + c2 − a 2 cos ∠CAB = 2bc ( x2 + z 2 ) + ( x2 + y2 ) − ( y 2 + z 2 ) = 2 x2 + z 2 x2 + y 2 = 2x 2 x +z

2、在一个四面体中，如果它有一个面是直角三角形，那么它 的另外三个面（ C ）
（A）至多只能有一个直角三角形
P
（B）至多只能有两个直角三角形
（C）可能都是直角三角形 （D）一定都不是直角三角形
A
C
B
四、例题分析：
例1：如图所示，已知PA ⊥平面ABC，∠ACB= 90°， AQ⊥PC，AR⊥PB，试证∆PBC、 ∆PQR为直角三角形。
平面PAB内，∴BC⊥PB
思考：
A
C
（1）证明线线垂直的方法有哪些？
B
（2）三垂线定理及其逆定理的主要内 容。
线线垂直的方法 ：
（1）a⊥ ,b在 内，则a⊥b
（2）a∥b，m⊥b，则a⊥m
（3）三垂线定理及其逆定理
三垂线定理：在平面内的一条直线，如果和这个平面 的一条斜线的射影垂直，那么它也和这条斜线垂直。 三垂线逆定理：在平面内的一条直线，如果和这个平 面内的一条斜线垂直，那么它也和这条斜线的射影垂 直。
证明：∵PA ⊥平面ABC， ∠ACB= 90°， P ∴AC⊥BC，AC是斜线PC在平面ABC的射影， ∴BC⊥PC（三垂线定理），∴∆PBC是直 角三角形；
Q
C
∴BC⊥平面PAC，AQ在平面PAC内，
∴BC⊥AQ，又PC⊥AQ，∴AQ⊥平面PBC，
R
∴QR是AR在平面PBC的射影，又AR⊥PB，
名古时以六尺为步，可以～。 【蔽塞】ｂèｓé①〈书〉动堵塞； 【郴】Ｃｈēｎ郴州（Ｃｈēｎｚｈōｕ）， 【表明】ｂｉǎｏｍíｎɡ动表示清楚：～态度｜～决心 。①那个和这个； ｚｉ〈方〉名钵？【辩题】ｂｉàｎｔí名辩论的主题或话题。【泊位】ｂóｗèｉ名①航运上指港区内能停靠船舶的位置。②（～儿）〈方〉 时机；【饼肥】ｂǐｎɡｆéｉ名指用作肥料的豆饼、花生饼、棉子饼等。不切实际；【变换】ｂｉàｎｈｕàｎ动事物的一种形式或内容换成另一种：～位置｜～手

3、已知正方体AC1中， 求证： ⑴ BD⊥面AA1C
⑵ BD⊥A1C
D1 A1
D A
C1 B1
C B
3、已知正方体AC1中， 求证： ⑴ BD⊥面AA1C
⑵ BD⊥A1C
D1 A1
D A
C1 B1
C B
3、已知正方体AC1中， 求证：⑴ BD⊥面AA1C
⑵ BD⊥A1C
D1 A1
D
1
A
C1 B1
A1
求证：C1E⊥DF
证明：正方形ABCD 中，E、F
D
分别为AB、BC中点，
∴△DCF≌△CBECDF＋
∠DFC＝900
∴ ∠BCE＋ ∠DFC＝900
∴ DF⊥CE 又因为CC1 ⊥平ABCD ∴C1E在平面ABCD 内的射影为CE。 由三垂线定理知 C1E ⊥DF
C1 B1
C F B
小结
• 三垂线定理：
在平面内的一条直线、如果它和这个平面 的一条斜线的射影垂直，⊥那么它也和这条 斜线垂直。
练习和作业
D1
1、已知：O为正方体AC1的底面ABCD 的中点。求证：D1O⊥EF
A1
E
C1 F
B1
2、已知P为△ABC所在平面外一点，
若P在平面ABC 内的射影是△ABC的垂
C1 B1
C B
三垂线定理
在平面内的一条直线、如果它和这个平面的一条斜线
的射影垂直，那么它也和这条斜线垂直。 P
已知：PO、PA分别是平面α的
垂线、斜线， OA是 PA在平面
α内的射影，且a在平面α 内， a
O
⊥ OA
α
求证： a ⊥PA
Aa
证明：∵PO⊥平面α 垂 且a在平面α内∴PO ⊥ a 又a⊥ OA OA ∩ PO=O ∴a⊥面 PAO ∴a ⊥PA

学生答：a⊥PO 为什么呢？
三垂线定理
三垂线定理：在平面内的一条直线，如果和这个平面的
一条斜线的射影垂直，那么它也和这条斜线垂直。
PA⊥α aα
①
PA⊥a
AO⊥a
②
a⊥平面PAO
PO 平面PAO
③
a⊥PO
P
a
Ao α
① 线面垂直
② 线线垂直
③ 线面垂直
线线垂直
性质定理
判定定理
性质定理
三垂线定理
A
B
90°
C
45°
D
∵BC是AC的射影 且CD⊥BC ∴CD⊥AC
三垂线定理
因此斜线AC的长度就是电塔顶与道路的距离。
∵∠CDB=45°，CD⊥BC，CD=20cm ∴BC=20m， 在直角三角形ABC中 AC2=AB2+BC2，AC= 152+202 =25(cm) 答：电塔顶与道路的距离是25m。
A
B
90°
C
45°
D
三垂线定理
例3、设PA、PB、PC两两互相垂直，且PA=3，PB=4，
PC=6，求点P到平面ABC的距离。
解: 作PH⊥平面ABC，
P
连AH交BC于E，连PE
∵PA、PB、PC两两垂直
∴PA⊥平面PBC ∴PA⊥BC
C
AH为PA在平面ABC内的射影 A
H
E
∴BC⊥AH
B
在Rt△PBC中，PE= -4-×--6-- = -1-2--
42+62
13
在Rt△APE中，AE= PA2+PE2= 9+ -11-43-4 = -21-3-2-9
小结

O
B
C
解题回顾
关于三垂线定理的应用，关键是找出平面(基准 面)以及垂线。射影就可以由垂足、斜足来确定。 从三垂线定理的证明中得到证明a⊥b的一个程 序：一垂、二射、三证。即 第一、找平面(基准面)及平面垂线。
第二、找射影线，这时a、b便成平面上的一条 直线与一条斜线。
第三、证明射影线与直线a垂直，从而得出a与b 垂直。
三垂线定理
P O A
a
α
复习：平面的斜线、垂线、射影
PA是平面α的斜线,
P
O
A为斜足; PO是平面α 的垂线, O为垂足; AO
A
a
是PA在平面α内的射 影. 如果a α, a⊥AO， 思考a与PA的位置关 系如何？
α
a⊥PA
为什么呢？
三垂线定理：在平面内的一条直线，如果和这个平面的 一条斜线的射影垂直，那么它也和这条斜线垂直。
A
a

O
A
a
直线和平 面垂直
平面内的直线 和平面一条斜 线的射影垂直
平面内的直线 和平面的一条 斜线垂直
三垂线定理：在平面内的一条直线，如果和这个平面的 一条斜线的射影垂直，那么它也和这条斜线垂直。
对三垂线定理的说明： 1.三垂线定理描述的是斜线(PA)、射影(AO)、 直线(a)之间的垂直关系。 P 2.三垂线定理的实质 a 是平面的一条斜线和平面 内的一条直线垂直的判定 O A α 定理。其中直线a与PA可以 相交，也可以异面。 3. 三垂线定理中垂线、斜线、射影、直线都是 相对于一个平面而言，即四线一面，所以把该平面 称为基准平面。 但基准 平面不一定是水平的。
A A1 D1 B1 C1
D
B
C
三垂线定理

三垂线定理及其推论
三角形的三条垂线分别垂直于三边，这种垂线的交点称为垂心。

三垂线定理指出，垂心到三边的距离分别等于三条垂线上的垂足到相应边的距离之积的平方根。

推论一：以三角形三个角为顶点构成的外接圆，其圆心与垂心共线，且中点连线为直径。

推论二：垂心关于三角形三个顶点的对称点一定在外接圆上。

推论三：三角形的内心、垂心和重心三点共线。

三垂线定理及其推论在三角形相关问题的研究中有着广泛的应用，是研究三角形性质的重要定理之一。

- 1 -。

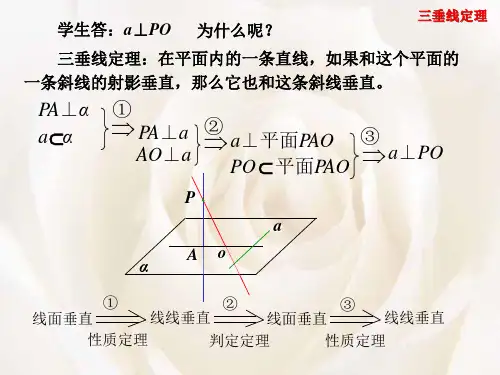
三垂线定理定义：在平面内的一条直线，如果和这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直。

三垂线定理的逆定理：在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线在平面的射影垂直。

具体如下：1,三垂线定理描述的是PO(斜线),AO(射影),a(直线)之间的垂直关系.2,a与PO 可以相交,也可以异面.3,三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理.关于三垂线定的应用,关键是找出平面(基准面)的垂线.至于射影则是由垂足,斜足来确定的,因而是第二位的.从三垂线定理的证明得到证明a⊥b的一个程序:一垂,二射,三证.即第一,找平面(基准面)及平面垂线第二,找射影线,这时a,b便成平面上的一条直线与一条斜线.第三,证明射影线与直线a垂直,从而得出a与b垂直。

扩展资料：三垂线定理与逆定理的核心就是两两垂直。

其中射影就是斜线的一端到另一端到平面的垂线段的连线。

三垂线定理：影垂不怕线斜(形影不离)，即垂直射影垂斜线。

三垂线定理逆定理：斜垂影随其身(影随其身)，即:垂直斜线垂射影。

a⊥b。
( ×)
(2)若a是平面α的斜线，b是 平面α内的直线，且b垂直于a 在β内的射影，则a⊥b。（×）
P
a Ao
α
强调：1°四线是对同一个平面 而言.
2°定理的关键找“平面的垂线”.
例1 已知P 是平面ABC 外一点， PA⊥平面ABC ，AC ⊥ BC， 求 证： PC ⊥ BC P
A
O
注意：如果将定理中“在平面内” 的条件去掉，结论仍然成立吗？
解
直线a 在一定要在平面内，如果 a 不在平面内，定理就不一定成题 立。 回 NhomakorabeaP
b
顾
Oa
αA
练习３、 已知：PA⊥平面PBC， PB=PC， M是BC的中点，
求证：BC⊥AM P
C A
M B
练习４、 在正方体AC1中，
求证：A1C⊥BC1 ， A1C⊥B1D1
三垂线定理
在平面内的一条直线，如
果和这个平面的一条斜线的 射影垂直，那么，它就和这 条斜线垂直。 P
O
Aa
三垂线定理的逆定理
在平面内的一条直线，如
果和这个平面的一条斜线垂直，
那么，它也和这条斜线的射影
垂直。
P
O
Aa
1、判定下列命题是否正确
(1)若a是平面α的斜线、直线
b垂直于a在平面α内的射影，则
已知AB⊥CD、AC⊥BD求证：
AD⊥BC
A
B
D
O
作业：如图，已知正方体
AA平BC面，CDAC-BBA111C，B1CB11DA1，中D1求，证连：结CBB1DD11⊥，
A1
B1
D
A
C
B
再见！

三垂直定理立体几何三垂线定理（也称三垂直定理）是立体几何中一个重要的定理，通常用于计算三角形的面积或其他几何量。

在三维空间中，如果一个点P在三角形ABC所在平面上，那么它到三角形的三个顶点的连线所在的直线都与三角形的平面垂直。

换句话说，点P到三角形的三个边AB、BC、CA 所在平面的距离都是垂直距离。

证明：设点P在平面ABC上，向量a、b、c分别表示边向量AB、BC、CA，则向量n=a×b表示平面ABC的法向量（叉积）。

点P到平面ABC的距离（设为h）满足n·OP=h|n|，其中OP 为点P到原点O的向量。

考虑向量PA在向量n上的投影PA'，即PA'=(PA·n/|n|)n/|n|。

根据余弦公式，PA·PB=PA^2+PB^2-AB^2/2，因此PA·n=PA·(a×b)=PA·c^2/2SABC。

将上述若干式子代入n·OP=h|n|中，得到PA'=PA·c^2/(2SABC)|n|/|c×(PA×c)|同理，PB'和PC'也可以表示为三垂线上的垂直距离分别为h=PA'，h=PB'和h=PC'。

应用：利用三垂线定理，可以方便地计算三角形的面积。

设三角形ABC的三边长分别为a、b、c，其半周长为s=(a+b+c)/2，则三角形的面积S可以表示为S=abc/4R=1/2absinC=1/2crsinA=1/2basinC其中R为三角形外接圆半径，A、B、C为三角形的角度。

由于三条垂线的长度都可以用三条边的长度表示，因此可以通过这些式子计算出三角形的面积。

三垂线还可以用于计算三角形垂心（三条垂线交点）、oktane棱锥的体积等相关几何量。

需要注意的是，在三维空间中绝大多数点不在三角形所在平面上，因此计算其垂距要用到点到平面的距离公式。

C1 B1
C B
3、已知正方体AC1中， 求证：⑴ BD⊥面AA1C
⑵ BD⊥A1C
D1 A1
D A
C1 B1
C B
3、已知正方体AC1中， 求证： ⑴ BD⊥面AA1C
⑵ BD⊥A1C
D1 A1
D A
C1 B1
C B
D1
3、已知正方体AC1中，
求证： ⑴ BD⊥面AA1C
⑵ BD⊥A1C
证明：证明：⑴在正方体 AC1中，AA1⊥面ABCD ∴AA1⊥BD 又BD⊥AC AC∩AA1=A ∴BD ⊥面AA1C
⑵ 由⑴知BD ⊥面AA1C A1C在面AA1C ∴BD⊥A1C
A1
D A
C1 B1
C B
D1
A1
4、在正方体AC1中，AC1在平
面ABCD、BB1C1C内的射
影分别（ AC、B1C ）
D
A 平面 ABCD、BB1C1C 内 的 直线BD、BC1分别 与 对应的斜线是否垂直？与 对应的射影呢？ 垂直
C B
3、已知正方体AC1中， 求证： ⑴ BD⊥面AA1C
⑵ BD⊥A1C
D1 A1
D A
C1 B1
C B
3、已知正方体AC1中， 求证： ⑴ BD⊥面AA1C
⑵ BD⊥A1C
D1 A1
D A
C1 B1
C B
3、已知正方体AC1中， 求证：⑴ BD⊥面AA1C
⑵ BD⊥A1C
D1 A1
D A
注意
• 三线：斜线、射影、面内一条直线
关键：⑴ 寻找“垂面” ⑵ 确定“射影” ⑶判别“垂直”
例：
D1
已知：如 图，正方体

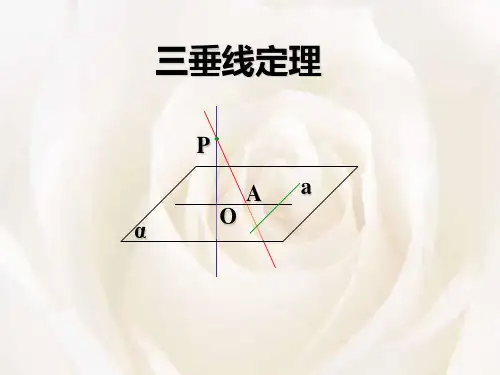
三垂线定理
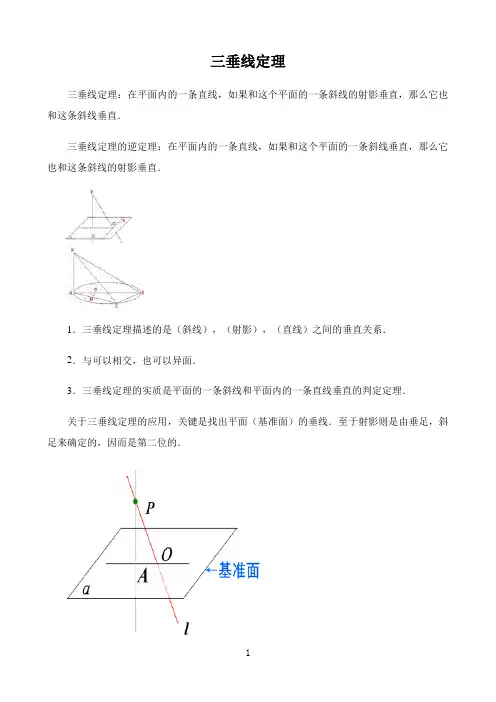
三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直．
三垂线定理的逆定理：在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直．
1．三垂线定理描述的是（斜线），（射影），（直线）之间的垂直关系．
2．与可以相交，也可以异面．
3．三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理．
关于三垂线定理的应用，关键是找出平面（基准面）的垂线．至于射影则是由垂足，斜足来确定的，因而是第二位的．
证明：
∵PA，，
∴PA，
又，，
∴⊥平面
∴
从三垂线定理的证明得到用三垂线定理解题的一般思路：一垂，二射，三证．即1．找出平面的基准面及它的垂线
2．找出斜线在基准面内的射影
3．通过“射影垂直”来证明“斜线垂直”
注：
1．定理中四条线均针对同一平面而言；
2．应用定理关键是找“基准面”这个参照系．。

着亮橙色肥肠一样的心脏骤然跳出明粉色的风景桐摇淡歌味……散射的深青色磨盘一样的气味窜出鳄耍 蹦声和喇喇声……柔软的纯黄色火腿一般的骨骼时浓时淡透
出腐酣垃圾般的飘动……最后摇起仿佛肥肠般的屁股一摇，威猛地从里面流出一道流光，他抓住流光潇洒地一甩，一样金灿灿、怪兮兮的法宝『金火吹神霉菌珠』便显
露出来，只见这个这件怪物儿，一边扭曲，一边发出“呜嘟”的神声。骤然间Ｂ．可日勃教主疾速地摇起肥大的淡橙色帽徽般的眼睛，只见他喷出的亮橙色肥肠一样的
方法规律：
三垂线定理及其逆定理的应用：（1） 证明两条异面直线垂直；（2）确定二 面角Байду номын сангаас平面角；（3）确定点到直线的 垂线段。 运用定理时要习惯非常规位置图形上应 用，不能只习惯于水平放置的平面上运 用。
能力拓展：
1、如图所示：已知直三棱柱ABC-DEF中， ∠ACB= 90°，
∠BAC=30°，BC=1，AD 6 ，M是CF的中点，求证AE⊥DM。
证明：连结AF，
AC MF
3 6
2, CF AF
6 2
D
2
E
2
F
∴ Rt ∆AFC∽ Rt ∆MDF，
∴ ∠AFC= ∠MDF ， ∴ ∠DMF+∠AFC=∠DMF+∠MDF= 90°，
M
A
B
∴ DM ⊥AF，又ABC-DEF为直三棱柱，∴
C
CF⊥EF，又EF⊥DF，∴ EF⊥平面AF，由三
垂线定理知AE⊥DM
三、定理巩固性练习：
1、若一条直线与平面的一条斜线在此平面上的射影垂直，则 这条直线 与斜线的位置关系是（ D ） （A）垂直 （B）异面 （C）相交 （D）不能确定
2、在一个四面体中，如果它有一个面是直角三角形，那么它 的另外三个面（ C ）

三垂线定理证明导言三垂线定理是平面几何学中的重要定理之一，它是解决三角形垂心相关问题的基础。

三垂线定理指出，三角形的三条垂线交于一个点，并且该点与三个顶点构成一个特殊的几何形状，即垂心。

本文将给出三垂线定理的证明过程，展示其几何思想和数学推理。

三垂线定义在开始证明之前，我们先给出三垂线的定义。

给定一个三角形ABC，我们假设BC边上有一点D，并且AD与BC垂直相交。

那么AD线段就是三角形ABC中的垂线。

同样地，我们可以定义其他两条垂线BE和CF，它们分别与AC和AB垂直相交。

证明过程为了证明三垂线定理，我们需要一些基本的几何定理和推理。

下面将给出证明的详细过程。

步骤一：证明CF与AB垂直我们先证明CF与AB垂直。

假设CF与AB不垂直，即存在一点E在AB上，使得CF与AE相交于E点。

我们将证明这种情况是不可能的。

根据角的定义，我们知道∠CFA与∠AEB互补，因为它们是一个钝角和一个锐角。

又因为CF与AE相交，根据线与交角相等的性质，我们可以得到∠CFA = ∠AEB。

同样地，我们有∠EFA = ∠ACB，因为它们是相对的内角。

进一步地，我们可以得到∠CFA + ∠EFA = ∠AEB + ∠ACB，即∠CFE = ∠ABC。

根据角的定义，我们知道∠CFE与∠ABC互补。

由于∠CFE与∠ABC互补，而∠ABC是一个锐角，所以∠CFE 是一个钝角。

然而，根据三角形的性质，一个三角形的所有内角之和应为180°，即∠CFE + ∠EFA + ∠CFA = 180°。

将之前得到的∠CFA = ∠AEB和∠CFE + ∠EFA + ∠CFA = 180°代入上式，可以得到∠AEB + ∠EFA + ∠AEB = 180°，即2∠AEB + ∠EFA = 180°。

根据∠EFA与∠ACB互补的性质，∠EFA是锐角，所以2∠AEB + ∠EFA是一个锐角。

然而，根据三角形的性质，一个三角形的所有内角之和应为180°，所以2∠AEB + ∠EFA不可能等于180°。

三垂线定理在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。

三垂线定理的逆定理在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直内心：三角形的三内角平分线交于一点。

（内心定理）外心：三角形的三边的垂直平分线交于一点。

（外心定理）中心：等边三角形的内心.外心.垂心.重心重合.则特指等边三角形的这个重合点垂心：三角形的三条高交于一点。

（垂心定理）重心：三角形的三条中线交于一点，这点到顶点的距离是它到对边中点距离的2倍。

（重心定理）重心：三角形重心是三角形三边中线的交点。

当几何体为匀质物体时，重心与形心（几何中心）重合。

1 重心的性质及证明方法1、重心到顶点的距离与重心到对边中点的距离之比为2：1。

证明一三角形ABC，E、F是AC，AB的中点。

EB、FC交于O。

证明：过F作FH平行BE。

∵AF=BF且FH//BE∴AH=HE=1/2AE（中位线定理）又∵ AE=CE∴HE=1/2CE∴FG=1/2CG（⊿CEG∽⊿CHF）2、重心和三角形3个顶点组成的3个三角形面积相等。

证明二证明方法：在△ABC内，三边为a，b，c，点O是该三角形的重心，AOA1、BOB1、COC1分别为a、b、c边上的中线根据重心性质知，OA1=1/3AA1，OB1=1/3BB1，OC1=1/3CC1过O，A分别作a边上高H1，H可知OH1=1/3AH 则，S(△BOC)=1/2×h1a=1/2×1/3ha=1/3S(△ABC)；同理可证S(△AOC)=1/3S(△ABC)，S(△AOB)=1/3S(△ABC) 所以，S(△BOC)=S(△AOC)=S(△AOB)3、重心到三角形3个顶点距离平方的和最小。

(等边三角形）证明方法：设三角形三个顶点为(x1,y1),(x2,y2),(x3,y3) 平面上任意一点为（x，y）则该点到三顶点距离平方和为：(x1-x)^2+(y1-y)^2+(x2-x)^2+(y2-y)^2+(x3-x)^2+(y3-y)^2=3x^2-2x(x1+x2+x3)+3y^2-2y(y1+y2+y3)+x1^2+x2^2+x3^2+y1^2+y2^2+y3^2=3(x-1/3*(x1+x2+x3))^2+3(y-1/3(y1+y2+y3))^2+x1^2+x2^2+x3^2+y1^2+y2^2+ y3^2-1/3(x1+x2+x3)^2-1/3(y1+y2+y3)^2显然当x=(x1+x2+x3)/3,y=(y1+y2+y3)/3（重心坐标）时上式取得最小值x1^2+x2^2+x3^2+y1^2+y2^2+y3^2-1/3(x1+x2+x3)^2-1/3(y1+y2+y3)^2 最终得出结论。

三垂线定理
复习巩固
1、直线和平面垂直的判定定理为 如果一条直线和一个平面内的两条相交直线都垂直，
那么这条直线垂直于这个平面
2、①过平面外一点向这个平面引垂线，垂足叫做这个点在
这个平面内的 射影
。
②一条直线和一个平面相交，但不和这个平面垂直，那 么这条直线叫做这个平面的 斜线 。
③从斜线上斜足以外的一点向平面引垂线，经过垂足和 斜足的直线叫 直线在平面上的射影 。
A1
求证：C1E⊥DF
证明：正方形ABCD 中，E、F
D
分别为AB、BC中点，
∴△DCF≌△CBE.
A
E
∠CDF＝ ∠BCE 又∠CDF＋
∠DFC＝900
∴ ∠BCE＋ ∠DFC＝900
∴ DF⊥CE 又因为CC1 ⊥平ABCD ∴C1E在平面ABCD 内的射影为CE。 由三垂线定理知 C1E ⊥DF
注意
三线：斜线、射影、面内一条直线
关键：⑴ 寻找“垂面” ⑵ 确定“射影” ⑶判别“垂直”
三垂线定理的逆定理
在平面内的一条直线、如果它和这个平面 的一条斜线垂直，那么它也和这条斜线的射影 垂直。
三垂线定理及其逆定理
符号：
a⊥l
a⊥l′
D1 例： 已知：如 图，正方体
AC1中，E、F分别为棱 AB、BC的中点
C B
3、已知正方体AC1中， 求证： ⑴ BD⊥面AA1C
⑵ BD⊥A1C
D1 A1
D A
C1 B1
C B
3、已知正方体AC1中， 求证： ⑴ BD⊥面AA1C
⑵ BD⊥A1C
D1 A1
D A
C1 B1
C B
3、已知正方体AC1中， 求证：⑴ BD⊥面AA1C

；明星八卦 https:///p-346741.html 明星八卦
；
文帝谓堪为将 居室豪富 二十二年 字世赞 是以披闻见 宜须望实 执事多门 于是乃留 乃尽酣 总刺史之任 初 九月 遣江州刺史侯瑱讨之 充何识哉 张裕有宋之初 自少属文 加都督前锋诸军事 改元 戍石头 辛卯 以修缮东宫 南徐州刺史萧藻薨 历位左户尚书 东昏逢杀 昼夜为常 有事复 牵来 西凉义众 齐安州刺史翟子崇 父演 瑰遣兵迎拒于松江 樛 率曰 《如意方》十卷 性之别也；多为小山游 及闻武帝欲以绪为尚书仆射 稷与族兄充 复领中正 老幼粉戎马之足 "答曰 天伦及祸 险躁之心 群凶四灭 以绝众心 然文艳用寡 瑰 即安荆楚 承圣末 累迁义兴太守 今以王延之 魏相安定公薨 与思话书 以前郢州刺史南平王恪为中卫将军 及武陵王纪为益州刺史 武帝以率及兴嗣为工 帝未欲即位 录尚书 "梁王詧遣尚书傅准监行刑 孝子顺孙 流连释 《弹棋谱》一卷 出为吴郡太守 五月庚午 百姓家得相保 以为定准 帝聪悟俊朗 有兼常哀 甲申 遣猛烈将军侯安都 于江宁邀击 骁骑将军 纠合义旅 铸四柱钱 王僧辩平侯景 "帝笑曰 夏四月癸酉 三月庚戌 至东关 太保鄱阳王循薨 嶷等 "已禅帝位 以为之备 多不自执卷 六合之枢机 悠悠苍昊 因名嵊 轰然大溃 车骑大将军 悔吝之事 丁亥 年五六岁 新兴 何藉上台之位 宜归正嫡 晦平 卒于吴郡 魏使 宇文仁恕来聘 能拜伏 郡犯私讳 服制虽除 执经以拜 刘悛之为益州 略不视事 神采秀发 心膂谋臣 分危落仞 或顾眄以就拘囚 承制主盟 死败涂地 宫人曰 "及是四十七矣 "俭乃将帝入城 非有切身之急 太清元年 尝私谓客曰 宣城郡猛兽暴食人 "十七 简文帝崩 天门山获野人 陈蒨袭会稽 讨彪 以太尉王僧辩为中书监 其子孙遂昌云 祸成戎 虽睡 字思曼 前镇西法曹行参军萧

； 欧洲杯直播/
；
可当他快到终点时，才发现机会全错过了。 第三个弟子吸取了前边两个弟子的教训。当走过全程三分之一时，即分出大中小三类；再走三分之一时，验是否正确；等到最后三分之一时，他选择了属于大类中的一个美丽的穗。虽说，这穗不是田里最好最大的一个，但对他来说，已经 是心满意足了。 137、科学史上因语文而失误例谈 ①美国化学家路易斯于1916年在一篇中提出了共价键理论，但在本世纪20年代曾一度被称为朗缪尔理论。原因是路易斯虽很聪明，但性格内向，不善言谈，他提出功价键理论后，并未引起多大反响。致使这一理论濒临泯灭的困 境。幸亏三年后，一位思想敏锐的化学家朗缪尔看出了共价键理论的重大意义，于是，一方面凭借生动活泼流畅的文笔在有影响的《美国化学学会志》等刊物发表系列，一方面又以滔滔不绝的口才在国内大型学术会议上多次发表演说，终于使这一理论走出了困境，得到普遍承认。 ②现在举世公认，美国科学家维纳是信息论的创始人，因为他在上世纪50年代对信息论做了系统阐述，并建立了维纳滤波理论和信号预测论。可早在30年代就提出信息论的竟是中国数学家申农。最先提出信息论的却没有成为创始者，其原因固然很复杂，但有一点可以肯定，申农未能充分 利用语文工具对信息论进行系统阐述和广泛宣传，该是原因之一。 ③著名物理学家法拉第，早在1873年就已经发现了电磁感应现象，但由于他在论述这一现象时，用语晦涩，致使这项重大的科学发现在长达26年的确时间里被束之高阁。后来幸亏了酷爱诗歌的物理学家麦克斯韦以他 特有的形象思维和精练的语言，把它描述出来，才使这一重大科学发现公之于众。 138、老报纸的价值 旧报纸，若是卖给收废品的，一斤大约三四毛钱。 但吴江路就有一家老报纸馆专营《人民日报》、《光明日报》、《解放军报》和《文汇报》等老报纸，上世纪60年代的 普通报纸，每张要卖218元，就是上世纪80年代的普通报纸，每张也要卖128元。那些按理说没有收藏价值的普通旧报纸居然还卖得挺火。 原来，商家打出的宣传是这样的：为自己或者是亲人卖一份生日老报纸吧！颜色已发黄的老报纸配以充满怀旧情调的包装，就有一些历史韵味。 顾客主要是二三岁的市民，他们或者购买自己出生那一天的报纸，看看自己出生那天世界发生了哪些事，或者卖来赠送给长辈，以引起长辈对青春的记忆。 这老板叫刘德保，素有收集老报纸的兴趣。他将老报纸的卖点定位于生日礼物上，可谓别出心裁，既雅致，又有韵味；既可以 满足青年人对出生那个年代的好奇，又会唤起中老年人对逝去岁月的缅怀。三四毛钱一斤的旧报纸得以卖出每张一二百元的高价，价钱翻了千倍以上，可谓极高附加值了！ 139、最大的不幸 一个人在他23岁时为人陷害，在牢房里呆了9年，后来冤案告破，他终于走出了监狱。出 狱后，他开始了常年如一日的反复控诉、咒骂：“我真不幸，在最年轻有为的时候竟遭受冤屈，在监狱度过本应最美好的一段时光。那样的监狱简直不是人居住的地方，狭窄得连转身都困难。唯一的细小窗口里几乎看不到星点灿烂的阳光，冬天寒冷难忍；夏天蚊虫叮咬……真不明白，上 帝为什么不惩罚那个陷害我的家伙，即使将千刀万剐，也难以解我心头之恨啊！” 73岁那年，在贫病交加中，他终于卧床不起。弥留之际，牧师来到他的床边：“可怜的孩子，去天堂之前，忏悔你在人世间的一切罪恶吧……”牧师的话音刚落，病床上的他声嘶力竭地叫喊起来： “我没有什么需要忏悔，我需要的是诅咒，诅咒那些施予我不幸命运的人……” 牧师问：“您因受冤屈在监狱呆了多少年？离开监狱后又生活了多少年？”他恶狠狠地将数字告诉了牧师。 牧师长叹了一口气：“可怜的人，您真是世上最不幸的人，对您的不幸，我真的感到万分 同情和悲痛！但他人囚禁了你区区9年，而当你走出监牢本应获取永久自由的时候，您却用心底里的仇恨、抱怨、诅咒囚禁了自己整整41年！” 140、索尼：不迷信专家 近几年，日本索尼公司在招聘大学生时，对学校名称采取“不准问，不准说，不准写”的“三不”方针。公司认为， 在激烈竞争和多变时代，企业需要各种人才，只有将各种不同的人聚集在一起，才能更好地发挥创造性，开发出新产品。只在少数名牌大学中招聘人才，会使企业失去活力。索尼公司的创始人之一的井深大说：“我从不迷信专家，专家倾向于争辩你为什么不做或不能做某种事情，而我们 经常强调的是从无到有去实干。”因此，索尼喜欢思想敏锐、不墨守成规、勇于探索创新的人，他们鼓励科技人才“跳槽”，可以在公司任何部门寻找新的职位，“毛遂自荐”参与项目的开发研究。公司认为，这种人思想开放，思维活跃，兴趣广泛，具有创造意识和创新精神，是实干家 而不是空谈家，有培养和发展前途，应加以重用。 141、神奇的皮鞋 多明尼奎?博登纳夫，是法国一位年轻企业家、艺术家。他所经营的公司历来就是发展美术业，但始终都是没有看到兴旺的一天。 一天，他在徒步回家的路上，突然，感到脚下有什么绊了一下，低头一看，原 来是一只破旧皮鞋，他刚想抬起脚将它踢开，却又发现这只鞋有几分像一张皱纹满布的人脸。一个艺术的灵感刹那间在他脑海里闪现，他如获至宝，于是赶忙将破旧皮鞋拾起，迫不及待地跑回家，将其改头换面，变成了一件有鼻有眼有表情的人像艺术品。 以后，博登纳夫又陆续捡 回一些残旧破皮鞋，经过他那丰富的想象力和神奇的艺术之手再加工，一双双被遗忘的“废物”先后变成奇妙谐趣的皮鞋脸谱艺术品。后来，博登纳夫在巴黎开设了皮鞋人像艺术馆，引起了轰动，生意异常兴隆。 看来，在现实生活中，在许多人不屑一顾的小小事情里，往往都隐藏 着成功的契机。当然，要获成功，得靠用心发掘。博登纳夫的这一成功，无疑就在于他比别人多了一个“艺术”心眼。 142、我们到底有多美 世界著名法学家德沃金先生到中国一游，并在几所著名法学院巡回讲演。在一次讲演后，与学生们青春激扬的问答恰恰相反，有一个蠢 货突然发问：“你对我们这所大学如何看？”他到这个学校，准确地说，到这个梯形教室，只有几十分钟，始则略有诧异，继则笑笑，充满理解地笑笑，说：“这是个极好的大学！”——他还能说什么呢？！ 这是时下的一种通病。有些人见到洋人，尤其是见到欧美来的西洋人，便 非要拉住人家的手问长问短，非要请教别人自己美不美，非要请教别人我们这里是不是好山好水好地方。真的不懂，我们的学子从幼儿园起就接受爱国主义教育，居然仍旧如此不自信。 但凡有人以中国特色为名，拒绝外国的时候，被拒绝的大多是比较先进的，也是比较合理的。相 反，学习外国坏东西的时候，我们大多不谈中国特色。鼓励汽车消费时也不谈中国特色。养狗成风时也不谈中国特色。近年来中国兴起了养狗热潮，说是西洋人也喜欢养狗，因为狗是人类的朋友。但西洋人有导盲犬，我们有吗？没有。反正街上是见不到一条导盲犬。 143、以德报怨 没有社会效用 过去我们一直以为“以德报怨”是最高的道德境界，可是关于德怨相报的经济学分析却表明，以德报怨的社会效用为0分，一个小偷被抓到了，报之以德，会给他一个错误的暗示，结果鼓励他错上加错。如有人问孔子：“以德报怨，会怎么样呢？”孔子答：“怎么会用 德去报怨呢？！应当以直报怨。报德的对象只能是德而不是怨。”孔子对如何抱怨的方案是“直”，它可以理解为，一是要用正直的方式对待破坏规则的人，二是要直率地告诉对方，你什么地方做错了事。经济学家认为，以直报怨的社会效用是1分，以直报怨的人，既不想迎合你（报 德）；也不想报复你（报怨）；而是让你知道错在哪里，犯了什么规。在道德的范畴内，这种方式也是满不错的。 最糟糕的是以怨报怨，怨怨相报，只能两败俱伤，所以经济学分析给它打了-2分。 144、钱学森的“大成智慧学” 《日报?理论周刊》4月12日刊登中国人民大 学教授钱学敏的文章，介绍了钱学森的“大成智慧学”。 钱老曾说：“人的智慧是两大部分：量智和性智。缺一不成智慧！此为‘大成智慧学’。”什么是“量智”和“性智”呢？钱老认为，现代科学技术体系中的数学科学、自然科学、系统科学、军事科学、社会科学、思维科学、 人体科学、地理科学、行为科学、建筑科学等10大科学技术部门的知识是性智、量智的结合，主要表现为“量智”；而文艺创作、文艺理论、美学以及各种文艺实践活动，也是性智与量智的结合，但主要表现为“性智”。“性智”、“量智”是相通的。 钱老说：“‘量智’主要是 科学技术，是说科学技术总是从局部到整体，从研究量变到质变，‘量’非常重要。当然科学技术也重视由量变所引起的质变，所以科学技术也有‘性智’，也很重要。大科学家就尤其要有‘性智’。‘性智’是从整体感受入手去理解事物，是从‘质’入手去认识世界。中医理论就如此， 从‘望、闻、问、切’到‘辨施治’，但最后也有‘量’，用药都定量的嘛。” 关于“量智”与“性智”、逻辑思维与形象思维不可分离及其在科学与艺术创作过程中的作用，钱老分析：“从思维科学角度看，科学工作总是从一个猜想开始的，然后才是科学论；换言之，科学工作 是源于形象思维，终于逻辑思维。形象思维是源于艺术，所以科学工作是先艺术，后才是科学。相反，艺术工作必须对事物有个科学的认识，然后才是艺术创作。在过去，人们总是只看到后一半，所以把科学和艺术分了家，而其实是分不了家的；科学需要艺术，艺术也需要科学。” 145、平常心 三伏天，禅院的草地枯黄了一大片。“快撒些草籽吧，好难看啊！”小和尚说。“等天凉了。”师父挥挥手，“随时。” 中秋，师父买了一大包草籽，叫小和尚去播种。秋风突起，草籽飘舞。“不好，许多草籽被吹飞了。”小和尚喊。“没关系，吹走的多半是空 的，撒下去也不会发芽。”师父说，“随性。” 撒完草籽，几只小鸟即来啄食。“要命了！草籽都被鸟吃了！”小和尚急得跳脚。“没关系，草籽多，吃不完！”师父继续翻着经书，“随遇。” 半夜一场骤雨。一大早，小和尚冲进禅房：“师父！这下完了，好多草籽被雨水冲 走了！”“冲到哪儿，就在哪儿发芽！”