西工大,西电孙肖子版模电第九章状态变量法--答案.

模拟电子技术_沈阳工业大学中国大学mooc课后章节答案期末考试题库2023年1.当OCL电路的最大输出功率为1W时，功放管的集电极最大耗散功率应大于1W。

（）答案:错误2.当温度升高时，二极管的正向导通压降将增大。

（）答案:错误3.直流稳压电源中滤波电路的目的是。

答案:将交、直流混合量中的交流成分滤掉4.集成运放工作在线性区的条件是。

答案:引入负反馈5.电容滤波电路适用于小负载电流，而电感滤波电路适用于大负载电流。

（）答案:正确6.场效管放大电路的放大能力没有晶体管放大电路的强。

( )答案:正确7.多级放大电路的输入电阻是（）。

答案:第一级的输入电阻8.为了使结型N沟道场效应管工作在恒流区，应使uGS（）答案:<09.场效管放大电路的输入电阻比晶体管放大电路的大。

( ）答案:正确10.场效应管是电压控制电流型器件。

（）答案:正确11.放大电路在低频信号作用时放大倍数数值下降的原因是。

答案:耦合电容和旁路电容的存在12.为了使滤波电路的输出电阻足够小，保证负载电阻变化时滤波特性不变，应选无源滤波电路。

答案:错误13.整流的目的是。

答案:将交流变为直流14.直流电源是一种将正弦信号转换为直流信号的波形变换电路。

（）答案:错误15.在单相桥式整流电容滤波电路中，若有一只整流管断开，输出电压平均值变为原来的一半。

（）答案:错误16.任何放大电路都有功率放大作用。

（）答案:正确17.集成运放的末级采用互补输出级是为了（）。

答案:以上都正确18.改善差分放大电路性能的措施有（）。

答案:以上都正确19.为了增大电压放大倍数，集成运放的中间级多采用（）。

答案:共射放大电路20.判断串联、并联反馈的方法是（）答案:反馈节点短路法21.欲将电压信号转换成与之成比例的电流信号，应在放大电路中引入答案:电流串联负反馈22.欲从信号源获得更大的电流，并稳定输出电流，应在放大电路中引入。

答案:电流并联负反馈23.为了稳定放大电路的输出电压，应引入负反馈。

《模拟电子技术基础》典型习题解答第一章半导体器件的基础知识1.1 电路如图P1.1所示，已知u i＝5sinωt (V)，二极管导通电压U D＝0.7V。

试画出u与u O的波形，并标出幅值。

i图P1.1 解图P1.1解：波形如解图P1.1所示。

1.2 电路如图P1.2（a）所示，其输入电压u I1和u I2的波形如图（b）所示，二极管导通电压U D＝0.7V。

试画出输出电压u O的波形，并标出幅值。

图P1.2解：u O的波形如解图P1.2所示。

解图P1.21.3 已知稳压管的稳定电压U Z ＝6V ，稳定电流的最小值I Zmin ＝5mA ，最大功耗P ZM ＝150mW 。

试求图P1.3所示电路中电阻R 的取值范围。

图P1.3解：稳压管的最大稳定电流 I ZM ＝P ZM /U Z ＝25mA电阻R 的电流为I ZM ～I Zmin ，所以其取值范围为Ω=-=k 8.136.0ZZ I ～I U U R1.4 已知图P1.4所示电路中稳压管的稳定电压U Z ＝6V ，最小稳定电流I Zmin ＝5mA ，最大稳定电流I Zmax ＝25mA 。

（1） 别计算U I 为10V 、15V 、35V 三种情况下输出电压U O 的值； （2） 若U I ＝35V 时负载开路，则会出现什么现象?为什么？图P1.4解：（1）当U I ＝10V 时，若U O ＝U Z ＝6V ，则稳压管的电流小于其最小稳定电流，所以稳压管未击穿。

故V33.3I LLO ≈⋅+=U R R R U当U I ＝15V 时，若U O ＝U Z ＝6V ，则稳压管的电流小于其最小稳定电流，所以稳压管未击穿。

故LO I L 5VR U U R R =⋅≈+当U I ＝35V 时，稳压管中的电流大于最小稳定电流I Zmin ，所以U O ＝U Z ＝6V 。

（2）=-=R U U I )(Z I D Z 29mA ＞I ZM ＝25mA ，稳压管将因功耗过大而损坏。

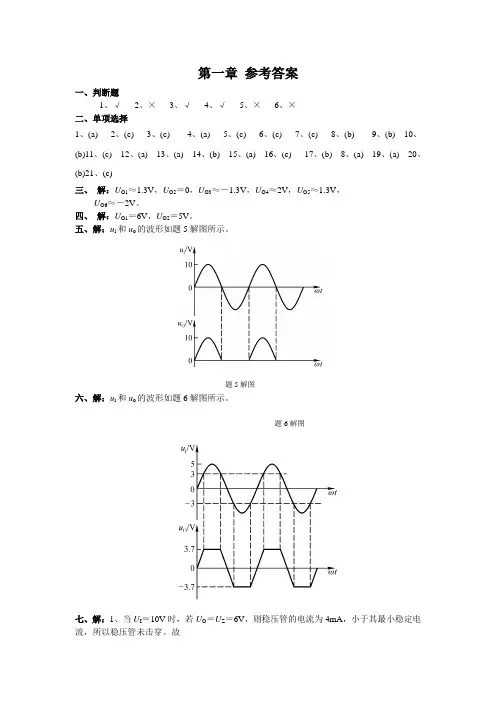
第一章参考答案一、判断题1、√2、×3、√4、√5、×6、×二、单项选择1、(a)2、(c)3、(c)4、(a)5、(c)6、(c)7、(c)8、(b)9、(b) 10、(b)11、(c) 12、(a) 13、(a) 14、(b) 15、(a) 16、(c) 17、(b) 8、(a) 19、(a) 20、(b)21、(c)三、解：U O1≈1.3V，U O2＝0，U O3≈－1.3V，U O4≈2V，U O5≈1.3V，U O6≈－2V。

四、解：U O1＝6V，U O2＝5V。

五、解：u i和u o的波形如题5解图所示。

题6解图题5解图六、解：u i和u o的波形如题6解图所示。

题6解图七、解：1、当U I＝10V时，若U O＝U Z＝6V，则稳压管的电流为4mA，小于其最小稳定电流，所以稳压管未击穿。

故V 33.3I LLO ≈⋅+=U R R R U当U I ＝15V 时，稳压管中的电流大于最小稳定电流I Zmin ，所以U O ＝U Z ＝6V同理，当U I ＝35V 时，U O ＝U Z ＝6V 。

2、 =-=R U U I )(Z I D Z 29mA ＞I ZM ＝25mA ，稳压管将因功耗过大而损坏。

八、解：波形如题8解图所示。

题8解图第二章 参考答案一、判断1、√2、×3、×4、√5、×6、√7、×8、×9、√ 10、× 11、√二、单项选择题1、(c)2、(a)3、(b)4、(b)5、(c)6、(a)7、(a)8、(a)9、(b) 10、(c) 11、(b) 12、(a) 13、(c) 14、(b) 15、(c) 16、(b) 17、(b) 18、(c) 19、(b) 20、(a) 21、(c) 22、(a) 23、(c) 24、(c) 25、(a) 26、(c) 27、(c) 28、(c) 29、(a) 30、(b) 31、(c) 32、(b) 33、(b) 34、(a) (a) (a) 35、(c) 36、(a) 37、(c) 38、(c) 39、(b) 40、(c) 41、(c) 42、(b) 43、(b) 44、(c) 45、(c) 46、(b) 47、(b) 48、(b) 49、(a) 50、(a) 51、(c) 52、(c) 53、(c) (c) 54、(c) (a)二、填空题1、NPN,PNP ；硅，锗；电子和空穴。

第六章习题图题所示电路，求u(t)对i(t)的系统函数H(s)=U(s)／ I(s) 。

11Fi(t)+CU(t)1H LR2 _(a)R1I(s)+1Ls LR2U(s)Cs_(b)图题答案解：图解 6.1 （a）电路的 s 域电路模型图解6.1 （b）所示。

故有Ls1 R2I (s) R1Cs U ( s)1Ls R2Cs代入数据得U(s)2s22s1H ( s)s2s1I(s)1Cs +U 1 (s)-1F13+C+U 1L1HU 2(t)-R 22-(a)R1+LsU 2R2-(b)图题图解（a）所示电路，求u2t对u1t的U 2 (s)H (s)系统函数U 1 (s) 。

答案解：图解 6.2 （a）所示电路的 s 域电路模型如图解 6.2 （b）所示。

故有U 2 (s)Ls R 2H(s)1U 1(s)Ls R22RCs代入数据得H (s)U 2s s22s U1s s25s 3已知系统的单位冲激响应h(t) 5te 5t U (t) ，零状态响应y(t ) U (t ) 2e 5t U (t)5te 5t U (t ) 。

求系统的激励f(t)。

答案5h s解：s 5125Y (s)s 5s 5 2s故得激励 f(t)的像函数为125Y (s) s s 5s 5 2311F(s)55s s 5H (s)s5故得f (t)3δ(t) U(t) e-5t U(t)3δ(t) 1 e-5t U(t)55s256.4 已知系统函数H (s)5s 5 ，初始状态为y 00 ，s2y / 0-2 。

(1). 求系统的单位冲激响应h(t);(2).当激励f(t)=δ(t)时，求系统的全响应y(t) ；(3) 当激励 f(t)=U(t)时，求系统的全响应y(t) 。

答案解: (1)s 2 5 12s 2s s 12H (s)5s 52s 511 s 12 4s 2s 2 s 22故h(t)δ (t)- 2e -2t costU (t ) e -2t sinU ( t) δ (t)- 2e -2t cos2t 2sin2t U (t )（2）系统的微分方程为y // t 2y / t 5y tf // t 5f / t对上式等号两边同时求拉普拉斯变换， 并考虑到拉普拉斯变换的微分性质，有s 2Y (s)sy 0y / 02sY (s) 2y 05Y (s) s 2F(s) 5F(s①今F(s) 1, y(0 )0, y / 02,代入上式得s 2 3 2 s 1Y (s)2s 514s 2s 1 2故得全响应为y(t )δ (t)- 2e -t costU( t)F(s)1, y(0 ) 0, y / 02（3）将s代入上式①，有Y (s)s 2 2s 5 1 2 2 4s s 2 5s 5s s 1 2故得全响应为y(t ) 1 2e t sin2t U (t)图题所示电路。

电子线路分析基础_西安电子科技大学中国大学mooc课后章节答案期末考试题库2023年1.电路如图所示，已知【图片】>>1，【图片】=0.7V，要求【图片】=1mA，则【图片】为（）【图片】。

【图片】参考答案:4.3k2.若想增大输入电阻，且保持放大器稳定，放大器应引入（）反馈。

参考答案:串联负3.放大器输入单一频率的信号时，不会出现线性失真。

参考答案:正确4.图示电路，若想实现输出电压稳定，则应该在（）引入反馈支路。

【图片】参考答案:①和③之间5.图示电路中，【图片】和【图片】特性完全相同，则输出电阻约为【图片】。

【图片】参考答案:正确6.图示电路是一个两级放大器。

【图片】参考答案:错误7.图示电路为三级放大器电路。

【图片】参考答案:错误8.图示电路中，【图片】和【图片】特性完全相同，下列叙述正确的是（）。

【图片】参考答案:为CE组态放大器、为CB组态放大器。

9.无外加电压时，PN结中没有载流子的运动。

参考答案:错误10.在OCL乙类功放电路中，若最大输出功率为12W，则电路中功放管的集电极最大功耗约为（）W。

参考答案:2.411.放大器的非线性失真与输入信号频率大小有关。

参考答案:错误12.电路如图所示，已知【图片】=4mS，【图片】=【图片】。

电路的输出电阻为（）【图片】。

【图片】参考答案:20k13.某放大器的交直流负载线如图所示，忽略晶体管的饱和压降，则最大不失真输出电压振幅值为（）V。

【图片】参考答案:314.某放大电路的幅频特性渐进线波特图如图所示，由此可知中频电压放大倍数为（）dB。

【图片】参考答案:4015.电路如图所示，深度负反馈条件下的电压放大倍数为（）。

【图片】参考答案:5116.若想减少输出电阻，且保持放大器稳定，放大器应引入（）反馈。

参考答案:电压负17.负反馈可以改善放大器的性能，相应的代价是使得放大倍数下降。

参考答案:正确18.直接耦合的放大器，带宽为无穷大。

9-1．（1）选取状态变量)(),(x 21t yx t y ==,则 ⎩⎨⎧+--=+--====u x x t u t y t y t y x x t y x1222145)()(4)(5)()( 故系统的状态空间表达式为：[]⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛⎥⎦⎥⎢⎣⎢--=⎪⎪⎭⎫ ⎝⎛21212101105410xx y u x x x x9-2．（1）选取状态变量6x ,6x ,6x 321yy y ===，则11233322167416676416x y u x x x u y y y y x x x x x =⎪⎪⎩⎪⎪⎨⎧+---=+---====故系统的状态空间表达式为[]⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎪⎪⎪⎭⎫ ⎝⎛3213213210061006417100010x x x y u x x x x x x或:选取状态变量yy ===321x ,x ,y x ，则同样可得系统的状态空间表达式为[]⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎪⎪⎪⎭⎫ ⎝⎛3213213210016006417100010x x x y u x x x x x x（3）同理，系统的状态空间表达式为[]⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎪⎪⎪⎭⎫ ⎝⎛3213212332100110033a 100010x x x y u x x x a a x x x（5）微分方程含有输入的导数项，可采用212P 的情形二：状态变量选择方法一：7,6,5,0;4,,2a 3210321=======b b b b a z a则⎪⎪⎩⎪⎪⎨⎧-=---=-=--==-===za a ab a a b a b b 51545003122133021122011100ββββββββββ故系统的状态空间表达式为：[]⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛--+⎪⎪⎪⎭⎫⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎪⎪⎪⎭⎫ ⎝⎛3213213210015154524100010x x x y u z x x x z x x x方法二（可控标准型）：[]⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎝+⎪⎪⎪⎭ ⎝⎥⎥⎥⎦⎢⎢⎢⎣---=⎪⎪⎪⎭ ⎝3213213215671024100x x x y u x x z x x9-3．（1）同9-2（3），可得[]⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎭⎫⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎪⎪⎪⎭⎫ ⎝⎛32132132100118626116100010x x x y u x x x x x x或（可控标准型）：[]⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎝+⎪⎪⎪⎭ ⎝⎥⎥⎥⎦⎢⎢⎢⎣---=⎪⎪⎪⎭ ⎝32132132121840106116100x x x y u x x x x或（特征值规范型）：由32212112611640182)()()(232+++-+-=+++++==s s s s s s s s s U s Y s G（部分分式展开）选取状态变量：)(31)(x ),(21)(x ),(11)(x 321s U s s s U s s s U s s +=+=-=即：321332211212123x2x x x x x y u x u x u x +-=⎪⎩⎪⎨⎧+-=+-=+=则系统的状态空间表达式为：[]⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎪⎪⎪⎭⎫ ⎝⎛32132132121212u 11130020001x x x y x x x x x x（3）同（1）[]⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎪⎪⎪⎭⎫ ⎝⎛321321321001322452100010x x x y u x x x x x x或：[]⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎪⎪⎪⎭⎫ ⎝⎛321321321265100452100010x x x y u x x x x x x或：[]⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎪⎪⎪⎭⎫ ⎝⎛321321321111110200010011x x x y u x x x x x x9-4．（3）要求掌握由传递函数求状态空间表达式的公式：53316)()(131253s 1)21-21-+++=+-=⎥⎦⎤⎢⎣⎡+-+++=-s s s D B A SI C s G s s s A SI （9-5．掌握状态转移矩阵的算法：法一：拉氏变换法⎥⎦⎤⎢⎣⎡-+++=-s s s A I 61553s 1)s (21-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++-+++-+-+++-++=3s 32s 23s 62s 63s 12s 13s 22s 3])[(e 11---=A sI L At⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--+=------)2sin(22)2cos()2sin(223)2sin(22)2sin(22)2cos(t e t e t e t e t e t e t t t tt t ⎥⎦⎤⎢⎣⎡--==---)2cos()2sin(2)2cos()0(e )(t e t e t e x t x tt tAt法二：先将A 变换成对角矩阵由0=-A I λ可得系统的特征根为：i 212,1±-=λA 为友矩阵，则变换阵P 可选为：⎥⎦⎤⎢⎣⎡--+-=i P 21i 2111⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=-ii i P 22122121221i 221211⎥⎦⎤⎢⎣⎡--+-=-i 21i 211AP P1)21()21(e ---+-⎥⎥⎦⎤⎢⎢⎣⎡=⇒P e e P t i ti At⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--+=------)2sin(22)2cos()2sin(223)2sin(22)2sin(22)2cos(t e t e t e t e t e t e t t t tt t⎥⎦⎤⎢⎣⎡--==---)2cos()2sin(2)2cos()0(e )(t e t e t e x t x tt tAt9-6．同9-5法一：拉氏变换法：])[(e 11---=A sI L At⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+-+-+--+--+--+-+-+-+-=---------------------------t t t t t t t t t t t t t t t t t t t t t t tt t t t e e e e e e e e e e e e e e e e e e 323232323232323232294e 2122716e 25912e 3232e 215.48e 2536e 321e 21234e 253e 3法二：化为对角阵系统特征值为321321-=-=-=λλλ，， 变换阵：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=941321111P ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡---=-21231143212531P132e e ----⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=Pe e P t tt At 9-7．状态转移矩阵：))(()(11---==ΦA sI L e t At⎥⎦⎤⎢⎣⎡+-+---=--------t t t ttt t t e e e e e e e e 32323232326623故状态方程的解为：τττd Bu t x t t t )()()0()()(x 0-Φ⎰+Φ=⎥⎦⎤⎢⎣⎡-+-+-=----t t t t e e e e 323234121 9-8．方法一：利用状态转移矩阵的性质 0|)(t =Φ=t A而 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+--=Φ-----t t t t t te e t e t e t e t 22224)21(0)84()44(000)( ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⇒010440001A 方法二：利用])[(e 11---=A sI L At⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡++++-++-++==⇒22221-)2(221)2(10)2(4)2(22100011)(A)-sI (s s s s s s s e L At ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++=-⇒01044000110440001)(A s s s A sI9-9．(2)根据)0()(x e t x At=，可得⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡++------111222At t t t t t t e te e ete e e ⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡-=⇒-------t t t t t t Atte e e te e e e 2211121⎥⎦⎤⎢⎣⎡+--=----t t t t e t tete e t )21(4)21(求系统矩阵A ，同9-8可采用两种方法：1) ⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-+--+-=Φ==----=1143)21()1()44()23(|)(00t t t tt t e t e t e t e t t A 2)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++-++-+==--22221)1(211)1(1)1(4)2(211)()(s s s s s s e L A sI At⎥⎦⎤⎢⎣⎡--=⇒⎥⎦⎤⎢⎣⎡+--+=-⇒11431143)(A s s A sI 9-10．(2)先求状态转移矩阵⎥⎥⎦⎤⎢⎢⎣⎡-=-==Φ----tt At e e A sI L e t 2211021211))(()( 则离散化后的系统矩阵⎥⎦⎤⎢⎣⎡====1353.004324.01e 1T t AtG⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-==---⎰4324.02838.021********220)(T T T t T A e e T Bdt e H 9-11．1时刻：)0()0()1(x Hu Gx +=2时刻：)1()0()0()1()1()2(x 2Hu GHu x G Hu Gx ++=+= 若使系统在第二个采样时刻转移到原点，即⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=00)1(4.03.0)0(4.03.01.005.01)0(x 1.005.01)2(x 2u u 可求得,282.3)0(-=u 3032.0)1(=u即施加上述控制作用，可使系统在第二个采样时刻转移到原点。

第九章 功率放大电路自测题一、（1）A （2）B （3）C （4）B D E （5）C二、（1）消除交越失真。

（2）最大输出功率和效率分别为%8.694W 162)(CC CES CC L2CES CC om ≈-⋅==-=V U V R U V P πη （3），，且3.1113.11215max ≈+=≈=R R A U U A u io u R 1＝1k Ω，故R 5至少应取10.3 k Ω。

习题9.1 （1）× （2）√ （3）× （4）× × √ （5）× × √ √（6）× √ √9.2 （1）C （2）B （3）C （4）C （5）A9.3 （1）最大输出功率和效率分别为%8.694πW 5.242)(CCCES CC L 2CES CC om ≈-⋅==-=V U V R U V P η（2）最大功耗 W 4.622.02.0L2CC oM Tmax =⨯=≈R V P P （3）输入电压 V 9.92CESCC om i ≈-≈≈U V U U9.4 （1）U B1＝1.4V U B3＝－0.7V U B5＝－17.3V（2）V 3.17 mA 66.1B5I 2B1CC CQ -=≈=-≈u u R U V I （3）若静态时i B1＞i B2，则应增大R 3。

（4）采用如图所示两只二极管加一个小阻值电阻合适，也可只用三只二极管。

9.5 最大输出功率和效率分别为%8.694πW 42)(CCCES CC L 2CES CC om ≈-⋅==-=V U V R U V P η9.6 应引入电压并联负反馈，由输出端经反馈电阻R f 接T 5管基极，图略。

R f ＝10 k Ω。

9.7 功放管的最大集电极电流、最大管压降、最大功耗分别为W 122.0V 342A5.0L2CC Tmax CES CC max CE L CESCC max C ≈⨯≈=-==-=R V P U V U R U V I9.8 （1）最大不失真输出电压有效值V 65.82)(CES CC L 4L om ≈-⋅+=U V R R R U （2）负载电流最大值A 53.1L4CES CC Lmax ≈+-=R R U V i （3）最大输出功率和效率分别为%644πW 35.92CC 4CES CC L2om om≈--⋅=≈=V U U V R U P R η9.9 当输出短路时，功放管的最大集电极电流和功耗分别为W46πA 26422Tmax 4CES CC Cmax ≈=≈-=R V P R U V i CC 9.10 （1）W 6.10)2( V 13L2Omax om Omax ≈=≈R u P u ， （2）引入电压串联负反馈。

计算和证明题.1 已知机械系统如图9-7所示，21,m m 为质量块，1m 受外力)(t F 作用。

弹簧的弹性系数如图示，如不计摩擦，自选一定数目的状态变量，建立系统的状态空间描述。

提示：设中间变量质量块1m 的位移为z ，根据牛顿定律有zm y z k t F 11)()(=-- ① 同理对质量块2m 有ym y k y z k 221)(=-- ② 设状态变量z x =1 12x zx == y x =3 34x y x == 由式① 13111112)(m t F x m k x m k z x++-== 由式② 32211214x m k k x m k y x+-== 因此有)(001000100000001143212212111114321t F m x x xx m k k m k m k m k x x x x ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+--=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡ []⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=43210100x x x x y .2 已知系统结构图如图9-8所示。

试写出系统的状态方程和输出方程（要求写成矢量形式）。

提示：[]xy u x x 01101212=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--= .3 已知系统的微分方程，试建立其相应的状态空间描述，并画出相应的状态结构图。

（1）u u u y y y y 86375++=+++（2）u u u y y y y 23375++=+++提示：（1）[]x u x x 168100573100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=y ，状态结构图略 （2）[]ux u x x +---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=54110057310001y ，状态结构图略。

.4判断下列矩阵是否满足状态转移矩阵的条件，如果满足，试求与之对应的A 阵。