初中数学几何每日一题

每日一题复习题数学题每日一题复习题 - 数学题数学是一门需要不断练习的学科，而每日一题的复习题目就是帮助我们巩固知识、提高技能的好方法。

在这篇文章中，我将为大家提供一些有趣的数学题目，帮助大家在日常生活中锻炼数学思维。

1. 数列求和已知等差数列的首项为a1，公差为d，前n项和为Sn。

请问Sn的公式是什么？如果给出a1=2，d=3，n=10，求Sn的值是多少？解析：等差数列的前n项和Sn可以通过以下公式求得：Sn = (n/2) * (2a1 + (n-1)d)。

代入a1=2，d=3，n=10，可得Sn = (10/2) * (2*2 + (10-1)*3) = 55。

2. 比例问题小明每天骑自行车上学，全程10公里。

他发现，如果他以每小时10公里的速度骑车，他需要一个小时到达学校。

但如果他以每小时15公里的速度骑车，他只需要多少时间到达学校？解析：根据速度、时间和距离的关系，我们可以得知速度与时间成反比。

设以每小时10公里的速度骑车到学校需要t小时，则根据比例关系，10/15 = t/1。

解得t = 2/3，即以每小时15公里的速度骑车，小明只需要40分钟就能到达学校。

3. 几何问题在一个正方形的内切圆中，有一个小圆切割出一个扇形。

扇形的圆心角为60度，小圆的半径为r。

请问，扇形的面积是多少？解析：首先，我们需要求出正方形的边长。

设正方形的边长为a，则内切圆的直径等于正方形的边长，即2r = a。

根据正方形的性质，我们知道对角线的长度等于边长的√2倍，即a√2 = 2r√2。

因此，a = 2r√2。

扇形的面积可以通过圆心角和圆的面积的比例得出，即扇形的面积为(60/360) * π * r^2 = (1/6) * π * r^2。

4. 概率问题一个袋子里有红、黄、蓝三种颜色的球各若干个，其中红球的数量是黄球的2倍，黄球的数量是蓝球的3倍。

现在从袋子中随机取出一个球，求取出的球是红色的概率。

解析：设红球的数量为x，黄球的数量为2x，蓝球的数量为6x。

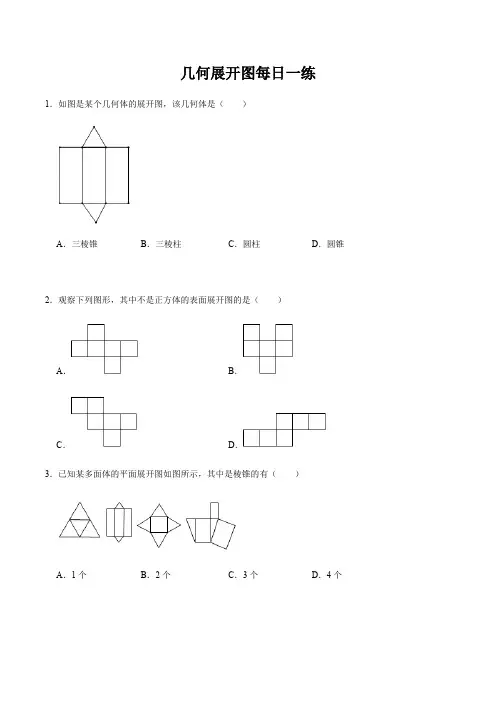
几何展开图每日一练1．如图是某个几何体的展开图，该几何体是（）A．三棱锥B．三棱柱C．圆柱D．圆锥2．观察下列图形，其中不是正方体的表面展开图的是（）A．B．C．D．3．已知某多面体的平面展开图如图所示，其中是棱锥的有（）A．1个B．2个C．3个D．4个4．一个几何体的表面展开图如图所示，这个几何体是（）A．圆柱B．圆锥C．长方体D．球5．如图，正方体的展开图中对面数字之和相等，则﹣x y＝（）A．9B．﹣9C．﹣6D．﹣86．下列各图是正方体展开图的是（）A．B．C．D．7．将正方体展开需要剪开的棱数为（）A．5条B．6条C．7条D．8条8．将一个无盖正方体形状盒子的表面沿某些棱剪开，展开后不能得到的平面图形是（）A．B．C．D．9．三个立体图形的展开图如图①②③所示，则相应的立体图形是（）A．①圆柱，②圆锥，③三棱柱B．①圆柱，②球，③三棱柱C．①圆柱，②圆锥，③四棱柱D．①圆柱，②球，③四棱柱10．下列图形中，（）是正方体的展开图．A．B．C．D．11．按如图所示图形中的虚线折叠可以围成一个棱柱的是（）A．B．C．D．12．在课题学习中，老师要求用长为12厘米，宽为8厘米的长方形纸片制作一个无盖的长方体纸盒．三位同学分别以下列方式在长方形纸片上截去两角（图中阴影部分），然后沿虚线折成一个无盖的长方体纸盒．甲：如图1，盒子底面的四边形ABCD是正方形；乙：如图2，盒子底面的四边形ABCD是正方形；丙：如图3，盒子底面的四边形ABCD是长方形，AB＝2AD．将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列，正确的是（）A．甲＞乙＞丙B．甲＞丙＞乙C．丙＞甲＞乙D．丙＞乙＞甲13．下列四组图中，每组左边的平面图形能够折叠成右边的立体图形的是（）A．①②B．①④C．②D．③14．如图，把一张边长为15cm的正方形硬纸板的四个角各剪去一个同样大小的正方形，再折成一个无盖的长方体盒子（纸板的厚度忽略不计），当剪去的正方形边长从4cm变为6cm后，长方体的纸盒容积变小（填大或小）了cm3．15．下面四个图形中不能围成下边三棱锥的是（）A．B．C．D．16．下列平面图形中不能围成正方体的是（）A．B．C．D．17．下图中哪个图形经过折叠后可以围成一个棱柱（）A．B．C．D．18．将图中的阴影部分剪下来，围成一个几何体的侧面，使AB和DC重合，所围成的几何体是（）A．B．C．D．几何展开图每日一练1．如图是某个几何体的展开图，该几何体是（）A．三棱锥B．三棱柱C．圆柱D．圆锥【分析】通过展开图的面数，展开图的各个面的形状进行判断即可．【解答】解：从展开图可知，该几何体有五个面，两个三角形的底面，三个长方形的侧面，因此该几何体是三棱柱，故选：B．【点评】本题考查棱柱的展开与折叠，掌握棱柱展开图的特征是正确判断的前提．2．观察下列图形，其中不是正方体的表面展开图的是（）A．B．C．D．【分析】利用正方体及其表面展开图的特点解题．【解答】解：A、C、D均是正方体表面展开图；B、是凹字格，故不是正方体表面展开图．故选：B．【点评】本题考查了正方体的展开图，熟记展开图的11种形式是解题的关键，利用不是正方体展开图的“一线不过四、田凹应弃之”（即不能出现同一行有多于4个正方形的情况，不能出现田字形、凹字形的情况）判断也可．3．已知某多面体的平面展开图如图所示，其中是棱锥的有（）A．1个B．2个C．3个D．4个【分析】根据三棱柱是各个侧面的高相等，底面是三角形，上表面和下表面平行且全等，所有的侧棱相等且相互平行且垂直于两底面的棱柱．并且上下两个三角形是全等三角形，可得答案．【解答】解：第1个图是三棱锥；第2个图是三棱柱；第3个图是四棱锥；第4个图是三棱柱．∴是棱锥的有2个．故选：B．【点评】考查了几何体的展开图，熟记常见立体图形的展开图的特征，是解决此类问题的关键．4．一个几何体的表面展开图如图所示，这个几何体是（）A．圆柱B．圆锥C．长方体D．球【分析】根据圆锥的侧面展开图得出答案．【解答】解：由几何体的表面展开图可知，这个几何体是圆锥．故选：B．【点评】此题主要考查了几何体的展开图，熟记常见立体图形的平面展开图的特征是解决此类问题的关键．5．如图，正方体的展开图中对面数字之和相等，则﹣x y＝（）A．9B．﹣9C．﹣6D．﹣8【分析】根据正方体的展开图的特点，找到向对面，再由相对面上的数字之和相等，可得出x、y的值，再代入计算即可求解．【解答】解：1与6相对，4与x相对，5与y相对，∵1+6＝4+x＝5+y，∴x＝3，y＝2，∴﹣x y＝﹣32＝﹣9．故选：B．【点评】本题考查了正方体的展开图，注意正方体的空间图形，从相对面入手，分析及解答问题．6．下列各图是正方体展开图的是（）A．B．C．D．【分析】正方体的展开图有“1+4+1”型，“2+3+1”型、“3+3”型三种类型，其中“1”可以左右移动．注意“一”、“7”、“田”、“凹”字型的都不是正方体的展开图．【解答】解：A、“田”字型，不是正方体的展开图，故选项错误；B、是正方体的展开图，故选项正确；C、不是正方体的展开图，故选项错误；D、不是正方体的展开图，故选项错误．故选：B．【点评】考查了几何体的展开图，解题时勿忘记四棱柱的特征及正方体展开图的各种情形．7．将正方体展开需要剪开的棱数为（）A．5条B．6条C．7条D．8条【分析】根据正方体的棱的条数以及展开后平面之间应有棱连着，即可得出答案．【解答】解：∵正方体有6个表面，12条棱，要展成一个平面图形必须5条棱连接，∴要剪12﹣5＝7条棱，故选：C．【点评】此题主要考查了正方体的展开图的性质，根据展开图的性质得出一个平面图形必须5条棱连接是解题关键．8．将一个无盖正方体形状盒子的表面沿某些棱剪开，展开后不能得到的平面图形是（）A．B．C．D．【分析】由平面图形的折叠及无盖正方体的展开图就可以求出结论．【解答】解：由四棱柱的四个侧面及底面可知，A、B、C都可以拼成无盖的正方体，但C拼成的有一个面重合，有两面没有的图形．所以将一个无盖正方体形状盒子的表面沿某些棱展开后不能得到的平面图形是D．故选：D．【点评】本题考查了正方体的平面展开图，解答时熟悉四棱柱的特征及无盖正方体展开图的各种情形是关键．9．三个立体图形的展开图如图①②③所示，则相应的立体图形是（）A．①圆柱，②圆锥，③三棱柱B．①圆柱，②球，③三棱柱C．①圆柱，②圆锥，③四棱柱D．①圆柱，②球，③四棱柱【分析】根据圆柱、圆锥、三棱柱表面展开图的特点解题．【解答】解：观察图形，由立体图形及其表面展开图的特点可知相应的立体图形顺次是圆柱、圆锥、三棱柱．故选：A．【点评】本题考查圆锥、三棱柱、圆柱表面展开图，记住这些立体图形的表面展开图是解题的关键．10．下列图形中，（）是正方体的展开图．A．B．C．D．【分析】根据正方体展开图的11种形式对各小题分析判断即可得解．【解答】解：A、中间4个正方形是“田字形”，不是正方体展开图；B、折叠不是正方体展开图；C、符合正方体展开图；D、不符合正方体展开图；故选：C．【点评】本题考查了正方体的展开图，熟记展开图的11种形式是解题的关键，利用不是正方体展开图的“一线不过四、田凹应弃之”（即不能出现同一行有多于4个正方形的情况，不能出现田字形、凹字形的情况，）判断也可．11．按如图所示图形中的虚线折叠可以围成一个棱柱的是（）A．B．C．D．【分析】利用棱柱的展开图中两底面的位置对A、D进行判断；根据侧面的个数与底面多边形的边数相同对B、C进行判断．【解答】解：棱柱的两个底面展开后在侧面展开图相对的两边上，所以A、D选项错误；当底面为三角形时，则棱柱有三个侧面，所以B选项错误，C选项正确．故选：C．【点评】本题考查了展开图折叠成几何体：通过结合立体图形与平面图形的相互转化，去理解和掌握几何体的展开图，要注意多从实物出发，然后再从给定的图形中辨认它们能否折叠成给定的立体图形．12．在课题学习中，老师要求用长为12厘米，宽为8厘米的长方形纸片制作一个无盖的长方体纸盒．三位同学分别以下列方式在长方形纸片上截去两角（图中阴影部分），然后沿虚线折成一个无盖的长方体纸盒．甲：如图1，盒子底面的四边形ABCD是正方形；乙：如图2，盒子底面的四边形ABCD是正方形；丙：如图3，盒子底面的四边形ABCD是长方形，AB＝2AD．将这三位同学所折成的无盖长方体的容积按从大到小的顺序排列，正确的是（）A．甲＞乙＞丙B．甲＞丙＞乙C．丙＞甲＞乙D．丙＞乙＞甲【分析】根据展开图分别求出每个同学的无盖长方体的容积，再比较大小即可．【解答】解：甲所折成的无盖长方体的容积为：5×3×3＝45（cm3），乙所折成的无盖长方体的容积为：10×2×2＝40（cm3），丙所折成的无盖长方体的容积为：6×4×2＝48（cm3），∴丙＞甲＞乙．故选：C．【点评】此题主要考查了展开图折叠成几何体，解题的关键是正确题意，然后根据题目的数量关系列出代数式解决问题．13．下列四组图中，每组左边的平面图形能够折叠成右边的立体图形的是（）A．①②B．①④C．②D．③【分析】根据几何体的展开图，可得答案．【解答】解：①不能折叠成正方体，②能折叠成长方体，③不能折成圆锥，④不能折成四棱锥，故选：C．【点评】本题考查了展开图折叠成几何体，熟记常见几何体的展开图是解题关键．14．如图，把一张边长为15cm的正方形硬纸板的四个角各剪去一个同样大小的正方形，再折成一个无盖的长方体盒子（纸板的厚度忽略不计），当剪去的正方形边长从4cm变为6cm后，长方体的纸盒容积变小（填大或小）了142cm3．【分析】分别求得剪去的正方形边长从4cm变为6cm后，长方体的纸盒容积即可得到结论．【解答】解：当剪去的正方形边长从4cm变为6cm后，长方体的纸盒容积从（15﹣4×2）2×4＝196cm3变为（15﹣6×2）2×6＝54cm3．故长方体的纸盒容积变小了196﹣54＝142cm3．故答案为：小，142．【点评】本题考查了展开图折叠成几何体，长方体的体积，熟记长方体的体积公式是解题的关键．15．下面四个图形中不能围成下边三棱锥的是（）A．B．C．D．【分析】对于能构成三棱锥的图形，将各面折起，不能重叠，也不能有空缺，据此进行判断．【解答】解：B、C、D都能构成三棱锥，但A将各面折起，出现重叠，不能构成三棱锥，故选：A．【点评】本题考查了三棱锥的展开图，熟记三棱锥展开图是解决问题的根本．16．下列平面图形中不能围成正方体的是（）A．B．C．D．【分析】根据常见的正方体展开图的11种形式以及不能围成正方体的展开图解答即可．【解答】解：根据常见的不能围成正方体的展开图的形式是“一线不过四，田、凹应弃之”，只有A选项不能围成正方体．故选：A．【点评】本题考查了正方体展开图，熟记展开图常见的11种形式与不能围成正方体的常见形式“一线不过四，田凹应弃之”是解题的关键．17．下图中哪个图形经过折叠后可以围成一个棱柱（）A．B．C．D．【分析】由平面图形的折叠及立体图形的表面展开图的特点解题．【解答】解：选项A、D缺少一个面，不能围成棱柱；选项C中折叠后底面重合，不能折成棱柱；只有B能围成三棱柱．故选：B．【点评】考查了展开图折叠成几何体，解题时勿忘记四棱柱的特征及正方体展开图的各种情形．18．将图中的阴影部分剪下来，围成一个几何体的侧面，使AB和DC重合，所围成的几何体是（）A．B．C．D．【分析】根据已知图形的特点和四个选项的特点进行判断．【解答】解：阴影部分剪下来，围成一个几何体的侧面，且是光滑的曲面，上下两个底面不相等，所以是圆台的侧面，故选：B．【点评】本题主要考查了展开图折成几何体，解题时注意发挥想象力，根据常见的几何体的特征进行解答．。

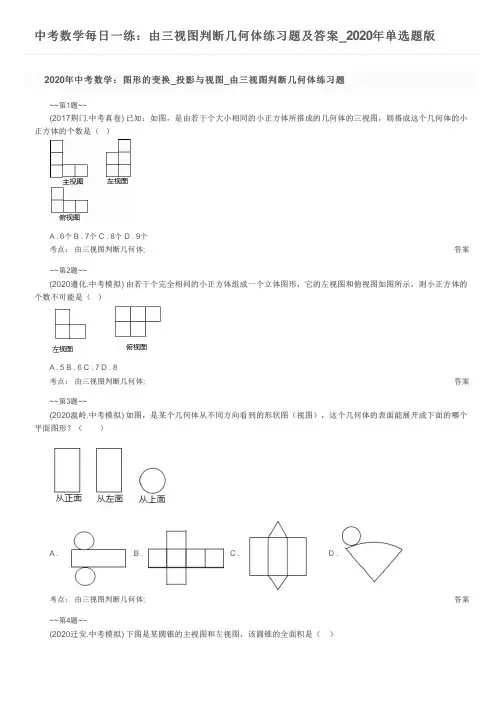
中考数学每日一练：由三视图判断几何体练习题及答案_2020年单选题版答案答案答案2020年中考数学：图形的变换_投影与视图_由三视图判断几何体练习题~~第1题~~(2017荆门.中考真卷) 已知：如图，是由若干个大小相同的小正方体所搭成的几何体的三视图，则搭成这个几何体的小正方体的个数是（ ）A . 6个B . 7个C . 8个D . 9个考点： 由三视图判断几何体;~~第2题~~(2020遵化.中考模拟) 由若干个完全相同的小正方体组成一个立体图形，它的左视图和俯视图如图所示，则小正方体的个数不可能是（ ）A . 5B . 6C . 7D . 8考点： 由三视图判断几何体;~~第3题~~(2020温岭.中考模拟) 如图，是某个几何体从不同方向看到的形状图（视图），这个几何体的表面能展开成下面的哪个平面图形？（ ） A . B . C . D .考点： 由三视图判断几何体;~~第4题~~(2020迁安.中考模拟) 下图是某圆锥的主视图和左视图，该圆锥的全面积是（ ）答案答案答案答案答案A . 36π B . 24π C . 20π D . 15π考点： 勾股定理;圆锥的计算;由三视图判断几何体;~~第5题~~(2019荆州.中考模拟) 如图，是从不同的方向看一个物体得到的平面图形，该物体的形状是（ ）A . 圆锥B . 圆柱C . 三棱锥D . 三棱柱考点： 由三视图判断几何体;~~第6题~~(2017平谷.中考模拟) 如图是某几何体从不同角度看到的图形，这个几何体是（ ）A . 圆锥B . 圆柱C . 正三棱柱D . 三棱锥考点： 由三视图判断几何体;~~第7题~~(2019通州.中考模拟) 如图是某个几何体的三视图，该几何体是（ ）A . 圆锥B . 四棱锥C . 圆柱D . 四棱柱考点： 由三视图判断几何体;~~第8题~~(2018青海.中考真卷) 由一些相同的小立方块搭成的几何体的三视图如图所示，则搭成该几何体的小立方块有（ ）A . 3块B . 4块C . 6块D . 9块考点： 由三视图判断几何体;~~第9题~~(2019呼和浩特.中考真卷) 如图是一个几何体的三视图，其中主视图与左视图完全一样，则这个几何体的表面积是（ ）答案答案 A . B . C . D .考点： 几何体的表面积;由三视图判断几何体;~~第10题~~(2019阜新.中考真卷) 如图所示的主视图和俯视图对应的几何体(阴影所示为右)是（ ）A .B .C .D .考点： 由三视图判断几何体;2020年中考数学：图形的变换_投影与视图_由三视图判断几何体练习题答案1.答案：B2.答案：A3.答案：A4.答案：A5.答案：A6.答案：A7.答案：B8.答案：B9.答案：B10.答案：C。

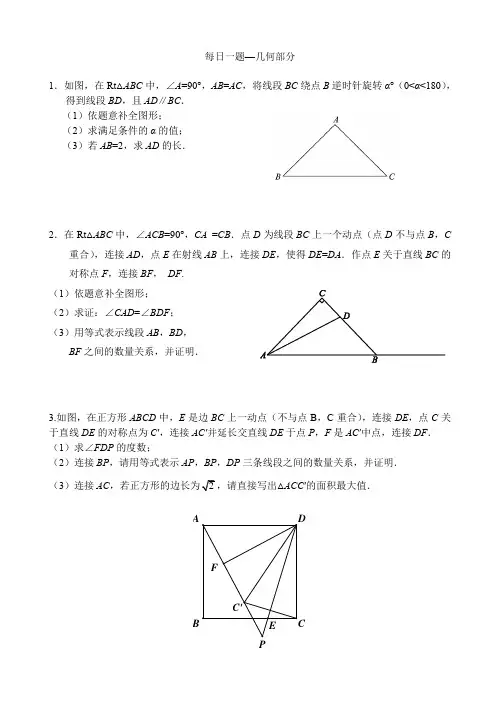
每日一题—几何部分1．如图，在Rt △ABC 中，∠A =90°，AB =AC ，将线段BC 绕点B 逆时针旋转α°（0<α<180），得到线段BD ，且AD ∥BC ． （1）依题意补全图形；（2）求满足条件的α的值； （3）若AB =2，求AD 的长．2．在Rt △ABC 中，∠ACB =90°，CA =CB ．点D 为线段BC 上一个动点（点D 不与点B ，C重合），连接AD ，点E 在射线AB 上，连接DE ，使得DE =DA ．作点E 关于直线BC 的对称点F ，连接BF ， DF . （1）依题意补全图形； （2）求证：∠CAD =∠BDF ； （3）用等式表示线段AB ，BD ，BF 之间的数量关系，并证明．3.如图，在正方形ABCD 中，E 是边BC 上一动点（不与点B ，C 重合），连接DE ，点C 关于直线DE 的对称点为C ʹ，连接ACʹ并延长交直线DE 于点P ，F 是AC ′中点，连接DF ． （1）求∠FDP 的度数；（2）连接BP ，请用等式表示AP ，BP ，DP 三条线段之间的数量关系，并证明． （3）连接AC ，若正方形的边长为2，请直接写出△ACC ′的面积最大值．FP C'BCA DE4.已知：Rt △ABC 中，∠ACB =90°，AC =BC .(1) 如图1，点D 是BC 边上一点(不与点B ，C 重合)，连接AD ，过点B 作BE ⊥AD ，交AD 的延长线于点E ，连接CE . 若∠BAD =α，求∠DBE 的大小 (用含α的式子表示) ； (2) 如图2，点D 在线段BC 的延长线上时，连接AD ，过点B 作BE ⊥AD ，垂足E 在线段AD 上，连接CE . ①依题意补全图2；②用等式表示线段EA ，EB 和EC 之间的数量关系，并证明.图1 图25.在△ABC 中，∠ACB =90°，AC =BC ， D 为AB 的中点，点E 为AC 延长线上一点，连接DE ，过点D 作DF ⊥DE 交CB 的延长线于点F ．（1）求证：BF= CE ； （2）若CE =AC ，用等式表示线段DF 与AB 的数量关系，并证明．ABA6．如图，在等腰直角△ABC中，90CA CD），连接BD，ABC°，D是线段AC上一点（2过点C作BD的垂线，交BD的延长线于点E，交BA的延长线于点F．（1）依题意补全图形；（2）若ACE α，求ABD的大小（用含α的式子表示）；（3）若点G在线段CF 上，CG BD，连接DG．①判断DG与BC的位置关系并证明；②用等式表示DG，CG，AB之间的数量关系为．7．如图，等边△ABC中，P是AB上一点，过点P作PD⊥AC于点D，作PE⊥BC于点E，M是AB的中点，连接ME，MD．（1）依题意补全图形；（2）用等式表示线段BE ，AD 与AB的数量关系，并加以证明；（3）求证：MD=ME．C8．如图，∠AOB = 90°，OC 为∠AOB 的平分线，点P 为OC 上一个动点，过点P 作射线PE交OA 于点E ．以点P 为旋转中心，将射线PE 沿逆时针方向旋转90°，交OB 于点F ． （1）根据题意补全图1，并证明PE = PF ；（2）如图1，如果点E 在OA 边上，用等式表示线段OE ，OP 和OF 之间的数量关系，并证明；（3）如图2，如果点E 在OA 边的反向延长线上，直接写出线段OE ，OP 和OF 之间的数量关系．图1 图29.已知ABC ∆为等边三角形，点D 是线段AB 上一点（不与A 、B 重合）.将线段CD 绕点C 逆时针旋转60︒得到线段CE.连结DE 、BE. （1）依题意补全图1并判断AD 与BE 的数量关系. （2）过点A 作AF EB ⊥交EB 延长线于点F.用等式表示线段EB 、DB 与AF 之间的数量关系并证明.PPEECCBBOOAA图2D CBA图1A B CD10.在△ABC 中，∠ABC =120°，线段AC 绕点A 逆时针旋转60°得到线段AD ，连接CD ，BD 交AC 于P ．（1）若∠BAC =α，直接写出∠BCD 的度数 （用含α的代数式表示）； （2）求AB ，BC ，BD 之间的数量关系；（3）当α=30°时，直接写出AC ，BD 的关系．11,如图，在等边△ABC 中，D 为边AC 的延长线上一点()CD AC ，平移线段BC ，使点C 移动到点D ，得到线段ED ，M 为ED 的中点，过点M 作ED 的垂线，交BC 于点F ，交AC 于点G ． （1）依题意补全图形； （2）求证：AG = CD ；（3）连接DF 并延长交AB 于点H ，用等式表示线段AH 与CG 的数量关系，并证明．12.已知：如图，在△ABC 中，AB >AC ，∠B =45°， 点D 是BC 边上一点，且AD=AC ，过点C 作CF ⊥AD 于点E ，与AB 交于点F ．（1）若∠CAD =α，求∠BCF 的大小（用含α的式子表示）； （2）求证：AC =FC ；（3）用等式直接表示线段BF 与DC 的数量关系．D BAB CDFE13.如图，在等边ABC △中，点D 是线段BC 上一点.作射线AD ，点B 关于射线AD 的对称点为E .连接CE 并延长，交射线AD 于点F .（1）设BAF α∠=，用α表示BCF ∠的度数；（2）用等式表示线段AF 、CF 、EF 之间的数量关系，并证明.14.如图，在△ABC 中，∠ABC =90°，BA =BC ．将线段AB 绕点A 逆时针旋转90°得到线段AD ，E 是边BC 上的一动点，连接DE 交AC 于点F ，连接BF ． （1）求证：FB =FD ；（2）点H 在边BC 上，且BH =CE ，连接AH 交BF 于点N ．①判断AH 与BF 的位置关系，并证明你的结论；②连接CN ．若AB =2，请直接写出线段CN 长度的最小值．H O DCBA15.已知：四边形ABCD 中，120ABC ∠=︒，60ADC ∠=︒，AD =CD ，对角线AC ，BD相交于点O ，且BD 平分∠ABC ，过点A 作AH BD ⊥，垂足为H ． （1）求证：ADB ACB ∠=∠；（2）判断线段BH ，DH ，BC 之间的数量关系；并证明．16.如图，在△ABC 中，AB ＝BC ，∠B ＝90°，点D 为线段BC 上一个动点(不与点B ，C 重合)，连接AD ，将线段AD 绕点D 顺时针旋转90°得到线段DE ，连接EC ．(1) ① 依题意补全图1；② 求证：∠EDC ＝∠BAD ；(2) ① 小方通过观察、实验，提出猜想：在点D 运动的过程中，线段CE 与BD 的数量关系始终不变，用等式表示，并证明.图1 D C B A备用图AB CD每日一题—新定义部分1．在平面直角坐标系xOy 中，如果等边三角形的一边与x 轴平行或在x 轴上，则称这个等边三角形为水平正三角形.(1)已知A （1，0），B （-1，0），若△ABC 是水平正三角形，则点C 坐标的是 （只填序号）； ①，②，③，④（2）已知点O ，E ，F ，以这三个点中的两个点及平面内的另一个点P为顶点，构成一个水平正三角形，则这两个点是 ，并求出此时点P 的坐标.2.在平面直角坐标系xOy 中，对于P ，Q 两点给出如下定义：若点P 到x 、y 轴的距离中的最大值等于点Q 到x 、y 轴的距离中的最大值，则称P ，Q 两点为“等距点”．下图中的P ，Q 两点即为“等距点”．(1)已知点A 的坐标为(-3，1)，①在点E (0，3)，F (3，-3)，G (2，-5)中，为点A 的“等距点”的是________；②若点B 在直线y =x +6上，且A ，B 两点为“等距点”，则点B 的坐标为________； (2)直线l ：y =kx -3(k >0)与x 轴交于点C ，与y 轴交于点D ，若T 1(-1,t 1)，T 2(4,t 2)，是直线l 上的两点，且T 1与T 2为“等距点”，求k 的值.()12,(0()01,-(0()00,(1()02,-3.对于平面直角坐标系xOy 中的点P 和图形G ，给出如下定义：若在图形G 上存在两个点A ，B ，使得以P ，A ，B 为顶点的三角形为等边三角形，则称P 为图形G 的“等边依附点”．已知M （-3，N （3，. ①在点C （-2,2），D （0,1），E （1,3）中，是线段MN 的“等边依附点”的是 ；②点P (m ，0)在x 轴上运动，若P 为线段MN 的“等边依附点”，求点P 的横坐标m 的取值范围。

(每日一练)七年级数学第四章几何图形初步知识总结例题单选题1、下列说法中，正确的是（）①己知∠A=40°，则∠A的余角是50°②若∠1+∠2=90°，则∠1和∠2互为余角．③若∠1+∠2+∠3=180°，则∠1、∠2和∠3互为补角．④一个角的补角必为钝角．A．①，②B．①，②，③C．③，④，②D．③，④答案：A解析：根据余角及补角的定义进行判断即可．∵和为180度的两个角互为补角，和为90度的两个角互为余角，∴①已知∠A=40°，则∠A的余角=50°，正确，②若∠1+∠2=90°，则∠1和∠2互为余角，正确，③∠1、∠2和∠3三个角不能互为补角，故错误，④若一个角为120°，则这个角的补角为60°，不是钝角，故错误，∴正确的是：①②．故选：A．小提示：本题考查了余角及补角，掌握余角和补角的定义是解题的关键．2、下列说法：（1）在所有连结两点的线中，线段最短；（2）连接两点的线段叫做这两点的距离；（3）若线段AC=BC，则点C是线段AB的中点；（4）经过刨平的木板上的两个点，能弹出一条笔直的墨线，是因为两点确定一条直线，其中说法正确的是（）A．（1）（2）（3）B．（1）（4）C．（2）（3）D．（1）（2）（4）答案：B解析：根据两点之间线段最短，数轴上两点间的距离的定义求解，线段的中点的定义，直线的性质对各小题分析判断即可得解．解：（1）在所有连结两点的线中，线段最短，故此说法正确；（2）连接两点的线段的长度叫做这两点的距离，故此说法错误；（3）若线段AC=BC，则点C不一定是线段AB的中点，故此说法错误；（4）经过刨平的木板上的两个点，能弹出一条笔直的墨线，是因为两点确定一条直线，故此说法正确；综上所述，说法正确有（1）（4）．故选：B．小提示：本题考查了线段的性质、两点间的距离的定义，线段的中点的定义，直线的性质等，是基础题，熟记各性质与概念是解题的关键．3、如图，BC=12AB，D为AC的中点，DC=3cm，则AB的长是()A．72cm B．4cm C．92cm D．5cm答案：B解析：先根据已知等式得出AB与AC的等量关系，再根据线段的中点定义可得出AC的长，从而可得出答案．∵BC=12AB∴AC=AB+BC=AB+12AB=32AB，即AB=23AC∵D为AC的中点，DC=3cm ∴AC=2CD=6cm∴AB=23AC=23×6=4(cm)故选：B．小提示：本题考查了线段的和差倍分、线段的中点定义，掌握线段的中点定义是解题关键．填空题4、如图，点C是线段AB上一点，点M、N、P分别是线段AC，BC，AB的中点．AC ＝3cm，CP＝1cm，线段PN＝__cm．答案：32解析：根据线段中点的性质求得线段CN的长度，即可求解．解：∵AP＝AC+CP，CP＝1cm，∴AP＝3+1＝4cm，∵P为AB的中点，∴AB＝2AP＝8cm，∵CB＝AB﹣AC，AC＝3cm，∴CB＝5cm，∵N为CB的中点，∴CN=12BC=52cm，∴PN=CN−CP=32cm所以答案是：32．小提示：本题考查的是两点间的距离的计算，掌握线段的中点的性质、灵活运用数形结合思想是解题的关键．5、单位换算：56°10′48″＝_____°．答案：56.18解析：先将48″换算成“分”，再将“分”换算成“度”即可．解：48×（160）′＝0.8′，则10.8×（160）°＝0.18°，故56°10′48″＝56.18°，所以答案是：56.18．小提示：本题考查度、分、秒的换算，掌握换算方法是正确计算的前提．解答题6、如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC=110°，将一直角三角板的直角项点放在O处，一直角边OM在射线O上，另一直角边ON在直线AB 的下方．(1)将图1中的三角形绕点O逆时针旋转至图2，使边OM在∠BOC的内部，且恰好平分∠BOC，问：此时直线ON是否平分∠AOC？计算出图中相关角的度数说明你的观点；(2)将图1中的三角板以每秒5°的速度绕点O逆时针方向旋转一周，在旋转过程中，第n秒时，直线ON恰好平分∠AOC，则n的值为____________（直接写出答案）；(3)将图1中三角板绕点O旋转至图3，使ON在∠AOC的内部时，求∠AOM与∠NOC 的数量关系，并说明理由．答案：(1)35°，见解析(2)11或47(3)∠AOM−∠NOC=20°，见解析解析：（1）如图，作射线NT,先求解∠BON,∠AOT,再求解∠COT,从而可得答案；（2）分两种情况：①如图2，当直线ON恰好平分锐角∠AOC时，此时逆时针旋转的角度为55°，②如图3，当NO平分∠AOC时，∠NOA=35°，此时逆时针旋转的角度为：180°+55°=235°，再求解时间t即可；（3）由∠AOM=90°−∠AON，∠NOC=70°−∠AON，消去∠AON即可得到答案.(1)解：如图，过点O作射线NT,∵OM平分∠BOC，∴∠MOC=∠MOB，又∵∠BOC=110°，∴∠MOB=55°，∵∠MON=90°，∴∠BON=∠MON−∠MOB=35°，∴∠AOT=35°,∠COT=180°−110°−35°=35°,∴∠AOT=∠COT,∴OT平分∠AOC,即直线ON平分∠AOC.(2)解：分两种情况：①如图2，∵∠BOC=110°，∴∠AOC=70°，当直线ON恰好平分锐角∠AOC时，∠AOD=∠COD=35°，∴∠BON=35°，∠BOM=55°，即逆时针旋转的角度为55°，由题意得，5t=55°解得t=11（s）；②如图3，当NO平分∠AOC时，∠NOA=35°，∴∠AOM=55°，即逆时针旋转的角度为：180°+55°=235°，由题意得，5t=235°，解得t=47（s），综上所述，t=11s或47s时，直线ON恰好平分锐角∠AOC；所以答案是：11或47；(3)解：∠AOM−∠NOC=20°.理由：∵∠MON=90°，∠AOC=70°，∴∠AOM=90°−∠AON，∠NOC=70°−∠AON，∴∠AOM−∠NOC=(90°−∠AON)−(70°−∠AON)=20°，∴∠AOM与∠NOC的数量关系为：∠AOM−∠NOC=20°.小提示：本题考查的是几何图形中角的和差关系，角的动态定义，角平分线的定义，掌握“几何图形中角的和差关系”是解本题的关键.。

(每日一练)人教版七年级数学几何图形初步基础知识点归纳总结单选题1、如图是一个正方体的平面展开图，把展开图折叠成正方体后，“红”字的面的对面上的字是（）A．传B．国C．承D．基答案：D解析：正方体的平面展开图中，相对面的特点是必须相隔一个正方形，据此作答．解：正方体的表面展开图，相对的面之间一定相隔一个正方形，则：“传”与“因”是相对面，“承”与“色”是相对面，“红”与“基”是相对面．故选：D．本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．2、下列说法：（1）在所有连结两点的线中，线段最短；（2）连接两点的线段叫做这两点的距离；（3）若线段AC=BC，则点C是线段AB的中点；（4）经过刨平的木板上的两个点，能弹出一条笔直的墨线，是因为两点确定一条直线，其中说法正确的是（）A．（1）（2）（3）B．（1）（4）C．（2）（3）D．（1）（2）（4）答案：B解析：根据两点之间线段最短，数轴上两点间的距离的定义求解，线段的中点的定义，直线的性质对各小题分析判断即可得解．解：（1）在所有连结两点的线中，线段最短，故此说法正确；（2）连接两点的线段的长度叫做这两点的距离，故此说法错误；（3）若线段AC=BC，则点C不一定是线段AB的中点，故此说法错误；（4）经过刨平的木板上的两个点，能弹出一条笔直的墨线，是因为两点确定一条直线，故此说法正确；综上所述，说法正确有（1）（4）．小提示：本题考查了线段的性质、两点间的距离的定义，线段的中点的定义，直线的性质等，是基础题，熟记各性质与概念是解题的关键．3、已知∠AOB=30°，如果用10倍的放大镜看，这个角的度数将（）A．缩小10倍B．不变C．扩大10倍D．扩大100倍答案：B解析：根据角是从同一点引出的两条射线组成的图形．它的大小与图形的大小无关，只与两条射线形成的夹角有关系，直接判断即可．解：角的大小只与角的两边张开的大小有关，放大镜没有改变顶点的位置和两条射线的方向，所以用10倍放大镜观察这个角还是30度．故选：B小提示：本题考查了角的概念．解题关键是掌握角的概念：从同一点引出的两条射线组成的图形叫做角，明确角的大小只与角的两边张开的大小有关．填空题4、如图，①~④是几何体的展开图，其中能围成三棱柱的有________（填序号）．答案：②解析：依据展开图的特征，即可得到围成的几何体的类型．解：图①能围成圆锥；图②能围成三棱柱；图③能围成正方体；图④能围成四棱锥；所以答案是：②．小提示：本题主要考查了展开图折成几何体，通过结合立体图形与平面图形的相互转化，去理解和掌握几何体的展开图，要注意多从实物出发，然后再从给定的图形中辨认它们能否折叠成给定的立体图形．5、如图所示的某种玩具是由两个正方体用胶水黏合而成的，它们的棱长分别为1dm和2dm, 为了美观，现要在其表面喷涂油漆，如果喷涂1dm2需用油漆5g，那么喷涂这个玩具共需油漆_________g．答案：140解析：根据题意先求出玩具的表面积，然后再求需要的油漆质量．解：玩具的表面积为：6×（2×2）+4×（1×1）=28平方分米，所以喷涂这个玩具共需油漆28×5=140克．所以答案是：140．小提示：本题主要考查了立体图形的视图问题．解题的关键是能把从不同的方向上看到的图形面积抽象出来（即利用视图的原理），从而求得总面积．解答题6、如图，已知线段AB=m（m为常数），点C为直线AB上一点（不与A、B重合），点P、Q分别在线段BC、AC上，且满足CQ=2AQ，CP=2BP．（1）如图1，点C在线段AB上，求PQ的长；（用含m的代数式表示）（2）如图2，若点C在点A左侧，同时点Р在线段AB上（不与端点重合），求2AP+CQ−2PQ的值．答案：（1）23m；（2）2AP+CQ−2PQ=0．解析：（1）根据已知AB=m(m为常数），CQ=2AQ，CP=2BP，以及线段的中点的定义解答；（2）根据题意，画出图形，求得2AP+CQ−2PQ=0，即可得出2AP+CQ−2PQ 与1的大小关系．解：（1）∵CQ=2AQ，CP=2BP，∴CQ=23AC，CP=23BC，∵点C恰好在线段AB中点，∴AC=BC=12AB，∵AB=m(m为常数），∴PQ=CQ+CP=23AC+23BC=23×12AB+23×12AB=23AB=23m；（2）如图示：∵CQ=2AQ，∴2AP+CQ−2PQ=2AP+CQ−2(AP+AQ)=2AP+CQ−2AP−2AQ=CQ−2AQ=2AQ−2AQ=0，∴2AP+CQ−2PQ=0．小提示：本题主要考查两点间的距离，掌握线段的中点的性质、线段的和差运算是解题的关键．。

(每日一练)人教版七年级数学几何图形初步知识点题库单选题1、一个几何体由大小相同的小立方块搭成，从上面观察这个几何体，看到的形状如图所示，其中小正方形中的数字表示在该位置小立方块的个数，则从正面看该几何体的形状图为（）A．B．C．D．答案：A解析：由已知条件可知，从正面看有3列，每列小正方形数目分别为4，2，3，据此可得出图形．解：根据所给出的图形和数字可得：从正面看有3列，每列小正方形数目分别为4，3，2，则符合题意的是：故选：A．小提示：本题考查了从不同方向看几何体等知识，能正确辨认从正面、上面、左面（或右面）观察到的简单几何体的平面图形．2、如图是一个正方体的平面展开图，把展开图折叠成正方体后，“红”字的面的对面上的字是（）A．传B．国C．承D．基答案：D解析：正方体的平面展开图中，相对面的特点是必须相隔一个正方形，据此作答．解：正方体的表面展开图，相对的面之间一定相隔一个正方形，则：“传”与“因”是相对面，“承”与“色”是相对面，“红”与“基”是相对面．故选：D．小提示：本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．3、下列语句，正确的是（）A．两条直线，至少有一个交点B．线段AB的长度是点A与点B的距离C．过不在同一条直线上的三点中任意两点画直线，最多只能画两条直线D．过一点有且只有一条直线答案：B解析：根据线段的性质，两点间的距离的定义对各选项分析判断后利用排除法求解．解：A、两条直线相交只有一个交点，故该选项不正确；B、线段AB的长度是点A与点B的距离，故该选项正确；C、同一平面内不在同一直线上的3个点，可画三条直线，故该选项不正确；D、过一点可以画无数条直线，故该选项不正确；故选：B．小提示：本题考查了直线、射线、线段，以及线段的性质，是基础题，熟记概念与性质是解题的关键．填空题4、若一个角的余角为35°，则它的补角度数为 ______．答案：125°##125度解析：若两个角的和为90°,则这两个角互余，若两个角的和为180°,则这两个角互补，根据定义直接可得答案.解：∵一个角的余角为35°，∴这个角为：90°−35°=55°,则它的补角度数为：180°−55°=125°,所以答案是：125°小提示：本题考查的是余角与补角的计算，掌握“余角与补角的含义”是解本题的关键.5、如图，将甲、乙、丙、丁四个小正方形中的一个剪掉，使余下的部分不能围成一个正方体，则剪掉的这个小正方形是________答案：丁解析：能围成正方体的“一四一”，“二三一”，“三三”，“二二二”的基本形态要记牢．解题时，据此即可判断答案．解：将如图所示的图形剪去一个小正方形，使余下的部分不能围成一个正方体，编号为甲乙丙丁的小正方形中剪去的是丁，所以答案是：丁.小提示：本题考查了展开图折叠成正方体的知识，解题关键是根据正方体的特征，或者熟记正方体的11种展开图，只要有“田”，“凹”字格的展开图都不是正方体的表面展开图．解答题6、如图，平面内有A、B、C、D四点．按下列语句画图．（1）画直线AB，射线BD，线段BC；（2）连接AC，交射线BD于点E．答案：（1）见解析；（2）见解析解析：（1）根据直线、射线、线段定义画出即可；（2）根据要求画出线段标出交点即可.解：（1）如图所示，直线AB，射线BD，线段BC即为所求（2）连接AC，点E即为所求小提示：本题考查了对直线、射线、线段定义的应用，主要考查学生的理解能力和画图能力．。

初二几何辅助线专题练习每日一题——截长补短法（欢迎加入群963700627）1.如图，AD∥BC，点E在线段A B 上，∠ADE=∠CDE，∠DC E=∠ECB.求证：CD=AD+BC.2.已知：如图，在△ABC中，∠C＝2∠B，∠1＝∠2.求证：AB=AC+CD.3.如图所示，△ABC中，∠C=90°，∠B=45°，AD 平分∠BAC 交B C 于D.求证：AB=AC+CD.4. 已知∆ABC 中，∠A=60，BD 、 CE分别平分 ∠A BС和.∠AСB B D C E交于点O求证：BE + CD = BC ．5.如图，ΔABC 是正三角形，∠ADC=120°,求证：BD=AD+CD.6.如图，四边形 ABCD 中，AB=AD，∠B=∠D=90°，点 E，F 分别在边 AB，AD 上，连接 CE，CF，且∠BCD=2∠ECF。

（1）求证：BC=BD；（2）求证：EF=BE+DF7.五边形A BCDE中，AB=AE，BC+DE=CD，∠ABC+∠AED=180°，求证：AD平分∠CDE8.如图所示，在ΔABC 中，AD 平分∠BAC,AD=AB,CM⊥AD于M,求证：AB+AC=2AM.9.如图，已知△ABC 为等边三角形，D 为B C 延长线上一点，连接A D，E 为A D 上一点，且满足AB=AE，连接B E，交A C 于点F.求证：AD=AF+CD10.已知，如图，△ABC 和△ADE 均为等腰直角三角形，∠BAC=∠DAE=90°.其中B、E、D 共线且DE 交AC 于F. 在AB 上取一点G，使EG∥AD，连接EG.若E 为BF 的中点，求证：BG+AB=BC.11.在R t△ABC 中，∠ABC=90°，点D是C B 上延长线上一点，点E是线段A B 上一点，连接D E，BF 平分∠ABC 交A C 于点F. AC=DE，BC=BE，点G是线段F B 延长线上一点，连接D G，点H是线段D G 上一点，连接A H 交B D 于点K，连接K G，当K B 平分∠AKG 时，求证：AK=DG+KG.12. 在R t∆ABC 中，∠BCA = 90︒，G 为A B 的中点，过点G 作D G ⊥AB 交A C 于点D.过点D作D E ⊥B D ，连接A E ，以点E为直角顶点，A E 为直角边向外作等腰直角三角形A EF ，使得点F刚好落在B D的延长线上，求证：B C =DE +DF .13.如图,在等边三角形ABC 中, ∠ABC 和∠ACB 的角平分线相交于点O,点E、F 分别在线段AB、BC 上,连接E O、FO ,满足∠EOF = 60︒,连接E F .(1)①求证: OB =OC ；②求∠BOC 的度数；14.如图，在∆ABC 中，∠ABC = 90 , D为BC 上一点，在∆ADE 中，∠E =∠C ，∠1 = 90 （1）∠1 =∠2（2）E D =BC +BD15.如图，△ABC 中，∠ABC=45°，过点C作C D⊥AB 于点D，过点B作B M⊥AC 于点M，BM 交C D 于点E，且点E为C D 的中点，连接M D，过点D作N D⊥MD 于点D，DN 交B M 于点N．求证：NE－ME=CM16．在△ABC 中，∠ACB＝90°，AC＝BC，过C 作C D∥AB 交∠ABC 的平分线于点D，∠ACB的平分线交B D 于点E。

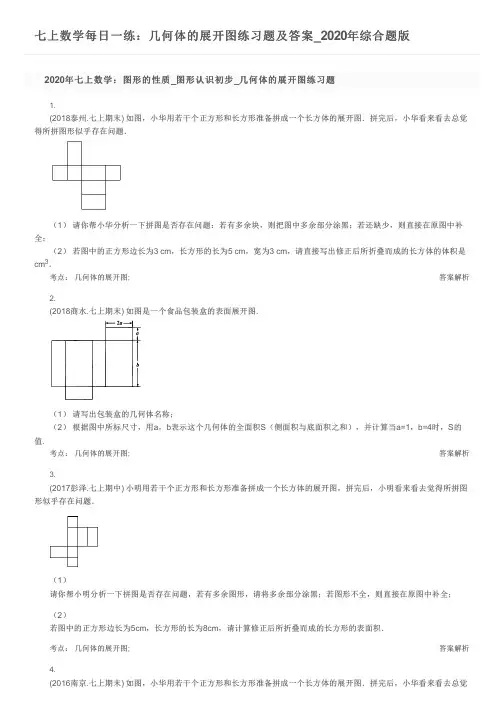
七上数学每日一练：几何体的展开图练习题及答案_2020年综合题版答案解析答案解析答案解析2020年七上数学：图形的性质_图形认识初步_几何体的展开图练习题1.(2018泰州.七上期末) 如图，小华用若干个正方形和长方形准备拼成一个长方体的展开图．拼完后，小华看来看去总觉得所拼图形似乎存在问题．（1） 请你帮小华分析一下拼图是否存在问题：若有多余块，则把图中多余部分涂黑；若还缺少，则直接在原图中补全；（2） 若图中的正方形边长为3 cm ，长方形的长为5 cm ，宽为3 cm ，请直接写出修正后所折叠而成的长方体的体积是cm ．考点： 几何体的展开图;2.(2018商水.七上期末) 如图是一个食品包装盒的表面展开图.（1） 请写出包装盒的几何体名称；（2） 根据图中所标尺寸，用a ，b 表示这个几何体的全面积S （侧面积与底面积之和），并计算当a=1，b=4时，S 的值.考点： 几何体的展开图;3.(2017彭泽.七上期中) 小明用若干个正方形和长方形准备拼成一个长方体的展开图，拼完后，小明看来看去觉得所拼图形似乎存在问题．（1）请你帮小明分析一下拼图是否存在问题，若有多余图形，请将多余部分涂黑；若图形不全，则直接在原图中补全；（2）若图中的正方形边长为5cm ，长方形的长为8cm ，请计算修正后所折叠而成的长方形的表面积．考点： 几何体的展开图;4.(2016南京.七上期末) 如图，小华用若干个正方形和长方形准备拼成一个长方体的展开图．拼完后，小华看来看去总觉3答案解析答案解析得所拼图形似乎存在问题．（1） 请你帮小华分析一下拼图是否存在问题：若有多余块，则把图中多余部分涂黑；若还缺少，则直接在原图中补全．（2） 若图中的正方形边长为2cm ，长方形的长为3cm ，宽为2cm ，请直接写出修正后所折叠而成的长方体的容积：c m ．考点： 几何体的展开图;5.(2016驻马店.七上期末) 如图是一个正方体盒子的表面展开图，该正方体六个面上分别标有不同的数字，且相对两个面上的数字互为相反数．（1） 把﹣16，9，16，﹣5，﹣9，5分别填入图中的六个小正方形中；（2） 若某相对两个面上的数字分别为 和 ﹣5，求x 的值．考点： 相反数及有理数的相反数;解一元一次方程;几何体的展开图;2020年七上数学：图形的性质_图形认识初步_几何体的展开图练习题答案1.答案：2.答案：3.答案：4.答案：35.答案：。

每日一题初中数学《每日一题初中数学，让我又爱又恨》嘿！同学们，你们知道吗？初中数学有个特别神奇的玩意儿，叫“每日一题”！这可真是让我又爱又恨呐！每天早上，数学老师就像个神奇的魔法师，准时在黑板的一角写下那道神秘的题目。

那题目就像是个小怪兽，张牙舞爪地等着我们去征服它。

“这题能难倒我？哼！”我心里暗暗想着，摩拳擦掌准备大干一场。

记得有一次，那道题是关于函数的。

函数啊，就像个调皮的小精灵，总是让人捉摸不透。

我盯着题目，眼睛都快瞪出来了，脑袋里像是有一团乱麻，怎么也理不清。

“哎呀，这可怎么办呀？”我急得直跺脚。

同桌小李凑过来，看了一眼题目，撇撇嘴说：“这有啥难的，你看啊……”听着他滔滔不绝地讲解，我却还是一脸懵，心里那个着急哟！“我怎么就不明白呢？”我不甘心就这样被打败，于是跑去请教班长。

班长可是我们班的数学大神，只见他拿着笔，在纸上轻轻一划，思路就像清澈的泉水一样涌了出来。

“原来是这样啊！”我恍然大悟，心里别提多高兴了。

还有一次，那道题是几何证明。

几何图形就像一个个神秘的城堡，每个边和角都藏着秘密。

我苦思冥想了好久，还是没有头绪。

这时候，后桌的小王拍了拍我的肩膀说：“嘿，咱们一起研究研究呗！”于是，我们俩你一言我一语地讨论起来，思维的火花不断碰撞。

“难道这样不行吗？”“哎呀，换个角度试试！”经过一番努力，终于把这道题给攻克了。

那种成就感，简直无法用言语来形容！每日一题，有时候就像一座高山，让我觉得怎么爬也爬不上去；有时候又像一条清澈的小溪，只要我用心，就能轻松地趟过去。

它就像个严厉的老师，不断鞭策着我前进；又像个贴心的朋友，陪伴着我成长。

你说，这每日一题是不是很有趣？虽然它常常让我头疼，但也让我学到了好多知识，让我的思维变得更加敏捷。

它让我明白，遇到困难不能退缩，只要坚持下去，就一定能找到解决的办法。

所以啊，我觉得这每日一题，真是初中数学学习中不可或缺的一部分！它虽然有时让我烦恼，但更多的是带给我挑战和成长的快乐！。

初二下册数学每日一练习题一、解方程1. 解方程：$2(x-3)+3(2x-5)=4(3x+1)-2(x+3)$。

解：展开并整理等式两边的式子，得到：$2x-6+6x-15=12x+4-2x-6$。

合并同类项，得到：$8x-21=10x-2$。

移项，得到：$8x-10x=21-2$。

得到：$-2x=19$。

两边同时除以-2，得到：$x=-\frac{19}{2}$。

所以，方程的解为$x=-\frac{19}{2}$。

2. 解方程：$4(2x+3)-2(4-x)=20$。

解：展开并整理等式两边的式子，得到：$8x+12-8+2x=20$。

合并同类项，得到：$10x+4=20$。

移项，得到：$10x=20-4$。

得到：$10x=16$。

两边同时除以10，得到：$x=\frac{16}{10}$。

所以，方程的解为$x=\frac{8}{5}$。

二、几何图形计算1. 计算正方形的面积和周长。

已知正方形的边长为8cm，根据正方形的性质，其面积等于边长的平方，周长等于边长的四倍。

所以，正方形的面积为$8^2=64$平方厘米，周长为$4 \times 8=32$厘米。

2. 计算圆的周长和面积。

已知圆的半径为5cm，根据圆的性质，其周长等于$2 \times \pi\times$ 半径，面积等于$\pi \times$ 半径的平方。

所以，圆的周长为$2 \times 3.14 \times 5=31.4$厘米，面积为$3.14 \times 5^2=78.5$平方厘米。

三、比例与百分数1. 一个成绩为63分的学生，如果总分为80分，请计算这个学生的百分比成绩。

已知百分比成绩可以通过成绩除以总分再乘以100来计算。

所以，这个学生的百分比成绩为$\frac{63}{80} \times 100=78.75$。

2. 某商店举行打折促销活动，所有商品都打8折，现在一件衣服的原价是120元，请问现在的促销价是多少？已知打8折可以通过原价乘以0.8来计算促销价。

148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
谢谢大家！
37
38
39
40
初中数学每日一题〔10〕
方法迁移——解决实验探究型问题 初中数学试卷的最后压轴题，总是实 验探究型问题：先在一种简单的背景 下证明某个结论，然后在条件变化后， 探究结论是否成立。解决问题的方法 就是：将第(1)问中的方法迁移到后面 (2)和(3)的问题中。
41
42
43
44
联想与“最短〞有关的知识点：两点之间线段最 短，垂线段最短，三角形两边之和大于第三边等。 将相关问题转化成这样的根本数学模型即可解决问 题。
20
21
22
23
24
25
26
初中数学每日一题〔6〕
分类讨论思想—探究图形个数
在几何问题中，经常会见到问:适合题 意的图形有几个，对于这种探究图形 个数问题，是典型的考查分类讨论思 想的问题，但是能否考虑全面，关键 却在于数学知识的掌握程度和运用的 灵活程度。
初中数学每日一题〔7〕 分类讨论思想—解决字母取值不确定性问题
每个数学结论都有其成立的条件，每一种数学方 法的使用也往往有其适用范围，在我们所遇到的 数学问题中，有些问题的结论不是唯一确定的， 有些问题的结论在解题中不能以统一的形式进行 研究，还有些问题的量是用字母表示数的形式给 出的，这样字母的取值不同也会影响问题的解决。 根据题目的特点和要求，分成假设干类，转化成假 设干个小问题来解决，这种按不同情况分类，然后 再逐一研究解决的数学思想，称之为分类讨论思想。

几何变换的类型每日一练1．如图，△PQR是三角形ABC经过某种变换后得到的图形．（1）分别写出点A与P，点B与Q，点C与R的坐标；（2）认真观察上述坐标，你发现了它们之间有怎样的关系？（3）△ABC内有一点M（a，b），点M经过这种变换后得到点N，请你写出点N的坐标；（4）如果网络图中每个小正方形的边长均为1，试求三角形ABC的面积．2．如图，如果将其中的甲图变成乙图，那么经过的变换正确的是（）A．旋转、平移B．对称、平移C．旋转、对称D．旋转、旋转3．一个图形无论经过平移还是旋转，有以下说法：（1）对应线段平行；（2）对应线段相等；（3）对应角相等；（4）不改变图形的形状和大小，其中正确的有（）A．（1）（2）（3）B．（1）（2）（4）C．（1）（3）（4）D．（2）（3）（4）4．如图，乙图案变为甲图案，需要用到（）A．旋转、对称B．平移、对称C．旋转、平移D．旋转、旋转5．请仔细观察下图，从图形（1）（2）（3）的变化规律，确定图形（4）为（）A．B．C．D．6．如图，四边形ABCD是正方形，点F，G在正方形的边上，点E在CB的延长线上，BE＝BF＝DC．下列说法正确的是（）A．将△ADG绕点A按顺时针方向旋转得到△ABFB．将△ADG绕点A按顺时针方向旋转得到△ABEC．将△ABE平移得到△ABFD．将△ADG平移得到△ABF7．如图，△ABC和△BDE是等边三角形，点A、B、D在一条直线上，并且AB＝BD．由一个三角形变换到另一个三角形（）A．仅能由平移得到B．仅能由旋转得到C．既能由平移得到，也能由旋转得到D．既不能由平移得到，也不能由旋转得到8．以下三组两个图形之间的变换分别属于（）A．平移、旋转、旋转B．平移、轴对称、轴对称C．平移、轴对称、旋转D．平移、旋转、轴对称9．从甲到乙的图形变换，判断全正确的是（）A．（1）翻折，（2）旋转，（3）平移B．（1）翻折，（2）平移，（3）旋转C．（1）平移，（2）翻折，（3）旋转D．（1）平移，（2）旋转，（3）翻折几何变换的类型每日一练1．如图，△PQR是三角形ABC经过某种变换后得到的图形．（1）分别写出点A与P，点B与Q，点C与R的坐标；（2）认真观察上述坐标，你发现了它们之间有怎样的关系？（3）△ABC内有一点M（a，b），点M经过这种变换后得到点N，请你写出点N的坐标；（4）如果网络图中每个小正方形的边长均为1，试求三角形ABC的面积．【分析】（1）利用坐标系直接得出各点坐标即可；（2）利用（1）中所求得出对应点之间的关系即可；（3）利用（2）中规律得出N点坐标即可；（4）利用△ABC所在矩形的面积进而减去周围三角形面积进而求出即可．【解答】解：（1）如图所示：点A与P的坐标分别为：（4，3），（﹣4，﹣3）；点B与Q的坐标分别为：（3，1），（﹣3，﹣1）；点C与R的坐标分别为：（1，2），（﹣1，﹣2）；（2）由（1）得：对应点坐标关于原点对称；（3）由（2）得：△ABC内有一点M（a，b），点M经过这种变换后得到点N，则点N的坐标为：（﹣a，﹣b）；（4）三角形ABC的面积为：2×3﹣×1×3﹣×1×2﹣×1×2＝2.5．【点评】此题主要考查了几何变换以及关于原点对称点的性质和三角形面积求法等知识，正确得出对应点坐标之间规律是解题关键．2．如图，如果将其中的甲图变成乙图，那么经过的变换正确的是（）A．旋转、平移B．对称、平移C．旋转、对称D．旋转、旋转【分析】观察本题中图案的特点，根据对称、旋转的性质即可得出答案．【解答】解：观察图形可得：将甲图先轴对称变化，再逆时针旋转即可变成乙图；故选：C．【点评】本题考查了几何变换的类型，用到的知识点是轴对称、旋转变化的性质：如果一个图形沿着一条直线对折，两侧的图形能完全重合，这个图形就是轴对称图形．折痕所在的这条直线叫做对称轴．旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变，两组对应点连线的交点是旋转中心．3．一个图形无论经过平移还是旋转，有以下说法：（1）对应线段平行；（2）对应线段相等；（3）对应角相等；（4）不改变图形的形状和大小，其中正确的有（）A．（1）（2）（3）B．（1）（2）（4）C．（1）（3）（4）D．（2）（3）（4）【分析】利用图形平移与旋转的定义判定即可．【解答】解：一个图形无论经过平移还是旋转，对应线段和角相等，不改变图形的形状和大小，旋转后对应的线段可能不平行．故选：D．【点评】本题主要考查了几何变换的类型，解题的关键是熟记图形平移与旋转的定义．4．如图，乙图案变为甲图案，需要用到（）A．旋转、对称B．平移、对称C．旋转、平移D．旋转、旋转【分析】根据旋转、平移的性质结合图形解答即可．【解答】解：由图可知，乙图案旋转、平移后可以变为甲图案．故选：C．【点评】本题考查了几何变换的类型，熟记各种变换的概念并准确识图是解题的关键．5．请仔细观察下图，从图形（1）（2）（3）的变化规律，确定图形（4）为（）A．B．C．D．【分析】根据已知的三个图形可以每次逆时针旋转90度，据此即可确定．【解答】解：根据已知的三个图形可以每次逆时针旋转90度，由（3）逆时针旋转90度得到B．故选：B．【点评】本题考查了图形的旋转，根据已知图形得到旋转的方法是关键．6．如图，四边形ABCD是正方形，点F，G在正方形的边上，点E在CB的延长线上，BE＝BF＝DC．下列说法正确的是（）A．将△ADG绕点A按顺时针方向旋转得到△ABFB．将△ADG绕点A按顺时针方向旋转得到△ABEC．将△ABE平移得到△ABFD．将△ADG平移得到△ABF【分析】结合图形，根据旋转变换与平移变换的定义进行解答．【解答】解：观察图形可得：将△ADG绕点A按顺时针方向旋转得到△ABE，△ABE与△ABF不能通过平移得到，△ADG平移也不能得到△ABF．故选：B．【点评】本题考查了几何变换的旋转变换与平移变换，准确识图是关键．7．如图，△ABC和△BDE是等边三角形，点A、B、D在一条直线上，并且AB＝BD．由一个三角形变换到另一个三角形（）A．仅能由平移得到B．仅能由旋转得到C．既能由平移得到，也能由旋转得到D．既不能由平移得到，也不能由旋转得到【分析】是轴对称图形，这三对全等三角形中的一个都是以其中另一个三角形绕点B旋转90°后得到或对折得到的．【解答】解：∵△ABC和△BDE是等边三角形，点A、B、D在一条直线上，并且AB＝BD．∴这三对全等三角形中的一个都是以其中另一个三角形绕点B旋转90°后得到或对折得到的．故选：C．【点评】本题考查了几何变换的类型，解题的关键是看清由两个三角形组成的图象是轴对称图形还是中心对称图形．8．以下三组两个图形之间的变换分别属于（）A．平移、旋转、旋转B．平移、轴对称、轴对称C．平移、轴对称、旋转D．平移、旋转、轴对称【分析】根据平移、旋转、轴对称的特点可知．【解答】解：第一个可沿水平线向右平移得到；第二个可绕对应点的中点旋转得到；第三个可沿对应点连线所在的垂直平分线翻折得到，即为轴对称．故选D．【点评】平移是沿直线移动一定距离得到新图形，旋转是绕某个点旋转一定角度得到新图形，轴对称是沿某条直线翻折得到新图形．观察时要紧扣图形变换特点，认真判断．9．从甲到乙的图形变换，判断全正确的是（）A．（1）翻折，（2）旋转，（3）平移B．（1）翻折，（2）平移，（3）旋转C．（1）平移，（2）翻折，（3）旋转D．（1）平移，（2）旋转，（3）翻折【分析】根据常见的几何变换类型，写出各小题的变化过程即可得解．【解答】解：由图可知，（1）把甲翻折即可得到乙；（2）绕甲的直角顶点顺时针旋转90°即可得到乙；（3）把甲先向右平移，再向上平移即可得到乙，所以，（1）翻折，（2）旋转，（3）平移．故选：A．【点评】本题考查了常见的几何变换类型，准确识图，判断出从甲到乙的变换过程是解题的关键．。

(每日一练)初中数学图形的性质几何图形初步基础知识点归纳总结单选题1、如图，△ABC内接于⊙O，∠A＝50°．E是边BC的中点，连接OE并延长，交⊙O于点D，连接BD，则∠D的大小为（）A．55°B．65°C．60°D．75°答案：B解析：连接CD，根据圆内接四边形的性质得到∠CDB＝180°﹣∠A＝130°，根据垂径定理得到OD⊥BC，求得BD＝CD，根据等腰三角形的性质即可得到结论．解：连接CD，∵∠A＝50°，∴∠CDB＝180°﹣∠A＝130°，∵E是边BC的中点，∴OD⊥BC，∴BD＝CD，∴∠ODB＝∠ODC＝1∠BDC＝65°，2故选：B．小提示：本题考查了圆内接四边形的性质，垂径定理，等腰三角形的性质等知识．正确理解题意是解题的关键．2、如图，已知⊙O的半径为4，M是⊙O内一点，且OM＝2，则过点M的所有弦中，弦长是整数的共有（）A．1条B．2条C．3条D．4条答案：C解析：过点M作AB⊥OM交⊙O于点A、B，根据勾股定理求出AM，根据垂径定理求出AB，进而得到答案．解：过点M作AB⊥OM交⊙O于点A、B，连接OA，AB，则AM＝BM＝12在Rt△AOM中，AM＝√OA2−OM2＝√42−22＝2√3，∴AB＝2AM＝4√3，则4√3≤过点M的所有弦≤8，则弦长是整数的共有长度为7的两条，长度为8的一条，共三条，故选：C．小提示：本题考查了垂径定理，勾股定理，掌握垂直于选的直径平分这条弦，并平分弦所对的两条弧是解题关键．3、如图所示，矩形纸片ABCD中，AD=6cm，把它分割成正方形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则AB的长为（）A．3.5cm B．4cm C．4.5cm D．5cm答案：B解析：设AB=xcm，则DE=（6-x）cm，根据扇形的弧长等于圆锥底面圆的周长列出方程，求解即可．设AB=x，则DE=（6-x）cm，=(6−x)π，由题意，得90π⋅x180解得x=4.故选B．小提示：本题考查了圆锥的计算，矩形的性质，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．4、已知：如图，PA，PB分别与⊙O相切于A，B点，C为⊙O上一点，∠ACB＝65°，则∠APB等于（）A．65°B．50°C．45°D．40°答案：B解析：连接OA，OB．根据圆周角定理和四边形内角和定理求解即可．连接OA，OB，∵PA、PB切⊙O于点A、B，∴∠PAO＝∠PBO＝90°，由圆周角定理知，∠AOB＝2∠ACB＝130°，∴∠APB＝360°﹣∠PAO﹣∠PBO﹣∠AOB＝360°﹣90°﹣90°﹣130°＝50°．故选：B．小提示：本题考查了切线的性质、圆周角定理、以及四边形的内角和为360度．5、如图，AB是⊙O的直径，点B是弧CD的中点，AB交弦CD于E，且CD=2√3，BD=2，则AB=（）A．2B．3C．4D．5答案：C解析：AB是⊙O的直径，点B是弧CD的中点，从而可知AB⊥CD，然后利用勾股定理即可求出AB的长度．解：设半径为r，连接OD，∵AB是⊙O的直径，点B是弧CD的中点，∴由垂径定理可知：AB⊥CD，且点H是CD的中点，CD=√3，∴HD=12∵BD=2，∴由勾股定理可知：HB=1，∴OH=r−1∴由勾股定理可知：r2=(r−1)2+(√3)2，解得：r=2∴AB=2r=4，故选：C．小提示：本题考查垂径定理，解题的关键是正确理解垂径定理以及勾股定理，本题属于中等题型。

(每日一练)通用版初中数学图形的性质几何图形初步真题单选题1、在正方形ABCD中，分别以B、D为圆心，以正方形的边长2为半径画弧，则图中阴影部分的面积为（）A．2π−4B．4−2πC．2D．π答案：A解析：由图可知，阴影部分的面积是两个圆心角为90°，且半径为2的扇形的面积与正方形的面积的差，可据此求出阴影部分的面积.S阴影=2S扇形-S正方形=2×90π×22-22=2π-4360故选：A小提示：本题利用了扇形的面积公式，正方形的面积公式求解，得出S阴影=2S扇形-S正方形是解题关键.2、已知⊙O的半径等于3，圆心O到点P的距离为5，那么点P与⊙O的位置关系是（）A．点P在⊙O内B．点P在⊙O外C．点P在⊙O上D．无法确定答案：B根据d，r法则逐一判断即可．解：∵r=3，d=5，∴d＞r，∴点P在⊙O外．故选：B．小提示：本题考查了点与圆的位置关系，熟练掌握ｄ，ｒ法则是解题的关键．3、如图，AB为⊙O的直径，C，D为⊙O上的两点，若∠ABD＝54°，则∠C的度数为（）A．34°B．36°C．46°D．54°答案：B解析：连接AD，如图，根据圆周角定理得到∠ADB=90°，∠C=∠A，然后利用互余计算出∠A，从而得到∠C的度数．解：连接AD，如图，∵AB为⊙O的直径，∴∠ADB=90°，∴∠A=90°−∠ABD=90°−54°=36°，∴∠C=∠A=36°．小提示：本题主要考查了同弦所对的圆周角相等，直径所对的圆周角是直角，解题的关键在于能够熟练掌握相关知识进行求解.解答题4、定义：对角线互相垂直且相等的四边形叫做垂等四边形．（1）下面四边形是垂等四边形的是；（填序号）①平行四边形；②矩形；③菱形；④正方形（2）图形判定：如图1，在四边形ABCD中，AD//BC，AC⊥BD，过点D作BD垂线交BC的延长线于点E，且∠DBC=45°，证明：四边形ABCD是垂等四边形．（3）由菱形面积公式易知性质：垂等四边形的面积等于两条对角线乘积的一半．应用：在图2中，面积为6的垂等四边形ABCD内接于⊙O中，∠BCD=60°．求⊙O的半径．答案：（1）④；（2）见解析；（3）r=2解析：（1）根据垂等四边形的性质对每个图形判断即可；（2）根据已知条件可证明四边形ACED是平行四边形，即可得到AC=DE，再根据等腰直角三角形的性质即可得到结果；（3）过点O作OE⊥BD，根据面积公式可求得BD的长，根据垂径定理和锐角三角函数即可得到⊙O的半径．解：（1）①平行四边形的对角线互相平分但不垂直和相等，故不是垂等四边形；②矩形对角线相等但不一定垂直，故不是垂等四边形；③菱形的对角线互相垂直但不一定相等，故不是垂等四边形；④正方形的对角线互相垂直且相等，故正方形是垂等四边形；故选：④；（2）∵AC⊥BD，ED⊥BD，∴AC∥DE，又∵AD∥BC，∴四边形ADEC是平行四边形，∴AC=DE，又∵∠DBC=45°，∴△BDE是等腰直角三角形，∴BD=DE，∴BD=AC，又∵BD⊥AC，∴四边形ABCD是垂等四边形；（3）如图，过点O作OE⊥BD，连接OD，∵四边形ABCD是垂等四边形，∴AC=BD，又∵垂等四边形的面积是24，∴12AC•BD=6，解得，AC=BD=2√3，又∵∠BCD=60°，∴∠DOE=60°，设半径为r，根据垂径定理可得：在△ODE中，OD=r，DE=√3，∴r=DEsin60°=√3√32=2，∴⊙O的半径为2．小提示：本题是一道圆的综合题，主要考查了平行四边形的性质、菱形的性质、矩形的性质、正方形的性质、新定义、圆周角定理、垂径定理，解答本题的关键是明确题意，找出所求问题需要的条件，利用新定义解答问题．5、如图，在⊙O中，AB是⊙O的弦，CD是⊙O的直径，且AB⊥CD，垂足为G，点E在劣弧AB⃗⃗⃗⃗⃗ 上，连接CE．（1）求证：CE 平分∠AEB ；（2）连接BC ，若BC //AE ，求证：BC =BE ．答案：（1）见解析；（2）见解析解析：（1）根据垂径定理，可得AC⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ ，从而得到 ∠AEC =∠BEC ，即可求证； （2）根据BC ∥AE ，可得到∠AEC =∠BCE ，再由∠AEC =∠BEC ，即可求证．（1）证明：∵CD ⊥AB ，CD 是直径，∴AC⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ ． ∴∠AEC =∠BEC ，∴CE 平分∠AEB ；（2）解：如图，∵BC ∥AE ，∴∠AEC =∠BCE ．又∵∠AEC =∠BEC ，∴∠BCE =∠BEC∴BE=BC．小提示：本题主要考查了垂径定理，平行线的性质，等腰三角形的性质，熟练掌握相关知识点是解题的关键．。

(每日一练)人教版七年级数学几何图形初步知识汇总大全单选题1、下列平面图形能围成圆锥体的是（）A．B．C．D．答案：A解析：根据几何体的展开图的特征即可求解．A、是圆锥的展开图，故选项正确；B、不是圆锥的展开图，故选项错误；C、是长方体的展开图，故选项错误；D、不是圆锥的展开图，故选项错误．故选：A．小提示：此题考查了展开图折叠成几何体，通过结合立体图形与平面图形的相互转化，去理解和掌握几何体的展开图，要注意多从实物出发，然后再从给定的图形中辨认它们能否折叠成给定的立体图形．2、下列几何体中，圆柱体是（）A．B．C．D．答案：C解析：根据圆柱体的定义，逐一判断选项，即可．解：A. 是圆锥，不符合题意；B. 是圆台，不符合题意；C. 是圆柱，符合题意；D. 是棱台，不符合题意，故选C．小提示：本题主要考查几何体的认识，掌握圆锥、圆柱、圆台、棱台的定义，是解题的关键．3、A，B，C，D四个村庄之间的道路如图，从A去D有以下四条路线可走，其中路程最短的是（）A．A→C→B→D B．A→C→D C．A→E→D D．A→B→D答案：C解析：利用两点之间线段最短可直接得出结论．利用两点之间线段最短的性质得出，路程最短的是：A→E→D，故选：C．小提示：本题考查了两点之间的距离，熟知两点之间线段最短是解题的关键．填空题4、如图，∠AOC=∠BOD=90°，∠AOB=70°，在∠AOB内画一条射线OP得到的图中有m对互余的角，其中∠AOP=x°，且满足0<x<50，则m=_______．答案：3或4或6解析：分三种情况下：①∠AOP＝35°，②∠AOP＝20°，③0＜x＜50中的其余角，根据互余的定义找出图中互余的角即可求解．∠AOB =35°时，∠BOP=35°①∠AOP＝12∴互余的角有∠AOP与∠COP，∠BOP与∠COP，∠AOB与∠COB，∠COD与∠COB，一共4对；②∠AOP＝90°-∠AOB =20°时，∴互余的角有∠AOP与∠COP，∠AOP与∠AOB，∠AOP与∠COD，∠COD与∠COB，∠AOB与∠COB，∠COP与∠COB，一共6对；③0＜x＜50中35°与20°的其余角，互余的角有∠AOP与∠COP，∠AOB与∠COB，∠COD与∠COB，一共3对．则m＝3或4或6．所以答案是：3或4或6．小提示：本题考查了余角和补角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．5、如图，∠AOC=∠BOD=90°，∠AOB=70°，在∠AOB内画一条射线OP得到的图中有m对互余的角，其中∠AOP=x°，且满足0<x<50，则m=_______．答案：3或4或6解析：分三种情况下：①∠AOP＝35°，②∠AOP＝20°，③0＜x＜50中的其余角，根据互余的定义找出图中互余的角即可求解．∠AOB =35°时，∠BOP=35°①∠AOP＝12∴互余的角有∠AOP与∠COP，∠BOP与∠COP，∠AOB与∠COB，∠COD与∠COB，一共4对；②∠AOP＝90°-∠AOB =20°时，∴互余的角有∠AOP与∠COP，∠AOP与∠AOB，∠AOP与∠COD，∠COD与∠COB，∠AOB与∠COB，∠COP与∠COB，一共6对；③0＜x＜50中35°与20°的其余角，互余的角有∠AOP与∠COP，∠AOB与∠COB，∠COD与∠COB，一共3对．则m＝3或4或6．所以答案是：3或4或6．小提示：本题考查了余角和补角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．解答题6、如图，线段AB=8cm,C是线段AB上一点，M是AB的中点，N是AC的中点．（1）AC=3cm，求线段CM、NM的长；（2）若线段AC=m，线段BC=n，求MN的长度（m<n用含m,n的代数式表示）．答案：（1）CM=1cm，NM=2.5cm；（2）1n2解析：（1）求出AM长，代入CM=AM-AC求出即可；分别求出AN、AM长，代入MN=AM-AN求出即可；（2）分别求出AM和AN，利用AM-AN可得MN．解：（1）∵AB=8cm，M是AB的中点，∴AM=1AB=4cm，2∵AC=3cm，∴CM=AM−AC=4−3=1cm；∵AB=8cm，AC=3cm，M是AB的中点，N是AC的中点，∴AM=12AB=4cm，AN=12AC=1.5cm，∴MN=AM−AN=4−1.5=2.5cm；（2）∵AC=m，BC=n，∴AB=AC+BC=m+n，∵M是AB的中点，N是AC的中点，∴AM=12AB=12(m+n)，AN=12AC=12m，∴MN=AM−AN=12(m+n)−12m=12n．小提示：本题考查了两点之间的距离，线段中点的定义的应用，解此题的关键是求出AM、AN的长．。

(每日一练)人教版初中数学图形的性质几何图形初步知识汇总笔记单选题1、已知⊙O的半径是4，圆心O到直线l的距离d＝6．则直线l与⊙O的位置关系是（）A．相离B．相切C．相交D．无法判断答案：A解析：根据直线和圆的位置关系的判定方法，即圆心到直线的距离大于半径，则直线与圆相离进行判断.解：∵圆心O到直线l的距离d=6，⊙O的半径R=4，∴d>R，∴直线和圆相离．故选：A．小提示：本题考查直线与圆位置关系的判定．掌握半径和圆心到直线的距离之间的数量关系是解答此题的关键.．2、计算弧长需要知道（）A．直径B．半径C．圆心角D．半径和圆心角答案：D解析：根据弧长公式确定即可．l=nC360=n2πr360=nπr180，所以计算弧长需要知道半径和圆心角．所以答案是：D．小提示：本题主要考查了弧长公式，熟练掌握公式是解题的关键．3、已知△ABC中，∠C=Rt∠，AC=3，BC=4，点P为边AB的中点，以点C为圆心，长度r为半径画圆，使得点A，P在⊙C内，点B在⊙C外，则半径r的取值范围是（）A．52<r<4B．52<r<3C．r>3D．3<r<4答案：D解析：根据勾股定理，得AB=5，由P为AB的中点，得CP=52，要使点A，P在⊙C内，r＞3，r＜4，从而确定r的取值范围.∵点A在⊙C内，∴r＞3，∵点B在⊙C外，∴r＜4，∴3<r<4，故选：D.小提示：本题考查了点和圆的位置关系，利用数形结合思想是解题的关键.填空题4、如图，把一个圆锥沿母线OA剪开，展开后得到扇形AOC，已知圆锥的高h为12cm，OA=13cm，则扇形⃗⃗⃗⃗⃗ 的长是_____cm（计算结果保留π）．AOC中AC答案：10π解析：⃗⃗⃗⃗⃗ 的长就是圆锥的底面周长即可求解．根据AC解：∵圆锥的高h为12cm，OA=13cm，∴圆锥的底面半径为√132−122=5cm，∴圆锥的底面周长为10πcm，∴扇形AOC中AC⃗⃗⃗⃗⃗ 的长是10πcm，故答案为10π．小提示：本题考查了圆锥的计算，解题的关键是了解圆锥的底面周长等于展开扇形的弧长．5、如图，从一块半径为1m的圆形铁皮上剪出一个圆周角为120°的扇形ABC，如果将剪下来的扇形围成一个圆锥，则该圆锥的底面圆的半径为_________m．答案：13解析：连接OA ，OB ，证明△AOB 是等边三角形，继而求得AB 的长，然后利用弧长公式可以计算出BOC⃗⃗⃗⃗⃗⃗⃗⃗ 的长度，再根据扇形围成圆锥底面圆的周长等于扇形的弧长即可作答．连接OA ，OB ，则∠BAO=12∠BAC=12×120°=60°，又∵OA=OB ，∴△AOB 是等边三角形，∴AB=OA=1，∵∠BAC=120°，∴B O C ⃗⃗⃗⃗⃗⃗⃗⃗ 的长为：120·π·AB 180=2π3， 设圆锥底面圆的半径为r2πr =2π3 r =13故答案为13．小提示：本题主要考查了弧长公式以及扇形弧长与底面圆周长相等的知识点，借助等量关系即可算出底面圆的半径．。